

东北大学 理学院,辽宁 沈阳 110819
收稿日期:2021-12-13
基金项目:国家自然科学基金资助项目(61673100)。
作者简介:杨冬梅(1966-),女,辽宁沈阳人,东北大学教授。
摘要:研究了阶次在0到1上的不确定奇异分数阶互联系统的非脆弱分散H∞控制问题.对现有的奇异分数阶线性系统容许且满足H∞性能的判定条件进行推广,以严格线性矩阵不等式的形式给出新的判定准则;通过对互联系统特殊结构的分析,利用线性矩阵不等式方法和矩阵分解技术,分别在加法和乘法控制器增益扰动下,给出非脆弱分散H∞控制器存在的充分条件和设计方法.在控制器的设计过程中,对互联矩阵没有加以限定,得到严格的线性矩阵不等式判据,在一定程度上降低了系统的保守性.利用LMI工具箱及Simulink数值仿真验证了结论的有效性.
关键词:分数阶奇异互联系统容许性H∞性能非脆弱控制
Non-fragile Decentralized H∞Control for Uncertain Singular Fractional-Order Interconnected Systems
YANG Dong-mei, SUN Yi-bing


School of Sciences, Northeastern University, Shenyang 110819, China
Corresponding author: SUN Yi-bing, E-mail: 2909529982@qq.com.
Abstract: The non-fragile decentralized H∞ control problems for uncertain singular fractional-order interconnected systems with commensurate order 0<α < 1 are studied. The existing criteria for admissibility and H∞ performance of singular fractional-order linear systems are extended. And the new criteria are given in the form of strict linear matrix inequality. Based on those conclusions, through analysis of the special structure of interconnected systems, under additive and multiplicative disturbances of controller gains, sufficient conditions for the existence of non-fragile decentralized H∞ controllers and their design methods are given by using linear matrix inequalities and matrix decomposition technology. In the design process of controllers, the interconnected matrices are not limited and strict linear matrix inequality criteria are obtained, which reduce conservatism of the systems to a certain extent. The effectiveness of the proposed methods is verified by LMI toolbox and Simulink numerical simulation.
Key words: fractional-ordersingular interconnected systemsadmissibilityH∞ performancenon-fragile control
近年来,奇异分数阶控制系统在应用领域引起人们的广泛关注[1].它既包含微分方程又包含代数方程,与正常整数阶控制系统相比更具一般性[2].对于阶次在0到1上的奇异分数阶系统,文献[3]给出了其容许的充要条件.文献[4-5]基于正常分数阶系统的稳定性判据,以严格线性矩阵不等式的形式给出了奇异分数阶线性系统容许的充要条件,有效降低了计算复杂度,得到保守性较低的控制器设计方法.目前,对奇异分数阶系统稳定化控制器设计的研究也越来越多,如状态反馈控制器、输出反馈控制器和滑模控制器等[6-7].
在工程应用中,被控对象很难用系统模型准确刻画,因此不确定系统更能反映其真实情况.与此同时,系统鲁棒稳定性的研究变得更加复杂,使控制器设计的难度增加,H∞控制理论可以较好地解决系统的鲁棒性问题[8].文献[9]给出了正常分数阶控制系统稳定且满足H∞性能的判定条件.对于奇异分数阶系统的H∞控制,文献[10]给出了容许且满足H∞性能的充分条件,将正常分数阶系统的有界实引理推广到奇异分数阶系统,由于其结论含有等式约束,求解比较复杂,这促使****进一步研究更简单的有界实引理,以便于设计容易求解且保守性较低的H∞控制器.
奇异分数阶互联系统可以更好地描述大型电力系统[11].在采用传统方法设计控制器时,只需找到控制器的增益,即可使闭环系统保持稳定.控制器对自身的微小变化非常敏感,非脆弱控制的思想就是设计对控制器增益的扰动不敏感的反馈控制,从而使系统拥有良好的性能[12].在非脆弱分散H∞控制方面,文献[13-14]分别研究了奇异整数阶互联系统和正常分数阶互联系统的非脆弱分散H∞控制器设计问题.然而,目前没有文献为奇异分数阶互联系统非脆弱分散H∞控制器的设计提供方法,因此本文所做如下:
对于奇异分数阶系统,提出了一种新的判定其容许且满足H∞性能的准则,结论不包含等式约束,与文献[10]相比更容易设计和求解控制器.
对于不确定奇异分数阶互联系统,利用以上结论,分别在控制器增益加法和乘法摄动下,设计非脆弱分散H∞控制器,使得闭环系统容许且满足H∞性能.
在控制器设计过程中,对互联矩阵没有限制,而文献[15]所得结论仅适用于互联矩阵为方阵的情形,相比之下,本文所提供的方法扩大了适用范围.
记号:M*表示矩阵M的共轭转置;z表示复数z的共轭;j是虚数单位,r=ejθ, θ=(1-α)·π/2;Re(·),Im(·)分别表示矩阵的实部和虚部;I是具有适当维数的单位矩阵,Hn表示n阶厄尔米特矩阵;sym{M }表示M+M*;(M)ij是分块矩阵,第i行第j列上的块为M,其余各块均为零矩阵.
一个复厄尔米特矩阵H满足H < 0当且仅当
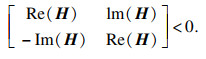 |
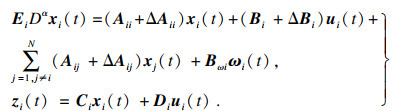 | (1) |
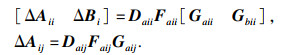 |
Dα表示如下的Caputo微分[16]:
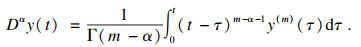 |
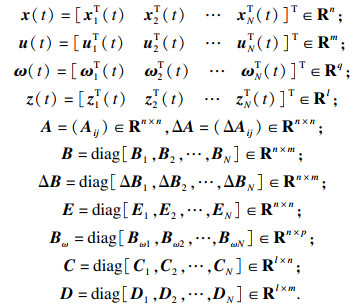 |
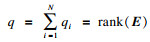
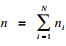
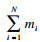
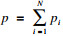
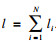
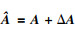
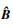
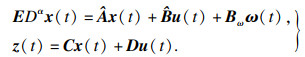 | (2) |
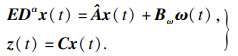 | (3) |
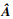
定义1[4-5] ??对于系统(3),若存在s∈C使得det(
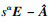
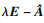

定义2[10] ??传递函数G(s)的H∞范数定义为
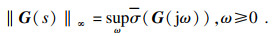 |
引理1 ??γ是给定正实数,若以下任意一种情况成立,则系统(3)容许且‖G(s)‖∞ < γ:
1) 存在矩阵Q∈Cn×n满足
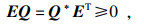 | (4a) |
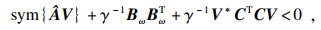 | (4b) |
2) 存在矩阵U∈Cn×n满足
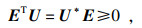 | (5a) |
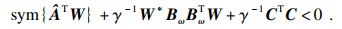 | (5b) |
引理2[17] ??对任意正数β,以及适当维数的矩阵X和Y,不等式成立:
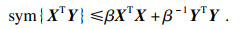 |
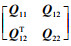
1) Q < 0;
2) Q11 < 0,Q22-Q12TQ11-1Q12 < 0;
3) Q22 < 0,Q11-Q12Q22-1Q12T < 0.
2 奇异分数阶系统的有界实引理定理1 ??γ是给定的正实数,若存在矩阵X>0,X=X*∈Cn×n,S∈R(n-q)×n,满足
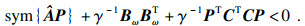 | (6) |

证明??只需证明定理1的条件与1)等价.
若存在矩阵Q满足式(4),则系统(3)容许,从而存在非奇异矩阵M,N∈Rn×n,使得
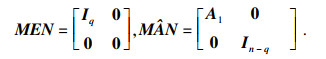 |
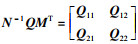
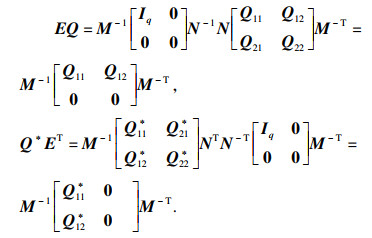 |
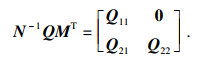 |
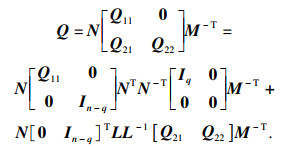 |
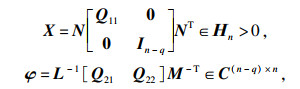 |
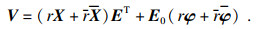 | (7) |
反之,对矩阵X和Q作分离实、虚部的处理得
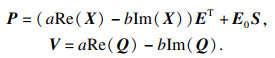 |
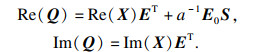 |
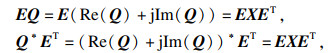 |
推论1 ??γ是给定的正实数,若存在矩阵X>0,X=X*∈Cn×n,S∈R(n-q)×n满足
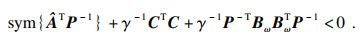 | (8) |
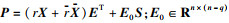
证明??在不等式(6)两端左乘P-T右乘P-1,即可得不等式(8).证毕.
注1 ??当α=1时,系统(3)退化为整数阶奇异系统,此时定理1与文献[13]一致;当E=I时,系统(3)退化为正常分数阶系统,E0=0,此时定理1与文献[14]一致,因此定理1更具有普适性.
注2 ??与文献[10]所得结论相比较,定理1不含等式约束,可以直接利用LMI工具箱求解,在一定程度上降低了计算复杂度,便于处理大规模系统.
定理2 ??γ是给定的正实数,若存在矩阵X>0,X=X*∈Cn×n,S∈R(n-q)×n使式(9)或式(10)成立:
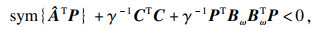 | (9) |
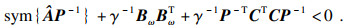 | (10) |
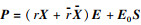
3 非脆弱分散H∞控制器设计对于奇异分数阶互联系统(1)的每个子系统,设计非脆弱分散控制器:
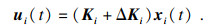 | (11) |
1) 加法摄动:
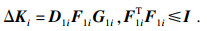 | (12) |
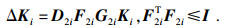 | (13) |
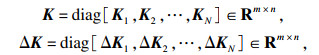 |
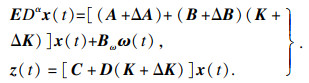 | (14) |
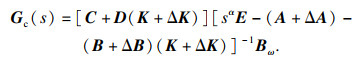 |
3.1 加法摄动下的控制器设计定理3 ??对于系统(1),给定γ>0,在形如式(12)的控制器增益加法摄动下,若存在对称矩阵X1i∈Rni×ni,反对称矩阵X2i∈Rni×ni,矩阵Si∈R(ni-qi)×ni,Yi∈Rmi×ni,以及正数αi,βi,σi和ε,使得对所有的i,j=1,2,?,N,i≠j,矩阵Qi=(aX1i-bX2i)EiT+E0iSi可逆,矩阵不等式为
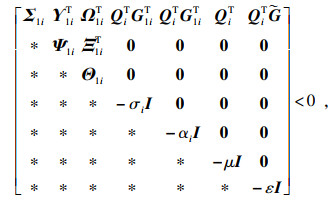 | (15) |
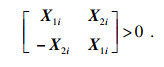 | (16) |
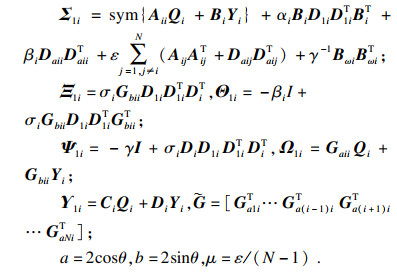 |
证明 ??令Xi=X1i+jX2i,若不等式(16)成立,则Xi∈Cni×ni且Xi=Xi*>0,记
 |
由推论1, 系统(14)容许且‖Gc(s)‖∞ < γ, 只需
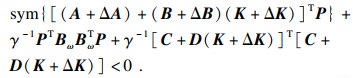 | (17) |
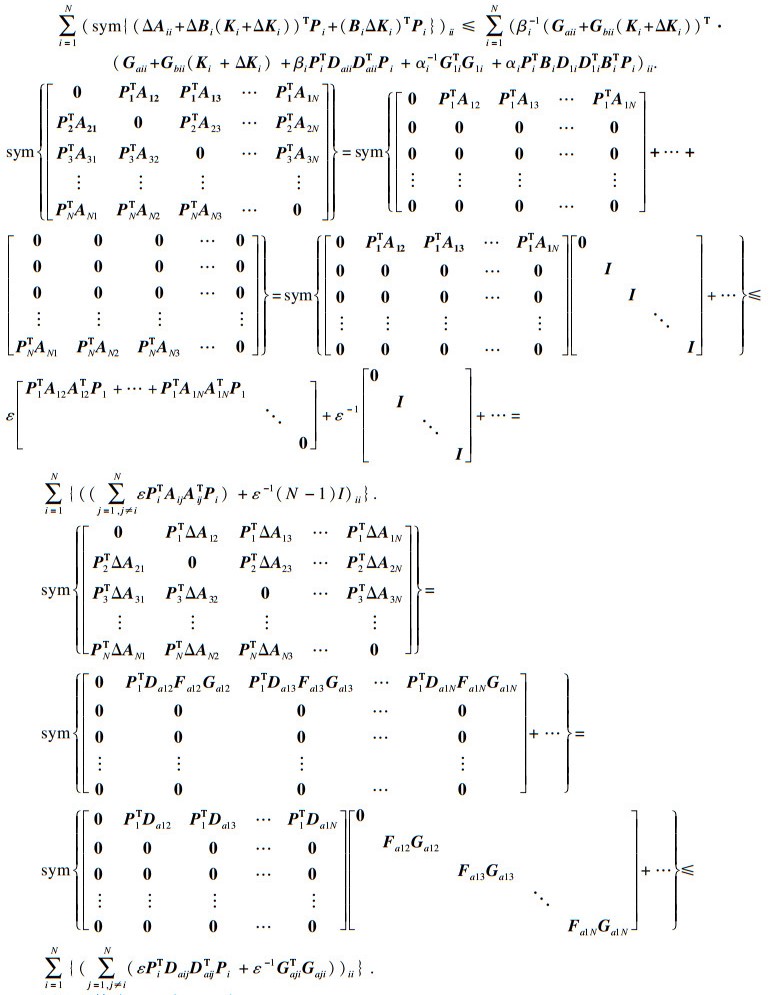 |
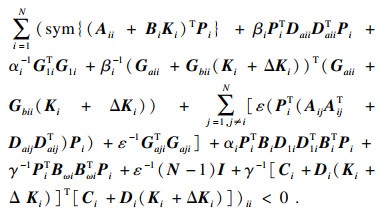 | (18) |
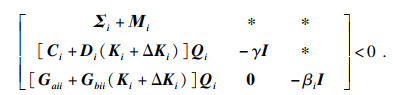 | (19) |
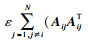
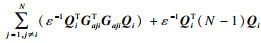
对式(19)左端进行如下处理:
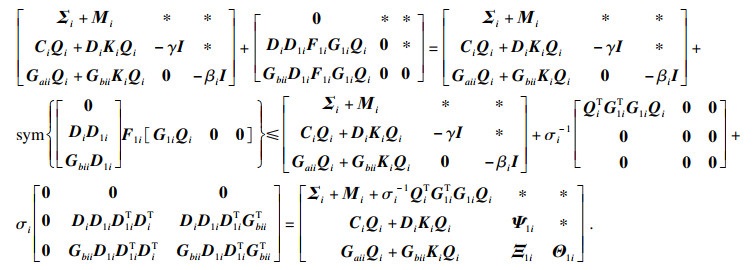 | (20) |
3.2 乘法摄动下的控制器设计定理4 ??对于系统(1),给定正数γ,在形如式(13)的控制器增益乘法摄动下,若存在对称矩阵X1i∈Rni×ni,反对称矩阵X2i∈Rni×ni,Si∈R(ni-qi)×ni,Yi∈Rmi×ni,以及正数αi,βi,σi,ε使得对所有的i,j=1,2,?,N,i≠j,矩阵Qi=(aX1i-bX2i)EiT+E0iSi可逆,且不等式(16)和如下不等式成立:
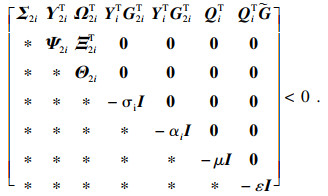 |
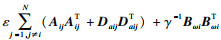
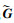
μ=ε/(N-1),a=2cosθ,b=2sinθ,E0i∈Rni×(ni-qi)为任意满足EiE0i=0的列满秩矩阵,那么闭环系统(14)容许且‖Gc(s)‖∞ < γ,此时Ki=YiQi-1是系统(1)的非脆弱分散H∞控制器增益.
注3 ??文献[15]为分数阶互联系统设计了非脆弱分散控制器,但其推导方法需要较强的限制条件,假设互联矩阵Aij∈Rni×ni为方阵,这导致所设计的控制器仅适用于各个子系统阶数均相同的情况.而本文方法不要求Aij为方阵,所得结论不但具有较大的适用范围,而且拥有良好的鲁棒性能.
注4 ??在为奇异分数阶互联系统设计分散控制器的过程中,需要对相应的复矩阵作分离实虚部的处理,以得到能利用LMI工具箱直接求解的实线性矩阵不等式.而整数阶奇异系统无需类似的处理,因此奇异分数阶系统的研究内容更加复杂.
4 数值仿真不确定奇异分数阶互联系统(1)在非脆弱分散控制器(11)作用下的闭环控制系统结构如图 1所示.
图 1(Fig. 1)
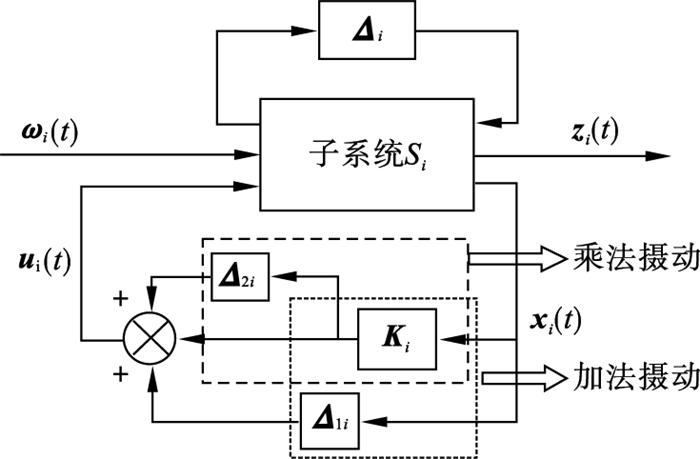 | 图 1 闭环控制系统结构图Fig.1 Structure diagram of closed-loop control system |
考虑由两个子系统组成的不确定奇异分数阶互联系统,假设α=0.45,其余参数如下:
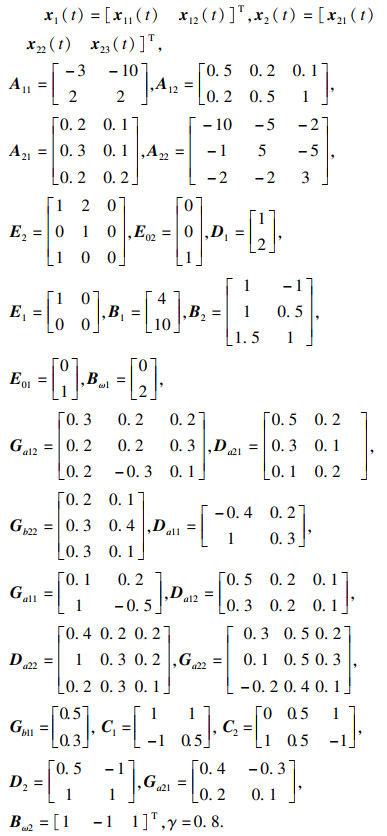 |
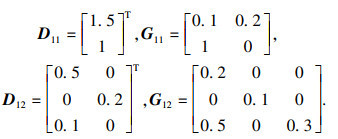 |
 |
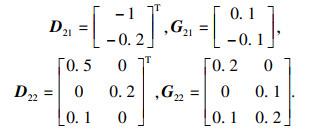 |
 |
图 2(Fig. 2)
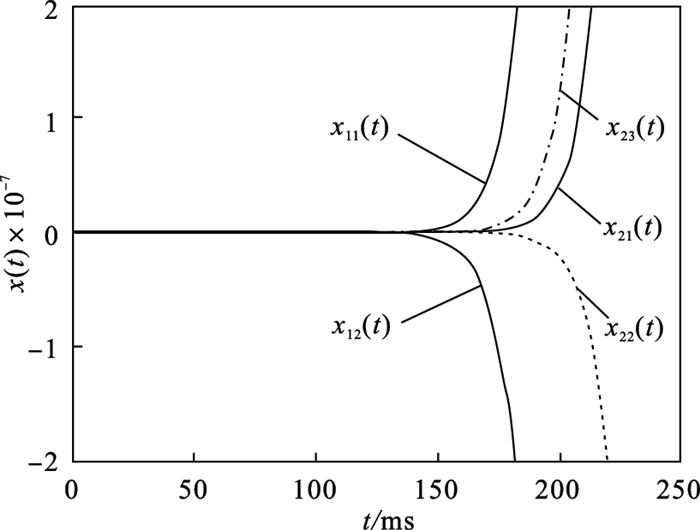 | 图 2 开环系统的状态响应Fig.2 State responses of open-loop system |
图 3(Fig. 3)
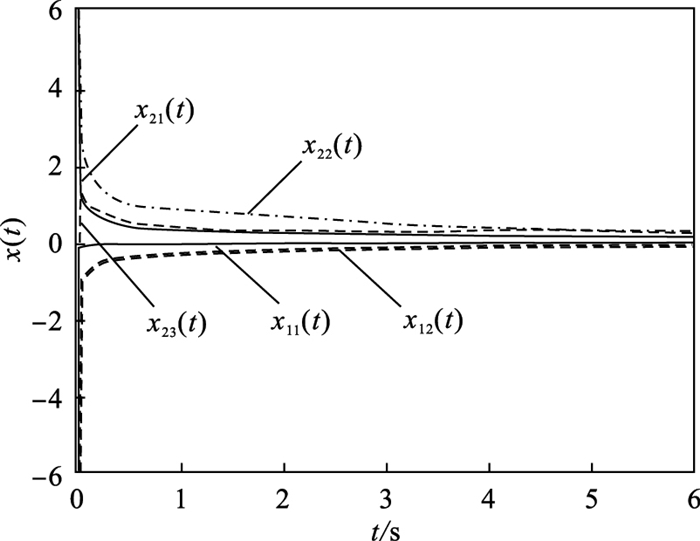 | 图 3 加法摄动下闭环系统的状态响应Fig.3 State responses of closed-loop system with additive perturbation |
图 4(Fig. 4)
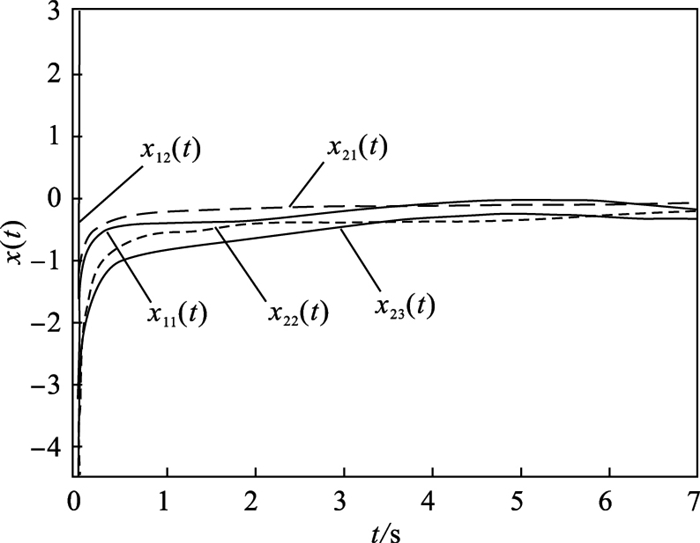 | 图 4 乘法摄动下闭环系统的状态响应Fig.4 State responses of closed-loop system with multiplicative perturbation |
利用FOTF工具箱[19],开环系统传递函数矩阵G(s)的H∞范数为2.610 0,频域响应如图 5所示.在控制器增益加法和乘法摄动下,闭环系统传递函数矩阵G(s)的H∞范数分别为0.518 0,0.509 9,频域响应分别如图 6和图 7所示,结果均小于预先给定的性能指标γ=0.8,闭环系统满足期望的H∞性能.
图 5(Fig. 5)
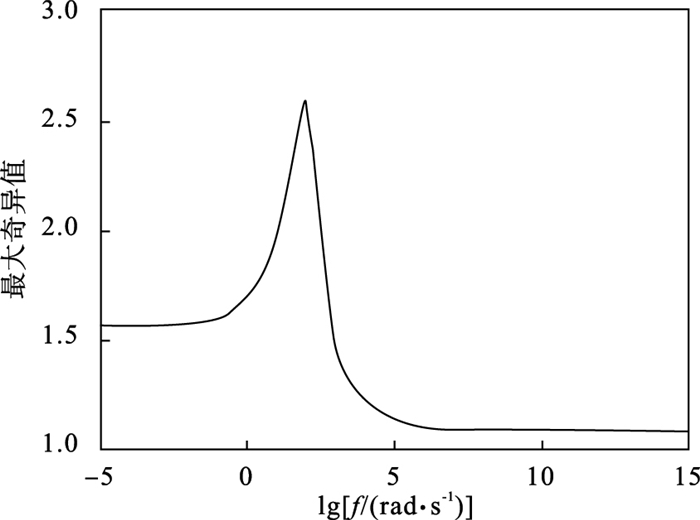 | 图 5 开环系统的最大奇异值Fig.5 Maximum singular values of open-loop system |
图 6(Fig. 6)
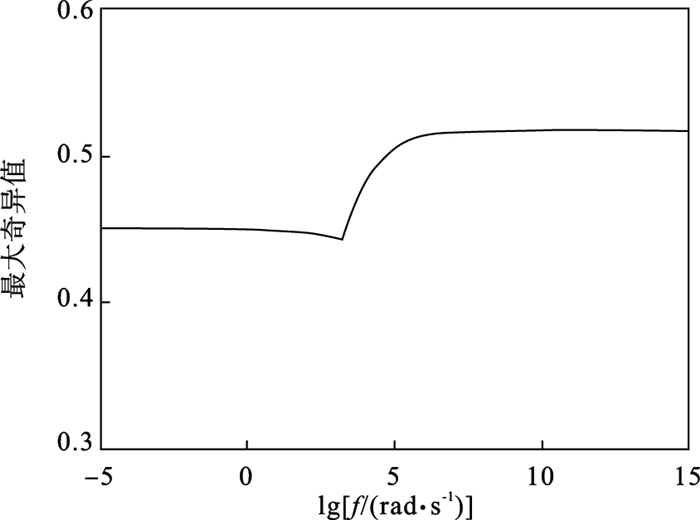 | 图 6 加法摄动下闭环系统的最大奇异值Fig.6 Maximum singular values of closed-loop system with additive perturbation |
图 7(Fig. 7)
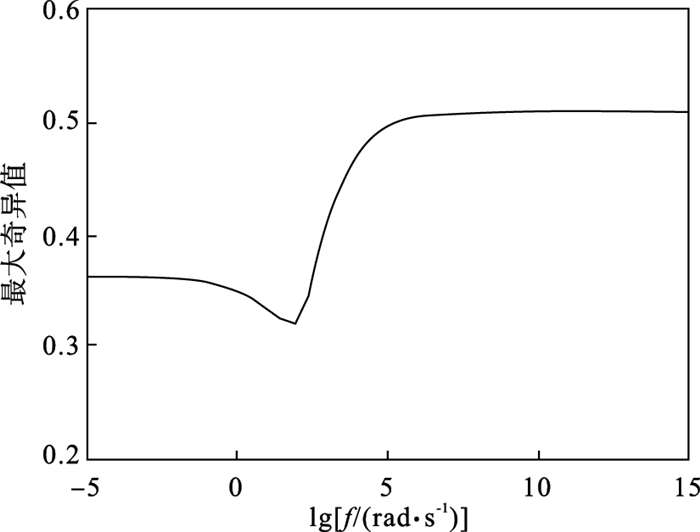 | 图 7 乘法摄动下闭环系统的最大奇异值Fig.7 Maximum singular values of closed-loop system with multiplicative perturbation |
注5 ??子系统S1是2阶的,子系统S2是3阶的,在各个子系统阶数不同的情况下,闭环系统可以在控制器作用下容许且满足H∞性能,因此本文结论比文献[15]更具有一般性.
5 结语本文提出了一种新的奇异分数阶线性系统容许且满足H∞性能的充分条件,结果以严格线性矩阵不等式的形式给出,适合处理复杂的大系统.在此基础上进一步研究了不确定奇异分数阶互联系统的非脆弱分散H∞控制问题,给出了保守性较低、容易求解且适用范围广泛的H∞控制器设计方法.通过仿真算例验证了所得结论的有效性.
参考文献
| [1] | Sabir Z, Raja M A Z, Guirao J L G, et al. A novel design of fractional Meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems[J]. Alexandria Engineering Journal, 2021, 60: 2641-2659. DOI:10.1016/j.aej.2021.01.004 |
| [2] | Marir S, Chadli M. Robust admissibility and stabilization of uncertain singular fractional-order linear time-invariant systems[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(3): 685-692. DOI:10.1109/JAS.2019.1911480 |
| [3] | Yu Y, Jiao Z, Sun C Y. Sufficient and necessary condition of admissibility for fractional-order singular system[J]. Acta Automatica Sinica, 2013, 39(12): 2160-2164. DOI:10.1016/S1874-1029(14)60003-3 |
| [4] | Zhan T, Ma S P. The controller design for singular fractional-order systems with fractional order 0 < α < 1[J]. The Anziam Journal, 2018, 60(2): 230-248. DOI:10.1017/S1446181118000202 |
| [5] | Zhang X F, Chen Y Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: the 0 < α < 1 case[J]. ISA Transactions, 2017, 82: 42-50. |
| [6] | Meng B, Wang X H, Zhang Z Y, et al. Necessary and sufficient conditions for normalization and sliding mode control of singular fractional-order systems with uncertainties[J]. Science China Information Sciences, 2020, 63(5): 1-10. |
| [7] | Zhang X F, Jin K X. State and output feedback controller design of Takagi-Sugeno fuzzy singular fractional order systems[J]. International Journal of Control Automation and Systems, 2021, 19(6): 2260-2268. DOI:10.1007/s12555-020-0078-5 |
| [8] | Marir S, Chadli M, Basin M V. Bounded real lemma for singular linear continuous-time fractional-order systems[J]. Automatica, 2022, 135: 1-9. |
| [9] | Farges C, Fadiga L, Sabatier J. H∞ analysis and control of commensurate fractional order systems[J]. Mechatronics, 2013, 23(7): 772-780. DOI:10.1016/j.mechatronics.2013.06.005 |
| [10] | Zhang Q H, Lu J G. H∞control for singular fractional-order interval systems: the 0 < α < 1 case[J]. ISA Transactions, 2021, 110: 105-116. DOI:10.1016/j.isatra.2020.10.003 |
| [11] | Li J, Lu J G, Chen Y Q. Robust decentralized control of perturbed fractional-order linear interconnected systems[J]. Computers & Mathematics with Applications, 2013, 66(5): 844-859. |
| [12] | Yang Y, He Y. Non-fragile observer-based robust control for uncertain systems via aperiodically intermittent control[J]. Information Sciences, 2021, 573: 239-261. DOI:10.1016/j.ins.2021.05.046 |
| [13] | 沃松林, 刘锋, 邹云. 广义大系统非脆弱分散H∞控制器设计[J]. 控制与决策, 2012, 27(4): 487-493. (Wo Song-lin, Liu Feng, Zou Yun. Non-fragile decentralized H∞ controller design for singular large-scale systems[J]. Control and Decision, 2012, 27(4): 487-493.) |
| [14] | Chen F Z, Lu J G, Miao Y B. Decentralized robust controller design for fractional order interconnected systems with element-bounded uncertainties[C]//Control & Decision Conference. Chongqing, 2017: 2790-2795. |
| [15] | Lin J Y. Robust resilient controller synthesis for uncertain fractional-order large-scale interconnected system[J]. Journal of the Franklin Institute, 2014, 351(3): 1630-1643. DOI:10.1016/j.jfranklin.2013.11.016 |
| [16] | Zhang X F, Huang W K. Adaptive sliding mode fault tolerant control for interval type-2 fuzzy singular fractional-order systems[J]. Journal of Vibration and Control, 2022, 28(3/4): 465-475. |
| [17] | Chen W B, Zhang G M, Xu S Y, et al. New results on stabilization for neutral type descriptor hybrid systems with time-varying delays[J]. Nonlinear Analysis: Hybrid Systems, 2022, 45: 1-12. |
| [18] | Yan Y Q, Zhang H G, Ming Z Y, et al. Observer-based adaptive control and faults estimation for T-S fuzzy singular fractional order systems[J]. Neural Computing and Applications, 2022, 34(6): 4265-4275. |
| [19] | 薛定宇. 分数阶微积分学与分数阶控制[M]. 北京: 科学出版社, 2018: 142-168. (Xue Ding-yu. Fractional calculus and fractional-order control[M]. Beijing: Science Press, 2018: 142-168.) |
