李寿涛¹, 魏玉博¹, 李秋媛¹, 于丁力^1,2
1. 吉林大学 通信工程学院，吉林 长春 130022;
2. 利物浦约翰摩尔大学，利物浦 英国 L35UX
收稿日期：2021-12-11
基金项目：吉林省科技厅自然科学基金资助项目(20190201099JC); 汽车仿真与控制国家重点实验室自由探索项目(ascl-zytsxm-202022)。
作者简介：李寿涛(1975-)，男，吉林长春人，吉林大学副教授。

摘要：针对侧向行驶车辆易发生转向失稳，构建了一种考虑轮胎侧偏刚度变化的车辆稳定性控制方法，以避免轮胎侧向力饱和，提高行车安全性.采用前、后轴轮胎侧偏角分段拟合方法建立轮胎侧偏刚度拟合模型，将拟合过的侧偏刚度引入到车辆动力学模型中，准确描述车辆当前的动态性能.为了避免轮胎侧向力饱和引起的转向失稳，本文提出一种基于模型预测控制(model predictive control, MPC)算法的前后轴约束的轮胎侧偏角的车辆稳定性控制方法，以优化车辆的转向性能.仿真结果表明，车辆稳定性控制方法能够将前后轴的轮胎侧偏角抑制在一定范围内，根据侧偏刚度的变化，避免车辆侧滑现象的发生，提高了车辆的稳定性.
关键词：主动安全性侧偏刚度拟合约束前轴侧偏角最小二乘法模型预测控制
MPC Stability Control Method Considering the Variation of Vehicle′s Cornering Stiffness
LI Shou-tao¹, WEI Yu-bo¹, LI Qiu-yuan¹, YU Ding-li^1,2
1. College of Telecommunication Engineering, Jilin University, Changchun 130022, China;
2. Liverpool John Moores University, Liverpool, UK
Corresponding author: LI Shou-tao，E-mail: list@jlu.edu.cn.

Abstract: In view of the easy steering instability of vehicles running sideways, this paper considers the variation of tire cornering stiffness to avoid saturation of tire lateral force and improve driving safety and constructs a vehicle stability control method. The front and rear axle tire sideslip angle segmented fitting method is used to establish a tire cornering stiffness fitting model, and then the fitted cornering stiffness is introduced into the vehicle dynamics model to accurately describe the current dynamic performance of the vehicle. In order to avoid the steering instability caused by the saturation of the tire lateral force, this paper proposes a vehicle stability control method based on the model predictive control(MPC)algorithm that considers the constraints of the front and rear axle tire sideslip angles to optimize the vehicle's steering performance. Simulation results show that the proposed vehicle stability control method can suppress the tire sideslip angle of the front axles within a certain range, while taking into account the changes in the cornering stiffness, thereby avoiding the occurrence of vehicle sideslip and improving the stability performance of the vehicle.
Key words: active safetycornering stiffness fittingconstrained front axle cornering angleleast square methodmodel predictive control
车辆操纵稳定性控制是一种提高汽车行驶主动安全性的关键技术，可有效防止侧翻、甩尾等交通事故的发生，目前电子稳定性控制(electronic stability control, ESC)单元多通过调节主动横摆力矩以达到稳定性控制效果，对于弯道的行车稳定性仍为车辆稳定性控制的难点及热点问题^[1].在行车过程中，车辆的行驶状态具有强非线性，车辆的动态参数会随路面状况及车辆的行驶状态变化^[2].其中，影响车辆结构参数不确定性的因素主要分为模型参数未知及未建模动态^[3-4].其中轮胎的垂直载荷会随车辆质量及行驶工况的改变而变化^[5-6]，轮胎侧偏刚度极易随车辆行驶工况及环境而发生改变，若不及时对轮胎侧偏刚度进行约束和处理，车辆极易发生失稳等不稳定工况.
车辆发生侧滑是造成重大交通事故的主要原因之一，考虑到因轮胎侧滑而导致的车辆失稳工况，Aligia等^[7]设计了一种基于观测器的牵引力控制系统，以消除侧向力与纵向牵引力之间的牵引效应，避免车辆因牵引力作用而出现打滑和侧翻.Han等^[8]对车辆进行合理控制，选择侧偏刚度的变化趋势作为指标对车辆行驶路面进行分类.由文献可知，由于轮胎侧偏刚度受多种因素影响而具有不确定性，所以基于侧偏刚度定量模型所设计的稳定控制器可能无法满足其驾驶过程中的稳定性要求.
针对以上问题，提出了一种基于轮胎侧偏角和垂直载荷转移量的侧偏刚度拟合模型，使当前侧向力在一定误差范围内跟踪真实值，此时车辆模型能更好描述车辆当前的运动状态，避免因轮胎侧偏角过大，使轮胎力进入非线性饱和区域造成不稳定工况，并设计模型预测控制器在约束可行域内求解控制序列及跟踪车辆理想的运动状态，提高了车辆的操纵稳定性与主动安全性.
1 二自由度车辆模型行驶过程中的车辆是一个具有强非线性的复杂系统，为简化控制器的求解过程，需要对车辆动力学模型进行线性化.定义坐标原点为质心位置，x, y轴分别表示车辆的纵向及侧向运动，由此建立如图 1所示的二自由度操纵模型，式(1)成立:

(1)

图 1(Fig. 1)

图 1 二自由度车辆模型Fig.1 Two-degree-of-freedom vehicle model

式中：m为车体质量；l_f, l_r分别为车辆质心到前、后轴之间的距离; δ_f为前轮转角；F_y1, F_y2, F_y3, F_y4分别为汽车的左前、右前、左后及右后轮胎侧向力；F_x1, F_x2, F_x3, F_x4分别为汽车的左前、右前、左后及右后轮胎纵向力；M_z为横摆力矩.
假设垂直载荷恒定且轮胎侧偏角足够小，轮胎侧向力为

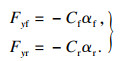(2)

式中：C_f，C_r分别为前、后轴轮胎侧偏刚度；α_f，α_r分别为前、后轴轮胎侧偏角，α_f=, α_r=；v_x为车辆纵向速度.
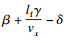
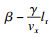
根据式(1)，式(2)整合状态空间方程：

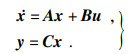(3)

式中：x=[β γ]^T; y= [δ M_z]^T;
考虑当前路面行驶要求，车辆进入稳态时，期望状态值为

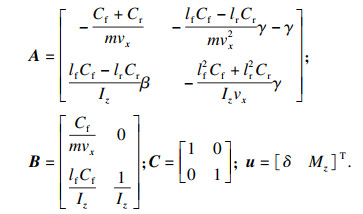(4)

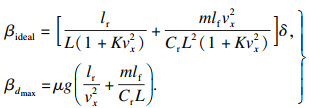(5)

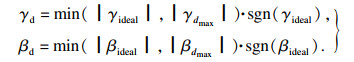(6)

式中：；L=l_f+l_r.
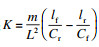
2 车载稳控单元结构设计控制系统的整体结构如图 2所示，控制器将使处于行驶工况的车辆的质心侧偏角和横摆角速度的实际值跟随期望值，从而计算出合适的附加横摆力矩.
图 2(Fig. 2)

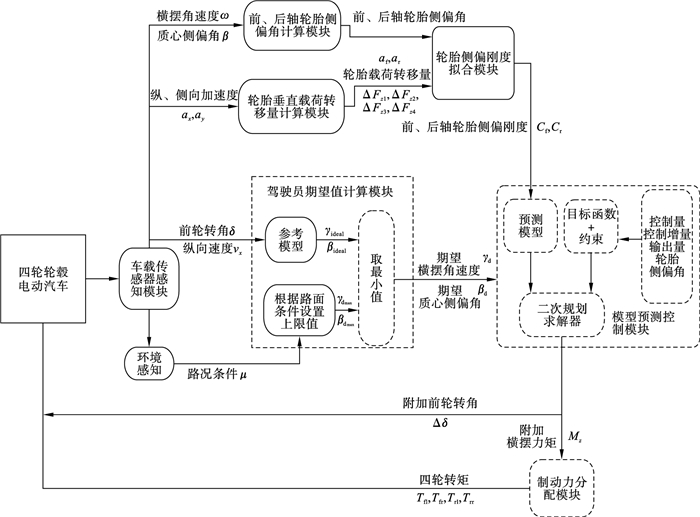图 2 车载稳控单元总体结构图Fig.2 Overall structure diagram of vehicle stability control unit

2.1 时变侧偏刚度拟合策略考虑轮胎侧偏刚度的实时变化性，应用最小二乘(least square, LS)作为拟合策略，通过拟合当前轮胎侧偏角及载荷传递对轮胎侧偏刚度进行实时处理.
最小二乘法的拟合二次多项式为

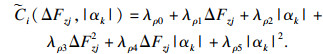(7)

式中：当i=fl, fr, rl, rr时，分别为左前、右前、左后、右后轮胎侧偏刚度; 当j=1, 2, 3, 4时，ΔF_zj分别为左前、右前、左后、右后轮胎垂直载荷变化量；α_k为轮胎侧偏角；当ω=1, 2, ?, 5时，λ_ρω为待拟合分段系数.
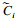
基于Carsim仿真平台进行模拟得到n组实验数据，为了提高拟合精度，引入残差平方和对λ_ρω进行求解：

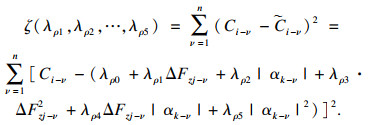(8)

对λ_ρ1, λ_ρ2, ?, λ_ρ5求偏导，求取ζ(λ_ρ1, λ_ρ2, ?, λ_ρ5)的最小值，可得

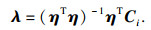(9)

式中：λ= [λ_ρ0, λ_ρ1, ?, λ_ρ5] ^T; C_i=[C_i-1, C_i-2, ?, C_i-n]^T;
通过计算匹配系数λ求得侧偏刚度拟合模型，拟合模型所得的轮胎侧偏刚度随轮胎侧偏角及载荷转移量实时变化，并对实际侧向力进行准确跟踪.
2.2 MPC稳定性控制模块采用模型预测控制(MPC)算法，求解最优附加前轮转角及横摆力矩.根据式(3)选取状态变量x=[β γ]^T，控制量y=[δ M_z]^T，将通过拟合得到的时变侧偏刚度代入到控制模型中，并采用增量形式消除静态误差：

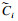
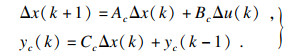(10)

式中：A_c=e^A_dT_c; B_c=;
基于式(9)对系统下一步状态进行预测，设定预测时域p及控制时域m，将当前k时刻测量的状态值作为初始状态，预测未来k+1到k+p的时刻表示为k+1|k, k+2|k, ?，k+p|k，则预测时域p内未来时刻的状态变量为

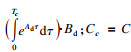
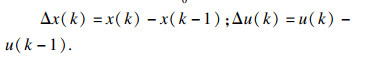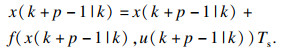(11)

式中, f(x(k), u(k))= 是k时刻系统状态变量的梯度.
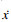
车辆在预测时域内选取横摆角速度及质心侧偏角的名义值作为跟踪项：

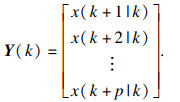(12)

为保证车辆在行驶过程中状态量始终以最小误差跟踪期望值，并在转弯过程中能保证一定的平滑性，目标函数为

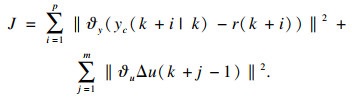(13)

式中: ?_y为误差加权因子；?_u为控制增量加权因子，将其转化为标准二次型问题进行求解最优的控制序列.
为保证车辆在行驶过程中的安全性，对控制量、控制增量及输出量进行约束的基础上，对轮胎侧偏角进行约束，各约束的表达形式分别为
控制量约束：

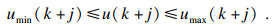(14)

控制增量约束：

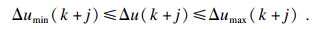(15)

输出量约束：

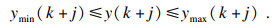(16)

式中: j=1, 2, ?, p; u_min(k+j)，u_max(k+j)分别为控制量的最小值和最大值；y_min(k+j)，y_max(k+j)分别为输出量的最小值和最大值；由式(4)可知，α_f, α_r需通过控制量与输出量之间的关系进行间接求解，因此需要对控制增量进行处理进而对侧偏角进行约束：

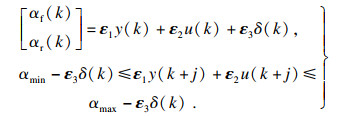(17)

式中:
j=1, 2, ?, p; α_min，α_max分别为前、后轴侧偏角的最小值和最大值.
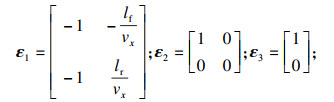将式(13)代入式(17)，可得

(18)

式中：
在以上约束条件下求解最优控制序列，在达到下一采样时刻，以当前时刻为初始状态重复以上步骤求解，从而实现滚动优化.
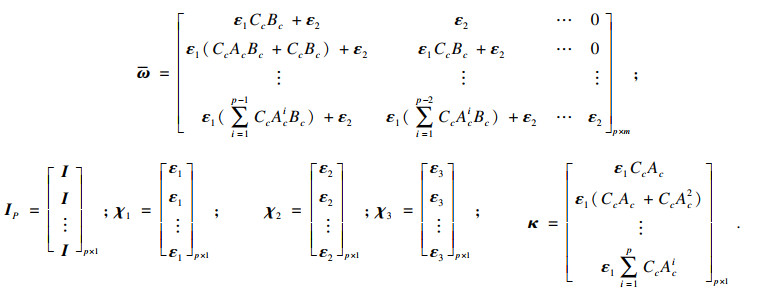3 仿真结果与分析通过仿真实验具体分析了控制器的控制效果.基于Carsim和Matlab/Simulink生成联合仿真平台，其中仿真车辆的相关参数如表 1所示，在单移线工况下进行仿真分析.
表 1(Table 1)

表 1 车辆的仿真参数Table 1 Vehicle simulation parameters 参数 参数名称 值 m/kg 整车质量 1 362 lf/m 质心到前轴的距离 1.06 lr/m 质心到后轴的距离 1.51 Iz/(kg·m-2) 车辆绕z轴的转动惯量 1 992.53 h/m 质心到地面的距离 0.513 c/m 车辆轮距 1.396

表 1 车辆的仿真参数 Table 1 Vehicle simulation parameters

设置路面摩擦系数μ=0.4，车速为100 km/h.由图 3可知，车辆在行驶过程中轮胎的侧偏刚度随垂直载荷不断变化而具有不确定性，最小二乘法与移动最小二乘法(moving least squares，MLS)都能对时变侧偏刚度进行一定的表达，但LS的吻合性能更好.拟合所得到的前轮胎侧偏刚度对真实值能进行有效跟踪.由图 4可知，通过补偿轮胎侧偏刚度可以在一定误差内准确追踪实际侧向力.
图 3(Fig. 3)

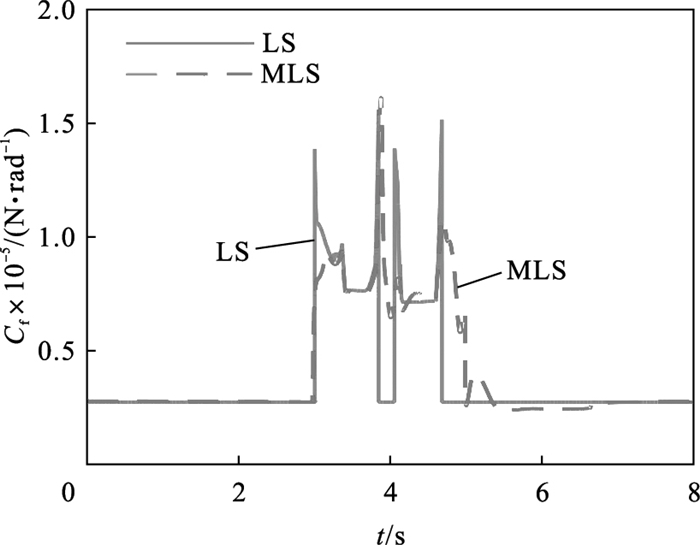图 3 前轴轮胎侧偏刚度Fig.3 Front axle tire cornering stiffness

图 4(Fig. 4)

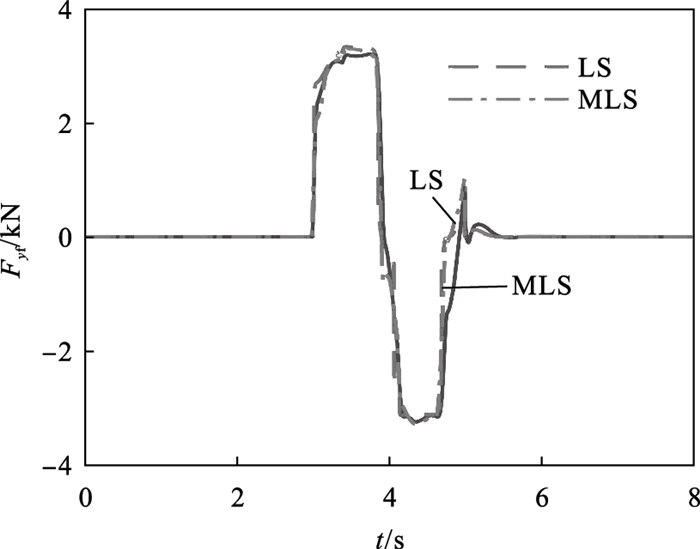图 4 前轴侧向力Fig.4 Front axle lateral force

由图 5可知，此时车辆的轮胎侧偏角过大，轮胎力处于非线性饱和区，车辆容易出现转弯失稳现象.在进行约束求解及稳定性控制后的前轴轮胎侧偏角在3~5 s仿真时长中明显减小.由图 6、图 7可知，与滑模自适应控制器(sliding mode controller, SMC)相比，基于MPC的稳定性控制方法能使车辆在较小误差内将状态参量控制在目标值附近，并能有效抑制轮胎侧滑角，更好改善车辆的动态性能.
图 5(Fig. 5)

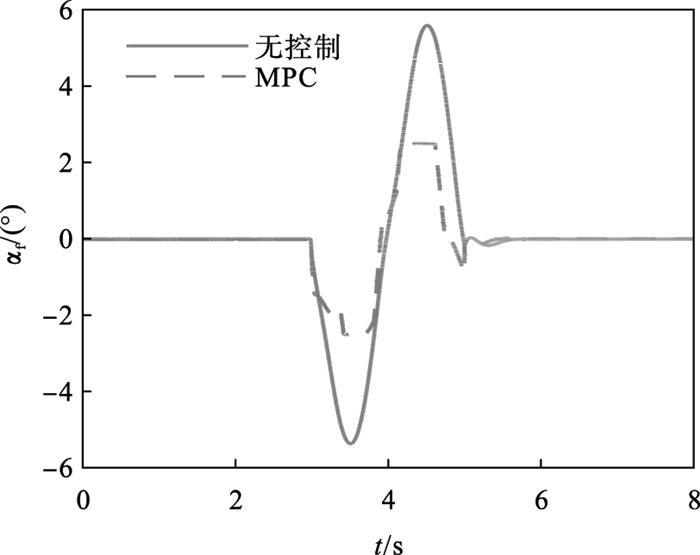图 5 前轴轮胎侧偏角Fig.5 Front axle tire slip angle

图 6(Fig. 6)

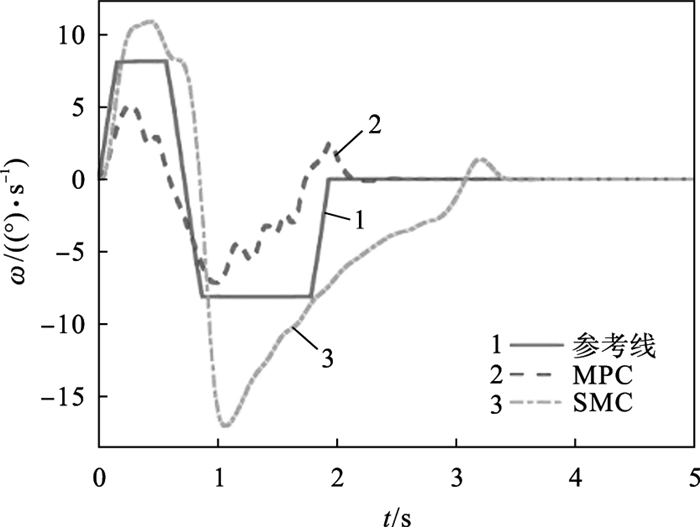图 6 横摆角速度Fig.6 Yaw rate

图 7(Fig. 7)

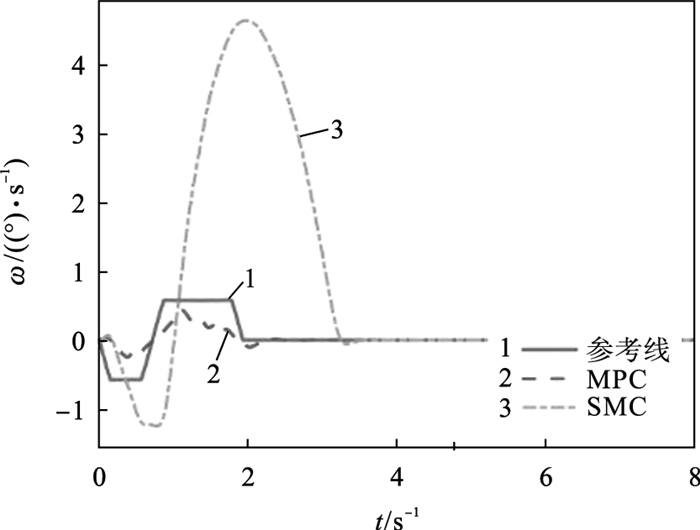图 7 质心侧偏角Fig.7 Sideslip angle of mass centre

4 结论1) 对侧偏刚度进行拟合，提高了侧偏刚度的表达精度，从而更好描述车辆当前的运动状态.
2) 设计了稳定性控制方法，引入轮胎侧偏角作为控制器的约束条件，使车辆的控制量实际值跟踪名义值，使所提出的控制方法有效减小超调，并能在较小误差内将状态参量控制在目标值附近，从而保证行驶过程中的稳定性与安全性.
参考文献

[1]	Ma X B, Wong P K, Zhao J, et al. Cornering stability control for vehicles with active front steering system using T-S fuzzy based sliding mode control strategy[J]. Mechanical Systems and Signal Processing, 2018, 3: 347-364.
[2]	Sun H, Zhao H, Huang K, et al. A new approach for vehicle lateral velocity and yaw rate control with uncertainty[J]. Asian Journal of Control, 2018, 20(1): 216-227. DOI:10.1002/asjc.1531
[3]	Mehdizadeh M, Soleymani M, Abolmasoumi A H. Stability control of a road vehicle considering model and parametric uncertainties[J]. International Journal of Vehicle Autonomous Systems, 2017, 13(3): 203-220. DOI:10.1504/IJVAS.2017.10004252
[4]	Guo N, Zhang Y, Zou B, et al. A computationally efficient path-following control strategy of autonomous electric vehicles with yaw motion stabilization[J]. IEEE Transactions on Transportation Electrification, 2020, 6(2): 728-739. DOI:10.1109/TTE.2020.2993862
[5]	Biase F D, Timpone L F. Vehicle sideslip angle estimation for a heavy-duty vehicle via extended Kalman filter using a rational tyre model[J]. IEEE Access, 2020, 8: 142120-142130. DOI:10.1109/ACCESS.2020.3012770
[6]	Kim J. Estimation of tire forces using vehicle linear accelerations and yaw rate[J]. Transactions of the Korean Society of Automotive Engineers, 2019, 27(10): 747-753. DOI:10.7467/KSAE.2019.27.10.747
[7]	Aligia D A, Magallan G A, Angelo C H. EV traction control based on nonlinear observers considering longitudinal and lateral tire forces[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(8): 2558-2571. DOI:10.1109/TITS.2017.2758343
[8]	Han K, Choi M, Choi S. Estimation of tire cornering stiffness as a road surface classification indicator using under steering characteristics[J]. IEEE Transactions on Vehicular Technology, 2018, 2: 13-21.