张顺尧¹, 桑爱军¹, 宋立军², 王世刚¹
1. 吉林大学 通信工程学院，吉林 长春 130022;
2. 吉林工程技术师范学院，吉林 长春 130052
收稿日期：2021-11-08
基金项目：吉林省自然科学基金资助项目(20200201295JC); 吉林省科技发展计划国际合作项目(20200801042GH)。
作者简介：张顺尧(1998-)，男，吉林省吉林市人，吉林大学硕士研究生;
桑爱军(1973-)，女，山东莱州人，吉林大学教授。

摘要：针对视频鬼成像重构采样次数少、清晰度低、噪声大等问题，提出了一种聚合型三维目标匹配滤波方法.首先将鬼成像视频中的每一帧图像与待优化帧进行块匹配，将块匹配后的每一帧图像按照时序排序组成三维矩阵.根据每一帧图片的帧序，赋予其不同的帧权值，对矩阵进行三维加权中值滤波.经过运动目标的欠采样仿真与实验对比后，结果表明本文方法相较于现存的三维滤波方法，不仅噪声系数更低、结构保留程度更好，同时获到了更好的主观评价(Brisque).对比原始实验恢复图，本文方法在噪声系数和边缘模糊度上分别下降34.25 %，6.86 %，在Brisque主观评价上提升了45.84 %.
关键词：计算鬼成像块匹配算法中值滤波三维加权滤波视频滤波
Convergent Three-dimensional Target Matching Filtering for Ghost Imaging
ZHANG Shun-yao¹, SANG Ai-jun¹, SONG Li-jun², WANG Shi-gang¹
1. College of Telecommunication Engineering, Jilin University, Changchun 130022, China;
2. Jilin Engineering Normal University, Changchun 130052, China
Corresponding author: SANG Ai-jun, E-mail: sangaj@jlu.edu.cn.

Abstract: Aiming at the problems of low sampling frequency, low resolution and high noise in video ghost imaging reconstruction, an aggregated three-dimensional target matching filtering method was proposed. Firstly, each frame of the ghost imaging video is block-matched with the frame to be optimized and each frame of images after block matching is arranged to form a three-dimensional matrix according to the time sequence. According to the frame sequence of each frame picture, different frame weights are assigned to it. Then the matrix is subjected to three-dimensional weighted median filtering. After under-sampling simulation and experimental comparison of moving targets, the method proposed has not only lower noise figure and better structure retention, but also a better subjective evaluation compared with the existing three-dimensional filtering methods. Compared with the original experimental restoration graph, the proposed method reduces the noise figure and edge ambiguity by 34.25 % and 6.86 %, respectively, and the Brisque subjective evaluation was improved by 45.84 %.
Key words: computational ghost imagingblock matching algorithmmedian filterthree-dimensional weighted filteringvideo filtering
鬼成像(ghost imaging, GI)是一种处于光学领域最前沿的成像系统^[1].不同于经典成像模式，鬼成像是通过关联光场能量重构目标图片的一种新型成像方式.在经典鬼成像中，分束器(beam splitter，BS)将光源分成两束，分别在不同路径上传播，高分辨相机(如CCD)所在的光路称为参考光路；无空间分辨能力的桶探测器所在的光路称为物体光路^[2].通过关联运算二者输出的光电流，即可重构出目标物体的像.美国麻省理工****Shapiro在2008年提出了计算鬼成像技术(computational ghost imaging，CGI), 利用空间光调制器(spatial light modulator，SLM)生成可控分布的散斑进行关联运算^[3].不仅简化了鬼成像系统的实验装置，还使用特定散斑提高重构质量.
与传统成像相比，鬼成像有着成像系统简单、容易实现、抗噪声能力强、采样速率可以超过奈奎斯特采样极限等优点，已应用到医学成像^[4]、激光雷达^[5]、光学加密^[6]、遥感卫星^[7]等领域.虽然鬼成像有着良好的应用前景，但仍存在采样次数多、重构时间长、成像质量差的问题.由于图像的成像质量往往与采样次数成正比，欠采样通常意味着低清晰度，严重影响视频鬼成像的重构.
Xu等提出了一种基于LED的结构化照明实现1000f/s的计算鬼成像方法，解决鬼成像系统采样速率过低的问题^[8].该方法的局限性在于LED模块需要较高的照明能量：虽然可以施加大的驱动电流为成像应用提供足够的照明功率，但密集的LED阵列将引起严重的发热问题.Nie等提出了运用粉色噪声散斑重建运动物体图像的CGI系统^[9].该方案利用粉色噪声散斑特有的正互相关特性，可以克服环境噪声、减少采样次数，进一步改善成像质量的鲁棒性.由于粉色噪声互相关特点，粉色噪声CGI往往会出现图片边缘清晰度低的现象.Yang等提出了一种TC-CGI方案：通过移动或旋转散斑矩阵，进行修正运算，以消除因目标移动超过单个像素距离导致的图像模糊问题^[10].在重建图像中，仍然存在一些噪声.可知，针对移动目标的鬼成像系统，均不同程度地受限于硬件、噪声、边缘清晰度等问题困扰.因此，提出一种针对视频鬼成像的优化方法.
本文提出一种聚合型三维目标匹配的鬼成像视频优化方法，多方面提升了鬼成像视频的还原质量.其原理是利用多个视频帧块匹配出当前帧的近似帧后，按时序组成三维矩阵.进行三维加权中值滤波，并经过锐化得到优化的当前帧.通过仿真和实验对比其他现存的三维滤波方法，本文所提的滤波方法在客观参数评价和人眼主观感受上都取得了更好的表现.
1 基本原理1.1 计算鬼成像计算鬼成像的实验装置如图 1所示^[11].激光发射器发出光源后，传播至计算机控制的数字微镜器件(digital micromirror device，DMD)上，模拟出已知光强分布的散斑，记为I(x, y).其中：x=1, 2, ?, m，表示行；y=1, 2, ?, n，表示列.光源在得到调制后照射至物体表面，物体反射光随后由透镜汇聚到桶探测器中.
图 1(Fig. 1)

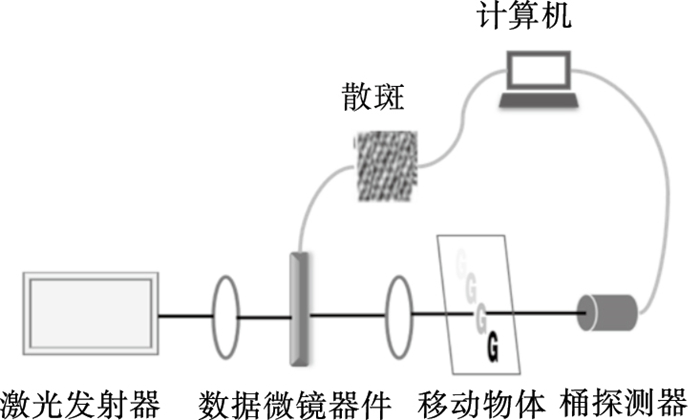图 1 计算鬼成像的实验装置图Fig.1 Diagram of experimental setup for computing ghost imaging

不断重复上述实验过程，将得到的数据汇总处理，即可恢复出物体的图像.设N次采样中，空间光调制器生成的第k个散斑矩阵为I(x, y, k), 与之对应的桶探测器测量的光强值为B(k), 待测物体的传输系数为T(x, y)，将散斑矩阵与光强值进行关联运算，即可还原出目标的像.计算鬼成像的重构式为

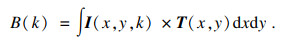(1)

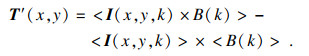(2)

式中：T′(x, y)为重构出的像；<·>为取平均值的运算；k=1, 2, ?, N，N为总采样次数.
1.2 聚合型三维目标匹配滤波在计算鬼成像的框架下提出了一种聚合型三维目标匹配的鬼成像视频优化方法.该方法首先利用块匹配准则，将视频中的每一帧与待优化帧做块匹配, 得到的所有图片按时序排列，组成一个三维矩阵.计算每一帧的帧权值，利用三维加权中值滤波去除视频中的噪声.使用Sobel边缘检测进行图像锐化，并还原出原视频.
1.2.1 块匹配算法块匹配准则是一种常用于图像去噪、运动估计的算法.现实生活中，相邻两帧间的物体运动可以视为位移量很小的直线运动，因此可以将一帧图片分为若干块计算目标物体的运动矢量，如图 2所示.前一帧的搜索区为(M+2W_x, N+2W_y), 当前帧块与前一帧块的位移为d(i, j)，在搜索区中若能找到与当前帧块匹配的前一帧块，则此d(i, j)为所需的运动矢量^[12].
图 2(Fig. 2)

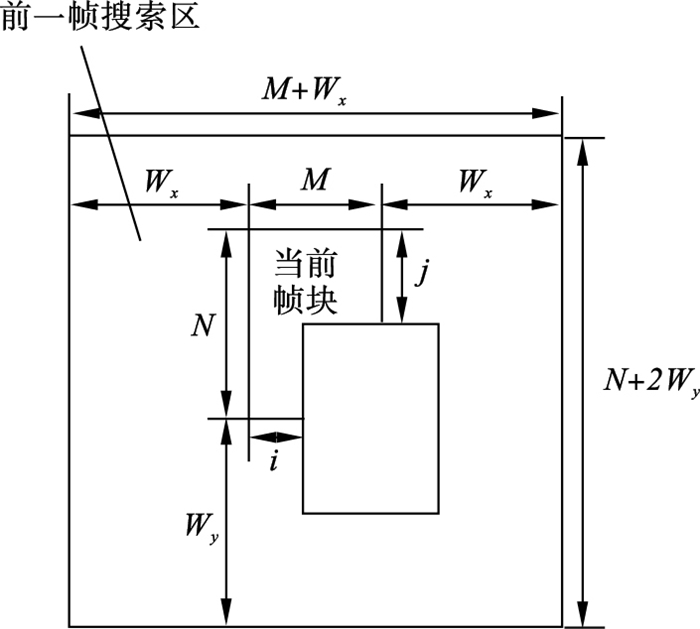图 2 块匹配算法Fig.2 Block matching algorithm

穷尽搜索法是块匹配准则中相对精准的匹配算法.对搜索窗内每一个点都用绝对误差均值(mean absolute deviation，MAD)最小准则进行计算，找到MAD最小时的点(i, j)值，作为所需的运动矢量d(i, j).绝对误差均值最小准则为

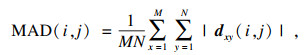(3)

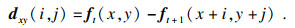(4)

式中：f_t(x, y)为前一帧图像；f_t+1(x+i, y+j)为当前帧图像；d_xy(i, j)为运动矢量，i=1, 2, ?, M+2W_x，j=1, 2, ?, N+2W_y.
本文提出一种聚合型块匹配方法.将视频中的每一帧都与目标帧进行块匹配，即视频中的所有帧都将重构成当前帧的近似图.将所有匹配后得到的图像按时序排序组成三维矩阵，该矩阵称为目标帧的重构矩阵，便于后续加权处理，如图 3所示.
图 3(Fig. 3)

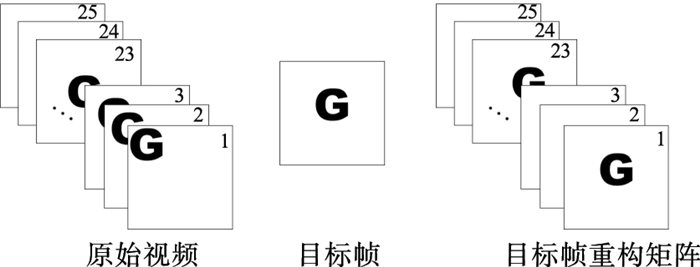图 3 目标帧的重构矩阵Fig.3 Reconstruction matrix of target frame

1.2.2 三维加权中值滤波为了去除噪声干扰，本文提出了一种基于时序的三维加权中值滤波方法，中值滤波是一种常用的消除噪声、保护边缘的滤波方法.将某领域集中的点按照像素值的大小依次进行排序，选取中间值作为当前像素值.中值滤波的计算式为

(5)

式中：median[]表示取中值函数；f(x, y)为图像坐标点(x, y)的灰度值；Z_xy为以(x, y)为中心的邻域内所有的坐标点；G(x_o, y_o)为(x, y)滤波后的像素值.
邻域集中的不同点对当前像素点的影响并不相同，加权中值滤波的提出针对性地解决了这一痛点.在加权中值滤波3×3的权值矩阵中，中心点的权重最大，四邻域的点权重次之，角邻域的点权重最小.3×3窗口的加权均值滤波式为^[13]

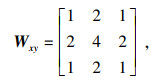(6)

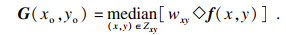(7)

式中：◇为加权符号；W_xy为权值矩阵；w_xy为权值矩阵W_xy中(x, y)点的值.
在鬼成像的视频中，帧与帧之间具有较强的关联性，可以利用其帧间关系去除噪声.为了更好地提升中值滤波对视频信号的降噪效果，在二维加权中值滤波的基础上考虑对第三维度时序的处理.对像素点的位置加权，通过计算每一帧与目标帧的绝对距离，得出每一帧的帧权值.三维加权中值滤波式为

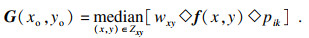(8)

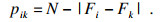(9)

式中：p_ik是帧权值；N为总帧数；F_i为待测帧帧序；F_k为目标帧帧序.
1.2.3 Sobel算子边缘检测锐化经中值滤波后，图像的噪声被大大降低，但边缘细节没有得到很好保留.边缘是图像中亮度值突变的区域，锐化可以恢复并增强目标物体被模糊掉的细节. 经测试，Sobel算子的边缘检测效果更佳.Sobel算子是一种3×3模板下的微分算子，可以很好地平滑噪声、增强边缘.Sobel算子表示为

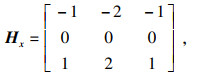(10)

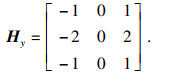(11)

2 仿真与实验为了检测聚合型三维目标匹配滤波方法，本文运用MATLAB进行仿真及实验，并与加权中值滤波、BM3D滤波^[14]和VBM4D滤波^[15]方法进行了对比.
2.1 仿真结果鬼成像重构出的图像分辨率普遍较低，使用PSNR评价重构图的噪声程度，SSIM评价重构图的模糊程度.为考查算法的普适性，分别模拟了高斯噪声、泊松噪声、椒盐噪声及乘性噪声4种不同噪声的污染情况.
仿真实验是以字母‘G’图像模拟成像的物体，其图片规格为64 pix×64 pix，zigzag序Walsh散斑与字母‘G’的尺寸相同，不同噪声污染后效果如图 4所示.对各种受噪声污染图进行滤波后的PSNR，SSIM进行比较，结果如表 1~表 4所示.
图 4(Fig. 4)

图 4 字母‘G’的鬼成像图Fig.4 Ghost imaging pictures of letter 'G' (a)—仿真原图；(b)—鬼成像后重构图；(c)—高斯噪声图；(d)—泊松噪声图；(e)—椒盐噪声图；(f)—乘性噪声图.

表 1(Table 1)

表 1 高斯噪声图的各种滤波方法比较Table 1 Comparison of various filtering methods of Gaussian noise map 方法 本文方法 加权中值滤波 BM3D VBM4D 重构图片 PSNR 13.866 6 13.246 9 13.366 5 12.972 8 SSIM 0.181 7 0.179 8 0.179 0 0.173 2

表 1 高斯噪声图的各种滤波方法比较 Table 1 Comparison of various filtering methods of Gaussian noise map

表 2(Table 2)

表 2 泊松噪声图的各种滤波方法比较Table 2 Comparison of various filtering methods of Poisson noise map 方法 本文方法 加权中值滤波 BM3D VBM4D 重构图片 PSNR 13.984 9 13.490 1 13.471 2 12.627 2 SSIM 0.187 3 0.190 1 0.184 1 0.187 6

表 2 泊松噪声图的各种滤波方法比较 Table 2 Comparison of various filtering methods of Poisson noise map

表 3(Table 3)

表 3 乘性噪声图的各种滤波方法比较Table 3 Comparison of various filtering methods of speckle noise map 方法 本文方法 加权中值滤波 BM3D VBM4D 重构图片 PSNR 14.066 1 13.496 2 12.795 2 12.452 2 SSIM 0.187 6 0.188 9 0.164 8 0.160 9

表 3 乘性噪声图的各种滤波方法比较 Table 3 Comparison of various filtering methods of speckle noise map

表 4(Table 4)

表 4 椒盐噪声图的各种滤波方法比较Table 4 Comparison of various filtering methods of salt and pepper noise map 方法 本文方法 加权中值滤波 BM3D VBM4D 重构图片 PSNR 13.970 9 13.218 0 13.245 7 13.227 9 SSIM 0.180 9 0.167 0 0.167 1 0.161 7

表 4 椒盐噪声图的各种滤波方法比较 Table 4 Comparison of various filtering methods of salt and pepper noise map

可知，本文方法较其他3种方法在不同噪声干扰下，PSNR, SSIM都取得了最大值.主观评价上，本文方法处理后的图片人眼感受更舒适.
2.2 实验结果为了考察聚合型三维目标匹配滤波方法在实际中的应用效果，进行目标为运动字母‘G’的鬼成像实验.目标物体分辨率为64pix×64pix，DMD显示频率为22kHz，散斑序列为Walsh散斑集.重构出的视频分别使用本文方法、加权中值滤波，BM3D，VBM4D进行优化.由于没有真实参考图片，评价指标需使用无参评价指标，本文采用了NRSS^[16]、噪声评价、模糊度评价^[17]、Brisque参数^[18]评价恢复图像的优劣.其中，4个参数的指标均是越小越好，结果如表 5和图 5所示.
表 5(Table 5)

表 5 优化后的重构图片的对比评价Table 5 Comparative evaluation of optimized reconstructed map 方法 原始重构图 本文方法 加权中值滤波 BM3D VBM4D 重构图片 NRSS 0.521 2 0.441 4 0.424 0 0.511 9 0.520 5 模糊度 0.220 0 0.204 9 0.205 3 0.244 8 0.224 6 噪声系数 0.396 7 0.260 8 0.266 3 0.211 8 0.270 8 Brisque 34.120 1 18.478 3 43.458 2 44.920 9 43.458 2

表 5 优化后的重构图片的对比评价 Table 5 Comparative evaluation of optimized reconstructed map

图 5(Fig. 5)

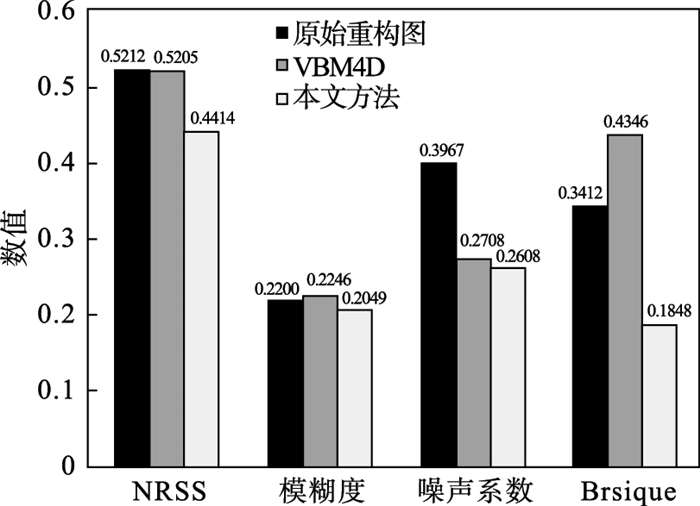图 5 本文方法与原始重构图及VBM4D滤波后图的评价比较Fig.5 Evaluation comparison of the method with the original image and the VBM4D filtered picture

由表 5可知，在进行滤波操作后，虽然其他方法都对图片噪声有一定抑制作用，但图片均出现了不同程度的边缘细节损失.本文方法不仅在去除噪声的情况下减少了边缘信息的损失，同时也得到了更好的主观评价.由图 5可知，相较于原始重构图，本文方法在无参考图形的主观和客观评价均有提升，其中噪声系数下降34.25 %，边缘模糊程度下降6.86 %，NRSS指标提升15.31 %，Brisque指标提升45.84 %.
3 结论1) 在计算鬼成像的框架下，将块匹配算法与加权中值滤波相结合，提出了一种聚合型三维目标匹配滤波算法.
2) 在重构出运动目标的鬼成像视频后，通过块匹配算法构建出目标帧的近似重构矩阵，进行三维加权中值滤波，得到优化后的目标帧.
3) 在经过运动物体的仿真和实验对比后，数据表明本文方法相较于传统加权中值滤波、BM3D，VBM4D算法，主观和客观评价均表现得更好.对比原始实验恢复图，本文方法在噪声系数和边缘模糊度上分别下降34.25 %，6.86 %，同时在Brisque主观评价上提升了45.84 %.
参考文献

[1]	Strekalov D V, Sergienko A V, Klyshko D N, et al. Observation of two-photon "ghost" interference and diffraction[J]. Physical Review Letters, 1995, 74(18): 3600-3612. DOI:10.1103/PhysRevLett.74.3600
[2]	Gatti A, Brambilla E, Bache M, et al. Ghost imaging with thermal light: comparing entanglement and classical correlation[J]. Physical Review Letters, 2004, 93(9): 093602. DOI:10.1103/PhysRevLett.93.093602
[3]	Shapiro J H. Computational ghost imaging[J]. Physical Review A, 2008, 78(6): 061802. DOI:10.1103/PhysRevA.78.061802
[4]	Koktzoglou I, Sheehan J J, Dunkle E E, et al. Highly accelerated contrast‐enhanced MR angiography: improved reconstruction accuracy and reduced noise amplification with complex subtraction[J]. Magnetic Resonance in Medicine, 2010, 64(6): 1843-1848. DOI:10.1002/mrm.22567
[5]	韩申生, 龚文林, 陈明亮, 等. 基于稀疏和冗余表象的鬼成像雷达研究进展[J]. 红外与激光工程, 2015, 44(9): 2547-2555. (Han Shen-sheng, Gong Wen-lin, Chen Ming-liang, et al. Research progress of GISC lidar[J]. Infrared and Laser Engineering, 2015, 44(9): 2547-2555. DOI:10.3969/j.issn.1007-2276.2015.09.002)
[6]	曹非, 赵生姝. 基于计算鬼成像的双密钥光学加密方案[J]. 光学学报, 2017, 37(1): 130-137. (Cao Fei, Zhao Sheng-shu. Optical encryption scheme with double secret keys based on computational ghost imaging[J]. Acta Optica Sinica, 2017, 37(1): 130-137.)
[7]	唐晓燕, 高昆, 倪国强. 量子光谱成像技术及其在对地观测中的应用前景[J]. 航天返回与遥感, 2011, 32(5): 80-88. (Tang Xiao-yan, Gao Kun, Ni Guo-qiang. Quantum spectral imaging technology and its prospect in earth observation application[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(5): 80-88.)
[8]	Xu Z H, Chen W, Penuelas J, et al. 1000 f/s computational ghost imaging using LED-based structured illumination[J]. Optics Express, 2018, 26(3): 2427-2434. DOI:10.1364/OE.26.002427
[9]	Nie X, Yang F, Liu X, et al. Noise-robust computational ghost imaging with pink noise speckle patterns[J]. Physical Review A, 2021, 104(1): 013513. DOI:10.1103/PhysRevA.104.013513
[10]	Yang Z, Li W, Song Z, et al. Tracking compensation in computational ghost imaging of moving objects[J]. IEEE Sensors Journal, 2020, 21(1): 85-91. DOI:10.3390/s21010085
[11]	陶勇, 王肖霞, 杨风暴. 基于高通滤波鬼成像的边缘检测方法[J]. 激光与光电子学进展, 2020, 57(2): 193-198. (Tao Yong, Wang Xiao-xia, Yang Feng-bao. Edge detection based on high-pass filter ghost imaging[J]. Laser & Optoelectronics Progress, 2020, 57(2): 193-198.)
[12]	毕厚杰, 王健. 新一代视频压缩编码标准——H.264/AVC[M]. 北京: 人民邮电出版社, 2009. (Bi Hou-jie, Wang Jian. New generation video compression coding standard—HH.264/AVC[M]. Beijing: Posts & Telecom Press, 2009.)
[13]	付萍, 陈贺新, 付宁阳. 全方位钟形加权中值滤波器[J]. 电子科学学刊, 1996, 18(4): 354-361. (Fu Ping, Chen He-xin, Fu Ning-yang. Omnidirectional bell-shaped weighted median filters[J]. Journal of Electronics & Information Technology, 1996, 18(4): 354-361.)
[14]	Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095. DOI:10.1109/TIP.2007.901238
[15]	Maggioni M, Boracchi G, Foi A, et al. Video denoising, deblocking, and enhancement through separable 4-D nonlocal spatiotemporal transforms[J]. IEEE Transactions on Image Processing, 2012, 21(9): 3952-3966. DOI:10.1109/TIP.2012.2199324
[16]	谢小甫, 周进, 吴钦章. 一种针对图像模糊的无参考质量评价指标[J]. 计算机应用, 2010, 30(4): 921-924. (Xie Xiao-fu, Zhou Jin, Wu Qin-Zhang. No-reference quality index for image blur[J]. Journal of Computer Applications, 2010, 30(4): 921-924.)
[17]	Choi M G, Jung J H, Jeon J W. No-reference image quality assessment using blur and noise[J]. International Journal of Computer Science and Engineering, 2009, 3(2): 76-80.
[18]	Mittal A, Moorthy A K, Bovik A C. No-reference image quality assessment in the spatial domain[J]. IEEE Transactions on Image Processing, 2012, 21(12): 4695-4708.