
 , 石宝龙1,2, 张小霞1,2, 吴法勇4
, 石宝龙1,2, 张小霞1,2, 吴法勇4 1. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动及控制教育部重点实验室,辽宁 沈阳 110819;
3. 东北大学 佛山研究生创新学院,广东 佛山 528312;
4. 中国航发沈阳发动机研究所,辽宁 沈阳 110015
收稿日期:2021-12-14
基金项目:广东省基础与应用基础研究基金联合基金资助项目(2020B1515120015);国家自然科学基金资助项目(11872148, U1908217)。
作者简介:罗忠(1978-), 男, 内蒙古集宁人, 东北大学教授, 博士生导师。
摘要:针对航空发动机装配过程中螺栓预紧力一致性差的问题,建立螺栓连接转子有限元模型,获得螺栓在顺序拧紧和星形拧紧时预紧力的衰减规律和分布特点.进行螺栓预紧力实验研究,分析了拧紧顺序及拧紧速度对螺栓预紧力的影响,并揭示了预紧力随时间的衰减机理.结果表明:拧紧相邻螺栓会使预紧力大幅衰减;提高拧紧速度会使螺栓获得较大预紧力,使得连接结构更加稳定;螺栓拧紧后预紧力会在短时间内大幅衰减,衰减规律与扭矩幅值息息相关.因此,在发动机装配中,严格控制螺栓拧紧工艺的同时,预紧力短时间内的衰减不可忽视.
关键词:螺栓连接拧紧工艺预紧力衰减残余预紧力实验研究
Variation Law of Preload of Bolted Joint in Tightening Process
LUO Zhong1,2,3

 , SHI Bao-long1,2, ZHANG Xiao-xia1,2, WU Fa-yong4
, SHI Bao-long1,2, ZHANG Xiao-xia1,2, WU Fa-yong4 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion System, Ministry of Education, Northeastern University, Shenyang 110819, China;
3. Foshan Graduate Innovation School of Northeastern University, Foshan 528312, China;
4. AECC Shenyang Engine Research Institute, Shenyang 110015, China. Corresponding author: LUO Zhong, E-mail: zhluo@mail.neu.edu.cn
Corresponding author: LUO Zhong, E-mail: zhluo@mail.neu.edu.cn.
Abstract: Aiming at such problems as poor consistency of bolt preload in aero-engine assembly, the decline rule and distribution characteristics of bolt preload in sequential tightening and star tightening were studied based on the FEM of bolted rotors. The experimental study of bolt preload was carried out, the influence of tightening sequence and tightening speed on the bolt preload were analyzed, and then the decline mechanism of the preload over time was revealed. The results showed that the preload decreases significantly when the adjacent bolts are tightened, and increasing tightening speed will make the bolt get larger preload, which makes the connection structure more stable. After tightening the bolts, the preload will decline significantly in a short period of time, and the decline rule is closely related to the torque amplitude. Therefore, in engine assembly, the decline of preload in a short period of time cannot be ignored while strictly controlling the bolt tightening process.
Key words: bolted jointtightening processpreload declineresidual preloadexperimental research
螺栓连接是航空发动机中应用最广泛的连接方式之一,诸如在涡轮、压气机等转子结构以及机匣等静子结构中.随着发动机推重比的逐代提升,同时又要满足其高可靠性的要求,提高螺栓连接结构稳定性变得愈发关键.螺栓预紧后残余预紧力的大小及分布特征是衡量连接结构稳健性的重要指标,直接关系到发动机的装配性能及工作可靠性,而螺栓拧紧顺序以及拧紧速度等拧紧工艺,对螺栓残余预紧力具有重要影响.因此,为保证螺栓连接结构获得足够的残余预紧力,拧紧工艺的考虑以及预紧力的控制需要更加严格.
众多****从预紧力控制方法、螺栓拧紧顺序、预紧力损失方式以及工艺参数等方面,讨论了螺栓预紧力的变化规律.预紧力控制方法方面,Abid等[1]建立了三维有限元螺栓法兰连接结构模型,基于扭矩控制法和拉伸控制法,开发了一种预紧力控制算法用于获取准确的目标预应力;Persson等[2]针对单螺栓连接结构,通过实验分析了不同预紧力控制方法下的夹紧力分散程度,得出分散程度从高到低排序为扭矩法、转角法、屈服点控制法.螺栓拧紧顺序方面,Grzejda[3]分析了螺栓装配顺序对非对称螺栓法兰连接结构螺栓装配过程中和装配后的预紧力的影响;Khan等[4]以垫圈法兰连接三维有限元模型为对象,研究了受载荷作用时,不同拧紧策略下连接结构的密封性和强度;李小强等[5]研究了拧紧工艺对单螺栓预紧力变化规律的影响,研究发现转角控制法、分步拧紧法、较高的拧紧速度均可提高螺栓预紧力的一致性.预紧力损失方式方面,郑劲松[6]讨论了螺栓拧紧工艺结构参数对缸盖螺栓预紧力不一致的影响,并进一步完善了扭矩-转角拧紧工艺,大幅提高了螺栓预紧力的一致性;Alkelani等[7]基于螺栓连接数学模型,结合实验研究了螺栓间距、紧固件预紧水平和螺栓拧紧顺序等对弹性相互作用的影响,导致预紧力分散的主要原因是弹性相互作用.工艺参数条件方面,杜永强等[8]通过实验研究从螺纹接触面微观滑移和微磨损的角度分析了螺栓连接结构的松动规律.Yu等[9]基于三维有限元仿真分析了螺栓连接结构在螺栓拧紧过程中的载荷分布,并讨论了装配间隙、摩擦系数、螺距以及弹性模量等对初始载荷的影响.
综上可知,多数****从理论研究和实验操作方面对螺栓预紧力的扩散机理进行了初步探索,但对于航空发动机转子螺栓预紧力一致性的研究尚且不足,且大部分局限于螺栓剩余预紧力的分析,没有对预紧力的衰减机理做出定量描述,导致优化拧紧工艺时缺乏精准参考.
根据上述讨论,建立了螺栓连接转子结构有限元仿真模型,研究螺栓在顺序拧紧和星形拧紧时预紧力的衰减规律及残余预紧力的分布特点.开展螺栓预紧力实验研究,获得了螺栓拧紧过程中预紧力的衰减规律,并与有限元仿真结果对比,然后研究了拧紧速度对预紧力的影响,最后分析了预紧力随时间的衰减机理.结果表明,在螺栓连接结构的装配中,严格控制螺栓拧紧工艺的同时,预紧力随时间的衰减也不可忽视.
1 螺栓残余预紧力仿真分析1.1 基于ANSYS的螺栓连接转子有限元建模基于ANSYS建立螺栓连接转子结构的有限元模型如图 1所示.图 1a为实验台转子系统,图 1b为有限元模型及其主要结构尺寸,模型包括非对称的左右转轴、周向分布的24颗螺栓以及由螺栓连接的两个盘.使用SOLID185单元模拟模型的盘、螺栓及转轴等实体结构,使用CONTA174和TARGE170单元建立模型接触界面的接触关系[10].边界条件设置为:约束转轴左右端面上所有节点的全部自由度.转子结构尺寸参数和材料参数如表 1所示.
图 1(Fig. 1)
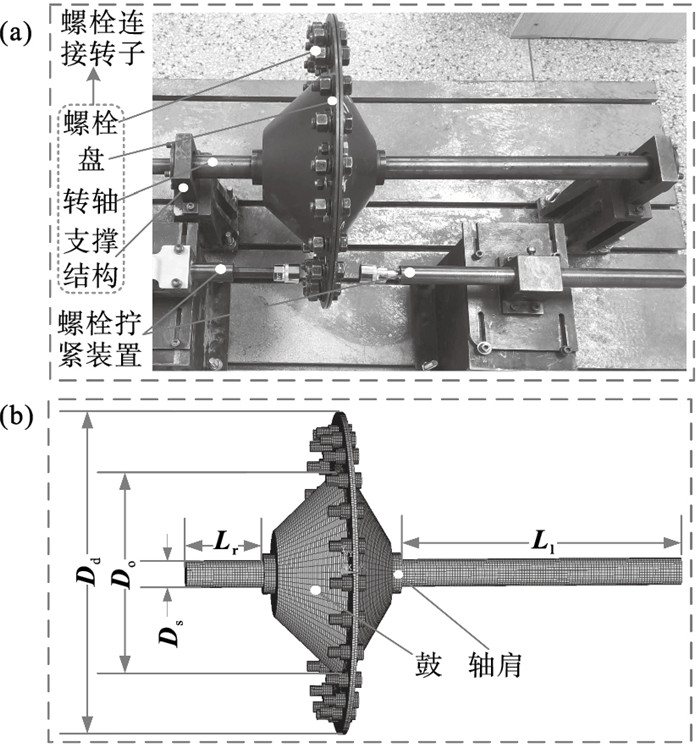 | 图 1 螺栓连接转子结构Fig.1 Bolt connected rotor structure (a)—实验台转子系统;(b)—有限元模型. |
表 1(Table 1)
| 表 1 螺栓连接转子主要参数 Table 1 Parameters of the bolted connectied rotor |
1.2 拧紧顺序对预紧力变化规律的影响在航空发动机转子系统进行装配时,涉及到大量的螺栓-盘连接结构装配,由于发动机复杂的结构特点,整个盘上的螺栓无法实现同时拧紧,因而存在多种拧紧顺序,其中顺序拧紧和星形两种拧紧顺序应用广泛,如图 2所示,两种拧紧方式的螺栓拧紧顺序均为1-2-…-23-24,其中星形拧紧的螺栓编号交叉分布.
图 2(Fig. 2)
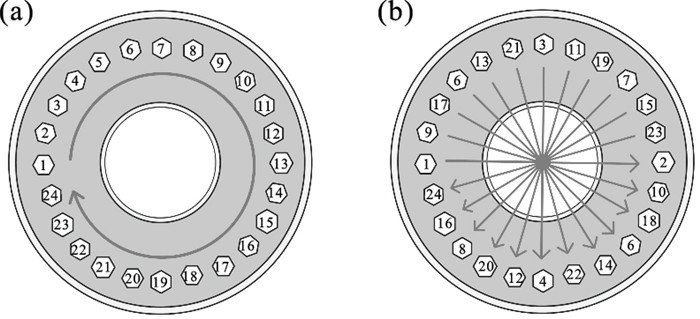 | 图 2 螺栓拧紧顺序Fig.2 Bolt tightening sequences (a)—顺序拧紧;(b)—星形拧紧. |
以图 1转子结构为研究对象,通过有限元仿真分析顺序拧紧和星形拧紧对螺栓残余预紧力的影响.为保证仿真结果的普适性,按预紧力大小分两种仿真工况:工况1,Fp=1 000 N;工况2,Fp=2 000 N.随螺栓拧紧个数的增加,由于弹性相互作用,后拧紧螺栓对已拧紧螺栓的预紧力存在一定影响.预紧力Fp=1 000 N时, 螺栓预紧力衰减曲线与残余预紧力分布如图 3所示.以顺序拧紧和星形拧紧为螺栓加载1 000 N预紧力时,前3颗拧紧螺栓的预紧力随螺栓拧紧个数的变化如图 3a和图 3b所示.不管哪种拧紧方式,随后续螺栓的拧紧,被拧紧螺栓的预紧力整体大幅衰减,最主要的衰减发生在拧紧相邻螺栓时,即如图 3a所示的顺序拧紧时,拧紧最后1颗螺栓对第1颗螺栓预紧力的影响远大于第2颗和第3颗.不同于顺序拧紧,星形拧紧某些位置的螺栓时,前3颗螺栓的预紧力随后续螺栓的拧紧会出现一定程度上的增加.全部螺栓完成拧紧时,2种拧紧顺序下各螺栓残余预紧力的分布曲线如图 3c所示,其中星形拧紧的残余预紧力分布曲线呈上下波动.
图 3(Fig. 3)
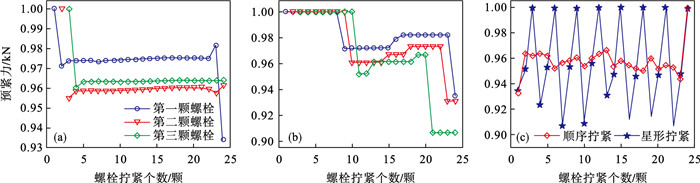 | 图 3 预紧力Fp=1 000 N时螺栓预紧力衰减曲线与残余预紧力分布Fig.3 Decline curves of bolt preload and distribution of residual preload when preload Fp=1 000 N (a)—顺序拧紧时预紧力衰减曲线;(b)—星形拧紧时预紧力衰减曲线;(c)—两种拧紧顺序下各螺栓最终预紧力. |
预紧力Fp=2 000 N时,螺栓预紧力衰减曲线与残余预紧力分布如图 4所示.由图可知,Fp=1 000 N与Fp=2 000 N时的结果几乎一致.
图 4(Fig. 4)
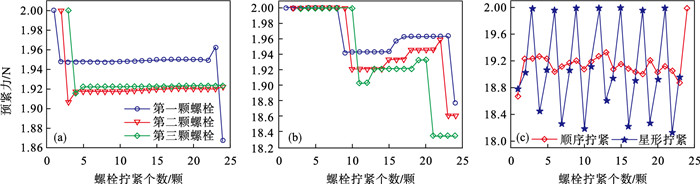 | 图 4 预紧力Fp=2 000 N时螺栓预紧力衰减曲线与残余预紧力分布Fig.4 Decline curves of bolt preload and distribution of residual preload when preload Fp=1 000 N (a)—顺序拧紧时预紧力衰减曲线;(b)—星形拧紧时预紧力衰减曲线;(c)—两种拧紧顺序下各螺栓最终预紧力. |
Coria等[11]得出星形拧紧时螺栓的残余预紧力分布曲线在一定范围内呈上下波动.出现这样的现象是因为存在弹性相互作用的影响,星形拧紧时最先拧紧的8棵螺栓受后续拧紧的16颗螺栓的影响最大,其预紧力衰减最多,接下来拧紧的8~16颗螺栓次之,先拧紧的螺栓均匀分布,使盘均匀变形,结合面粗糙度和摩擦系数降低,最后拧紧的8颗螺栓的预紧力几乎与目标预紧力一致.
为进一步分析所得残余预紧力特征,得到表 2所示不同预紧力幅值下残余预紧力平均值Fa、预紧力衰减比η和残余预紧力标准差Fst.3个特征参数见式(1).
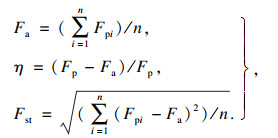 | (1) |
| 表 2 不同预紧力下特征参数对比 Table 2 Comparison of characteristic parameters under different preloading forces | ||||||||||||||||||||||||||
式中: Fpi为第i颗螺栓残余预紧力; n为螺栓总个数; Fp为加载的预紧力.
由表 2可知,顺序拧紧和星形拧紧的残余预紧力平均值和预紧力衰减比相差无几,但顺序拧紧的残余预紧力标准差远小于星形拧紧,随加载预紧力的增加,两种拧紧顺序的残余预紧力标准差几乎都在成倍增加.
单从特征参数来看,顺序拧紧时螺栓残余预紧力分布更加均匀,对应的连接结构预紧效果更好.大量研究表明,星形拧紧时螺栓残余预紧力扩散较小,无论从连接结构的应力状态还是残余预紧力的角度分析,星形拧紧的连接性能更加优越[12].结合图 3c和图 4c所得结果,对螺栓分布较多的连接结构,星形拧紧时一部分螺栓的残余预紧力值接近于加载值,且螺栓位置分布均匀,在一定程度上能提高连接结构的性能.
2 拧紧工艺对预紧力的影响2.1 拧紧顺序对预紧力衰减规律的影响基于ANSYS仿真可以高效且较为准确地分析螺栓预紧力的变化规律,但不能完全考虑真实的环境条件,有必要从实验角度作进一步分析,同时验证仿真结果的准确性.
螺栓残余预紧力实验测试系统如图 5所示,控制器控制拧紧枪以扭矩的形式为盘外圈的螺栓加载一定的预紧力,由测力传感器采集压力信号,信号经过放大并转换为预紧力的形式显示.
图 5(Fig. 5)
 | 图 5 残余预紧力实验测试系统Fig.5 Test system of residual preload |
实验过程:控制拧紧枪以10 N·m的扭矩按顺序拧紧的方式装配螺栓,随螺栓逐个拧紧,采集拧紧每颗螺栓时第1颗拧紧螺栓的预紧力值;以星形拧紧的方式装配螺栓,完成与顺序拧紧相同的采集操作,两种拧紧方式的预紧力衰减曲线如图 6所示.
图 6(Fig. 6)
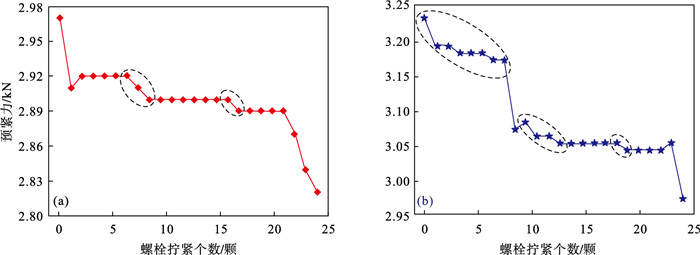 | 图 6 螺栓预紧力衰减曲线Fig.6 Decline curve of bolt preload (a)—顺序拧紧;(b)—星形拧紧. |
由图 6可知,在拧紧与第1颗螺栓相近的螺栓时,两种拧紧顺序下的第1颗螺栓预紧力都会大幅衰减,且衰减位置与仿真时的相同.不同于仿真,除了拧紧第1颗螺栓附近的螺栓外,拧紧其他位置的螺栓会使第1颗螺栓预紧力出现明显衰减,如圈内曲线所示.星形拧紧完成时预紧力衰减了260 N,远大于顺序拧紧时的150 N.这可能是因为螺栓与被连接件受力发生弹塑性变形,使得螺栓拧紧后预紧力在短时间内发生了自行衰减,而顺序拧紧时第2颗拧紧的螺栓与第1颗相邻,一定程度上阻止了预紧力随时间的衰减.
2.2 拧紧速度对螺栓预紧力的影响文献[13]提出,在螺栓拧紧时,由于接触面并非光滑,拧紧时接触面的相对滑移会产生微观磨损,使得接触面温度升高.拧紧速度不同时,表面磨损及表面温度均不同,表面摩擦系数会随之改变,进而影响预紧力.因此,研究拧紧速度对螺栓预紧力的影响十分必要.
基于图 5所示的预紧力测试系统,以单螺栓为研究对象,螺栓扭矩分别5, 10, 15, 20, 25 N·m,拧紧速度分别为20,40,60,80,100,120 r/min,采集各扭矩在不同拧紧速度下的预紧力,预紧力随拧紧速度的变化曲线如图 7所示.
图 7(Fig. 7)
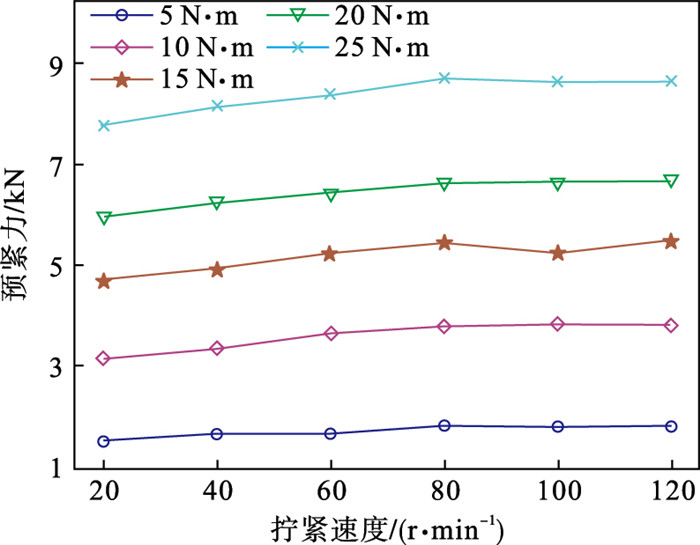 | 图 7 预紧力随拧紧速度的变化曲线Fig.7 Variation of preload with tightening speed |
由图 7可知,整体上各扭矩下螺栓的预紧力随拧紧速度的增加而增加,但在拧紧速度高于80 r/min时,这种增加趋势不再明显,扭矩大时更加无序.
由文献[5]可知,为螺栓施加扭矩进行拧紧时,加载的扭矩T等于螺纹副摩擦力矩T1、螺栓与被连接件接触面间的端面摩擦力矩T2之和见式(2):
 | (2) |
由式(2)可得:
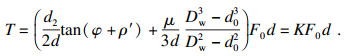 | (3) |
由式(3)可知,当加载扭矩T不变时,F0增加,d恒定,扭矩系数K随拧紧速度的增加而减小.扭矩系数K与接触面加工精度、表面温度等有关,提高拧紧速度,会使接触面温度升高、磨损加快,接触面趋于平整光滑,扭矩系数减小,进而提高了连接结构的稳定性.受限于工艺稳定性及拧紧装置精度等技术要求,实际操作中拧紧速度并非越高越好.大扭矩下拧紧速度高于80 r/min时,预紧力的变化不明显.
3 螺栓预紧力随时间衰减机理由文献[14]可知,在实际操作中,螺栓完成拧紧后预紧力会在一段时间内发生很大程度的降低,造成获得的预紧力不足进而导致连接结构工作性能的不稳定.因此对于图 1所示螺栓连接转子结构而言,研究螺栓拧紧顺序对预紧力在短时间内衰减机理的影响具有重要意义.
设定30 N·m拧紧扭矩,分别以顺序拧紧和星形拧紧两种螺栓拧紧顺序,将图 5中连接结构的全部螺栓拧紧,在拧紧最后一颗螺栓的同时开始检测该螺栓预紧力随时间的变化规律.分别采集最后1颗螺栓0,10,30 s及1,2,…,10 min时的预紧力,两种拧紧顺序下预紧力随时间的衰减曲线如图 8所示.
图 8(Fig. 8)
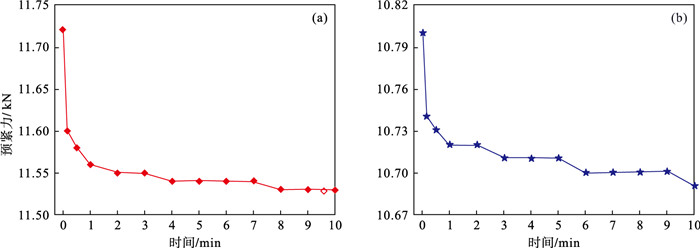 | 图 8 预紧力随时间的衰减曲线Fig.8 Decline curve of preload with time (a)—顺序拧紧;(b)—星形拧紧. |
由图 8可知,螺栓预紧力在拧紧后的10 min内发生了很大程度的衰减,其中最主要的衰减发生在螺栓拧紧后的前1 min;螺栓在顺序拧紧时预紧力10 min内衰减了190 N,而星形拧紧只衰减了110 N.在实际应用中,螺栓星形拧紧后预紧力的扩散程度远小于顺序拧紧,相应的连接结构装配性能更加稳定,如文献[12]所述,螺栓星形拧紧时预紧效果更好.
进一步研究各扭矩下螺栓预紧力随时间的衰减情况.以图 5测试系统中的单螺栓为研究对象,研究分别以10, 20, 30, 40 N·m拧紧螺栓时预紧力随时间的衰减规律,预紧力采集时间节点与上述一致,不同扭矩下预紧力随时间的衰减曲线如图 9所示.
图 9(Fig. 9)
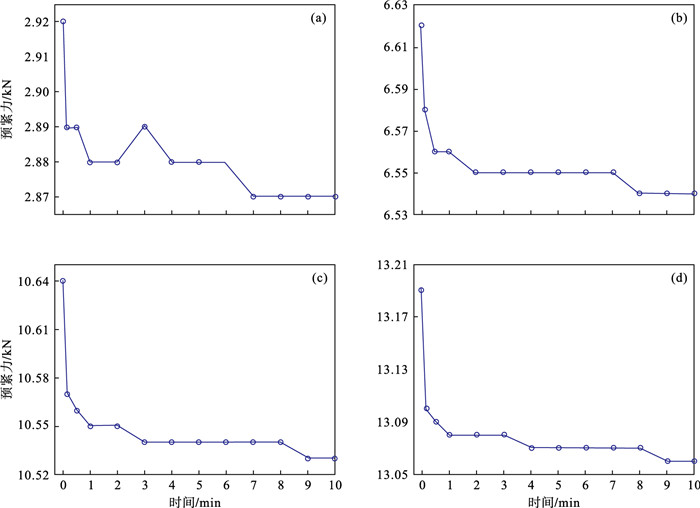 | 图 9 不同扭矩下预紧力随时间的衰减曲线Fig.9 Decline curve of preload with time under different torques (a)—10 N·m;(b)—20 N·m;(c)—30 N·m;(d)—40 N·m. |
不难发现,预紧力的衰减主要发生在前几分钟,后几分钟螺栓预紧力基本趋于稳定;同时各扭矩下预紧力衰减规律基本一致,符合指数或幂函数形式.预紧力之所以衰减,是因为拧紧时螺栓与被拧紧工件发生了弹塑性变形,微观组织产生了位错、滑移等微观运动,同时接触表面微凸体受挤压逐渐减小,导致预紧力发生衰减.
不同扭矩下螺栓的预紧力衰减比如表 3所示,可知,各扭矩下预紧力整体衰减比均在1%左右,且随扭矩增加,衰减比小幅降低.
表 3(Table 3)
| 表 3 不同扭矩下预紧力衰减比例 Table 3 Ratio of preload decline under different torques |
不同扭矩下各时间段预紧力衰减数值占总衰减值的比例如图 10所示,前5 min预紧力衰减接近90%;前10 s内预紧力衰减占比约三分之二.随扭矩增大,各阶段衰减占比略微提高.扭矩为40 N·m时,前5 min的衰减比已达到92.3%,结合表 3可推断,螺栓预紧力扩散程度随扭矩增加而减小,扩散周期随扭矩增加而变短.
图 10(Fig. 10)
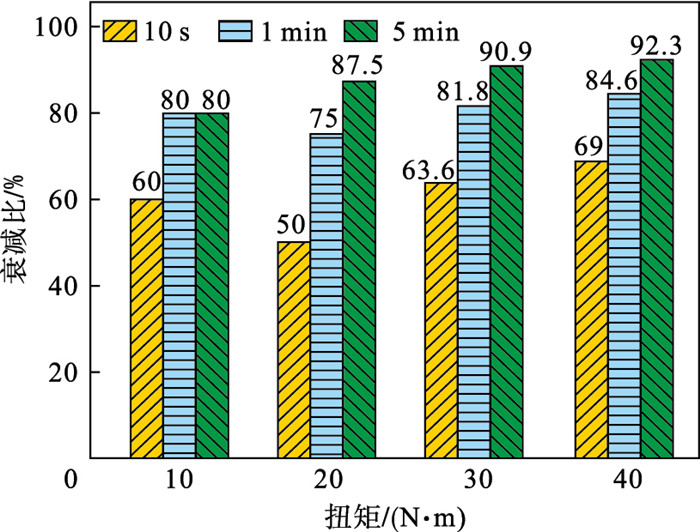 | 图 10 不同扭矩各时间段衰减比Fig.10 Decline ratio of different torques at intervals |
综上所述,在航空发动机中的螺栓-盘连接结构装配时,由于存在弹性相互作用,应尽量避免先拧紧相邻螺栓而导致预紧力大幅衰减,适当增加螺栓拧紧速度可以提高预紧力一致性;采用星形拧紧方式拧紧螺栓,并尽可能缩短螺栓装配时间,可有效减少预紧力随时间的衰减.
4 结论1) 以顺序拧紧和星形拧紧相邻螺栓时,螺栓预紧力均会大幅衰减,不同预紧幅值下螺栓衰减规律以及残余预紧力分布几乎相同,顺序拧紧时螺栓残余预紧力分布标准差小于星形拧紧.
2) 提高拧紧速度会使螺栓预紧力增加的同时扭矩系数K减小,进而提高连接结构稳定性,但在拧紧速度高于80 r/min时趋势不再明显.
3) 螺栓拧紧后预紧力会在短时间内发生明显的衰减现象,螺栓拧紧后预紧力在前10 s内衰减占比高达三分之二,而星形拧紧可大幅降低这种衰减.随扭矩增加,预紧力衰减程度减小,衰减周期变短.因此,采用星形拧紧的方式并施加较大的拧紧力矩可有效降低螺栓预紧力随时间的衰减.
参考文献
| [1] | Abid M, Khan A, Nash D H. Optimized bolt tightening strategies for gasketed flanged pipe joints of different size[J]. International Journal of Pressure Vessels & Piping, 2016, 139(3): 22-37. |
| [2] | Persson E, Roloff A. Ultrasonic tightening control of a screw joint: a comparison of the clamp force accuracy from different tightening methods[J]. Proceedings of the Institution of Mechanical Engineers. Part C: Journal of Mechanical Engineering Science, 2015, 230(15): 2595-2602. |
| [3] | Grzejda R. Analysis of the tightening process of an asymmetrical multi-bolted connection machine dynamics research[J]. Machine Dynamics Research, 2015, 39(3): 25-32. |
| [4] | Khan N B, Abid M, Jameel M. Joint strength of gasketed bolted pipe flange joint under combined internal pressure plus axial load with different(industrial and ASME)bolt-up strategy[J]. Proceedings of the Institution of Mechanical Engineers. Part E: Journal of Process Mechanical Engineering, 2017, 231(3): 555-564. DOI:10.1177/0954408915614460 |
| [5] | 李小强, 孟庆阔, 杜一凡, 等. 拧紧策略对航空发动机单螺栓连接预紧力的影响[J]. 机械工程学报, 2020, 56(13): 231-241. (Li Xiao-qiang, Meng Qing-kuo, Du Yi-fan, et al. Influence of tightening strategy on pre-tightening force of aero-engine single-bolt connection[J]. Journal of Mechanical Engineering, 2020, 56(13): 231-241.) |
| [6] | 郑劲松. 发动机缸盖螺栓拧紧工艺与实验研究[D]. 上海: 上海交通大学, 2008. (Zheng Jin-song. Studies on techniques and experiments of the bolts tightening for engine's cylinder head[D]. Shanghai: Shanghai Jiao Tong University, 2008. ) |
| [7] | Alkelani A A, Nassar S A, Housari B A. Formulation of elastic interaction between bolts during the tightening of flat-face gasketed joints[J]. Journal of Mechanical Design, 2009, 131(2): 519-528. |
| [8] | 杜永强, 刘建华, 刘学通, 等. 偏心载荷作用下螺栓连接结构的松动行为研究[J]. 机械工程学报, 2018, 54(14): 74-81. (Du Yong-qiang, Liu Jian-hua, Liu Xue-tong, et al. Research on self-loosening behavior of bolted joints under eccentric excitation[J]. Journal of Mechanical Engineering, 2018, 54(14): 74-81.) |
| [9] | Yu Q, Zhou H, Wang L. Finite element analysis of relationship between tightening torque and initial load of bolted connections[J]. Advances in Mechanical Engineering, 2015, 7(5): 1-8. |
| [10] | Liu S G, Ma Y H, Zhang D Y. Studies on dynamic characteristics of the joint in the aero-engine rotor system[J]. Mechanical Systems and Signal Processing, 2012, 29: 120-136. |
| [11] | Coria I, Abasolo M, Aguirrebeitia J, et al. Study of bolt load scatter due to tightening sequence[J]. International Journal of Pressure Vessels and Piping, 2020, 182(C): 104054. |
| [12] | 聂晓东, 胡军, 李旋旋, 等. 拧紧工艺对螺栓预紧力影响的实验研究[J]. 中国工程机械学报, 2019, 17(1): 75-78. (Nie Xiao-dong, Hu Jun, Li Xuan-xuan, et al. Experimental study of tightening process effect to bolt preload[J]. Chinese Journal of Mechanical Engineering, 2019, 17(1): 75-78.) |
| [13] | 王晓斌, 蒋佳桉, 陈平, 等. 拧紧转速对螺栓联接可靠性分析[J]. 机电工程技术, 2016, 45(3): 101-104. (Wang Xiao-bin, Jiang Jia-an, Chen Ping, et al. Reliability analysis of tightening speed on the bolt connection[J]. Mechanical & Electrical Engineering Technology, 2016, 45(3): 101-104.) |
| [14] | Nechache A, Bouzid A H. On the use of plate theory to evaluate the load relaxation in bolted flanged joints subjected to creep[J]. International Journal of Pressure Vessels and Piping, 2008, 85(7): 486-497. |
