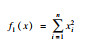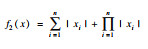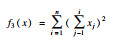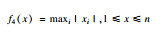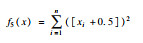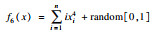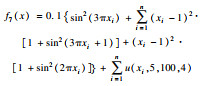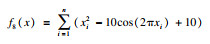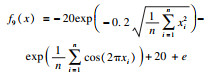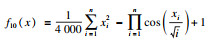, 张婷1, 刘永刚2, 陈晶1
, 张婷1, 刘永刚2, 陈晶1 1. 长安大学 道路施工技术与装备教育部重点实验室,陕西 西安 710064;
2. 河南卫华重型机械有限公司,河南 长垣 453400
收稿日期:2021-12-11
基金项目:陕西省自然科学基金资助项目(2019JQ-556, 2022JQ-576, 2022JM-295);河南省博士后科研项目启动资助;陕西省国际科技合作项目(2019KW-015)。
作者简介:陈一馨(1984-),女,甘肃天水人,长安大学副教授,研究生导师。
摘要:针对樽海鞘群算法在优化过程中存在收敛速度慢、求解精度低、易于陷入局部最优解等缺点,提出了基于柯西和高斯混合变异的一种自适应变异策略的樽海鞘群算法,该算法通过选出适应度值最好的前S个个体进行自适应变异,可避免算法陷入局部最优解.通过柯西和高斯变异动态调整参数的变化提高算法的局部搜索能力和收敛速度.选取10个测试函数分别对樽海鞘群算法及改进樽海鞘群算法进行测试比较.数值分析表明,改进的樽海鞘群算法收敛速度快,寻优能力强且精度高.将改进后的算法用于提梁机主梁结构的优化设计中,该结构在满足强度、刚度、稳定性等设计要求条件下,主梁的截面积减少了13.58%,轻量化效果显著,表明该算法具有良好的工程应用价值.
关键词:樽海鞘群算法自适应变异策略柯西变异高斯变异提梁机主梁轻量化
Lightweight Design Method of Girder Hoist Based on Improved Salp Swarm Algorithm
CHEN Yi-xin1,2

 , ZHANG Ting1, LIU Yong-gang2, CHEN Jing1
, ZHANG Ting1, LIU Yong-gang2, CHEN Jing1 1. Key Laboratory of Road Construction Technology & Equipment, Ministry of Education, Chang'an University, Xi'an 710064, China;
2. Henan Weihua Heavy Machinery Co., Ltd., Changyuan 453400, China
Corresponding author: CHEN Yi-xin, E-mail: chenyx@chd.edu.cn.
Abstract: In view of the disadvantages of slow convergence, low solution accuracy and tendencies to fall into local optimal solutions in the optimization process, an improved adaptive mutation strategy of salp swarm algorithm based on Cauchy and Gaussian mixture mutation was proposed. The algorithm tend not to fall into local optimal solution by selecting the first S individuals with the best fitness value for adaptive variations, and the local search capability and convergence speed of the algorithm is improved by dynamically adjusting the size variation of the parameters through the Cauchy and Gaussian variants. Ten test functions were selected to test and compare the salp swarm algorithm and the improved adaptive mutation salp swarm algorithm respectively. Numerical analysis showed that the improved salp swarm algorithm has fast convergence speed, strong search ability and high accuracy. The improved algorithm was applied to the optimization design of the main beam structure of the beam lifter. Under the condition of meeting the design requirements of strength, stiffness and stability, etc., the cross-sectional area of the main beam is reduced by 13.58 %, and the weight reduction effect is significant, indicating that the algorithm has good engineering application value.
Key words: salp swarm algorithmadaptive mutation strategyCauchy mutationGaussian mutationgirder hoistweight reduction
樽海鞘群算法(salp swarm algorithm, SSA)[1]是Mirjalili等受到樽海鞘在海洋中的群体行为的启发,于2017年提出一种新型的智能优化算法.与布谷鸟算法、海鸥算法及鲸鱼算法等相比较,樽海鞘群算法数学模型简单,寻找最优解时的原理简单且算法中所涉及参数较少[2],被广泛应用于多个专业方向.张凡等[3]把樽海鞘群算法应用于电力系统最优潮流问题的求解中,研究了樽海鞘群算法适应度值较好的领导者个体个数对计算结果的影响.沈平等[4]把布谷鸟算子引入到樽海鞘群算法中,用于优化可见光通信多载波调制器的参数,提高了传输速率.刘景森等[5]提出了一种新的改进樽海鞘群算法,其融合了有效缩放和随机交叉策略的自适应动态角色,并将改进算法应用于一些较复杂的工程优化设计问题当中,例如求解焊接梁、压力容器、三杆桁架.经测试结果对比分析,证明改进后的算法在问题适应性、寻优稳定性和收敛速度方面都得到了改善.王秋萍等[6]提出一种多策略集成的改进樽海鞘群算法,将其应用于机器人路径规划中,获得了最短的安全路径.刘芳瑞等[7]将Tent映射和惯性权重结合于樽海鞘群算法中,应用于垃圾邮件分类的案例中,采用增强算法优化分类器参数,提高了垃圾邮件分类的准确度和辨识度.陈涛等[8]将樽海鞘群算法应用于无源时差定位的非线性问题中,SSA在搜索边界也能够快速稳定地收敛至目标值.与其他群智能算法一样,收敛速度慢、收敛精度低及易陷入局部最优解,这些缺陷的存在也限制了其应用范围.
鉴于樽海鞘群算法存在的缺点,采用诸多措施对其进行改进.王彦军等[9]提出一种结合精英反向学习策略、差分策略及Gauss变异的樽海鞘群算法,通过测试函数及焊接梁工程优化实例分析,发现改进后的算法提高了寻优速度及最优解的精度.陈连兴等[10]通过将加权重心引入领导者位置更新公式并将自适应权重引入追随者位置更新公式中,降低了领导者对自身的依赖,提升了算法的全局搜索和局部寻优能力,最后对个体进行逐维随机差分变异,提高了种群的多样性.白珏等[11]通过引入惯性权重因子对追随者的位置进行更新并结合种群成功率与非线性递减函数来平衡算法的全局和局部搜索能力,引入差分变异思想对非最优个体进行变异,避免算法陷入局部最优解.陈忠云等[12]利用正弦、余弦算法对樽海鞘个体进行正弦和余弦优化并对领域空间进行差分演化变异策略来增强算法局部搜索能力.刘景森等[13]将上一代领导者更新的位置加入到新的位置更新公式中,并在此基础上加入惯性权重来增加算法搜索的充分性;通过引入领导者-跟随者数量自适应调整策略来提高算法的收敛速度.Faris等[14]用8种不同的传递函数将SSA从连续型转换为离散型二进制,在此基础上引入交叉算子进行更新,提高了算法的搜索能力,与已有的5种特征选择方案进行比较,优化效果显著.Sayed等[15]提出了一种基于混沌理论的SSA,利用混沌映射转换而来的混沌变量对影响更新位置的参数进行一定的优化,提高了寻找最优特征子集的能力,提升了算法的全局搜索能力.Wu等[16]在基本SSA中引入动态权重因子和自适应突变策略,通过变异概率的变化,提高了全局搜索能力,增强了算法跳出局部最优解的能力.Wang等[17]利用单纯形法对樽海鞘的最坏位置进行更新,提高了算法的收敛速度,增加了种群的多样性.陈忠云等[18]在初始种群中引入改进的混沌序列,可以增强初始种群的多样性,同时选取当前最优个体对其采用精英质心拉伸机制,提高了算法的搜索能力.
到目前为止,已有很多方法来改进SSA,在一定程度上均提升了算法的性能.针对基本SSA存在的问题,本文从3个方面提出了改进方法:
1) 基于黄金正弦算法的原理,引入黄金分割系数对领导者位置进行更新,提高了全局搜索能力;
2) 融合柯西变异对最优个体附近产生一个随机扰动来增加种群多样性,避免陷入局部最优解;
3) 提出一种柯西与高斯混合变异的自适应变异策略改进算法,主要对种群中适应度值最好的前S个个体进行变异操作,增强了算法跳出局部最优解的能力,柯西和高斯变异的动态调整参数的大小变化提高了算法的搜索能力和收敛精度.
选取10个标准测试函数分别对原始樽海鞘群算法、基于黄金正弦的樽海鞘群算法、基于柯西变异的樽海鞘群算法以及基于柯西和高斯混合变异的自适应变异策略来改进樽海鞘群算法,对收敛速度、寻优精度及时间复杂度进行测试.最后,将改进后的算法用于提梁机主梁结构的轻量化设计.
1 樽海鞘群算法及其改进方法1.1 樽海鞘群算法(SSA)樽海鞘群算法源于樽海鞘在移动和觅食时的链式群行为,如图 1所示.在樽海鞘链中存在领导者和追随者,领导者位于樽海鞘链的最前端,朝着食物移动并且引导追随者的移动,追随者互相跟随,种群通过个体间的互相协作寻找全局最优位置[1],即食物源位置.
图 1(Fig. 1)
 | 图 1 樽海鞘链[1]Fig.1 Salp chain[1] |
SSA的基本原理和算法步骤如下所述:
步骤1种群初始化,根据搜索空间里每一维对应的上、下限值,确定初始樽海鞘的位置为
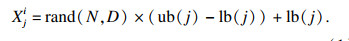 | (1) |
步骤2计算个体的适应度值,并对其进行排序.
步骤3选取适应度值排序中最优的樽海鞘的位置作为初始食物源位置.
步骤4通过更新式(2)变换樽海鞘群中领导者的位置:
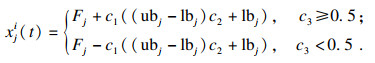 | (2) |
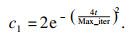 | (3) |
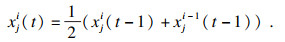 | (4) |
1.2 融合黄金正弦的樽海鞘群算法(GSSSA)黄金正弦算法(golden sine algorithm)是Tanyildizi等[19]提出的一种新型元启发式算法,该算法利用正弦函数和黄金分割系数的数学模型进行位置更新求解,在算法迭代过程中,通过式(5)更新领导者的位置:
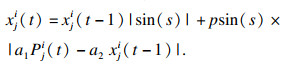 | (5) |
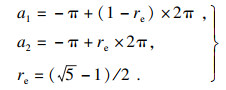 | (6) |
1.3 融合柯西变异的樽海鞘群算法(CSSA)结合柯西变异算子, 改进樽海鞘群算法,使其个体具备能迅速逃离局部极值的能力,由于柯西分布函数的特点,樽海鞘群个体在变异后会把更多的时间放在搜寻全局最优值上,使得改进后的樽海鞘群算法在寻找全局最优解时具备最好的调节能力,并对樽海鞘群最优个体产生一个随机扰动,扩大分布函数的范围, 增加种群的多样性,增强跳出局部最优解的能力.标准柯西分布函数式为
 | (7) |
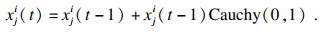 | (8) |
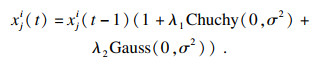 | (9) |
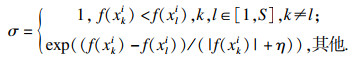 | (10) |
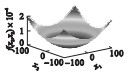
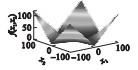
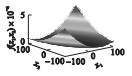
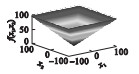
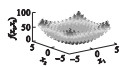
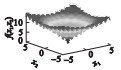
2 SSA,GSSSA,CSSA及CGSSA算法比较分析2.1 测试函数选择采用10个标准测试函数对SSA,GSSSA,CSSA,CGSSA 4种算法进行性能测试,测试函数式、函数图及参数设置如表 1所示.
表 1(Table 1)
| 表 1 测试函数及参数设置 Table 1 Test function and parameter setting |
2.2 收敛速度和寻优精度的测试结果与分析原始算法结合柯西和高斯混合变异的自适应变异策略不仅提高了算法的局部开发能力,扩大了搜索范围,而且避免了算法过早收敛,降低了算法陷入局部最优解的概率.利用表 1中的测试函数进行4种算法的测试,选择种群大小为50,迭代500次,运行30次,对运行结果进行统计,获得各算法运行所得30组最优值的最小值、最大值、平均值、标准差和变异系数,测试结果曲线图和测试结果见图 2和表 2.
图 2(Fig. 2)
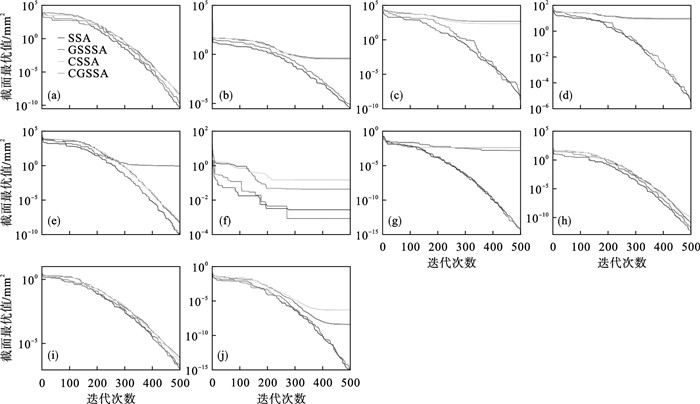 | 图 2 基于10个标准测试函数的算法迭代图Fig.2 Iteration graph of each algorithm based on 10 standard test functions (a)—f1(x);(b)—f2(x);(c)—f3(x);(d)—f4(x);(e)—f5(x);(f)—f6(x);(g)—f7(x);(h)—f8(x);(i)—f9(x);(j)—f10(x). |
表 2(Table 2)
| 表 2 测试结果 Table 2 Test results |
在上述测试函数中,f1~f6为单峰函数,均仅有唯一的全局最小值,没有局部极值,可以用来评价算法的开发能力.由图 2中的测试函数f1~f5测试结果可知,CGSSA呈指数级下降,相比其他算法,收敛速度较快,GSSSA整体也呈指数级下降趋势,但比CGSSA下降速度慢,同时在测试函数f5中收敛速度明显下降.f7~f10为多峰函数,均会产生一定量的局部极值,但全局最优解仅有一个,可用来评价算法的搜索能力.由图 2可知,测试函数f7~f10迭代曲线趋势大致相同.由表 2数据分析可知,在上述分析的10个测试函数中,CGSSA在6个测试函数中的平均值和5个测试函数中标准差均为最小,收敛速度较快,收敛精度较高.在寻找最优解时,在9个测试函数中,CGSSA均为最小值,而GSSSA仅在1个测试函数上为最小值,CSSA和原始SSA均未取得最小值,寻找最优解能力还有待提高.变异系数同标准差一样可以反应数据的离散程度,但变异系数与平均值有很大关系,当平均值非常接近于0时,很微小的变动也会给变异系数造成较大误差.CGSSA的平均值非常接近于0,导致测试函数f2,f3计算所得的变异系数较大.其余测试函数变异系数较小,说明CGSSA的鲁棒性较好.但变异系数不应单独作为评价算法好坏的标准,应将表 2中所有数据结合起来分析算法的可行性.
综上所述,4种算法中CGSSA有较高的收敛精度和收敛速度,选择CGSSA对提梁机主梁进行轻量化设计.
2.3 改进后算法的时间复杂度分析时间复杂度是指执行算法时的运行时间,是判断算法性能的关键指标之一.改进算法的种群数量为N,空间维度为D,最大迭代次数为Max_iter,目标函数计算量假设为M,则可知SSA的时间复杂度为O(Max_iter(N·D+N·M))[11].
由CGSSA步骤可知,在算法迭代一次时,增加的时间复杂度为O(N/2),因此,CGSSA算法在进行Max_iter迭代后,时间复杂度为O(Max_iter(N·D+N·M+N/2)).根据时间复杂度的计算规则,不包括此函数的最低项和首项系数,所以CGSSA的时间复杂度为O(Max_iter(N·D+N·M)).CGSSA和SSA的时间复杂度一样,在数量级上没有增加,即未增加多余的计算量,算法的执行速度没变.
3 提梁机主梁轻量化设计3.1 优化数学模型的建立5 000 kN提梁机的结构如图 3所示.提梁机主梁结构由两个主梁结构及连接主梁的两个横梁组成.起重机主梁为箱形截面,由上下盖板、腹板、加劲肋和横隔板焊接而成.在满足设计强度、刚度和稳定性的前提下,主梁质量最轻,截面面积最小,建立优化目标主函数:
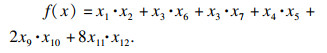 | (11) |
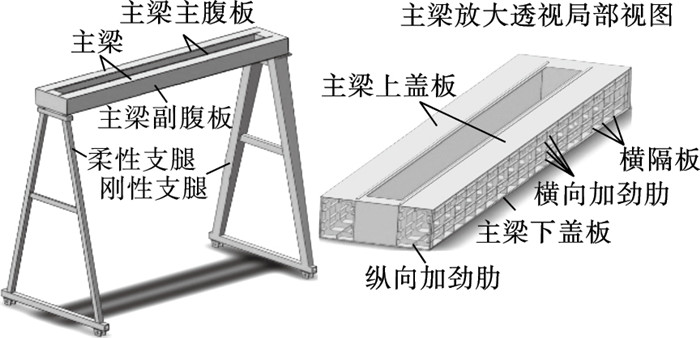 | 图 3 提梁机结构图Fig.3 Structure diagram of girder hoist |
式中:x1,x2为上盖板宽度和厚度;x4,x5为下盖板厚度和宽度;x3,x6为副腹板高度和厚度;x3,x7为主腹板的高度和厚度;x8为腹板间距;x9,x10为上、下盖板加劲肋的厚度和宽度;x11,x12为腹板加劲肋宽度和厚度;x13为加劲肋与下盖板间距;x14为加劲肋间的距离.
3.2 约束函数3.2.1 强度准则1) 弯曲应力:根据约束函数σ-[σ]≤0可知,跨中截面翼缘板角点最大弯曲正应力σ为
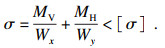 | (12) |
图 4(Fig. 4)
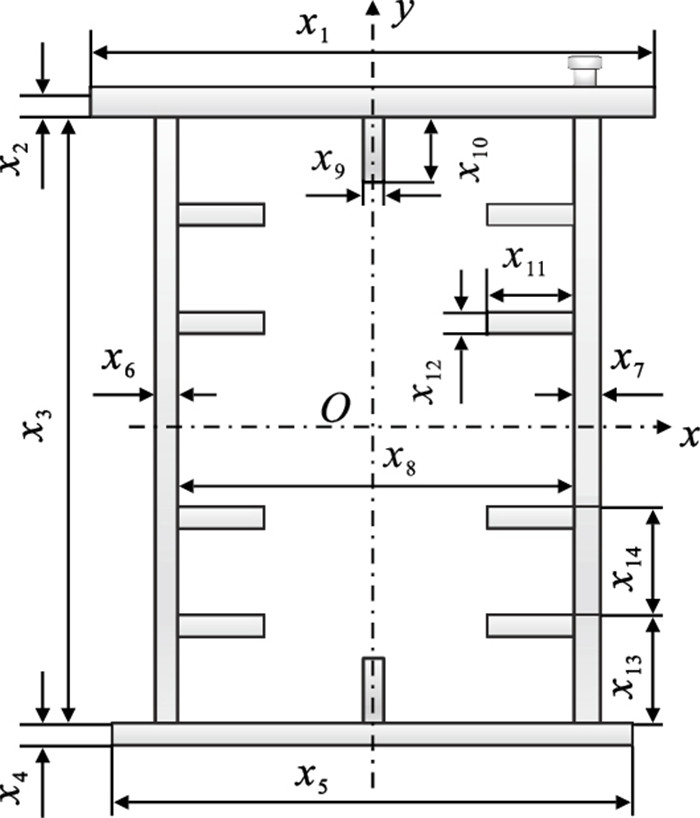 | 图 4 主梁截面图Fig.4 Diagram of main beam's cross section |
图 5为主梁在垂直方向上的受力示意图.
图 5(Fig. 5)
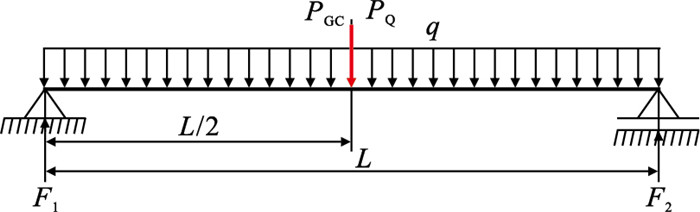 | 图 5 主梁垂直方向受力示意图Fig.5 Diagram of vertical force on main girder |
主梁在垂直方向跨中的弯矩为
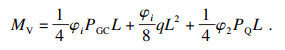 | (13) |
主梁在水平方向受力分析如图 6所示.
图 6(Fig. 6)
 | 图 6 主梁水平方向受力示意图Fig.6 Diagram of horizontal force on main girder |
由大车水平惯性力PDG和桥架惯性力qG引起的跨中水平弯矩为
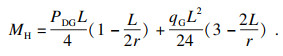 | (14) |
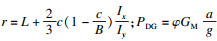
在偏载工况下,主梁受力分析如图 7所示,主梁所受剪力最大,其值为F1与F2中的较大值.
图 7(Fig. 7)
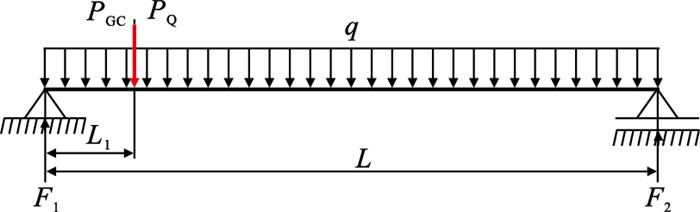 | 图 7 偏载工况下主梁受力示意图Fig.7 Force diagram of main beam under eccentric load condition |
根据以上受力分析,力及力矩平衡式为
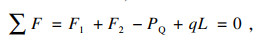 | (15) |
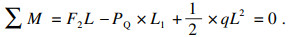 | (16) |
2) 主、副腹板的剪应力强度:因主、副腹板的板厚不同,根据约束函数
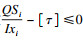
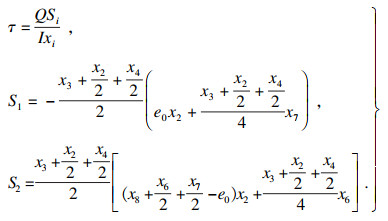 | (17) |
3.2.2 刚度准则根据约束函数f-[f]≤0,挠度应满足
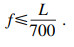 | (18) |
3.2.3 稳定性校核通过宽厚比值进行受压翼缘板的稳定性校核.当宽度较大时,应设置纵向加劲肋,降低宽厚比,由加劲肋划分出来的区格应满足:
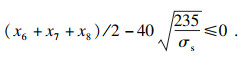 | (19) |
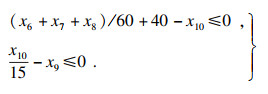 | (20) |
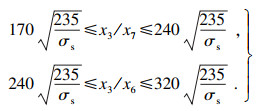 | (21) |
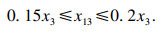 | (22) |
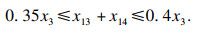 | (23) |
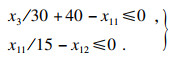 | (24) |
图 8(Fig. 8)
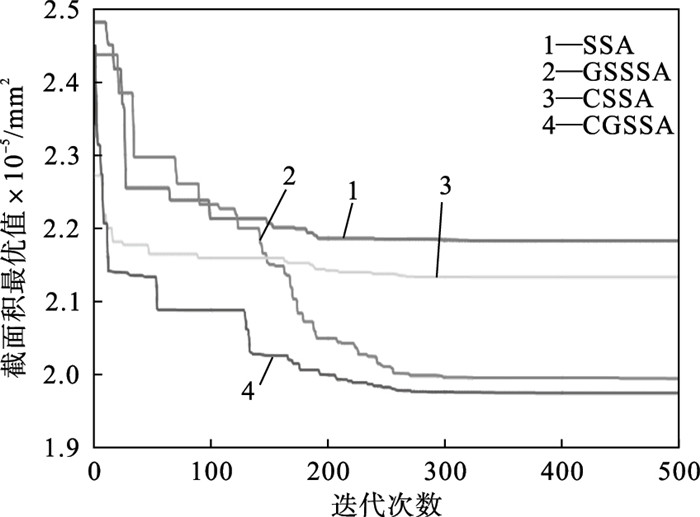 | 图 8 各个算法最优值迭代计算图Fig.8 Optimal value iterative calculation diagram of each algorithm |
3.3.2 算法控制参数种群大小对算法的运行时间、收敛速度及算法精度均有很大影响,如图 9所示.
图 9(Fig. 9)
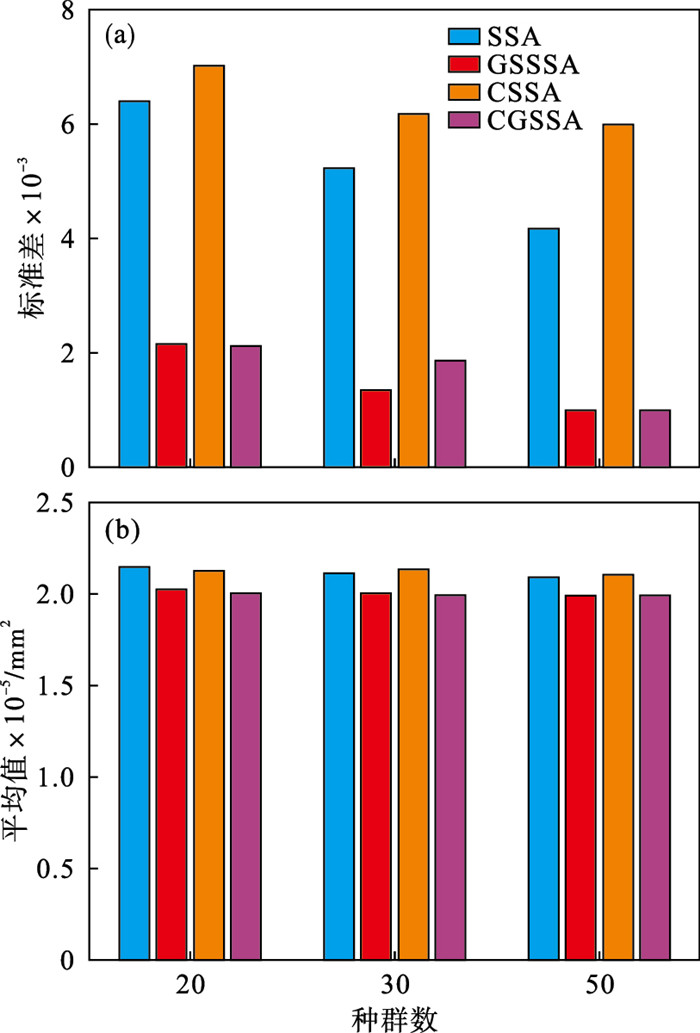 | 图 9 4种算法测试结果Fig.9 Test results of four algorithms (a)—标准差;(b)—平均值. |
对于樽海鞘群算法,种群越大越具有多样性,收敛速度和算法精度也越好,但随种群大小的增加,算法运行时间增加,因此,要选择合理的种群大小.设置迭代次数为500,种群大小分别为20,30,50,运行30次可计算获得优化后提梁机主梁截面积的平均值和标准差.
由图 9可知,当种群大小为50时,测得的平均值和标准差都比种群大小为20和30时小,说明种群大小为50时的最优解更精确且算法稳定性好.
分别选择20,30和50个种群,测试算法的运行时间,分别运行30次,测得运行时间的平均值分别为103,146,211 s,因此种群数为50时的运行速率并不慢.
种群大小为50,迭代次数为500,将4种算法分别运行30次,取最优的一组计算结果,如表 3所示.结果表明:提梁机的主梁经过CGSSA优化设计后,截面积由原来的239 298 mm2减少到206 794 mm2,减少了32 504 mm2,降幅达到了13.58%,优化效果明显.
表 3(Table 3)
| 表 3 各参数优化计算结果 Table 3 Optimized calculation results of each parameter |
4 结论1) 本文提出一种基于柯西和高斯混合变异的一种自适应变异策略的樽海鞘群算法(CGSSA),该算法通过选出适应度值最好的前S个个体进行自适应变异,优化了原先存在的收敛速度慢、收敛精度低、容易陷入局部最优解的缺点,提高了算法的搜索能力和收敛精度,降低了陷入局部最优解的概率.
2) 通过10个基准测试函数的测试,从随机运行30次统计获得的最优值的最小值、最大值、平均值、标准差和变异系数等5个方面进行对比,结合各个测试函数图说明CGSSA具有较高的收敛速度和收敛精度.经过时间复杂度的计算,改进后的CGSSA与原SSA时间复杂度一样,没有增加多余的计算负担,体现出改进后的CGSSA性能好.
3) 以提梁机主梁结构自重最轻为目标函数,以强度、刚度和稳定性等设计要求为约束条件,利用CGSSA算法进行优化设计,优化后的主梁截面积减少了13.58%,提梁机主梁质量减小,可有效节省制造成本.
参考文献
| [1] | Mirjalili S, Gandomi A H, Mirjalili S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114(6): 163-191. |
| [2] | 周新, 邹海. 融合黄金正弦混合变异的自适应樽海鞘群算法[J]. 计算机工程与应用, 2021, 57(12): 75-85. (Zhou Xin, Zou Hai. Adaptive salp swarm algorithm with golden sine mixed mutation[J]. Computer Engineering and Applications, 2021, 57(12): 75-85. DOI:10.3778/j.issn.1002-8331.2006-0011) |
| [3] | 张凡, 王雷, 赵娟, 等. 樽海鞘群算法在电力系统最优潮流计算中的应用[J]. 分布式能源, 2021, 6(1): 35-43. (Zhang Fan, Wang Lei, Zhao Juan, et al. Application of salp swarm algorithm in optimal power flow calculation of power system[J]. Distributed Energy, 2021, 6(1): 35-43.) |
| [4] | 沈平, 张彬彬, 袁瑛. 樽海鞘群算法在可见光通信调制器的应用[J]. 光学技术, 2021, 47(4): 477-482. (Shen Ping, Zhang Bin-bin, Yuan Ying. Application of the salp swarm algorithm in the visible light communication modulator[J]. Optical Technology, 2021, 47(4): 477-482. DOI:10.13741/j.cnki.11-1879/o4.2021.04.016) |
| [5] | 刘景森, 袁蒙蒙, 李煜. 基于改进樽海鞘群算法求解工程优化设计问题[J]. 系统仿真学报, 2021, 33(4): 854-866. (Liu Jing-sen, Yuan Meng-meng, Li Yu. Solving engineering optimization design problem based on improved salp swarm algorithm[J]. Journal of System Simulation, 2021, 33(4): 854-866. DOI:10.16182/j.issn1004731x.joss.19-0645) |
| [6] | 王秋萍, 王彦军, 戴芳. 多策略集成的樽海鞘群算法的机器人路径规划[J]. 电子学报, 2020, 48(11): 2101-2113. (Wang Qiu-ping, Wang Yan-jun, Dai Fang. Robot path planning based on multi-strategy integrated salp swarm algorithm[J]. Journal of Electronics, 2020, 48(11): 2101-2113.) |
| [7] | 刘芳瑞, 陈宏伟. 基于改进樽海鞘群算法的垃圾邮件分类[J]. 湖北工业大学学报, 2021, 36(1): 61-64. (Liu Fang-rui, Chen Hong-wei. Spam classification based on improved salp swarm algorithm[J]. Journal of Hubei University of Technology, 2021, 36(1): 61-64.) |
| [8] | 陈涛, 王梦馨, 黄湘松. 基于樽海鞘群算法的无源时差定位[J]. 电子与信息学报, 2018, 40(7): 1591-1597. (Chen Tao, Wang Meng-xin, Huang Xiang-song. Passive TDOA location based on salp swarm algorithm[J]. Electronic and Informatics, 2018, 40(7): 1591-1597.) |
| [9] | 王彦军, 王秋萍, 王晓峰. 改进的樽海鞘群算法及在焊接梁问题中的应用[J]. 西安理工大学学报, 2019, 35(4): 484-493. (Wang Yan-jun, Wang Qiu-ping, Wang Xiao-feng. The improved salp swarm algorithm and its application in the welding beam problem[J]. Journal of Xi 'an University of Technology, 2019, 35(4): 484-493.) |
| [10] | 陈连兴, 牟永敏. 一种改进的樽海鞘群算法[J]. 计算机应用研究, 2021, 38(6): 1648-1652. (Chen Lian-xing, Mou Yong-min. An improved salp swarm algorithm[J]. Computer Application Research, 2021, 38(6): 1648-1652.) |
| [11] | 白钰, 彭珍瑞. 基于自适应惯性权重的樽海鞘群算法[J]. 控制与决策, 2022, 37(1): 237-246. (Bai Yu, Peng Zhen-rui. A salp swarm algorithm based on adaptive inertia weight[J]. Control and Decision, 2022, 37(1): 237-246.) |
| [12] | 陈忠云, 张达敏, 辛梓芸. 正弦余弦算法的樽海鞘群算法[J]. 计算机应用与软件, 2020, 37(9): 209-214. (Chen Zhong-yun, Zhang Da-min, Xin Zi-yun. A salp swarm algorithm of sine cosine algorithm[J]. Computer Application and Software, 2020, 37(9): 209-214.) |
| [13] | 刘景森, 袁蒙蒙, 左方. 面向全局搜索的自适应领导者樽海鞘群算法[J]. 控制与决策, 2021, 36(9): 2152-2160. (Liu Jing-sen, Yuan Meng-meng, Zuo Fang. Global search-oriented adaptive leader salp swarm algorithm[J]. Control and Decision, 2021, 36(9): 2152-2160.) |
| [14] | Faris H, Mafarja M M, Heidari A A, et al. An efficient binary salp swarm algorithm with crossover scheme for feature selection problems[J]. Knowledge-based Systems, 2018, 154: 43-67. |
| [15] | Sayed G I, Khoriba G, Haggag M H. A novel chaotic salp swarm algorithm for global optimization and feature selection[J]. Applied Intelligence, 2018, 48(10): 3462-3481. |
| [16] | Wu J, Nan R, Chen L. Improved salp swarm algorithm based on weight factor and adaptive mutation[J]. Journal of Experimental & Theoretical Artificial Intelligence, 2019, 31(3): 493-515. |
| [17] | Wang D, Zhou Y, Jiang S, et al. A simplex method based salp swarm algorithm for numerical and engineering optimization[C]//International Conference on Intelligent Information Processing. Tours: Springer, 2018: 150-159. |
| [18] | 陈忠云, 张达敏, 辛梓芸, 等. 混沌精英质心拉伸机制的樽海鞘群算法[J]. 计算机工程与应用, 2020, 56(10): 44-50. (Chen Zhong-yun, Zhang Da-min, Xin Zi-yun, et al. Chaotic elite centroid stretching mechanism of salp swarm algorithm[J]. Computer Engineering and Application, 2020, 56(10): 44-50.) |
| [19] | Tanyildizi E, Demir G. Golden sine algorithm: a novel math-inspired algorithm[J]. Advances in Electrical & Computer Engineering, 2017, 17(2): 71-78. |
| [20] | 毕孝儒, 牟琦, 龚尚福. 融合动态概率阈值和自适应变异的鲸鱼优化算法[J]. 微电子学与计算机, 2019, 36(12): 78-83, 88. (Bi Xiao-ru, Mu Qi, Gong Shang-fu. Whale optimization algorithm combined with dynamic probability threshold and adaptive mutation[J]. Microeletronics & Computer, 2019, 36(12): 78-83, 88.) |