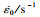卢晓红, 顾瀚, 丛晨, 阮飞翔
大连理工大学 机械工程学院，辽宁 大连 116024
收稿日期：2021-11-29
基金项目：国家自然科学基金资助项目(51875080)；中央高校基本科研业务费专项资金资助项目(DUT20ZD204)；大连市科技创新基金资助项目(2020JJ26GX041)。
作者简介：卢晓红(1978-)，女，内蒙古赤峰人，大连理工大学教授。

摘要：Inconel 718介观尺度薄壁件在航空航天、医疗和通讯等领域的需求日益增长.薄壁微铣削变形是领域内的难题，而微铣削力是引起加工变形的重要因素.为实现薄壁微铣削力的预测，建立了Inconel 718薄壁微铣削加工过程的有限元仿真模型，以及微铣刀和薄壁件的几何模型，完成了网格划分，并验证了网格独立性.采用Johnson-Cook本构模型和失效准则描述材料本构关系和切屑分离准则，修正库仑模型描述摩擦特性.对比薄壁微铣削过程仿真模型输出的微铣削力与实验测量结果，最大和平均相对误差分别为11.23%，7.04%，验证了模型的有效性和准确性.
关键词：微铣削薄壁件力预测有限元仿真Inconel 718
Micro-milling Force Prediction of Inconel 718 Thin-walled Parts
LU Xiao-hong, GU Han, CONG Chen, RUAN Fei-xiang
School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China
Corresponding author: LU Xiao-hong, E-mail: lxhdlut@dlut.edu.cn.

Abstract: Inconel 718 mesoscopic thin-walled parts are in increasing demands in aerospace, medicine, communication equipment and other fields. Thin-wall micro-milling deformation is a difficult problem in the field, and micro-milling force is an important factor causing machining deformation.In order to predict the force of thin-wall micro-milling, the finite element simulation model of Inconel 718 thin-wall micro-milling process was established together with the geometric models of the micro-milling tool and thin-wall parts, the mesh division was completed, and the mesh independence was verified. The Johnson-Cook constitutive model and failure criterion were used to describe the material constitutive relationship and chip separation criterion respectively. The modified Coulomb model was used to describe the friction characteristics. The results show that the maximum and average relative errors are 11.23% and 7.04%, respectively, by comparing the micro milling force output of the simulation model with the experimental results, which verifies the effectiveness and accuracy of the model.
Key words: micro-millingthin-walled partsforce predictionfinite element simulationInconel 718
介观尺度薄壁件是指特征尺寸在0.01~1 mm，高、厚比大于5 mm的微小零件，通常要求具有较高的加工精度和表面质量^[1].介观尺度薄壁件被广泛应用于微小结构零件或部件，如微型燃料电池、芯片上的微通道、微型叶轮或涡轮叶片等.很多微小薄壁件要求高温情况下性能稳定，具有抗热疲劳性、良好的韧性和耐腐蚀性，镍基高温合金Inconel 718能够满足微小零件在高温条件下工作可靠的需要，需求日益广泛.微铣削能加工特征尺寸在微米级的零件，是加工微小薄壁件的潜在有效技术手段.微小薄壁件的尺寸在微米级，刚性差、强度低，在微铣削加工过程中极易发生变形，导致零件壁厚不均匀，产生较大尺寸误差，加工精度难以保证.因此，微小薄壁件的微铣削加工变形是该领域内的典型难题.微铣削力对加工变形有重要影响, 因此，准确预测微铣削力是实现薄壁零件微铣削变形预测和抑制的前提.
目前，介观尺度薄壁件微铣削力的预测研究刚刚起步，微铣削力预测方法主要有经验法、解析法和有限元法.经验法依据微铣削试验建立微铣削力经验模型，通过微铣削试验采集微铣削力数据，对数据进行回归分析和插值计算，建立微铣削力与主要影响因素(如切削参数、刀具几何参数及振动等)之间的关系.孙雅洲等^[2]、张福霞^[3]均进行了微铣削正交试验，建立了微铣削力经验模型.李光俊^[4]设计完成了Inconel 718材料微槽铣正交试验，建立了微铣削力试验预测模型，研究了工艺参数对微铣削力的影响规律.Zhou等^[5]进行了微铣削试验，建立了基于二阶响应面法的微铣削力预测模型，研究了切削参数对微铣削力的影响.微铣削实验需要加工、测量、辅助设备和大量实验材料，成本较高, 且基于经验法的微铣削力预测模型只适用于特定材料和设备，不能反映微铣削机理.
解析法综合考虑微铣削过程中刀具和材料的力学、机械、物理和几何特性，建立微铣削系统输出和输入之间的关系.解析法可以很好表征加工过程的机理, 许多****用解析法建立了微铣削力预测模型.富宏亚等^[6]用UG软件建立了刀具及工件三维模型，经过布尔运算提取实际切削的微铣刀刃段，用解析方法建立综合考虑微铣削尺度效应、主轴径向跳动和单齿、多齿切削现象的球头微铣刀的微铣削力模型.王华^[7]以Inconel 718为研究对象，考虑微铣削温度的影响，建立了微铣削力-热耦合模型.吴继华等^[8]考虑材料在微切削时的应变梯度效应，建立的微切削模型能够较好地体现微切削不同于传统切削的尺度效应.Bao等^[9-11]建立的微铣削力解析预测模型考虑了刀具跳动、刀尖轨迹等.Malekian等^[12]基于刀具与工件间的过盈体积，建立了考虑弹性恢复、径向跳动的微铣削耕犁力模型.Bissacco等^[13]建立了考虑切削刃半径尺寸效应和刀具跳动微铣削力模型.Fang^[14-15]建立了一种新的用于预测微铣削力的滑移线场模型，该模型考虑了刀刃圆弧半径、剪切效应和尺寸效应的影响.Yi等^[16]建立了考虑刀具和工件变形、刀具跳动和材料强度影响的微铣削力解析预测模型.Moges等^[17]建立的微铣削力解析模型可以迭代修改刀具中心位置和刀齿轨迹，可以较好预测刀具偏转时的微铣削力.Wan等^[18]将塑性成形理论与滑移线场理论相结合，建立了材料分离模型及微铣削剪切力和耕犁力预测模型.Lu等^[19]建立的微铣削力三维解析预测模型考虑了切削温度的影响及剪切效应为主导的切削过程中由于刃口圆弧导致的耕犁力的影响.微铣削力解析模型中简化了微铣削过程中的诸多影响因素，由于微铣削的加工机理还不够清楚，对于剪切角、材料本构模型的研究还不够充分，影响了模型的预测精度.
有限元法被越来越多的研究者用于微铣削力预测.刘宇等^[20]利用Deform-3D软件对AL6061材料的微铣削加工过程进行模拟仿真.Thepsonthi等^[21]利用Deform-2D软件建立了有限元模型，对比无涂层硬质合金刀具，揭示了CBN涂层微铣刀对微铣削力的影响规律. Thepsonthi等^[22]利用Deform-3D软件建立了Ti6Al4V钛合金材料的微铣削加工过程三维仿真模型，明确了微铣削力与刀具磨损之间的关系.Attanasio等^[23]基于有限元法利用Deform-3D软件预测了CuZn37材料微铣削力.Sahoo等^[24]利用Deform-3D软件建立了考虑刀具跳动影响的微铣削有限元仿真模型，并获得微铣削力系数，建立了Ti6Al4V微铣削力预测模型.Pratap等^[25]利用ABAQUS对铜材料工件的微铣槽加工进行了仿真，实现了微铣削力的预测，发现在转速和切深一定时，微铣削力随进给率的增加而增大.Afazov等^[26]利用ABAQUS软件对AISI 4340钢在不同的未变形切屑厚度和切削速度下进行了大量的有限元分析，用非线性方程描述了微铣削力、未变形切屑厚度和切削速度之间的关系，综合正交切削有限元模型预测力和方程计算的切削厚度建立了微铣削力预测模型.Gao等^[27]将解析法与有限元法相结合，利用ABAQUS软件建立了微铣削力的预测模型，并研究了不同材料(镍基高温合金DD98、多晶高温合金GH4169和单晶铝)和不同工艺参数微铣削力的影响.Jin等^[28]用ABAQUS软件建立的黄铜微铣削力有限元模型综合考虑了刀具轨迹、刀具跳动等.有限元法可以降低实验成本，较为直观地表达切削力和应力分布情况，反映切削过程的物理本质，对于分析整个切削过程具有重要意义.目前在微铣削领域常用的有限元仿真软件有Deform和ABAQUS等，ABAQUS软件对微铣削这一非线性过程的分析功能强大，并具有强大的材料模型自定义功能.本文基于有限元法利用ABAQUS软件建立薄壁微铣削加工过程有限元仿真模型，以实现薄壁微铣削力的预测.
1 薄壁件微铣削加工过程仿真基于ABAQUS建立薄壁件微铣削加工过程仿真模型，主要包括前处理、分析计算和后处理三部分，如图 1所示.有限元仿真模型所有输入的量纲须一致，本文采用SI(mm)国际单位制.
图 1(Fig. 1)

图 1 基于ABAQUS的薄壁件微铣削过程仿真流程图Fig.1 Flow chart of thin-walled parts micro-milling process simulation based on ABAQUS

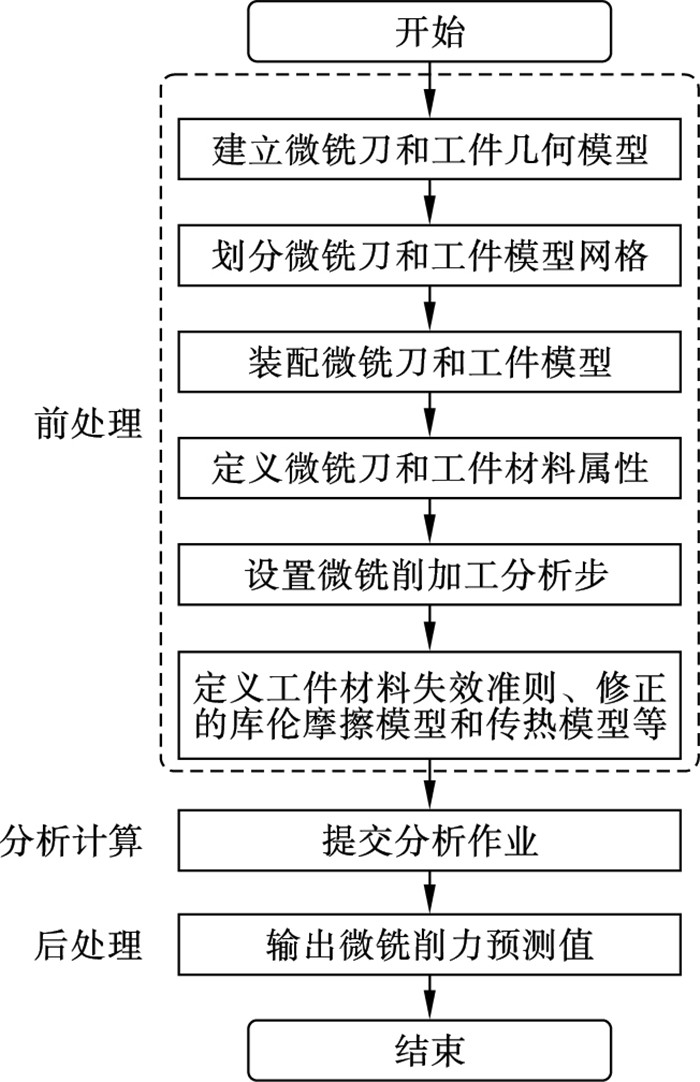
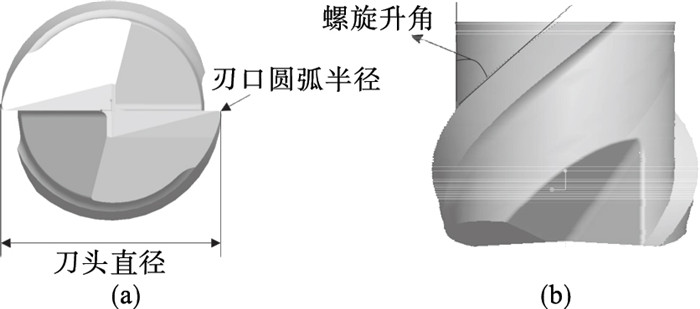
1.1 几何模型、网格划分和装配微铣刀的结构特征和几何尺寸体现了微铣削加工的重要特征，微铣刀几何模型的精确程度直接影响仿真模型的准确度.利用NS刀具有限公司生产的型号为MX230微铣刀，采用FEI公司Q45扫描电镜拍摄了微铣刀的SEM照片，如图 2所示.微铣刀的三维几何模型通过Pro/E三维建模软件建立，如图 3所示.微铣刀的刀头半径为0.3 mm，刀柄半径为2 mm，悬伸量为15 mm，切削刃长度为1.2 mm，如图 4所示.微铣刀的几何参数如表 1所示.考虑仿真效率的问题，薄壁件模型的长度、厚度和高度分别为1，0.12，1 mm.薄壁件模型直接在ABAQUS中建立.
图 2(Fig. 2)

图 2 微铣刀SEM照片Fig.2 SEM images of micro-milling tool (a)—俯视图；(b)—主视图.

图 3(Fig. 3)

图 3 微铣刀几何模型Fig.3 Model of the micro-milling tool (a)—俯视图；(b)—主视图.

图 4(Fig. 4)

图 4 微铣刀结构示意图Fig.4 Structure schematic diagram of the micro-milling tool

表 1(Table 1)

表 1 微铣刀几何参数Table 1 Geometric parameters of the micro-milling tool 几何参数 符号/单位 数值 刀头半径 rc/mm 0.3 刀柄半径 rs/mm 2 刀具全长 Ltool/mm 45 悬伸量 l/mm 15 切削刃长度 lc/mm 1.2 颈锥角 γ/mm 12 螺旋升角 β/mm 30 刃口圆弧半径 r/mm 0.002 切削刃数目 — 2

表 1 微铣刀几何参数 Table 1 Geometric parameters of the micro-milling tool

仿真模型的计算精度和计算效率受网格划分的影响较大，网格数量越少，计算效率越高.网格划分的质量越高，计算精度越高.刀具模型的网格类型采用C3D4T，并在刀尖、主切削刃和副切削刃等关键部位局部细化，如图 5所示.薄壁件模型的网格类型采用C3D8RT.为减少网格数量，在薄壁件模型被加工部分划分相对细密的网格，而在非加工部分划分相对稀疏的网格，如图 6所示.完成网格划分后，根据后续实验切削参数(轴向切削深度300 μm，径向切削深度20 μm)进行装配，如图 7所示.
图 5(Fig. 5)

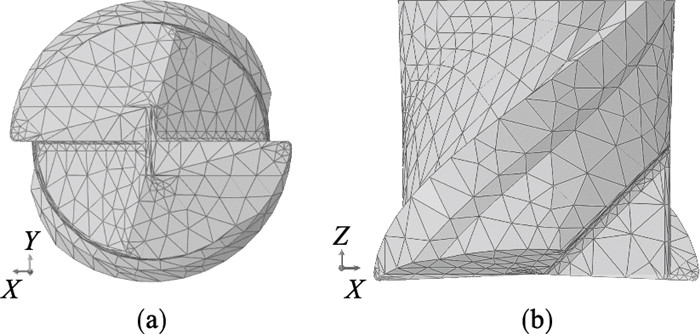图 5 微铣刀的网格划分Fig.5 Mesh division of the micro-milling tool (a)—俯视图；(b)—主视图.

图 6(Fig. 6)

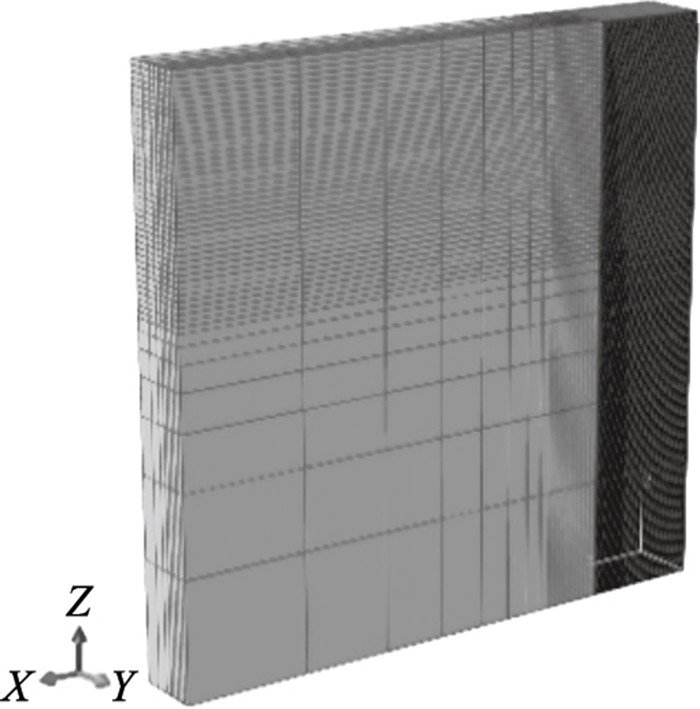图 6 薄壁件模型的网格划分Fig.6 Mesh division of thin-walled models

图 7(Fig. 7)

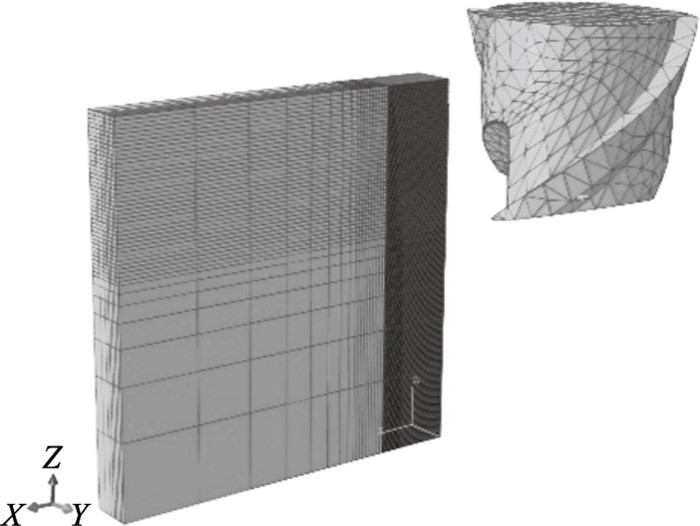图 7 微铣刀和薄壁件模型的装配Fig.7 The assembly of the micro-milling cutter and thin wall model

为验证网格划分的合理性，在主轴转速40 000 r/min、进给速度1.5 mm/s、轴向切削深度0.3 mm、径向切削深度0.02 mm的工艺参数条件下，通过改变刀具模型和薄壁件模型的网格密度进行了网格独立性测试，不同网格数量组合如表 2所示.网格数量的不同对仿真结果有一定影响，相同切削参数通过微铣削实验测量的微铣削力为0.2974 N，与微铣削力的仿真值基本一致.对比可知，提高网格密度在一定程度上可以提高模型的预测精度.
表 2(Table 2)

表 2 网格独立性测试网格数量和微铣削力仿真值Table 2 Mesh number and micro-milling force simulation values for mesh independence test 仿真次数 1 2 3 4 刀具模型的网格数 5 031 7 342 9 753 10 981 工件模型的网格数 165 578 225 960 289 015 312 359 微铣削力仿真值Fy/N 0.347 9 0.330 8 0.325 8 0.322 6

表 2 网格独立性测试网格数量和微铣削力仿真值 Table 2 Mesh number and micro-milling force simulation values for mesh independence test

1.2 材料模型薄壁件材料为Inconel 718，微铣刀材料为YG8，两种材料的热物理参数如表 3所示，并据此建立工件和微铣刀的材料模型.
表 3(Table 3)

表 3 Inconel 718和YG8的热物理参数[29]Table 3 Thermophysical parameters of Inconel 718 and YG8 热物理参数 符号/单位 Inconel 718 YG8 密度 ρ/(kg·m-3) 8 280 14 700 弹性模量 E/MPa 1.85×105 6.4×105 泊松比 μ 0.33 0.22 线膨胀率 Δ/K-1 13.2×10-6 4.5×10-6 热导率 κ/(W·(m·k)-1) 11.4 75.4 比热 c/(J·(kg·k)-1) 435 220

表 3 Inconel 718和YG8的热物理参数[29] Table 3 Thermophysical parameters of Inconel 718 and YG8

在微铣削难加工材料Inconel 718的过程中，材料的应变和应变率较大，同时大量产热.这种大应变、高应变率、高温下金属材料的强度极限及失效过程可以由Johnson-Cook(以下简称“J-C”)材料模型较好地描述.因此，选择J-C模型描述工件材料Inconel 718的本构关系和失效准则.经典的J-C本构模型如式(1)所示.Inconel 718的J-C本构模型参数如表 4所示.

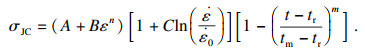(1)

表 4(Table 4)

表 4 Inconel 718的J-C本构模型参数[29]Table 4 Parameters of J-C constitutive model for Inconel 718 A/MPa B/MPa C n m tm/℃ 985 949 0.01 0.4 1.61 0.001 1 320

表 4 Inconel 718的J-C本构模型参数[29] Table 4 Parameters of J-C constitutive model for Inconel 718

式中：σ_JC为应力; A为屈服应力; B为应变硬化系数；C为应变率系数；n为加工硬化系数；m为温度软化系数；ε为应变；为应变率；为参考应变率；t为变形温度；t_r为室温；t_m为熔点.
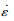
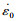
微铣削过程中存在尺度效应，传统尺度下的J-C本构模型不能反映尺度效应.因此，本文基于介观力学中的应变梯度理论和位错理论，建立描述材料介观力学性能的材料本构模型，描述材料在介观尺度下的本构关系.介观尺度下的J-C本构模型为

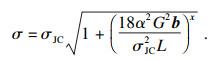(2)

式中：α为刀具前角；G为剪切模量；b为Burgers矢量；L为剪切带长度；x为修正因子.介观尺度下Inconel 718的应变梯度参数如表 5所示.
表 5(Table 5)

表 5 介观尺度下Inconel 718的应变梯度参数[30]Table 5 Parameters of strain gradient for Inconel 718 at mesoscopic scale α G/MPa b/nm x 0.5 -0.022 5 t(℃)+860.003 0.249 0.38

表 5 介观尺度下Inconel 718的应变梯度参数[30] Table 5 Parameters of strain gradient for Inconel 718 at mesoscopic scale

1.3 切屑分离准则切屑分离准则是实现切削过程精确模拟的关键.采用J-C动态失效准则描述高应变率的金属材料变形失效.如式(3)所示，J-C动态失效准则基于单元积分点的等效塑性应变定义破坏参数，当失效参数X达到1时，工件材料的刚度逐渐退化，发生失效，切屑开始形成：

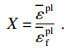(3)

式中：X为失效参数；为等效塑性应变；为等效失效应变.
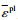
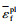
由J-C失效准则得到等效失效应变:

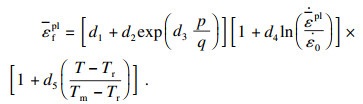(4)

式中：为等效失效应变；p为压应力；q为von Mises应力；为等效塑性应变率；d₁~d₅分别为J-C模型的失效参数.20 ℃条件下Inconel 718的J-C失效模型参数如表 6所示.
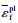
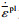
表 6(Table 6)

表 6 Inconel 718的J-C失效模型参数[31]Table 6 Parameters of J-C failure model for Inconel 718 d1 d2 d3 d4 d5 0.04 0.75 -1.45 0.04 0.89

表 6 Inconel 718的J-C失效模型参数[31] Table 6 Parameters of J-C failure model for Inconel 718

1.4 刀具和工件的相互作用在微铣削过程中，微铣刀前刀面与切屑之间的摩擦是切削力和切削热的重要来源之一.同时，微铣刀后刀面和工件已加工表面产生相互摩擦作用，影响加工表面的质量和残余应力.微铣刀与工件摩擦产生的热量大部分会传递到工件材料中，引起材料温度升高，使材料软化，引起材料的力学性能改变，最终影响切削力大小和工件变形.因此，建立能够准确描述微铣削过程中摩擦特性的力学模型是有限元仿真能够反映实际切削力和变形的基础.
采用修正的库仑模型描述微铣削过程的摩擦特性.将切屑与刀具之间的接触摩擦面根据摩擦特性的不同分为滑移区和黏结区两个部分，以不同的表达式计算摩擦应力.滑移区是距离工件较远的刀尖部分，该区域切削热量散去较快，温度相对较低，切屑材料没有黏结到刀具上.滑移区摩擦应力的大小与刀具和切屑接触摩擦面的正应力大小成正比，符合库伦定律，如式(5)所示.黏结区是与切屑根部相接触距离工件最近的刀尖部分，该区域的切削热量聚集现象严重，温度较高，刀具和工件材料原子活跃，并且刀具-切屑之间存在很大的压应力，二者材料原子相互渗透，产生黏结现象.黏结区的摩擦应力是恒定不变的，等于材料的最大剪切应力：

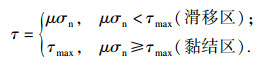(5)

式中：τ为摩擦应力；μ为摩擦系数；σ_n为正应力；τ_max为最大剪切应力.
在ABAQUS中，定义薄壁件被加工部分节点集与微铣刀几何表面集之间为点-面接触模式.薄壁件被加工部分与微铣刀的切向接触通过“罚”接触和有限滑移描述二者的相互作用，硬质合金刀具和Inconel 718工件之间的摩擦系数设置为0.4^[32-33].法向接触在金属切削过程有限元模型中一般设置为“硬”接触，以避免刀具和工件在仿真过程中相互穿透.
1.5 传热模型微铣削过程中产生的热量不断变化，设定初始环境温度为20 ℃，材料的塑性应变作功绝大部分转换成为热能，转换效率为0.9.
热量的传递方式有热传导、热对流和热辐射.热传导是发生于工件材料内部和刀具-切屑接触区域的主要传热方式，基于傅里叶定律和能量守恒定律^[33]，建立三维瞬态热传导能量微分方程：

(6)

式中：ρ_w，k_w和c_w分别为工件材料的密度、导热系数和比热容；为热流密度；v_x为X方向的速度；v_y为Y方向上的速度；v_z为Z方向上的速度.式(6)等号左边的分别表示X，Y和Z方向的传热项. 为内部热源产生的热量，即工件塑性变形和刀具-切屑界面滑动摩擦产生的热流密度.式(6)等号右侧描述了材料在微铣削过程中的动态吸热过程.
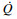
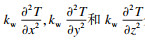
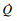
微铣削过程中的主要产热来源是刀具-切屑和刀具-工件的摩擦.从摩擦接触面到工件和切屑表面的传热系数为

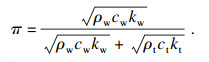(7)

式中：π为传热系数；ρ_w，c_w和k_w分别为工件材料的密度、比热容和导热系数；ρ_t，c_t和k_t分别为刀具材料的密度、比热容和导热系数.
微铣削过程中伴随着刀具和工件表面向周围空气传递热量，因此分别设置刀具表面-空气和工件表面-空气两个热对流边界，并将热对流系数设定为150 W·m^-2·K^-1，以描述热对流对加工过程所产生的影响.热辐射对微铣削过程中传热影响较小，因此不考虑热辐射的影响.
1.6 边界条件和载荷如图 8所示，通过对工件底面的节点集设置全约束以实现为薄壁件底面的固定约束(U_x=U_y=U_z=U_Rx=U_Ry=U_Rz=0).微铣刀绕Y轴旋转，并沿着X方向进给.因此约束微铣刀沿Y方向和Z方向的自由度(U_y=U_z=0)以及绕X轴和Z轴的自由度(U_Rx=U_Rz=0).根据切削参数为刀具模型上的参考点(图 8中的点R)设置旋转速度和进给速度，以实现微铣刀边界条件的定义.
图 8(Fig. 8)

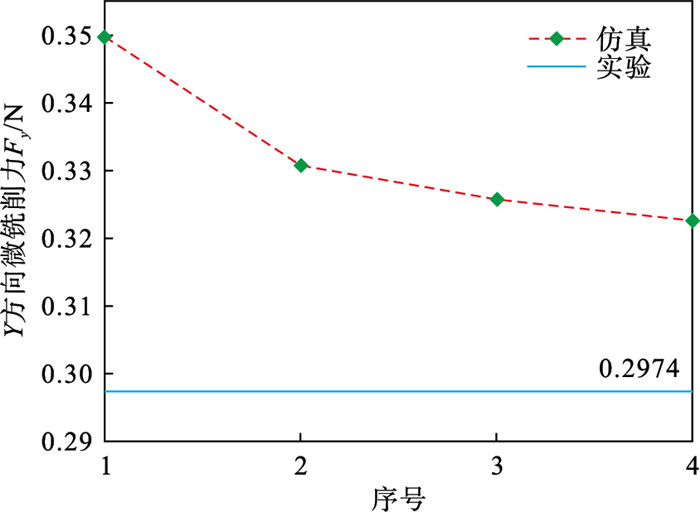图 8 边界条件和载荷Fig.8 Boundary conditions and loads

微铣削开始时，刀具与工件的相对位置关系如图 8所示.微铣削过程中，微铣刀沿X方向进给，径向和轴向切削深度保持不变，Z向的微铣削力较小，对加工影响较小.X方向的薄壁件长度大，刚度大，因此X方向的微铣削力对加工的影响较小.只有Y方向的微铣削力对薄壁微铣削过程中的变形有显著影响.根据作用力和反作用力之间的关系，工件和刀具所受微铣削力值相同，故仿真模型中选择刀具参考点所受微铣削力作为微铣削力模型的预测输出.
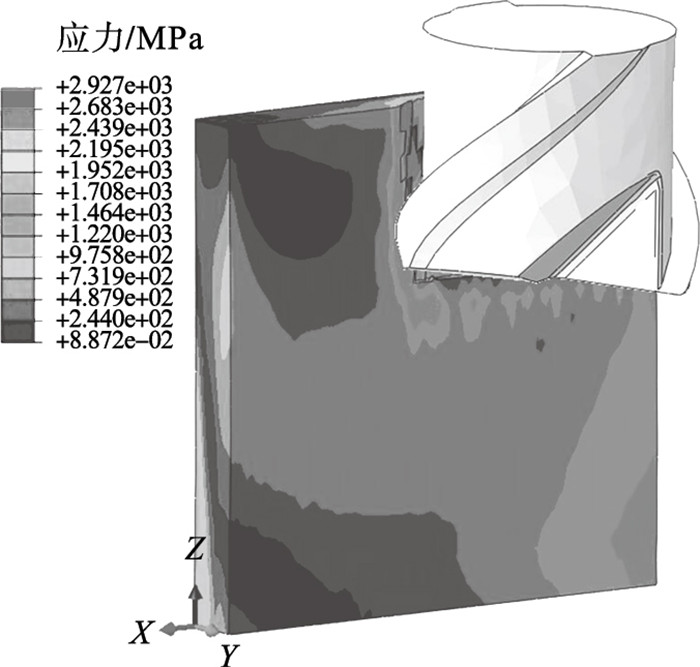
薄壁件的长度、厚度和高度分别为5，0.12，1 mm.薄壁件微铣削加工的切削参数如表 7所示，径向和轴向切削深度分别为0.02，0.3 mm.微铣削薄壁件模拟结果如图 9所示.
表 7(Table 7)

表 7 薄壁微铣削加工的切削参数Table 7 Cutting parameters of micro-milling thin-walled parts 序号 转速N/(r·min-1) 进给速度fz/(mm·s-1) 轴向切深ap/mm 径向切深ae/mm 1 40 000 1.5 0.3 0.02 2 50 000 1.5 0.3 0.02 3 60 000 1.5 0.3 0.02

表 7 薄壁微铣削加工的切削参数 Table 7 Cutting parameters of micro-milling thin-walled parts

图 9(Fig. 9)

图 9 薄壁微铣削加工过程仿真应力云图Fig.9 Simulation stress cloud diagram of thin-wall micro-milling process

2 微铣削力预测与实验验证为验证薄壁微铣削过程仿真模型的有效性，进行了微铣削实验，微铣床及测力仪如图 10所示.利用Kistler公司生产的动态测力仪9256C1实现了微铣削力的测量.根据采样定理，微铣削力的采样频率设定为20 kHz.
图 10(Fig. 10)

图 10 微铣床及测力仪Fig.10 Micro-milling machine and dynamometer

与仿真模型保持一致，实验所用刀具为NS刀具有限公司生产的型号为MX230微铣刀.Inconel 718薄壁件的长度、厚度和高度分别为5, 0.12, 1 mm.工件通过压板固定在微铣床平台上, 夹紧完成前，用千分尺调整工件的平面度和水平度.通过试切法定位刀具，观察测力软件中显示的图像，当图像发生突变时，表示刀具刚好接触到工件，通过该方法可以实现刀具定
实验与仿真模型所采取的切削参数相同，如表 8所示.实验测量和仿真模型预测的Y向微铣削力在不同主轴转速下的对比结果分别如图 11~图 13所示.Y向微铣削力峰值平均值对比结果如表 8所示.
图 11(Fig. 11)

图 11 Y向微铣削力对比(N=40 000 r/min)Fig.11 Comparison of micro-milling force in Y direction(N=40 000 r/min)

图 12(Fig. 12)

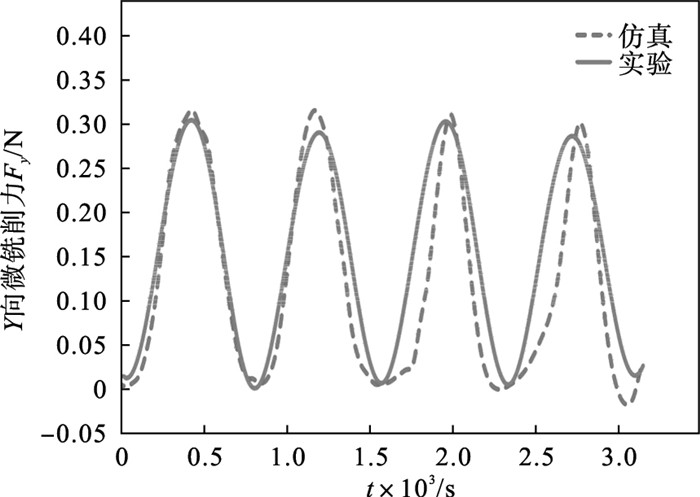图 12 Y向微铣削力对比(N=50 000 r/min)Fig.12 Comparison of micro-milling force in Y direction(N=50 000 r/min)

图 13(Fig. 13)

图 13 Y向微铣削力对比(N=60 000 r/min)Fig.13 Comparison of micro-milling force in Y direction(N=60 000 r/min)

由图 11~图 13可知，仿真模型输出的微铣削力的变化趋势与实验所测一致.由于仿真模型忽略了环境干扰、夹紧误差等因素的影响，仿真结果与实验结果仍存在误差.由于微铣削是断续切削，因此微铣削力呈周期性波动.随主轴转速从40 000 ~60 000 r/min，Y方向的微铣削力增大，可能是由于随切削区温度的升高，工件材料与刀具之间的摩擦逐渐从滑动摩擦过渡到黏着摩擦，从而增加了第一变形区和第三变形区之间的摩擦，导致微铣削力增加.
表 8(Table 8)

表 8 Y方向微铣削力峰值平均值对比Table 8 Comparison of average value of peak value of the micro-milling force in the Y direction 序号 转速N/(r·min-1) 实验值/N 仿真值/N 相对误差/% 1 40 000 0.297 4 0.330 8 11.23 2 50 000 0.442 2 0.462 3 4.54 3 60 000 0.645 7 0.611 2 5.34

表 8 Y方向微铣削力峰值平均值对比 Table 8 Comparison of average value of peak value of the micro-milling force in the Y direction

由表 8可知，Y方向微铣削力的实验值与预测值的最大相对误差为11.23%，平均相对误差为7.04%，验证了所建立的薄壁微铣削加工过程仿真模型的有效性和微铣削力预测的准确性.
3 结论1) 基于有限元法利用ABAQUS软件建立了Inconel 718薄壁件微铣削加工过程的有限元仿真模型，实现了薄壁微铣削力的预测.建立了刀具的精确几何模型，完成了不均匀的网格划分以提高计算效率并验证了网格独立性.采用J-C本构模型描述考虑尺度效应的材料特性，采用J-C动态失效准则作为切屑分离准则.采用修正的库仑模型描述摩擦特性.考虑热传导和热对流的影响，根据切削参数定义了边界条件和载荷.
2) 进行了薄壁微铣削实验，对比薄壁微铣削过程仿真模型输出的微铣削力与实验测量结果，最大和平均相对误差分别为11.23%，7.04%，验证了所建立的薄壁微铣削过程仿真模型的有效性和微铣削力预测结果的准确性.所建立的仿真模型实现了薄壁件微铣削力的预测，为实现薄壁零件的高精度加工提供了一定技术依据.
参考文献

[1]	Liu Y, Li P, Liu K, et al. Micro milling of copper thin wall structure[J]. The International Journal of Advanced Manufacturing Technology, 2017, 90(1/2/3/4): 405-412.
[2]	孙雅洲, 孟庆鑫, 王波, 等. 基于微小型机床的微细铣削力实验研究[J]. 航空精密制造技术, 2009, 45(3): 1-4. (Sun Ya-zhou, Meng Qing-xin, Wang Bo, et al. Experimental study of micro milling forces based on miniature machine tool[J]. Aviation Precision Manufacturing Technology, 2009, 45(3): 1-4. DOI:10.3969/j.issn.1003-5451.2009.03.001)
[3]	张福霞. 微细铣削力的建模与分析[D]. 哈尔滨: 哈尔滨工业大学, 2007. (Zhang Fu-xia. Modelling and analysis of micro-end milling force[D]. Harbin: Harbin Institute of Technology, 2007. )
[4]	李光俊. 镍基高温合金微细铣削过程切削力建模研究[D]. 大连: 大连理工大学, 2013. (Li Guang-jun. Research on the cutting force modeling during micro-end milling nickel-based superalloy processing[D]. Dalian: Dalian University of Technology, 2013. )
[5]	Zhou M, Chen Y, Zhang G. Force prediction and cutting-parameter optimization in micro-milling al7075-t6 based on response surface method[J]. Micromachines, 2020, 11(8): 766-782. DOI:10.3390/mi11080766
[6]	富宏亚, 张翔, 韩振宇, 等. 微径球头铣刀铣削力建模与仿真[J]. 计算机集成制造系统, 2011, 17(7): 1448-1453. (Fu Hong-ya, Zhang Xiang, Han Zhen-yu, et al. Modeling and simulation of micro-ball-end milling forces[J]. Computer Integrated Manufacturing Systems, 2011, 17(7): 1448-1453.)
[7]	王华. 镍基高温合金微铣削热-力耦合分析及加工硬化研究[D]. 大连: 大连理工大学, 2017. (Wang Hua. Research on thermal-mechanical coupled analysis and work hardening on micro-milling nickel-base superalloy[D]. Dalian: Dalian University of Technology, 2017. )
[8]	吴继华, 刘战强. 正交微切削中切削力预测模型研究[J]. 武汉理工大学学报(交通科学与工程版), 2010, 34(1): 130-133. (Wu Ji-hua, Liu Zhan-qiang. Prediction of forces in orthogonal micro-cutting bases on strain gradient theory[J]. Journal of Wuhan University of Technology(Transportation Science and Engineering), 2010, 34(1): 130-133. DOI:10.3963/j.issn.1006-2823.2010.01.032)
[9]	Bao W Y, Tansel I N. Modeling micro-end-milling operations. Part I: analytical cutting force model[J]. International Journal of Machine Tools & Manufacture, 2000, 40(15): 2155-2173.
[10]	Bao W Y, Tansel I N. Modeling micro-end-milling operations. Part Ⅱ: tool run-out[J]. International Journal of Machine Tools & Manufacture, 2000, 40(15): 2175-2192.
[11]	Bao W Y, Tansel I N. Modeling micro-end-milling operations. Part Ⅲ: tool run-out[J]. International Journal of Machine Tools & Manufacture, 2000, 40(15): 2193-2211.
[12]	Malekian M, Park S S, Jun M B G. Modeling of dynamic micro-milling cutting forces[J]. International Journal of Machine Tools and Manufacture, 2009, 49(7/8): 586-598.
[13]	Bissacco G, Hansen H N, Slunsky J. Modelling the cutting edge radius size effect for force prediction in micro milling[J]. CIRP Annals, 2008, 57(1): 113-116. DOI:10.1016/j.cirp.2008.03.085
[14]	Fang N. Slip-line modeling of machining with a rounded-edge tool. Part I: new model and theory[J]. Journal of the Mechanics and Physics of Solids, 2003, 51(4): 715-742. DOI:10.1016/S0022-5096(02)00060-1
[15]	Fang N. Slip-line modeling of machining with a rounded-edge tool. Part Ⅱ: analysis of the size effect and the shear strain-rate[J]. Journal of the Mechanics and Physics of Solids, 2003, 51(4): 743-762. DOI:10.1016/S0022-5096(02)00061-3
[16]	Yi J, Wang X, Jiao L, et al. Micro-flank milling forces considering stiffness of thin-walled parts[J]. The International Journal of Advanced Manufacturing Technology, 2018, 95(5): 2767-2782.
[17]	Moges T M, Desai K A, Rao P V M. Modeling of cutting force, tool deflection, and surface error in micro-milling operation[J]. The International Journal of Advanced Manufacturing Technology, 2018, 98(9/10/11/12): 2865-2881.
[18]	Wan M, Wen D, Ma Y, et al. On material separation and cutting force prediction in micro milling through involving the effect of dead metal zone[J]. International Journal of Machine Tools and Manufacture, 2019, 146: 103452-103466. DOI:10.1016/j.ijmachtools.2019.103452
[19]	Lu X, Wang H, Jia Z, et al. Coupled thermal and mechanical analyses of micro-milling Inconel 718[J]. Part B: Journal of Engineering Manufacture, 2019, 233(4): 1112-1126. DOI:10.1177/0954405418774586
[20]	刘宇, 别海楠. 6061铝合金微铣削切削力仿真与预测[J]. 工具技术, 2016, 50(12): 29-35. (Liu Yu, Bie Hai-nan. Simulation and prediction of micro-milling force for 6061[J]. Tool Engineering, 2016, 50(12): 29-35.)
[21]	Thepsonthi T, ?zel T. Experimental and finite element simulation based investigations on micro-milling Ti-6Al-4V titanium alloy: effects of CBN coating on tool wear[J]. Journal of Materials Processing Technology, 2013, 213(4): 532-542. DOI:10.1016/j.jmatprotec.2012.11.003
[22]	Thepsonthi T, ?zel T. 3-D finite element process simulation of micro-end milling Ti-6Al-4V titanium alloy: experimental validations on chip flow and tool wear[J]. Journal of Materials Processing Technology, 2015, 221: 128-145. DOI:10.1016/j.jmatprotec.2015.02.019
[23]	Attanasio A, Abeni A, Zel T, et al. Finite element simulation of high speed micro milling in the presence of tool run-out with experimental validations[J]. The International Journal of Advanced Manufacturing Technology, 2019, 100(1): 25-35.
[24]	Sahoo P, Patra K, Singh V K, et al. Modelling dynamic stability and cutting forces in micro milling of Ti6Al4V using intermittent oblique cutting fem simulation-based force coefficients[J]. Journal of Manufacturing Science and Engineering, 2020, 142(9): 1-29.
[25]	Pratap T, Patra K. Finite element method based modeling for prediction of cutting forces in micro-end milling[J]. Journal of the Institution of Engineers(India): Mechanical Engineering Division, 2017, 98(1): 17-26.
[26]	Afazov S M, Ratchev S M, Segal J. Modelling and simulation of micro-milling cutting forces[J]. Journal of Materials Processing Technology, 2010, 210(15): 2154-2162. DOI:10.1016/j.jmatprotec.2010.07.033
[27]	Gao Q, Chen X. Experimental research on micro-milling force of a single-crystal nickel-based superalloy[J]. International Journal of Advanced Manufacturing Technology, 2019, 102: 595-604. DOI:10.1007/s00170-018-03211-x
[28]	Jin X, Altintas Y. Prediction of micro-milling forces with finite element method[J]. Journal of Materials Processing Technology, 2012, 212(3): 542-552.
[29]	Hao Z, Li J, Fan Y, et al. Study on constitutive model and deformation mechanism in high speed cutting Inconel 718[J]. Archives of Civil & Mechanical Engineering, 2019, 19(2): 439-452.
[30]	Ding H, Shen N, Shin Y C. Thermal and mechanical modeling analysis of laser-assisted micro-milling of difficult-to-machine alloys[J]. Journal of Materials Processing Technology, 2012, 212(3): 601-613.
[31]	Erice B, Gálvez F. A coupled elastoplastic-damage constitutive model with Lode angle dependent failure criterion[J]. International Journal of Solids & Structures, 2014, 51(1): 93-110.
[32]	Sharman A, Dewes R C, Aspinwall D K. Tool life when high speed ball nose end milling Inconel 718[J]. Journal of Materials Processing Technology, 2001, 118(1/2/3): 29-35.
[33]	Lewis R W, Nithiarasu P, Seetharamu K N. Fundamentals of the finite element method for heat and fluid flow[M]. Chichester: John Wiley & Sons, Ltd, 2004: 10-12.