王述红, 李友明, 尹宏, 侯钦宽
东北大学 资源与土木工程学院，辽宁 沈阳 110819
收稿日期：2022-03-17
基金项目：辽宁省重点科技计划项目(2019JH2-10100035)；中央高校基本科研业务费专项资金资助项目(N170108029，N180701005)。
作者简介：王述红(1969-)，男，江苏泰州人，东北大学教授，博士生导师。

摘要：针对传统边坡体建模精确度不高的问题，引入多约束离散平滑插值(discrete smooth interpolation，DSI)算法，通过改进团队自主研发的三维数值分析系统GeoSMA-3D，获得多约束DSI拟合建模新模块.利用原始钻孔和物探数据辅以离散结构面信息对边坡整体进行插值，通过互异的约束条件对不同特征的地质对象进行标定，进而采用改进的修正函数对边坡体进行拟合建模，通过高精度的三维边坡体模型获取结构面信息并进行聚类分组.结果表明：该方法提高了离散介质岩体分析的准确性，具有较好的理论意义及工程应用价值.
关键词：多约束DSI算法三维拟合建模GeoSMA-3D结构面块体分析
Improvement of GeoSMA-3D Program Based on Multi-constrained DSI Algorithm
WANG Shu-hong, LI You-ming, YIN Hong, HOU Qin-kuan
School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: LI You-ming, E-mail: neuliyouming@126.com.

Abstract: Aiming at overcoming the low accuracy of traditional slope modeling, a new multi-constraint DSI fitting modeling module was established by introducing multi-constraint discrete smooth interpolation(DSI)algorithm in improving the self-developed 3D numerical analysis system GeoSMA-3D. Firstly, the original drilling and geophysical data were used to interpolate the whole slope with discrete structural plane information, then the geological objects with different characteristics were calibrated through different constraints, and then the slope body is fitted by the improved correction function. Finally, the structural plane information was obtained through the high-precision three-dimensional slope model and the clustering group was carried out. The results show that the method improves the accuracy of discrete rock mass analysis with good theoretical significance and engineering application value.
Key words: multi-constrained DSI algorithmthree-dimensional fitting modelingGeoSMA-3Dstructural surfaceblock analysis
非连续变形分析(discontinuous deformation analysis, DDA)方法^[1]是一种对离散介质岩体模型大变形问题进行分析求解且适用性较强的数值计算方法.该方法以位移为基本未知量，并以最小势能原理为基本原理，全部块体不但允许本身的变形与位移，而且可以在块体之间旋转、延伸与滑动，具有完备的运动学与动力学理论、高效率的计算过程、精确的平衡条件和符合能量守恒定律等特点，可以计算静力学与动力学问题，经过多年发展与完善，获得了巨大进步和拓展应用.
块体理论(block theory)以“刚体”、“平动”假设为基础，其核心是结合刚体极限平衡的静力分析在临空面上识别关键块体.所谓的关键块体就是失去稳定性的可动块体.在块体理论中，首先利用有限性原理对一个块体作出是否有限的判断，再使用可动性原理判断出这个块是否为可移动的，然后通过移动块体进行力学性分析，进一步确定实际的关键块体.块体理论的定义清晰、方法简便、容易使用，适合对块体结构岩体的稳定性分析.在边坡与洞室工程中，可以选取最佳的边坡倾角与倾向，以优化洞室轴线的走向和横切面形态，从而判断不稳定岩石坍塌的形态和加固措施的强度.对于采矿及隧道项目，可以选择最佳开挖方向以获得最佳开挖效果.
构建模型是工程分析问题的先决条件，而非连续岩体中蕴含的结构面大多都是随机和不确定的，这给建模带来了巨大困难.所有的工程分析软件程序都无法摆脱的问题就是所建立的模型是否能够反映工程岩体的实际情况.本文使用GeoSMA-3D系统以块体模型间的相互组合原理为基础，构建符合岩体基本情况的复杂岩体模型.
GeoSMA-3D全称是“岩土工程结构与模型分析系统(geotechnical structure and model analysis system)”，由笔者所在东北大学团队自主研发.系统使用Visual C++语言，利用OpenGL作为媒介平台，基于非连续变形分析理论与块体理论自主研发的三维岩体结构分析软件.目前该软件已经实现对边坡(主要针对岩质边坡)多个台阶和多个斜面的建模，基于三维网络对岩体结构面进行模拟、显示与分析；对结构面信息进行赤平投影分析，由关键块体的搜索、显示及分析计算可知岩质边坡块体动态滑落的过程及块体稳定性等.
目前GeoSMA-3D仍然存在许多不足，如建立模型时需输入岩体边坡模型的少量相关几何参数就能生成所需要的简单几何模型.虽然几何模型精度并非与几何参数数量成正比，但由少量几何参数生成的模型精确度必然大打折扣，这也是笔者一直想改进的地方.
与此同时，笔者团队的诸多****也在GeoSMA-3D原有基础上，做出了不断探索和应用.王述红等^[2]运用虚拟网格技术和随机结构面切割岩体工艺，并通过现场采集的结构面非接触式摄影技术，构建了岩质边坡空间的块体模型.王述红等^[3]根据多单元块体间通过交叉覆盖而形成独立块体的基本原理，在GeoSMA-3D系统中接入了一种基于覆盖技术的新方式，进行了块体搜索.
近年来，三维地质建模已广泛应用于各种岩土领域，如隧道开挖、边坡稳定性分析、石油和采矿勘探、地质调查和学术界的研究^[4-5]都取得了可观的成果.随研究的深入，复杂地质体三维模型构建受到越来越多的关注.众多****和专家进行了诸多探索，Dhont等^[6]实现了区域建模；刘琳^[7]提出一种以多个参数为基础的复杂地质面重网格化算法，实现了对复杂地质曲面的重构；李昌领^[8]类比面元模型和体元模型的建模方法，使复杂地层建模的无缝连接融合难题得到解决.但是，部分建模方法构建的地质模型为封闭的表面模型或块体模型.其中，有实体概念的算法不能充分展现地质体形态，而能充分展现地质体形态的算法又没有实体概念，所以仍然没有有效方法能用于构建复杂地质体实体模型.
根据复杂地质体的特征，将GO-CAD软件^[9]中基于多约束DSI算法的真三维建模技术，引入团队自主研发的GeoSMA-3D软件中，对该程序进行了进一步的开发和利用.利用三维地质块体模型对空间数据进行处理，提取异常信息并实现可视化，对复杂地质体中较典型的边坡体进行三维实体建模，提高了对岩体结构面分析的准确性，从而为边坡稳定性分析提供了一种准确、高效的新方法.
1 多约束DSI算法1.1 DSI原理离散平滑插值方法^[10-11]是由法国****Mallet教授提出的，是基于离散数学中的地质建模核心理论与原理.
国内外****的众多研究表明，地质体之所以具有空间连续性，是因为其由大量离散互异的地质单元所构成.由此设定如下离散拓扑模型：

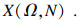(1)

式中：Ω=Ω(S)；N是Ω集合中所有点的数量，定义为，N=|Ω|.
该模型实质上是利用离散数学的原理描述地质结构曲面S在欧几里德三维空间上有限节点的集合，如图 1所示.
图 1(Fig. 1)

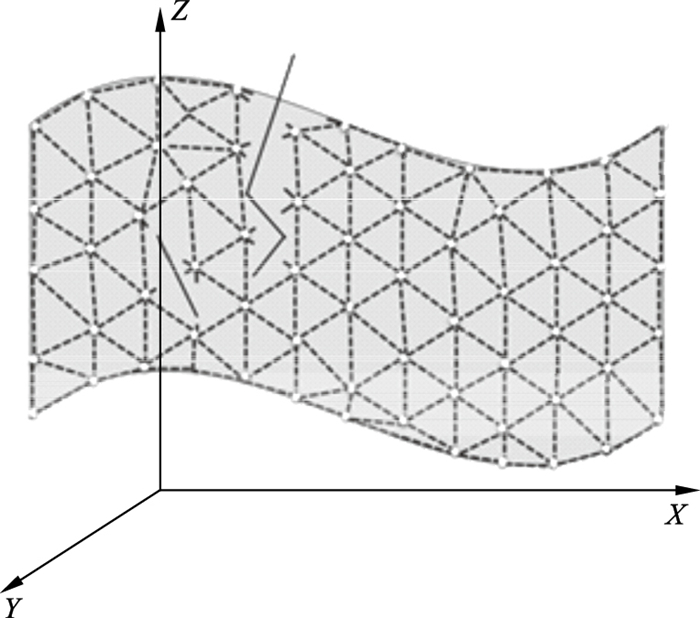图 1 地质曲面网格节点示意图Fig.1 Schematic diagram of grid nodes of geological surface

拟定离散模型为

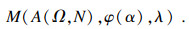(2)

式中：φ(α)={φ₁(α), φ₂(α), φ₃(α), …, φ_v(α), …}；?α∈Ω, λ={λ₁, λ₂, …}；{λ_i}?；系数A_{v, i}(α)和b_{v, i}是可变化的，随约束条件的差异而随时变动.
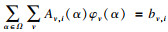
设定集合Ω中某一点k的属性函数集合为

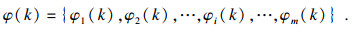(3)

式中：m为k点属性函数的数量，定义为m∈|Ω|；{φ₁(k), φ₂(k), φ₃(k)}表示k点的三维几何坐标.φ₄(k)表示k点上的曲面法向量；φ₅(k)(5≤i≤m)为用以确定曲面S除三维坐标和法向矢量外的全部张量属性.
为了精确描述任意曲面S的属性空间分布特征与位置，可以先将点k的属性函数集合φ(k)转换成m维行矩阵φ′(k)进行表述，再利用曲面S上n个点的φ′(k)矩阵组成的N×M矩阵，记为矩阵Φ，继而为后续的插值拟合求解提供了便利.
为使Φ矩阵表达更加清晰简洁，设定在Ω集合中所有点的某一个张量属性为i(1≤i≤m)，并用n维列矩阵表述：

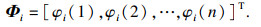(4)

式中，n为集合Ω上点的个数.
Φ矩阵可换一种表述为

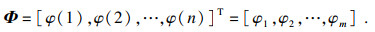(5)

式中：n为集合Ω上点的个数；m为集合Ω上每个点的张量属性个数.
由于插值拟合不受网格节点的排列顺序和编号的影响，可将Φ矩阵作变换后再求解.通过调换Φ矩阵中各个元素的排列顺序，将Φ矩阵分解为两部分，其中前一部分为已知矩阵、后一部分为未知矩阵，如式6所示：

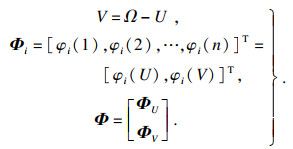(6)

式中：U为节点u∈Ω的集合且节点u的张量属性已知；V为节点v∈Ω的集合且节点v的张量属性未知.
由于工程实际因素的限制，部分节点的函数φ(k)已知，其余节点是未知的，对于未知函数值则可用离散平滑插值(DSI)求解.
1.2 算法的改进在三维地质建模过程中，基于多约束DSI算法，通过对模糊或精确约束的各种数据进行解译与拟合，任意复杂地质对象的快速建模已被众多****所接受，同时可以通过人机智能化合作、以数字孪生驱动高性能控制等方式随时编辑修正，使模型不连贯的地方通过迭代插值拟合得以连接融合.为了对地质体对象进行拟合建模，就必须综合利用测量、物探、平硐等数据以及之间的相互关系，进而利用原始钻孔数据对一些比较模糊的岩层结构进行了拟合插值, 从而估计初始钻孔数据和优化后调整结果之间的残差，进而分析比较，由此得出不同地质区域拟合模型的拟合有效区间，从而提高了拟合建模的真实性.
为了表达更加简洁明了，定义一个n维列矩阵：

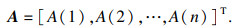(7)

式中：n为Ω集合中第i个属性的地质解释约束条件数量.
由上述n维列矩阵经转置得到n维行矩阵后，再添加一个常数则可表述为

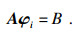(8)

式中，B是常数.
要使得到的模型能够较为准确地应用于边坡结构面分析中，需根据各种特征的地质对象使用互异的可靠度约束，并相应选择不同处理应对数据的方法，才能正确表示实际空间位置与各个曲面的产状数据(包括测量、物探、平硐与钻孔数据).在处理这类可靠性不同数据的时候，需要增加对地质面进行描述的空间结点量(即增加集合空间的容量).在原DSI算法基础上改进并提出了多约束DSI算法，根据地质曲面的繁杂性，需利用多约束DSI技术为地质人员的地理、钻孔等资料进行了数据解译与模糊性的数据拟合，如根据曲面S形成了各种不同的限制条件, 以及根据曲面S上的约束条件, 使用互异的约束条件对应不同特征的地质对象，从而降低曲面S上约束条件对模型精确度的限制.对式(9)中未知子矩阵进行修正，并定义了一个修正系数V_α(k)，使得V_α(k)|Aφ_i-B|达到最小甚至趋于0.
在GeoSMA-3D程序中进行三维拟合建模时，为了应对不同的可靠度约束，须选择适当的修正函数，修正函数的选择应完全自由.为了更好地贴合实际，对V_α(k)修正函数作了改进：

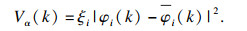(9)

其中，ξ_i为约束权重系数.
2 基于多约束DSI算法的高精度三维拟合建模与优化赤平投影2.1 多约束DSI拟合建模在原有GeoSMA-3D程序基础上，对该程序进行了进一步的开发和利用，将多约束DSI算法核心技术引入到该程序中，开发出针对于拟合建模的新模块，从而实现了通过非接触式摄像技术对测量、物探、平硐及钻孔等数据及其关联的综合利用，共同构建地质边坡模型，大大提高了模型的真实性，如图 2所示.在建模过程中针对岩土层穿插、尖灭及透镜体等复杂条件进行及时修正(如生成尖灭线、透镜体、杜绝薄层起伏岩土层面模型之间出现穿插等)，从而大大节省了后期调整的时间.与此同时还能拟合地质表面三维高精度模型，构建出参差错落的地质结构光滑曲面，不仅保证了模型的地质合理性，也为后续的结构面识别与获取以及三维块体搜索与切割提供了高精度模型，使之更加精确、清晰.
图 2(Fig. 2)

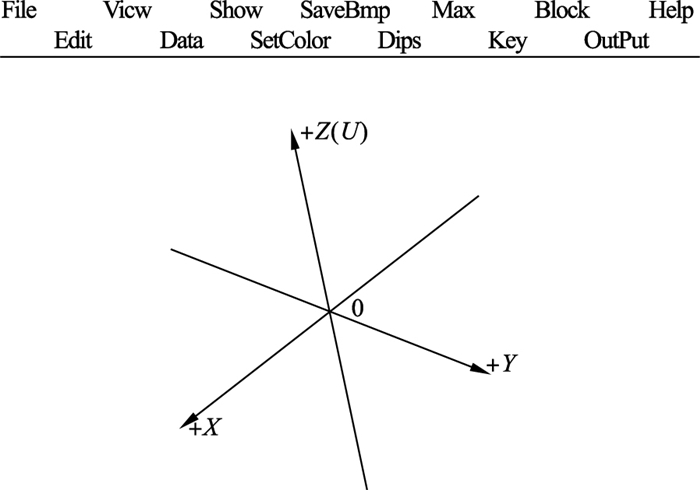图 2 GeoSMA-3D系统界面示意图Fig.2 GeoSMA-3D system interface diagram

多约束DSI拟合建模的过程如图 3所示.
图 3(Fig. 3)

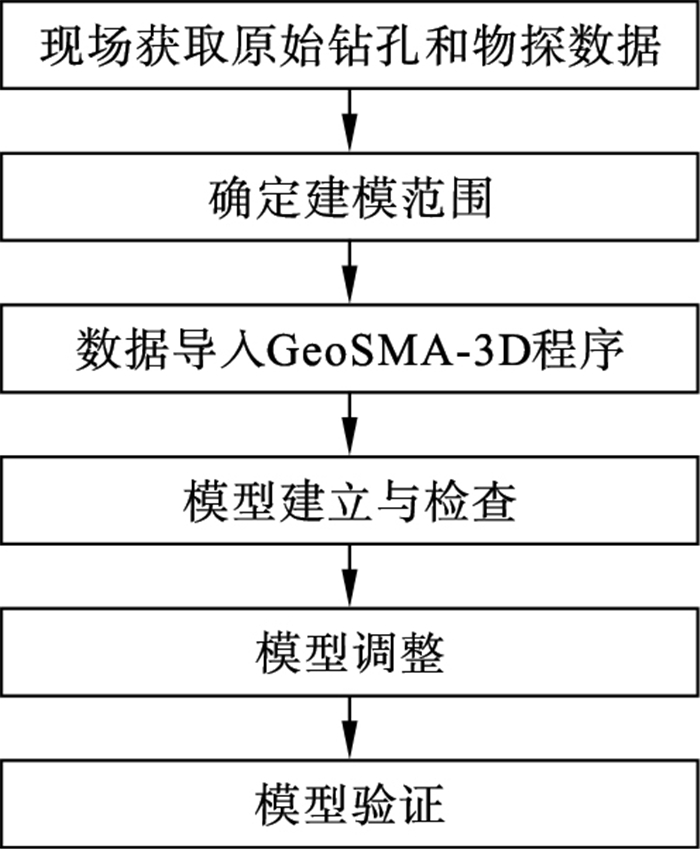图 3 多约束DSI拟合建模流程图Fig.3 Flowchart multi-constraint DSI fitting modeling

1) 现场获取原始钻孔和物探数据，并对原始数据进行检查和预处理，确保数据遵循关联关系，从而确保数据质量.
2) 确定建模范围：程序设计有裁剪箱插件，可自行裁剪建模范围，裁剪完成后形成立方网格，并定义网格的全局参数(包含网格的边长及数量)及网格精细控制参数，使每个网格中有两到三个控制点，从而确定网格密度.
3) 将现场数据导入GeoSMA-3D系统中：利用现场测绘的点云等高线数据形成地表面，再将钻孔数据中地层空间信息导入程序中.需要说明的是，钻孔孔口点是基本精确控制点，其点位是否正确影响整个三维模型的精确性，需对其进行精确定位.若前期处理时将原始数据导入Excel表格中，转换模型效率会比较高.
4) 模型建立与检查：利用多约束DSI插值自动拟合生成三维模型，再对模型根据现场实际情况进行检查；需要指出的是，现场实际地层中可能还有众多复杂的夹层和透镜体，拟合模型虽然能尽可能贴合实际，但局部区域的拟合可能无法识别具体实际情况而提示错误，这时需要人为操作进行剖面检查；在进行剖面检查时，选取的剖面要尽可能截取多个钻孔，选取的剖面个数直至截取到所有的钻孔时为止.
5) 模型调整：在逐个进行剖面检查时，对于与实际情况不符的夹层或透镜体，要及时进行调整.剖面调整结束后，再次生成完整模型，此模型即为高精度三维模型，如图 4所示.
图 4(Fig. 4)

图 4 多约束DSI高精度局部剖面模型示意图Fig.4 Schematic diagram of multi-constrained DSI high-precision three-dimensional model

6) 模型验证：为了判断模型是否符合钻孔接入条件，需在三维模型中通过全方位确认剖面与钻孔的联系，从而确定其合理性.其中有钻孔的界面须有模型的接入，而无钻孔的位置无须模型的接入.
2.2 优化赤平投影赤平投影法是一种应用比较广泛的图形投影方法.该方法使用图像描述垂直与解析平面之间的空间关系, 用以测定和描述垂直倾角、方位及空间平面.它可以作为一种求解图形的方法，而不是复杂的数学计算，因此具有很高的准确性，并且能达到预期目的和效果.其绘图主要涉及两个步骤：
1) 在投影球中心位置处放置对象的几何要素，然后为获得球面投影需将几何要素从球中心投影到球面上，从而创建了一个球面投影.
2) 为了球面投影的几何要素转换至赤平投影上，需由极向球面投影作射线，使其与投影的赤道平面相交，交集即为赤平投影.
自1960年以来，该方法已广泛应用于工程地质领域，不仅可以确定岩石的结构特性，而且可以分析岩石的力学状态.因此，可以使用赤平投影将岩石强度、受力和边界条件整合到投影系统中进行分析，评价和研究岩石的稳定性.
针对于GeoSMA-3D系统中原有的赤平投影分析功能进行了完善.基于Python的pandas库等多个基础库，依托由团队项目云南鲁奎山露天矿获取的CSV数据，创建一个带有网格线的立体网格，在裂隙组上循环，用不同的颜色绘制，并为每一组添加部分统计数据，从而绘制了两组裂隙，如图 5所示.其中每个裂隙都被绘制为代表裂缝面的极点的点，这不仅使赤平投影绘图具有交互性，同时仍然保留一定的灵活性，可以随时重构代码.
图 5(Fig. 5)

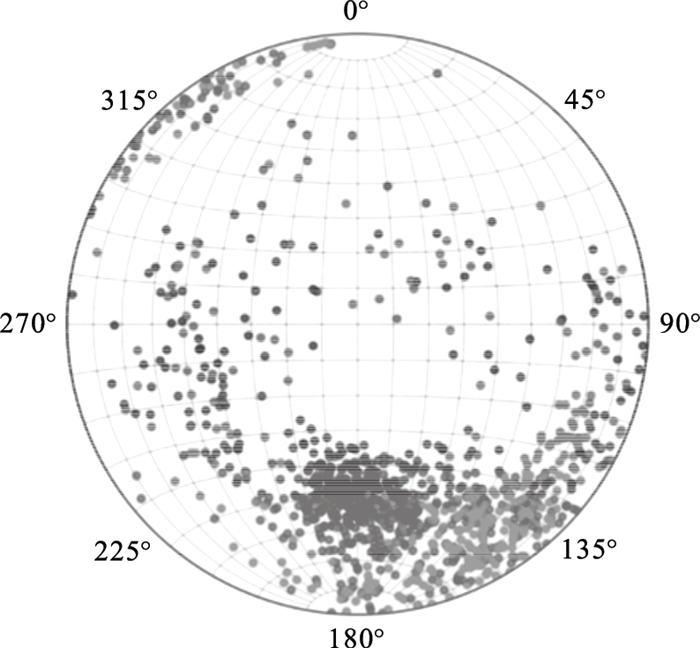图 5 两组裂隙极点示意图Fig.5 Schematic diagram of stereographic projection analysis of two groups of fissures

3 对比分析与验证3.1 多约束DSI误差对比分析目前DSI算法对钻孔资料的插值效果优于其他几类常用插值算法^[4-11].为体现其强大的适用性，将采用云南鲁奎山露天矿某一标段采集获取的边坡点云模型，对比分析多尺度DSI算法和其他几类常用插值算法所产生的误差.该边坡采集的密集点云模型经降采样处理后包含151 839个离散点云，其中136 164个点用作插值计算，15 675个点用作数值验证.本文引入平均绝对误差(MAE)、误差均方根(RMSE)和残差(R²)三个较为常用的精确度评价指标，采用多约束DSI算法与Kriging插值算法、薄板样条插值算法、临近点插值算法、线性内插算法等进行点距离的计算，并将其结果运用以上三种精度评价指标进行误差分析，如表 1所示.可以看出多尺度DSI算法验证点的残差基本都落在0~2 mm范围内，数据吻合度较高，结合模型的尺度可知，其精确度符合工程实际的要求.
表 1(Table 1)

表 1 几类常用插值算法的误差对比分析Table 1 Comparison and analysis of errors of commonly used interpolation algorithms? m 插值算法 平均绝对误差 误差均方根 残差 多尺度DSI 0.013 0.121 0.000 28 Kriging插值 0.029 0.192 0.000 52 薄板样条插值 0.028 0.189 0.000 49 临近点插值 0.037 0.513 0.001 16 线性内插 0.045 0.598 0.001 39

表 1 几类常用插值算法的误差对比分析 Table 1 Comparison and analysis of errors of commonly used interpolation algorithms?

3.2 程序对比验证为了验证GeoSMA-3D系统及多约束DSI拟合建模新模块的实用性，选取辽宁庄盖高速建设工程某标段的边坡^[12]作为研究对象，由于该边坡场址范围内有多处起伏褶皱、陡立断层扭曲、侵入界面不规则，加上层位变化复杂、考虑水流作用和复杂出露等情况.岩层岩体有严重风化，比较破碎，岩体条件较差，节理裂隙发育较严重，单靠现场钻孔和物探数据不足以有效控制空间形态，这成为该工程项目难以攻克的一个难点.
根据钻孔和物探资料确定地层空间关系，辅以钻孔摄像技术^[13]获取的离散结构面信息，并经统计处理，如表 2所示.然后再针对这些复杂因素利用多约束DSI模块采用逐层插入、部分模型表征、显示查看、调整数据、重新表征模型等循环方式生成更加贴合该边坡特点的模型.
表 2(Table 2)

表 2 结构面坐标及产状信息Table 2 Structural surfaces coordinates and occurrence Information 结构面编号 坐标/m 倾向 倾角 x y z (°) (°) 01 3.805 -0.497 2.612 250.34 23.93 02 0.142 -5.323 3.617 94.13 45.28 03 6.674 8.536 4.487 265.96 65.76 04 12.113 2.809 7.129 284.75 98.11 05 12.635 5.516 7.785 250.32 77.95 06 14.549 -3.346 4.891 94.17 88.24 07 12.189 8.466 2.918 265.95 82.95 08 1.514 11.485 0.932 282.38 82.97 09 1.926 13.321 3.692 26.59 8.71 10 5.943 15.537 2.472 284.76 84.03 11 14.258 18.469 6.587 170.25 28.82 12 15.524 20.002 5.715 196.74 58.66 13 6.297 -23.042 2.068 70.05 28.07 14 0.711 24.925 0.824 246.12 69.94 15 1.415 26.527 2.536 204.58 83.75 16 2.895 27.486 3.512 33.72 35.53

表 2 结构面坐标及产状信息 Table 2 Structural surfaces coordinates and occurrence Information

钻孔摄像技术是一门现场原位测量技术，由于近年来频繁的使用和发展，已日趋完善.该技术采用了现场原位检测钻孔侧壁，以便使岩石结构表面的信息都能够收集.同时其作为现场测量深入坚硬岩层的主要构造面的重要技术方法之一，不但可以鉴定出孔壁剖面线的形态特点，还能够获得岩性构造面倾向、倾角、间距、数量等产状的准确信息.
钻孔摄像技术是以光学成像为基本原理，通过应用全景技术，可以同时观测任意埋深的360°全方位孔壁，将观测到的全方位孔壁图像转换为孔壁平面图，再基于最小二乘法原理进行空间方位信息拟合.通过对取样长度与精度的归一化处理，分析二维形貌特征的计算和结构面形貌特征的近似描述，进而可得到孔壁结构面的形貌特征.
按GeoSMA-3D系统中流程顺序进行：确定裂隙生成的范围、模拟生成的随机裂隙、三维结构面的网格模拟、岩体表面上结构面的迹线统计和显示、关键块体搜索和结构面聚类的检测；优化的赤平投影分析、表征构成可移动块体的结构面和岩体表面的结构面迹线、生成结构面切割整个岩体模型时所产生的最大块体，以及分析多组优势结构面所产生的最大关键块体.提取关键块体的空间几何形态及相关数据信息(其中包含滑动面数、滑动块体的数量和体积、安全系数等)；最终得到了如图 6和图 7所展示的关键块体示意图，同时生成了相对应的关键块体信息，如表 3和表 4所示.
图 6(Fig. 6)

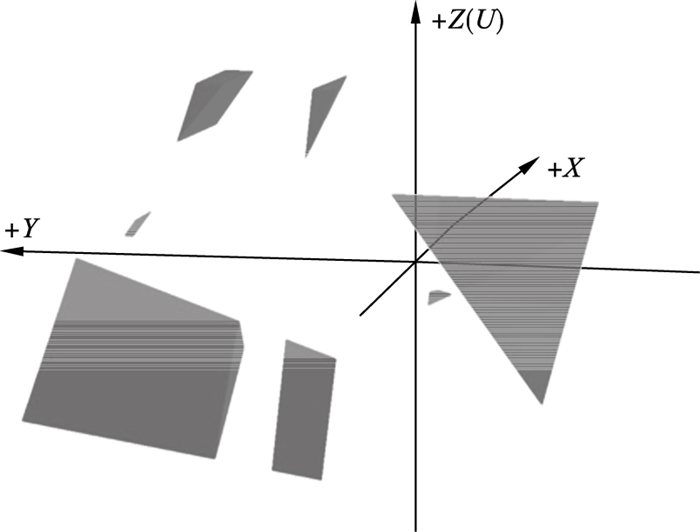图 6 程序改进前可移动块体示意图Fig.6 Schematic diagram of movable blocks before program improvement

图 7(Fig. 7)

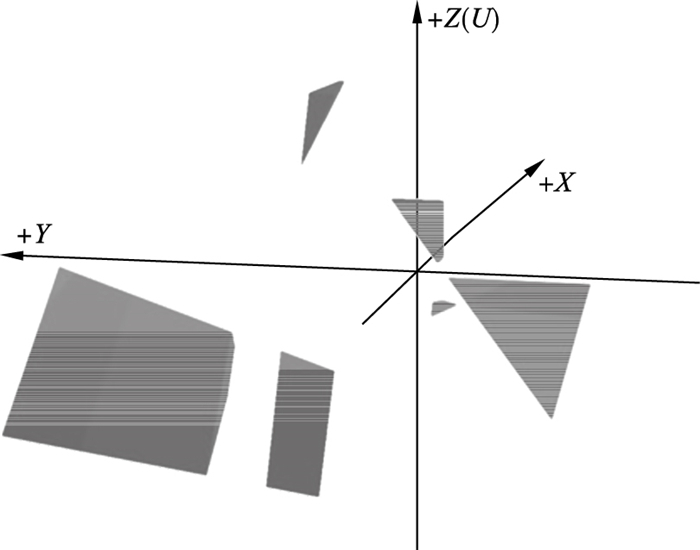图 7 程序改进后可移动块体示意图Fig.7 Schematic diagram of movable blocks after program improvement

表 3(Table 3)

表 3 程序改进前生成的关键块体信息Table 3 Key block information generated before program improvement 块体编号 体积/m3 滑动面数 安全系数 01 0.003 5 1 0.971 02 1.458 3 1 0.182 03 0.901 8 1 0.278 04 10.513 2 2 0.551 05 0.002 5 1 0.984 06 3.193 8 1 0.739 07 9.989 5 2 0.565

表 3 程序改进前生成的关键块体信息 Table 3 Key block information generated before program improvement

表 4(Table 4)

表 4 程序改进后生成的关键块体信息Table 4 Key block information generated after program improvement 块体编号 体积/m3 滑动面数 安全系数 01 0.793 7 1 0.491 02 0.916 3 2 0.265 03 5.758 7 2 0.618 04 0.002 8 1 0.958 05 3.023 5 1 0.771 06 9.967 4 2 0.571

表 4 程序改进后生成的关键块体信息 Table 4 Key block information generated after program improvement

通过对比分析改进前后GeoSMA-3D系统中所获得的关键块体信息，发现经多约束DSI模块拟合建模后搜索的关键块体信息更加精确，这验证了多约束DSI算法的有效性.
4 结论1) 基于多约束DSI算法原理，开发得到多约束DSI拟合建模新模块，利用该模块实现了对边坡体进行高精度的三维拟合建模.通过对比分析发现，该模块不仅有效提高了拟合边坡体模型的准确性，避免了复杂边坡体内部结构建模与实际不相符的技术难题，更加强了后续结构面分析过程的准确性.
2) 基于GeoSMA-3D系统，利用三维数值计算对岩体结构面进行建模和表征；对结构面信息进行赤平投影分析及对关键块体进行搜索、显示和分析计算.通过边坡模型与现场实测数据的对比分析，进一步预测工程岩块破裂和失稳趋势，为工程现场施工提供参考和借鉴.
3) 通过对工程实例的应用，可移动块体和结构面表征更加清晰、明显，进一步验证多约束DSI算法的适用性，同时也体现了GeoSMA-3D系统的优异性.
参考文献

[1]	Shi G H, Goodman R E. Two dimensional discontinuous deformation analysis[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1985, 9: 541-556. DOI:10.1002/nag.1610090604
[2]	王述红, 张航, 张艳桥, 等. 随机结构面切割岩质边坡空间块体模型及关键块体分析[J]. 东北大学学报(自然科学版), 2011, 32(3): 431-434. (Wang Shu-hong, Zhang Hang, Zhang Yan-qiao, et al. Spatial block model and key block analysis of rock slope cut by random structural surfaces[J]. Journal of Northeastern University(Natural Science), 2011, 32(3): 431-434. DOI:10.3969/j.issn.1005-3026.2011.03.032)
[3]	王述红, 王斐笠, 张紫杉. 基于覆盖技术的块体搜索及程序开发[J]. 东北大学学报(自然科学版), 2017, 38(2): 265-269, 289. (Wang Shu-hong, Wang Fei-li, Zhang Zi-shan. Block search and program development based on overlay technology[J]. Journal of Northeastern University(Natural Science), 2017, 38(2): 265-269, 289. DOI:10.3969/j.issn.1005-3026.2017.02.023)
[4]	Lemon A M, Jones N L. Building solid models from boreholes and user-defined cross-sections[J]. Computers & Geosciences, 2003, 29: 547-555. DOI:10.3969/j.issn.1001-4160.2003.05.001
[5]	Zanchi A, Salvi F, Zanchetta S H, et al. 3D reconstruction of complex geological bodies: examples from the Alps[J]. Computers & Geosciences, 2009, 35: 49-69.
[6]	Dhont D, Monod B, Hervouet Y, et al. 3D geological modeling of the Trujillo block: insights for crustal escape models of the Venezuelan Andes[J]. Journal of South American Earth Science, 2012, 39: 245-251. DOI:10.1016/j.jsames.2012.04.003
[7]	刘琳. 复杂地质体三维建模参数化的研究[D]. 北京: 中国地质大学, 2017. (Liu Lin. Research on 3D modeling parameterization of complex geological bodies[D]. Beijing: China University of Geosciences, 2017. )
[8]	李昌领. 复杂地层体三维建模算法研究[D]. 徐州: 中国矿业大学, 2014. (Li Chang-ling. Research on 3D modeling algorithm of complex stratum[D]. Xuzhou: China University of Mining and Technology, 2014. )
[9]	Tomas S I, Hantuch I H. GO-CAD: virtual reality simulation[J]. IFAC Proceedings Volumes, 2003, 36(18): 274-283.
[10]	Mallet J L. Geomodeling[M]. Oxford(USA): Oxford University Press, 2002.
[11]	Mallet J L. Discrete smooth interpolation in geometric modeling[J]. ACM-Transactions on Graphics, 1989, 8(2): 121-144. DOI:10.1145/62054.62057
[12]	穆檄江. 碎裂岩体块体力学分析及其岩坡稳定性评价[D]. 沈阳: 东北大学, 2013. (Mu Xi-jiang. Block mechanics analysis and cataclastic rock slope stability assessment[D]. Shenyang: Northeastern University, 2013. )
[13]	王益腾, 王川婴, 邹先坚, 等. 基于钻孔摄像技术的孔壁剖面线形貌特征描述方法及其应用研究[J]. 岩石力学与工程学报, 2020, 39(sup2): 3412-3420. (Wang Yi-teng, Wang Chuan-ying, Zou Xian-jian, et al. Research on the feature description method and application of hole wall profile line based on borehole camera technology[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(sup2): 3412-3420.)