唐秀洁¹, 赵文¹, 路博¹, 李伟伟²
1. 东北大学 资源与土木工程学院，辽宁 沈阳 110819;
2. 广州地铁设计研究院股份有限公司，广东 广州 510010
收稿日期：2021-12-04
基金项目：国家自然科学基金资助项目(51878127)。
作者简介：唐秀洁(1994-)，女，山东日照人，东北大学博士研究生;
赵文(1962-)，男，辽宁沈阳人，东北大学教授，博士生导师。

摘要：依托咬合管幕结构的抗弯性能试验，利用ABAQUS有限元软件建立了咬合管幕结构模型，在对模型的准确性进行验证的基础上，对咬合管幕结构在集中荷载作用下的抗弯性能进行分析. 选取咬合距离、钢管直径、钢管壁厚及钢筋直径进行研究，得到不同参数组合下结构的抗弯承载力水平.结果表明：加载过程中，钢管与核心混凝土中存在明显的应力重分布，咬合管幕结构具有良好的抗弯性能，钢管直径是影响咬合管幕结构抗弯性能的主要因素，当钢管直径增加45.7%时，结构抗弯承载力最大可提高294.3%.
关键词：咬合管幕结构有限元模型抗弯性能应力重分布参数分析
Flexural Behavior and Influencing Parameters of Secant-Pipe-Roof Structure
TANG Xiu-jie¹, ZHAO Wen¹, LU Bo¹, LI Wei-wei²
1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China;
2. Guangzhou Metro Design & Research Institute Co., Ltd., Guangzhou 510010, China
Corresponding author: ZHAO Wen, E-mail: wenneu@163.com.

Abstract: Based on the flexural behavior test of the secant-pipe-roof structure(SPRS), the ABAQUS finite element software was used to establish the SPRS model. After verifying the model's accuracy, the SPRS′s flexural behavior under loading was studied. The parameters of secant distance, steel tube diameter, steel tube thickness and steel bar diameter were selected for parameter analysis, and the flexural capacities of the structure under different parameter combinations were obtained. The results show that during the loading process, there is a significant redistribution of stress in the steel tube and the core concrete, and the SPRS has good anti-flexural behavior. The steel tube diameter is the most important factor affecting the flexural behavior of the SPRF. When the steel tube diameter is increased by 45.7%, the maximum flexural capacity of the structure can be increased by 294.3 %.
Key words: secant pipe roofing structurefinite element modelflexural behaviorstress redistributionparameter analysis
随着基础设施建设水平的不断提高，城市轨道交通系统已成为现代化城市建设的重要主题之一.截至2020年底，中国共有38个城市开通地铁，运营里程7 108.49 km，位居世界第一^[1].
随着地上建筑风格的复杂化和地下空间的不断开发，地下工程的施工环境越来越复杂，传统的浅埋暗挖法、洞桩法及双侧壁导洞法等施工方法已经不能满足现有的工程需要^[2].管幕工法是一种新型的施工方法，在施工过程中使用顶管机将多根钢管推入待挖土中，并将推入的钢管水平连接成一个整体，形成支撑结构，之后在其支撑下进行地下土开挖^[3-4].管幕法最早出现于20世纪70年代的欧洲^[5]，比利时的安特卫普地铁站就是应用此工法建设而成，这是管幕工法在实际工程中早期的应用之一^[6-7].管幕工法逐渐被应用于世界各地地下工程的施工中，并被不断完善和改进.
针对管幕结构的受力机制，相关****开展了大量研究.Xiao等^[8]利用试验与数值模拟相结合的方法研究了开挖过程中管幕的受力机制.Shimada等^[9]利用数值模拟方法模拟了管幕工法的施工过程，对管幕结构的受力形式和承载力水平进行了研究.Zhang等^[10]研究了浅层隧道中管幕结构的荷载传输机制.Xie等^[11-12]研究了管幕在地下结构中的作用，揭示了其对土体变形机制的影响，给出了土体变形的计算公式，并将其与有限元分析法相结合模拟了实际工程的施工过程.传统管幕结构中的钢管仅通过锁扣进行连接，这在很大程度上限制了结构的承载力和整体刚度. 为了满足施工要求，开挖过程中需要设立大量的临时支撑，增加了施工过程的难度^[13].针对这一问题，韩国提出了新管幕工法(new tubular roof method, NTR)，这一新技术在中国的沈阳地铁2号线和港珠澳沉管隧道得到了成功应用.黎永索等^[14-15]基于沈阳地铁2号线工程，研究了新管幕结构的变形规律及衬砌结构与围岩的相互作用机制.Liu等^[16]详细介绍了NTR管幕工法配合冻结法施工的过程.赵文等^[17]在已有的管幕工法的基础上提出了新管幕工法(steel tube slab, STS)，通过使用高强螺栓和焊接下翼缘板的方式提高了结构的刚度和抗弯能力.Jia等^[18]对STS结构的抗弯性能和破坏模式进行了研究，证明了STS结构作为一种永久支撑的优越性.
传统的管幕结构极限承载力低，NTR由于受到拱形截面的限制，空间利用率低，STS在横向使用螺栓连接，对顶管顶进的精度要求较高，施工复杂.已有的管幕工法在施工过程中难以清除管间土，会影响混凝土浇筑的密实度，降低结构承载力.随着地上结构形式和规模的发展变化，地下工程所面临的周边环境也越来越复杂多变，传统的管幕工法已经不能满足工程需求，迫切需要一种新型的施工方法.
咬合管幕工法是近几年新出现的一种管幕施工方法^[19].目前关于咬合管幕的研究还十分有限，在使用过程中的受力机制和破坏形式尚不明确.本文通过数值模拟的方法对咬合管幕结构的弯曲性能进行分析，得到了咬合管幕结构的受力破坏规律，为其在工程中的应用提供参考.
1 咬合管幕结构简介咬合型管幕结构由拼装钢管、混凝土及钢筋组成.其中拼装钢管分为主体结构部分(钢弧)和可回收部分，如图 1所示.相邻钢管间的横向连接方式为主体结构部分(钢弧)以咬合形式搭接，可回收部分开口处的两个侧壁上设有限位螺栓与滚珠，用以防止在顶进过程中主体结构部分(钢弧)与可回收部分发生相对错动，以及减少它们之间的摩擦力.
图 1(Fig. 1)

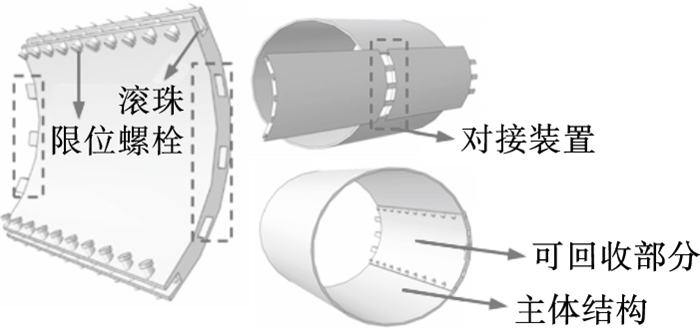图 1 拼装钢管构造图Fig.1 Structure of the assembled steel pipe

1.1 施工步序在施工过程中，首先顶进第一根上述拼接钢管，并在顶进过程中掏除钢管内部土体.松开第一根钢管可回收部分上的限位螺栓，然后开始顶进下一根钢管，在顶进过程中钢管的主体结构部分将顶出并取代上一根钢管的可回收部分，进而实现与上一根钢管的咬合搭接，并对相邻顶管的搭接处进行焊接，在相互连接的顶管侧壁的特定位置开孔并在孔内植入钢筋，最后在钢管内部灌注混凝土形成最终的整体结构.其结构形式和连接方式如图 2所示.
图 2(Fig. 2)

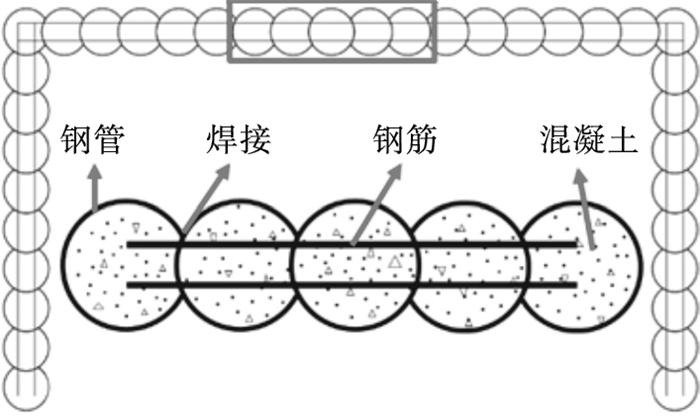图 2 咬合管幕结构示意图Fig.2 Schematic diagram of the secant pipe roofing structure

1.2 结构特点咬合型管幕结构与传统管幕结构相比具有以下优势：本结构横向采用咬合形式搭接，具有较高的承载力，避免了施工过程中架设临时支撑的繁琐步序；本结构取消管间连接，降低了对顶管精度的要求，解决了管间土难以清除的问题；本结构为矩形断面形式，提高了地下空间的利用率.在结构上具有很强的优越性.
2 咬合管幕结构有限元模型的建立2.1 单元选取使用ABAQUS/Standard 6.14软件建立咬合管幕结构的有限元模型.有限元模型中的钢管、混凝土和钢垫块采用实体单元，以8节点减缩积分格式(C3D8R)进行模拟，钢管内植入的钢筋使用三维桁架单元(T3D2)进行模拟.模型的主要构件及其网格划分如图 3所示.
图 3(Fig. 3)

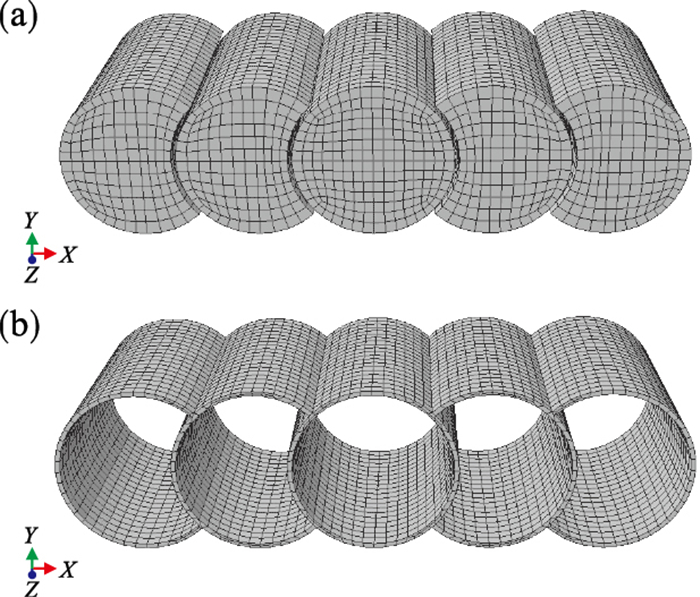图 3 有限元模型网格划分Fig.3 The mesh of finite element model (a)—管内混凝土；(b)—钢管.

2.2 材料本构模型及属性在咬合管幕结构模型中，钢管和混凝土都采用弹塑性材料.在本构关系上，钢管采用韩林海提出的二次塑流模型^[20]，管内混凝土不同于普通混凝土，其受到钢管的约束，弹塑性会有所改变，因此采用韩林海提出的混凝土塑性损伤模型对管内混凝土进行模拟^[21]，把钢筋看作理想的弹塑性材料对其应力-应变关系进行模拟.其中钢材的密度为7 800 kg/m³, 弹性模量和泊松比分别为E_s=206 GPa，υ_s=0.30.管内混凝土的弹性模量E_c=25 GPa，密度ρ_c=2 400 kg/m³，泊松比υ_c=0.20.
2.3 接触设置钢管与混凝土的相互作用是通过设置接触面来实现的，相互作用力通过接触面传递，包括向心力和切向力.本研究认为钢管与混凝土之间不存在相对运动，即它们之间的接触是一种“硬”接触，因此，钢管与混凝土之间的向心力通过“硬”接触来模拟.切向力则通过罚函数进行模拟，罚因子取0.25.钢筋尺寸较小，因此使用嵌入区域命令将其嵌入到模型中.试验中采用的是手工电弧焊，焊条选用的是J422碳钢电焊条，有限元分析中钢管之间的连接采用等强处理，抗拉强度为420 MPa.
2.4 边界条件及加载方式模型加载方式采用单点集中荷载.首先在模型中设置参考点，然后通过coupling约束将参考点与钢垫块耦合到一起，再对参考点RP-3进行加载时，荷载通过钢垫块传递到模型，以此来实现单点弯曲加载.在模型两端设置参考点，分别限制参考点RP-1的Y，Z向的位移和参考点RP-2的X, Y, Z方向的位移，模拟简支梁的约束条件.模型的约束条件及加载方式如图 4所示.
图 4(Fig. 4)

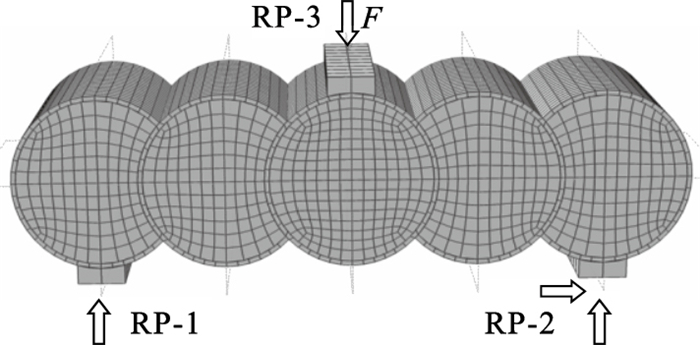图 4 模型的约束条件及加载方式Fig.4 Model constraints and loading methods

3 试验验证3.1 试验概况李伟伟^[22]设计试验对咬合管幕的抗弯性能进行了研究，可知不同咬合距离的咬合管幕结构在集中荷载下的弯曲性能.试件加载破坏形态如图 5所示.
图 5(Fig. 5)

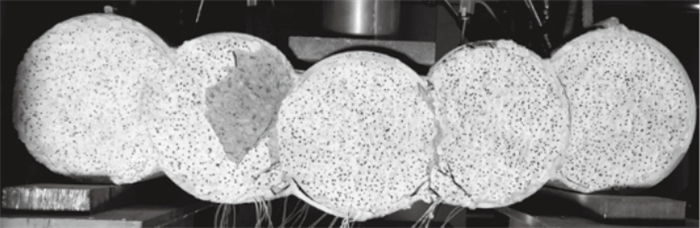图 5 咬合管幕结构加载破坏形态Fig.5 Loading failure mode of secant pipe roofing structure

3.2 有限元模型参照试验中试件SPRF-1的参数建立有限元分析基础模型，模型主体主要由3部分组成，分别为钢管、核心混凝土及内部钢筋.所用钢材为Q235钢，混凝土为C30混凝土，钢筋为HRB400热轧带肋钢筋.构件的计算长度为636 mm，纵向长度为300 mm，其余各项模型参数如表 1所示.
表 1(Table 1)

表 1 基础模型参数Table 1 Parameters of the model? mm 参数 钢管直径 钢管壁厚 咬合距离 钢筋直径 取值 219 6 60 12

表 1 基础模型参数 Table 1 Parameters of the model?

3.3 试验结果与模拟结果对比将模型计算得到的结果与试验结果进行对比分析，试验测得的屈服荷载和极限荷载分别为411.3，567.7 kN，通过数值模拟计算得到的屈服荷载和极限荷载分别为414.2，560.3 kN，两组荷载分别相差0.7%，1.2%.数值模拟结果与试验结果对比如图 6所示，可知，两者一致性较好，说明本文建立的有限元模型可以对咬合管幕结构进行模拟.
图 6(Fig. 6)

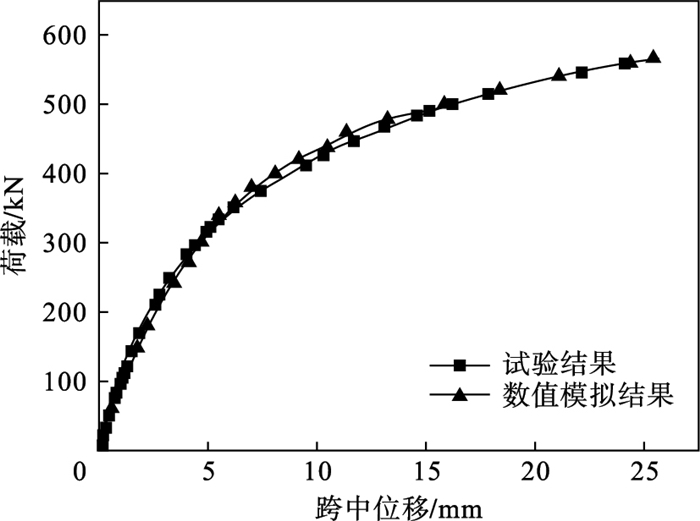图 6 数值模拟结果与试验结果对比Fig.6 Comparison of numerical results and test results

由数值模拟和试验得到的咬合型管幕结构的破坏形式对比如图 7所示，数值模拟准确反映了试件在荷载作用下的破坏过程，试件经历了钢筋屈服、受拉区钢管屈服、受压区混凝土屈服直至试件破坏阶段，试件表现出良好的延性，最终发生弯曲破坏，试验和数值模拟结果保持一致.
图 7(Fig. 7)

图 7 咬合管幕结构的破坏形式对比Fig.7 Comparison of the failure modes of secant pipe roofing structure (a)—破坏形式；(b)—数值模拟.

4 咬合管幕结构抗弯性能分析4.1 破坏流程在模型加载直至破坏的过程中经历了3个阶段：弹性工作阶段、弹塑性工作阶段及强化工作阶段.模型的荷载位移曲线如图 8所示，图中, a，b，c分别为模型的弹性极限荷载、屈服荷载及极限荷载，其值分别为285.4，414.2，560.3 kN.构件在oa段处于弹性受力阶段，此时的荷载位移曲线近似接近于一条直线，荷载急剧增加直到屈服点a，而位移的增加十分有限.构件在ab段进入弹塑性阶段，构件的弯曲刚度逐渐减小，构件在加载过程中开始表现出非线性行为.构件在bc段进入塑性阶段，该阶段内荷载有一定增加，之后趋于稳定，而位移有较大增加.在整个过程中没有观察到明显的曲线下降，这说明构件在弯曲下具有良好的延性.
图 8(Fig. 8)

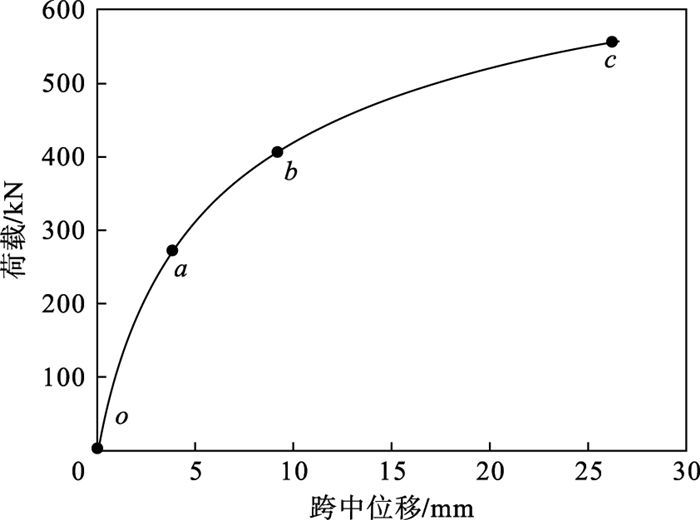图 8 模型的荷载位移曲线Fig.8 Load-displacement curve

4.2 钢管与混凝土的应力重分布随着荷载的增加，构件的变形不断增大，构件各组成部分的应力也会随之增加.当应力增大到一定程度时，如钢管达到屈服状态或混凝土开裂时，构件的应力不再随变形的增大而增大，甚至会有所减小，这时就会出现钢筋和混凝土的应力重分布.
不同加载阶段钢管的竖向应力分布如图 9所示，可知随加载的进行，构件的竖向应力逐渐增大，所有加载阶段中应力最大的钢管都位于中间位置，并且其最大竖向应力出现在截面的中间位置，故取中间钢管混凝土为研究对象，进一步分析加载过程中钢管及混凝土的应力变化.
图 9(Fig. 9)

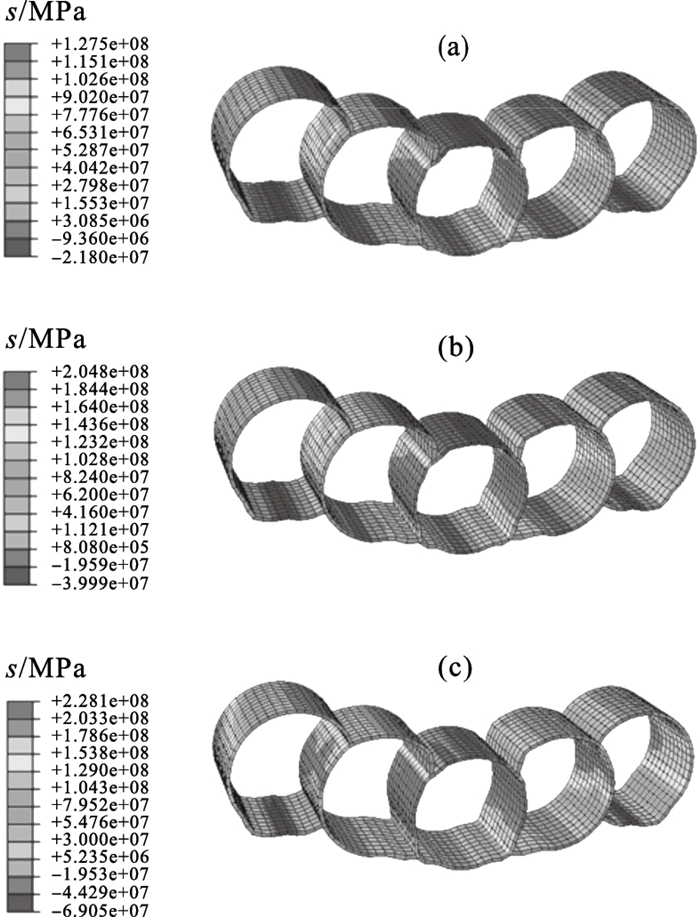图 9 不同阶段钢管竖向应力分布Fig.9 Vertical stress distribution of steel tube at different stages (a)—阶段a；(b)—阶段b；(c)—阶段c.

构件加载过程中，中间钢管不同点的应力-位移曲线如图 10所示，其中横坐标为点13处的竖向位移.由图 10a可知，点7处钢管的Mises应力始终没有达到屈服，这是因为点7位于钢管截面的中性轴附近.点1，点2，点3处的Mises应力始终较小，这是因为在加载过程中，试件发生弯曲变形，两侧钢管对中间钢管有水平向挤压力及向上的作用力，抵消了一部分荷载作用力.由图 10b可知，钢管中竖向应力较大的位置为两侧位置，在整个加载过程中，点1~点3承受纵向压应力，点13的竖向应力始终较小，接近于0.
图 10(Fig. 10)

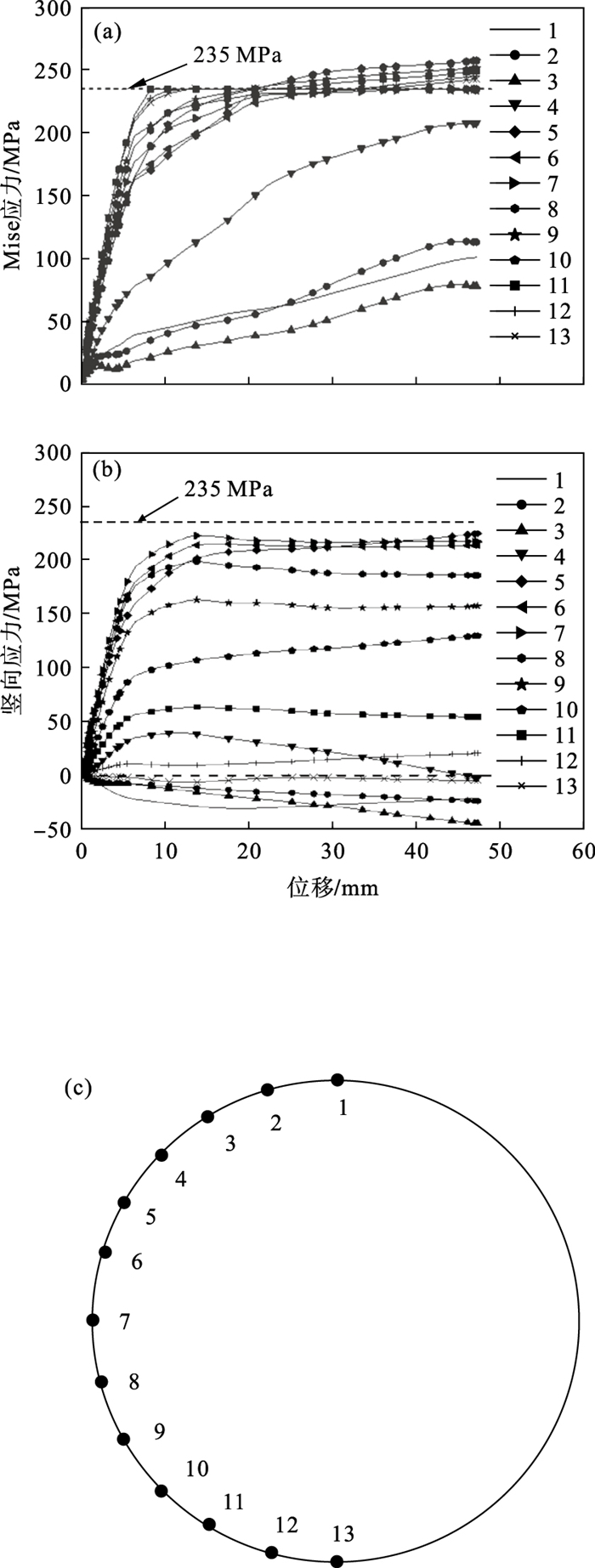图 10 钢管不同位置的应力-位移曲线Fig.10 Stress-displacement curves in the steel tube at different points (a)—Mises应力；(b)—竖向应力；(c)—位置点分布.

构件在不同加载阶段的中间位置钢管的跨中截面沿周长方向的Mises应力发展情况如图 11所示，可知，随荷载的增加，钢管各点的Mises应力逐渐增大，当达到极限荷载时，钢管在点5，点12，点13，点14及点21处达到屈服.点5和点21处的应力屈服是由钢管屈曲变形引起的应力集中造成的.由图 10b及图 11b可知，点12~点14位置处的竖向应力较小，横向压力较大，因此点12~点14位置处的屈服是由钢管底部承受较大的横向拉应力造成的.通过对比不同阶段的应力分布可以看出，在整个加载过程中，模型的中性轴位置没有发生变化.
图 11(Fig. 11)

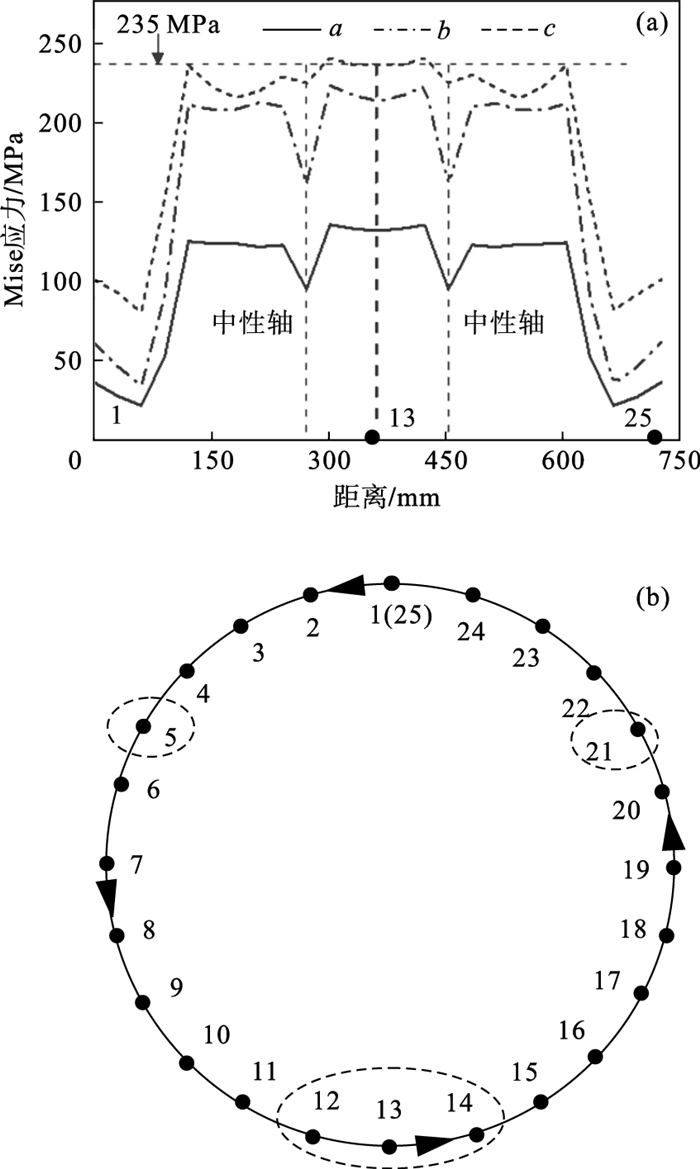图 11 不同阶段钢管Mises应力沿周向变化Fig.11 Development of Mises stress along the circumferential direction of the steel tube at different stages (a)—Mises应力；(b)—位置点分布.

针对加载过程中构件的纵向应力分布情况，取点7为研究对象，其竖向应力沿钢管分布如图 12所示.可知，钢管的最大受力侧所受应力为拉应力，且在阶段a和阶段b，钢管中间位置的应力大于两端的应力；当加载到阶段c时，钢管两端的应力增大超过中间位置，并接近于屈服，这是因为加载到阶段c，钢管的屈曲变形增大进而出现应力集中现象.
图 12(Fig. 12)

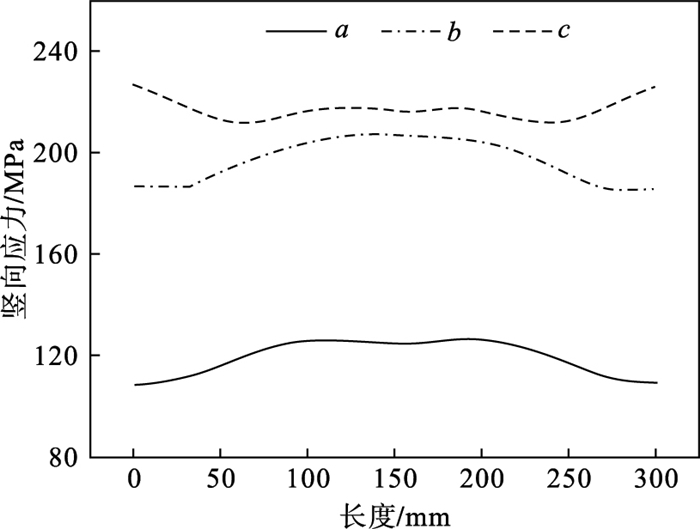图 12 不同阶段钢管竖向应力沿构件长度的变化Fig.12 Variation of vertical stress of steel pipe along the length of the specimen at different stages

不同加载阶段钢管中点1，点7及点13处的横向应力分布及发展情况如图 13所示.可知，在整个加载过程中，钢管在点1和点13承受拉应力.随加载的进行，应力逐渐增大，当加载到阶段c时，钢管在点13处的长度范围内，中间位置的点开始进入屈服状态，这是因为在加载过程中，底部钢管承受较大的拉应力.钢管在点7处承受压应力, 在整个加载过程中，应力变化呈先减小后增大的趋势，这是由钢管两侧在加载过程中的屈曲变形导致的.
图 13(Fig. 13)

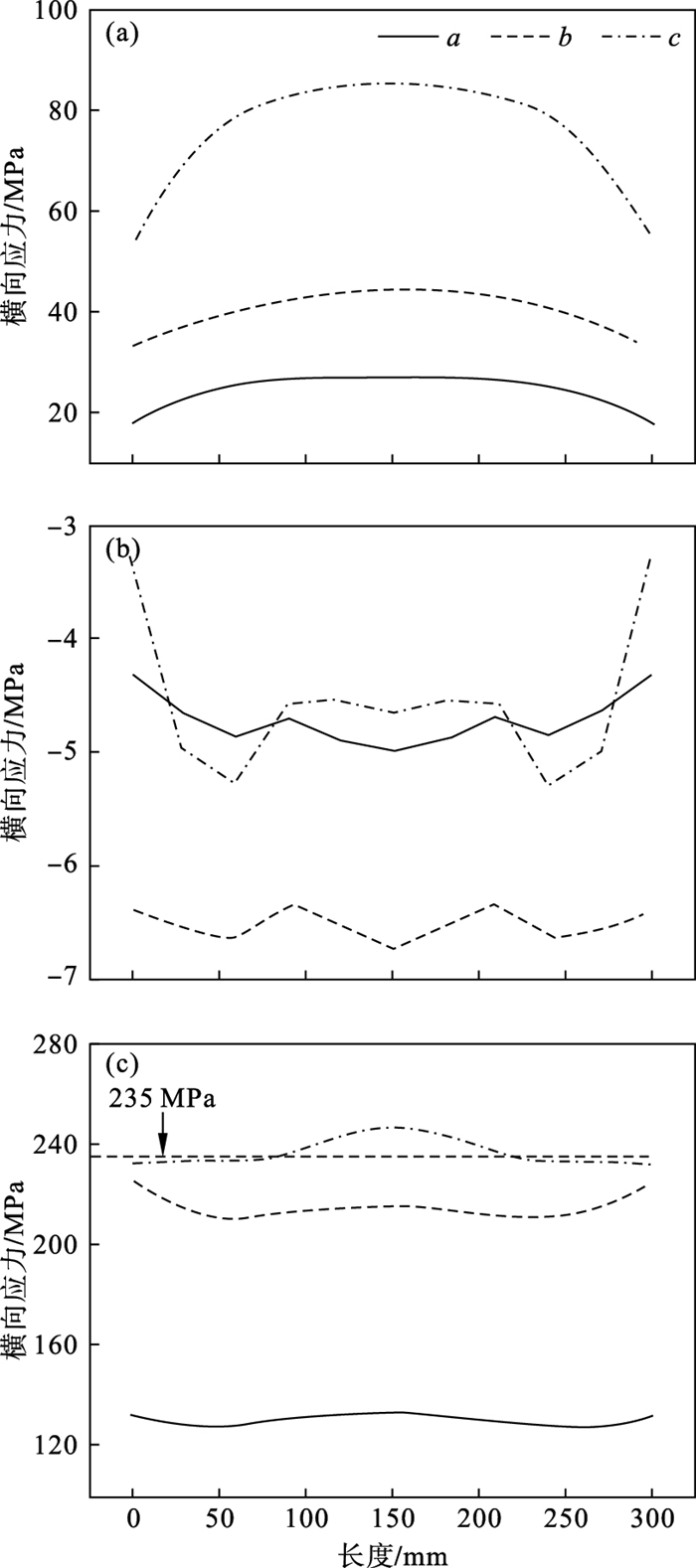图 13 不同阶段钢管横向应力沿构件长度变化Fig.13 Variation of transverse stress of steel pipe along the length of the specimen at different stages (a)—点1；(b)—点7；(c)—点13.

构件中间钢管内核心混凝土的中间位置截面内不同点的竖向应力随混凝土最低点竖向应变的变化曲线如图 14所示.可知，在整个加载过程中，截面内混凝土承受的都是压应力，应力随位置变化的总体趋势是由上到下逐渐减小，这说明越往下点的位置越接近中性轴.位置1处的竖向应力最大值为36.4 MPa，超过了混凝土的抗压强度，这是因为周围钢管的约束作用，使得核心混凝土的抗压强度有所提高.
图 14(Fig. 14)

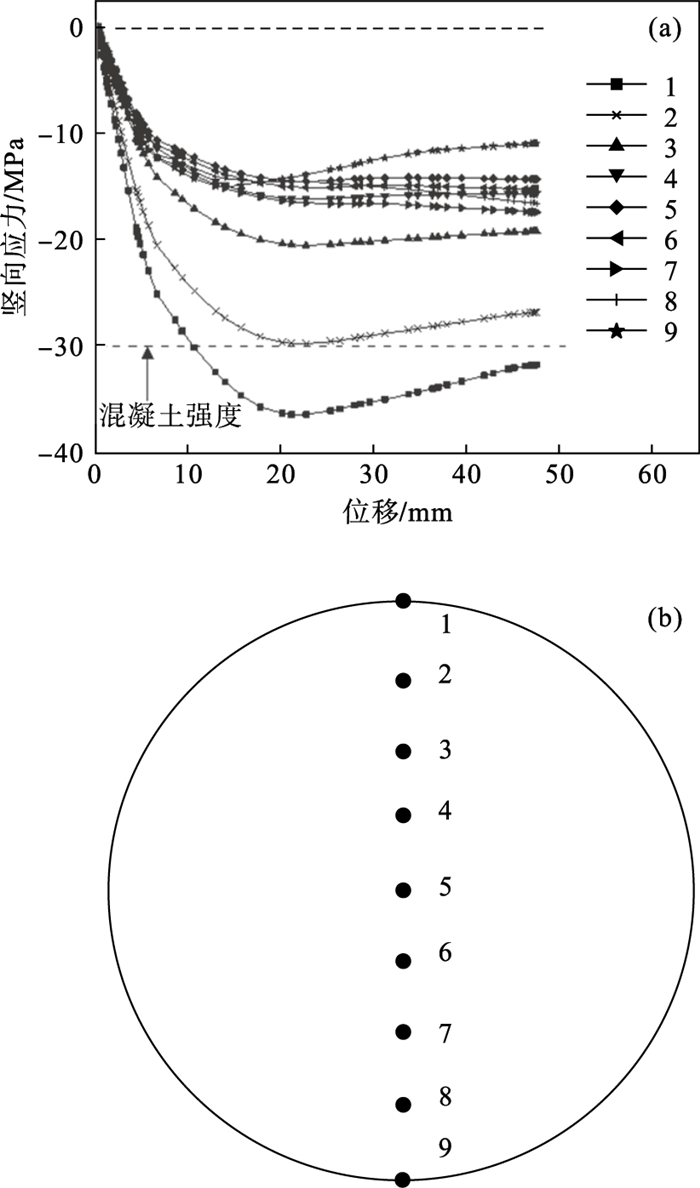图 14 混凝土不同位置的应力-位移曲线Fig.14 Stress-displacement curves of concrete at different locations (a)—应力-位移曲线；(b)—位置点分布.

不同加载阶段构件中间位置钢管内的核心混凝土的竖向应力的分布及发展如图 15所示.可知，截面混凝土在上、中、下3个位置承受的都是压应力，顶点处的压应力最大，当加载到第3阶段时，沿钢管长度的中间段位置的竖向应力超过了混凝土的抗压强度，这是因为钢管对核心混凝土的约束作用提高了核心混凝土的抗压强度.
图 15(Fig. 15)

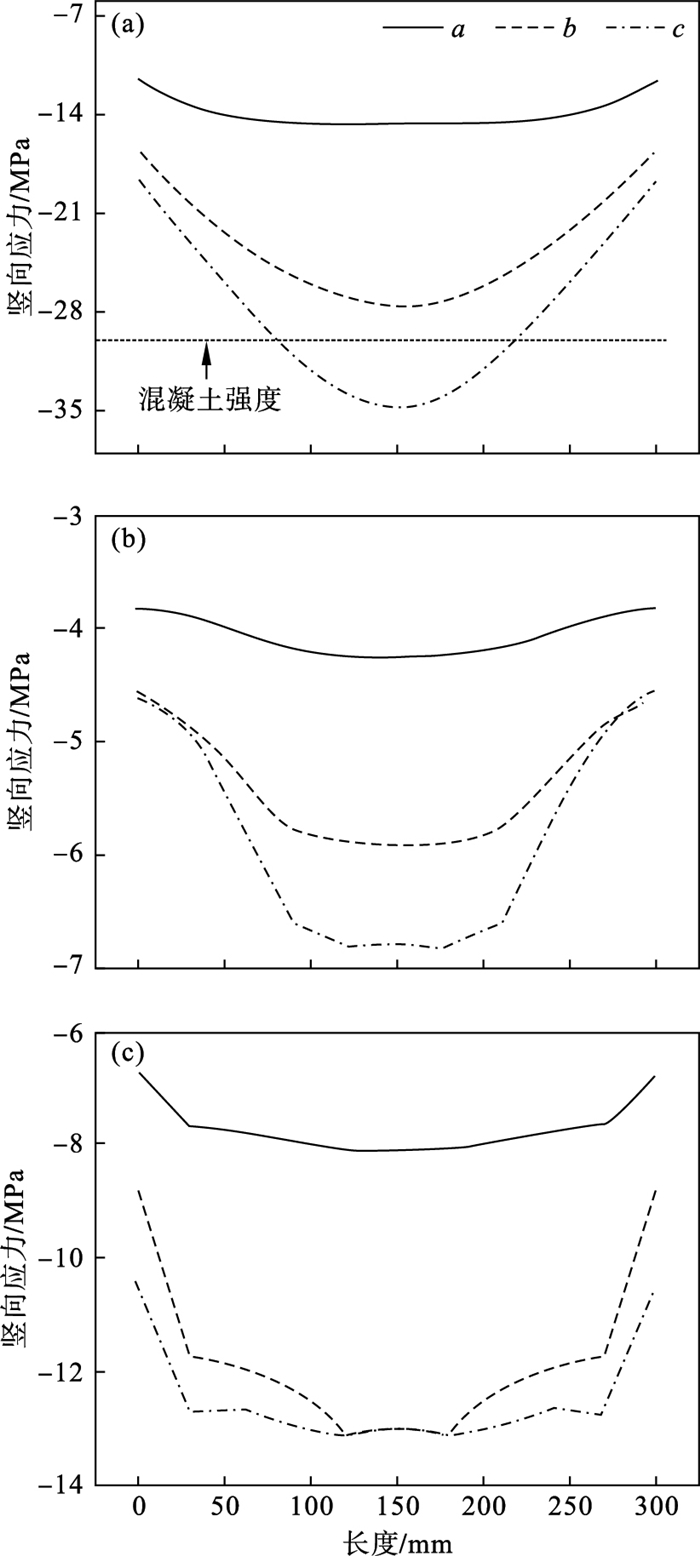图 15 不同阶段混凝土竖向应力沿构件长度的变化Fig.15 Variation of vertical stress of cocrete along specimen length at different stages (a)—点1；(b)—点5；(c)—点7.

核心混凝土不同加载阶段竖向应力的分布如图 16所示，加载到阶段a时，截面内的竖向应力并没有出现明显的分布变化，最大竖向压力随荷载的增加而不断增大，截面在整个加载过程中持续受压，并未出现拉应力.加载到阶段b后，竖向应力开始出现明显的分布变化，沿截面长度方向的应力呈两端小、中间大的趋势，就上、下位置来看，上部应力大于中间及下部应力.
图 16(Fig. 16)

图 16 核心混凝土竖向应力分布图Fig.16 Vertical stress distribution of core concrete (a)—阶段a；(b)—阶段b；(c)—阶段c.

5 咬合管幕结构参数分析选取咬合程度、钢管直径、钢管壁厚及钢筋直径建立不同参数组合下的数值模型，通过数值模拟研究不同参数组合下咬合管幕结构的抗弯性能.
5.1 咬合程度与钢管直径对抗弯性能的影响钢管直径分别为219，244，269，294，319 mm时，咬合程度分别为40，50，60，70，80，90 mm的试件展开交叉模拟，对比分析不同参数组合下咬合管幕结构的抗弯性能.
不同咬合长度与钢管直径组合下咬合管幕结构的抗弯性能如图 17所示.当咬合长度保持不变时，构件的抗弯承载力随钢管直径的增大而增加.当钢管直径保持不变时，弯曲性能随咬合长度的变化未表现出统一的变化规律.对于不同的咬合，钢管直径为219，244，269，294，319 mm时，构件抗弯承载力分别增加104.1%，118.4%，144.4%，165.0%，197.8%，294.3%，增加的百分比值均大于1且随咬合的增加而增大，说明钢管直径对构件抗弯性能有较大影响，咬合长度越大，钢管直径的影响效果越大.
图 17(Fig. 17)

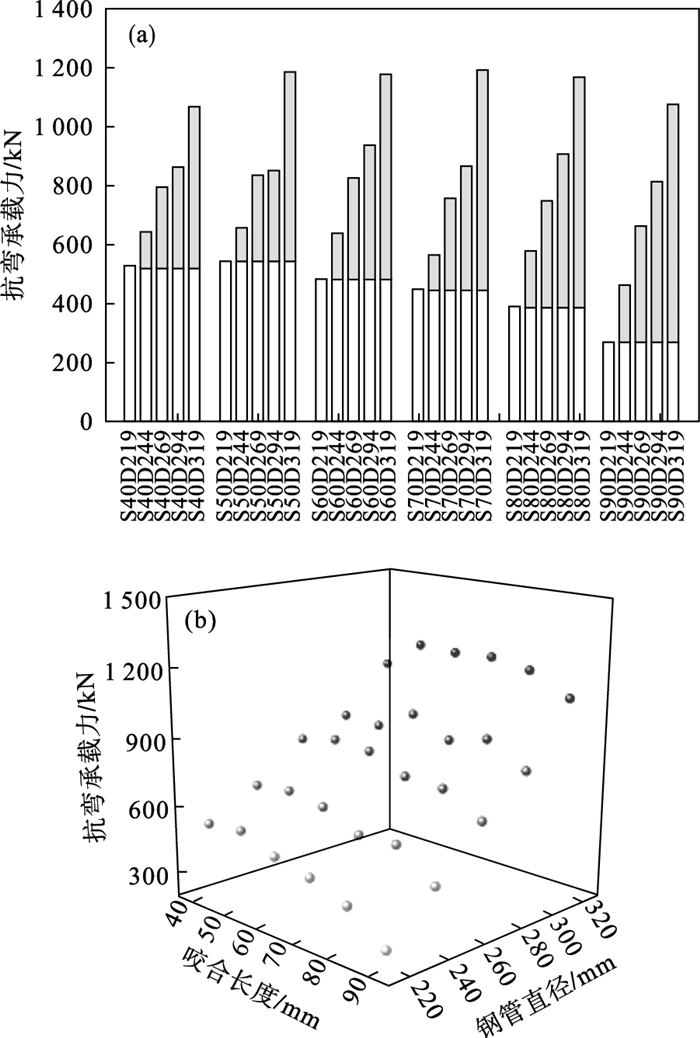图 17 咬合长度与钢管直径组合下的结构抗弯性能Fig.17 The flexural behavior of structure under the combination of secant distance and steel pipe diameter (a)—柱状图；(b)—散点图.

5.2 钢管直径与钢管壁厚对抗弯性能的影响钢管直径分别为219，244，269，294，319 mm，钢管壁厚分别为4，5，6，7，8 mm的试件展开交叉模拟，对比分析不同参数组合下咬合管幕结构的抗弯性能.
钢管直径与钢管壁厚组合下咬合管幕结构的抗弯性能如图 18所示.可知，当钢管直径保持不变时，构建的抗弯承载力随钢管壁厚的增加而增大，但增大的百分比远低于图 16中由于钢管直径的增大而引起的抗弯承载力增大的百分比，说明钢管壁厚对构件抗弯承载力的影响远低于钢管直径对构件抗弯承载力的影响.
图 18(Fig. 18)

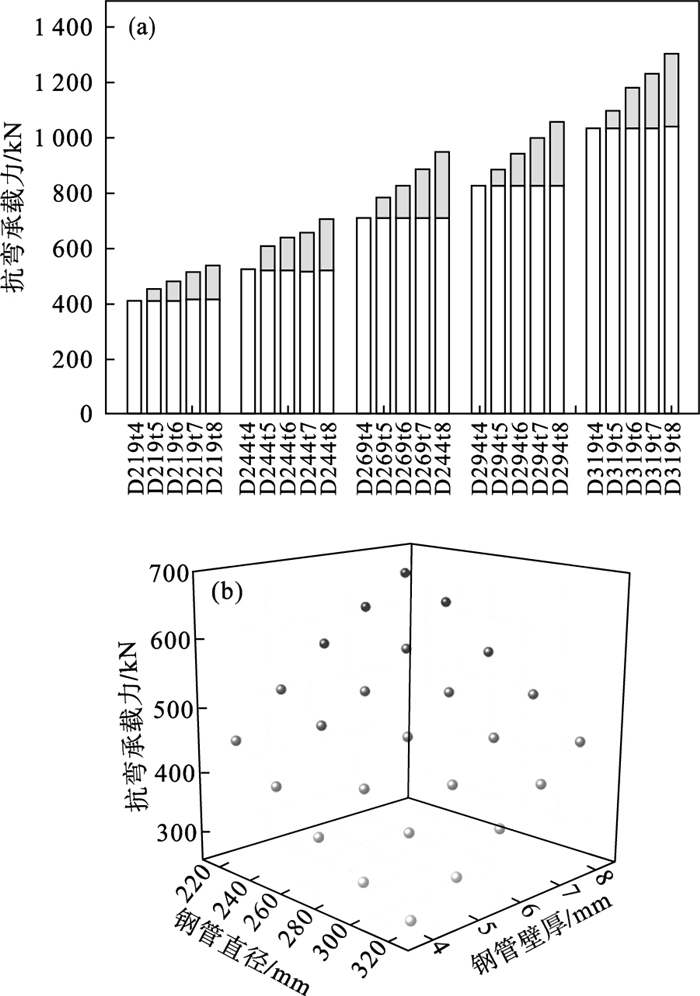图 18 钢管直径与钢管壁厚组合下结构的抗弯性能Fig.18 The flexural behavior of the structure under the combination of steel tube diameter and steel tube thickness (a)—柱状图；(b)—散点图.

5.3 钢管壁厚与钢筋直径对抗弯性能的影响钢管壁厚分别为4，5，6，7，8 mm，钢筋直径分别为8，10，12，14，16 mm的试件展开交叉模拟，对比分析不同参数组合下咬合管幕结构的抗弯性能.
钢管壁厚与钢筋直径组合下咬合管幕结构的抗弯性能如图 19所示.可知，当钢管壁厚保持不变时，构件的抗弯承载力随钢筋直径的增大而逐渐增大，但增大的百分比较小.随钢管壁厚的增加，抗弯承载力随钢筋直径的增大而增大的百分比逐渐减小，说明钢管壁厚越大，钢筋直径对承载力的影响效果越不明显.当钢管壁厚为8 mm时，钢筋直径从8 mm增加到16 mm，构件的抗弯承载力仅增加了3.6%，可以忽略不计.这说明增大钢筋直径对提高构件的抗弯承载力作用较小.
图 19(Fig. 19)

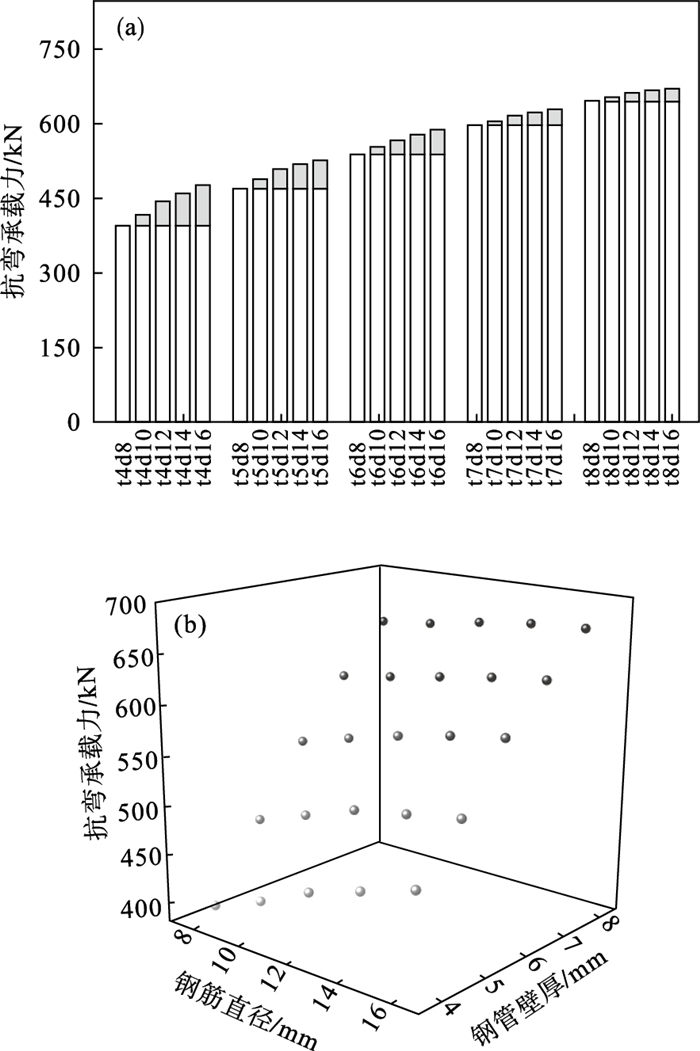图 19 钢管壁厚与钢筋直径组合下结构的抗弯性能Fig.19 The flexural behavior of the structure under the combination of steel tube thickness and steel bar diameter (a)—柱状图；(b)—散点图.

6 结论1) 建立了咬合管幕结构的有限元模型，对比了构件屈服荷载和极限荷载的数值模型计算结果和试验结果，二者分别相差0.7%，1.2%，表现出较高的一致性，证明了数值模拟结果的合理性.
2) 咬合管幕结构在加载过程中经历了弹性阶段、弹塑性阶段及强化阶段，表现出良好的延展性，其最终破坏模式为弯曲破坏.最终的破坏位置为钢管的两侧及底部，钢管两侧的破坏是由钢管屈曲导致，钢管底部的破坏是横向受拉破坏.
3) 在加载过程中钢管发生屈曲变形而出现应力集中，核心混凝土受到钢管的约束抗压强度增大.随加载的进行，钢管与核心混凝土之间出现明显应力重分布及黏结滑移.
4) 得到了多结构参数对咬合管幕结构抗弯性能的联合影响，咬合距离越大，钢管直径对抗弯强度的影响效果越明显；对于咬合距离分别为40，90 mm的构件，当钢管直径增加45.7%时，结构抗弯承载力分别提高104.1%，294.3%.钢筋直径对抗弯承载力的影响随钢管壁厚的增大而逐渐减小.
参考文献

[1]	韩宝明, 杨智轩, 余怡然, 等. 2020年世界城市轨道交通运营统计与分析综述[J]. 都市快轨交通, 2021, 34(1): 5-11. (Han Bao-ming, Yang Zhi-xuan, Yu Yi-ran, et al. Statistical analysis of urban rail transit operation in the world in 2020:a review[J]. Urban Rapid Rail Transit, 2021, 34(1): 5-11.)
[2]	Fang Q, Zhang D, Wong L N Y. Environmental risk management for a cross interchange subway station construction in China[J]. Tunnelling and Underground Space Technology, 2011, 26(11): 750-763.
[3]	Zhang Z Q, Li H Y, Liu H Y, et al. Load transferring mechanism of pipe umbrella support in shallow-buried tunnels[J]. Tunnelling and Underground Space Technology, 2014, 43: 213-221. DOI:10.1016/j.tust.2014.05.018
[4]	Xiao H, Zhou S, Sun Y. Stability analysis and case study of shallow tunnel using pipe roof support[J]. Geotechnical and Geological Engineering, 2019, 37(3): 1249-1260. DOI:10.1007/s10706-018-0681-x
[5]	Coller P J, Abbott D G. Microtunneling techniques to form an insitu barrier around existing structures[J]. American Society of Civil Engineers, 1994, 2: 386-394.
[6]	Musso G. Jacked pipe provides roof for underground construction in busy urban area[J]. Civil Engineering, 1979, 49(11): 79-82.
[7]	Ire H. Tubular trust jacking for underground roof construction on the Antwerp Metro[J]. Tunnelling, 1985, 5: 13-15.
[8]	Xiao J Z, Dai F C, Wei Y Q, et al. Analysis of mechanical behavior in a pipe roof during excavation of a shallow bias tunnel in loose deposits[J]. Environmental Earth Sciences, 2016, 75(4): 293-301. DOI:10.1007/s12665-015-5176-y
[9]	Shimada H, Hamanakal A, Sasaoka T, et al. Effect of application of pipe roof method by using pipe jacking on behavior of surrounding soil[J]. Physical Science and Application, 2013, 6: 353-358.
[10]	Zhang Z, Li H, Liu H, et al. Load transferring mechanism of pipe umbrella support in shallow-buried tunnels[J]. Tunnelling and Underground Space Technology, 2014, 43: 213-221. DOI:10.1016/j.tust.2014.05.018
[11]	Xie X, Zhao M, Shahrour I. Experimental study of the behavior of rectangular excavations supported by a pipe roof[J]. Applied Sciences, 2019, 9(10): 2082-2091. DOI:10.3390/app9102082
[12]	Xie X, Zhao M, Shahrour I. Face stability model for rectangular large excavations reinforced by pipe roofing[J]. Tunnelling and Underground Space Technology, 2019, 94: 103132. DOI:10.1016/j.tust.2019.103132
[13]	Jia P J, Zhao W, Chen Y, et al. A case study on the application of the steel tube slab structure in construction of a subway station[J]. Applied Sciences, 2018, 8(9): 1437-1445. DOI:10.3390/app8091437
[14]	黎永索, 张可能, 黄常波, 等. 管幕预筑隧道地表沉降分析[J]. 岩土力学, 2011, 32(12): 3701-3707. (Li Yong-suo, Zhang Ke-neng, Huang Chang-bo, et al. Analysis of surface subsidence of tunnel built by pipe-roof pre-construction method[J]. Rock and Soil Mechanics, 2011, 32(12): 3701-3707. DOI:10.3969/j.issn.1000-7598.2011.12.027)
[15]	黎永索, 张可能, 黄常波. 管幕预筑隧道衬砌结构现场监测分析[J]. 岩土工程学报, 2012, 34(8): 1541-1547. (Li Yong-suo, Zhang Ke-neng, Huang Chang-bo. Monitoring of lining structure of tunnels built by using pipe-roof pre-construction method[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1541-1547.)
[16]	Liu J, Ma B, Cheng Y. Design of the Gongbei tunnel using a very large cross-section pipe-roof and soil freezing method[J]. Tunnelling and Underground Space Technology, 2018, 72: 28-40. DOI:10.1016/j.tust.2017.11.012
[17]	赵文, 贾鹏蛟, 王连广, 等. 地铁车站STS新管幕构件抗弯承载力试验研究[J]. 工程力学, 2016, 33(8): 167-176. (Zhao Wen, Jia Peng-jiao, Wang Lian-guang, et al. Experimental study on the flexural capacity of steel tube slab members of subway stations[J]. Engineering Mechanics, 2016, 3(8): 167-176.)
[18]	Jia P J, Zhao W, Guan Y P, et al. Experimental study on the flexural behavior of steel tube slab composite beams and key parameters optimization[J]. Advances in Structural Engineering, 2019, 6(2): 181035.
[19]	赵文, 李伟伟, 金文强, 等. 地下咬合型管幕构件抗弯刚度参数分析[J]. 东北大学学报(自然科学版), 2020, 41(7): 1014-1019. (Zhao Wen, Li Wei-wei, Jin Wen-qiang, et al. Parameter analysis of flexural stiffness of underground secant pipe roof structure[J]. Journal of Northeastern University(Natural Science), 2020, 41(7): 1014-1019.)
[20]	Ding F X, Ying X Y, Zhou L C, et al. Unified calculation method and its application in determining the uniaxial mechanical properties of concrete[J]. Frontiers of Architecture and Civil Engineering in China, 2011, 5(3): 381-393.
[21]	韩林海. 钢管混凝土结构——理论与实践[M]. 北京: 科学出版社, 2007: 67-75. (Han Lin-hai. Concrete filled still tubular structure—theory and practice[M]. Beijing: Science Press, 2007: 67-75.)
[22]	李伟伟. 地下工程咬合型管幕结构的抗弯性能研究[D]. 沈阳: 东北大学, 2019. (Li Wei-wei. Study on flexural behavior of secant pipe roofing structure on subsurface engineering[D]. Shenyang: Northeastern University, 2019. )