王宏民^1,2, 禅亮^1,2
1. 哈尔滨理工大学 自动化学院, 黑龙江 哈尔滨 150080;
2. 黑龙江省复杂智能系统与集成重点实验室，黑龙江 哈尔滨 150080
收稿日期：2021-10-28
基金项目：黑龙江省自然科学基金资助项目(F201310)。
作者简介：王宏民(1962-)，男，黑龙江哈尔滨人，哈尔滨理工大学教授。

摘要：基于振动分析的齿轮故障检测已被证明在故障识别中是有效的，但对表征早期磨损的振动信号的提取和识别仍没有得到很好的解决.本文提出一种基于频谱相关性分析的变分模态分解(VMD)和核支持向量机(SVM)相结合的齿轮早期磨损诊断方法，对能够揭示早期磨损状态的微弱齿轮振动信号采用近似完全重构的准则来初始化模式数，并采用信号功率谱密度最大值对应的频率初始化VMD方法的中心频率，用以有效提取齿轮磨损信息，进而结合核支持向量机进行齿轮的早期磨损诊断.实验结果表明，所提方法可有效克服背景噪声大无法预设模式数的问题，对噪声具有更好的鲁棒性，诊断准确率达到94.4%，可为齿轮早期磨损检测提供解决方法.
关键词：齿轮振动信号的提取早期磨损诊断频谱相关性分析变分模态分解支持向量机
Early Wear Diagnosis of Gears Based on Spectrum Correlation Analysis
WANG Hong-min^1,2, CHAN Liang^1,2
1. School of Automation, Harbin University of Science and Technology, Harbin 150080, China;
2. Heilongjiang Provincial Key Laboratory of Complex Intelligent System and Integration, Harbin 150080, China
Corresponding author: WANG Hong-min, E-mail: 13904810908@163.com.

Abstract: Gear fault detection based on vibration analysis has been proven to be effective in fault identification. However, the extraction and identification of vibration signals characterizing early wear have not been solved well. This paper proposes a method for early wear diagnosis of gears, combining variational mode decomposition (VMD) based on spectrum correlation analysis with kernel support vector machine (SVM). For weak gear vibration signals that can characterize early wear, the modal numbers are initialized by an approximate complete reconstruction criterion. Meanwhile, the frequency corresponding to the maximum value of the signal power spectral density is used to initialize the center frequency of the VMD method. It is used to effectively extract gear wear information from gear vibration signals and then be combined with kernel support vector machines for early wear diagnosis of gears. The experimental results show that the proposed method can effectively overcome the problem that the modal numbers cannot be preset with large background noise, be with better robustness to noisy situations, and achieve a diagnostic accuracy of 94.4%, which provides a solution for early wear detection of gears.
Key words: extraction of gear vibration signalsearly wear diagnosisspectrum correlation analysisvariational mode decomposition (VMD)support vector machines (SVM)
随着新能源汽车在工业生产中的普及，其传动系统的故障、磨损和损伤，尤其是齿轮的早期磨损和故障，已经造成了诸多的故障停机和经济损失.为了保证机器安全、平稳运行，必须跟踪磨损的生长状况并预测其未来的发展趋势，以便在机器出现进一步损伤之前及时进行维修或更换^[1-2].
在早期的磨损阶段，局部磨损(如点蚀、裂纹或剥落)是导致故障的主要来源.一般情况下，齿轮的故障会产生冲击，结果是在振动信号中可以观察到瞬态激励.然而，齿轮齿面的局部磨损通常会导致振动信号的微弱瞬变，由于齿轮箱复杂的结构和运行环境，振动传感器采集信号的精度受背景噪声和测点位置的影响较大，导致齿轮产生的微弱振动信号往往被噪声掩盖，使得弱故障特征提取变得困难.具体来说，对于含有噪声的非平稳时间序列，具有时、频域多解析能力的小波变换及其改进型^[3]能够弥补频谱分析的局限，以检测非平稳信号的多瞬态现象，但是主观确定的小波基函数和降噪阈值不适用于多特征匹配.经验模态分解^[4]在处理非平稳信号时特别有效，并且不需要在分解时选择基函数.然而，在实际应用中，分解的精度受噪声的影响很大，同时噪声会导致严重的模式混叠.经过研究人员的努力，提出了集成经验模态分解(ensemble empirical mode decomposition, EEMD)^[5]和完全集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)^[6]的方法，虽然计算效率和精度有所提升，但是噪声干扰和模式混叠的问题并没有得到根本解决^[7-8].
为了解决早期磨损检测中噪声干扰和模式混叠问题，基于自适应模态分解的概念，Dragomiretskiy等^[9]提出了一种非递归的变分模态分解(variational mode decomposition, VMD)方法.VMD方法能在不考虑先验变换条件的情况下揭示微弱的瞬态信息，是一种有效的旋转机械故障诊断方法^[10].该方法通过构建变分求解和自适应滤波器组来检测微弱的齿轮信号，在一定程度上避免了EEMD和CEEMDAN方法的模态混叠问题.但是，由于背景噪声大，无法预先设置模式数，导致分解不充分或过分解的问题.模式数的合理性对齿轮磨损检测结果有显著影响，限制了VMD方法的适应性.在文献中，Yang等^[11]为检测液压管早期故障，提出了最优模态分解，应用遗传算法优化VMD参数，但是优化算法加重了计算负担，适应度函数的选取会严重影响超参数的设定.Gai等^[12]为揭示轴承的早期故障特征，采用混合灰狼优化器来寻找VMD最优的参数组合.朱永利等^[13]采用双阈值法确定最佳模式数，但是其计算结果取决于主观定义阈值，缺乏普遍适应性.
关联齿轮磨损与齿轮振动信号之间的关系是实现齿轮健康状态诊断的基础.对包含齿轮磨损信息的固有模态函数(intrinsic mode function，IMF)分量实施特征提取，得到稳定的磨损特征矩阵，才能识别齿轮的磨损程度.SVM(support vector machines)可以在输入和输出之间建立更稳定、更有效的非线性关系，其性能高度依赖于核函数和核参数.自适应粒子群算法可以通过迭代寻优改善性能, Ma等^[14]构建了自适应粒子群算法优化的最优加权最小二乘SVM辨识非线性模型.Han等^[15]采用核主成分分析和混合核的支持向量机模型预测金融危机.Gao等^[16]采用广义多核学习支持向量机诊断复杂电气系统的早期故障.Yao等^[17]采用优化的支持向量机来诊断电动汽车电池组中的故障.Wu等^[18]提出了一种基于堆叠集成学习和广义多类支持向量机的健康状态评估方法，并将其应用于复杂降解系统的健康状态评估.
针对上述问题，本文提出了一种基于频谱相关性分析的VMD方法，对磨损齿轮振动信号进行特征提取，并结合改进的支持向量机(SVM)识别磨损程度.首先，采用局部加权回归散点平滑(locally weighted scatter smoothing, LOWESS)算法平滑信号，通过近似完全重构的准则确定合适的模式数.其次，为了减少迭代次数，求解信号的功率密度谱，以最大值对应的频率初始化中心频率.最后，通过VMD方法获取相应的磨损特征，并结合自适应粒子群优化(adaptive particle swarm optimization, APSO)算法的SVM进行分类.
1 基于频谱相关性分析的VMD方法1.1 VMD方法的局限性由于VMD方法将目标信号视为调幅调频信号，在分解时自适应地分配模式.如果事先设定合适的模式数，可以准确地识别齿轮的特征频率.为了验证这一点，本文采用式(1)所示的3个调幅信号产生混合模拟信号，代表实际应用中的多重调制现象.模拟信号的采样频率为10 kHz，测试模拟信号x(t)的波形和频谱如图 1和图 2所示.可以观察到3个子信号的频带在频域中被明显划分，在此基础上确定模式数k=3.

(1)

图 1(Fig. 1)

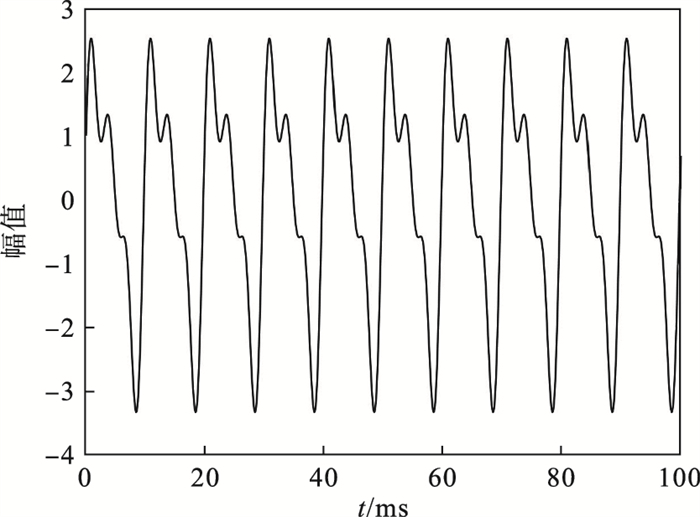图 1 模拟信号的波形Fig.1 Waveform of analog signal

图 2(Fig. 2)

图 2 模拟信号的频谱Fig.2 Spectrum of analog signal

使用VMD方法分解模拟信号，分解后的子信号频谱结果如图 3所示.对比图 2可以观察到，VMD方法在频谱中准确地分解混合模拟调幅信号，分解获得的频率分量与原信号一致，3种模式在频域中清晰可见，3个微弱的信号分量具有稳定的频率，瞬时振幅接近原始信号.这意味着VMD可以提取隐藏在不同子信号中的脉冲特征.
图 3(Fig. 3)

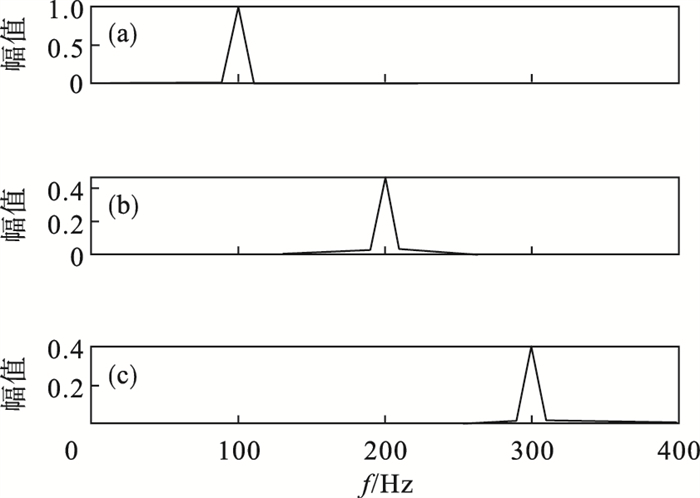图 3 VMD方法分解后子信号频谱Fig.3 Sub-signal spectrum after VMD decomposition (a)—IMF1；(b)—IMF2；(c)—IMF3.

为了说明VMD方法的局限性，本文在构造的原始信号中加入了高斯白噪声，样本的信噪比为-10 dB，噪声信号波形和频谱如图 4和图 5所示.对比图 1和图 2原始信号时域波形和频谱，加入噪声后信号频谱更加复杂，出现了许多无意义的极值点，同时改变了信号波形.
图 4(Fig. 4)

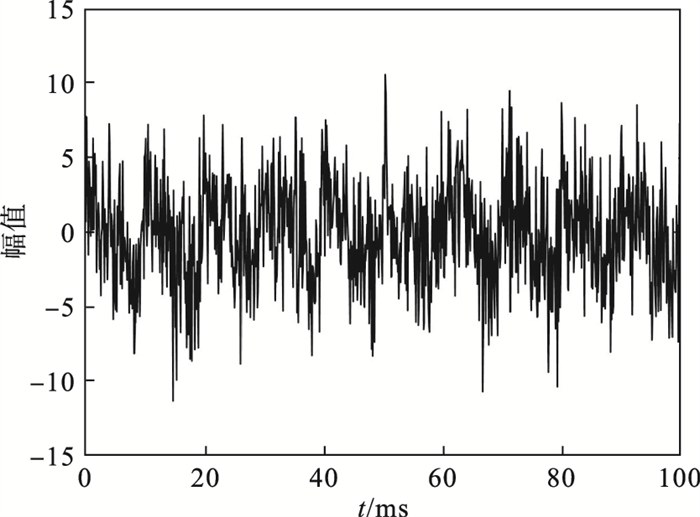图 4 噪声信号的波形Fig.4 Waveform of noise signal

图 5(Fig. 5)

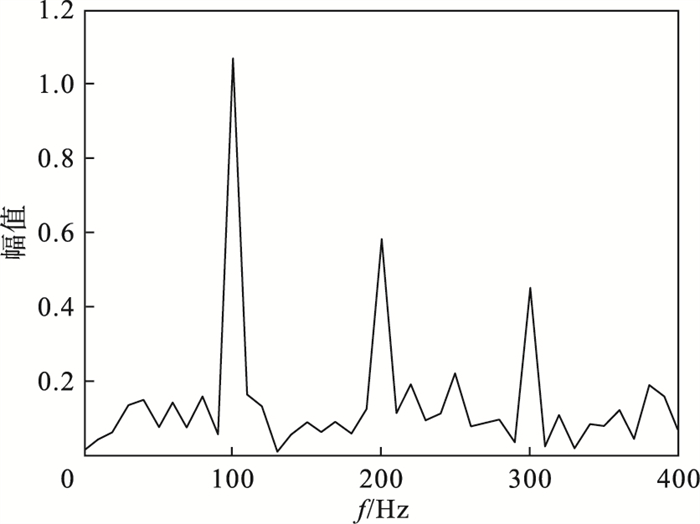图 5 噪声信号频谱Fig.5 The spectrum of the noise signal

为了观察噪声对原始信号的影响，采用VMD分解噪声信号，模式数仍设置为3，图 6为噪声信号经过分解后子信号频谱.可以注意到模式1，2，3的幅值和波形发生了变化，其中模式3已经无法辨识，这也意味着子信号的信息在分解后丢失，
图 6(Fig. 6)

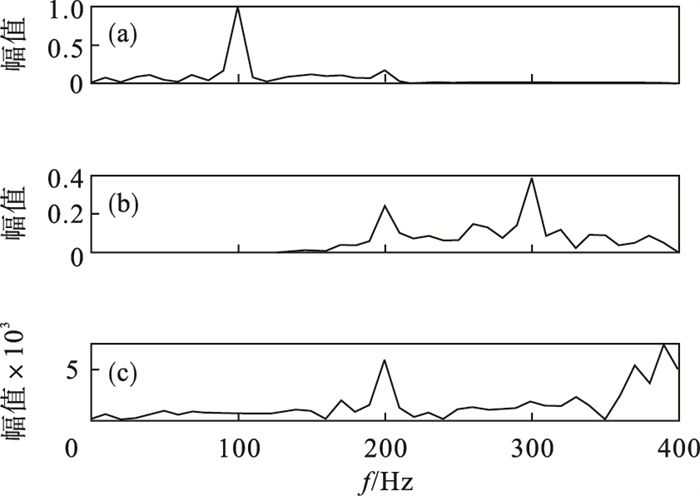图 6 VMD分解噪声信号后子信号频谱Fig.6 Sub-signal spectrum after VMD decomposition of noise signal (a)—IMF1；(b)—IMF2；(c)—IMF3.

这是由于添加噪声造成的.IMF2和IMF3中的信号频谱被噪声覆盖，信号幅值在分解后发生了变化，无法获取有关子信号特征.因此，通过分解后得到的子信号重构原始信号，以期获得相关原始信号特征是不可能的.
虽然VMD方法可以准确地识别模拟信号的脉冲特征，但由于背景噪声大，无法准确地设置模式数，导致很难准确地识别隐藏在实际信号中的弱故障特征.分解不足时，部分模式被丢弃或被相邻模式共享.齿轮的弱故障特征可能被子信号中的噪声掩盖，分解过大时，齿轮信号的故障特征可能被分解为不同的模式，无法识别.
1.2 基于频谱相关性分析的VMD方法在上节，VMD方法使用时，需要预设目标信号的模式数，这就需用户提前掌握原始信号的一些先验信息，否则会导致信号的过分解或分解不足.然而，含噪信号的分解结果通常会在子信号中混有一定量的噪声，这意味着强噪声背景可能会造成信息丢失和过分解的问题，削弱磨损特征的可视化.为了解决这个问题，本文提出了一种改进的VMD方法，有序地解决了信息丢失和过分解的问题.
首先，使用LOWESS算法对信号频谱预处理，计算出目标信号的频谱分量个数，将其分配给模式数k，以实现原始信号的近似完全重构.将信号功率谱密度最大值对应的频率作为f_k的初值，以较少迭代次数加快计算速度.噪声的调制使得频谱中产生了许多无意义的极值点，为了剔除频谱中无意义的极值点，本文选取信号长度的3%作为匹配长度，保证了信号频谱的局部结构得到保护，消除了无意义的极值点.
实值信号Z根据式(2)更新模态函数和中心频率，被分解为k个具有一定稀疏性的模态u_k，且每个模态围绕一个中心频率f_k.直到满足∑_k‖u_kⁿ⁺¹-u_kⁿ‖₂²/‖u_kⁿ‖₂² < e的约束条件，然后获得预设模式数下具有稀疏特性的IMFs.

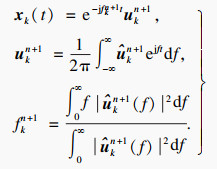(2)

在获得几乎包含了所有信息的IMF之后，可以得到几种包含故障特征的组合模式.然后通过模式函数x_k(t)重构原始信号，以显示故障的明显特征.

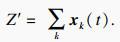(3)

为了解决原始的VMD方法对含有噪声的信号进行分解时存在信息丢失的问题，本文使用改进的方法解决这个问题.首先实施LOWESS算法平滑第2节中构造的含噪信号，通过降噪平滑后的频谱图如图 7所示，从图中可以观察到频谱分量有11个，因此k=11，确定初始f_k=100，VMD方法分解后的子信号的前3个分量的频谱图如图 8所示.其中每一个IMF分量仅包含一个显著频率，特征频率非常明显，说明改进后的方法故障特征可视化能力优于原始方法，可以应用于齿轮振动信号的弱故障诊断.
图 7(Fig. 7)

图 7 LOWESS算法平滑后噪声信号频谱分量Fig.7 Spectral component of the noise signal after LOWESS algorithm

图 8(Fig. 8)

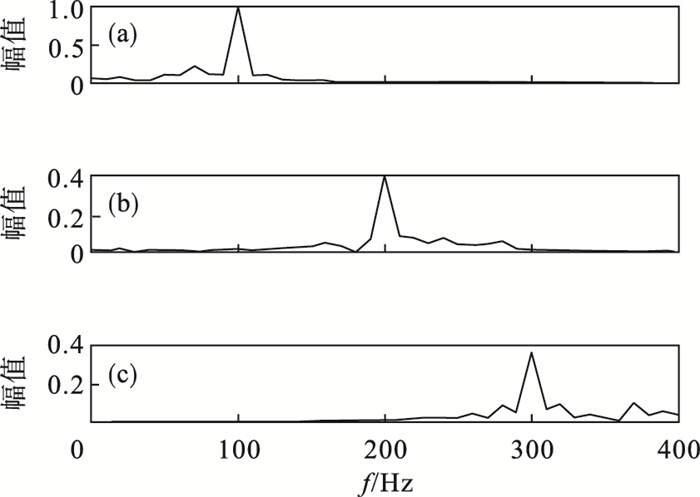图 8 改进的VMD方法分解后前3个分量频谱Fig.8 Spectrum of the first three components after decomposition of the improved VMD method (a)—IMF1；(b)—IMF2；(c)—IMF3.

1.3 仿真实验分析为了验证所提方法在齿轮健康状态特征提取中的有效性，采用文献[7]中带Bootstrap重采样优化的CEEMD方法进行比较.Bootstrap重采样通过对原始信号中的噪声进行重新计算，得到最佳噪声输入值，来减小输入噪声对分解结果的影响.CEEMD自适应地将混合信号分解成7个固有模态函数.混合信号的前3个IMF的时域图如图 9所示.
图 9(Fig. 9)

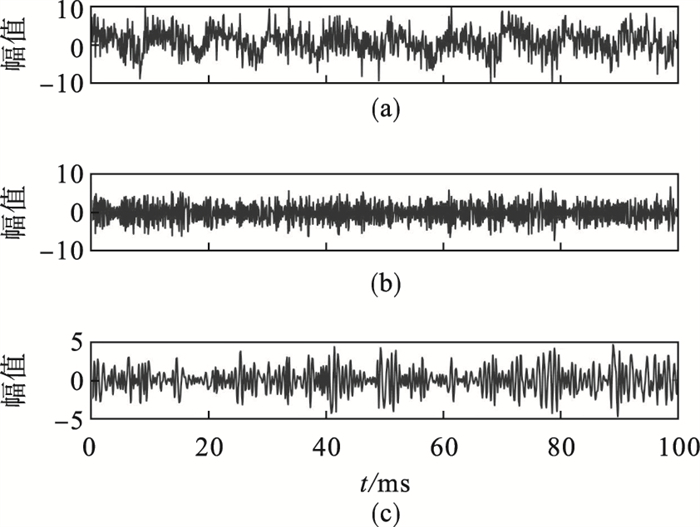图 9 CEEMD分解前3个IMF的时域图Fig.9 Time domain diagrams of the first three IMFs after CEEMD decomposition (a)—IMF1；(b)—IMF2；(c)—IMF3.

将前3个IMF变换到频域，其时域波形和频谱如图 10所示，混合信号x(t)可以在IMF1中清晰观察到，IMF2和IMF3中均含有大量的噪声，频域波形复杂，无法获取信号的特征.
图 10(Fig. 10)

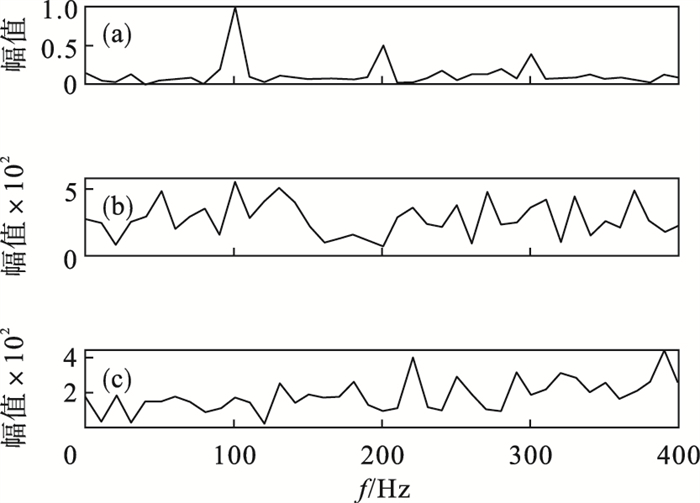图 10 CEEMD分解前3个IMF的频谱Fig.10 Spectrum of the first three IMFs after CEEMD decomposition (a)—IMF1；(b)—IMF2；(c)—IMF3.

所提方法和Bootstrap重采样优化的CEEMD方法均能在含有噪声的混合信号中提取齿轮振动信号，区别在于VMD方法将混合信号视为调幅调频信号，能够把混合信号中的子信号一一分解出来，不会存在信号混叠的情况，可通过特征提取实现齿轮磨损诊断.CEEMD方法虽成功分解出了由3个子信号组成的混合信号，但对信号的深度分解存在不足，因此，存在调幅调频的齿轮磨损诊断中VMD方法具有更好的噪声鲁棒性.
2 VMD辅助SVM的齿轮磨损诊断本文通过提取IMF分量中的特征参数，来表征齿轮早期磨损程度，并结合SVM实现齿轮健康状态的监控.
2.1 改进的SVM诊断模型在获得齿轮磨损特征集{x_i, y_i}_i=1^N，齿轮样本标签y_i∈{1, 2, 3, 4, 5, 6}的条件下，SVM分类器通过搜索超平面来解决分类问题，该超平面通过一组来自原始齿轮磨损特征数据集的支持向量建立，分离的最优超平面由w·x+b=0确定，类别y_i与输入向量x_i之间满足以下不等式：

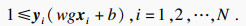(4)

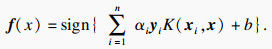其中，w是决策面权重系数.通过权衡风险(对样本的拟合能力)和结构风险(对测试样本的预测能力)求解方程(5)实现分类功能.

(5)

其中：α_i是拉格朗日乘数；K(x_i, x)=φ(x_i)是预定义的核函数，核函数将原本非线性不可分的特征空间映射到高维的线性可分空间.
2.2 基于自适应粒子群算法的参数优化由于使用核支持向量机进行辅助检测，惩罚因子和核函数宽度对SVM的分类精度有很大的影响，针对参数的离散性和不确定性，需要一种迭代寻优算法计算2个参数的最优值.
粒子群算法通过个体经历位置中的适应度最优位置和种群中所有粒子搜索的适应度最优位置来更新个体位置.为避免早熟收敛、局部最优的问题，引入变异操作，使得粒子跳出当前搜索的最优位置，在更大的空间中开展搜索，粒子速度和位置更新迭代如下:

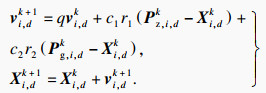(6)

其中：X_{i, d}^k和v_{i, d}^k是粒子位置和速度；P_{z, i, d}^k和P_{g, i, d}^k是粒子的个体极值和群体极值；q是惯性因子；c₁和c₂是学习因子；r₁, r₂为[0, 1]范围内的随机数.
2.3 基于改进的VMD和核SVM的齿轮早期磨损诊断模型提出的基于改进的VMD、核SVM的齿轮早期磨损诊断模型如图 11所示.
图 11(Fig. 11)

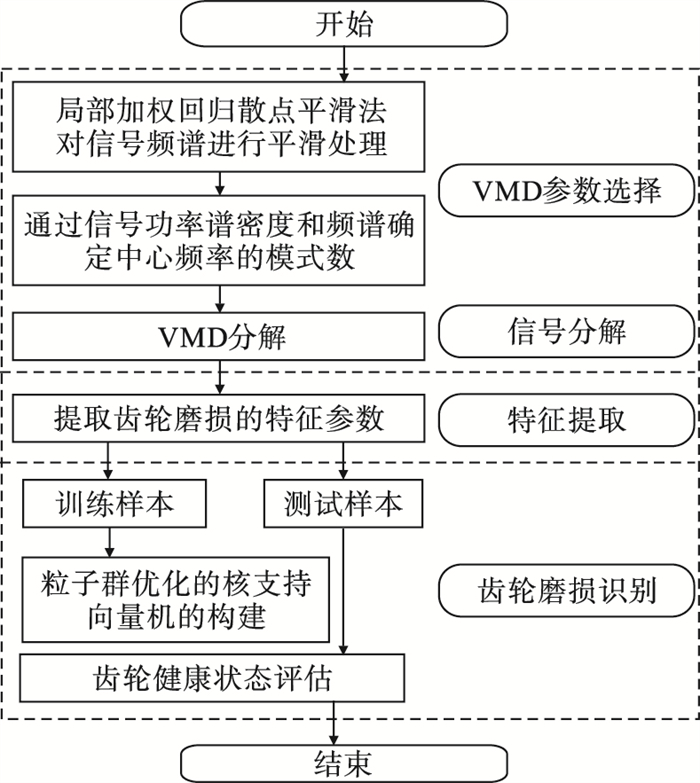图 11 齿轮早期磨损诊断模型Fig.11 Gear early wear diagnosis model

由图 11可知，算法流程主要分为四部分，分别为信号预处理、VMD分解信号、特征参数提取、齿轮健康状态识别，具体的步骤如下：
Step?1搭建实验测试平台并利用振动传感器采集齿轮振动信号；
Step?2采用LOWESS算法平滑振动信号噪声，并确定目标信号FFT频谱上的分解模数k；
Step?3计算目标信号功率谱密度最大值所对应的频率，作为VMD方法的初始中心频率；
Step?4利用VMD方法将目标信号分解为一系列的IMFs；
Step?5利用希尔伯特变换对所有IMF分量进行处理，找出含有齿轮信号的IMF分量，进而得到齿轮的故障特征；
Step?6从含有齿轮故障特征的IMF分量中提取能有效描述齿轮磨损特征的特征参数，组成特征向量；
Step?7分析磨损类型的数目，设计SVM分类器的输入、输出；
Step?8输入特征参数向量对SVM进行训练，得到齿轮磨损诊断模型；
Step?9使用测试样本验证方法的有效性，并分析和评估实验结果.
3 方法验证和实验结果分析齿轮表面的局部磨损必须尽早发现，为了避免故障的发生，建立单极齿轮箱实验平台对齿轮的缺陷特征进行研究.
3.1 实验环境与设备设计并构建的齿轮箱实验平台如图 12所示，实验装置主要由齿轮箱、信号采集装置两部分组成.其中齿轮箱有直流无刷电机驱动，主动轮22个齿.信号由振动传感器在转速880 r/min下完成采集，采样频率为5 120 Hz，信号采集传感器位于主动轮上方1 cm处，速度计位于主轴齿轮的另一端.
图 12(Fig. 12)

图 12 齿轮箱实验平台Fig.12 Gearbox test bench

所有的实验数据均在相同的条件下获得，且齿轮的负载和速度恒定.共采集6种类型的齿轮振动信号，分为3种不同级别的齿面磨损和3种不同级别的齿面裂纹，齿轮的健康状态描述如表 1所示.
表 1(Table 1)

表 1 齿轮健康状态描述Table 1 Description of gear health status 齿轮类型 磨损深度/mm 齿轮类型 裂纹深度/mm 轻度磨损 公法线缩短 0.05 轻度裂纹 0.35 中度磨损 (点蚀产生) 公法线缩短 < 0.1 中度裂纹 0.68 重度磨损 (点蚀严重) 公法线缩短 0.1~0.2 重度裂纹 1.23

表 1 齿轮健康状态描述 Table 1 Description of gear health status

3.2 实验结果及分析图 13为原始信号的时域波形，首先通过LOWESS算法平滑目标信号频谱，得到处理后频谱中的频谱分量.图 14展示的频谱分量的个数为10，并把该数量分配给VMD的模式数k.通过求解目标信号功率谱，得到f_k=147 Hz.经过VMD分解之后，信号被自适应地分解为10个IMF，图 15为前5个IMF分量的时域波形，其中内膜函数IMF2包含齿轮的特征频率，IMF2的频谱图如图 16所示，其中齿轮的特征频率322 Hz在图中可以观察到.
图 13(Fig. 13)

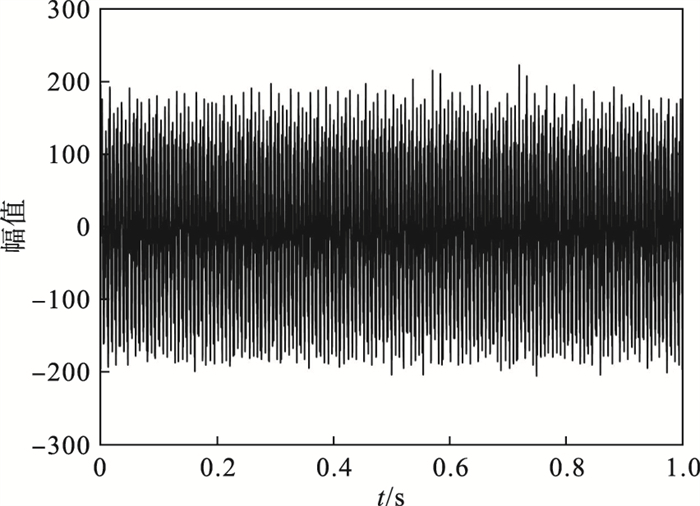图 13 原始信号波形Fig.13 Waveform of original signal

图 14(Fig. 14)

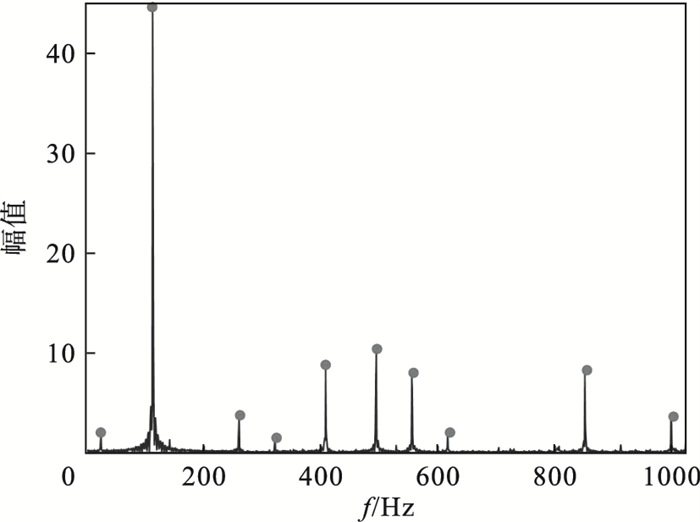图 14 频谱分量个数Fig.14 Number of spectrum components

图 15(Fig. 15)

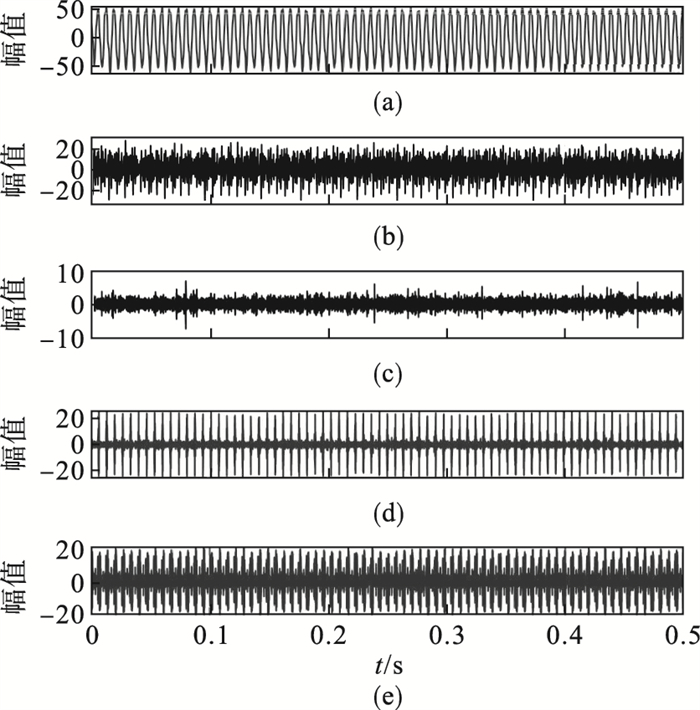图 15 信号经改进的VMD分解后的前5个IMFFig.15 The first 5 IMFs after the improved VMD decomposed signal (a)—IMF1；(b)—IMF2；(c)—IMF3；(d)—IMF4；(e)—IMF5.

图 16(Fig. 16)

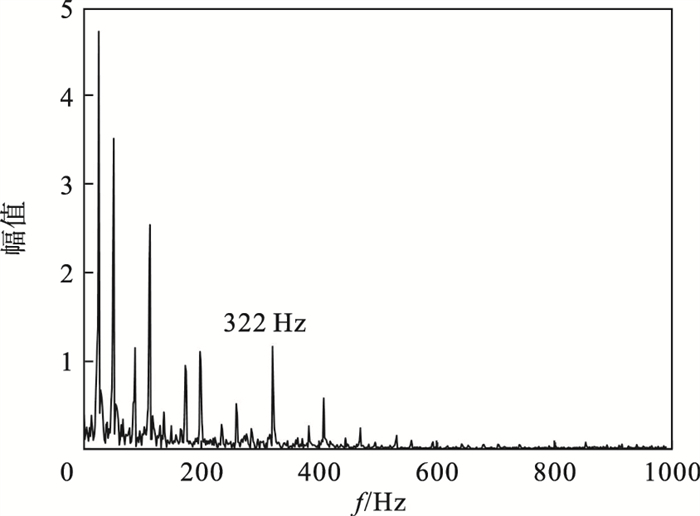图 16 LOWESS后的IMF2频谱Fig.16 IMF2 spectrum after LOWESS

为了说明平滑噪声的重要性，对目标信号不进行LOWESS，其他参数不变的情况下实施VMD，图 17为分解后IMF2的频谱图.其中特征频率被诸多脉冲围绕，这意味着噪声和其他振动分量影响弱故障的表达.通过对比图 16可以发现，实施LOWESS可在局部频谱结构得到保护的前提下，频谱中的一些无意义的极值点被剔除，特征频率明显，磨损特征的可视化进一步得到增强.
图 17(Fig. 17)

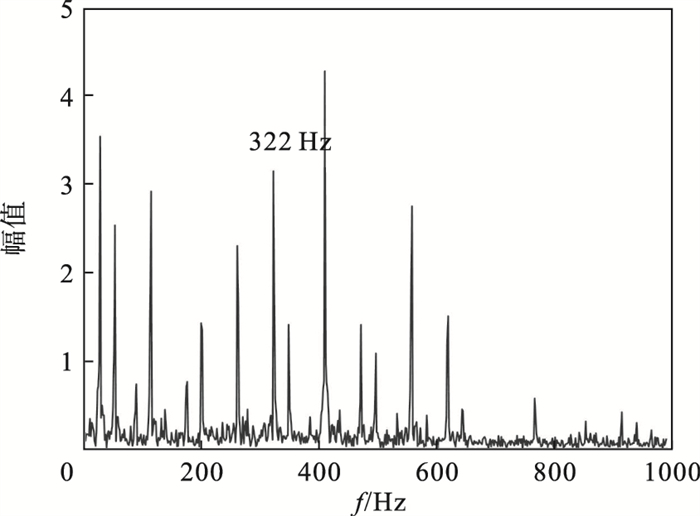图 17 原始信号未进行LOWESS的IMF2频谱Fig.17 IMF2 spectrum of the original signal without LOWESS

本文从IMF2中提取7特征参数用于齿轮的早期磨损诊断，分别为标准差、峰度、平均值、偏斜度、裕度因子、均方根、波峰因数.6种不同的齿轮类型，轻度磨损、中度磨损、重度磨损、轻度裂纹、中度裂纹、重度裂纹，类别标签设置为1，2，3，4，5，6.每个样本采集30组数据，共产生1 260个特征参数组成磨损特征的数据集.
图 18为特征参数数量与模型诊断准确率的关系，可以观察到随着特征参数数量的增加，识别准确率呈增长趋势，特征参数数量为7时，准确率最高，达到了94.4%.为进一步研究特征参数的敏感度，在相同的条件下，测试了不同特征参数数量下的单一类别的准确率.表 2展示了属于相同特征参数数量下不同健康状态的单一类别的测试结果.可以观察到特征参数数量不同，诊断的准确率不同，所提的方法在整个特征参数数量的变化区间内保持了较高的准确率，不同的类别被很好地区分.7个特征参数从信号的幅值分布、冲击间隔、能量、数据分布、波形等方面表征齿轮的磨损程度，促成了模型的精准分类.
图 18(Fig. 18)

图 18 特征参数数量与准确率的关系Fig.18 Relationship between the number of feature parameters and the accuracy rate

表 2(Table 2)

表 2 不同特征参数数量下的模型诊断准确率Table 2 Diagnostic accuracy rate of the model with different number of feature parameters ? % 特征参 数数量 类别标签 1 2 3 4 5 6 3 100 80 90 100 86.6 100 4 100 100 90 90 93.3 96.7 5 100 93.3 90 96.7 96.7 96.7 6 100 96.7 90 96.7 100 96.7 7 100 100 90 96.7 100 96.7

表 2 不同特征参数数量下的模型诊断准确率 Table 2 Diagnostic accuracy rate of the model with different number of feature parameters ?

4 结论1) 磨损、点蚀、裂纹对振动信号变化的作用依次增大，呈弱不连续的变化规律.
2) 本文方法可有效克服因背景噪声大而无法预先设置合适模式数的问题，具有高效、快捷的优点，同时实现了齿轮早期健康状态的监控.
3) 本文方法的准确率达到了94.4%，相比故障后的检测，该方法更具有实际意义，实现了故障预警和缺陷的跟踪.
参考文献

[1]	Liu L H, Chen L Q, Wang Z L, et al. Early fault detection of planetary gearbox based on acoustic emission and improved variational mode decomposition[J]. IEEE Sensors Journal, 2020, 21(2): 1735-1745.
[2]	Liang P F, Deng C, Wu J. Intelligent fault diagnosis of rotating machinery via wavelet transform, generative adversarial nets and convolutional neural network[J]. Measurement, 2020, 159: 107768. DOI:10.1016/j.measurement.2020.107768
[3]	Yan R Q, Gao R X, Chen X F. Wavelets for fault diagnosis rotary machines: a review with applications[J]. Signal Processing, 2013, 96: 1-15.
[4]	Huang N E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, 1998, 454: 903-995. DOI:10.1098/rspa.1998.0193
[5]	Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047
[6]	Torres M E, Colominas M A, Schlotthauer G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP). Prague: IEEE, 2011: 4144-4147.
[7]	Lu Y F, Xie R, Liang S. CEEMD-assisted kernel support vector machines for bearing diagnosis[J]. The International Journal of Advanced Manufacturing Technology, 2020, 106(7): 3063-3070.
[8]	Dutta S, Singh M, Kumar A. Classification of non-motor cognitive task on EEG based brain-computer interface using phase space features in multivariate empirical mode decomposition domain[J]. Biomedical Signal Processing and Control, 2017, 39: 378-389.
[9]	Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675
[10]	Li H D, Xu Y, An D, et al. Application of a flat variational modal decomposition algorithm in fault diagnosis of rolling bearings[J]. Journal of Low Frequency Noise Vibration and Active Control, 2020, 39(2): 335-351. DOI:10.1177/1461348419846730
[11]	Yang T G, Yu X G, Li G C, et al. An early fault diagnosis method based on the optimization of a variational modal decomposition and convolutional neural network for aeronautical hydraulic pipe clamps[J]. Measurement Science and Technology, 2020, 31(5): 055007. DOI:10.1088/1361-6501/ab5342
[12]	Gai J B, Shen J X, Hu Y F, et al. An integrated method based on hybrid grey wolf optimizer improved variational mode decomposition and deep neural network for fault diagnosis of rolling bearing[J]. Measurement, 2020, 162: 107901. DOI:10.1016/j.measurement.2020.107901
[13]	朱永利, 贾亚飞, 王永旺, 等. 基于改进变分模态分解和Hilbert变换的变压器局部放电信号特征提取及分类[J]. 电工技术学报, 2017, 32(9): 221-235. (Zhu Yong-li, Jia Ya-fei, Wang Yong-wang, et al. Feature extraction and classification on partial discharge signal of power transformers based on improved variational mode decomposition and Hilbert transform[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 221-235.)
[14]	Ma L, Liu X G. A novel APSO-aided weighted LSSVM method for nonlinear hammerstein system identification[J]. Journal of the Franklin Institute, 2017, 354(4): 1892-1906.
[15]	Han T T, Zhao Q C. Financial crisis predictions based on biorthogonal wavelet hybrid kernel support vector machine[C]//2015 11th International Conference on National Computation. Zhangjiajie: IEEE, 2015: 719-724.
[16]	Gao T Y, Yang J L, Jiang S D, et al. A novel incipient fault diagnosis method for analog circuits based on GMKL-SVM and wavelet fusion features[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 70: 3502315.
[17]	Yao L, Fang Z P, Xiao Y Q, et al. An intelligent fault diagnosis for lithium battery systems based on grid search support vector machine[J]. Energy, 2021, 214: 118866.
[18]	Wu J, Guo P F, Cheng Y F, et al. Ensemble generalized multiclass support-vector-machine-based health evaluation of complex degradation systems[J]. IEEE/ASME Transactions on Mechatronics, 2020, 25(5): 2230-2240.