魏琳扬¹, 郭馨², 王存海³, 李国军¹
1. 东北大学 冶金学院，辽宁 沈阳 110819;
2. 哈尔滨锅炉厂有限责任公司，黑龙江 哈尔滨 150046;
3. 北京科技大学 能源与环境工程学院，北京 100083
收稿日期：2021-11-15
基金项目：国家自然科学基金资助项目(52106079); 中国博士后科学基金资助项目(2020M680968)。
作者简介：魏琳扬(1992-)，男，河北邢台人，东北大学讲师，博士;
李国军(1972-)，男，吉林扶余人，东北大学副教授，博士生导师。

摘要：针对半透明介质光学参数估计问题，建立了脉冲激光辐照下半透明介质光学参数反演模型，采用量子微粒群优化(QPSO)算法反演了折射率和吸收系数，分析了测量误差、热物性参数对反演结果的影响，并利用敏感性分析揭示了反演精度与测量误差的关系.计算结果表明：建立的反演模型和采用的QPSO算法可以精确估计折射率和吸收系数，即使人为添加10%的测量误差，反演结果依然具有较强的鲁棒性和准确度.本研究可为半透明介质物性参数获取提供技术参考.
关键词：光学参数反演量子微粒群优化算法辐射-导热耦合半透明介质脉冲激光
Inversion of Optical Parameters of Semitransparent Media Based on Quantum Particle Swarm Optimization Algorithm
WEI Lin-yang¹, GUO Xin², WANG Cun-hai³, LI Guo-jun¹
1. School of Metallurgy, Northeastern University, Shenyang 110819, China;
2. Harbin Boiler Company Limited, Harbin 150046, China;
3. School of Energy and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China
Corresponding author: WEI Lin-yang, E-mail: weilinyang@smm.neu.edu.cn.

Abstract: Aiming at the problem of optical parameter estimation for semitransparent media, an inversion model for optical parameters of semitransparent media exposed to pulse laser irradiation is established. The quantum particle swarm optimization (QPSO) algorithm is adopted to estimate the refractive index and absorption coefficient. The effects of measurement error and thermophysical parameters on the inversion results are analyzed. The relationship between the inversion accuracy and measurement error is revealed by sensitivity analysis. The calculation results show that the established inversion model and the QPSO algorithm can accurately estimate the refractive index and absorption coefficient. Even with measurement error of 10%, the retrieval results still have strong robustness and high accuracy. This study can provide technical reference for obtaining the physical parameters of semitransparent media.
Key words: inversion of optical parametersquantum particle swarm optimization (QPSO) algorithmcoupled radiation-conductionsemitransparent mediapulse laser
半透明介质又称参与性介质或弥散介质，是介于透明和不透明之间的一类介质^[1]，广泛应用于航空航天、能源利用、生物医学等高新技术领域^[2-5].热辐射在半透明介质内传输时会呈现出一些特有的性质，而这些特性是由其介质的物性参数决定的，如折射率决定了光线传输轨迹，吸收系数决定了能量衰减程度等.因此，准确掌握半透明介质的光学参数是深入研究光热辐射传输机理的基础，也是设计和利用半透明介质的关键.
目前，对于半透明介质物性参数的测量，常规测量方法仅能获得介质的等效物性，因其与真实物性相差甚远而无法采信，这就导致无法精确了解介质内的光热辐射传输过程，难以对其进行调控.基于辐射反问题的参数反演技术可以精确获得半透明介质的光学参数分布，是一种具有潜力和应用前景的方法.通过测量边界上的响应信息反演出介质内部的物性和几何参数，模型简单，对材料没有损伤，在很多领域得到应用.Das等^[6]采用遗传算法研究了辐射-导热耦合反问题，成功反演了半透明介质的散射反照率、导热-辐射耦合系数和壁面发射率.Chopade等^[7]采用差分进化算法研究了瞬态辐射-导热耦合反问题，反演了半透明介质的衰减系数、散射反照率、发射率及辐射-导热耦合系数，并分析差分进化算法参数对反演结果的影响.Qi等^[8]在国内率先开展了辐射反问题的研究，将群体智能优化策略应用于辐射反问题的求解，采用随机微粒群优化算法反演了介质的衰减系数、散射反照率及非均匀分布的吸收系数.之后，又提出了混合的微粒群算法，研究了辐射-导热耦合反问题，同时反演了一维半透明介质的多个参数^[9].Zhang等^[10]提出了一种改进的蚁群算法，基于激光作用下瞬态辐射-导热耦合模型反演了一维半透明介质的热物性参数(导热系数)和光学参数(吸收系数及散射系数).Ren等^[11]研究了光热参数同时反演的串扰问题，通过敏感性分析指出了出现串扰的原因是测量信息对待反演参数敏感性差异巨大，并基于不同测量信息提出了二次反演方案，实现了与温度有关的光热参数同时反演.
但是基于辐射反问题的物性参数估计具有严重的病态性和高度的不适定性，是目前热辐射研究领域极具挑战性的课题之一^[12].近年来虽然关于辐射反问题的研究层出不穷，但其病态性、多解性、串扰问题至今没有得到彻底解决.因此，本文对半透明介质光学参数反演问题进行研究，建立基于辐射响应测量信息的反演模型，引入量子微粒群算法进行反问题求解，实现半透明介质的光学参数准确反演，为半透明介质物性参数获取提供理论和技术支撑.
1 正问题模型1.1 激光辐照作用下辐射-导热耦合模型半透明平板介质如图 1所示，平面脉冲激光辐照介质左侧进行加热，介质的边界为漫射灰体壁面，当没有内热源时，能量方程可以表示为

(1)

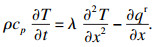图 1(Fig. 1)

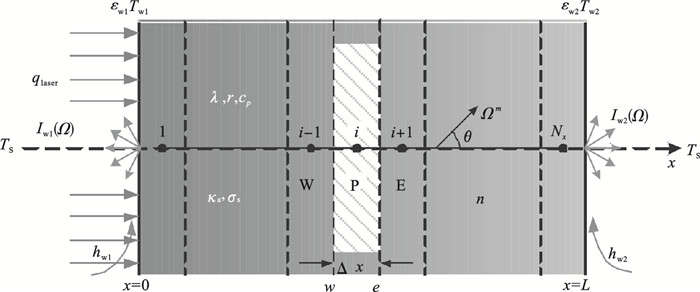图 1 激光辐照作用下半透明介质瞬态辐射-导热耦合模型Fig.1 Transient radiation-conduction coupled model for semitransparent medium exposed to laser irradiation

式中：T表示介质温度，K；t表示时间，s；ρ表示介质的密度，kg/m³；c_p表示介质的比定压热容，J/(kg·K)；λ表示介质的热导率，W/(m·K)；q^r表示辐射热流，W/m².
初始条件和边界条件设置为

(2)

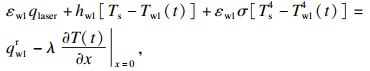(3a)

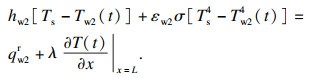(3b)

式中：T_s为环境温度/介质初始温度，这里取值为T_s=300 K；T_w为壁面温度；q_laser是辐照激光强度；ε_w1，h_w1，q_w1^r分别是左壁面的发射率、与空气的对流换热系数和辐射热流；ε_w2，h_w2，q_w2^r分别是右壁面的发射率、与空气的对流换热系数和辐射热流.
在半透明介质内，辐射传输方程可以表示为

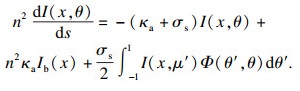(4)

式中：I(x, θ)表示在位置x和沿极角θ的辐射强度，W/(m²·sr)；s为辐射(光线)传播距离；I_b(x)是在位置x的黑体辐射强度，W/(m²·sr)；Φ(θ′, θ)是散射相函数；κ_a和σ_s分别是介质的吸收系数和散射系数，m^-1；n表示折射率.然后，对应的q_w1^r，q_w2^r及?q^r/?x可以表示为

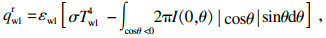(5)

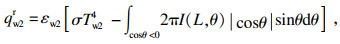(6)

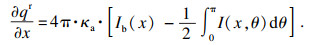(7)

本文采用有限体积法(finite volume method, FVM)对该耦合传热模型进行求解，有限体积法的相关描述可参考文献[1]，故不再赘述.
1.2 辐射-导热耦合模型求解验证本文首先对建立的激光辐照作用下半透明介质瞬态辐射-导热耦合传热模型进行验证，采用文献[13]中的一个一维算例(射线踪迹法求解)，表 1列出了介质物性参数和模型边界条件.图 2给出了介质右边界的动态温度响应，从图中可以看出，本文的模拟结果与射线踪迹法的计算结果吻合很好，最大偏差仅有2.35%，说明本文采用的有限体积法求解模型可以准确计算半透明介质内的瞬态辐射-导热耦合换热问题.
表 1(Table 1)

表 1 半透明介质物性参数及边界条件Table 1 Physical parameters and boundary condition of semitransparent media 参数 符号 单位 数值 介质厚度 L m 0.01 体积比热容 c=ρcp J/(m3·K) 2.2×106 导热系数 λ W/(m·K) 0.7 对流换热系数 hw1, hw2 W/(m2·K) 7.0 环境/初始温度 Ts K 300 激光作用时间 tlaser s 1.0 激光强度 qlaser W/m2 3.0×106 吸收系数 κa m-1 1.0或30.0 散射系数 σs m-1 0.0 折射率 n 1.5 边界条件 黑体边界

表 1 半透明介质物性参数及边界条件 Table 1 Physical parameters and boundary condition of semitransparent media

图 2(Fig. 2)

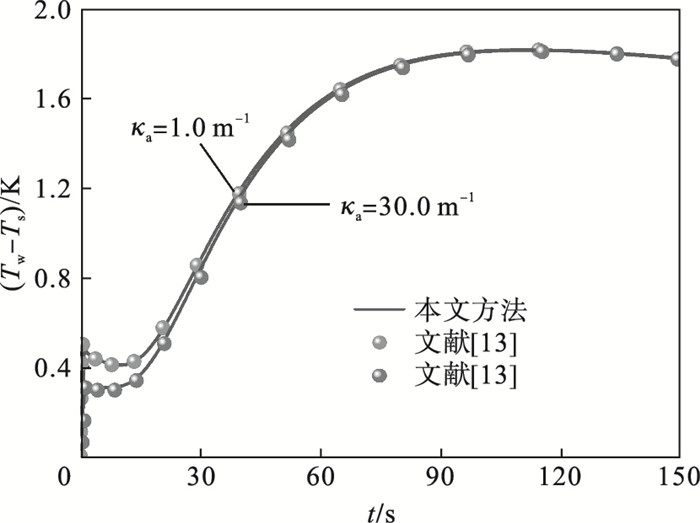图 2 激光辐照作用下半透明介质右边界温度响应Fig.2 Temperature response at right wall of semitransparent medium exposed to laser irradiation

2 反问题模型2.1 光学参数反演模型对于半透明纯吸收介质光学参数(折射率和吸收系数)反演问题，利用平面脉冲激光辐照作用下边界位置的时变辐射信号作为已知信息，利用QPSO(quantum particle swarm optimization)算法估计光学参数值，反演模型如图 3所示.在室温环境下(介质的2个边界与空气存在对流换热和辐射换热)，激光持续辐射介质左侧10 s，右边界的方向辐射强度信息构建目标函数.

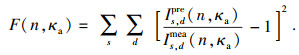(8)

图 3(Fig. 3)

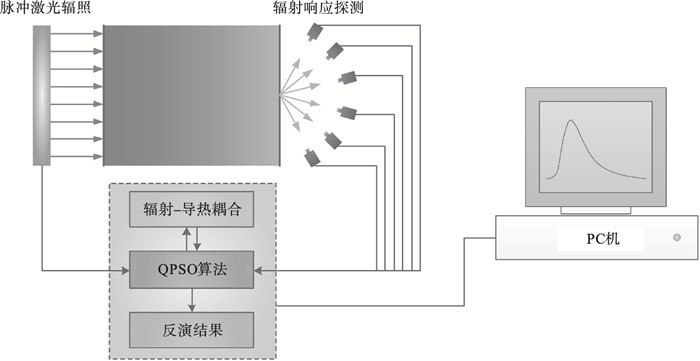图 3 半透明介质折射率和吸收系数反演模型Fig.3 Retrieval model for refractive index and absorption coefficient of semitransparent medium

式中，I_{s, d}^pre(n, κ_a)和Imea_{s, d}(n, κ_a)分别是预测和测量的瞬态方向辐射强度.
为了更加符合实际情形，本文在模拟实验数据中人为添加测量噪音，随机标准偏差模型如下：

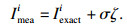(9)

式中：I_meaⁱ为模拟的测量辐射强度；I_exactⁱ为精确辐射强度；ζ表示期望值为0，标准差为1的正态分布随机数；σ表示标准差，置信区间为99%的标准差可以定义为

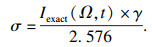(10)

式中，γ为测量误差.本文采用相对误差(relative error，RE)来评价反演结果的好坏，其可以定义为如下形式

(11)

式中，Y_est和Y_exact分别是反演光学参数的估计值和真实值.
2.2 量子微粒群优化算法半透明介质光学参数反演问题本质是反问题寻优问题，需要借助优化算法来进行求解，本文采用量子微粒群优化(QPSO)算法^[14]作为反问题求解器.在QPSO算法中，假定每个粒子具有量子行为，其状态可由波函数ψ决定.其中，|ψ|²是粒子位置X_i=(x_i1, x_i2, …, x_ij, …, x_iN)的概率密度.在第k次迭代中，粒子i在N维搜索空间以粒子局部吸引因子Q_i=(q_i1, q_i2, …, q_ij, …, q_iN)为中心，其可以表示为

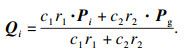(12)

式中：c₁和c₂为加速系数，这里取值为1.0；r₁和r₂为[0, 1]区间均匀分布的随机数；P_i是粒子i的个体历史最优位置；P_g是群体历史最优位置.波函数可以表示为

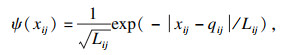(13)

式中L_ij为双指数分布的标准偏差.
故概率密度函数可以表示为

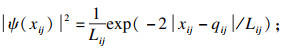(14)

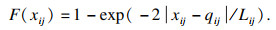粒子位置的概率分布函数可由式(15)确定:

(15)

经蒙特卡洛法模拟后，粒子的位置X_i可以表示为

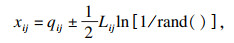(16a)

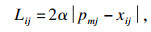(16b)

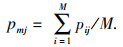(16c)

式中，α为吸引扩散系数，为了保证量子微粒群的全局收敛，通常采用α < 1.781.迭代的收敛精度设为ε=1.0×10^-10，最大迭代次数设为N_k=1 000，量子微粒群优化的详细流程如图 4所示.
图 4(Fig. 4)

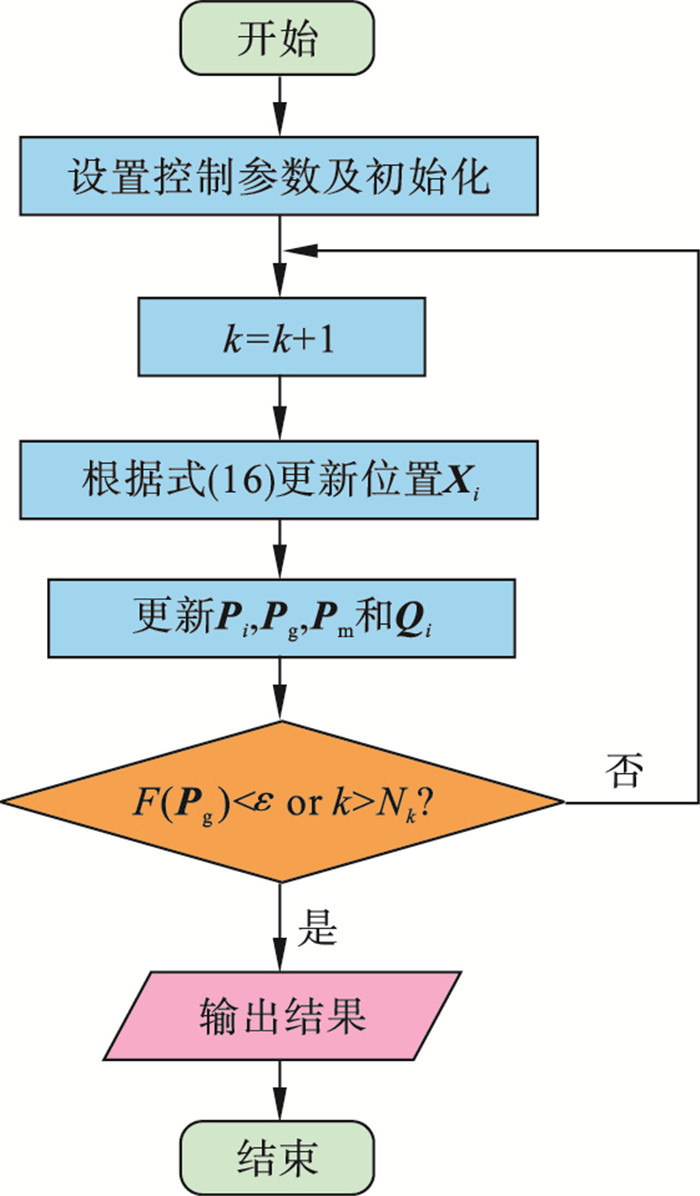图 4 量子微粒群优化算法流程图Fig.4 Flowchart of QPSO algorithm

3 半透明介质光学参数反演结果分析3.1 测量误差对反演结果的影响测量误差在实际测量中是无法避免的，因此首先分析测量误差对反演结果的影响.样品介质的物性参数采用表 1中的数据，以n=1.5和κ_a=5.0 m^-1为例进行反演计算.图 5给出了10次计算的结果，可以看到在5%和10%测量误差下，反演结果与真实值很接近，表明反演精度较高；同时也可以看出每次的反演结果均存在一定差异，这是由于QPSO算法具有随机性，模拟测量误差也具有随机性.为了消除随机性带来的负面影响，本文采用10次计算的平均值作为最终反演结果，即表示为a±δ的形式(a表示折射率或吸收系数平均值，δ表示标准偏差).
图 5(Fig. 5)

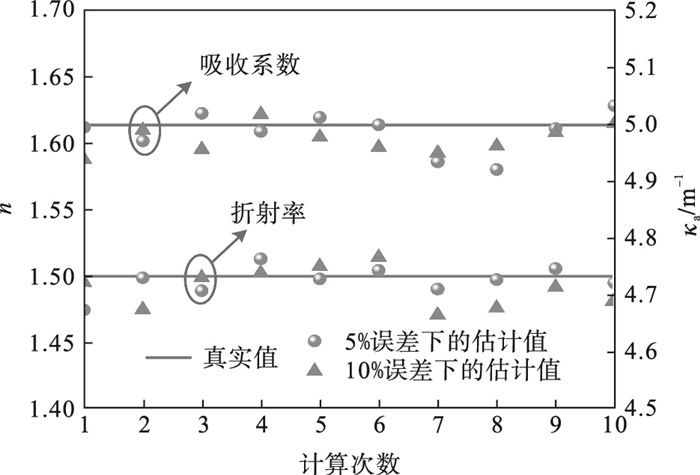图 5 10次反演计算的结果Fig.5 Retrieval results of 10 calculations

表 2给出了反演的折射率和吸收系数，可以看出不同组合的反演结果均与真实值非常吻合，特别是在考虑5%的测量误差时，最大相对误差仅为1.74%；即使考虑10%的测量误差，最大相对误差也仅为6.71%，这表明基于边界辐射响应信息的反演模型具有很高的反演精度，量子微粒群优化算法具有很好的鲁棒性，可以容忍较大的测量误差的干扰.同时，当测量误差为5%时，折射率的反演精度要高于吸收系数，但当测量误差为10%时，吸收系数的反演精度要高于折射率，为了分析导致这一现象的原因，本文进行了测量信息的敏感性分析，对应的敏感系数定义为

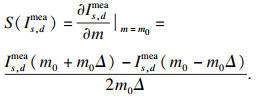(17)

表 2(Table 2)

表 2 不同折射率和吸收系数组合的反演结果Table 2 Retrieval results of different combinations of refractive index and absorption coefficient 真实值 5%误差下的估计值 相对误差/% 10%误差下的估计值 相对误差/% n = 1.50 1.497±1.06×10-2 0.22 1.492±1.49×10-2 0.57 κa = 5.00 m-1 4.987±3.58×10-2 0.26 4.974±2.49×10-2 0.51 n = 1.50 1.498±1.16×10-2 0.15 1.601±2.69×10-2 6.71 κa = 10.00 m-1 10.016±3.36×10-2 0.16 10.107±2.18×10-1 1.07 n = 2.00 1.981±1.93×10-2 0.94 1.932±2.59×10-2 3.40 κa = 5.00 4.927±3.57×10-2 1.46 4.919±6.87×10-2 1.62 n = 2.00 2.010±1.29×10-2 0.50 2.088±6.46×10-2 4.41 κa = 10.00 m-1 9.826±5.71×10-2 1.74 9.970±4.71×10-2 0.30

表 2 不同折射率和吸收系数组合的反演结果 Table 2 Retrieval results of different combinations of refractive index and absorption coefficient

式中：m表示待反演的参数；Δ表示0.5%的小变化量；m₀表示待反演参数的某值.
敏感系数本质是测量信息对反演参数的一阶导数，反映测量信息对反演参数的敏感程度.如果敏感系数太小，表示测量信息对反演参数不敏感，容易导致反演失败；如果敏感系数太大，表示测量信息对反演参数十分敏感，容易受到测量误差的干扰.图 6给出了右壁面不同方向辐射强度对折射率和吸收系数的敏感系数，可以看出测量信息对折射率和吸收系数都较为敏感，说明可以利用辐射信息反演出折射率和吸收系数.同时也可以看到测量信息对折射率更为敏感，这就解释了为什么在测量误差小时，折射率反演精度较高，而在测量误差大时，吸收系数反演精度较高.这一发现可以为后续实验研究提供指导.
图 6(Fig. 6)

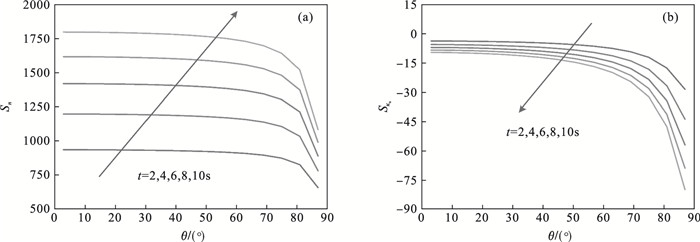图 6 辐射强度对反演参数的敏感系数Fig.6 Sensitivity coefficients of radiative response to retrieval parameters (a)—折射率；(b)—吸收系数.

3.2 热物性参数对反演结果的影响本节分析半透明介质热物性参数(导热系数λ和体积比热容c=ρc_p)对折射率和吸收系数反演结果的影响.首先考察导热系数的影响，待反演的折射率和吸收系数设置为n=1.50和κ_a=10.00 m^-1，介质体积比热容设置为c=ρc_p=1.0×10⁶ J/(m³·K)，其他参数采用表 1中的数据.在反演过程中，折射率的搜索范围为[0, 10]，吸收系数的搜索范围为[0, 100 m^-1].表 3给出了反演的折射率和吸收系数，可以看出不同导热系数下的反演结果均有较高精度，考虑5%测量误差时，折射率最大反演误差为1.37%，吸收系数最大反演误差为2.39%；考虑10%测量误差时，折射率最大反演误差为5.05%，吸收系数最大反演误差为2.79%，表明导热系数对光学参数的反演结果影响较小.
表 3(Table 3)

表 3 不同导热系数下的折射率和吸收系数反演结果Table 3 Retrieved results of refractive index and absorption coefficient with different conduction coefficients 真实值 5%误差下的估计值 相对误差/% 10%误差下的估计值 相对误差/% λ=0.70 1.484±1.66×10-2 1.04 1.461±1.51×10-2 2.63 9.831±1.24×10-1 1.69 9.820±1.64×10-1 1.81 λ=3.50 n=1.50 1.508±5.55×10-3 0.55 1.424±5.00×10-2 5.05 κa=10.00 m-1 9.904±5.26×10-2 0.96 9.916±2.18×10-1 0.84 λ=7.00 1.521±1.29×10-2 1.37 1.448±2.32×10-2 3.47 9.761±2.06×10-1 2.39 9.721±1.49×10-1 2.79

表 3 不同导热系数下的折射率和吸收系数反演结果 Table 3 Retrieved results of refractive index and absorption coefficient with different conduction coefficients

同样地，表 4给出了不同体积比热容下的折射率和吸收系数反演结果(导热系数λ=0.70 W/(m·K))，可以看出体积比热容对折射率和吸收系数的反演精度影响很小，考虑5%测量误差时，折射率最大反演误差为1.04%，吸收系数最大反演误差为1.69%；考虑10%测量误差时，折射率最大反演误差为6.71%，吸收系数最大反演误差为1.81%.说明热物性参数对本文建立的反演模型影响很小，换句话说，具有不同热物性的半透明介质均可以采用本文的反演模型进行光学参数反演.因此，本文的反演模型具有一定的普适性.
表 4(Table 4)

表 4 不同体积比热容下的折射率和吸收系数反演结果Table 4 Retrieved results of refractive index and absorption coefficient with different heat capacities c/(J·m-3·K-1) 真实值 5%误差下的估计值 相对误差/% 10%误差下的估计值 相对误差/% 1.0 ×106 1.484 4±1.66×10-2 1.04 1.460 6±1.51×10-2 2.63 9.831 0±1.24×10-1 1.69 9.819 5±1.64×10-1 1.81 2.0×106 n=1.50 1.497 7±1.16×10-2 0.15 1.600 7±2.69×10-2 6.71 κa=10.00 m-1 10.015 8±3.36×10-2 0.16 10.106 6±2.18×10-1 1.07 3.0 ×106 1.494 8±5.06×10-3 0.35 1.519 8±2.03×10-2 1.32 9.906 9±4.57×10-2 0.93 10.114 7±8.11×10-2 1.15

表 4 不同体积比热容下的折射率和吸收系数反演结果 Table 4 Retrieved results of refractive index and absorption coefficient with different heat capacities

4 结论1) 建立的反演模型和采用的量子微粒群算法可以很好地解决半透明介质光学参数反演问题，具有较高的反演精度和鲁棒性.
2) 敏感性分析表明测量误差对反演结果有重要影响，较小测量误差时，折射率反演精度较高；较大测量误差时，吸收系数反演精度较高.
3) 介质的热物性(导热系数和热容)对光学参数的反演影响较小，该反演模型具有较好的普适性.
参考文献

[1]	Howell J R, Mengüc M P, Daun K, et al. Thermal radiation heat transter[M]. Boca Raton: CRC Press, 2020.
[2]	王伟臣, 魏志军, 张峤, 等. 后燃对火箭发动机羽流红外特性的影响[J]. 航空动力学报, 2010, 25(11): 2612-2618. (Wang Wei-chen, Wei Zhi-jun, Zhang Qiao, et al. Influence of afterburning on infrared signature of rocket motor exhaust plume[J]. Journal of Aerospace Power, 2010, 25(11): 2612-2618.)
[3]	韩炜, 赵跃进, 胡新奇, 等. 超高声速飞行器光学窗口气动光学效应分析[J]. 光学技术, 2010, 36(4): 622-626. (Han Wei, Zhao Yue-jin, Hu Xin-qi, et al. Study on aerooptical effects of hypersonic vehicles optical window[J]. Optical Technique, 2010, 36(4): 622-626.)
[4]	Farooq M, Green A A, Hutchins M G. High performance sputtered Ni: SiO2 composite solar absorber surfaces[J]. Solar Energy Materials and Solar Cells, 1998, 54: 67-73. DOI:10.1016/S0927-0248(97)00265-1
[5]	Dominguez J B, Berube-Lauziere Y. Diffuse optical tomographic imaging of biological media by time-dependent parabolic SPN equations: a two-dimensional study[J]. Journal of Biomedical Optics, 2012, 17(8): 86012-1.
[6]	Das R, Mishra S C, Ajith M, et al. An inverse analysis of a transient 2-D conduction-radiation problem using the lattice Boltzmann method and the finite volume method coupled with the genetic algorithm[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2008, 109(11): 2060-2077. DOI:10.1016/j.jqsrt.2008.01.011
[7]	Chopade R P, Mohan V, Mayank R, et al. Simultaneous retrieval of parameters in a transient conduction-radiation problem using a differential evolution algorithm[J]. Numerical Heat Transfer, Part A, 2013, 63: 373-395. DOI:10.1080/10407782.2013.733179
[8]	Qi H, Ruan L M, Zhang H C, et al. Inverse radiation analysis of a one-dimensional participating slab by stochastic particle swarm optimizer algorithm[J]. International Journal of Thermal Sciences, 2007, 46(7): 649-661. DOI:10.1016/j.ijthermalsci.2006.10.002
[9]	Qi H, Niu C Y, Gong S, et al. Application of the hybrid particle swarm optimization algorithms for simultaneous estimation of multi-parameters in a transient conduction-radiation problem[J]. International Journal of Heat and Mass Transfer, 2015, 83(7): 428-440.
[10]	Zhang B, Qi H, Ren Y T, et al. Application of homogenous continuous ant colony optimization algorithm to inverse problem of one-dimensional coupled radiation and conduction heat transfer[J]. International Journal of Heat and Mass Transfer, 2013, 66(3): 507-516.
[11]	Ren Y T, Qi H, Zhao F Z, et al. Simultaneous retrieval of temperature-dependent absorption coefficient and conductivity of participating media[J]. Scientific Reports, 2016, 6: 21998. DOI:10.1038/srep21998
[12]	Liu D, Yan J H, Wang F, et al. Inverse radiation analysis of simultaneous estimation of temperature field and radiative properties in a two-dimensional participating medium[J]. International Journal of Heat and Mass Transfer, 2010, 53(21): 4474-4481.
[13]	Tan H P, Ruan L P, Tong T W. Temperature response in absorbing, isotropic scattering medium caused by laser pulse[J]. International Journal of Heat and Mass Transfer, 2000, 43(2): 311-320. DOI:10.1016/S0017-9310(99)00131-3
[14]	Sun J, Feng B, Xu W B. Particle swarm optimization with particles having quantum behavior[C]//Congress on Evolutionary Computation. Portland, OR, USA: IEEE, 2004: 325-331.