查从燚¹, 孙志礼¹, 潘陈蓉², 王健¹
1. 东北大学 机械工程与自动化学院，辽宁 沈阳 110819;
2. 安徽新华学院 通识教育部，安徽 合肥 230088
收稿日期：2021-12-02
基金项目：国家自然科学基金资助项目(51775097，51875095)。
作者简介：查从燚(1993-)，男，安徽六安人, 东北大学博士研究生;
孙志礼(1957-)，男，山东巨野人，东北大学教授，博士生导师。

摘要：现有的自适应加点策略多局限于Kriging模型，或在每次迭代过程中只能选取一个最佳样本点，效率较低.为解决上述问题，本文提出了一种通用的并行自适应加点策略CF-K.该方法考虑了样本点的局部不确定性并确保所选样本点分布在极限状态函数附近；此外，结合k-means算法以实现并行计算，即利用多台计算机在每次迭代的同时进行多个样本的仿真.算例分析表明，与其他方法相比，所提方法在满足精度要求的条件下具有更少的迭代次数，更节省时间.基于所提方法的结构可靠性分析不仅在计算效率和精度之间取得了较好的平衡，在理论上还可用于任何现有的代理模型.
关键词：代理模型自适应加点策略k-means算法并行结构可靠性
Parallel Adaptive Sampling Strategy for Structural Reliability Analysis
ZHA Cong-yi¹, SUN Zhi-li¹, PAN Chen-rong², WANG Jian¹
1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Department of General Education, Anhui Xinhua University, Hefei 230088, China
Corresponding author: ZHA Cong-yi, E-mail: congyizha@163.com.

Abstract: Many existing adaptive sampling strategies are limited to the Kriging models, or are with low efficiency for only selecting one best sample point at each iteration. To solve the above issues, a general parallel adaptive sampling strategy CF-K is proposed. The proposed method considers the local uncertainty of the sample points and ensures that the selected sample points distribute around the limit-state function. Furthermore, the k-means algorithm is incorporated to achieve parallel computation, which means that several sample points can be simulated simultaneously at each iteration on several computers. The numerical cases show that the proposed method has less iterations and saves more time than other methods under the condition of satisfying the precision. The structural reliability analysis based on the proposed method not only achieves a good balance between computational efficiency and accuracy, but also be available for any existing surrogate models in principle.
Key words: surrogate modeladaptive sampling strategyk-means algorithmparallelstructural reliability
在实际工程中，不确定性参数广泛存在于结构的设计、制造及使用等各个阶段.单个不确定性参数的影响虽小，但多个耦合往往使结构响应产生意想不到的偏差，甚至引发灾难性的后果.因此, 对结构可靠性分析方法及其应用进行探索和研究，以保证结构的可靠性，具有重要的科学价值和实际意义.
结构的功能函数常分为显式和隐式，解决显式功能函数可靠性问题的方法已较为成熟，经典方法有蒙特卡洛模拟(Monte Carlo simulation, MCS)法、一阶可靠性方法及二阶可靠性方法^[1-3]等.工程实际中，结构的功能函数多为隐式，往往需要借助有限元仿真分析，而复杂结构的仿真分析即使借助高速计算机也需要较长时间.如汽车侧碰撞的有限元分析一次计算时间约20 h.开展可靠性分析则需要多次仿真，耗时更长，传统的可靠性方法已无法满足实际需求.为解决以上问题, ****们提出了代理模型法，即通过插值或回归方法构建模型代替结构的隐式功能函数.该方法既能保证所需的精度，又可以提高计算效率.常见的代理模型有响应面、支持向量机^[4]、神经网络^[5]、Kriging^[6]及径向基函数^[7]等.
代理模型法的关键在于训练样本的获取.目前，训练样本的获取方法主要包括：一次采样和序列采样^[8].序列采样因以自适应加点的方式更新训练样本集并更新代理模型，能在确保代理模型精度的前提下提高样本点的利用率等优点而被广泛应用.对此，****们开发了一系列的自适应加点策略(又称学习函数)，如U学习函数^[9]、LIF学习函数^[6]、REIF学习函数^[10]、FNEIF学习函数^[11]、RLCB学习函数^[12]等.现有学习函数大多需要未知样本点的预测均值和预测方差，其他代理模型无法像Kriging模型一样可以估计样本点的标准差，导致学习函数局限于Kriging模型而无法用于其他代理模型，而Kriging模型本身具有一定的不确定性，该特性会影响计算结果的稳定性.此外，现有的通用学习函数在迭代过程中大多只能挑选一个最佳样本点更新代理模型.此类选点方式未能充分利用计算机资源，效率有待进一步提高.为解决上述问题，本文提出一种基于通用学习函数的并行自适应加点策略CF-K，该方法考虑了样本点的局部不确定性并保证所选的样本点分布在极限状态函数附近，进一步地结合k-means算法，在每次迭代过程中从多区域分别选择最佳样本点以提高代理模型精度，减少搜索最佳样本点算法的迭代次数. 减少迭代次数能有效地节省时间，尤其是评估仿真复杂耗时的结构可靠性.所提方法在理论上可用于现有的所有代理模型，具有较高的普适性.
1 理论基础1.1 Kriging模型Kriging模型源于地质统计，是一种半参数化模型，目前已广泛应用于可靠性分析领域.Kriging模型的基本形式为^{[6, 13]}

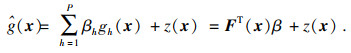(1)

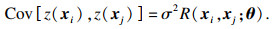式中：β_h为回归系数；g_h(x)为变量x多项式；z(x)服从高斯分布N(0, σ²)，其协方差表示为

(2)

式中：σ²是高斯过程的方差；R(x_i, x_j; θ)是x_i和x_j的空间相关函数，具体表达式为

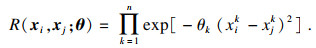(3)

式中：θ是相关参数向量；x_i^k和x_j^k分别为x_i和x_j的第k个分量；θ_k是θ的第k个分量.
已知样本集S_DoE=[x₁, x₂, …, x_N]及对应的响应值Y=[y₁, y₂, …, y_N]^T，G(x)最小方差无偏估计为

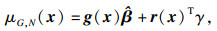(4)

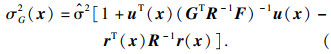(5)

式中：
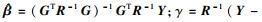
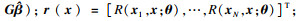
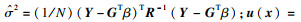
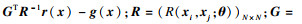
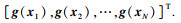
1.2 径向基函数模型径向基函数(radial basis function, RBF)是一种常用的多元分散数据插值代理模型.假设训练样本有n个且记为^[7]

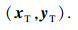(6)

式中：x_T=[x_T1, x_T2, …, x_Tn]^T; y_T=[y_T1, y_T2, …, y_Tn]^T; 下标T表示该样本为训练样本.
径向基函数插值模型可以表示如下线性组合形式：

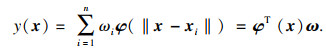(7)

其中：ω_i是系数向量ω的第i个分量；φ(‖x-x_i‖)是核函数向量φ(x)的第i个分量.核函数向量有多种选择，如高斯函数、薄板样条函数、逆多二次函数等(见表 1)^[7].如表 1所示, r=‖x-x_i‖表示欧氏距离，c为形状参数，e为常数.
表 1(Table 1)

表 1 常见的核函数Table 1 Common kernel function 类型 核函数 高斯函数 e(-cr2) 薄板样条函数 r2lg(1+cr2) 逆多二次函数 (1+cr2)-1/2

表 1 常见的核函数 Table 1 Common kernel function

将式(6)中的样本代入式(7)中得

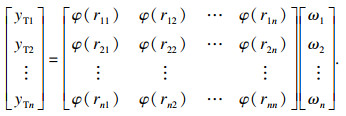(8)

改写为矩阵形式：

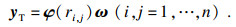(9)

式中，ω=[ω₁, ω₂, …, ω_n]^T.
若各训练样本点之间两两互不相同，则φ可逆，式(9)有唯一解.因此，其权重系数矩阵可以改写为

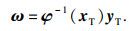(10)

因此，基于RBF代理模型得到预测样本点数值的最终表达式如下：

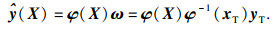(11)

其中，?(X)表示的是样本集X=[x₁, x₂, …, x_n]^T对应的预测值矩阵.
2 基于并行自适应加点策略CF-K的结构可靠性分析2.1 通用的学习函数CF基于代理模型的结构可靠性分析的关键在于选择恰当的自适应加点策略以高效地构建高精度的代理模型.若自适应加点策略选择的训练样本过多，则计算负担大，效率低；反之，无法保证代理模型的精度.因此，提出一种基于交叉验证的新学习函数辅助构建有效的代理模型.
交叉验证是一种模型准确性评估的常用方法.其基本原理是从训练样本点中删除一个或多个样本点，并利用剩余的样本点构建代理模型.交叉验证法的种类较多，本文采用k折交叉验证法.所谓k折交叉验证法即将n个训练样本点尽可能均匀地分成k个子集^[7-8]，记为

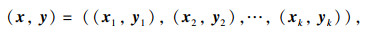(12)

则测试样本表示为S_Testⁱ=(x_i, y_i), 训练样本为S_Train^-i=((x₁, y₁), …, (x_i-1, y_i-1), (x_i+1, y_i+1), …, (x_k, y_k))，i=1, 2, …, k.
利用所有训练样本(x, y)构建的代理模型记为.依次去除第i个子集S_Testⁱ，利用剩下的训练样本S_Train^-i构建的代理模型为.通过k折交叉验证法，可以获得k个不同的代理模型，由k个代理模型预测值的差异可确定局部不确定性的大小.则候选样本点x_j^c处的不确定性可表示为

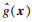
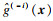
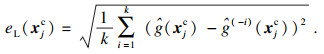(13)

式中上标c表示样本为候迭样本
由式(13)可知，当e_L(x_j^c)数值较大时，表明x_j^c是对代理模型的分类不确定性影响较大的危险点，故被选为新训练样本.然而，式(13)仅考虑了代理模型的认知不确定性，却忽略了添加的训练样本点应分布在极限状态函数附近.假设为已构建的代理模型，为确保所选的训练样本点落在极限状态函数附近，可表示为

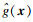
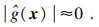(14)

根据式(13)和式(14)可得一种新的通用自适应学习函数CF：

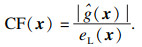(15)

使学习函数CF最小的点将从候选样本集中被自适应选为新的训练样本点，具体表达如下：

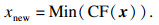(16)

2.2 k-means算法k-means算法实现简单，聚类效果好，因此被广泛应用.其基本原理是根据样本点到聚类中心距离最小的原则，将样本点分为k个簇.其中样本点到聚类中心的距离表达式为^[13]

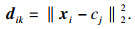(17)

k-means算法的基本流程如下：
1) 从样本集中随机抽取k个样本作为初始的聚类中心{c₁, c₂, …, c_k}；
2) 计算样本点x_i和各个中心c_j, j=1, 2, …, k的距离，依据d_ik最小原则进行分组；
3) 重新计算k个簇新的聚类中心c_j, j=1, 2, …, k；
4) 若前后两次k个聚类中心点的位置都没有变化，则输出分类结果, 否则返回2).
k-means算法迭代过程图解如图 1所示.
图 1(Fig. 1)

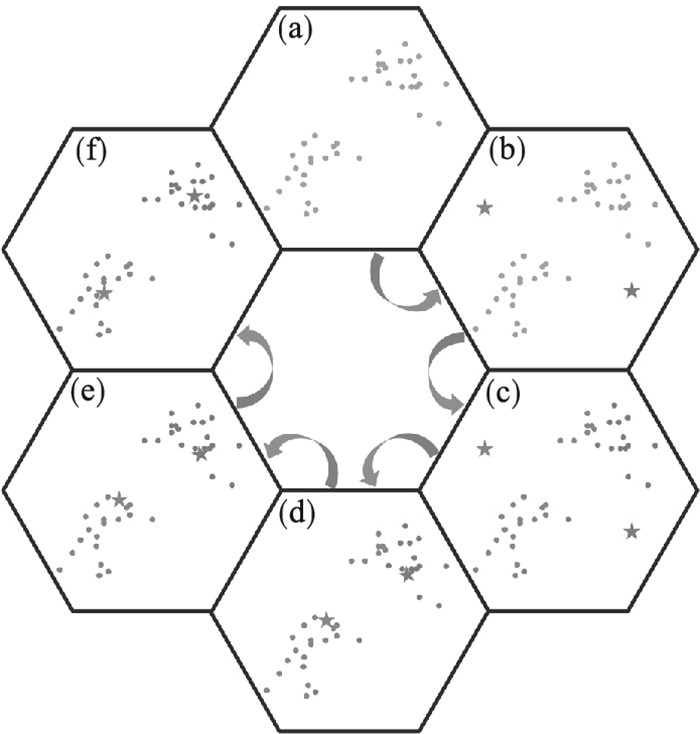图 1 k-means算法迭代过程示意图Fig.1 Iteration process diagram of the k-means algorithm

k-means算法迭代过程大致由图 1所示的六步组成.其中：图 1a为待分类样本.设k=2，随机选择两类样本对应的初始聚类中心(以下简称中心)，即图 1b中黑色和灰色五角星.然后计算所有样本到两中心的距离，并标记各样本的类别及该样本距离最小的中心的类别，如图 1c所示，即第一次迭代后的样本类别.接着对当前黑灰样本分别求其新的中心，如图 1d所示，新的黑灰中心的位置发生了变化.图 1e和图 1f重复了图 1c及图 1d的过程，即将样本的类别标记为距离最近的中心的类别并求新的中心.最后的样本分类见图 1f.
2.3 CF-K方法原理学习函数CF与其他大多数学习函数一样，在更新代理模型的迭代过程中，每次迭代只能选取一个最佳样本点.因此，对学习函数CF的加点方式进行改进以进一步提高计算效率.拟在每次迭代过程中，通过一次仿真选择多个最佳样本点，同时从多区域对代理模型进行拟合，以减少迭代次数提高效率.
综上，本文引入k-means算法，提出一种并行自适应加点策略CF-K.其基本流程为：首先，利用k-means算法对候选样本点进行分类，分成k组；然后，在每一组中各选取满足Min(CF(x))的最佳样本点.应用k-means算法可以从多区域同时让代理模型“逼近”真实极限状态函数, 并且在一定程度上可以缓解所选样本点过密，提高样本利用率及计算效率^[13].自适应加点策略CF-K的停止准则为^[8]

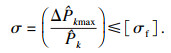(18)

式中：, 分别是由第k次迭代的代理模型和估计的失效概率；[σ_f]为停止准则阈值.
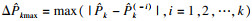
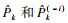
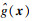
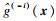
2.4 失效概率的计算假设最终构建的代理模型为，则失效概率估计如下^[13]：

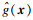
(19)

式中：x_i是由蒙特卡洛法生成的候选样本x=(x₁, x₂, …, x_NMCS)中的第i个样本；为指示函数，当时, ，反之，.
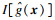
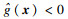
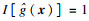
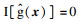
2.5 基于CF-K方法的结构可靠性分析流程步骤1??采用拉丁超立方抽样法选取N个初始样本点x=[x₁, x₂, …, x_N]，各变量的取值范围为[-5, 5].计算对应的响应值y=[y₁, y₂, …, y_N]，并构建初始训练样本集(x, y).
步骤2??基于初始训练样本集(x, y)构建初始代理模型，记迭代次数i=0.
步骤3??使用蒙特卡洛法构建候选样本空间S=[x₁, x₂, …, x_NMCS].
步骤4??应用k-means算法将候选样本分成k组.
步骤5??在每一组中选取满足Min(CF(x))的样本点作为最佳样本点.k折交叉验证法多用5折或10折交叉验证.文中采用10折交叉验证以兼顾效率和精度.若在可接受的精度范围内进一步提高计算效率，可用5折交叉验证.
步骤6??计算对应的响应值并加入初始训练样本中，重新构建代理模型，记迭代次数i=i+1.
步骤7??根据当前迭代对应的代理模型所估计的失效概率，并由式(18)判断是否收敛.如果满足收敛要求，则获取最终的代理模型和失效概率估计值，否则返回步骤4.具体流程示意图见图 2.
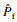
图 2(Fig. 2)

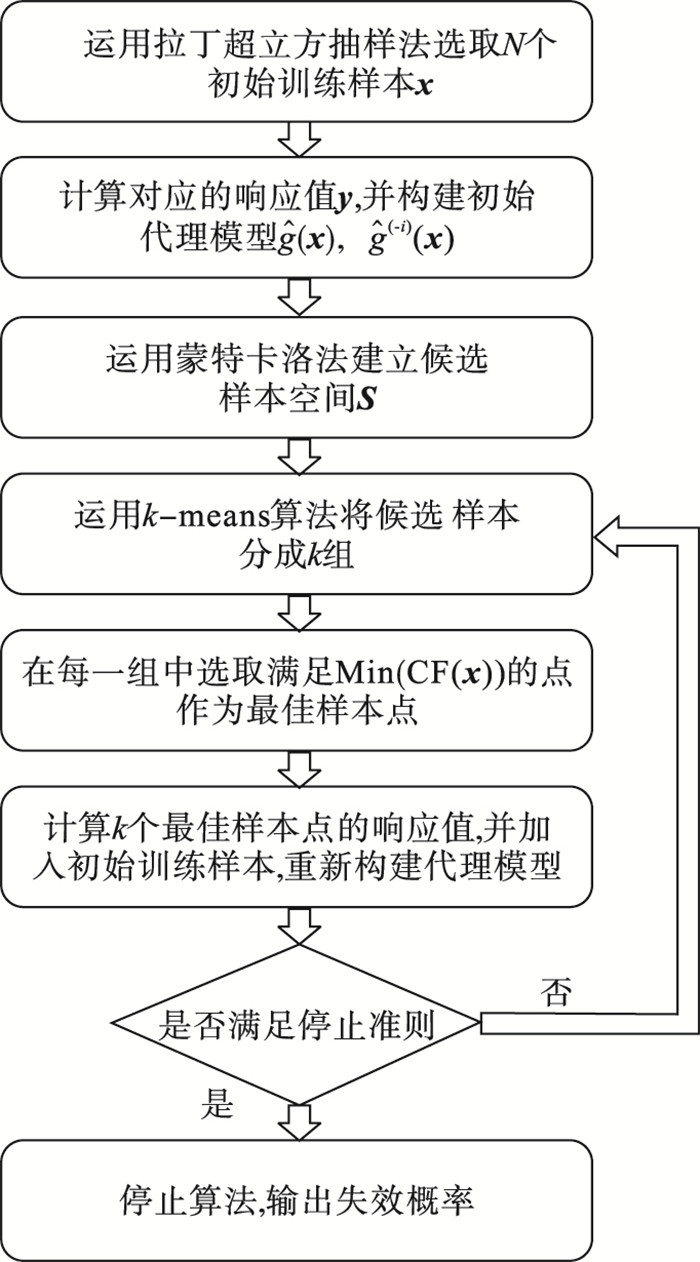图 2 基于CF-K法的结构可靠性分析流程图Fig.2 Flowchart of the structural reliability analysis based on the CF-K method

需要注意的是，在使用MCS法计算失效概率时，应满足式(20)，其中阈值[δ]可取0.05^[14].

(20)

3 算例分析在本节中，一个数值算例和一个实际工程算例被用来验证所提方法的有效性.在算例分析中，失效概率估计值与精确解的相对误差定义为^[8]

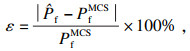(21)

其中：为失效概率估计值；P_f^MCS为蒙特卡洛法求得的失效概率值.
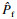
3.1 强非线性算例为验证所提方法的有效性和优势，首先对二维强非线性的算例进行分析，其功能函数为^[8]

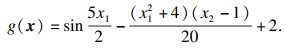(22)

其中，变量x₁和x₂相互独立且均满足正态分布，具体参数为x₁~N(1.5, 1), x₂~N(2.5, 1).
本例中, 初始训练样本的数量均为12个，停止准则阈值[σ_f]=0.02，MCS法生成样本量为5×10⁵个，所得结果=3.131×10^-2作为“精确解”^[8].为减少不确定性，基于所提加点策略的可靠性分析方法重复运行5次，平均结果见表 2和图 3，其他方法结果源于文献[8].将基于所提方法指导Kriging模型和RBF模型获得的极限状态函数与实际极限状态函数进行对比，结果如图 4所示. N为迭代次数.
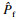
表 2(Table 2)

表 2 不同方法的平均结果Table 2 Average results with different methods 方法 k N ε/% MCS[8] — — 3.131×10-2 — AK-MCS+U[8] — 40.9 3.137×10-2 0.192 Kriging+CF-K k=2 7.6 3.138×10-2 0.497 k=3 5.6 3.133×10-2 0.595 k=4 4.2 3.151×10-2 0.638 k=5 3.2 3.130×10-2 0.577 RBF+CF-K k=2 20.6 3.142×10-2 0.519 k=3 15.4 3.133×10-2 0.431 k=4 13.4 3.118×10-2 0.691 k=5 10.2 3.122×10-2 0.504

表 2 不同方法的平均结果 Table 2 Average results with different methods

图 3(Fig. 3)

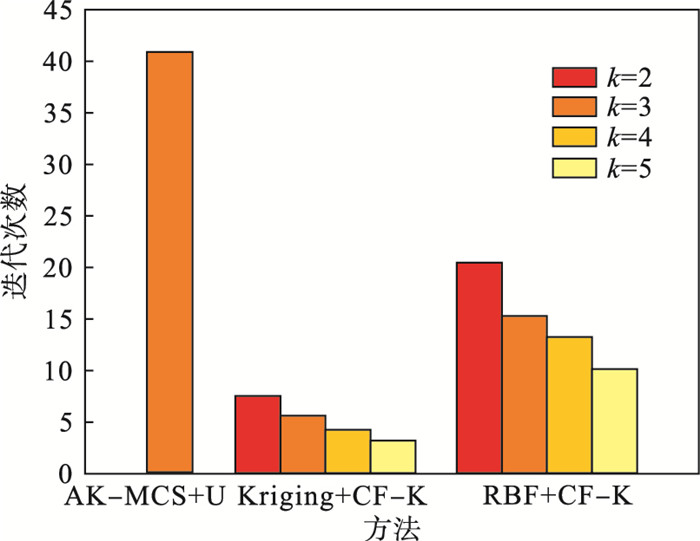图 3 不同方法的迭代次数Fig.3 Iterations with different methods

图 4(Fig. 4)

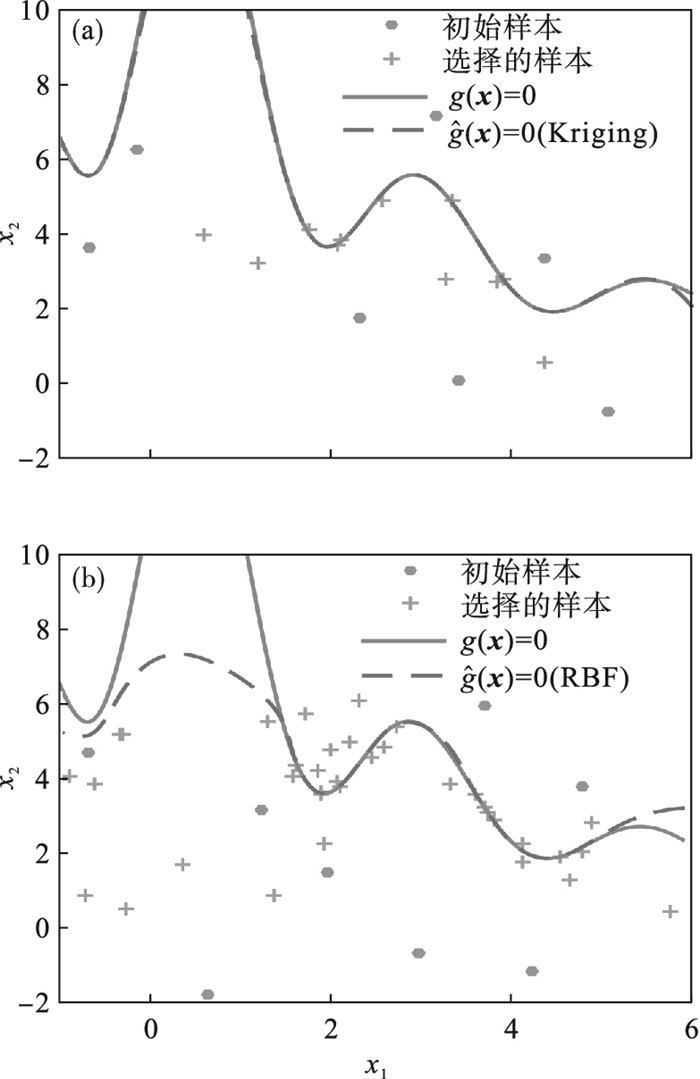图 4 基于CF-K的代理模型与真实极限状态函数的对比Fig.4 Comparison of surrogate models based on the CF-K and real limit-state function (a)—Kriging+CF-K (k=2); (b)—RBF+CF-K (k=2).

由表 2和图 3可知，基于所提方法的各代理模型得到的失效概率与MCS在大量样本下计算的结果几乎相同.AK-MCS+U和Kriging+CF-K均采用Kriging模型，在精度相差较小的情况下，基于所提自适应加点策略CF-K的算法迭代次数远远少于U学习函数，计算效率得到较大幅度的提升.此外，迭代次数随着k值的增加而逐渐减少，可有效节省仿真时间，但也会增加并行运算使用的计算机数量.
根据算例及文献[14]可知，可取k=4，具体可进一步根据实际情况对k值进行放大或缩小. Kriging+CF-K和RBF+CF-K对比可知，所提方法在理论上能适用于其他现有的代理模型，且在精度和效率之间取得了令人满意的折中.RBF+CF-K需要相对较多的迭代次数，造成这种现象的原因可能有以下几点：1)每个代理模型均有各自擅长解决的问题领域，这也是研究通用自适应加点策略的目的之一，即解决现有自适应加点策略多局限于Kriging模型的问题，为充分发挥各代理模型的优势，解决它们各自擅长的问题领域提供理论与技术支撑；2)RBF模型需要确定合适的形状参数c才能充分发挥RBF模型的优势，而文中用于确定形状参数c的算法可能存在一些不足.
由图 4可知，基于CF-K的Kriging模型和RBF模型均能很好地拟合真实极限状态函数.RBF模型全局近似相对较弱，但局部近似精度高，而基于代理模型的可靠性分析法关注的正是代理模型在关键区域而非全局的精度.
3.2 工程算例以一个经典的实际工程问题即桁架结构为算例，进一步验证所提方法的有效性，其结构简图如图 5所示^[15].该结构由23个杆件构成，其中水平杆为11根，倾斜杆为12根，水平杆的截面积和杨氏模量为(A₁，E₁)，倾斜杆的截面积和杨氏模量为(A₂，E₂).所受随机载荷为P₁~P₆，随机载荷均服从Gumbel型分布(6个载荷分别作用在6个节点上(见图 5)).上述随机变量相互独立，具体参数见表 3.
图 5(Fig. 5)

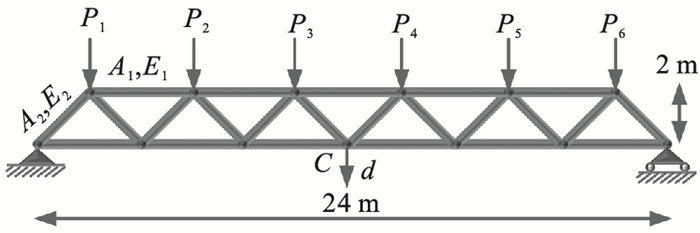图 5 桁架结构Fig.5 The truss structure

表 3(Table 3)

表 3 变量的分布Table 3 Distribution of variables 变量 分布 均值 标准差 (P1~P6)/N Gumbel 5×104 7.5×103 A1/m2 对数正态 2×10-3 2×10-4 A2/m2 对数正态 1×10-3 1×10-4 E1/Pa 对数正态 2.1×1011 2.1×1010 E2/Pa 对数正态 2.1×1011 2.1×1010

表 3 变量的分布 Table 3 Distribution of variables

根据文献[15]，该桁架结构的失效定义为图 5中的位置C在竖直方向的位移d(x)大于给定阈值，其阈值为0.12 m.该结构的功能函数可表示为

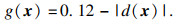(23)

式中，|d(x)|由有限元分析软件ANSYS计算.
本算例中，取20个初始训练样本，停止准则阈值[σ_f]=0.025，使用MCS法随机生成1×10⁶个样本，所得失效概率=1.52×10^-3作为精确解^[15].为减少不确定性，基于所提加点策略的可靠性分析方法重复运行5次，平均结果如表 4和图 6所示，其他方法结果源于文献[15].
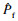
表 4(Table 4)

表 4 不同方法的平均结果Table 4 Average results with different methods 方法 k N ε/% MCS[8] — 1.52×10-3 — AK-MCS+U[8] 300 1.52×10-3 0 Kriging+CF-K k=2 26.4 1.524×10-3 0.90 k=3 21.6 1.511×10-3 0.93 k=4 14.8 1.525×10-3 0.62 k=5 11.6 1.521×10-3 0.63 RBF+CF-K k=2 36.6 1.520×10-3 0.61 k=3 24.4 1.522×10-3 0.87 k=4 18.6 1.521×10-3 0.86 k=5 16 1.506×10-3 0.97

表 4 不同方法的平均结果 Table 4 Average results with different methods

图 6(Fig. 6)

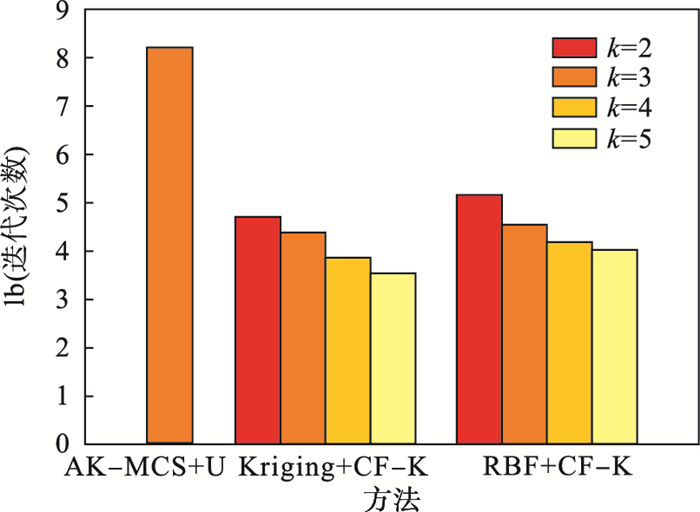图 6 不同方法的迭代次数Fig.6 Iterations results with different methods

由表 4和图 6可知，由所提方法CF-K分别指导Kriging模型和RBF模型进行结构可靠性分析，均以较少的迭代次数获得的失效概率值与MCS法得到“精确解”大致相同，再次验证所提自适应加点策略具有良好的性能和通用性.与AK-MCS+U相比，其精度虽处于同一水平，但迭代次数远少于AK-MCS+U，表明基于所提方法的结构可靠性分析在保证精度的前提下，能以较少的迭代次数完成可靠性分析，即所提方法的学习能力在一定程度上优于U学习函数.此外，由于U学习函数仅适用于Kriging模型，而所提方法适用于其他现有的代理模型，故其普适性高于U学习函数.
4 结论1) 所提方法CF-K基于交叉验证原理构建，因此不局限于Kriging模型，还适用于现有的其他代理模型，拓展了代理模型方法在结构可靠性分析领域的适用性.
2) 在保证精度的前提下, CF-K法改进了大多数自适应加点策略每次迭代仅选取一个最佳样本点的不足，减少了迭代次数，提高了计算效率.
3) 通过算例分析可知，所提自适应加点策略不仅适用多种代理模型用于结构可靠性分析，还较好地兼顾了计算精度和效率.
参考文献

[1]	Melchers R E. Structural reliability analysis and prediction[M]. 2nd ed. New York: Wiley, 1999.
[2]	Zhao W A, Chen Y, Liu J C. An effective first order reliability method based on Barzilai-Borwein step[J]. Applied Mathematical Modelling, 2020, 77: 1545-1563. DOI:10.1016/j.apm.2019.08.026
[3]	Lee C H, Kim Y. Probabilistic flaw assessment of a surface crack in a mooring chain using the first- and second-order reliability method[J]. Marine Structures, 2019, 63(1): 1-15.
[4]	Keshtegar B, Seghier M, Zio E, et al. Novel efficient method for structural reliability analysis using hybrid nonlinear conjugate map-based support vector regression[J]. Computer Methods in Applied Mechanics & Engineering, 2021, 381: 113818.
[5]	Papadopoulos V, Giovanis D G, Lagaros N D, et al. Accelerated subset simulation with neural networks for reliability analysis[J]. Computer Methods in Applied Mechanics & Engineering, 2012, 223/224: 70-80.
[6]	Sun Z, Wang J, Li R, et al. LIF: a new Kriging based learning function and its application to structural reliability analysis[J]. Reliability Engineering & System Safety, 2017, 157: 152-165.
[7]	Shi L J, Sun B B, Ibrahim D S. An active learning reliability method with multiple kernel functions based on radial basis function[J]. Structural and Multidisciplinary Optimization, 2019, 60(1): 211-229. DOI:10.1007/s00158-019-02210-0
[8]	Xiao N C, Zuo M J, Guo W. Efficient reliability analysis based on adaptive sequential sampling design and cross-validation[J]. Applied Mathematical Modelling, 2018, 58: 404-420. DOI:10.1016/j.apm.2018.02.012
[9]	Echard B, Gayton N, Lemaire M. AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation[J]. Structural Safety, 2011, 33(2): 145-154. DOI:10.1016/j.strusafe.2011.01.002
[10]	Zhang X F, Wang L, Sorensen J D. REIF: a novel active-learning function toward adaptive Kriging surrogate models for structural reliability analysis[J]. Reliability Engineering & System Safety, 2019, 185: 440-454.
[11]	Shi Y, Lu Z, He R, et al. A novel learning function based on Kriging for reliability analysis[J]. Reliability Engineering & System Safety, 2020, 198: 106857.
[12]	Yi J X, Zhou Q, Cheng Y, et al. Efficient adaptive Kriging-based reliability analysis combining new learning function and error-based stopping criterion[J]. Structural and Multidisciplinary Optimization, 2020, 62(5): 2517-2536. DOI:10.1007/s00158-020-02622-3
[13]	曹汝男, 孙志礼, 张毅博, 等. 基于主动学习的复杂机械结构的可靠性分析[J]. 东北大学学报(自然科学版), 2020, 41(2): 223-228. (Cao Ru-nan, Sun Zhi-li, Zhang Yi-bo, et al. Reliability analysis based on active learning for complex mechanical structure[J]. Journal of Northeastern University (Natural Science), 2020, 41(2): 223-228.)
[14]	Cao R N, Sun Z L, Wang J, et al. An efficient and time-saving reliability analysis strategy for complex mechanical structure[J]. IEEE Access, 2020, 8: 171281-171291. DOI:10.1109/ACCESS.2020.3020314
[15]	Marelli S, Sudret B. An active-learning algorithm that combines sparse polynomial chaos expansions and bootstrap for structural reliability analysis[J]. Structural Safety, 2018, 75: 67-74. DOI:10.1016/j.strusafe.2018.06.003