
 , 于苏扬1, 赵伍端1, 陈杰4
, 于苏扬1, 赵伍端1, 陈杰4 1. 长安大学 道路施工技术与装备教育部重点实验室,陕西 西安 710064;
2. 芜湖哈特机器人产业技术研究有限公司博士后工作站,安徽 芜湖 241007;
3. 哈尔滨工业大学 芜湖机器人产业技术研究院,安徽 芜湖 241007;
4. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819
收稿日期:2022-06-29
基金项目:国家自然科学基金资助项目(52275005, 52175004); 中国博士后科学基金资助项目(2022M722435);机器人技术与系统国家重点实验室开放基金(SKLRS-2020-KF-08); 河南省重点研发与推广专项(科技攻关)项目(222102320417); 河南省市场监督管理局科技计划项目(2022sj145)。
作者简介:郭万金(1983-), 男, 内蒙古赤峰人, 长安大学副教授。
摘要:为了解决打磨过程中打磨控制系统存在扰动问题,设计了一种机器人力控末端执行器,并提出了一种机器人主动柔顺恒力打磨自抗扰模糊变阻抗控制方法.所提方法的内环控制采用模糊变阻抗控制器,外环控制采用自抗扰打磨控制器.采用Lyapunov稳定性理论证明了所提方法的跟踪误差收敛为零.通过仿真和实验,验证了所提方法的有效性和适用性.研究结果表明:在内环控制相同情况下,与外环控制为PID控制器相比,所提出的机器人主动柔顺恒力打磨自抗扰模糊变阻抗控制方法减小了打磨过程中的力跟踪误差和位置超调量,提高了机器人打磨力控制系统的控制效果和鲁棒性,实现机器人柔顺恒力控制.
关键词:机器人打磨主动柔顺自抗扰控制机器人末端执行器恒力控制
Grinding Control Method of Robotic Active Compliance Constant-Force
GUO Wan-jin1,2,3

 , YU Su-yang1, ZHAO Wu-duan1, CHEN Jie4
, YU Su-yang1, ZHAO Wu-duan1, CHEN Jie4 1. Key Laboratory of Road Construction Technology and Equipment of MOE, Chang'an University, Xi'an 710064, China;
2. Post-Doctoral Research Center, Wuhu HIT Robot Technology Research Institute Co., Ltd., Wuhu 241007, China;
3. Wuhu Robot Technology Research Institute, Harbin Institute of Technology, Wuhu 241007, China;
4. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: GUO Wan-jin, E-mail: guowanjin@chd.edu.cn.
Abstract: In order to solve the problem of disturbance in grinding control system, a robotic force control end-effector is designed, and a grinding control method of robotic active compliance constant-force is proposed, based on the active disturbance rejection control and the fuzzy variable impedance control. A fuzzy variable impedance controller is adopted by the inner-loop control of the proposed method, and an active disturbance rejection grinding controller is adopted by the outer-loop control. Convergence of the tracking error to zero for the proposed method is guaranteed by the Lyapunov stability theory. The effectiveness and applicability of the proposed method are verified by the co-simulation and experiment. By comparing the proposed method and the PID controller, which is used to replace the outer-loop control, when the inner-loop control is same, the former has better ability to reduce force tracking error and position overshoot during simulation experiments. Meanwhile, using the proposed method, the control effects and the robustness of the force control system for the robotic grinding are improved, and the robotic compliant constant-force control is realized.
Key words: robotic grindingactive complianceactive disturbance rejection controlrobotic end-effectorconstant-force control
随着制造业智能化发展,工业机器人技术广泛应用于打磨等连续接触式作业[1].打磨是一种提高工件表面精度的精密加工方法,打磨环节有很多影响因素,其中打磨力是一个关键因素,直接影响工件质量.
为了以可控方式进行机器人柔顺恒力打磨[1],国内外****对机器人力控末端执行器开展了诸多研究.黄智等[2]提出一种气囊式力控打磨装置,对打磨压力进行控制;林文强等[3]提出一种可调节压力的气囊支撑装置,用于提高薄壁件加工精度.Chen等[4]提出一种末端执行器,用于对薄壁整体叶盘磨抛过程中主动接触力的控制.Dai等[5]设计一种具有较好阻尼性能的气电混合式末端执行器,改善控制系统的响应时间和控制带宽.Mohammad等[6]提出一种力控末端执行器,通过调节音圈电机的伸缩实现刀具柔度.Ma等[7]设计一种主动力控末端执行器,通过将其原型化为微型机械手研磨系统进行位置和力控制.Ding等[8]提出一种基于正负组合刚度机构的恒力装置.Jin等[9]设计一种调节旋转方向和气压来主动控制接触力大小的末端执行器.Mohammad等[10]提出一种可集成到机器人抛光单元中的力控末端执行器.Tommasino等[11]设计一种能够承受碰撞冲击力的双稳态机构末端执行器.
为了实现恒力打磨,提高末端执行器从自由空间过渡到约束空间的顺应能力,解决控制过程中鲁棒性等问题,****对机器人主动柔顺恒力控制方法开展了大量研究.史家顺等[12]提出一种跟随轨迹的变抛光力气动加载系统.许家忠等[13]提出一种基于位置控制的自适应阻抗控制器,解决机械臂末端位置判断问题和打磨轨迹在线补偿问题.张雷等[14]提出一种气动伺服抛光系统.王磊等[15]提出一种模糊预测算法.Xu等[16]提出一种将力/位置混合控制与PI/PD控制相结合方法.Mohsin等[17]提出一种基于刀具路径规划和抛光参数的复杂曲面机器人抛光控制方法.Gracia等[18]提出一种基于任务优先级和滑模控制的机器人表面处理混合位置/力控制方法.Kakinuma等[19]提出一种基于宏-微机构的机器人抛光控制系统,实现主轴快速动态力控制.Lakshminarayanan等[20]提出一种用于跟踪工件轮廓并实现位置和力实时调整的阻抗控制迭代学习控制器.Kana等[21]提出一种基于阻抗控制的协同曲线跟踪控制方法.在接触环境多变且不可预测的打磨加工场景下,上述控制方法[13, 14, 16, 17, 21]的控制性能对模型精度要求较高,且由于机器人打磨作业存在低刚度、小驱动带宽和低定位分辨率等问题[6],控制方法[18]与控制器[20]计算量较大.
由于机器人加工过程中打磨力非线性变化对工件的加工精度影响较大,传统PID控制并不能满足非线性系统的要求,而且会对系统的扰动放大[22].自抗扰控制技术具有实时估计系统内外部未知扰动并予以补偿、鲁棒性强和对模型依赖性低等特点[23],近年来逐渐被应用于机器人领域,如机器人关节角跟踪[24]、机器人轨迹控制[25-27]等.本文将自抗扰控制技术应用于机器人打磨恒力控制,解决打磨过程中打磨控制系统存在的扰动问题.设计一种力控末端执行器,使机器人控制位置,末端执行器调节工件表面法线方向的打磨力,为实现恒力打磨的力和位置解耦控制提供结构基础;在末端执行器结构基础上,提出一种机器人主动柔顺恒力打磨控制方法,为机器人柔顺恒力控制提供一种实现途径.
1 机器人力控末端执行器本文设计一种力控末端执行器结构,如图 1a所示,其中,打磨电机通过连接主轴传递旋转运动到打磨工具,音圈电机提供打磨工具的伸缩平移控制,并采用滚珠花键副实现伸缩平移及旋转运动的解耦.所设计结构具有高集成化和通用性强等特点,其主要优势是可通过调节音圈电机伸缩量进而控制接触力,有效地避免了使用刚性末端执行器时因运动不准确导致工件变形或过切现象,为实现主动柔顺恒力控制提供优良结构基础.
图 1(Fig. 1)
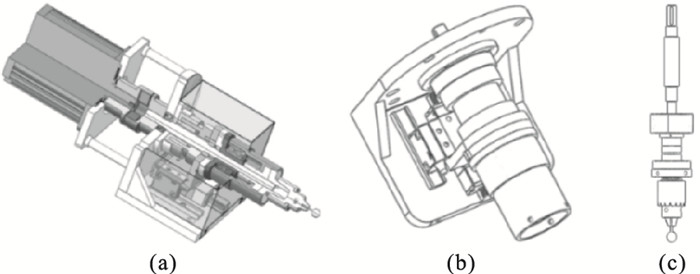 | 图 1 机器人力控末端执行器Fig.1 Robotic force control end-effector (a) —执行器结构;(b)—伸缩平移组件;(c) —旋转运动组件. |
所设计结构关键部分包括伸缩平移组件(如图 1b所示)和旋转运动组件(如图 1c所示).其中:1) 伸缩平移组件主要由音圈电机、导轨连接板、双列角接触球轴承与传力连接件组成.其主要优点有:①伸缩平移运行平稳.这得益于用于位置控制的中空型音圈电机的磁性外壳固定安装于腕部连接板上,线圈连接到导轨连接板上,可以确保设计刚性并防止运行期间打磨工具颤振对伸缩平移的影响.②结构紧凑.传递到导轨连接板的伸缩平移通过传力连接件和中空型力传感器传输到双列角接触球轴承的内侧,双列角接触球轴承的外侧与传力架过盈配合,同时允许传力架和传力连接件之间相对旋转运动,在平稳传递伸缩平移运动的同时,仅占用较小轴向空间,使末端执行器运动部件质量大幅度减小.
2) 旋转运动组件主要由打磨电机、主轴、深沟球轴承、传力架、法兰型滚珠花键副与打磨工具组成.其主要特点有:①平移和旋转运动可靠解耦.采用主轴将打磨电机输出的旋转运动通过机械传动形式传递给打磨工具,主轴上部连接至打磨电机,中间部分采用深沟球轴承支撑以承载径向负载,下部为具有滚道槽的花键轴段,与法兰型滚珠花键副连接,传力架连接至滚珠花键副将旋转运动传递给打磨工具,具备实现可靠伸缩平移同时传递扭矩的特点及打磨电机和主轴保持静止、打磨工具处旋转运动和伸缩平移互不干扰的优势.②通用性强.能够实现打磨工具与可胀锥度套之间无间隙的可靠夹紧和方便拆卸功能;且可与不同串联、并联型式机器人适配,适应多场景的打磨作业.
2 机器人主动柔顺控制方法为了解决打磨过程中打磨控制系统存在扰动问题,本文设计一种自抗扰打磨控制器.同时,为了适应打磨作业接触环境多变工况,结合容易控制、计算量小的阻抗控制[13],设计一种模糊变阻抗控制器.在此基础上,针对打磨非线性系统力波动影响打磨期望力跟踪效果、打磨力动态变化对控制精度影响较大等问题,提出一种机器人主动柔顺恒力打磨自抗扰模糊变阻抗控制方法.其中,内环控制采用所设计的模糊变阻抗控制器,用于补偿末端执行器位置误差并调节阻抗特性使得刚性与柔顺性主动适应多变打磨作业环境,外环控制采用所设计的自抗扰打磨控制器,用于动态调整打磨工具工作位置;内外环控制共同构成闭环控制回路,实现机器人主动柔顺恒力打磨.
2.1 自抗扰打磨控制器本文的控制模型为二阶控制系统,可将其表示为如式(1)所示的非线性系统模型.
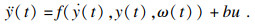 | (1) |
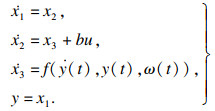 | (2) |
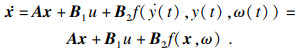 | (3) |

在非线性系统中通常需要设计扩张状态观测器估计时变扰动[28-30].为了实现对打磨过程中时变扰动的估计与补偿,本文设计的扩张状态观测器如式(4)所示:
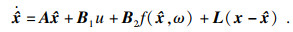 | (4) |
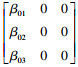
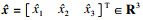
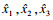
为了获得更好的控制效果,将扩张状态观测器的状态误差信息输出
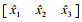
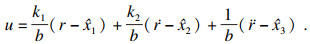 | (5) |
将式(5)代入式(1)得
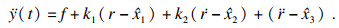 | (6) |
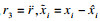
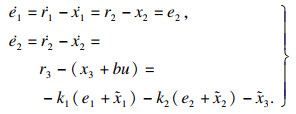 | (7) |
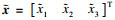
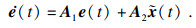 | (8) |
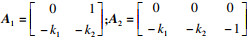
由于机器人打磨作业属于减材加工方式,通常不允许产生过切等现象.为了实现闭环系统的信号过渡,引入最速综合函数fhan() [23],在保证快速跟踪的前提下使输入信号不产生超调,提高系统鲁棒性.具体形式如式(9)所示:
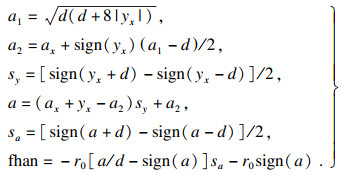 | (9) |
由式(4)设计的扩张状态观测器和式(5)设计的误差反馈控制律,并结合式(9)中提供微分信号过渡的最速综合函数,得出以下离散自抗扰打磨控制器:
1) 跟踪微分器:
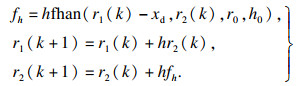 | (10) |
2) 误差反馈控制律:
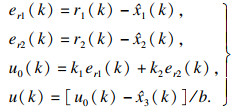 | (11) |
3) 扩张状态观测器:
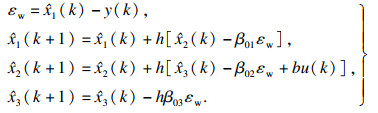 | (12) |
由式(10)~式(12)得出自抗扰打磨控制器,实现对位置误差估计与补偿.其对模型依赖性低,具有更高控制精度、稳定性和较强的鲁棒性.所设计自抗扰打磨控制器对应的控制框图如图 2所示,具体流程为:1)采用跟踪微分器对给定期望位置xd信号进行平滑过渡处理,得到期望信号r1及其微分信号r2;2)误差反馈控制律将位置误差er1和位置误差的微分er2进行处理,获得控制量u0;3)扩张状态观测器对打磨过程中系统内外扰动总和进行状态观测
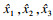
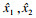
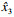
图 2(Fig. 2)
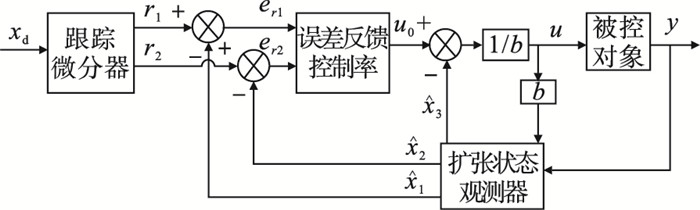 | 图 2 自抗扰打磨控制器控制框图Fig.2 Control block diagram of active disturbance rejection grinding controller |
2.2 扩张状态观测器收敛性分析扩张状态观测器将系统总扰动扩张成一个新的系统状态量,通过控制系统输入、输出将误差观测出来并加以补偿[31].本文采用Lyapunov稳定性理论对扩张状态观测器进行收敛性分析,证明在求解打磨非线性系统问题时自抗扰打磨控制器的跟踪误差收敛为零.由式(3)和式(4)得
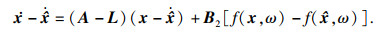 | (13) |
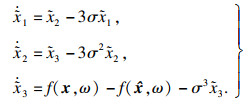 | (14) |
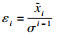
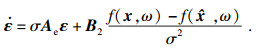 | (15) |
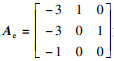
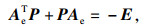 | (16) |
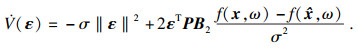 | (17) |

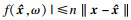
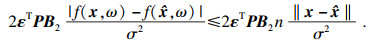 | (18) |
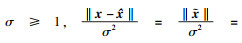
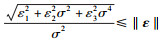
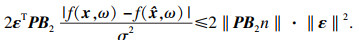 | (19) |
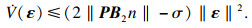 | (20) |
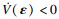
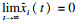
2.3 模糊变阻抗控制器本文为了实现恒力跟踪,将打磨作业过程的力与位置的动态变化通过阻抗来表征,并采用基于位置的阻抗控制间接控制力,即不直接控制音圈电机输出的伸缩驱动力,而是根据位置偏差信号间接控制音圈电机,通过与工件接触改变系统实际接触力,使实际接触力相对于期望接触力的力误差Fe逐渐趋近于零,实现打磨期望力Fn跟踪.打磨机器人作业系统经简化后建立基于位置的阻抗控制模型如式(21)所示:
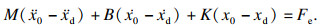 | (21) |
对于接触环境多变且不可预测的打磨作业场景,固定参数的阻抗控制无法根据任务或环境变化对输出值进行动态规划调整[32],变参数阻抗控制可以较好地解决这一问题.模糊控制具有不依赖于被控对象精确数学模型和便于操作等特点[33].本文结合变参数阻抗控制和模糊控制的各自优点,根据力反馈信息得到的力误差Fe和误差变化ΔFe对阻抗参数M,B和K进行优化和输出,从而达到适应打磨多变接触环境和提高控制效果的目的.
本文设计的模糊变阻抗控制器控制框图如图 3所示.在模糊变阻抗控制器设计中,设定输入误差Fe和误差变化ΔFe两者的论域为[-3, 3],通过三角形隶属函数建立负大、负中、负小、零、正小、正中、正大共7个语言变量的模糊子集(NB,NM,NS,Z0,PS,PM,PB),根据控制要求设置每个值所取范围宽度相等,在模糊推理时采用并行法;输入模糊控制器的精确量经过模糊量化处理为模糊量,通过查询模糊规则表[33],确定阻抗参数模糊量,将输出的模糊量通过加权平均法进行去模糊化得到精确输出变量ΔWM,ΔWB和ΔWK,将其代入修正关系式得到精确量输出WM,WB和WK,修正关系式为
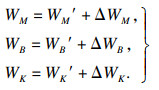 | (22) |
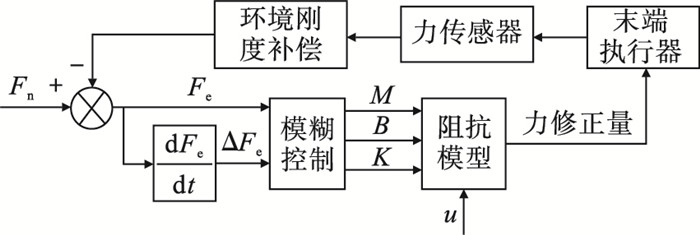 | 图 3 模糊变阻抗控制器控制框图Fig.3 Control block diagram of fuzzy variable impedance controller |
式中,WM′,WB′和WK′为设定的阻抗参数初始值.通过变参数实现动态调节力修正量,解决控制系统稳定性问题,实现对被控制对象的控制,满足任意时刻对阻抗参数进行优化和输出.
2.4 机器人主动柔顺恒力打磨控制方法为了补偿末端执行器的位置误差并调节阻抗特性使得刚性与柔顺性主动适应多变打磨作业环境,本文结合以上设计的模糊变阻抗控制器和自抗扰打磨控制器,提出一种机器人主动柔顺恒力打磨自抗扰模糊变阻抗控制方法(简称为机器人主动柔顺恒力打磨控制方法),实现动态调整打磨工具工作位置较好收敛到期望位置和恒力打磨.本文所提出的机器人主动柔顺恒力打磨控制方法对应控制框图如图 4所示,具体流程如下:
图 4(Fig. 4)
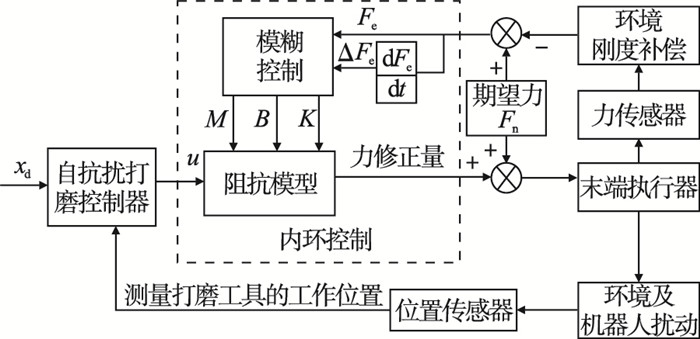 | 图 4 机器人主动柔顺恒力打磨控制方法控制框图Fig.4 Control block diagram of grinding control method of robotic active compliance constant-force |
1) 给定期望位置xd,自抗扰打磨控制器根据位置传感器反馈的打磨工具当前工作位置,对打磨模型和机器人扰动进行在线状态估计和信号补偿;
2) 自抗扰打磨控制器输出值作为阻抗模型的输入,通过阻抗模型建立末端执行器伸缩位移与接触力之间的关系,输出力的修正量进行力补偿,使力偏差趋近于零,避免力超调而产生过切现象;
3) 阻抗模型的阻抗参数采用模糊控制并考虑环境刚度补偿的力反馈信息进行优化和输出.
在所构建的自抗扰模糊变阻抗闭环控制回路中,外环自抗扰打磨控制器根据在打磨初始条件下以及打磨过程中的期望位置和误差扰动,对位置误差进行估计与补偿,解决打磨过程中控制系统存在扰动的问题;内环模糊变阻抗控制器通过变参数实现动态调节力修正量,达到适应打磨多变接触环境和提高控制效果的目的.本文所提出的机器人主动柔顺恒力打磨控制方法,对末端执行器的打磨力进行补偿使其不发生超调,实现机器人主动柔顺恒力打磨.
3 控制方法仿真与实验本文建立如图 5所示机器人打磨虚拟样机,其由所设计的力控末端执行器、六自由度串联工业机器人及工件组成,并在该虚拟样机上开展Matlab与Adams联合仿真实验,验证提出的机器人主动柔顺恒力打磨控制方法的有效性.其中,工件为45号钢的非球面曲面.为避免末端执行器位姿变化量过大致使机器人系统影响打磨作业精度,将末端执行器设置为沿着工件非球面曲面的母线进行打磨(如图 5b所示),设置打磨力方向始终沿着非球面曲面法线方向,并指向非球面曲面.打磨电机转速设置为3 000 r/min,将内环控制均设计为模糊变阻抗控制器,外环控制分别设计为PID控制器和自抗扰打磨控制器,分别得到PID模糊变阻抗控制器和自抗扰模糊变阻抗控制器,进行打磨仿真对比实验.两个控制器的参数是根据经验先进行粗调整,再作微调整,多次优化调整后,使期望目标值的接近程度达到约90%.
图 5(Fig. 5)
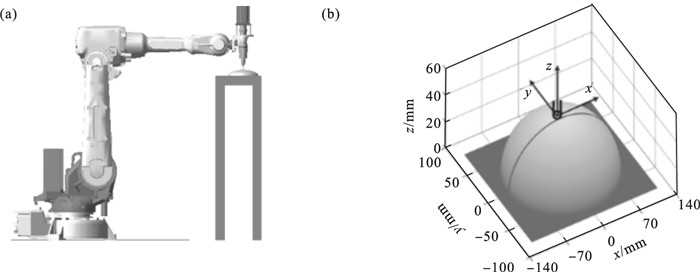 | 图 5 工件与机器人及末端执行器虚拟样机Fig.5 Virtual prototype of workpiece, robot, and end-effector (a) —机器人及末端执行器;(b)—工件. |
采用两种控制器的仿真实验结果如图 6和图 7所示,打磨期望力均设置为20 N,对应材料去除深度为0.07 mm.图 8为稳定打磨阶段打磨工具末端位置的误差分析对比图.通过对比可知,PID模糊变阻抗控制器虽然能达到期望打磨力,但打磨力控制精度难以满足要求,力稳定性较差,最大力波动量为0.8 N,稳定打磨阶段打磨工具末端位置的误差变化量较大,最大超调为1.26%;而自抗扰模糊变阻抗控制器能够显著地减小力变化量和打磨工具末端位置的误差变化量,对应的最大力波动量为0.52 N,位置误差最大超调为0.67%.
图 6(Fig. 6)
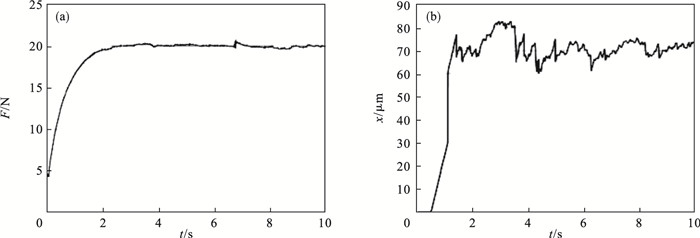 | 图 6 PID模糊变阻抗控制器仿真(期望力20 N)Fig.6 Simulation of PID fuzzy variable impedance controller (desired force 20 N) (a)—打磨力;(b) —打磨工具位移量. |
图 7(Fig. 7)
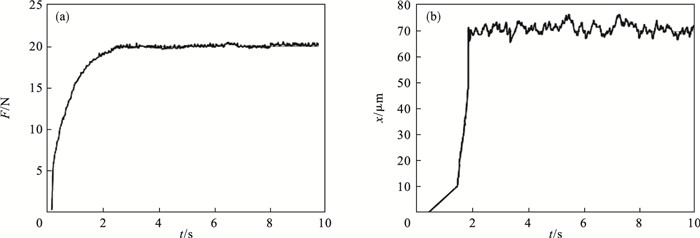 | 图 7 自抗扰模糊变阻抗控制器仿真(期望力20 N)Fig.7 Simulation of active disturbance rejection fuzzy variable impedance controller (desired force 20 N) (a) —打磨力;(b) —打磨工具位移量. |
图 8(Fig. 8)
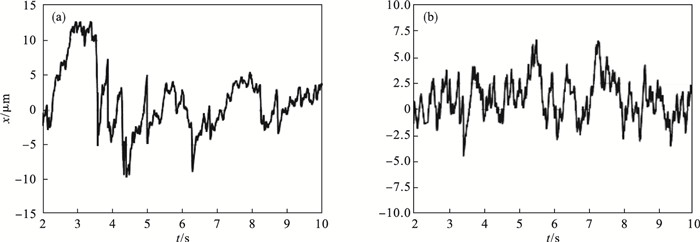 | 图 8 稳定打磨阶段打磨工具末端位置误差分析对比图(期望力20 N)Fig.8 Comparison diagram of error value analysis of grinding tool end position in stable grinding stage(desired force 20 N) (a)— PID模糊变阻抗控制器;(b) —自抗扰模糊变阻抗控制器. |
PID模糊变阻抗控制器和自抗扰模糊变阻抗控制器的仿真实验结果如表 1所示.其中,Fmax为最大打磨力,Fmin为最小打磨力,Fb为最大力波动量,EF为打磨力平均误差,SF为打磨力方差,ΔX0为稳定打磨阶段打磨工具末端位置的误差波动范围.
表 1(Table 1)
| 表 1 仿真实验数据 Table 1 Simulation data |
对比PID模糊变阻抗控制器的仿真结果可以看出,自抗扰模糊变阻抗控制器能显著地减小力波动,打磨力稳定性提高35%,打磨力平均误差减小33%,打磨力方差减小67%,稳定打磨阶段打磨工具末端位置的误差波动范围减小49.8%.上述分析结果表明,所提出的机器人主动柔顺恒力打磨控制方法能够较好地实现恒力打磨、减小打磨力波动与稳定打磨阶段打磨工具末端位置的误差波动范围.
在机器人打磨作业时,应根据所需材料去除量调节打磨力.为了进一步验证所提出的机器人主动柔顺恒力打磨控制方法在不同打磨力下的适用性,对打磨期望力分别为30 N和40 N的工况在上述相同打磨条件下开展仿真对比实验.仿真实验结果如图 9至图 14所示.
图 9(Fig. 9)
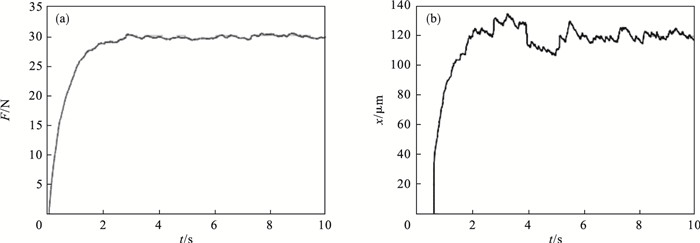 | 图 9 PID模糊变阻抗控制器仿真(期望力30 N)Fig.9 Simulation of PID fuzzy variable impedance controller (desired force 30 N) (a) —打磨力;(b)—打磨工具位移量. |
图 10(Fig. 10)
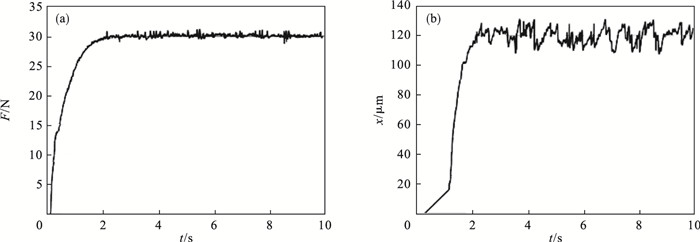 | 图 10 自抗扰模糊变阻抗控制器仿真(期望力30 N)Fig.10 Simulation of active disturbance rejection fuzzy variable impedance controller (desired force 30 N) (a) —打磨力;(b)—打磨工具位移量. |
图 11(Fig. 11)
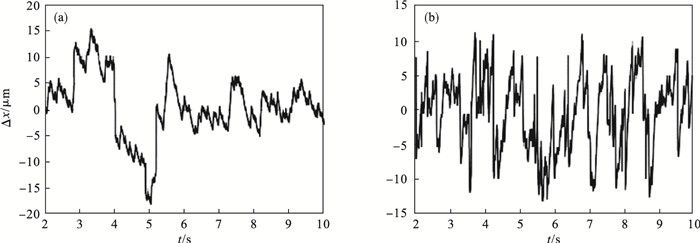 | 图 11 打磨期望力稳定打磨阶段打磨工具末端位置误差分析对比图(期望力30 N)Fig.11 Analysis and comparison diagram of position error value at the end of grinding tool at the stage of stable grinding with desired force (desired force 30 N) (a) —PID模糊变阻抗控制器;(b)—自抗扰模糊变阻抗控制器. |
图 12(Fig. 12)
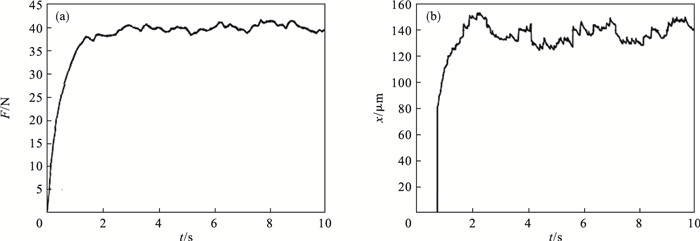 | 图 12 PID模糊变阻抗控制器仿真(期望力40 N)Fig.12 Simulation of PID fuzzy variable impedance controller (desired force 40 N) (a)—打磨力;(b)—打磨工具位移量. |
图 13(Fig. 13)
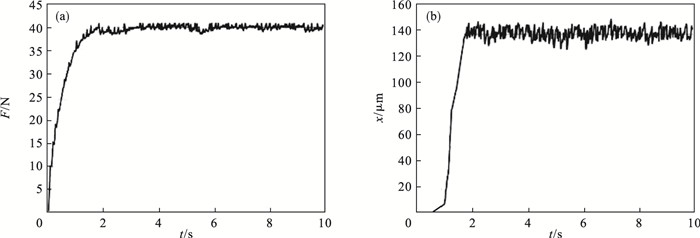 | 图 13 自抗扰模糊变阻抗控制器仿真(期望力40 N)Fig.13 Simulation of active disturbance rejection fuzzy variable impedance controller (desired force of 40 N) (a) —打磨力;(b)—打磨工具位移量. |
图 14(Fig. 14)
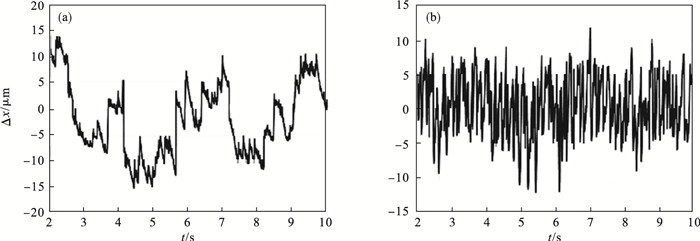 | 图 14 打磨期望力稳定打磨阶段打磨工具末端位置误差分析对比图(期望力40 N)Fig.14 Analysis and comparison diagram of position error value at the end of grinding tool at the stage of stable grinding with desired force (desired force 40 N) (a) —PID模糊变阻抗控制器;(b)—自抗扰模糊变阻抗控制器. |
由图 9至图 14可知,相同的打磨转速下,自抗扰模糊变阻抗控制器能够更准确跟踪期望力,稳定打磨阶段打磨工具末端位置的误差变化量更小,不会出现较大超调.因此,本文所提出的机器人主动柔顺恒力打磨控制方法能够获得更小力/位置误差,同时解决了控制系统稳定性和收敛性问题,对于机器人打磨作业具有较好的有效性与适用性.
在相同打磨转速(3 000 r/min)下,设置打磨期望力初始值为20 N,然后上升至25 N,开展打磨期望力跟踪仿真实验,PID模糊变阻抗控制器和自抗扰模糊变阻抗控制器的力跟踪仿真对比结果如图 15所示.
图 15(Fig. 15)
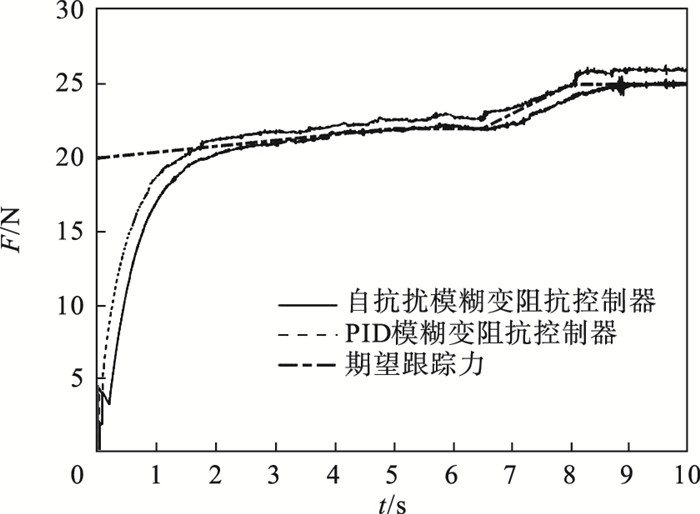 | 图 15 力跟踪效果对比Fig.15 Comparison of force tracking effect |
分析可知,在初始阶段自抗扰模糊变阻抗控制器能够减小力的波动量,尽管在过渡阶段由于跟踪微分器的作用致使调节时间延长,但是最终能够在不发生超调情况下跟踪变化的期望跟踪力,有效避免机器人打磨作业中发生过切问题,而PID模糊变阻抗控制器为了较快完成过渡阶段易引起超调而致使打磨作业发生过切现象;在力跟踪实验中,自抗扰模糊变阻抗控制器的最大力波动量为0.49 N,而PID模糊变阻抗控制器的最大力波动量为0.96 N.仿真结果表明,所提出的机器人主动柔顺恒力打磨控制方法能够较好地实现从某个期望力切换到另一个期望力,可以有效提高打磨力控制系统的稳定性和鲁棒性.
本文机器人实验平台如图 16所示,选用ABB IRB-4600机器人及IRC5控制器和示教器作为机器人实验平台,BECKHOFF公司CX-260354嵌入式控制器作为实验平台控制设备,上位机控制器采用基于PC的控制软件TwinCAT3.上位机控制器与机器人IRC5控制器之间采用套接字通讯,与传感器之间采用EtherCAT通讯.实验中机器人运行提前示教的目标点,上位机控制器连接力传感器,力传感器将接收的实时力信息转换为数字信号输入到BECKHOFF控制器,经本文所提出的力控方法计算出相关控制修正量;机器人末端执行器作为下位机向上位机发送实时位姿信息,并接收所提出力控方法计算的修正位姿信息修改当前运动轨迹,从而控制机器人进行恒力打磨实验.
图 16(Fig. 16)
 | 图 16 机器人打磨实验平台Fig.16 Robotic grinding experiment platform |
在机器人恒力打磨实验中,打磨期望力均设置为10 N,分别采用PID模糊变阻抗控制方法和本文所提出的机器人主动柔顺恒力打磨控制方法,对应力控制结果分别如图 17和图 18所示.实验结果表明,PID模糊变阻抗控制方法有明显的力控延时,实时性效果差,在稳定阶段力误差波动约±3.4 N.与之比较,本文所提出的控制方法虽然初始阶段力超调量略大,但能够较快调整,在稳定阶段力误差波动在±1.8 N以内,与前者实验结果比较,力误差波动较小,力控制性能更加稳定,有效改善了力控延时.通过机器人实验验证了所提出方法的有效性.
图 17(Fig. 17)
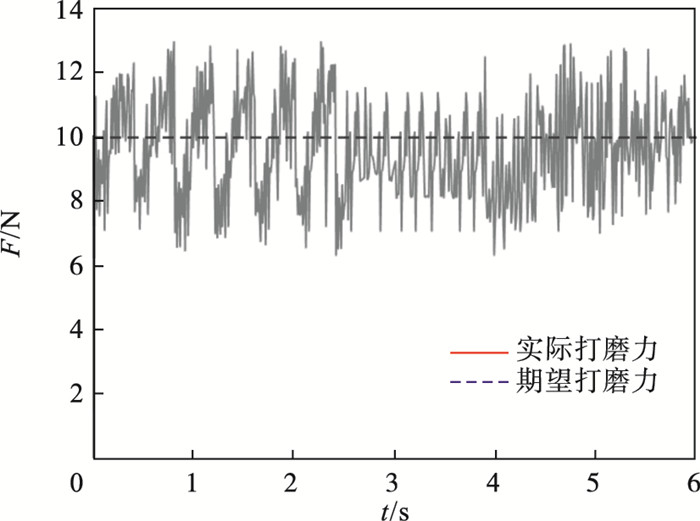 | 图 17 PID模糊变阻抗控制打磨力Fig.17 Grinding force of PID fuzzy variable impedance control |
图 18(Fig. 18)
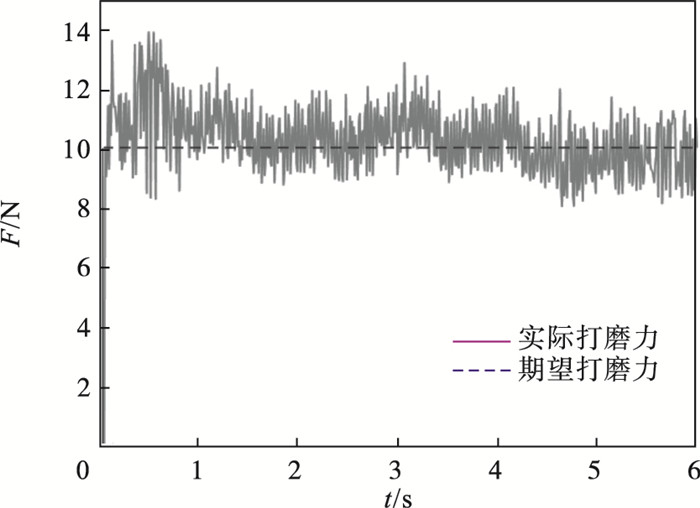 | 图 18 自抗扰模糊变阻抗控制打磨力Fig.18 Grinding force of active disturbance rejection fuzzy variable impedance control |
4 结论1) 本文针对机器人在打磨过程中采用刚性末端执行器控制精度不足问题,设计了一种力控末端执行器,实现机器人力控制和位置控制的解耦,在保证机器人恒力控制前提下,又能保证位置控制精度和响应速度,具有高集成化和通用性强等特点.
2) 提出了一种机器人主动柔顺恒力打磨自抗扰模糊变阻抗控制方法,内环控制为模糊变阻抗控制器,外环控制为自抗扰打磨控制器.采用Lyapunov稳定性理论开展了收敛性分析,证明了所提方法的无误差估计能力,并通过Matlab与Adams联合仿真验证了所提方法的有效性和适用性.
3) 对比PID模糊变阻抗控制器仿真结果表明,在相同打磨条件下,本文方法使打磨力稳定性提高35%,打磨力平均误差减小33%,打磨力方差减小67%,稳定打磨阶段打磨工具末端位置误差的波动范围减小49.8%,具有更好的力跟踪效果,能够有效地提高打磨力控制系统的稳定性和鲁棒性.并通过机器人对比实验,验证了所提方法较PID模糊变阻抗控制方法具有更小的力误差波动与更加稳定的力控性能,有效改善了力控延时,在稳定打磨阶段力误差波动控制在±1.8 N以内.本文方法可为机器人实现恒力打磨提供一种力控方法参考.
参考文献
| [1] | Zhu W L, Beaucamp A. Compliant grinding and polishing: a review[J]. International Journal of Machine Tools and Manufacture, 2020, 158: 103634. DOI:10.1016/j.ijmachtools.2020.103634 |
| [2] | 黄智, 周涛, 吴湘, 等. 机器人气囊抛光SiC光学元件加工特性研究[J]. 西安交通大学学报, 2020, 54(12): 22-29. (Huang Zhi, Zhou Tao, Wu Xiang, et al. SiC optical element processing under robot bonnet polishing[J]. Journal of Xi'an Jiaotong University, 2020, 54(12): 22-29.) |
| [3] | 林文强, 焦明裕, 赵西松, 等. 可调节气囊提高航空薄壁件加工精度的研究[J]. 东北大学学报(自然科学版), 2017, 38(3): 390-394. (Lin Wen-qiang, Jiao Ming-yu, Zhao Xi-song, et al. Study on improving the machining accuracy of aviatic thin-walled parts with the adjustable airbag[J]. Journal of Northeastern University(Natural Science), 2017, 38(3): 390-394. DOI:10.3969/j.issn.1005-3026.2017.03.018) |
| [4] | Chen F, Zhao H, Li D, et al. Contact force control and vibration suppression in robotic polishing with a smart end effector[J]. Robotics and Computer-Integrated Manufacturing, 2019, 57: 391-403. DOI:10.1016/j.rcim.2018.12.019 |
| [5] | Dai J, Chen C Y, Zhu R, et al. Suppress vibration on robotic polishing with impedance matching[J]. Actuators, 2021, 10(3): 59-78. DOI:10.3390/act10030059 |
| [6] | Mohammad A E K, Hong J, Wang D. Design of a force-controlled end-effector with low-inertia effect for robotic polishing using macro-mini robot approach[J]. Robotics and Computer-Integrated Manufacturing, 2018, 49: 54-65. DOI:10.1016/j.rcim.2017.05.011 |
| [7] | Ma Z, Poo A N, Ang M H, et al. Design and control of an end-effector for industrial finishing applications[J]. Robotics and Computer-Integrated Manufacturing, 2018, 53: 240-253. DOI:10.1016/j.rcim.2018.04.010 |
| [8] | Ding B, Zhao J, Li Y. Design of a spatial constant-force end-effector for polishing/deburring operations[J]. The International Journal of Advanced Manufacturing Technology, 2021, 116(11): 3507-3515. |
| [9] | Jin M, Ji S, Pan Y, et al. Effect of downward depth and inflation pressure on contact force of gasbag polishing[J]. Precision Engineering, 2017, 47: 81-89. DOI:10.1016/j.precisioneng.2016.07.007 |
| [10] | Mohammad A E K, Hong J, Wang D, et al. Synergistic integrated design of an electrochemical mechanical polishing end-effector for robotic polishing applications[J]. Robotics and Computer-Integrated Manufacturing, 2019, 55: 65-75. DOI:10.1016/j.rcim.2018.07.005 |
| [11] | Tommasino D, Bottin M, Cipriani G, et al. Development and validation of an end-effector for mitigation of collisions[J]. Journal of Mechanical Design, 2022, 144(4): 043301. DOI:10.1115/1.4052443 |
| [12] | 史家顺, 董金龙, 刘聪, 等. 随五轴加工轨迹变抛光力的控制策略与方法[J]. 东北大学学报(自然科学版), 2020, 41(1): 89-94. (Shi Jia-sun, Dong Jin-long, Liu Cong, et al. Control strategy and method for variable polishing force adapting to the 5-axis machining trajectory[J]. Journal of Northeastern University (Natural Science), 2020, 41(1): 89-94.) |
| [13] | 许家忠, 郑学海, 周洵. 复合材料打磨机器人的主动柔顺控制[J]. 电机与控制学报, 2019, 23(12): 151-158. (Xu Jia-zhong, Zheng Xue-hai, Zhou Xun. Active and compliant control of the composite polishing robot[J]. Electric Machines and Control, 2019, 23(12): 151-158.) |
| [14] | 张雷, 周宛松, 卢磊, 等. 抛光力实时控制策略研究[J]. 东北大学学报(自然科学版), 2015, 36(6): 853-857. (Zhang Lei, Zhou Wan-song, Lu Lei, et al. Research on real-time control strategies of polishing force[J]. Journal of Northeastern University(Natural Science), 2015, 36(6): 853-857. DOI:10.3969/j.issn.1005-3026.2015.06.021) |
| [15] | 王磊, 柳洪义, 王菲. 在未知环境下基于模糊预测的力/位混合控制方法[J]. 东北大学学报(自然科学版), 2005, 26(12): 1181-1184. (Wang Lei, Liu Hong-yi, Wang Fei. Position/force control based on fuzzy prediction in unknown environment[J]. Journal of Northeastern University(Natural Science), 2005, 26(12): 1181-1184.) |
| [16] | Xu X H, Zhu D H, Zhang H Y, et al. Application of novel force control strategies to enhance robotic abrasive belt grinding quality of aero-engine blades[J]. Chinese Journal of Aeronautics, 2019, 32(10): 2368-2382. DOI:10.1016/j.cja.2019.01.023 |
| [17] | Mohsin I, He K, Li Z, et al. Path planning under force control in robotic polishing of the complex curved surfaces[J]. Applied Sciences, 2019, 9(24): 5489-5511. DOI:10.3390/app9245489 |
| [18] | Gracia L, Solanes J E, Mu?oz-Benavent P, et al. Adaptive sliding mode control for robotic surface treatment using force feedback[J]. Mechatronics, 2018, 52: 102-118. DOI:10.1016/j.mechatronics.2018.04.008 |
| [19] | Kakinuma Y, Ogawa S, Koto K. Robot polishing control with an active end effector based on macro-micro mechanism and the extended Preston's law[J]. CIRP Annals, 2022, 71(1): 341-344. DOI:10.1016/j.cirp.2022.04.074 |
| [20] | Lakshminarayanan S, Kana S, Mohan D M, et al. An adaptive framework for robotic polishing based on impedance control[J]. The International Journal of Advanced Manufacturing Technology, 2020, 112(1/2): 401-417. |
| [21] | Kana S, Lakshminarayanan S, Mohan D M, et al. Impedance controlled human-robot collaborative tooling for edge chamfering and polishing applications[J]. Robotics and Computer-Integrated Manufacturing, 2021, 72: 102199. DOI:10.1016/j.rcim.2021.102199 |
| [22] | 张铁, 吴圣和, 蔡超. 基于浮动平台的机器人恒力控制研磨方法[J]. 上海交通大学学报, 2020, 54(5): 515-523. (Zhang Tie, Wu Sheng-he, Cai Chao. Constant force control method for robotic disk grinding based on floating platform[J]. Journal of Shanghai Jiao Tong University, 2020, 54(5): 515-523.) |
| [23] | 韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008. (Han Jing-qing. Active disturbance rejection control technology: control technology for estimating and compensating uncertain factors[M]. Beijing: National Defense Industry Press, 2008.) |
| [24] | Cui X, Wang B, Lu H, et al. Design and passive training control of elbow rehabilitation robot[J]. Electronics, 2021, 10(10): 1147-1163. DOI:10.3390/electronics10101147 |
| [25] | Shi D, Zhang J, Sun Z, et al. Composite trajectory tracking control for robot manipulator with active disturbance rejection[J]. Control Engineering Practice, 2021, 106: 104670. DOI:10.1016/j.conengprac.2020.104670 |
| [26] | Hai X, Wang Z, Feng Q, et al. Mobile robot ADRC with an automatic parameter tuning mechanism via modified pigeon-inspired optimization[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(6): 2616-2626. DOI:10.1109/TMECH.2019.2953239 |
| [27] | Chen F, Liao J, Xiong J, et al. High-precision trajectory tracking design and simulation for six degree of freedom robot based on improved active disturbance rejection control[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2019, 233(10): 3659-3669. |
| [28] | Huang Y, Xue W. Active disturbance rejection control: methodology and theoretical analysis[J]. ISA Transactions, 2014, 53(4): 963-976. |
| [29] | Meng X, Yu H, Zhang J, et al. Liquid level control of four-tank system based on active disturbance rejection technology[J]. Measurement, 2021, 175: 109146. |
| [30] | Lakomy K, Madonski R, Dai B, et al. Active disturbance rejection control design with suppression of sensor noise effects in application to DC-DC buck power converter[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 816-824. |
| [31] | 张勇, 陈增强, 张兴会, 等. 基于自抗扰的四旋翼无人机动态面姿态控制[J]. 吉林大学学报(工学版), 2019, 49(2): 562-569. (Zhang Yong, Chen Zeng-qiang, Zhang Xing-hui, et al. Dynamic surface attitude control of quad-rotor UAV based on ADRC[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(2): 562-569.) |
| [32] | 李超, 张智, 夏桂华, 等. 基于强化学习的学习变阻抗控制[J]. 哈尔滨工程大学学报, 2019, 40(2): 304-311. (Li Chao, Zhang Zhi, Xia Gui-hua, et al. Learning variable impedance control based on reinforcement learning[J]. Journal of Harbin Engineering University, 2019, 40(2): 304-311.) |
| [33] | Hamedani M H, Zekri M, Sheikholeslam F, et al. Recurrent fuzzy wavelet neural network variable impedance control of robotic manipulators with fuzzy gain dynamic surface in an unknown varied environment[J]. Fuzzy Sets and Systems, 2021, 416: 1-26. |
