
 , 刘彦彤, 谢海修
, 刘彦彤, 谢海修 东北大学 信息科学与工程学院, 辽宁 沈阳 110819
收稿日期:2021-11-03
基金项目:国家自然科学基金资助项目(61773108)。
作者简介:井元伟(1956-), 男, 辽宁西丰人, 东北大学教授, 博士生导师。
摘要:研究了具有用户数据报协议(user datagram protocol, UDP)数据流干扰和不确定项的TCP/AQM网络拥塞控制问题.首先考虑由丢包率范围而导致的输入饱和的问题, 从而对丢包率进行限制.其次, 利用模糊逼近的方法处理系统中的干扰和不确定项.为节约网络资源, 引入事件触发机制, 结合输入饱和、模糊逼近以及Backstepping技术, 提出了一种主动队列管理算法, 不仅可以使队列长度跟踪到期望队列长度, 而且减少了触发次数, 节约了网络资源.最后, 仿真验证和分析表明了所提方法的有效性和优越性.
关键词:TCP/AQM网络系统拥塞控制输入饱和模糊逼近事件触发
Event Triggering Control of TCP/AQM Network System with Input Saturation
JING Yuan-wei

 , LIU Yan-tong, XIE Hai-xiu
, LIU Yan-tong, XIE Hai-xiu School of Information Science & Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: JING Yuan-wei, E-mail: ywjjing@mail.neu.edu.cn.
Abstract: The TCP/AQM network congestion control problem with user datagram protocol(UDP) data flow interference and uncertain terms is dealt with. Firstly, the problem of input saturation due to the range of packet loss rate is considered to limit the packet loss rate. Secondly, the fuzzy approximation method is used to deal with the interference and uncertain items in the system. In order to save network resources, an event trigger mechanism is introduced. Combining the input saturation, the fuzzy approximation and Backstepping technology, an active queue management algorithm is proposed, which can not only track the queue length to the expected queue length, but also reduce the numbers of triggers and save network resources. Finally, simulation verification and analysis show the effectiveness and superiority of the proposed method.
Key words: TCP/AQM network systemcongestion controlinput saturationfuzzy approximationevent triggering
近年来, 随着用户的爆炸式增长以及对网络服务质量(quality of service, QoS)要求的增加, 网络拥塞成为一个热点问题.因此, 传输控制协议(transmission control protocol, TCP)网络拥塞问题越来越成为人们关注的话题.如何设计出高效且服务质量好的控制器成为关键.目前, 主动队列管理(active queue management, AQM)算法[1]是一种有效的TCP网络拥塞控制算法.在1993年, Floyd和Jacobson提出了随机早期检测(random early detection, RED)算法[2], 是最早提出和实现的一种AQM算法.由于RED算法对参数配置过于敏感, 控制效果并不是很好,之后出现许多改进的RED算法[3-6].Misra等[3]基于流体流理论建立了TCP网络与路由器队列的非线性微分方程模型, 取得了很好的效果.基于此模型, 分别出现了基于PI[4], PD[5]和PID[6]的算法.相比于传统的RED算法, 这些算法大大提高了系统的性能.但由于算法参数设置的固定性, 使得算法对网络环境变化的适应性较差.后来又出现了基于优化理论的AQM算法[7].
对于实际网络来说, 在TCP网络中, 非响应用户数据报协议(user datagram protocol, UDP)会占用网络资源, 如链路容量等, 进而影响整个TCP网络服务质量, 导致网络吞吐量下降.可将UDP流等非响应流视为外部干扰.许多研究者在处理UDP数据流干扰的同时, 还会对链路容量C进行处理.对于外部扰动, 大多采用H∞控制理论或Minimax理论来处理, 也可以采用模糊逼近或神经网络逼近的方法.文献[8]利用Minimax理论求出影响最大的干扰, 采用反步法设计出控制器.
上述网络拥塞控制算法的设计是以网络信道作为媒介的, 而控制律则是以固定频率的方法(即时间触发机制)进行更新的.这种方法会降低网络的利用率, 也就降低了网络的控制效率, 同时也会引起不必要的计算和通信资源的浪费.为解决此类问题, 文献[9]提出了事件触发控制机制.其主要思想是, 设定一个基于事件的条件, 当此条件满足时, 控制器保持原值(即不动作), 一旦条件不满足则执行控制任务(即控制器更新), 从而达到降低控制任务的执行次数、节约网络资源的目的.文献[10]针对非线性系统, 利用事件触发策略解决了时间触发机制降低网络系统效率的问题.文献[11]针对非线性系统, 在反步法框架下, 结合模糊逼近和神经网络等方法设计出了基于事件触发的控制器.
目前, 在TCP网络控制系统中应用事件触发机制的研究还很少.文献[12]将事件触发机制应用到了TCP/AQM网络系统中, 处理了输入饱和问题, 设计了事件触发网络拥塞预设性能控制器.
在上述讨论的启发下, 本文将结合模糊逼近、事件触发和Backstepping技术去解决带有干扰、不确定项及由于丢包率受限引起的输入饱和的TCP/AQM网络系统的拥塞控制问题.
1 问题描述1.1 TCP/AQM网络模型考虑文献[13]所描述的TCP/AQM网络模型如下所示:
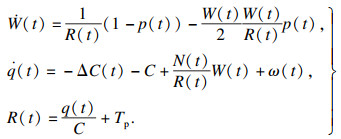 | (1) |
注1 ??由于网络是有时延的, 在一段时间内, 可认为N(t), R(t)是固定不变的常数, 因此可以写为N, R.因为C(t)是一个未知的变量, 受UDP数据数据流的干扰, C(t)=C+ΔC(t).其中, C是固定值, ΔC(t)是受UDP数据流干扰引起的不确定项, 简写为ΔC.
根据文献[14], TCP网络系统的源端发送速率r(t)的导数和
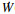
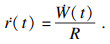 | (2) |
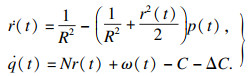 | (3) |
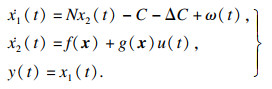 | (4) |
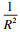
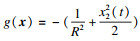
控制输入u(t)代表丢包率, 故应控制在[0, 1]之间, TCP网络动态系统模型可以表达为
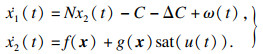 | (5) |
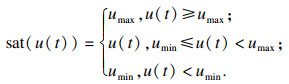 | (6) |
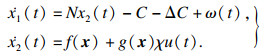 | (7) |
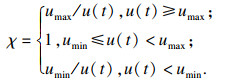 | (8) |
1.2 预备知识为使本文后续分析具有依据, 需要介绍一些预备知识, 以假设和引理的形式给出.
假设1 ??非响应流引起的外部干扰Δω(t)和不确定项ΔC是连续且有界的.
假设2 ??期望队列长度qref(t)及其一阶导数连续可微.
假设3[15] ??对于式(8)中的χ, 存在常数Δh0使得
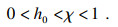 |
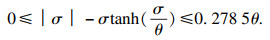 | (9) |
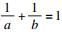
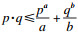
引理3[18](模糊逻辑系统) ??对于有界闭集ΩZ上的一个连续函数F(Z), 及任意的λ>0, 存在一个模糊逻辑系统(FLS)WTS(Z), 使得
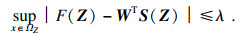 | (10) |
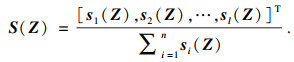 | (11) |
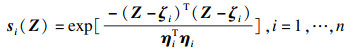 | (12) |
2 主要结论2.1 自适应事件触发控制器设计在本节中, 主要是在Backstepping控制方法的框架下设计能使系统稳定且节约网络资源的控制器.设计过程分为两步,具体如下:
步骤1 ??令z1=x1(t)-qref(t), z2=x2(t)-α, qref(t)为期望队列长度,并选择Lyapunov函数为
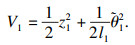 | (13) |
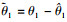

将V1关于时间t求导得
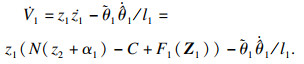 | (14) |
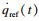
应用模糊逻辑系统W1TR1(Z1)来近似TCP系统中的外部扰动, 有
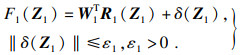 | (15) |
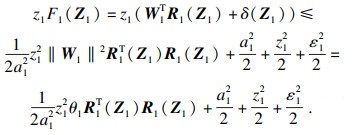 | (16) |
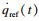
将式(16)代入式(14)可得
 | (17) |
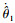
 | (18) |
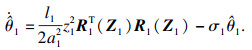 | (19) |
将式(18)和(19)代入到式(17)得
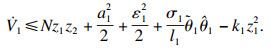 | (20) |
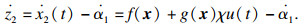 | (21) |
 | (22) |
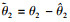
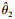
将V2关于时间t求导得
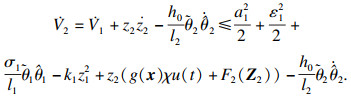 | (23) |
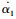
应用模糊逻辑系统W1TR1(Z1)来逼近非线性函数F2(Z2):
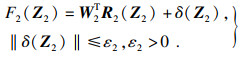 | (24) |
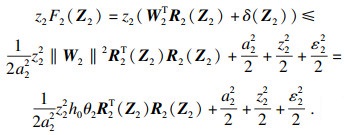 | (25) |
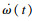
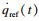
将式(25)代入到式(23)得
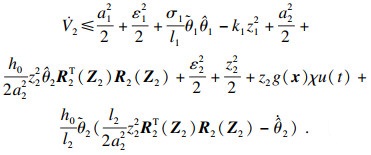 | (26) |
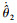
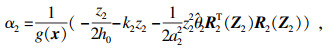 | (27) |
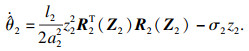 | (28) |
式(28)中,
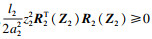

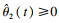

按照固定阈值策略设计事件触发控制器:
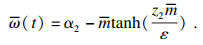 | (29) |
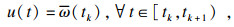 | (30) |
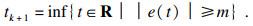 | (31) |
至此, TCP/AQM网络系统的自适应控制器设计完成.
2.2 稳定性证明定理1 ??对于系统(5), 如果假设1~假设3满足, 设计事件触发条件为式(30)和式(31), 同时虚拟控制律为式(27), 控制器为式(29), 则闭环系统(5)是半全局一致最终有界(semi-globally ultimately uniformly bounded, SGUUB)的.
证明??由式(29)可得
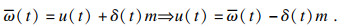 | (32) |
将式(32)代入式(26)可得
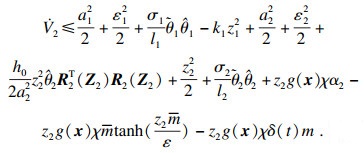 | (33) |
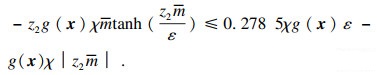 | (34) |
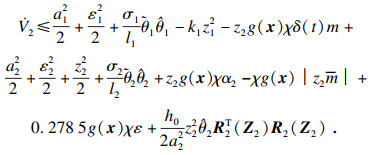 | (35) |
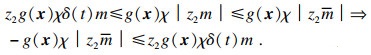 | (36) |
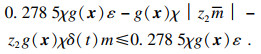 | (37) |
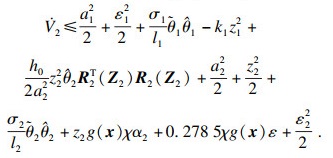 | (38) |
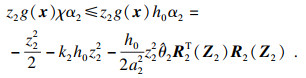 | (39) |
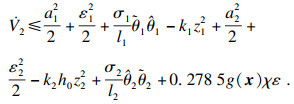 | (40) |
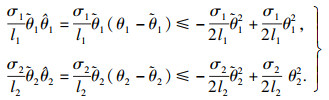 | (41) |
 | (42) |
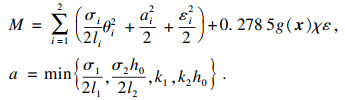 |
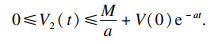 | (43) |
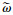
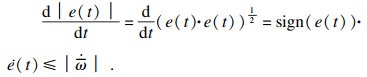 | (44) |
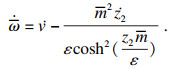 | (45) |
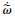
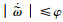
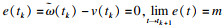
综上所述, TCP/AQM网络系统在控制器式(29)以及触发条件式(31)的作用下, 不仅可以保证系统的所有信号都是有界的, 而且也减少了网络资源的浪费.通过证明该算法可以有效地避免Zeno行为的发生.
3 仿真及结果考虑了如图 1所示的一个典型的哑铃拓扑, 利用MATLAB/SIMULINK进行仿真.从图 1可以看出, 瓶颈链路位于路由器1和路由器2之间, 源端通过瓶颈向各自的接收器发送数据流.
图 1(Fig. 1)
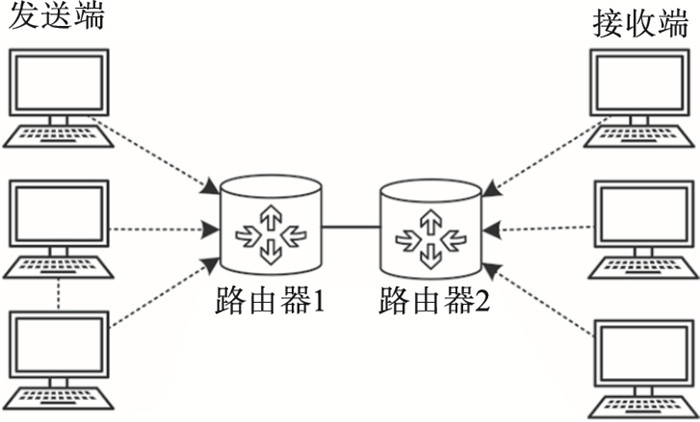 | 图 1 哑铃型网络拓扑结构Fig.1 Dumbbell network topology |
首先给出系统(5)中相应的系统参数和设计参数如下:
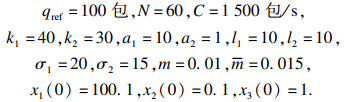 |
图 2(Fig. 2)
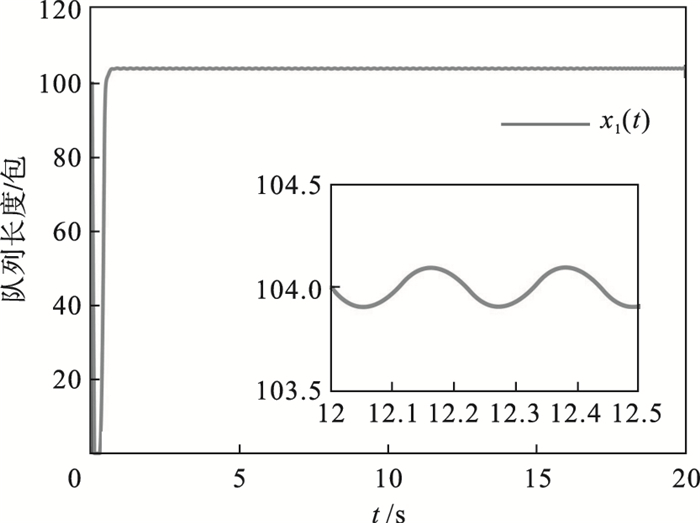 | 图 2 系统的队列长度响应曲线Fig.2 Queue length response curve of the system |
注2 ??为了获得更少的触发次数, 牺牲了队列长度.若为获得更高的精度, 可以适当调整参数.
图 3为丢包率的变化曲线, 亦即控制律曲线.丢包率始终在[0, 1], 且最终丢包率稳定在0.24左右.由于引入了事件触发机制, 当满足事件触发条件时, 控制器更新.当事件触发条件不满足时, 控制器保持不变.故基于事件触发的丢包率u(t)呈阶梯状变化.
图 3(Fig. 3)
 | 图 3 丢包率u(t)的阶梯图Fig.3 Step diagram of the packet loss rate u(t) |
图 4为系统的事件触发时间间隔.从图中可以看出, 在控制初始阶段, 控制器几乎一直在更新, 更新的次数较多.在控制器的作用下, 系统逐渐趋于稳定, 事件触发条件满足的概率也在减小, 控制器的更新次数也就在减少.仿真过程中, 选择的采样步长为0.001s, 意味着对于连续的控制器在20s内需要更新20000次, 而在事件触发机制下设计的控制器在20s内一共触发了313次, 其更新次数相比于连续控制器的更新次数减少了90% 左右, 大大地降低了计算量, 减少了控制器的执行次数, 达到了节约网络资源的目的.图 5显示了自适应律
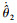
图 4(Fig. 4)
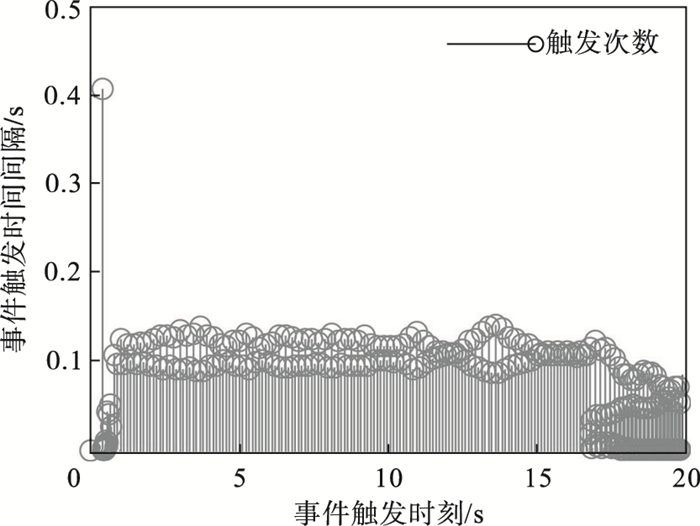 | 图 4 系统的事件触发时间间隔Fig.4 The event-triggered time interval for the system |
图 5(Fig. 5)
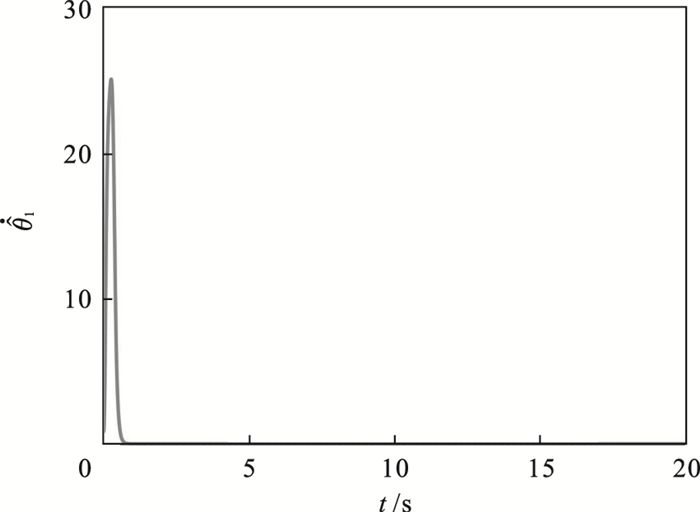 | 图 5 自适应律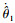 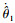 |
图 6(Fig. 6)
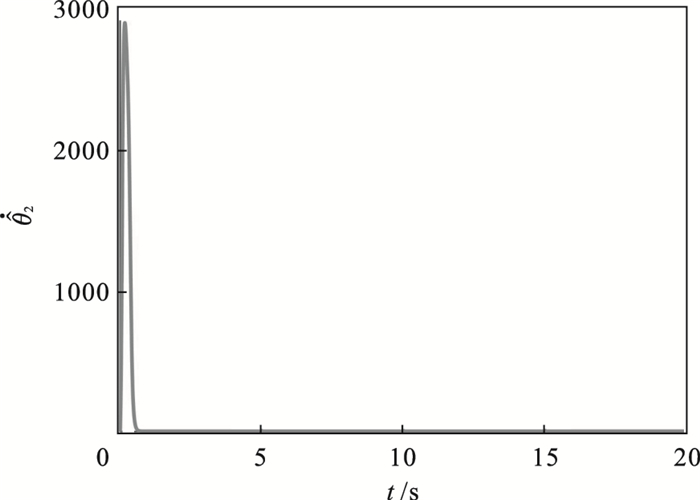 | 图 6 自适应律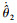 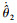 |
为了说明本文算法的优越性, 与PID控制算法[6]进行对比.其中, 网络参数选择和本文保持一致, 控制参数为
Kp=1.103×10-5, Ki=1.168×10-4, Kd=1.801×10-6.
仿真结果如图 7, 图 8所示.首先, 从图 7中可以明显看出, 虽然本文所提控制方法的最终队列长度稳定值比PID方法最终队列长度稳定值要大, 但本文设计的控制器的超调量更小.因此, 本文设计的方法可以为TCP/AQM系统获得更好的瞬态性能.其次, 将本文控制方法的丢包率和PID控制方法的丢包率进行比较, 结果如图 8所示.PID控制方法的丢包率稳定在0.425左右, 而本文所提出的控制方法的丢包率稳定在0.25左右.因此本文设计的控制方法具有更好的控制效果.此外, PID控制方法是基于时间触发策略进行设计的, 而本文提出的控制方法是基于事件触发策略进行设计的, 减少了触发次数, 在保证一定的系统性能的同时, 节约了网络资源, 这也是相较于PID控制方法的优势所在.
图 7(Fig. 7)
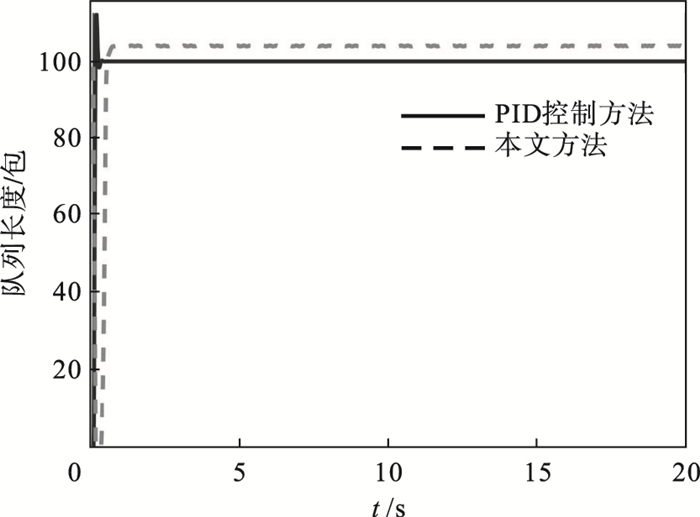 | 图 7 系统的队列长度对比曲线Fig.7 Queue length comparison curves of the system |
图 8(Fig. 8)
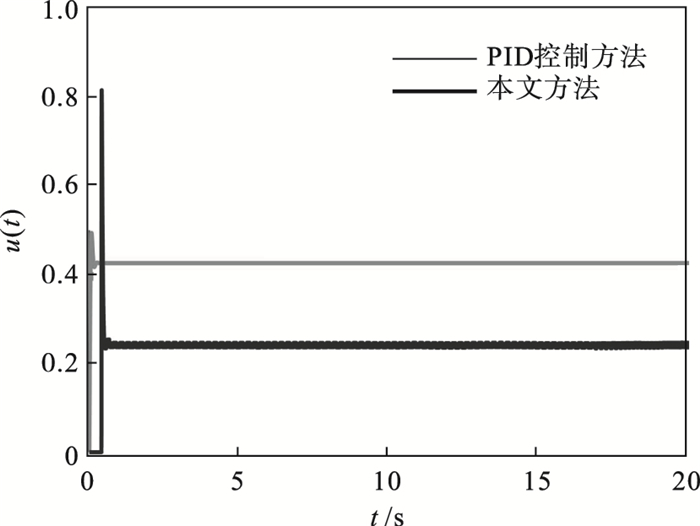 | 图 8 丢包率u(t)的对比结果Fig.8 The comparison results of the packet loss rate u(t) |
4 结语本文结合事件触发机制和模糊逼近的方法, 提出了一种新的非线性TCP/AQM网络拥塞控制算法, 并且采用饱和函数处理了输入受限的问题.这种方法不仅可以保证系统状态在有界范围内稳定, 获得更小的丢包率, 而且可以减少控制器更新次数, 有效节省网络资源.本文所提出的控制方法通过仿真进一步验证了有效性.在后续研究中, 将所提出的方法扩展到多瓶颈网络模型中.
参考文献
| [1] | Braden B, Clark D, Crowcroft J, et al. Recommendations on queue management and congestion avoidance in the Internet: RFC 2309[S]. Reston: Internet Society, 1998. |
| [2] | Floyd S, Jacobson V. Random early detection gateways for congestion avoidance[J]. IEEE/ACM Transactions on Networking, 1993, 1(4): 397-413. DOI:10.1109/90.251892 |
| [3] | Misra V, Gong W B, Towsley D. Fluid-based analysis of a network of AQM routers supporting TCP flows with an application to RED[C]//Proceedings of the 19th IEEE International Conference on SIGCOMM. Stockholm, 2000: 151-160. |
| [4] | Unal H U, Melchoraguilar D, Ustebay D, et al. Comparison of PI controllers designed for the delay model of TCP/AQM networks[J]. Computer Communication, 2013, 36(10): 1225-1234. |
| [5] | Tang Y H, Xiao M, Jiang G P, et al. Fractional-order PD control at Hopf bifurcations in a fractional-order congestion control system[J]. Nonlinear Dynamics, 2017, 90(3): 2185-2198. DOI:10.1007/s11071-017-3794-5 |
| [6] | Bisoy S K, Pattnaik P K. Design of feedback controller for TCP/AQM networks[J]. Engineering Science and Technology—an Internatinal Journal, 2017, 20(1): 116-132. DOI:10.1016/j.jestch.2016.10.002 |
| [7] | Zhou C, He J W, Chen Q W. A robust active queue management scheme for network congestion control[J]. Computers and Electrical Engineering, 2013, 39(2): 285-294. DOI:10.1016/j.compeleceng.2012.11.008 |
| [8] | 井元伟, 李赞华, 刘婷. 一类TCP网络系统的Minimax拥塞控制[J]. 东北大学学报(自然科学版), 2019, 40(8): 1065-1069. (Jing Yuan-wei, Li Zan-hua, Liu Ting. Minimax congestion control for a class of TCP network systems[J]. Journal of Northeastern University(Natural Science), 2019, 40(8): 1065-1069.) |
| [9] | ?str?m K J, Bernhardsson B. Comparison of periodic and event based sampling for first-order stochastic systems[J]. IFAC Proceedings Volumes, 1999, 32(2): 5006-5011. DOI:10.1016/S1474-6670(17)56852-4 |
| [10] | Henningsson T, Johannesson E, Cervin A. Sporadic event-based control of first-order linear stochastic systems[J]. Automatica, 2008, 44(11): 2890-2895. DOI:10.1016/j.automatica.2008.03.026 |
| [11] | Huang J S, Wang W, Wen C Y, et al. Adaptive event-triggered control of nonlinear systems with controller and parameter estimator triggering[J]. IEEE Transactions on Automatic Control, 2019, 65(1): 818-324. |
| [12] | 井元伟, 白云. 基于事件触发的TCP网络滑模控制[J]. 东北大学学报(自然科学版), 2021, 42(4): 457-462. (Jing Yuan-wei, Bai Yun. Sliding mode control of TCP network based on event-triggered[J]. Journal of Northeastern University(Natural Science), 2021, 42(4): 457-462.) |
| [13] | Liu Y, Liu X P, Jing Y W, et al. Adaptive back-stepping H∞ tracking control with prescribed performance for Internet congestion[J]. ISA Transactions, 2018, 72: 92-99. DOI:10.1016/j.isatra.2017.10.004 |
| [14] | Ariba Y, Gouaisbaut F, Labit Y. Feedback control for router management and TCP/IP network stability[J]. IEEE Transactions on Network and Service Management, 2009, 6(4): 255-266. DOI:10.1109/TNSM.2009.04.090405 |
| [15] | Zhao S Y, Pan Y N, Du P H, et al. Adaptive control for non-affine nonlinear systems with input saturation and output dead zone[J]. Applied Mathematics and Computation, 2020, 386: 125506. DOI:10.1016/j.amc.2020.125506 |
| [16] | Polycarpou M M, Ioannou P A. A robust adaptive nonlinear control design[J]. Automatica, 1996, 32(3): 423-427. DOI:10.1016/0005-1098(95)00147-6 |
| [17] | Polycarpou M M. Stable adaptive neural control scheme for nonlinear systems[J]. IEEE Transactions on Automatic Control, 1996, 41(3): 447-451. DOI:10.1109/9.486648 |
| [18] | Wang L X, Mendel J M. Fuzzy basis functions, universal approximation, and orthogonal least squares learning[J]. IEEE Transactions on Neural Networks, 1992, 3(5): 807-810. DOI:10.1109/72.159070 |
