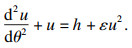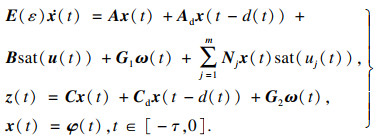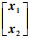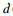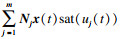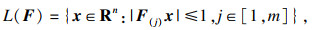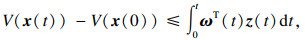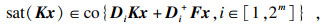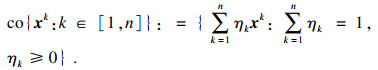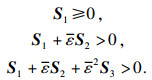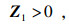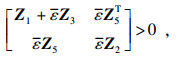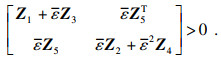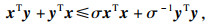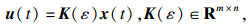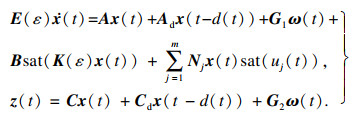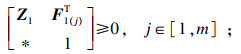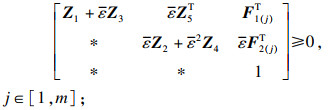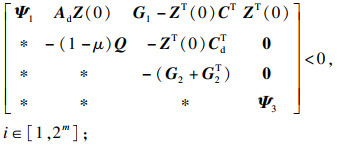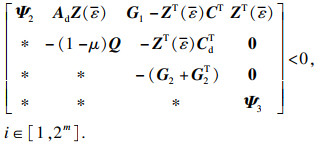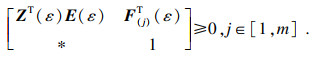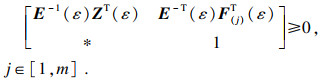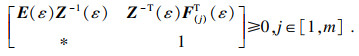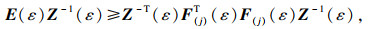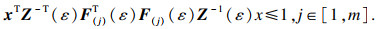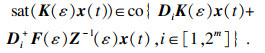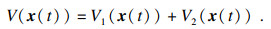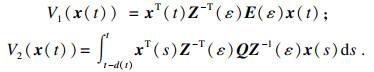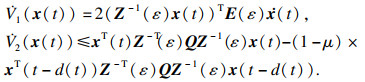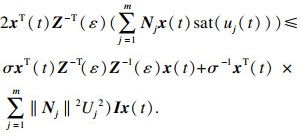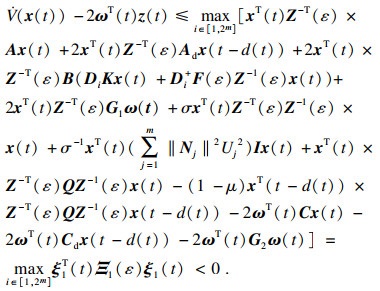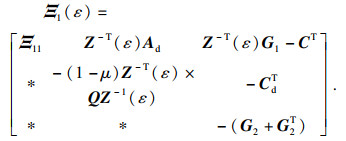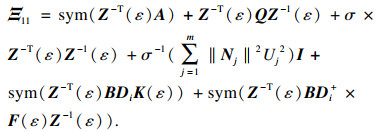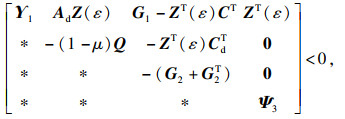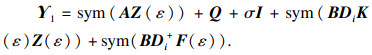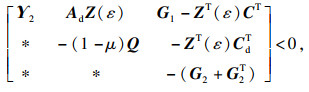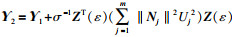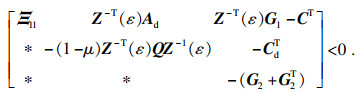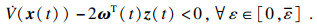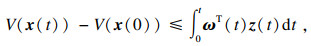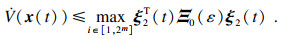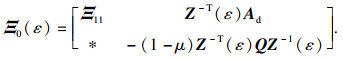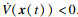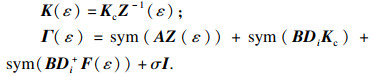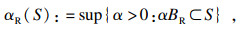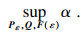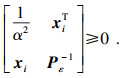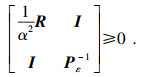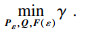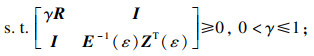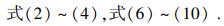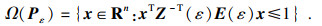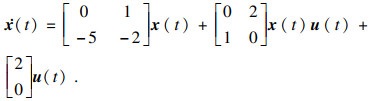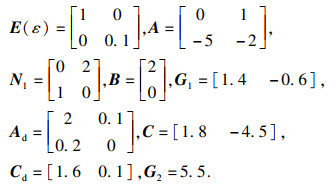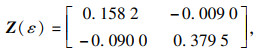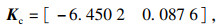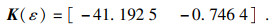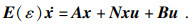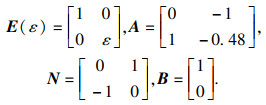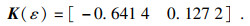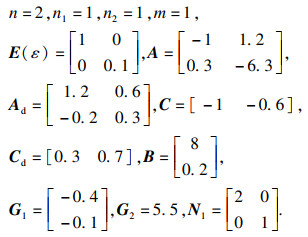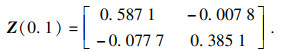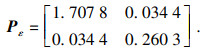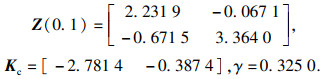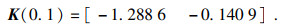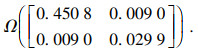张秀华, 任佳旭
东北大学 理学院，辽宁 沈阳 110819
收稿日期：2022-04-16
基金项目：国家自然科学基金资助项目(61673100)。
作者简介：张秀华(1963-), 女, 辽宁铁岭人, 东北大学教授。

摘要：针对具有输入约束和变时滞的奇异摄动双线性系统，提出一种状态反馈无源控制器的设计方法，以消除时滞因素和输入饱和对闭环系统的影响.首先，在Lyapunov稳定性理论和无源性理论的框架下，应用线性矩阵不等式技术和凸组合技术，将系统状态反馈控制器的设计归结为求解一组与时滞上界无关的线性矩阵不等式问题.所得控制器使闭环系统渐近稳定且无源，同时构造了与奇异摄动参数相关的椭圆吸引域估计，并将上述方法推广到不含时滞和外部输入的系统.然后，提出凸优化问题，得到闭环系统吸引域的极大估计，其中奇异摄动参数稳定界也是设计的目标之一.最后，通过数值仿真算例说明了所提理论方法的有效性.
关键词：奇异摄动双线性系统输入饱和无源控制线性矩阵不等式吸引域奇异摄动参数
Passive Control of Singularly Perturbed Bilinear Systems with Input Saturation
ZHANG Xiu-hua, REN Jia-xu
School of Sciences, Northeastern University, Shenyang 110819, China
Corresponding author: ZHANG Xiu-hua, E-mail: zhangxiuhua@mail.neu.edu.cn.

Abstract: For singularly perturbed bilinear systems with input constraints and time-varying delays, a design method of state feedback passive controller is proposed to eliminate the effects of delay factors and input saturation on the closed-loop system. Firstly, in the framework of Lyapunov stability theory and passivity theory, using linear matrix inequality technology and convex combination technology, the design of the system state feedback controller is reduced to solve a set of linear matrix inequalities independent of the upper bound of time delay. The obtained controller makes the closed-loop system asymptotically stable and passive, and constructs the estimation of the elliptic domain of attraction related to singular perturbation parameters. The above method is extended to the system without time delay and external input. Then, a convex optimization problem is proposed to obtain the maximum estimation of the domain of attraction of the closed-loop system, and the stability bound of singular perturbation parameter is also one of the design objectives. Finally, numerical simulation examples illustrate the effectiveness of the proposed theoretical method.
Key words: singularly perturbed bilinear systemsinput saturationpassive controllinear matrix inequalitydomain of attractionsingular perturbation parameter
许多过程本质上具有双时间尺度的动态特性，可以用奇异摄动系统(singularly perturbed systems, SPSs)精确地建模^[1].通过引入一个小的正参数ε，将SPSs分解为快、慢子系统.由于SPSs模型提供了方便和自然的表示方式，因此SPSs在电力系统、航天工程和大型系统中得到了广泛的应用^[2].奇异摄动方法最早应用于天体力学中.例如，由牛顿经典力学得出的单个行星围绕太阳的轨道方程，根据爱因斯坦的引力理论进行修正时，方程为
其中：θ为轨道的极角；u为与轨道的径向坐标成反比的量；h是测量行星的角动量；ε>0是一个小参数，比如水星约为10^-7.这样便建立了一个SPSs模型^[3].近年来，奇异摄动方法受到了越来越多的关注，在奇异摄动方法的帮助下，出现了许多关于SPSs的稳定分析和控制器设计的研究.例如，文献[4]利用LMI技术，构造了基于动态事件的马尔可夫跳跃SPSs的一个异步弹性滤波器，并得到了具有耗散性能的滤波误差系统的随机稳定的有效判据.
双线性系统是一类在生物学、经济学、化学工程等领域具有广泛应用的特殊非线性系统^[5].它相对于状态或控制分别是线性的，但同时相对于状态和控制则不是线性的.现实生活中许多系统都表现出非线性行为，而双线性系统可以更准确地模拟非线性现象，因此对于双线性系统的分析和设计是很有必要的.
在许多实际的控制应用中，特别是在工业设计过程中，输入限制是不可避免的，这意味着输入饱和问题必然存在.输入饱和的存在可能会恶化控制系统的性能，甚至破坏闭环系统的稳定性.文献[6]在故障估计设计过程中考虑了输入饱和，将饱和函数用一个连续函数逼近，提出了三种针对3自由度直升机系统的鲁棒执行器故障估计方法.文献[7]通过设计一个辅助系统来处理输入饱和，利用Lyapunov方法为具有输入饱和的n连杆机器人设计了自适应神经阻抗控制器.
无源性理论在电力系统、车辆系统等领域也发挥了重要作用^[8].文献[9]对具有区间时变时滞的不确定奇异摄动Markov跳跃系统进行了无源性分析和无源控制器设计，给出了LMI形式的时滞相关条件，但条件维数过大，增加了计算的复杂度.文献[10]研究了基于无源性的奇异摄动系统的多目标最优控制问题，但没有考虑奇异摄动参数稳定界的估计问题.文献[11]讨论了不确定奇异摄动系统的无源性和渐近稳定性，并通过求解广义特征值问题得到稳定界的估计.然而，到目前为止，对于带有输入饱和、变时滞和双线性项的奇异摄动系统的无源控制的研究还很少.如何在该领域获得一个更好的、更全面的设计规则仍然是一个重要的问题.
本文讨论了一类具有输入饱和与变时滞的奇异摄动双线性系统的无源控制问题.目的是在给定闭环系统奇异摄动参数稳定界的前提下，提出一种状态反馈无源控制器的设计方法.首先，在Lyapunov稳定性理论和无源性理论的框架下，利用凸包法将系统饱和非线性部分表示为状态反馈和辅助矩阵反馈的凸组合，结合LMI技术，设计一种状态反馈控制器，给出闭环SPSs无源和渐近稳定的时滞无关的充分条件，并构造了椭圆吸引域估计.在此基础上，提出一个凸优化问题，得到闭环系统吸引域的极大估计.最后，通过数值仿真算例验证了所提方法的可行性和有效性.文中得出的结论是由更加通用的存储函数推导得到的，而且没有等式约束，可应用于多种SPSs中.
1 问题描述符号说明：R^n×m表示n×m阶实矩阵集合；Rⁿ表示n维实数列向量集合；L₂[0, ∞)表示在[0, ∞)上平方可积的函数集合；0和I分别表示具有适当维数的零矩阵和单位矩阵；M>0(< 0)表示M是正定矩阵(负定矩阵)；sym(N)表示N+N^T；diag{·, ·}表示对角矩阵；.
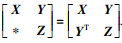
考虑一类含有输入饱和的变时滞奇异摄动双线性系统：

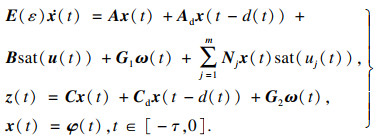(1)

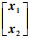
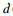
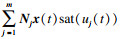
其中：E(ε)=diag{I_n1, εI_n2}，其中n₁+n₂=n；x(t)=∈Rⁿ是状态变量，x₁^T∈R^n₁，x₂^T∈R^n₂；φ(t)是连续向量初始值函数；A, A_d, B, C, C_d, G₁, G₂是已知的具有适当维数的常数矩阵；ω(t)∈R^p是L₂[0, ∞)空间的外部输入；z(t)∈R^q是被控输出；d(t)是系统的状态滞后，满足0≤d(t)≤τ < ∞，(t)≤μ < 1；u(t)∈R^m是控制输入，sat: R^m→R^m是标准饱和函数，且sat(u(t))=[sat(u₁(t)), sat(u₂(t)), …, sat(u_m(t))]^T，不失一般性，sat(u_j(t))=sign(u_j(t))min{U_j, |u_j(t)|}，其中U_j表示正常数；表示双线性项，其中N_j∈R^n×n是控制向量与状态向量之间耦合的加权矩阵.
令D是m×m对角元素为0或1的对角矩阵的集合，可知D的元素个数是2^m.假设D={D_i: i∈[1, 2^m]}，定义D_i+D_i⁺=I.如果D_i∈D，那么D_i⁺∈D.
给定矩阵F∈R^m×n，定义集合：
其中F_(j)是矩阵F的第j行.
定义椭圆区域Ω(P, ρ)={x∈Rⁿ: x^TPx≤ρ}，Ω(P)={x∈Rⁿ: x^TPx≤1}.
定义1^[11]?? 对于系统(1)，若存在一个连续的非负定储存函数V(x(t))≥0，V(0)=0，使得对所有的零初始条件的轨迹，任意的输入信号ω(t)∈R^p，有如下不等式成立：
则系统(1)是无源的.
引理1^[12]?? 令K，F∈R^m×n，对于任何x∈L(F)，都有
其中co{·}代表集合的凸包，集合{x¹, x², …, xⁿ}的凸包定义为
引理2^[13]?? 给定正数ε>0，对称矩阵S₁，S₂和S₃，如果下面矩阵不等式条件成立：
则S₁+εS₂+ε²S₃>0，?ε∈(0, ε].
引理3^[13] ??如果存在矩阵Z_k(k=1, 2, 3, 4, 5)且Z_k=Z_k^T(k=1, 2, 3, 4)，满足下列LMI条件：

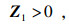(2)

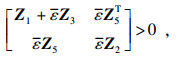(3)

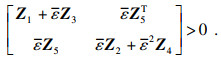(4)

则E(ε)Z(ε)=Z^T(ε)E(ε)>0，?ε∈(0, ε].
其中，
引理4^[14]?? 对于任意n维向量x, y∈Rⁿ，有
其中σ为任意正数.
本文的目的是设计以下形式的状态反馈控制器：
使闭环系统

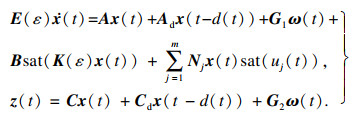(5)

是渐近稳定且无源的.
2 主要结果给出具有输入约束的闭环系统(5)的无源控制器设计方法和闭环系统的椭圆吸引域估计.
2.1 控制器设计定理1 ??给定奇异摄动参数ε的上界ε，如果G₂+G₂^T>0，存在对称正定矩阵Q∈R^n×n，矩阵K_c∈R^m×n，F₁∈R^m×n₁，F₂∈R^m×n₂以及矩阵Z₁∈R^n₁×n₁，Z₂∈R^n₂×n₂，Z₃∈R^n₁×n₁，Z₄∈R^n₂×n₂，Z₅∈R^n₂×n₁且Z_k=Z_k^T(k=1, 2, 3, 4)，使得线性矩阵不等式(2)~(4)和下列LMI可行：

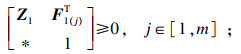(6)

(7)

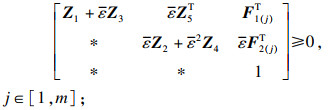(8)

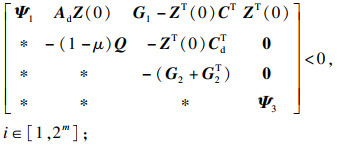(9)

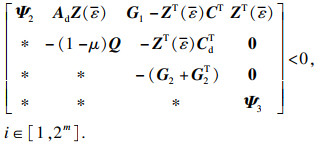(10)

式中：
其中，F(ε)=[F₁??εF₂]，ε=0或ε.
则对任意ε∈(0, ε]，存在无记忆状态反馈控制器u(t)=K(ε)x(t)，K(ε)=K_cZ^-1(ε)，使得系统(5)是渐近稳定且无源的，椭圆区域Ω(P_ε, 1)={x∈Rⁿ: x^TP_εx≤1}是闭环系统吸引域的估计，P_ε=Z^-T(ε)E(ε).
证明??由线性矩阵不等式(6)~(8), 根据引理2和引理3可知，对任意ε∈(0, ε]，有
即对任意ε∈(0, ε]，有

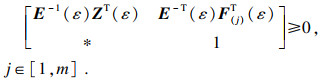(11)

在式(11)左右两侧分别乘以diag(Z^-T(ε)×E(ε), 1)和diag((Z^-T(ε)E(ε))^T, 1)，有

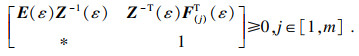(12)

由式(12)可知,
所以对任意x∈Ω(P_ε)，一定有
因此Ω(P_ε)?L(F(ε)Z^-1(ε)).根据引理1，对任意x∈Ω(P_ε)，有

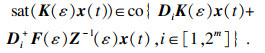(13)

定义下列与ε相关的能量存储函数：
其中：
式中, Q为待定的对称正定矩阵.
根据引理3，线性矩阵不等式(2)~(4)能保证Z^-T(ε)E(ε)=E(ε)Z^-1(ε)>0，因此V(x(t))是正定的.
对V(x(t))沿系统(5)的轨迹对t进行求导，得
应用引理4和范数定义，有

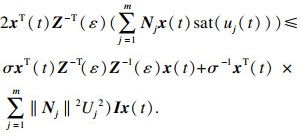(14)

根据式(13)及式(14)，有

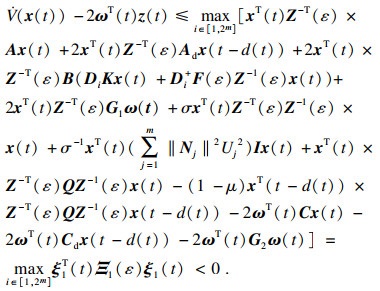(15)

式中：ξ₁(t)=[x^T(t)??x^T(t-d(t))??ω^T(t)]^T;
其中，
根据引理2，式(9)和式(10)可得，?ε∈(0, ε],
其中，
由Schur补引理，?ε∈(0, ε]，上式等价于

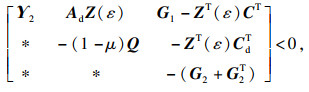(16)

式中, .
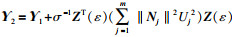
在式(16)左右两侧分别乘以diag{Z^-T(ε), Z^-T(ε), I}和diag{Z^-1(ε), Z^-1(ε), I}，?ε∈(0, ε]，有
因此，定理中的条件可使式Ξ₁(ε) < 0成立.
由式(15)可知

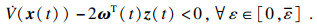(17)

将式(17)从0到t积分可得
因此由定义1可知系统(5)是无源的.
下面证明渐近稳定性：
当ω(t)=0时，有
其中ξ₂(t)=[x^T(t)??x^T(t-d(t))]^T，且?ε∈(0, ε]，
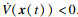
由Schur补引理知，当G₂+G₂^T>0时，若Ξ₁(ε) < 0，有Ξ₀(ε) < 0，所以.闭环系统(5)渐近稳定且无源.证毕.
注1 ??对于一个给定的奇异摄动参数上界ε(也称稳定界)，定理1中推导出的条件依赖于稳定界ε，而不依赖于奇异摄动参数ε，这样可以避免由小的奇异摄动参数引起的病态问题.
注2 ??由于SPSs结构的特殊性，本文构造了一个依赖于奇异摄动参数ε的吸引域估计.这种构造有利于进一步制定凸优化问题，来扩大闭环系统的吸引域估计.
当ω(t)=0，时滞d(t)=0时，定理1简化为如下推论：
推论1 ??给定奇异摄动参数ε的上界ε，如果存在矩阵K_c∈R^m×n，F₁∈R^m×n₁，F₂∈R^m×n₂以及矩阵Z₁∈R^n₁×n₁，Z₂∈R^n₂×n₂，Z₃∈R^n₁×n₁，Z₄∈R^n₂×n₂，Z₅∈R^n₂×n₁且Z_k=Z_k^T(k=1, 2, 3, 4)，使得线性矩阵不等式(2)~(4)，(6)~(8)和下列LMI可行：
则对任意ε∈(0, ε]，闭环系统是渐近稳定的.u(t)=K(ε)x(t)是该系统的状态反馈控制器，椭圆区域Ω(P_ε, 1)={x∈Rⁿ: x^TZ^-T(ε)×E(ε)x≤1}是闭环系统吸引域的估计.其中：
下面将提出一种凸优化算法，以获得尽可能大的吸引域估计.
2.2 吸引域优化令B_R是一个预期形状的有界凸集，对于一个正实数α，定义αB_R={αx: x∈B_R}.对于一个集合S∈Rⁿ，定义
显然，如果α_R(S)≥1，那么B_R?S.
在本文中，B_R有两个典型区域，一个是椭圆区域，B_R={x∈Rⁿ: x^TRx < 1}，R>0；另一个是多边形区域，B_R=co{x₁, x₂, …, x_l}.
给定一个正标量ε，对于任意ε∈(0, ε]，本文将通过求解优化问题得到吸引域的极大估计，优化问题可以表示为

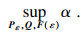(18)

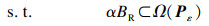(19a)

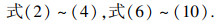(19b)

将式(19a)转化为线性矩阵不等式的形式，这样就可以得到如下凸优化问题：
当B_R为多边形区域时，条件(19a)等价于α²x_i^TP_εx_i≤1，由于P_ε>0，由Schur补引理可知条件(19a)可转化成：
当B_R为椭圆区域Ω(R, 1)时，条件(19a)等价于α²P_ε≤R，由于P_ε>0，由Schur补引理可知条件(19a)可转化成：
选定B_R为椭圆区域Ω(R, 1)，可得如下定理：
定理2?? 给定奇异摄动参数ε的上界ε，如果G₂+G₂^T>0，存在对称正定矩阵Q∈R^n×n，矩阵K_c∈R^m×n，F₁∈R^m×n₁，F₂∈R^m×n₁以及矩阵Z₁∈R^n₁×n₁，Z₂∈R^n₂×n₂，Z₃∈R^n₁×n₁，Z₄∈R^n₂×n₂，Z₅∈R^n₂×n₁且Z_k=Z_k^T(k=1, 2, 3, 4)，使得下列LMI优化问题可行：

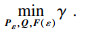(20)

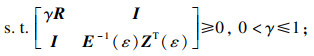(21a)

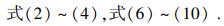(21b)

则对任意ε∈(0, ε]，存在无记忆状态反馈控制器u(t)=K(ε)x(t)，K(ε)=K_cZ^-1(ε)，使得闭环系统(5)是渐近稳定且无源的.当γ取最小值时，闭环系统吸引域的一个极大估计为
注3 ??求解以上凸优化问题所得到的吸引域都是系统真实吸引域的子集.
注4 ??有界凸集B_R的选取和优化后得到γ的大小均会影响吸引域估计范围的大小，所以选取合适的B_R并且在算例仿真时尽可能得到较小的γ(0 < γ≤1)能有效扩大闭环系统的吸引域估计.
推论2 ??为了得到闭环系统稳定界的最大估计ε_max，可以使用LMI工具箱，在保证定理2中LMI优化问题可行的前提下，通过一维折半查找法，得到当前实例下奇异摄动参数稳定界ε的最大估计.
对比已有的关于受输入饱和影响的奇异摄动系统的研究，本文加入了奇异摄动参数稳定界的估计方法，在具体实例中能更直观地判断出所给奇异摄动参数是否在稳定界内.
3 仿真算例例1 ??考虑文献[15]中的系统：

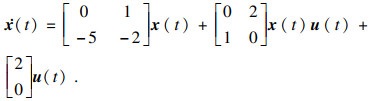(22)

系统(22)可以转化为带有外部输入ω(t)和变时滞x(t-d(t))的形式，系统参数为
取σ=0.3，μ=0.1，U₁=0.6，利用Matlab中的LMI工具箱求解定理1中得到的线性矩阵不等式，得到
从而状态反馈控制器增益矩阵为
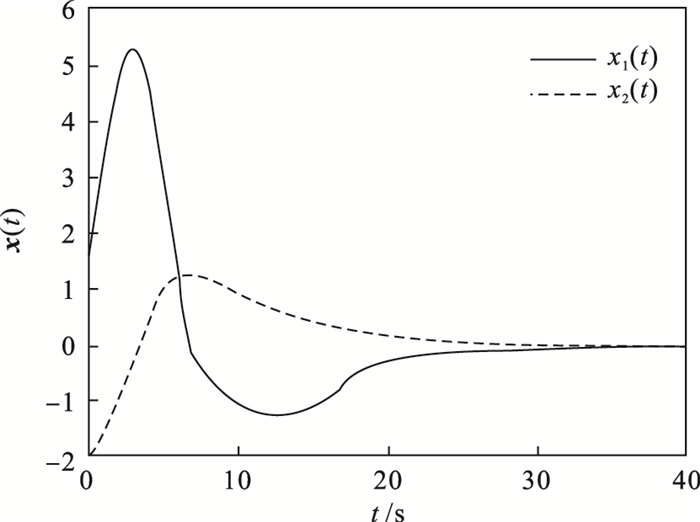
选取初态x(0)=[-0.2 ??1]^T，外部输入ω(t)=1/(1+2t)，由于本文得到的判据与时滞上界无关，为了验证该结论，此处选取变时滞x(t-d(t))=0.1sint+9999.9，时滞上界τ=10000，该闭环系统的状态轨迹如图 1所示.
图 1(Fig. 1)

图 1 闭环系统的状态轨迹(例1)Fig.1 State trajectories of closed-loop system(example 1)

例2 ??考虑文献[16]中描述的Boost转换器双线性系统，该系统的状态空间表达式为
其中，
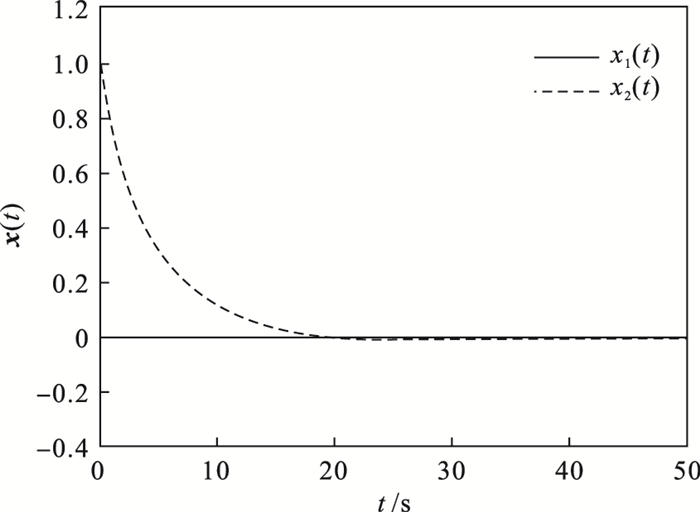
取ε=0.1，σ=3，U₁=0.4，通过推论1，求得状态反馈增益矩阵为
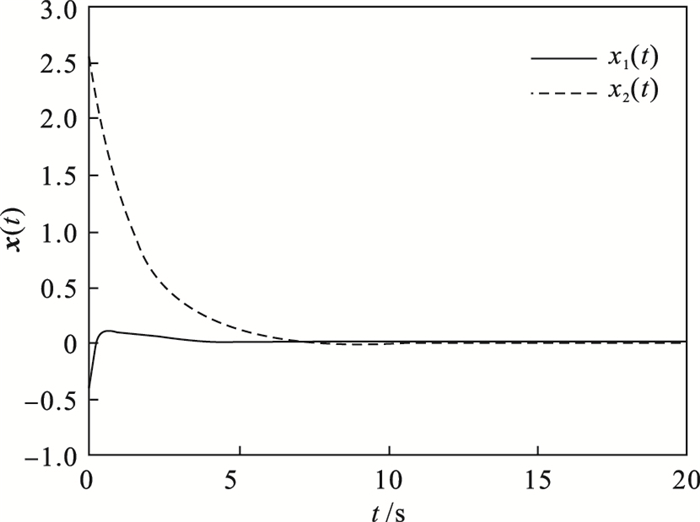
选取初态x(0)=[1.5 ??-2]^T，该闭环系统的状态轨迹如图 2所示.
图 2(Fig. 2)

图 2 闭环系统的状态轨迹(例2)Fig.2 State trajectories of closed-loop system (example 2)

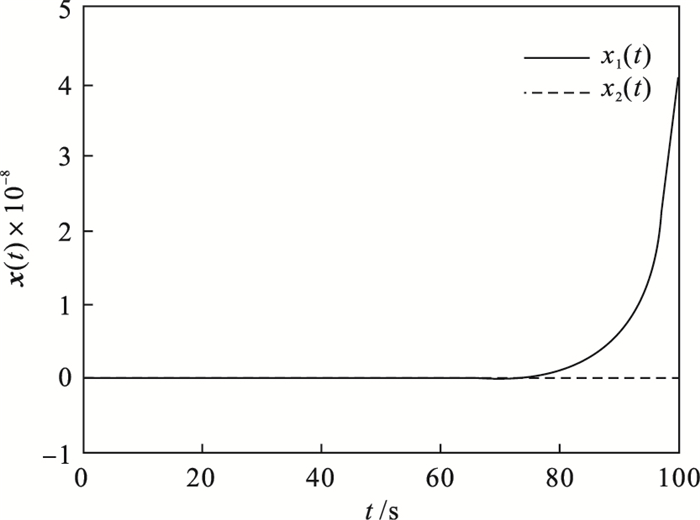
例3 ??考虑形式类似于式(5)系统的相关参数：
选取初态x(0)=[-0.8 ??2.6]^T，U₁=2，外部输入ω(t)=0.5sin(2t)e^-0.3t，时变时滞d(t)=0.2sin(0.5t)+0.2，时滞上界τ=0.4，时滞微分上界μ=0.1，得到开环系统状态轨迹见图 3.
图 3(Fig. 3)

图 3 开环系统的状态轨迹Fig.3 State trajectories of open loop system

令σ=1，根据定理1，使用LMI工具箱，得到
闭环系统的吸引域Ω(P_ε)={x∈Rⁿ: x^TP_εx≤1}，其中，
为了优化吸引域估计，选定B_R为单位圆Ω(I)，根据定理2，调整参数σ的值，利用LMI工具箱的mincx求解器求解该凸优化问题，得到
状态反馈增益矩阵为
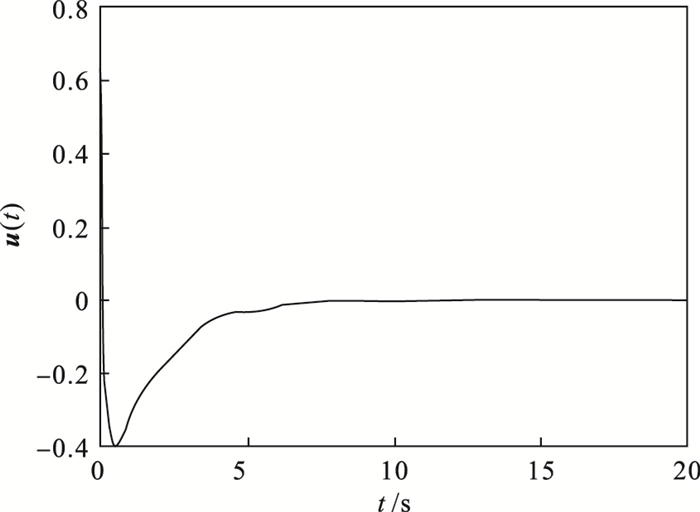
选取相同的初态，闭环系统状态轨迹见图 4，控制输入轨迹见图 5.
图 4(Fig. 4)

图 4 闭环系统的状态轨迹(例3)Fig.4 State trajectories of closed-loop system(example 3)

图 5(Fig. 5)

图 5 闭环系统的输入轨迹Fig.5 Input trajectory of closed-loop system

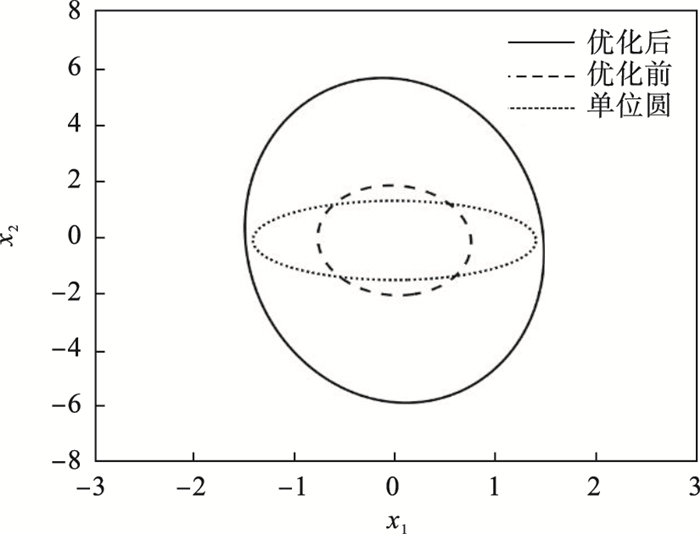
优化后的闭环系统的吸引域估计为
该闭环系统的吸引域如图 6所示.
图 6(Fig. 6)

图 6 闭环系统的吸引域Fig.6 Attractive domain of closed-loop system

以上选值不变，限定γ≤1，运用一维折半搜索法，求得最大奇异摄动参数稳定界ε_max约为7.0425.
表 1给出不同时滞微分上界与奇异摄动参数上界的关系(限定γ≤1).由表 1可知，时滞微分上界越小，摄动参数上界越大.结果表明，时滞微分上界会影响奇异摄动参数稳定界，从而影响系统的无源性能.
表 1(Table 1)

表 1 μ与ε的关系Table 1 The relationship between μ and ε 时滞上界μ 摄动参数上界ε 0.1 7.0425 0.2 6.9751 0.3 6.8859 0.4 6.7563 0.5 6.4283 0.6 5.2227

表 1 μ与ε的关系 Table 1 The relationship between μ and ε

4 结语本文研究了一类带有输入饱和的变时滞奇异摄动双线性系统的无源控制问题.通过构造保守性较小的Lyapunov函数，结合LMIs，提出一种状态反馈无源控制器的设计方法，给出保证奇异摄动参数小于或等于稳定界ε时，闭环SPSs是渐近稳定的和无源的，同时构造了一个与奇异摄动参数ε相关的椭圆吸引域.此外，给出了最大稳定界ε的估计方法.在此基础上，提出凸优化问题来进一步扩大闭环系统吸引域估计.最后，通过数值算例及仿真说明了本文所提方法的有效性.本文中的LMI条件不受时滞上界影响，所提出的方法可以应用到更多的SPSs模型中，在一定程度上降低了所得结果的保守性.
参考文献

[1]	Kokotovic P, Khalil H K, O'Reilly J. Singular perturbation methods in control: analysis and design[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1999: 1-8.
[2]	Ganjefar S, Mohammadi A. Variable speed wind turbines with maximum power extraction using singular perturbation theory[J]. Energy, 2016, 106(13): 510-519.
[3]	Kumar M. Methods for solving singular perturbation problems arising in science and engineering[J]. Mathematical and Computer Modelling, 2011, 54(1/2): 556-575.
[4]	Wang Y Q, Chen F, Zhuang G M, et al. Event-based asynchronous and resilient filtering for Markov jump singularly perturbed systems against deception attacks[J]. ISA Transactions, 2021, 112: 56-73. DOI:10.1016/j.isatra.2020.11.029
[5]	Mohler R R. Bilinear control processes: with applications to engineering, ecology, and medicine[M]. New York: Academic Press, 1973: 4-7.
[6]	Zhu X, Li D. Robust fault estimation for a 3-DOF helicopter considering actuator saturation[J]. Mechanical Systems and Signal Processing, 2021, 155(10): 107624.
[7]	He W, Dong Y T, Sun C Y. Adaptive neural impedance control of a robotic manipulator with input saturation[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 46(3): 334-344.
[8]	杨冬梅, 王傲. 基于观测器的时滞T-S模糊广义切换系统的异步无源控制[J]. 东北大学学报(自然科学版), 2021, 42(11): 1521-1526. (Yang Dong-mei, Wang Ao. Observer-based asynchronous passive control for T-S fuzzy generalized switched systems with time delay[J]. Journal of Northeastern University(Natural Science), 2021, 42(11): 1521-1526.)
[9]	Wang Y Y, Wang Q B, Zhou P F, et al. Delay-dependent passivity and passification for uncertain singularly perturbed Markovian jump systems with time-varying delay[J]. Circuits, Systems, and Signal Processing, 2012, 31(6): 2179-2194. DOI:10.1007/s00034-012-9427-9
[10]	Liu L, Feng Z J, Han C W. Multi-objected optimal control problem for singularly perturbed systems based on passivity[C]//The 35th Chinese Control Conference(CCC). Chengdu, 2016: 2626-2630.
[11]	Gao Y B, Lu G P, Wang Z M. Passivity analysis of uncertain singularly perturbed systems[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2010, 57(6): 486-490. DOI:10.1109/TCSII.2010.2048378
[12]	Hu T S, Lin Z L. Control systems with actuator saturation: analysis and design[M]. Boston: Birkhauser, 2001: 158-162.
[13]	Yang C Y, Che Z Y, Zhou L N. Integral sliding mode control for singularly perturbed systems with mismatched disturbances[J]. Circuits, Systems, and Signal Processing, 2019, 38(4): 1561-1582. DOI:10.1007/s00034-018-0925-2
[14]	Kim J H, Bien Z. Robust stability of uncertain linear system saturating actuators[J]. IEEE Transactions on Automatic Control, 1994, 39(1): 202-206. DOI:10.1109/9.273369
[15]	Benallou A, Mellichamp D A, Seborg D E. Optimal stabilizing controllers for bilinear systems[J]. International Journal of Control, 1988, 48(4): 1487-1501. DOI:10.1080/00207178808906264
[16]	Bichiou S, Bouafoura M K, Braiek N B. Time optimal control laws for bilinear systems[J]. Mathematical Problems in Engineering: Theory, Methods and Applications, 2018, 2018: 1-10.