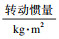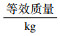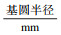胡蛟^1,2, 胡茑庆^1,2, 沈建^1,2, 罗鹏^1,2
1. 国防科技大学 智能科学学院, 湖南 长沙 410073;
2. 国防科技大学 装备综合保障技术重点实验室, 湖南 长沙 410073
收稿日期：2021-09-29
基金项目：国家重点研发计划项目(2018YFB1702401)；国家自然科学基金资助项目(51975576)。
作者简介：胡蛟(1984-)，男，湖南益阳人，国防科技大学博士研究生;
胡茑庆(1967-)，男，湖南永州人，国防科技大学教授，博士生导师。

摘要：针对直升机主减系统关键部件智能化故障诊断的迫切需求，从动力学建模的角度分析典型故障状态下系统的动态响应特性有助于深化故障机理和先进诊断算法的研究.采用集中参数法对直升机主减系统典型结构建立了考虑多非线性因素的故障动力学模型，并采用多体软件进行仿真建模与校验.仿真结果表明，啮合频率与局部故障特征频率调制现象清晰明显，行星轮周向响应明显大于平移响应.该类模型能有效揭示典型故障下的振动特性，为直升机传动系统故障诊断提供指导.
关键词：直升机主减速器典型部件故障动力学建模振动响应特性频谱分析
Fault Dynamic Modeling and Simulation for Typical Components of Helicopter Main Reducers
HU Jiao^1,2, HU Niao-qing^1,2, SHEN Jian^1,2, LUO Peng^1,2
1. College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410073, China;
2. Laboratory of Science and Technology on Integrated Logistics Support, National University of Defense Technology, Changsha 410073, China
Corresponding author: HU Niao-qing, E-mail: hnq@nudt.edu.cn.

Abstract: Aiming at the urgent demands of intelligent fault diagnosis for the key components of helicopter main reducers, the dynamic response characteristics of the system under the typical fault state are analyzed from the perspective of dynamic modeling, which is conducive to deepening the understanding of fault mechanism and advanced diagnosis algorithm. The fault dynamic models considering multi-nonlinear factors are developed for the typical components of a helicopter main reducer using the lumped-parameter method, and the multi-body software is applied for simulation modeling and verification. The results show that the modulation phenomenon between meshing frequency and local fault characteristic frequency is clear and the circumferential responses of the planet gear are obviously greater than the translational responses. these models can effectively reveal the vibration characteristics under typical faults and provide guidance for fault diagnosis of the helicopter transmission system.
Key words: helicopter main reducertypical componentfault dynamic modelingvibration response characteristicsspectrum analysis
直升机被广泛应用于抗震救灾、紧急救援、旅游观光、反恐维稳等诸多领域，在国民经济发展和国防建设中发挥着重要作用.传动系统作为直升机无冗余备份的关键核心部件，常见结构主要由三器两轴(主减速器、中间减速器、尾减速器、动力传动轴和尾传动轴)等组成.直升机的使用特性决定了其将常常运行于恶劣的变工况环境，齿轮箱部件容易出现疲劳和各种故障，如果故障不能被及时发现和排除，将导致整个传动系统的失效，进而造成重大的经济损失.
国内外****对于直升机传动系统的建模做过不少工作.文献[1-2]以某型直升机主减速器行星轮系为研究对象，分别建立了行星轮系集中参数模型和有限元模型以研究裂纹故障下的动态响应.盛冬平^[3]考虑了齿面摩擦、多间隙等非线性因素的影响，按照由低到高的层级顺序对某型直升机主减系统进行了建模及特性分析.
Liang等^[4]分别从建模方式、啮合刚度评估、损伤建模与诊断技术、传递路径影响和验证方式对齿轮系统研究进行了综述.Lei等^[5]对各类故障建模进行了归纳总结.Hammami等^[6]对行星轮系统非平稳负载下的非线性特性进行了深入研究.Parra等^[7]为方便对比现象模型与集中参数模型的仿真结果，提出一种将集中参数模型解分解为固定参考坐标系函数的方法，并将两种模型与实验结果进行了比较.Xue等^[8]采用有限元方法计算不同故障程度的时变啮合刚度并代入集中参数模型求解了行星轮系统动态响应.马辉等^[9]通过建立行星轮系有限元模型，研究了齿顶修形、减重孔和杆系柔性对啮合刚度的影响.
以上关于传动系统建模的文献大多基于研究传动系统的动态特性，旨在提升如可靠性、系统稳定性、振动噪声优化等性能从而指导设计，而在健康状态监测和诊断领域，从动力学建模的角度深入分析传动系统动态特性及故障机理，对故障进行隔离诊断具有十分重要的意义.因此，本文以某型直升机主减速器典型部件定轴轮系和行星轮系为研究对象，分别建立正常状态和典型故障状态的集中参数模型，并通过多体动力学软件进行仿真验证，分析结果可为直升机传动系统的故障诊断和预测提供指导，并为健康状态监测系统的开发提供理论依据及数据支撑.
1 齿轮时变啮合刚度计算齿轮副啮合刚度的周期时变性是引起齿轮振动的主要因素，影响齿轮故障响应最重要且最直接的原因是啮合刚度的异化.因此，要建立带有故障的齿轮系统动力学模型，首要任务便是寻求合适的方法计算故障工况下的时变啮合刚度.轮齿裂纹和断齿作为占比较大的典型故障，受到了国内外许多****的关注，针对该类工况下的啮合刚度计算与试验验证也开展了很多工作^[10-11].目前，关于齿轮啮合刚度的算法种类较多，综合考虑各类算法优缺点，本文采用改进的势能法计算齿轮在不同故障程度下的时变啮合刚度.改进势能法是将轮齿等效成悬臂梁，根据材料力学、弹性力学等理论计算储存在啮合齿轮对中的赫兹能U_H、弯曲势能U_b、剪切势能U_s、压缩势能U_a和基体变形势能U_f，分别求取各部分刚度，即可计算齿轮副的啮合刚度如下^[11]：

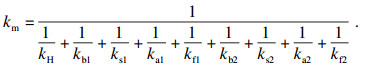(1)

齿轮系统参数如表 1所示，采用改进势能法计算时变啮合刚度结果如图 1所示，q表示裂纹长度.
表 1(Table 1)

表 1 定轴齿轮系统参数Table 1 Fixed-shaft gearbox system parameters 参数 数值 参数 数值 z1 43 fm/Hz 430 z2 53 TD/(N·m) 81.1 ID/(kg·m2) 0.002 1 TL/(N·m) 100 IL/(kg·m2) 0.010 5 kb/(N·m-1) 6.56×107 I1/(kg·m2) 4.365 9×10-4 cb/(N·s·m-1) 1.8×105 I2/(kg·m2) 8.360 2×10-4 kt/(N·m·rad-1) 4.4×104 cm/(N·s·m-1) 67 ct/(N·m·s·rad-1) 5.0×105 M1/kg 4.250 模数/mm 3 M2/kg 5.238 R1/mm 60.6 fz/Hz 10 R2/mm 74.7

表 1 定轴齿轮系统参数 Table 1 Fixed-shaft gearbox system parameters

图 1(Fig. 1)

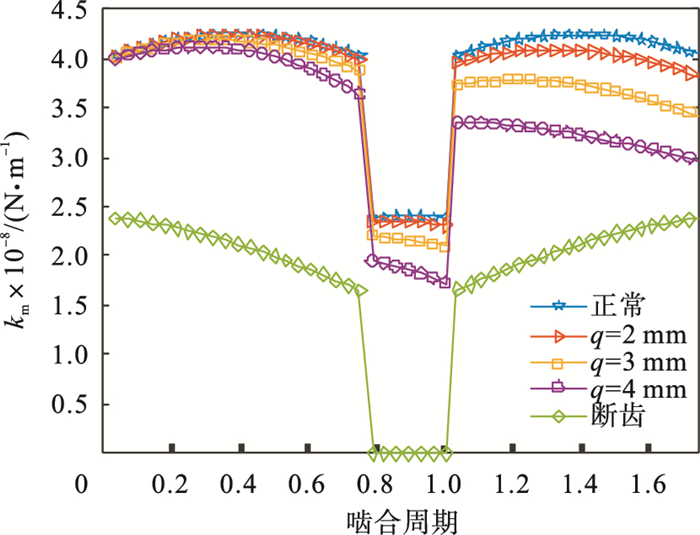图 1 主动轮齿不同故障程度下的啮合刚度Fig.1 Mesh stiffness of the gear tooth under different failure levels

2 定轴轮系动力学建模2.1 定轴轮系集中参数建模与仿真以定轴轮系为研究对象，本文构建的5自由度动力学模型如图 2所示，系统结构及运行参数如表 1所示.
图 2(Fig. 2)

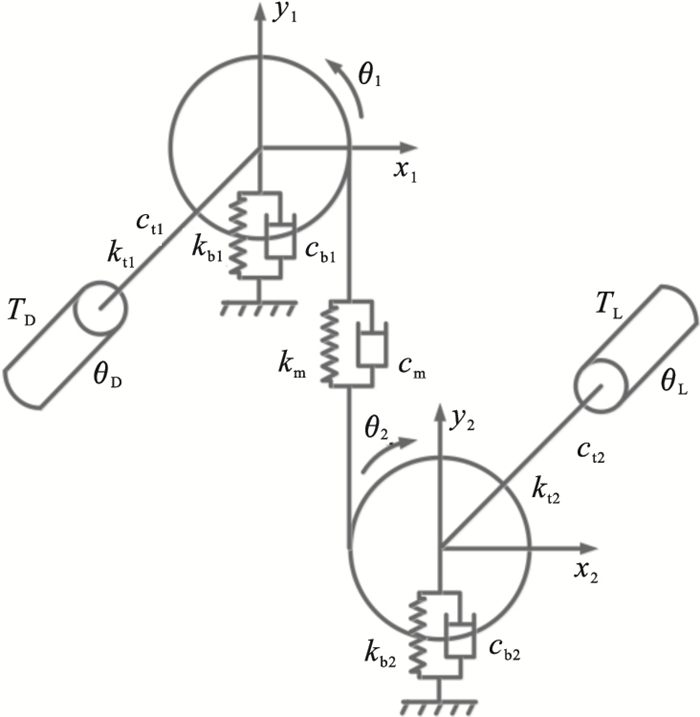图 2 单级齿轮系统Fig.2 Single-stage gear system

采用牛顿第二定律对图 2定轴系统建立动力学方程组如下：

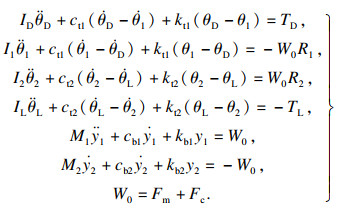(2)

式中：F_m，F_c分别为啮合刚度k_m和阻尼系数c_m对应的力元；I，T分别表示转动惯量和转矩；k_b，c_b分别为齿轮支撑轴承的径向刚度和阻尼系数；k_t，c_t分别为轮轴的扭转刚度和阻尼系数；y，θ分别表示垂向位移和转角；下标1，2，D，L分别表示主动轮、从动轮、驱动和负载电机.
不失一般性，令k_t1=k_t2=k_t，c_t1=c_t2=c_t，k_b1=k_b2=k_b，c_b1=c_b2=c_b.齿轮啮合刚度力与阻尼力计算如式(3)所示.

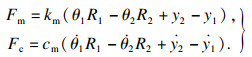(3)

为突出故障现象，典型故障选取断齿工况，分别将第1节求取的正常状态和主动轮断齿时变啮合刚度代入式(2)，并求解响应结果，主动轮加速度响应如图 3所示.
图 3(Fig. 3)

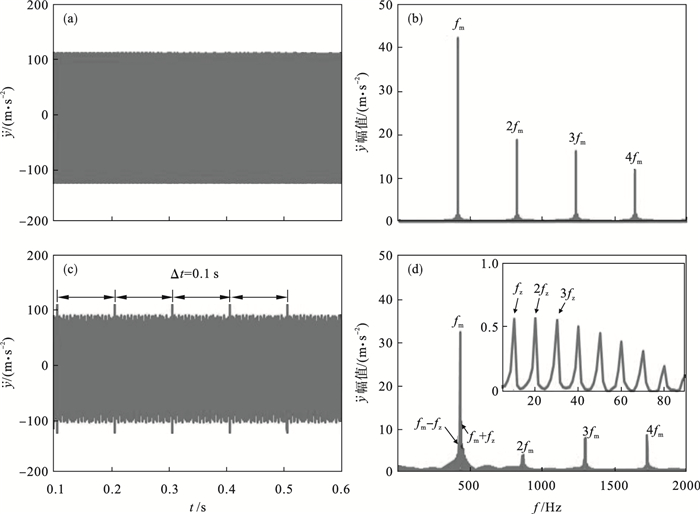图 3 主动轮集中参数模型响应Fig.3 Lumped-parameter model responses of the gear (a)—正常状态时域；(b)—正常状态频域；(c)—断齿状态时域；(d)—断齿状态频域.

对比图 3a, 3c可以看出，故障状态响应信号较正常状态存在明显的周期性突峰，间隔时间为Δt=0.1 s，对应主动轮转频f_z.图 3b为正常状态频谱图，其主要成分为时变啮合刚度引起的啮频f_m及其倍频(2f_m, 3f_m，…)，且加速度幅值随阶次升高基本呈现下降趋势；图 3d断齿状态除上述主要成分外，啮频及倍频两侧非对称分布有故障轮转频10 Hz的调制边带，且调制现象存在于整个频段，低频段存在明显的故障轮转频及其倍频分量.
2.2 定轴轮系多体建模与仿真采用多体动力学软件对2.1节建立的定轴集中参数模型进行仿真校验，切除主动轮齿部分实体以模拟断齿故障，定轴齿轮箱多体模型如图 4所示.
图 4(Fig. 4)

图 4 定轴齿轮箱系统多体模型Fig.4 Multi-body model of the fixed-shaft gearbox (a)—正常状态；(b)—断齿状态.

设置采样频率10 kHz，仿真时长0.6 s，分别提取正常状态与断齿故障下主动轮垂向加速度信号，结果如图 5所示，其时、频域所呈现的特征结构与图 3基本一致.
图 5(Fig. 5)

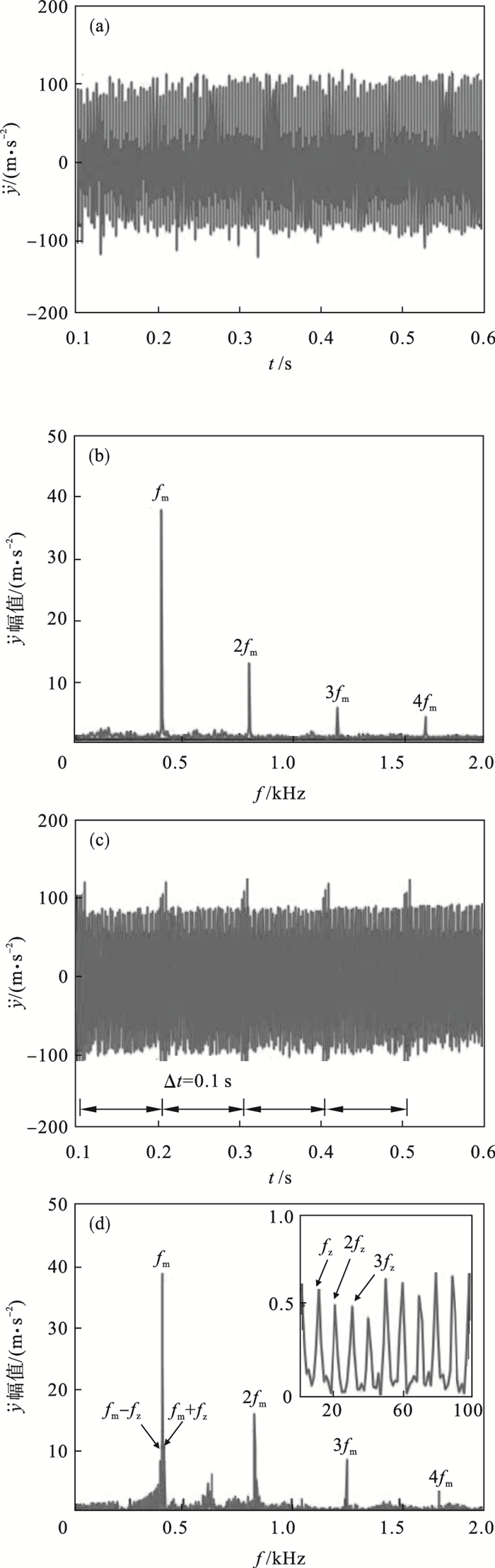图 5 主动轮多体模型响应Fig.5 Multi-body model responses of the gear (a)—正常状态时域；(b)—正常状态频域；(c)—断齿状态时域；(d)—断齿状态频域.

以上仿真结果表明，所建立的定轴集中参数模型与多体模型是一致的，且与理论分析相吻合.
3 行星轮系动力学建模3.1 行星轮系集中参数建模与仿真以单级行星轮组件为研究对象建立平移﹣扭转模型，如图 6所示，行星轮系结构参数见表 2，系统中轴承刚度k_s=k_p=k_r=10⁸ N·m^-1；周向刚度k_st=k_ct=0; k_rt=10×10⁹ N·m^-1；压力角α=20°；模数m=2.5 mm；齿宽L=10 mm; 外部扭矩T_pd=23.33 N·m；T_pl=100 N·m.
图 6(Fig. 6)

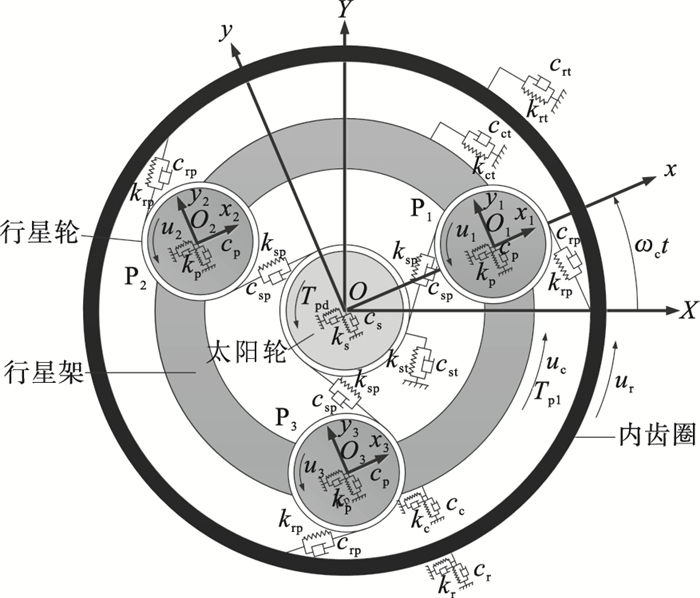图 6 行星轮系平移-扭转模型Fig.6 Translational-rotational model of the planetary gear set

表 2(Table 2)

表 2 行星轮系结构参数Table 2 Parameters of the planetary gear set 基本参数 太阳轮 行星轮 齿圈 行星架 齿数 28 32 92 — 0.000 6 0.001 5 0.057 0.05 0.39 0.64 2.30 5.38 32.9 37.6 108.1 —

表 2 行星轮系结构参数 Table 2 Parameters of the planetary gear set

平移﹣扭转模型相比纯扭转模型需要考虑更多的非线性因素和自由度，其动力学建模和求解更加复杂.为此，先定义如下三类坐标系：OXY为固定的全局坐标系，原点在太阳轮中心，坐标系不随行星架旋转；Oxy为随行星架角速度ω_c等速旋转的随动坐标系，原点固定在行星架中心；局部坐标系O_nx_ny_n(n=1，2，3)原点在行星轮中心，也以ω_c等速随行星架旋转，坐标轴与Oxy的两平移轴系平行对齐.下标c, r, s分别代表行星架、齿圈和太阳轮.每个构件都具有两个平移方向和一个旋转方向的自由度，模型共计18个自由度.
根据牛顿第二定律建立计入外部载荷的18自由度平移﹣扭转模型，行星架、齿圈、太阳轮和行星轮各构件的动力微分方程组分别如下：

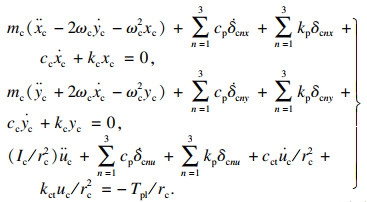(4)

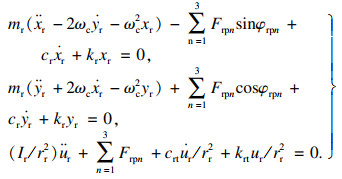(5)

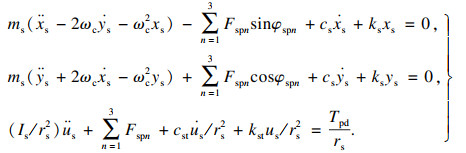(6)

(7)

式中, F_spn，F_rpn分别为太阳轮、齿圈与行星轮之间的啮合力，，j=spn，rpn，n=1，2，3.
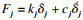
本文假定综合传递误差按正弦函数变化，即e_j(t)=E_jsin(2πf_mt+φ_j)，E_j为误差幅值，φ_j为啮合初相位.加入齿轮副传递误差的影响，将上述方程组写成矩阵形式：

(8)

式中：M为系统质量矩阵；K_b，C_b，K_m，C_m分别为轴承支撑刚度、阻尼矩阵和齿轮啮合刚度、阻尼矩阵；G，K_Ω分别为陀螺力矩阵和向心力矩阵；Q为广义坐标矩阵，由各构件横向x，y和周向u的位移组成；T_p，E分别为力矩阵和误差矩阵.
考虑齿轮安装等因素造成齿侧间隙的影响，f(x, B)表示非线性间隙函数，其数学表达式为^[3]

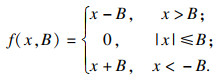(9)

式中，B为间隙常量.
将式(9)代入方程组(4)~(7)，得到包含间隙影响的广义坐标矩阵方程.
假定齿圈固定，太阳轮和行星架分别作为输入、输出构件，对系统参数进行相应设置：综合传递误差幅值E_j=20 μm，间隙常量B=25 μm，太阳轮输入转速为2 572 r/min，根据表 2可计算行星轮至行星架传动比i_pc和太阳轮至行星架传动比i_sc如下，系统运行参数见表 3.

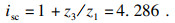(11)

表 3(Table 3)

表 3 行星轮系运行参数Table 3 Operation parameters of the planetary gear set 参数 数值 啮合频率fm/Hz 920 输出转频fc/Hz 10 行星轮转频fp/Hz 18.8 输入转频fs/Hz 43

表 3 行星轮系运行参数 Table 3 Operation parameters of the planetary gear set

Newmark-β法是一种将线性加速度方法普遍化的方法，以其设定参数下无条件收敛和求解速度快等优势被广泛应用于求解系统动力学微分方程组^[12].因此，本文采用Newmark-β法对上述建立的行星轮系动力学方程组进行数值求解.设置采样频率为50 kHz，仿真时长为0.1 s，求解行星轮系动力学微分方程.根据行星轮系结构参数，注意方程中各处齿轮啮合副的刚度设置应满足相应的相位关系^[13]，如表 4所示.提取行星轮3个自由度的加速度响应信号，并按行星架转频作归一化处理后的阶次谱如图 7，图 8所示.
表 4(Table 4)

表 4 行星轮系相对相位Table 4 Relative phases of the planetary gear set γs1 γs2 γs3 γr1 γr2 γr3 γrs 0 0.333 0.667 0 -0.667 -0.333 0.5

表 4 行星轮系相对相位 Table 4 Relative phases of the planetary gear set

图 7(Fig. 7)

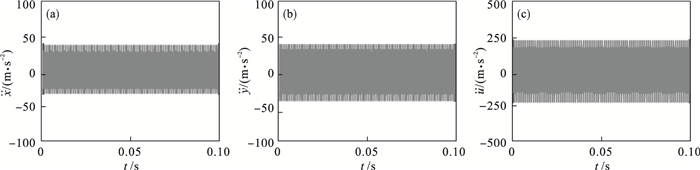图 7 正常状态行星轮P1时域响应Fig.7 Time domain responses of the planet gear P1 in the normal state (a)—x向；(b)—y向；(c)—周向.

图 8(Fig. 8)

图 8 正常状态行星轮P1频域响应Fig.8 Frequency domain responses of the planet gear P1 in the normal state (a)—x向；(b)—y向；(c)—周向.

由图 7可知，在正常状态下，行星轮各向时域响应均较为平稳，因时变啮合刚度影响而产生的周期振动明显.图 8频域谱线分布明晰，啮频及其倍频峰值明显，且各向响应幅值基本满足依阶次升高而递减的规律.总体而言，平移坐标系下的加速度响应幅值较小，周向响应幅值明显大于平移响应幅值，这与行星轮系的结构特点有关，周向均匀分布的各行星轮在平移方向的响应会有相互消减的作用.
采用改进势能法植入太阳轮断齿故障，仿真时长为0.5 s.为便于图形显示截取0.1~0.2 s时段，结果如图 9~图 11所示.图 9所示的行星轮3向时域响应较图 7均呈现明显因断齿故障造成的非平稳波动，故障轮齿与3个行星轮依次啮合，因传递误差和齿侧间隙的影响，响应信号中局部故障周期为Δt_d=0.030 4 s，对应的特征频率为太阳轮相对转频f_d=f_s-f_c^[14].由图 10，图 11频谱图及局部放大图可看出，各阶啮频及其倍频附近均存在故障调制边频，低频段故障频率及其倍频清晰可见，由于3个行星轮啮合的差异性造成了3N阶啮合频率和故障频率谐波的幅值增强效应，N=1, 2, 3, ….
图 9(Fig. 9)

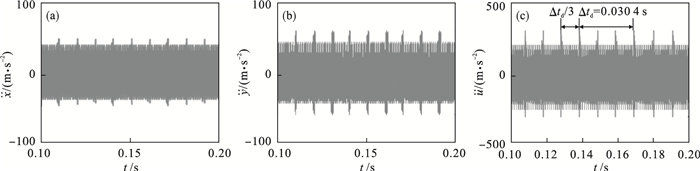图 9 断齿状态行星轮P1时域响应Fig.9 Time domain responses of the planetary gear P1 with a broken tooth (a)—x向；(b)—y向；(c)—周向.

图 10(Fig. 10)

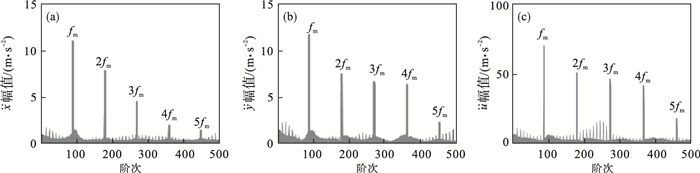图 10 断齿状态行星轮P1频域响应Fig.10 Frequency domain responses of the planetary gear P1 with a broken tooth (a)—x向；(b)—y向；(c)—周向.

图 11(Fig. 11)

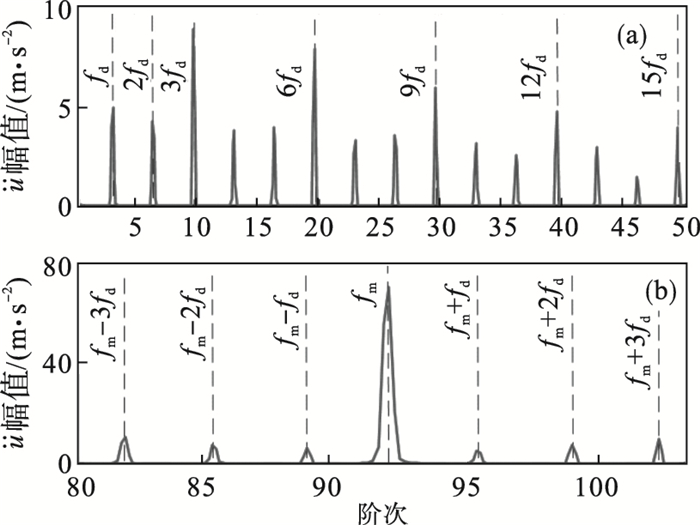图 11 断齿状态行星轮P1周向响应局部频谱图Fig.11 Local frequency spectrum of the planet gear P1 circumferential responses with a broken tooth (a)—0至50阶; (b)—80至103阶.

需要强调的是，由于此类建模是采用引入随动坐标系的“类定轴轮系”方法，故上述直接求解的响应信号均未计入传递路径，特别是因行星架旋转而造成的时变效应影响，所得结果与文献[8]的部分研究结论是吻合的，在与试验信号进行对比时，应继续加入行星架的旋转效应.
3.2 行星轮系多体建模与仿真按照表 2所列参数建立行星轮系多体仿真模型，见图 12，轮系驱动和约束设置与集中参数模型保持一致.
图 12(Fig. 12)

图 12 行星齿轮箱多体模型Fig.12 Multi-body model of the planetary gearbox

仿真时长1 s，截取0~0.4 s时段并提取正常状态和断齿故障状态下行星轮周向加速度曲线，如图 13所示.
图 13(Fig. 13)

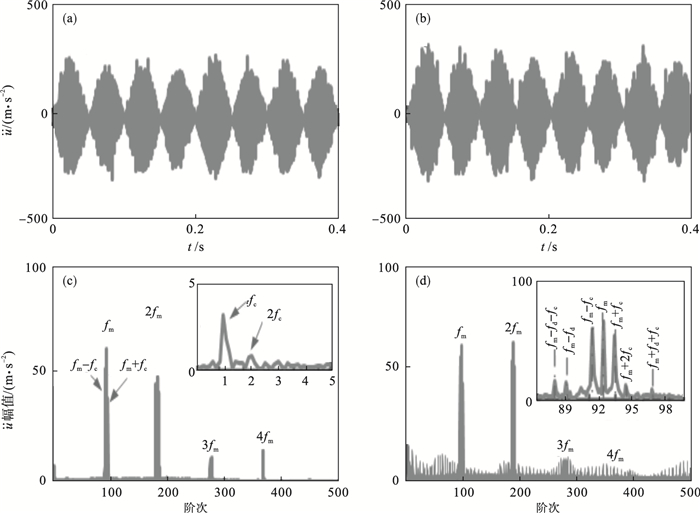图 13 行星轮P1周向加速度响应Fig.13 Angular acceleration of the planetary gear P1 (a)—正常时域响应；(b)—断齿时域响应；(c)—正常阶次谱；(d)—断齿阶次谱.

对比图 9，图 10可以看出，正常状态下时域曲线出现了明显的因为行星架公转而产生的大幅度周期调制现象，而频域则是在啮频两侧出现了f_c的调制边带和低频段f_c的多阶谐波.故障工况下时域响应非平稳性增强，频谱图中呈现的特征是在gf_m±hf_d±wf_c处存在明显的调制边带，其中g，h，w均为正整数，这与文献[14]的研究结论是一致的.对比集中参数模型的仿真结果可知，造成此种差异的原因为集中参数建模是基于与行星架同等转速ω_c的随动坐标系，而多体动力学模型则是参照固定于大地的全局坐标系建立的.虽然两类模型仿真的行星轮响应信号因建模方式存在差异，但两者对于故障机理的反映是一致且有效的.
4 结论1) 采用商用软件建立的多体模型能够有效地对直升机主减典型部件的非线性集中参数模型进行仿真验证，结果表明，两类模型对于齿轮系统故障状态的机理和响应特性仿真是一致且有效的.
2) 齿轮故障的响应特征均表现为系统啮合频率和故障特征频率的调制现象，且行星轮周向振动明显大于平移方向.
3) 该系列模型的建立不仅能指导传动系统的优化设计，也能为直升机健康监测方法的开发，特别是为现阶段基于人工智能的热点方法提供有效的参考和大数据支撑.
参考文献

[1]	Cheng Z, Hu N Q, Zhang X P. Crack level estimation approach for planetary gearbox based on simulation signal and GRA[J]. Journal of Sound and Vibration, 2012, 331(26): 5853-5863. DOI:10.1016/j.jsv.2012.07.035
[2]	Fan L, Wang S P, Wang X J, et al. Nonlinear dynamic modeling of a helicopter planetary gear train for carrier plate crack fault diagnosis[J]. Chinese Journal of Aeronautics, 2016, 29(3): 675-687. DOI:10.1016/j.cja.2016.04.008
[3]	盛冬平. 直升机主减速器传动系统的动力学研究[D]. 南京: 南京航空航天大学, 2015. (Sheng Dong-ping. Research on key dynamic problems of helicopter main reducer transmission system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. )
[4]	Liang X H, Zuo M J, Feng Z P. Dynamic modeling of gearbox faults: A review[J]. Mechanical Systems and Signal Processing, 2018, 98(1): 852-876.
[5]	Lei Y G, Lin J, Zuo M J, et al. Condition monitoring and fault diagnosis of planetary gearboxes: a review[J]. Measurement, 2014, 48(1): 292-305.
[6]	Hammami A, Alfonso F D R, Chaari F, et al. Effects of variable loading conditions on the dynamic behaviour of planetary gear with power recirculation[J]. Measurement, 2016, 94(6): 306-315.
[7]	Parra J, Vicuna C M. Two methods for modeling vibrations of planetary gearboxes including faults: comparison and validation[J]. Mechanical Systems and Signal Processing, 2017, 92(4): 213-225.
[8]	Xue S, Howard I. Torsional vibration signal analysis as a diagnostic tool for planetary gear fault detection[J]. Mechanical Systems and Signal Processing, 2018, 100(1): 706-728.
[9]	马辉, 段田堂, 孙衍宁, 等. 齿顶修形行星轮系啮合刚度分析[J]. 东北大学学报(自然科学版), 2019, 40(3): 380-385. (Ma Hui, Duan Tian-tang, Sun Yan-ning, et al. Mesh stiffness analysis of planetary gear system with gear tip relief[J]. Journal of Northeastern University(Natural Science), 2019, 40(3): 380-385.)
[10]	Chen Z G, Zhu Z F, Shao Y M. Fault feature analysis of planetary gear system with tooth root crack and flexible ring gear rim[J]. Engineering Failure Analysis, 2015, 49(2): 92-103.
[11]	Wan Z G, Cao H R, Zi Y Y, et al. An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack[J]. Engineering Failure Analysis, 2014, 42(4): 157-177.
[12]	张子明, 杜成斌, 周星德. 结构动力学[M]. 北京: 清华大学出版社, 2008: 88-90. (Zhang Zi-ming, Du Cheng-bin, Zhou Xing-de. Dynamics of structures[M]. Beijing: Tsinghua University Press, 2008: 88-90.)
[13]	Parker R G, Lin J. Mesh phasing relationships in planetary and epicyclic gears[J]. Journal of Mechanical Design, 2004, 126(2): 365-370. DOI:10.1115/1.1667892
[14]	Feng Z P, Zuo M J. Vibration signal models for fault diagnosis of planetary gearboxes[J]. Journal of Sound and Vibration, 2012, 331(22): 4919-4939.