

1. 吉林大学 机械与航空航天工程学院,吉林 长春 130022;
2. 吉林大学 生物与农业工程学院,吉林 长春 130022;
3. 吉林大学 工程仿生教育部重点实验室,吉林 长春 130022
收稿日期:2021-11-12
基金项目:国家自然科学基金资助项目(31970454)。
作者简介:张志君(1974-),男,吉林舒兰人,吉林大学教授,博士生导师;
孙霁宇(1976-),女,吉林省吉林市人,吉林大学教授,博士生导师。
摘要:通过采用计算流体力学方法对不同相对厚度的椭圆翼型在低雷诺数范围下进行了数值模拟,研究了椭圆翼型在低雷诺数下的层流分离现象及流场结构.结果表明:在低雷诺数下,薄椭圆翼型在小攻角时前缘出现层流分离泡是其具有高的升力系数及升阻比的原因,随厚度的增加,前缘层流分离泡逐渐消失,在后缘形成时均小泡.随着雷诺数升高,薄椭圆翼型时均分离泡都出现在前缘,但外形缩小,而在较低雷诺数下,薄椭圆翼型小攻角时没有发生转捩再附现象;同时层流分离泡的出现也对翼型后缘分离涡的尺寸和位置产生了重要影响.相对厚度和雷诺数通过影响椭圆翼型上表面层流分离泡的尺寸、位置以及后缘分离涡的形态结构,进而改变了气动特性.
关键词:椭圆翼型低雷诺数相对厚度气动特性层流分离泡
Study on Laminar Flow Separation of Elliptic Airfoils at Low Reynolds Numbers
ZHANG Zhi-jun1, LI Tian-ge1, SI Teng-fei1, SUN Ji-yu2,3


1. School of Mechanical and Aerospace Engineering, Jilin University, Changchun 130022, China;
2. School of Biological and Agricultural Engineering, Jilin University, Changchun 130022, China;
3. Key Laboratory of Biomimetic Engineering, Ministry of Education, Jilin University, Changchun 130022, China
Corresponding author: SUN Ji-yu, professor, E-mail: sjy@jlu.edu.cn.
Abstract: The different relative thickness of elliptic airfoils was simulated to study the laminar flow separation and the structure of flow field in the range of low Reynolds numbers by the method of computational fluid dynamics. The results showed that a leading-edge separation bubble forms on the thin elliptical airfoil at low Reynolds numbers, which accounts for high lift coefficient and lift-drag ratio at a small angle of attack. The laminar separation bubbles gradually disappear at the leading edge and appear at the trailing edge with the increase of relative thickness. The size of the leading-edge separation bubbles of the thin elliptic airfoil gradually reduces with the increase of Reynolds numbers. However, the phenomenon of transition and reattachment disappears at lower Reynolds numbers; at the same time, the size and position of the vortex at the trailing edges of the airfoil are also greatly affected by the appearance of laminar separation bubbles. The relative thickness and Reynolds number change the aerodynamic characteristics by influencing the size and position of laminar separation bubbles on the upper surface of the elliptic airfoil and the structure of separation vortex at the trailing edge.
Key words: elliptic airfoillow Reynolds numberrelative thicknessaerodynamic characteristicslaminar separation bubble
近年来,微型飞行器因其体积小、灵活性强等突出优点被广泛应用到各个领域,而翼型在低雷诺数下的气动特性决定了微型飞行器的性能,从而使低雷诺数下翼型流动分析成为了研究者的焦点.低雷诺数下,由于空气黏性效应的增强,翼型表面易发生流动分离,甚至发生转捩、再附等现象,形成层流分离泡,使翼型的气动特性急剧恶化,对此国内外****进行了大量的理论和实验研究.Horton[1]提出了短层流分离泡模型,并描述了其基本特征.Selig等[2]利用风洞试验测量了34个翼型在低雷诺数下的升阻力,发现低雷诺数下翼型的气动力与层流分离泡有关,并给出了改善翼型气动特性的方法.白鹏等[3]采用数值模拟方法对对称翼型SD8020在低雷诺数下的流场进行了分析,得出了不同于经典层流分离泡模型的一种后缘层流分离泡模型,并利用了该模型解释了对称翼型小攻角下低雷诺数流场特性以及升力系数非线性效应.Kojima等[4]对NACA0002和NACA0012两种翼型进行了数值模拟,对比两种翼型非定常与时均流场得出了厚度对翼型的层流分离有着重要的影响.Ma等[5]采用试验与数值模拟结合的方法细致地研究了相对厚度和最大相对厚度位置对翼型气动性能的影响,结果表明翼型厚度改变了层流分离泡的尺寸及位置进而影响翼型的升阻力特性.朱志斌等[6]采用大涡模拟(large eddy simulation,LES)方法精细研究了低雷诺数范围内雷诺数对翼型SD7003气动特性的影响规律及作用机理,指出造成不同时均分离泡形态和气动特性的原因在于翼型上表面分离剪切层的失稳与转捩特征.
上述研究针对的均是尖后缘翼型在不同雷诺数下的流动分离现象,而对钝后缘翼型的研究大多数在较高雷诺数范围内.Kwon等[7]在雷诺数Re=3×105下对相对厚度为16%的椭圆翼型进行了风洞试验研究,发现翼型后缘的速度分布和涡流结构与常规翼型大不相同.Assel[8]采用Spalart-Allmaras湍流模型对厚度从5%到25%的椭圆翼型在4种雷诺数下进行了CFD模拟,研究了相对厚度对椭圆翼型气动力的影响,但由于使用完全湍流模型,其无法准确捕捉到翼型表面的流动分离,致使计算结果没有体现椭圆翼型独有的气动特性.Chitta等[9]利用5种湍流模型对厚度为16%的椭圆翼型进行了数值模拟,对比实验结果得出:Transition SST和k-kL-ω湍流模型能清晰地捕捉到翼型前缘层流分离泡的形成,显示的流动分离区域与实验结果吻合很好.Sun等[10]采用风洞实验与数值模拟结合的方法揭示了椭圆翼型在雷诺数Re=5×105时非常规气动特性的流动机理,认为翼型前缘层流分离和后缘分离涡的产生是翼型小攻角下高升力的原因.
本文选取不同相对厚度的椭圆翼型为研究对象,采用数值模拟方法对不同雷诺数下的气动特性进行分析,计算结果与实验数据[7]进行对比,验证了数值模拟方法的准确性;进而比较了不同厚度椭圆翼型在不同雷诺数下的气动力,分析了椭圆翼型在低雷诺数下具有高升力系数的原因.通过不同相对厚度和雷诺数下时均流场的对比,探究了翼型表面层流分离泡的变化规律,分析了相对厚度和雷诺数对流动分离的影响,为钝尾缘翼型在低雷诺数下流动机理的研究提供参考.
1 数值模拟和算例验证1.1 基本控制方程控制方程为时均连续性方程和Reynolds时均Navier-Stokes方程:
 | (1) |
 | (2) |
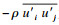
1.2 湍流模型选取带转捩修正的四方程Transition SST湍流模型,该模型结合了
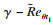
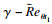
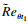
 | (3) |
关于动量厚度雷诺数
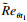
 | (4) |
 | (5) |
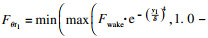
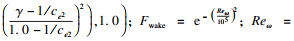
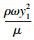
k-ω SST湍流模型的控制方程[14]为
 | (6) |
与
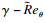
 | (7) |
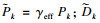
1.3 数值模拟方法本文基于有限体积法求解不可压缩Navier-Stokes方程,在低雷诺数范围下(Re=40 000,80 000)对不同相对厚度(t/c=6%,8%,12%,16%,18%,t表示翼型厚度,c表示翼型弦长)的椭圆翼型进行了数值模拟,椭圆翼型前后左右对称,翼型光滑对称,弦长c=1 m,利用ICEM软件进行网格划分,流场域的范围为20倍弦长,如图 1所示.利用CFD仿真软件对翼型气动性能进行数值模拟,流体域介质为空气,压力和速度耦合采用SIMPLEC算法,方程离散格式采用二阶迎风格式,边界条件入口采用速度入口,出口采用压力出口.
图 1(Fig. 1)
 | 图 1 计算域及网格示意图Fig.1 Schematic of computational domain and grids (a)—计算域示意图;(b)—网格示意图. |
1.4 算例验证为了验证本文数值模拟方法的准确性,对相对厚度为16%的椭圆翼型在雷诺数Re=3×105条件下进行了数值计算.为了提高效率以及消除网格密度对计算结果的影响,进行了网格无关性验证,网格1、网格2和网格3的壁面第一层网格厚度分别为50,500和10 μm,如图 2所示,计算结果与实验数据[7]对比发现网格1与网格3计算的升力系数和阻力系数一致,与实验结果吻合很好,表明本文的数值模拟方法是准确的.为了节省计算时间,提高计算效率,文中选取网格1进行模拟计算.从图 2中可以看出在攻角α为0°~5°范围内,升力线斜率大于2π,这与常规翼型的气动特性有很大的不同[7],并且在攻角α为0°时,与尖后缘的对称翼型不同,升力系数曲线没有出现“平台”,这是由于椭圆翼型特殊的钝后缘结构导致气体流过翼型后缘产生了非常规的流动分离.
图 2(Fig. 2)
 | 图 2 数值方法准确性验证Fig.2 Accuracy validation of numerical methods (a)—不同攻角下的升力系数对比;(b)—不同攻角下的阻力系数对比. |
2 计算结果分析2.1 相对厚度和雷诺数对椭圆翼型气动力的影响利用上述数值模拟方法对5种不同相对厚度的椭圆翼型进行仿真分析,图 3对比了5种相对厚度的椭圆翼型在雷诺数Re=4×104条件下的升力系数CL、阻力系数CD、升阻比CL/CD,不同相对厚度的翼型升力系数曲线均随攻角的增加而增大,在小攻角下(< 6°),相对厚度为6%的翼型的升力系数大于其他4种翼型,当攻角变大时,薄翼型过早发生流动分离,相对厚度较大的翼型表现出良好的升力特性,随相对厚度的增加,升力系数增加,失速攻角后移,最大升力系数增大,相对厚度为16%的翼型的最大升力系数出现在攻角12°附近.对于阻力系数曲线,在小攻角下,翼型的阻力系数随相对厚度的增加而增加,而在大攻角下表现出截然相反的特性,较厚翼型的阻力系数小于薄翼型,相对厚度为16%的椭圆翼型最小阻力系数没有出现在0°,而出现在7°附近.整体而言,所有翼型的阻力系数随攻角的变化趋势相同.由升阻比曲线可知,薄翼型的最大升阻比小于厚翼型,对应的临界攻角随相对厚度的增加而增加,在攻角较小时,翼型的最大升阻比随相对厚度的增加而减小,在大攻角时则相反,可以看出较厚的椭圆翼型在大攻角下的气动特性优于薄椭圆翼型.
图 3(Fig. 3)
 | 图 3 不同相对厚度下的椭圆翼型气动特性(Re=4×104)Fig.3 Aerodynamic characteristics of elliptic airfoils with different relative thickness(Re=4×104) |
图 4是5种不同相对厚度的椭圆翼型在雷诺数Re=8×104时的气动力曲线.椭圆翼型的升力系数曲线随攻角的增加均呈非线性,对比雷诺数Re=4×104时翼型的气动力曲线可知,相对厚度对翼型的阻力系数和升阻比特性影响规律差别不大,薄翼型相对厚翼型在较小攻角下的高升力趋势并不明显,当攻角较大时,翼型的升力系数也随着相对厚度的增加而增加;由此可看出雷诺数也对椭圆翼型的气动特性产生了影响.
图 4(Fig. 4)
 | 图 4 不同相对厚度下的椭圆翼型气动特性(Re=8×104)Fig.4 Aerodynamic characteristics of elliptic airfoils with different relative thickness(Re=8×104) |
图 5为相对厚度8%的椭圆翼型在低雷诺数范围内的气动力对比曲线,椭圆翼型的升力系数在攻角较小时随雷诺数的增加而增大,在攻角6° < α < 10°时,不同雷诺数下的升力系数值差别不大,翼型在雷诺数Re=2×104条件下的最大升力系数及临界攻角最大,而在其余4种雷诺数条件下,翼型的最大升力系数都出现在攻角α=8°附近.随着雷诺数的增加,椭圆翼型的阻力系数降低,而最大升阻比升高.总体而言,薄椭圆翼型在低雷诺数下虽然具有较高的最大升力系数,但其阻力系数更大,导致其最大升阻比较小.
图 5(Fig. 5)
 | 图 5 椭圆翼型在不同雷诺数下的气动特性曲线Fig.5 Aerodynamic characteristics of elliptic airfoils with different Reynolds numbers |
2.2 相对厚度对翼型流场的影响图 6为雷诺数Re=4×104时不同相对厚度的椭圆翼型在攻角为4°的时均流场图,相对厚度为6%的薄椭圆翼型前缘出现层流分离泡,而厚度较大的椭圆翼型表面则是大范围层流,对比图 7中不同相对厚度椭圆翼型在此条件下的平均升、阻力系数可以看出,翼型的升力和阻力系数随相对厚度的增加均呈非线性,这是由于薄翼型前缘分离泡的存在,变相地改变了椭圆翼型结构,使其升力系数增大.当翼型厚度增加到8%时,由于前缘分离泡消失,导致升力骤降,阻力也降低到最低值,并且随着厚度的继续增加,阻力又逐渐增大.从时均流场可看出,不同相对厚度的椭圆翼型在钝后缘产生分离涡,并且随着厚度的增加,翼型后缘上表面分离涡向上游移动,对翼型表面影响范围逐渐变大,结合图 7升力系数和阻力系数对比曲线可得,薄翼型前缘分离泡的形成和尾缘小分离涡是其在低雷诺数下具有高升力的原因.
图 6(Fig. 6)
 | 图 6 不同相对厚度椭圆翼型时均流场结构(Re=4×104)Fig.6 Time-average flow field structures of elliptic airfoil swith different relative thickness(Re=4×104) (a)—t/c=6%,前缘;(b)— t/c=6%,后缘;(c)—t/c=8%,前缘; (d)—t/c=8%,后缘; (e)—t/c=12%,后缘; (f)—t/c=16%,后缘. |
图 7(Fig. 7)
 | 图 7 不同相对厚度椭圆翼型平均升力和阻力系数Fig.7 Average lift and drag coefficients of elliptic airfoils with different relative thickness |
图 8给出了不同相对厚度的椭圆翼型在雷诺数Re=8×104、攻角为6°时上表面分离点Xs、再附点位置Xp以及层流分离泡的相对长度(|Xp-Xs|),薄翼型在前缘出现层流分离泡,相对厚度为4%椭圆翼型的前缘分离泡最长,再附点距离前缘约为弦长的34.7%,长度为34.1%c,随着厚度的增加,分离泡的分离点略微后移,再附点位置前移,长度逐渐变短,当厚度增加到10%时,分离泡长度最短,约为12%c,厚度进一步增加时,分离点保持在前缘基本不动,再附点位置后移,长度增加,而当厚度增加到16%时,椭圆翼型在后缘发生流动分离.
图 8(Fig. 8)
 | 图 8 不同相对厚度椭圆翼型时均化分离点和再附点位置Fig.8 Positions of time-average separation points and reattachment points of elliptic airfoils with different relative thickness |
如图 9所示,不同相对厚度的椭圆翼型在雷诺数Re=8×104、攻角为6°条件下的时均流场存在显著差异,薄椭圆翼型在前缘发生了流动分离、再附现象,当厚度增加时,时均分离泡虽然在长度上先缩短再变长,但在高度上逐渐变薄,直至消失,在厚度增加到16%时,前缘层流分离泡消失,在后缘形成了时均小分离泡,从时均流场中也可看出,在椭圆翼型后缘上下表面存在两个大小不等的分离涡,翼型较薄时,后缘表面分离出的两个分离涡大小相似,随着厚度的增加,上表面分离涡分离点前移,向翼型的上游移动,分离区变大,影响范围增加,而下表面分离涡虽然对翼型后缘的影响同样增加,但分离涡先减小再增大,并且逐渐远离翼型后缘,当前缘不发生流动分离、再附时,在后缘分离出时均小泡,同时后缘下表面分离涡增大.前缘的流动分离导致了翼型后缘表面两个分离涡的分离状态发生了很大的改变.可见,椭圆翼型相对厚度影响了前缘分离泡的形态,进而影响了后缘分离涡的大小和位置,改变了翼型的流场结构,使翼型的气动性能大不相同.
图 9(Fig. 9)
 | 图 9 不同相对厚度椭圆翼型时均流场结构(Re=8×104)Fig.9 Time-average flow field structures of elliptic airfoils with different relative thickness (Re=8×104) (a)—t/c=6%,前缘;(b)—t/c=6%,后缘;(c)— t/c=8%,前缘; (d)— t/c=8%,后缘;(e)—t/c=14%,前缘;(f)— t/c=14%,后缘; (g)— t/c=16%,前缘;(h)—t/c=16%,后缘;(i)— t/c=18%,前缘; (j)—t/c=18%,后缘. |
2.3 雷诺数对翼型流场的影响下面分析雷诺数对层流分离现象的影响,图 10为相对厚度为8%的椭圆翼型在攻角为4°时不同雷诺数下的时均流场对比,可以看出在较低雷诺数下,翼型前缘在小攻角下没有发生流动分离,后缘上表面分离涡的分离点随雷诺数的增加而前移,分离区变大,当雷诺数增加到6×104时,椭圆翼型上表面出现前缘层流分离泡,并且随着雷诺数增加,时均分离泡长度缩短,但高度基本保持不变,而翼型后缘流场结构与没有形成前缘分离泡的翼型后缘不同,前缘形成分离泡的翼型在后缘分离出两个大小基本相等的小分离涡,影响范围减小,对比图 11中不同雷诺数下的升、阻力系数可知,从雷诺数4×104增加到6×104时,升力系数突增的原因是椭圆翼型上表面层流分离泡的出现以及后缘分离涡影响范围的减小.
图 10(Fig. 10)
 | 图 10 不同雷诺数下时均流场结构(t/c=8%)Fig.10 Time-average flow field structures at different Reynolds numbers(t/c=8%) (a)—Re=2×104,前缘;(b)—Re=2×104,后缘;(c)— Re=4×104,前缘; (d)— Re=4×104,后缘;(e)—Re=6×104,前缘;(f)— Re=6×104,后缘; (g)— Re=8×104,前缘;(h)—Re=8×104,后缘;(i)— Re=1×105,前缘; (j)—Re=1×105,后缘. |
图 11(Fig. 11)
 | 图 11 不同雷诺数下平均升力和阻力系数Fig.11 Average lift and drag coefficients at different Reynolds numbers |
在攻角为6°时,相对厚度为8%的椭圆翼型在不同雷诺数下的平均压力系数(Cp)曲线如图 12所示,翼型上表面存在明显的压力梯度,下表面压力系数分布基本相同,可见层流分离泡主要出现在上表面前缘,雷诺数主要影响椭圆翼型上表面的气流流动,随着雷诺数的增加,翼型上表面前缘分离点位置几乎不变,再附点位置前移,层流分离泡长度减小,雷诺数从2×104增加到4×104,翼型再附点前移量最大,由距离前缘29.7%前移到18%,层流分离泡长度从38%c缩短到17.2%c,随着雷诺数的增加,黏性效应减弱,翼型上表面的逆压梯度减弱,层流分离泡逐渐消失.
图 12(Fig. 12)
 | 图 12 不同雷诺数下平均压力系数分布Fig.12 Average pressure coefficient distributions at different Reynolds numbers |
3 结论1) 采用Transition SST湍流模型可以精确模拟出椭圆翼型的非常规气动力特性,准确地捕捉到了椭圆翼型在低雷诺数下的层流分离现象,与实验结果对比,验证了数值模拟方法的准确性.
2) 通过比较5种不同相对厚度的椭圆翼型的气动力可知,薄椭圆翼型在低雷诺数、小攻角下有高的升力系数和升阻比;而厚椭圆翼型在大攻角下具有较高的最大升力系数和最大升阻比;相对厚度相同时,翼型的升阻比随雷诺数的增加而增大.
3) 在低雷诺数、小攻角条件下,相对厚度较小的椭圆翼型在上表面前缘形成了时均分离泡,时均分离泡的出现,改变了翼型的气动特性;在较大攻角下,随着翼型相对厚度的增加,层流分离泡变得扁平直至消失,当相对厚度达到16%时,时均分离泡由前缘分离泡转变为后缘分离泡,同时椭圆翼型后缘大小几乎相等的分离涡影响范围增加,上表面后缘分离涡分离点随厚度的增加而前移,下表面分离涡逐渐远离后缘.
4) 对比不同雷诺数下椭圆翼型的时均流场可知,在攻角较小时,较高雷诺数出现了时均分离泡,同时椭圆翼型后缘上表面由影响范围较大的分离涡转变为与下表面分离涡大小相似的小分离涡,导致升力突增;在攻角较大时,时均分离泡在不同雷诺数下均出现在椭圆翼型的前缘,并且随雷诺数的增加而缩小;上表面尾缘分离涡随雷诺数的增加而靠近后缘,下表面分离涡位置、大小基本不变.
参考文献
| [1] | Horton H P. Laminar separation bubbles in two and three dimensional incompressible flow[D]. London: University of London, 1968. |
| [2] | Selig M, Guglielmo J, Broern A. Experiments on airfoils at low Reynolds numbers[C]//The 34th Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1996: 1-8. |
| [3] | 白鹏, 崔尔杰, 李锋, 等. 对称翼型低雷诺数小攻角升力系数非线性现象研究[J]. 力学学报, 2006, 38(1): 1-8. (Bai Peng, Cui Er-jie, Li Feng, et al. Study of the non-linear lift coefficient of the symmetric airfoil at low Reynolds number near the 0° angle of attack[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 1-8.) |
| [4] | Kojima R, Nonomura R, Oyama A, et al. Large-eddy simulation of low Reynolds number flow over thick and thin NACA airfoils[J]. Journal of Aircraft, 2013, 50(1): 187-196. DOI:10.2514/1.C031849 |
| [5] | Ma D, Zhao Y, Qiao Y, et al. Effects of relative thickness on aerodynamic characteristics of airfoil at a low Reynolds number[J]. Chinese Journal of Aeronautics, 2015, 28(4): 1003-1015. DOI:10.1016/j.cja.2015.05.012 |
| [6] | 朱志斌, 尚庆, 白鹏, 等. 翼型低雷诺数层流分离现象随雷诺数的演化特征[J]. 航空学报, 2019, 40(5): 57-67. (Zhu Zhi-bin, Shang Qing, Bai Peng, et al. Evolution of laminar separation phenomenon on low Reynolds number airfoil at different Reynolds numbers[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(5): 57-67.) |
| [7] | Kwon K, Park S O. Aerodynamic characteristics of an elliptic airfoil at low Reynolds number[J]. Journal of Aircraft, 2005, 42(6): 1642-1644. DOI:10.2514/1.16740 |
| [8] | Assel T W. Computational study of flow over elliptic airfoils for rotor/wing unmanned aerial vehicle applications[D]. Columbia: University of Missouri-Rolla, 2007. |
| [9] | Chitta V, Walters D K. Prediction of aerodynamic characteristics of an elliptic airfoil at low Reynolds number[C]// Proceedings of the ASME 2012 Fluids Engineering Summer Meeting. New York: AMSE, 2012: 1297-1308. |
| [10] | Sun W, Gao Z H, Du Y M, et al. Mechanism of unconventional aerodynamic characteristics of an elliptic airfoil[J]. Chinese Journal of Aeronautics, 2015, 28(3): 687-694. DOI:10.1016/j.cja.2015.03.009 |
| [11] | Langtry R B, Menter F R. Transition modeling for general CFD applications in aeronautics[C]//The 43rd AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2005: 1131-1134. |
| [12] | Langtry R B, Menter F R, Likki S R, et al. A correlation based transition model using local variables.Part Ⅱ: test cases and industrial applications[J]. Journal of Turbomachinery, 2006, 128(3): 413-422. DOI:10.1115/1.2184352 |
| [13] | Langtry R B, Menter F R, Likki S R, et al. A correlation-based transition model using local variables.Part I: model formulation[J]. Journal of Turbomachiner, 2006, 128(3): 57-67. |
| [14] | Menter F R. Two-equation eddy viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
