付亚平^1,2, 闻妲^1,2, 王巧云^1,2
1. 东北大学 信息科学与工程学院，辽宁 沈阳 110819;
2. 微纳精密光学传感与检测技术河北省重点实验室，河北 秦皇岛 066400
收稿日期：2021-10-29
基金项目：国家自然科学基金青年项目(61601104)；河北省自然科学基金资助项目(F2019501025, F2020501040，F2017501052)；中央高校基本科研业务费专项资金资助项目(N172304032, 2020GFYD026)。
作者简介：付亚平(1995-)，女，河北石家庄人，东北大学硕士研究生;
王巧云(1980-)，女，河北秦皇岛人，东北大学副教授，硕士生导师。

摘要：针对光纤Fabry-Perot(F-P)传感器的解调，提出一种基于快速傅里叶变换与余弦相似度(FFT-COSS)的腔长解调算法.首先利用快速傅里叶变换确定腔长的粗测值，然后结合余弦相似度算法求取精确腔长值，作为F-P腔的最终解调结果.仿真结果表明，FFT-COSS算法将解调误差控制在±0.2 nm, 单次解调的平均时间控制在1 s.将该算法应用于石墨烯与聚甲基丙烯酸甲酯(PMMA)混合膜制作的薄膜式F-P传感器微压测试系统.实验结果表明，FFT-COSS算法的拟合度达到0.990 8，腔长分辨率优于0.621 8 nm，单次解调的平均时间控制在1 s，与仿真结果相符.
关键词：光纤F-P传感器薄膜式传感器快速傅里叶变换余弦相似度腔长解调
A Demodulation Algorithm for Fiber-Optic F-P Sensor Based on Fast Fourier Transform and Cosine Similarity
FU Ya-ping^1,2, WEN Da^1,2, WANG Qiao-yun^1,2
1. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China;
2. Hebei Key Laboratory of Micro-Nano Precision Optical Sensing and Measurement Technology, Qinhuangdao 066004, China
Corresponding author: FU Ya-ping, E-mail: 905251154@qq.com.

Abstract: Aiming at the demodulation of the Fabry-Perot(F-P)sensor, a cavity length demodulation algorithm based on fast Fourier transform and cosine similarity(FFT-COSS)is proposed. Firstly, the fast Fourier transform is used to determine the rough measurement value of the cavity length, and then the exact cavity length value is obtained in combination with the cosine similarity algorithm as the final demodulation result of the F-P cavity. Simulation results show that the FFT-COSS algorithm controls the demodulation error to ±0.2 nm and the average time of a single demodulation to 1 s. The algorithm is applied to a thin-diaphragm F-P sensor micro-pressure test system made of a mixed graphene diaphragm and polymethyl methacrylate(PMMA). Experimental results show that the fitted R-squared of the FFT-COSS algorithm reaches 0.990 8 and the cavity length resolution is better than 0.621 8 nm.The average time of a single demodulation is controlled at 1 s, which agrees with the simulation results.
Key words: fiber-optic F-P sensorthin film sensorfast Fourier transformcosine similaritycavity length demodulation
光纤Fabry-Perot(F-P)传感器具有体积小、精度高、测量范围广、抗电磁干扰能力强等优势，已广泛应用于工业、军事、航天等诸多领域^[1-2].因F-P传感器的腔长敏感特性，温度、应力和应变等外界参量的变化^[3-4]都会引起F-P传感器腔长发生变化，可以通过腔长改变来检测外界物理量变化，因此对F-P腔解调研究很有必要.
现有的解调方法分为强度解调法和相位解调法两大类.在强度解调法中一般使用单色激光光源，利用输出光谱信号的线性区域进行解调^[5].该方法原理简单、成本低，但腔长解调精度不高、解调范围有限.在相位解调法中采用宽谱光源，通过采集的输出光谱信号来进行腔长解调^[6].常用的相位解调法有条纹计数法、相关解调法、最小二乘法、快速傅里叶变换法(fast Fourier transform, FFT)等.条纹计数法通过跟踪波峰对应的波长信息来实现腔长解调，解调速度快，可以实现腔长的绝对测量，但解调的精度仅为微米级别.相关解调法通过模拟不同腔长下的输出光谱信号与光谱仪上采集到的原始输出光谱信号做相关运算解调出腔长，该方法原理简单，但算法运算量较大，且分辨率和精度不高的缺点限制了其广泛应用^[7].刘嘉静等利用最小二乘法进行腔长解调，解调误差为±2.5 nm^[8].FFT算法将光谱信号从波长域转化到频率域，通过提取光谱信号的频率，解调出腔长，该方法解调速度快，但解调的准确度不高.雷小华等提出了基于三次样条差的快速傅里叶变换解调法，解决了光波长域转化到光频率域采样不均匀的问题，将解调误差成功控制在0.06 μm以内^[9].Zhou等提出了快速傅里叶变换-最小均方差的联合算法(fast Fourier transform and minimum mean square error, FFT-MMSE), 实现了大的动态腔长测量范围^[10].尹嘉笛等针对FFT-MMSE联合算法提出了一种Fibonacci的搜索方法来减小计算量，实现了2.5 mm的大动态范围解调^[11].冯嘉双等提出了幅值归一化-最小均方差的解调算法(normalization-minimum mean square error, N-MMSE)，相比于传统方法而言，提高了解调精度，实现了0.72 nm的高分辨率测量^[12].
为了实现对F-P传感器的多样化解调，本文提出了一种基于快速傅里叶变换-余弦相似度的新型联合解调算法(fast Fourier transform-cosine similarity, FFT-COSS)，解决了原始FFT算法解调精度不高的问题.通过FFT算法获得腔长的粗测值，然后利用COSS算法求精确腔长，算法原理简单，易于实现.
1 光纤F-P传感器原理光纤F-P传感器的典型结构如图 1所示，将单模光纤插入毛细玻璃管中，并用环氧树脂胶固定，单模光纤端面与薄膜端面共同构成F-P腔，腔长记为L_FP.当宽谱光源(ASE light)由单模光纤传入F-P腔时，会在两个端面发生透射和反射，最终会在F-P腔表面形成多束透射光和反射光.反射光与透射光具有相同的振动频率和振动方向，满足干涉条件，从而产生多光束干涉现象^[13-14]，根据多光束干涉原理，反射光干涉光谱信号为

(1)

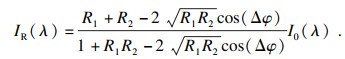图 1(Fig. 1)

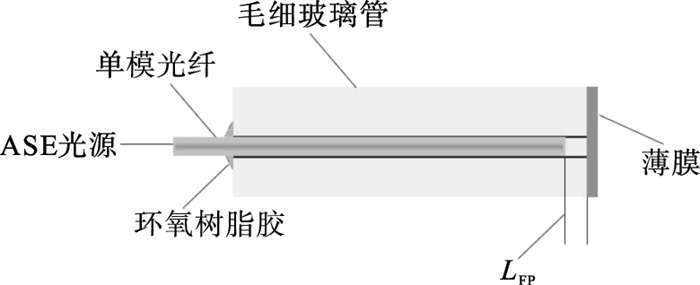图 1 F-P腔的典型结构及干涉原理Fig.1 Typical structure and interference principle of F-P cavity

透射光干涉光谱为

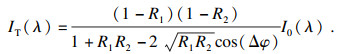(2)

由于单模光纤端面的反射率较低，可将F-P腔内的干涉近似为双光束干涉，式(1)可简化为

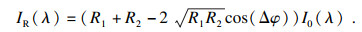(3)

式中：I₀(λ)表示入射光光强，幅值为1;R₁, R₂分别表示构成F-P腔的两个端面的反射率, 其中相邻光束之间的相位差表示为

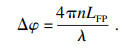(4)

式中：L_FP表示传感器的腔长; n表示F-P腔内介质的折射率(空气腔内的折射率为1);λ表示入射光的波长.当F-P传感器受到温度或应力等外界环境影响时，其腔长L_FP会发生改变，进而导致相位差Δφ发生变化，I_R(λ)也会随之发生变化.通过对I_R(λ)进行解调可得到腔长L_FP的变化量，从而得到外部参量的变化.
2 解调算法原理为实现F-P腔的多样化解调，本文提出了一种基于快速傅里叶变换和余弦相似度的腔长解调算法(FFT-COSS)，首先将从光谱仪上采集到的1×n维光谱信号I_R(λ)通过快速傅里叶变换获得腔长的粗测值，然后利用余弦相似度算法获得腔长的精确值.FFT-COSS算法的具体过程：
1) 对光谱仪上采集到的光谱信号进行预处理并通过快速傅里叶变化确定腔长粗测值L′_FP；
2) 在粗测值附近确定合适的搜索范围(L′_FP-d~L′_FP+d)，设定合适的搜索间隔Δd，生成一系列的模拟光谱信号I₁, I₂, …, I_i, …, I_2d/Δd；
3) 将模拟光谱信号I_i与真实光谱信号I_R进行余弦相似度计算得到COSS(L_i)，并初始记录i=1时所对应的COSS(L₁)为最大余弦相似度值Max(COSS)；
4) 将COSS(L_i)同Max(COSS)进行比较，若COSS(L_i)>Max(COSS)，则将COSS(L_i)更新为最大余弦相似度值，反之，最大余弦相似度值不变；
5) 判断当前模拟序列号i是否小于等于2d/Δd，若没有超出范围，则进入新的一轮循环，若超出范围，则输出最终Max(COSS)所对应的腔长为准确腔长L_i值.
算法流程图如图 2所示.
图 2(Fig. 2)

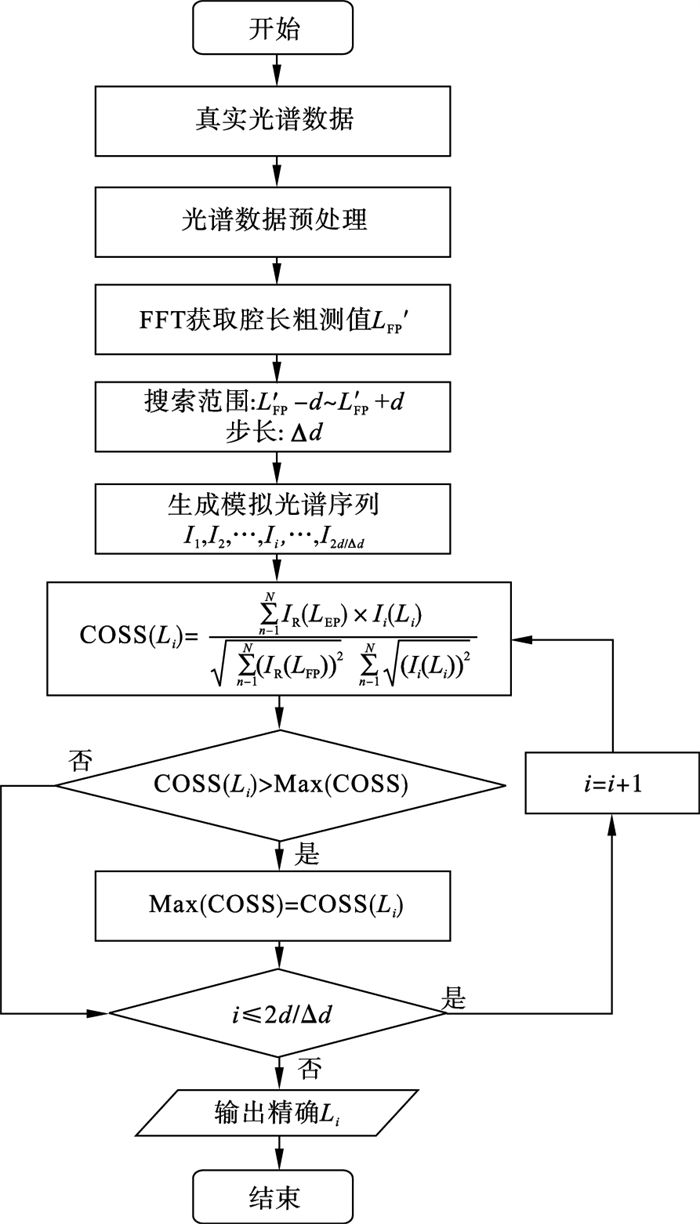图 2 FFT-COSS算法流程图Fig.2 FFT-COSS algorithm flowchart

2.1 快速傅里叶变换原理将波长域的光谱信号转化到波数域，并通过三次样条差进行等间隔采样，使其满足均匀采样.式(3)可表示为

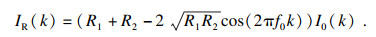(5)

式中: k表示波数，为波长λ的倒数; f₀为光谱信号的采样频率.此时F-P传感器腔长为

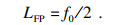(6)

假设I₀(k)为线性光源，对式(5)进行快速傅里叶变换：

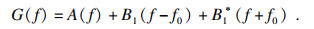(7)

通过FFT算法即可求得F-P传感器的腔长.该方法抗干扰性强，解调速度快，能够实现大范围的绝对腔长测量.但FFT算法得到的腔长精度较低，记为粗测值L′_FP, 还需进一步辅助其他算法对精确腔长进行求解.
2.2 余弦相似度算法原理余弦相似度，也称余弦相似性，是通过计算向量空间中两个向量夹角的余弦值来评估二者的相似度，二者余弦值越接近于1，说明两个向量越相似.COSS算法属于腔长匹配算法，其主要流程为：首先确定合适的腔长搜索范围L_start=L′_FP-d, L_end=L′_FP+d和搜索步长Δd，得到模拟腔长L₁, …, L_i-1, L_i, L_i+1, …, L_2d/Δd；并生成一系列模拟光谱信号I_i(L_i)，最后将获得的模拟光谱信号与实际光谱信号进行余弦相似度计算，得到与腔长相对应的余弦值COSS(L_i)，选取最大余弦相似度值Max[COSS(L_i)]所对应的腔长为腔长精确值.COSS(L_i)是衡量模拟腔长L_i与真实腔长L_FP趋紧程度的参数，取值越接近于1，代表模拟腔长L_i越趋近于真实腔长L_FP的值，表示为

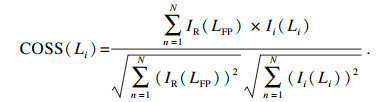(8)

式中: I_R(L_FP)表示真实的光谱信号; I_i(L_i)表示模拟的光谱信号; N表示光谱信号的采样点.
3 FFT-COSS算法仿真分析为验证FFT-COSS算法在F-P传感器解调中的可行性与准确性，首先进行了仿真实验.根据F-P腔的反射原理，利用式(3)模拟反射光谱信号, 为更加接近真实光谱信号，在仿真过程中加入噪声，不同的噪声类别会对光谱信号产生不同的干扰，根据ASE宽谱光源的特点选定高斯噪声.设置反射率R为0.04，波长λ范围为1 520~1 570 nm，采样点N为2 048，得到的仿真结果如图 3所示.
图 3(Fig. 3)

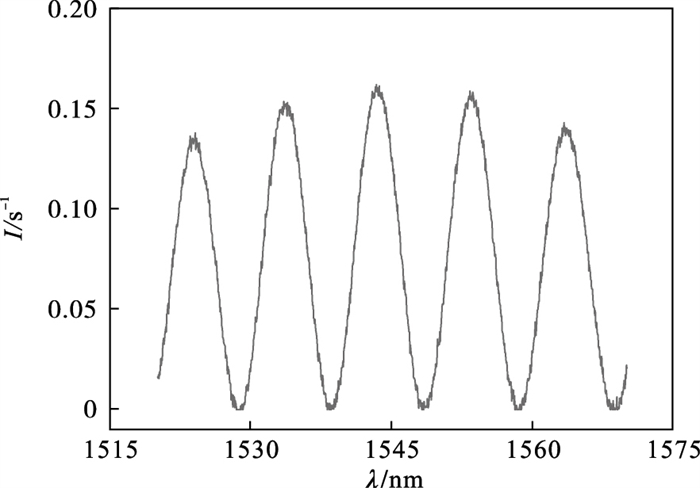图 3 F-P的干涉光谱输出Fig.3 F-P interference spectrum output

对模拟光谱信号进行去噪处理.常见的去噪方法有巴特沃斯低通滤波器算法、中值滤波算法、均值滤波算法、维纳滤波算法、小波变换算法、傅里叶变换算法等，去噪的结果如图 4所示.由对比结果可以看出来，巴特沃斯低通滤波器算法和均值滤波算法会使光谱发生一定量的偏移，而中值滤波算法、维纳滤波算法和小波变换算法不能很好去除光谱的尖峰和毛刺，傅里叶变换算法既去除了尖峰、毛刺, 又保证光谱不发生偏移，因此选择傅里叶变换算法对光谱进行去噪.
图 4(Fig. 4)

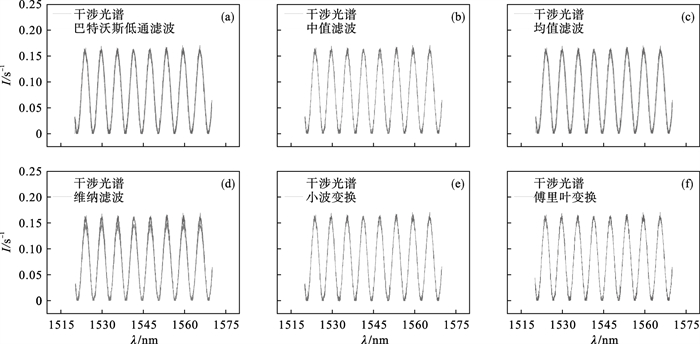图 4 F-P干涉光谱的不同去噪方法对比结果Fig.4 Comparison results of different denoising methods for F-P interference spectrum (a)—巴特沃斯低通滤波算法；(b)—中值滤波算法；(c)—均值滤波算法; (d)—维纳滤波算法; (e)—小波变换算法；(f)—傅里叶变换算法.

如图 5所示，当腔长从100 μm以5 μm为步长均匀增大至200 μm时，FFT-COSS算法的腔长误差L_e最大值为0.209 0 nm，标准误差SD为0.103 877 nm，解调的平均时间为0.949 281 s.FFT-MMSE算法的腔长误差L_e最大值为0.236 8 nm，标准误差SD为0.169 884 nm，解调的平均时间为4.242 038 s.由对比结果可知，FFT-COSS算法不仅在解调结果上优于FFT-MMSE算法，且在解调时间方面比FFT-MMSE算法也缩短了近4倍.经过仿真分析可知FFT-COSS算法可以实现F-P腔的高精度快速解调.
图 5(Fig. 5)

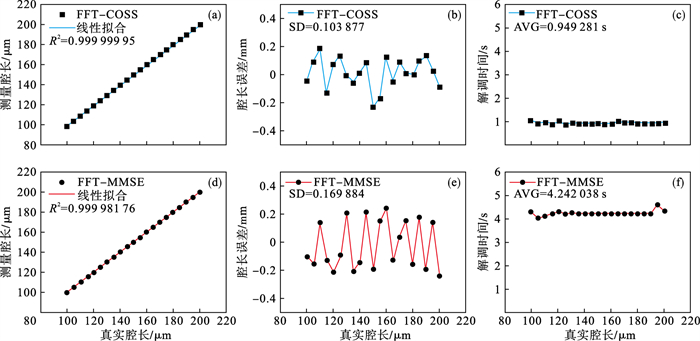图 5 FFT-COSS与FFT-MMSE算法仿真对比结果Fig.5 FFT-COSS algorithm and FFT-MMSE algorithm simulation comparison results (a)—FFT-COSS算法拟合度仿真；(b)—FFT-COSS算法标准误差仿真；(c)—FFT-COSS算法解调时间仿真; (d)—FFT-MMSE算法拟合度仿真; (e)—FFT-MMSE算法标准误差仿真；(f)—FFT-MMSE算法解调时间仿真.

4 FFT-COSS算法可行性验证为验证FFT-COSS算法的性能，利用石墨烯与PMMA混合膜制作了膜片式光纤F-P传感器并进行了微压测试，系统结构如图 6所示.系统由ASE宽谱光源，光纤环形器，膜片式光纤F-P传感器探头和光谱仪等几部分组成.实验中设置光源的波长范围是1 530~1 570 nm，光谱仪的采样点N为2 048，水的深度变化范围是0~17 cm，经过液体压强计算公式得到压强的相对变化范围为0~1 666 Pa.首先光源经过光纤环形器到达F-P传感器，将F-P传感器放置在装满水的量筒的水面位置，初始位置为量筒中的水面位置，对此时的干涉光谱信号进行采集，记录此时的腔长为初始腔长.随后传感器开始没入水中，每次没入水中的深度变化均为1.7 cm，根据计算得出，每次压强增加166.6 Pa，随着传感器没入水面的深度增加，光谱仪接收到的干涉光谱信号也将发生变化.待水面稳定后采集光谱信号，并上传至计算机利用算法进行解调.
图 6(Fig. 6)

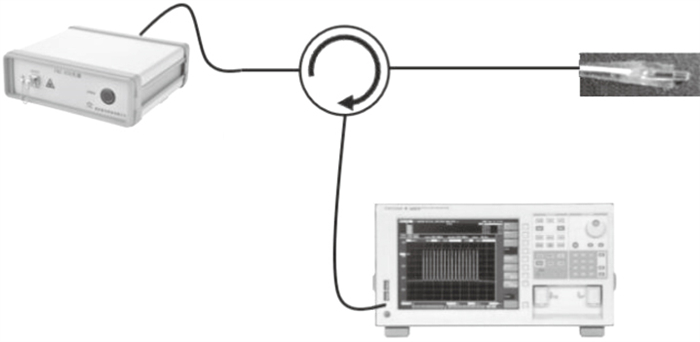图 6 薄膜式F-P传感器腔长解调系统Fig.6 The cavity length demodulation system of diaphragm F-P sensor

由于受到压力的作用导致膜片发生形变，F-P传感器的腔长随之发生改变，进而导致干涉光谱信号变化，如图 7a所示，当压强增大时，腔长减小，实际的光谱信号是向着波长减小的方向漂移.且由于受到光源的非理想化以及反射面的不平整性，光在光纤传输中的损耗等因素的影响，实际所接收到的反射信号呈现出明显的尖峰、毛刺，需要对接收到的光谱信号进行预处理，去噪的结果如图 7b所示，从结果可以看出，去除了大部分的尖峰、毛刺.
图 7(Fig. 7)

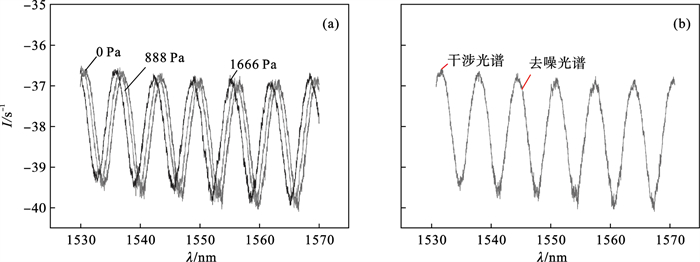图 7 F-P传感器真实光谱及去噪结果Fig.7 F-P sensor true spectrum and denoising result (a)—压强对干涉光谱的影响；(b)—干涉光谱的去噪对比图.

随着F-P传感器没入水中的深度变化，F-P传感器所受的压强发生变化，腔长随之发生改变.分别采用FFT-COSS算法和FFT-MMSE算法进行解调，解调结果如图 8所示，通过FFT-COSS算法计算腔长得到的算法拟合度为0.990 795 81，FFT-MMSE算法拟合度为0.989 033 16.由算法拟合度R²的结果可以看出，FFT-COSS算法的拟合度优于FFT-MMSE算法的拟合度.由于传感器进入水下的深度是通过人眼进行观测的，会产生读数误差，以及在实验时水下温度的变化，均会对实验结果产生一定影响，因此实验结果所得到的拟合度R²与仿真结果有一定差别.
图 8(Fig. 8)

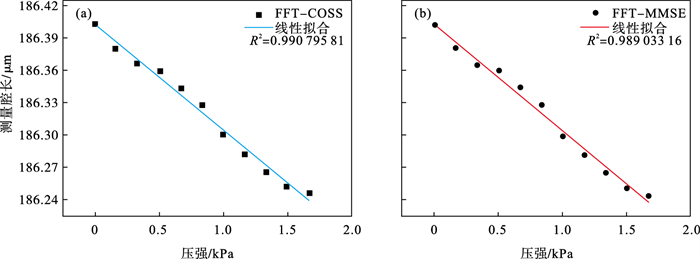图 8 FFT-COSS与FFT-MMSE算法腔长测量实验对比结果Fig.8 FFT-COSS algorithm and FFT-MMSE algorithm cavity length measurement experiment comparison results (a)—FFT-COSS算法拟合度；(b)—FFT-MMSE算法拟合度.

在标准大气压下进行腔长分辨率测量实验，结果如图 9所示，FFT-COSS算法的平均腔长值186.204 505 6 μm, 腔长的标准差为0.310 903 52 nm，FFT-MMSE算法的平均腔长值为186.402 474 6 μm，腔长的标准差为0.330 006 06 nm.记腔长分辨率RSE为腔长标准差的2倍，得到FFT-COSS算法和FFT-MMSE算法的腔长分辨率分别为0.621 807 04和0.660 012 12 nm，可以看出FFT-COSS算法的腔长分辨率优于FFT-MMSE算法的腔长分辨率.
图 9(Fig. 9)

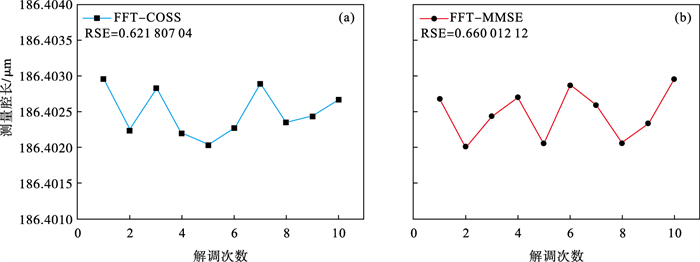图 9 FFT-COSS与FFT-MMSE算法分辨率对比结果Fig.9 FFT-COSS algorithm and FFT-MMSE algorithm resolution comparison results (a)—FFT-COSS算法；(b)—FFT-MMSE算法.

选取110组数据的解调时间，对算法的解调时间进行对比，如图 10所示，FFT-COSS算法的平均解调时间为0.951 598 s, FFT-MMSE算法的平均解调时间为3.893 438 s，FFT-COSS算法比FFT-MMSE算法缩短了近3倍，与仿真时间相符.因此通过FFT-COSS算法与FFT-MMSE算法对比实验可以证明，基于快速傅里叶变换-余弦相似度的光纤F-P传感器解调算法可应用于光纤F-P传感器的腔长解调中，具有解调精度高、速度快的优势.
图 10(Fig. 10)

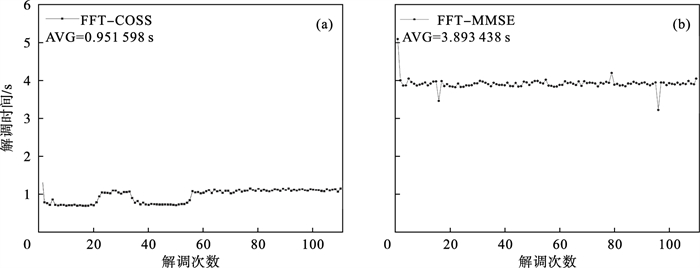图 10 FFT-COSS与FFT-MMSE算法解调时间对比结果Fig.10 FFT-COSS algorithm and FFT-MMSE algorithm demodulation time comparison results (a)—FFT-COSS算法；(b)—FFT-MMSE算法.

5 结语本文提出基于快速傅里叶变换-余弦相似度的光纤F-P传感器解调算法，首次将余弦相似度算法(COSS)应用于F-P传感器的腔长解调中.首先通过快速傅里叶变换确定腔长的粗测值和腔长范围，并构建一系列模拟光谱信号.然后通过COSS算法计算模拟干涉光谱信号与实际干涉光谱信号的余弦相似度值来求取腔长的精确值，实现F-P传感器的腔长解调.仿真和实验结果证明，FFT-COSS算法相比于应用广泛的FFT-MMSE解调算法，解调精度和分辨率优于FFT-MMSE算法，且解调时间比FFT-MMSE算法缩短了近3倍，可以应用于F-P传感器的高精度快速解调.
参考文献

[1]	Wei H, Krishnaswamy S. Adaptive fiber-ring lasers based on an optical fiber Fabry-Perot cavity for high-frequency dynamic strain sensing[J]. Applied Optics, 2020, 59(2): 530-535. DOI:10.1364/AO.377368
[2]	Yang Y Q, Wang Y G, Zhao Y X, et al. Sensitivity-enhanced temperature sensor by hybrid cascaded configuration of a Sagnac loop and a FP cavity[J]. Optics Express, 2017, 25(26): 33290-33296. DOI:10.1364/OE.25.033290
[3]	Chen K, Yang B L, Deng H, et al. Simultaneous measurement of acoustic pressure and temperature using a Fabry-Perot interferometric fiber-optic cantilever sensor[J]. Optics Express, 2020, 28(10): 15050-15061. DOI:10.1364/OE.387195
[4]	Li H, Zhao Q C, Jing S D, et al. FP cavity and FBG cascaded optical fiber temperature and pressure sensor[J]. Chinese Optics Letters, 2019, 17(4): 040603. DOI:10.3788/COL201917.040603
[5]	Chen K, Yu Z H, Yu Q Y, et al. Fast demodulated white-light interferometry-based fiber-optic Fabry-Perot cantilever microphone[J]. Optics Letters, 2018, 43(14): 3417-3420. DOI:10.1364/OL.43.003417
[6]	Liao H, Lu P, Liu L, et al. Phase demodulation of short-cavity Fabry-Perot interferometric acoustic sensors with two wavelengths[J]. IEEE Photonics Journal, 2017, 9(2): 1-9.
[7]	Cui J W, Niu Y Z, Dang H, et al. Demodulation method of F-P sensor based on wavelet transform and polarization low coherence interferometry[J]. Sensors, 2020, 20(15): 4249-4266. DOI:10.3390/s20154249
[8]	刘嘉静, 涂子维, 周次明, 等. 基于最小二乘法的光纤法布里-珀罗传感器相位校正解调算法[J]. 光子学报, 2019, 48(9): 81-96. (Liu Jia-jing, Tu Zi-wei, Zhou Ci-ming, et al. Algorithm of phase correction on least square estimation for optic fiber Fabry-Perot sensor[J]. Acta Photonica Sinica, 2019, 48(9): 81-96.)
[9]	雷小华, 陈伟民, 章鹏, 等. 基于三次样条插值的光纤F-P传感器傅里叶变换解调研究[J]. 光子学报, 2008, 37(4): 705-708. (Lei Xiao-hua, Chen Wei-min, Zhang Peng, et al. Demodulation method based on Fourier transform with cubic spline interpolation for optical fiber Fabry-Perot sensors[J]. Acta Photonica Sinica, 2008, 37(4): 705-708.)
[10]	Zhou X L, Yu Q X. Wide-range displacement sensor based on fiber-optic Fabry-Perot interferometer for subnanometer measurement[J]. IEEE Sensors Journal, 2010, 11(7): 1602-1606.
[11]	尹嘉笛, 周次明, 欧艺文, 等. 光纤Fabry-Perot传感器的Fibonacci-MMSE联合解调算法[J]. 光子学报, 2015, 44(9): 168-173. (Yin Jia-di, Zhou Ci-ming, Ou Yi-wen, et al. Combined algorithm of Fibonacci-MMSE for optical fiber Fabry-Perot sensor[J]. Acta Photonica Sinica, 2015, 44(9): 168-173.)
[12]	冯嘉双, 王伟, 张雄星, 等. 光纤法布里-珀罗传感器幅值归一化-最小均方差联合解调算法[J]. 光子学报, 2020, 49(9): 99-106. (Feng Jia-shuang, Wang Wei, Zhang Xiong-xing, et al. Combined interrogation algorithm of amplitude normalization and minimum mean square error for fiber-optic Fabry-Perot sensors[J]. Acta Photonica Sinica, 2020, 49(9): 99-106.)
[13]	Cui Q S, Thakur P, Rablau C, et al. Miniature optical fiber pressure sensor with exfoliated graphene diaphragm[J]. IEEE Sensors Journal, 2019, 19(14): 5621-5631. DOI:10.1109/JSEN.2019.2904020
[14]	Liu Q, Jing Z G, Liu Y Y, et al. Absolute measurement of dynamic low-finesse Fabry-Perot cavity using phase-shifting white-light interferometry[J]. Journal of Lightwave Technology, 2021, 39(12): 3926-3931. DOI:10.1109/JLT.2020.3036407