刘芳¹, 刘彦鹏¹, 李静东¹, 卜凡涛²
1. 天津工业大学 天津市自主智能技术与系统重点实验室，天津 300387;
2. 东软睿驰汽车技术(沈阳)有限公司，辽宁 沈阳 110179
收稿日期：2021-09-08
基金项目：国家重点研发计划项目(2021YFB2501800)；国家自然科学基金资助项目(61802280, 61806143, 61772365, 41772123)；天津市技术创新引导专项(基金)(21YDTPJC00130)。
作者简介：刘芳(1983-)，女，辽宁沈阳人，天津工业大学副教授。

摘要：针对电动汽车无规则随机充放电特点及在线检测需求，考虑到由于电池一致性问题导致难以保证离线实验数据分析法估计精度的问题，提出一种以离线获取的电池健康状态(SOH)外在指征函数为基础的基于无迹卡尔曼滤波(unscented Kalman filter, UKF)思想的在线闭环校正SOH估算架构.该方法优点在于：能够在随机放电过程中快速估算出高精度的SOH值，算法复杂度相对降低，易于实际工程实现且具有较好的鲁棒性.通过验证可以证明, 提出的车载动力电池放电过程SOH估算方法具有较好的实用性及较高的估算精度.
关键词：健康状态无迹卡尔曼滤波自回归模型电动汽车锂离子电池
Online Estimation of State of Health During Discharging of Vehicle Power Battery
LIU Fang¹, LIU Yan-peng¹, LI Jing-dong¹, BU Fan-tao²
1. Tianjin Key Laboratory of Autonomous Intelligence Technology and Systems, Tiangong University, Tianjin 300387, China;
2. Neusoft Reach Automotive Technology, Co., Ltd, Shenyang 110179, China
Corresponding author: LI Jing-dong, E-mail: lijingdong@tiangong.edu.cn.

Abstract: According to the characteristics of irregular random charge and discharge of electric vehicles and the requirements of on-line detection, it is difficult to ensure the accuracy of off-line experimental data analysis methods due to battery consistency problems. In this paper, an on-line closed-loop correction SOH (state of health) estimation architecture based on the idea of unscented Kalman filter(UKF)is proposed, which is based on the off-line SOH external indicator function. The advantage of this method is that it can quickly estimate the high-precision SOH value in the random discharge process and the algorithm complexity is relatively reduced. It is easy to implement in practical engineering and the proposed method has better robustness. Through verification, it can be proved that the SOH estimation method proposed in this paper has better practicability and higher estimation accuracy.
Key words: state of health (SOH)unscented Kalman filterauto regression modelelectric vehiclelithium ion battery
锂离子电池因其具有高密度、长寿命以及低成本等特点得到了广泛的应用^[1].但在使用过程中由于电化学成分的降解，其性能会随时间和使用而退化^[2].因此锂离子电池的健康状态(SOH)在线、精准鲁棒估算对于车载动力电池系统乃至整车系统的安全有效运行和精准管控至关重要.
近年来，随着锂离子电池应用领域的不断扩展，各种SOH估计方法也得到了快速发展.其估算思想大致如下：从SOH的定义出发，通过小电流平稳充/放电的满充满放方式实现SOH的测量，其优点在于简单、直观.但就电动汽车领域而言，其相对苛刻的测量条件难以得到满足.从可获得数据出发，以神经网络算法^[3]为代表的智能算法，将动力电池视为黑箱，利用可获得电池数据构建SOH估算模型，实现SOH的估算^[4].但电池老化样本数据获取周期相对较长，大量训练样本难以获得，加之神经网络模型结构复杂等问题的存在，使得此类估算思想难以实现实际应用.不同于上述两类算法，有些研究人员从寻找电池老化与外在表征关系出发，提出通过挖掘电池容量与欧姆内阻、电容等关系的基于电池等效电路的支持向量机一类的机器学习方法^[5].此类算法具有相对明确的物理意义^[6-7]，但为了追求电池欧姆内阻、电容的精确表达形式，导致电池模型复杂度不断提高.因此一些研究人员绕开等效电路模型，寻找更为直观的外在指征变化规律，如利用恒流恒压充放电时的单位电压下的容量增量曲线(dQ/dV)——容量增量曲线(incremental capacity，IC)法^[8-10]，但这种方法仅适用于低倍率恒流充放电情况下的SOH估算，应用范围相对较小.针对高倍率充放电过程，有人又提出了应力微分SOH方法——基于测量力的增量曲线法(incremental capacity curve based on measured force，ICF)^[11-12]，优势在于不再受限于低倍率、恒流率的电池循环条件，但对于电池表面应力变化的测量却需要更精密的仪器，因此并不适用于车载动力电池这类复杂工作条件下的电池SOH估算问题.文献[13]提出了仅基于车载动力电池易获得数据(温度、电压、电流)的基于温度变化率曲线的SOH估算方法——温度变化特征曲线法，该方法通过电池表面温度与时间的积分获得温度变化特征曲线(dT/dt)，并建立波谷点对应时间t_min与SOH之间的对应关系.较前两类增量曲线法而言，其不但适用于高倍率电流下的SOH估算，而且数据更易获得.然而，此类估算方法(统称为“外在指征函数法”)中对于“对应关系”确定的过程仅能在离线实验条件下进行，另外，即使同种工艺下的动力电池也势必存在差异，因此离线获取的电池外在特性与老化对应关系不能广泛应用.
综合分析以上方法的不足以及电动汽车领域对于SOH在线、精确估算的实际需求，本文提出了一种以离线获取的SOH外在指征函数曲线^[14]为基础的基于滤波思想在线闭环具有自校正能力的SOH估算架构.
1 基于外在指征函数的SOH估算方法1.1 基于外在指征函数的SOH估算方法简介本文以基于温度变化率曲线的SOH估算方法为代表，介绍外在指征函数一类SOH估算方法的基本思路、步骤以及局限性.
文献[13]指出电池在CC-CV充电过程中熵引起的温度变化存在两个波谷，两个波谷之间的距离与SOH具有函数关系，因此温度变化率可以作为SOH的外在指征，其计算如下：

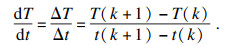(1)

其中: T(k)和T(k+1)分别为k和k+1时刻电池温度; t(k+1)和t(k)分别为k+1与k时刻测量温度时间; Δt为采样周期，波谷点对应时间即为熵引起温度变化的两个波谷之间的距离，文献[13]将其定义为t_min可作为SOH的外在指征值.建立外在指征值t_min与SOH的对应函数关系：

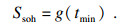(2)

以美国国家航空航天局(NASA)数据库中B0005号磷酸铁锂电池充电数据为例，图 1为基于温度变化率的SOH估算方法拟合得到的公式(2)中的函数g(t_min).基于温度变化率曲线的SOH估算方法即是以图 1中拟合函数为依据对同一型号电池进行SOH估算.
图 1(Fig. 1)

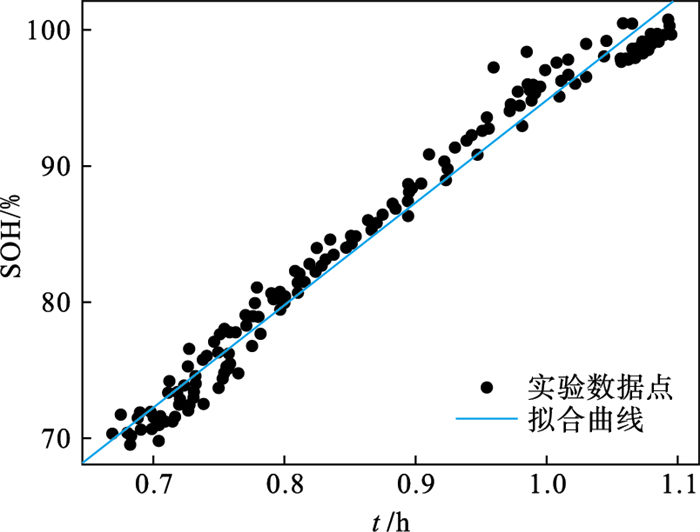图 1 B0005号电池的g(tmin)函数Fig.1 The function of B0005 battery

1.2 车载动力电池不适用分析首先，车载动力电池应用环境以及运行方式不同于实验室环境，其在实际应用中引起电池温度变化的原因多种多样.此外，即使同种工艺制造下的电池也不可避免存在差异，因此仅依据电池样本得到的外在指征函数在大规模车载动力电池应用时，必定产生误差.图 2给出一个实例说明.
图 2(Fig. 2)

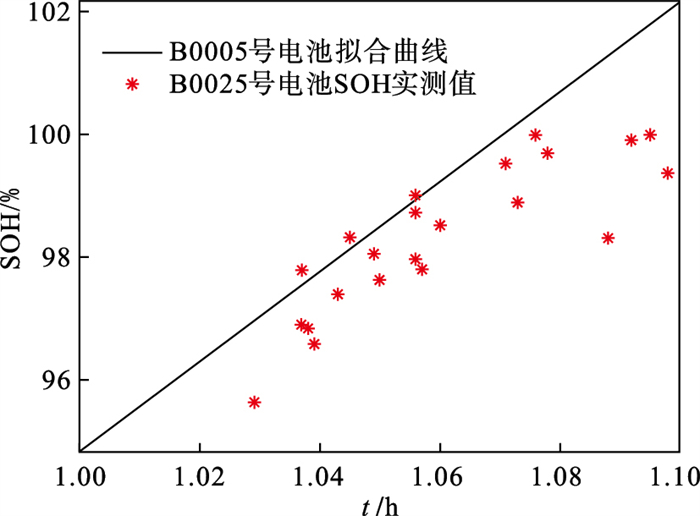图 2 实测值与g(tmin)函数对比Fig.2 Comparison of measured data and g(tmin)function

图 2中实线为基于温度变化率曲线的SOH估算方法得到的B0005号电池SOH拟合曲线；“*”为同种材质的B0025号磷酸铁锂电池实测的SOH值.可以看出B0025号电池实测的SOH值与依据B0005号电池实验数据得到的拟合曲线存在一定偏差.因此上述实例可以从一个侧面说明基于电池外在指征函数一类的SOH估算方法在车载动力电池上应用将会存在一定偏差的问题.
2 基于外在指征函数的放电过程SOH在线估算架构本文针对电动汽车领域对于SOH在线、精确估算的实际需求，提出一种以离线获取的SOH外在指征函数曲线为基础的结合滤波思想在线闭环具有自校正能力的SOH估算架构.在此框架内，本文将外在SOH指征函数与滤波算法相融合，依据外在指征函数的SOH先验信息赋予SOH初始值S_soh(0).进一步利用滤波算法在S_soh(0)基础上进行闭环修正以此弥补外在指征函数法在大规模电池应用时估算精度不足的问题.最后利用滤波算法修正后SOH值反馈在线修正外在指征函数的SOH函数曲线.这种良性循环架构，提高算法整体的收敛速度及鲁棒性.
2.1 外在指征函数——温度变化率函数基于上述车载动力电池SOH在线估算架构，本文提出基于温度变化率函数的无迹卡尔曼滤波SOH估算方法(differential temperature-unscented Kalman filter，DT-UKF).其中，SOH外在指征函数关系部分，本文采用易于车载动力电池实现的基于温度变化率函数法，其外在指征值t_min与SOH的函数离线获得过程如前所述，依据文献[13]给出拟合函数：

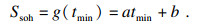(3)

其中，a，b为参数.依据式(3)得到初始SOH值S_soh(0).
2.2 “灰箱”等效电路模型由于AR模型在模型阶次恰当的条件下具有无限逼近真实值的能力^[15]，本文提出将动力电池放电过程内部电压的变化看作以电流序列l_k(k=1, 2, 3, …)为输入，内部压降U_in为输出的黑箱结构, 并利用自回模型对其进行建模，此结构与动力电池开路电压U_ocv组成如图 3所示的“灰箱”等效电路模型.
图 3(Fig. 3)

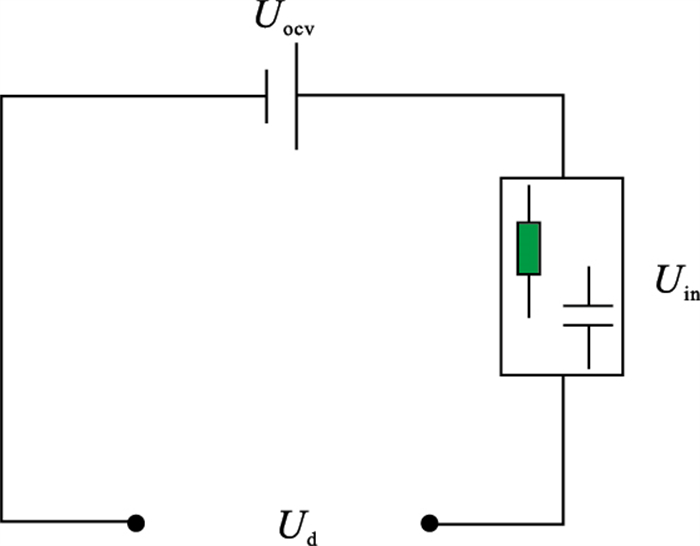图 3 基于AR模型的等效电路模型Fig.3 Equivalent circuit model based on AR model

图 3中, U_ocv为电池开路电压，U_in为电池内部压降，Ud为电池测量端电压.基于AR模型的等效电路模型表达式：

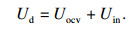(4)

式中，依据文献[16], k时刻的开路电压U_ocv(k)可以表示为k时刻电池电量S_soc(k)的函数：

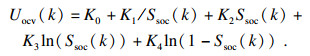(5)

式中：K₀, K₁, K₂, K₃, K₄为待定参数.
式(4)中内部电压U_in的AR模型如式(6)所示：

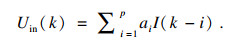(6)

式中：U_in(k)为k时刻内部电压; p为AR模型阶数；a_i(i=1, …, p)为待定系数.依据文献[17], 当AR模型阶次p恰当时，其可以无限逼近真实值.
由于基于AR模型的等效电路模型为线性模型，因此考虑低计算复杂度的需求及递归最小二乘算法(RLS)全局最优的快速收敛速度，这里决定采用RLS算法对基于AR模型的等效电路模型进行参数辨识.
2.3 基于无迹卡尔曼滤波在线SOH修正由于电池的老化过程在电池的全生命周期内属于慢时变过程，且代表电池老化程度SOH的变化范围仅为[1, 0.8]，因此在一次充放电循环内的前后两个采样时刻可以视其为恒值.因此：

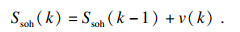(7)

式中，v(k)为状态残差.
依据图 3，得到如下观测方程：

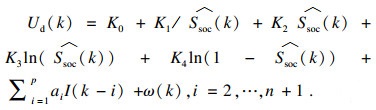(8)

式中，定义放电电流为负；采用库仑积分方式：

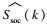
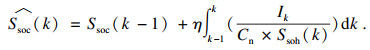(9)

式中：S_soc(k-1)为k-1时刻的电池剩余电量，采至电池管理系统(BMS)；η为与放电倍率及温度相关的库仑系数；C_n为电池的额定容量.
由于式(8)为非线性方程，因此本文采用更适用于非线性状态方程状态求解的UKF方法实现SOH的在线修正^[18].
以下给出UKF算法关键步骤.
步骤1??采样——产生2n+1(n为状态的维度，本文中n=1)个sigma点集.

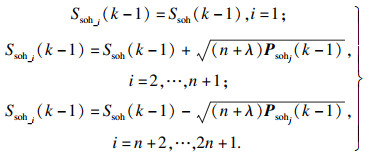(10)

P_sohj(k-1)表示P_soh(k-1)方阵中第j列，j=1, …, n；λ=α²(n+e)-n，α为采样点集到均值点的距离，e为比例因子，一般取0或3-n.
步骤2??一步估计——利用式(7)对sigma点集S_{soh_i}(k-1)进行一步估计得到S_{soh_i}(k|k-1).
步骤3??状态统计——计算sigma点集一步估计结果S_{soh_i}(k|k-1)的统计量：

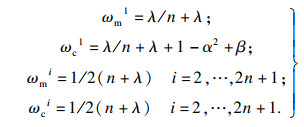(11)

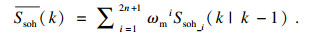(12)

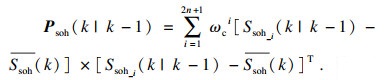(13)

其中，β满足正态分布, 取2.
步骤4??重采样——利用状态一步估计的均值统计量S_soh(k)替换式(10)中的S_soh(k-1)，式(13)中方差统计量P_soh(k|k-1)中每一列P_{soh_j}(k|k-1), j=1, …, n替换式(10)中P_{soh_j}(k-1)产生新的sigma点集S_{soh_i}(k), i=1, …, 2n+1.
步骤5??观测值计算——利用式(8)对新的sigma点集S_{soh_i}(k)进行观测值计算，得到U_{d_i}(k), i=1, …, 2n+1.
步骤6??观测统计——计算U_{d_i}(k)的统计量：

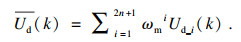(14)

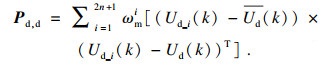(15)

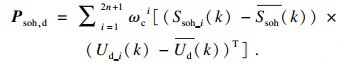(16)

步骤7??更新估计——更新S_soh及方差P_soh.

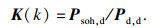(17)

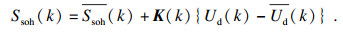(18)

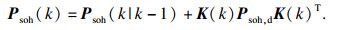(19)

2.4 基于DT-UKF算法的总体流程依据实际需求给出DT-UKF算法的总体流程图如图 4所示.图 4各部分简要说明如下：
图 4(Fig. 4)

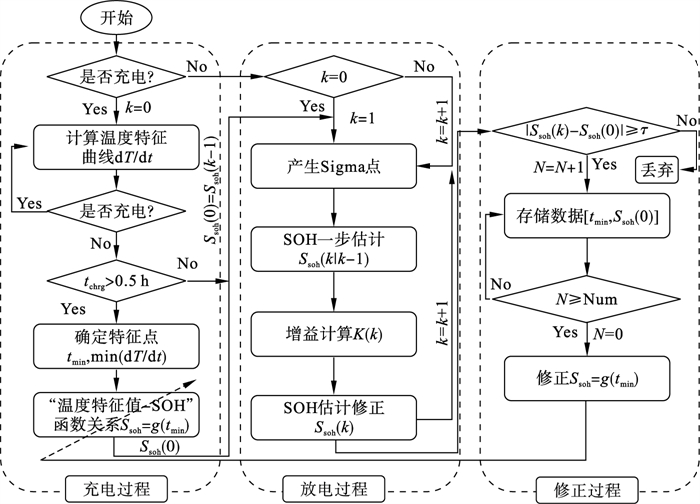图 4 基于DT-UKF的SOH估计流程图Fig.4 SOH estimation flow chart based on DT-UKF

1) 充电过程——确定SOH初始值：此过程为CC-CV充电过程，利用离线获取温度变化率特征函数S_soh=g(t_min)获得SOH初始值的过程.即在车辆上电瞬间，首先判断电池是否处于充电状态，若处于充电状态，则依据BMS实时采集的温度T计算dT/dt，直至出现dT/dt的波谷点(依据文献[13]，波谷点t_min∈[0.3 h, 0.5 h]).依据波谷点t_min，得到SOH的起始值S_soh(0)：

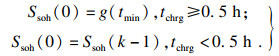(20)

式中，S_soh(k-1)表示上一次放电循环过程中依据DT-UKF算法得到的最终SOH估计值.
2) 放电过程——修正SOH估计：利用DT-UKF算法对SOH初始值S_soh(0)进行UKF修正.当k≠0时，说明上一次车辆上电时为放电，此时继续时间累积k，利用S_soh(k)进行UKF修正.
3) 修正过程——修正函数S_soh=g(t_min)：利用最终SOH估计值对S_soh=g(t_min)进行更新.
3 算法验证3.1 数据来源本文选取NASA开源数据库中的锂离子电池随机游走放电数据集进行算法验证.节选NASA随机游走放电数据集，其随机放电电流图如图 5所示.
图 5(Fig. 5)

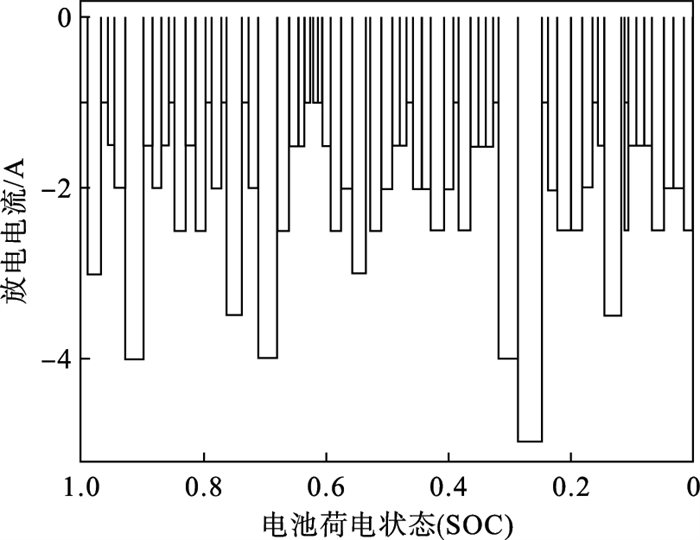图 5 RW13号电池放电电流Fig.5 Discharge current of RW13 battery

从图 5可知，其放电过程随机，符合车载电池的放电特征.另外其SOH跨度较大，在[1, 0.75]范围内，完全涵盖车载电池SOH∈[1, 0.8]的变化范围，因此随机游走放电数据集数据特征贴近实际车载电池特征.
3.2 基于NASA随机游走放电数据集的算法验证3.2.1 噪声下DT-UKF算法与传统UKF算法比较数据集中的RW13, RW14, RW15, RW16号磷酸铁锂电池均是以恒流恒压模式充电至4.2 V后，以[0.5 A, 5 A]的随机电流放电至端电压降至3.2 V的模式循环50次后，测量一次SOH，直至SOH降至0.5左右.本文选取RW14, RW15, RW16号磷酸铁锂电池CC-CV充电数据离线拟合温度变化率外在指征函数关系(式(21))，如图 6所示(仅截取电池寿命范围内数据).

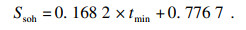(21)

图 6(Fig. 6)

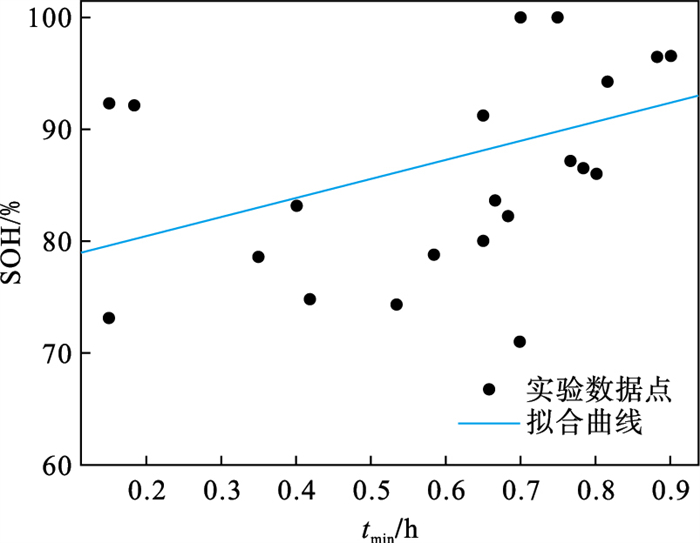图 6 RW13号电池的g(tmin)函数Fig.6 The function g(tmin)of RW13 battery

从图 6可以看出，随机游走实测数据质量较差，基于此数据，依据文献[13]算法拟合出的式(21)较为牵强，因此在实际应用过程中会带来一定误差，这也从一个侧面说明仅基于实验室条件下实测的外在指征函数进行大规模车载电池SOH估算的不适性.
这里将式(21)作为同一材质的RW13号电池的外在指征函数，同时在RW13号电池的电流、电压数据中加入40 dB的高斯白噪声，以模拟实际传感器采集信号含有噪声的情况.基于上述数据及式(21)的外在指征函数，利用本文提出的SOH估算方法对其进行SOH估算，结果如图 7所示.
图 7(Fig. 7)

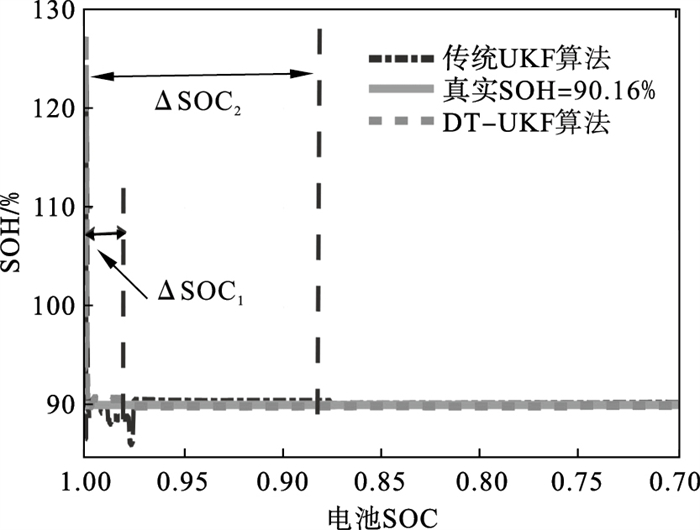图 7 噪声下估计结果对比Fig.7 Comparison results under noise

图 7中，实线为RW13号电池实测的SOH值，虚线为基于本文提出的DT-UKF算法的估计SOH值.点划线为传统UKF算法估计的SOH值，这里SOH初值为[80%，100%]之间的随机数.可以看出，对于随机游走数据，在40 dB的高斯白噪声下，本文提出的SOH估算方法由于采用了具有先验信息的外在指征函数给出的SOH初始值，依然能够在短时间内(ΔSOC₁ < 0.04)高精度收敛于真实值；相比而言，传统的UKF收敛速度较慢(ΔSOC₂ < 0.13).因此可以证明，对于随机放电过程，本文提出的基于DT-UKF的SOH估算方法较传统UKF算法收敛速度大幅度提高.
3.2.2 全寿命周期下算法的验证首先将提出的基于DT-UKF的SOH估算方法与基于外在指征函数的SOH估算法比较.已验证本文提出的SOH估算方法的闭环在线自校正效果及良性的循环效果.比较结果如图 8所示，误差如图 9所示.
图 8(Fig. 8)

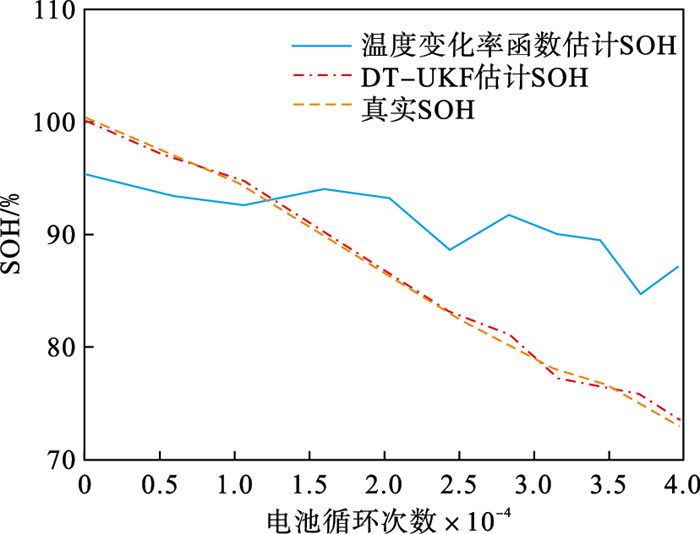图 8 RW13号电池算法对比结果Fig.8 Comparison results of RW13 battery

图 9(Fig. 9)

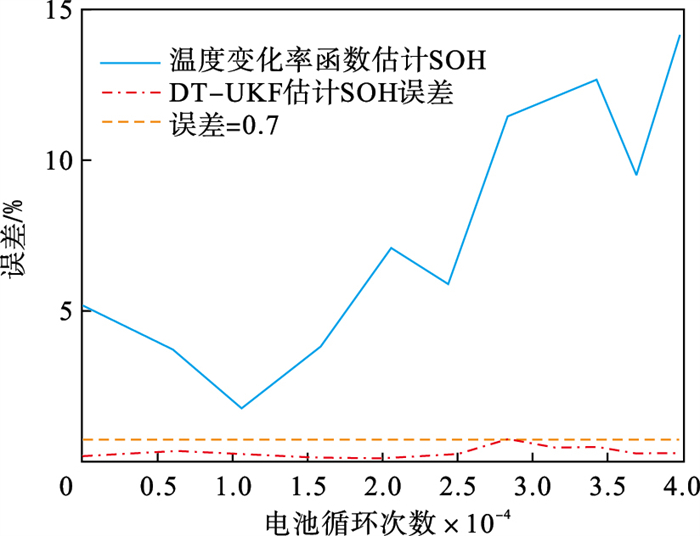图 9 RW13号电池误差对比结果Fig.9 Comparison error of RW13 battery

从图 8及图 9中可以明显看出，仅基于外在指征函数(温度变化率函数)的SOH估算方法在实际应用中的效果较本文提出的估算方法要差.尤其在电池老化末期，其与真实的SOH值之间的偏差不断扩大，分析其原因在于，基于实验的拟合函数在实际应用中并没有依据实际采集数据进行修正，因此其误差将始终保留.而本文利用架构中的闭环结构及UKF算法内部的闭环结构不断依据实际数据对SOH结果进行修正，使其能够精准逼近真实值.这也说明本文提出的SOH估算方法具有较强的鲁棒性.
进一步，通过图 10以及图 11展现出本文提出的DT-UKF算法框架的闭环结构对于外在指征函数的在线修正过程.
图 10(Fig. 10)

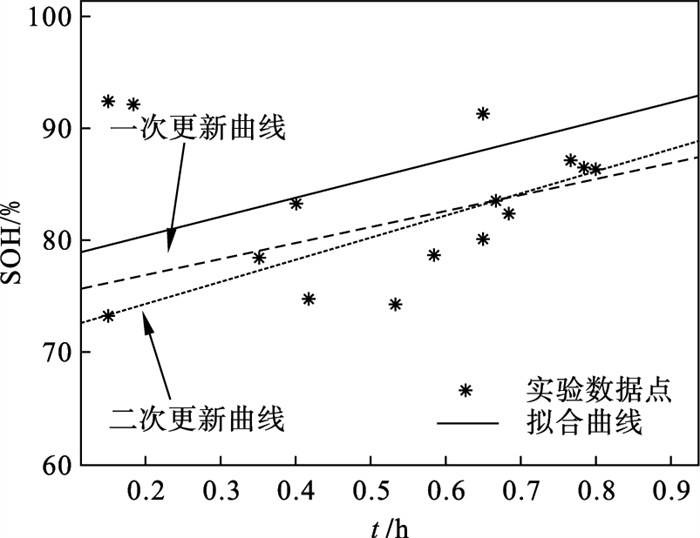图 10 外在指征函数的两次修正过程Fig.10 The twice correction process of the external indication function

图 11(Fig. 11)

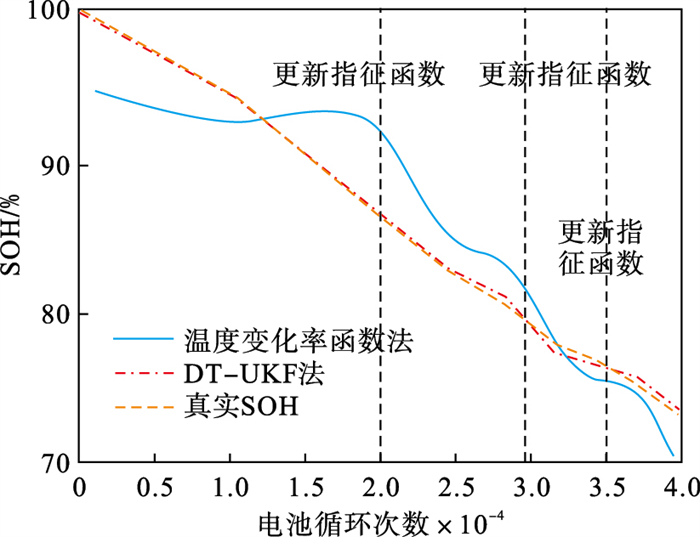图 11 两次修正后的精度对比Fig.11 Accuracy comparison after two corrections

图 10中实线为利用星号得到的外在指征函数离线拟合结果.虚线及点划线分别为依据本文提出的DT-UKF算法的闭环架构总体流程图对外在指征函数进行的一次修正及二次修正结果.经过两次对外在指征函数的修正，使得仅基于外在指征函数的SOH估算精度大幅度提高.其结果可以通过对比图 8中的实线与图 11中的实线看出.图 8中实线为仅依据离线获得的外在指征函数式(21)求得的SOH结果，可以看出其与同种材质的RW13真实SOH相差较大.而图 11中实线为离线获得的外在指征函数经过图 10中的两次修正后估算的SOH结果，可以看出，经过两次修正，仅基于外在指征函数的SOH估算精度与同种材质的RW13真实SOH(虚线)较接近，且效果明显好于图 8.此实验可以证明本文提出的DT-UKF算法闭环架构能够在精确估算SOH的同时，实现对外在指征函数的在线修正，有效缓解由于电池一致性问题使得外在指征函数方法在大规模应用时表现出的局限性.
4 结论1) 本文针对电动汽车领域对于SOH在线、精确、鲁棒估算的需求，提出一种以离线获取的SOH外在指征函数曲线为基础的结合滤波思想在线闭环具有自校正能力的SOH估算架构.在此架构内，提出基于DT-UKF的SOH估算方法以及基于AR模型的“灰箱”等效电路模型结构.
2) 在NASA数据库下，利用随机游走数据集对算法在精度、鲁棒性进行验证.并与传统的基于外在指征函数的SOH估算方法进行比较，从多角度证明本文提出的基于DT-UKF的SOH估算方法针对随机放电过程的SOH估算具有较好的精度和较强的鲁棒性，能够在线修正由于电池一致性问题带来的估算误差.
3) 如何评估车载电池包(多单体)的整体健康寿命还需进一步研究，如：以模组为单位，评估电池包的老化程度.
参考文献

[1]	孙丙香, 任鹏博, 陈育哲, 等. 锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测[J]. 电工技术学报, 2021, 36(3): 666-674. (Sun Bing-xiang, Ren Peng-bo, Chen Yu-zhe, et al. Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 666-674. DOI:10.19595/j.cnki.1000-6753.tces.200071)
[2]	Hannan M A, Lipu M S H, Hussain A, et al. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: challenges and recommendations[J]. Renewable and Sustainable Energy Reviews, 2017, 78: 834-854. DOI:10.1016/j.rser.2017.05.001
[3]	李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119. (Li Chao-ran, Xiao Fei, Fan Ya-xiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119. DOI:10.19595/j.cnki.1000-6753.tces.191617)
[4]	Hannan M A, Lipu M S H, Hussain A, et al. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm[J]. IEEE Access, 2018, 6: 10069-10079. DOI:10.1109/ACCESS.2018.2797976
[5]	Chen Z, Sun M, Shu X, et al. Online state of health estimation for lithium-ion batteries based on support vector machine[J]. Applied Sciences, 2018, 8(6): 925. DOI:10.3390/app8060925
[6]	Richardson R R, Birkl C R, Osborne M A, et al. Gaussian process regression for in-situ capacity estimation of lithium-ion batteries[J]. IEEE Transactions on Industrial Informatics, 2018, 15: 127-138.
[7]	Li Y, Zou C, Berecibar M, et al. Random forest regression for online capacity estimation of lithium-ion batteries[J]. Applied Energy, 2018, 232: 197-210. DOI:10.1016/j.apenergy.2018.09.182
[8]	Tang X, Zou C, Yao K, et al. A fast estimation algorithm for lithium-ion battery state of health[J]. Journal of Power Sources, 2018, 396: 453-458. DOI:10.1016/j.jpowsour.2018.06.036
[9]	Berecibar M, Garmendia M, Gandiaga I, et al. State of health estimation algorithm of LiFePO4 battery packs based on differential voltage curves for battery management system application[J]. Energy, 2016, 103(15): 784-796.
[10]	Li Y, Abdel-Monem M, Gopalakrishnan R, et al. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter[J]. Journal of Power Sources, 2018, 373: 40-53. DOI:10.1016/j.jpowsour.2017.10.092
[11]	Schiffer Z J, Cannarella J, Arnold C B. Strain derivatives for practical charge rate characterization of lithium ion electrodes[J]. Journal of Electrochemical Society, 2016, 163(3): A427-A433. DOI:10.1149/2.0091603jes
[12]	Samad N A, Kim Y, Siegel J B, et al. Battery capacity fading estimation using a force-based incremental capacity analysis[J]. Journal of the Electrochemical Society, 2016, 163(8): A1584-A1594. DOI:10.1149/2.0511608jes
[13]	Wu Y, Jossen A. Entropy-induced temperature variation as a new indicator for state of health estimation of lithium-ion cells[J]. Electrochimica Acta, 2018, 276: 370-376. DOI:10.1016/j.electacta.2018.04.203
[14]	Liu F, Ma J, Su W X, et al. SOC estimation based on data driven exteaded Kalman filter algorithm for power battery of electric vehicle and plug-in electric vehicle[J]. Journal of Central South University, 2019, 26(6): 1402-1415.
[15]	陈文帅. 基于灰色-AR模型的电动汽车锂离子电池寿命预测研究[D]. 长春: 长春工业大学, 2018. (Chen Wen-shuai. Research on life prediction of lithium-ion battery in electric vehicles based on gray-AR model[D]. Changchun: Changchun University of Technology, 2018. )
[16]	Yang D, Wang Y, Pan R, et al. State-of-health estimation for the lithium-ion battery based on support vector regression[J]. Applied Energy, 2018, 227: 273-283.
[17]	Liu F, Ma J, Su W X. Unscented particle filter for SOC estimation algorithm based on a dynamic parameter identification[J]. Mathematical Problems in Engineering, 2019, 2019: 7452079.
[18]	颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948. (Yan Xiang-wu, Deng Hao-ran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3937-3948.)