
 , 陈昭, 赵岐, 梁力
, 陈昭, 赵岐, 梁力 东北大学 资源与土木工程学院,辽宁 沈阳 110819
收稿日期:2021-10-14
基金项目:中央高校基本科研业务费专项资金资助项目(N2001015)。
作者简介:李明(1980-),男,辽宁沈阳人,东北大学副教授;
梁力(1955-),男,辽宁丹东人,东北大学教授,博士生导师。
摘要:采用PHF-LSM(permeability-based hydraulic fracture-level set method)水力压裂数值计算模型,模拟并分析了均质与分层岩石材料中分段压裂过程引起的应力阴影效应.通过与单一裂缝诱发应力理论解的对比,验证了PHF-LSM考虑应力阴影效应的可行性.以此模型为基础分析了单一裂缝发展过程中,岩石材料参数与初始应力条件对诱发应力场的影响,以及均质与分层岩石材料的多裂缝起裂过程中不同压裂间距与压裂顺序产生的应力阴影效应.数值计算结果表明:泊松比、抗拉强度与孔隙率的增加会增大裂缝引起的诱发应力与净压力比值的峰值,而弹性模量和水平主应力差的增大会减小该峰值;裂缝间距的扩大可以减弱裂缝间应力阴影效应;两步压裂与顺序压裂的裂缝总面积均大于同时压裂时的面积,但顺序压裂与两步压裂会带来更高的起裂压力;产层厚度与压裂间距的减小会增大应力阴影效应.
关键词:分段水力压裂应力阴影PHF-LSM模型分层岩石材料
The Stress Shadow Effect of Multistage Hydraulic Fracturing of Rock Material Based on PHF-LSM Model
LI Ming

 , CHEN Zhao, ZHAO Qi, LIANG Li
, CHEN Zhao, ZHAO Qi, LIANG Li School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: LI Ming, E-mail: liming@mail.neu.edu.cn.
Abstract: The PHF-LSM(permeability-based hydraulic fracture-level set method)hydraulic fracturing numerical model is used to simulate and analyze the stress shadow effect caused by staged fracturing in homogeneous and layered rock materials. Compared with the theoretical solution of single crack induced stress, the feasibility of considering stress shadow effect in PHF-LSM is verified. Based on this model, the influence of rock material parameters and initial stress conditions on induced stress field during the development of single fracture, and the stress shadow effect caused by different fracturing spacing and fracturing sequence during the initiation of multiple fractures in homogeneous and layered rock materials were analyzed. The numerical results show that the increase of Poisson′s ratio, tensile strength and porosity will increase the peak value of the ratio of induced stress to net pressure, while the increase of elastic modulus and horizontal principal stress difference will decrease the peak value. The expansion of crack spacing can weaken the stress shadow effect between cracks. The total fracture area of the two-step fracturing and the sequential fracturing are larger than that of simultaneous fracturing, but sequential fracturing and two-step fracturing will cause higher fracture initiation pressure. The decrease of pay layer thickness and fracturing spacing will increase the stress shadowing effect.
Key words: multistage hydraulic fracturingstress shadowPHF-LSM modellayered rock material
随着世界页岩油气资源探明储量不断增加,水力压裂开采技术得到了长足发展,分段压裂广泛用于加强油气开采产量.在分段压裂过程中同时或连续产生的裂缝之间会产生局部强烈的应力场变化,导致裂缝几何形态产生差别,即应力阴影效应[1].该效应会对应力场产生显著的改变,因此综合研究影响应力阴影效应的因素对控制裂缝与缝网形态,以期增加油气产量是十分必要的.
应力阴影效应的研究可以通过理论分析、物理试验和数值模拟等手段开展.Green等[2]研究了理想状态单裂缝附近应力场分布的理论解,发现应力场的改变主要体现在最小水平主应力的增大;杨正明等[3]通过物理模拟试验研究了低渗致密油藏分段水平井的渗流规律,并发现水平井压裂的最佳分段数的设置与储层渗透率存在着较大联系;Bai等[4]通过真三轴实验与混合动力FDEM(hybrid finite-discrete element method)数值模型结合研究了不同应力差与射孔参数对受应力阴影影响下的裂缝偏转角度和起裂压力的影响;Ju等[5]通过三维数值计算模型研究了同时压裂与顺序压裂对应力场的影响;Yang等[6]使用DDM(displacement discontinuity method)模型探讨了压裂时簇个数、直径以及间距等参数对改善多裂缝不均匀扩展的影响;Zhang等[7]探究了天然裂缝长度、与水力裂缝角度和间距对水力裂缝的影响; Liu等[8]使用一种基于离散格点理论和合成岩体技术研究了在水平天然裂缝影响下的多裂缝扩展形态.
本文采用基于渗透率修正的水力压裂数值计算模型(permeability-based hydraulic fracture-level set method,PHF-LSM)研究均质和分层岩石材料中分段压裂过程引起的应力阴影效应,探讨岩石材料性质、压裂点间距和压裂顺序影响下的应力阴影效应,及其对起裂压力和裂缝发展过程的影响.
1 PHF-LSM水力压裂模型1.1 基本方程PHF模型基于流固耦合理论,采用线弹性本构关系和Mohr-Coulomb破坏及强化准则描述饱和岩石材料固体骨架的力学行为,采用达西定律描述多孔岩石材料中的孔隙流体,并假设处于开裂区域的岩石材料渗透率是平均应力σm的函数[9-10].采用LSM建立岩石的非均质特征[11].PHF模型的主要控制方程为
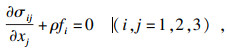 | (1) |
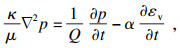 | (2) |
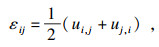 | (3) |
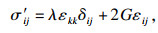 | (4) |
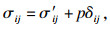 | (5) |
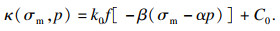 | (6) |
本文依托软件ABAQUS实现水力压力过程的模拟.利用渗透率κ与渗透系数K之间的关系
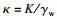
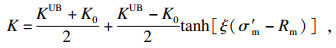 | (7) |
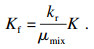 | (8) |
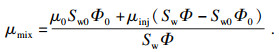 | (9) |
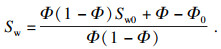 | (10) |
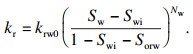 | (11) |
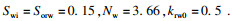
LSM采用高一维的方程
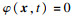
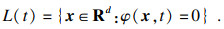 | (12) |
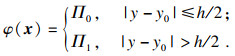 | (13) |
图 1(Fig. 1)
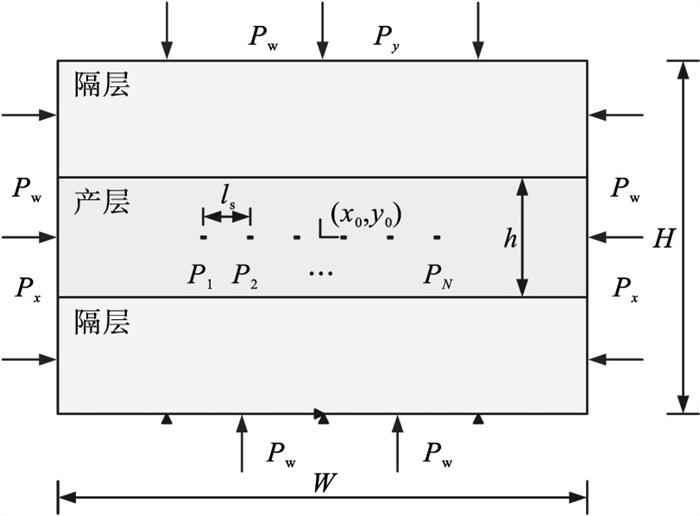 | 图 1 分层岩石材料分段水力压裂力学模型Fig.1 Mechanical model of multistage hydraulic fracturing for layered rock material |
1.2 PHF-LSM模型在ABAQUS中实现采用ABAQUS软件实现PHF-LSM水力压裂弥散裂缝数值计算模型,程序流程图如图 2所示.求解共需8个场变量和用于存储对应初值的8个状态变量,分别为弹性模量(E)、泊松比(ν)、抗拉强度(Rm)、渗透系数(K)、密度(ρ)、饱和度(Sw)、孔隙比(e)和混合黏滞系数(μmix).所用到的关键子程序有UEXTERNALDB,SDVINI和USDFLD,分别用于实现材料参数及控制参数的读取和初始化,依据式(13)给出的水平集方程初始化状态变量(材料参数)和依据式(7)~(11)修正水力压裂过程中渗透系数随有效应力改变.
图 2(Fig. 2)
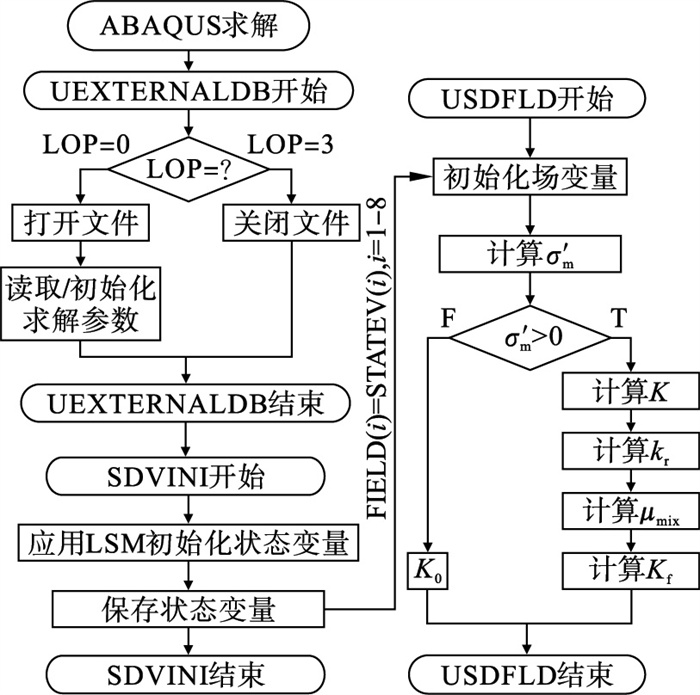 | 图 2 PHF-LSM模型流程图Fig.2 Flow chart of PHF-LSM model |
1.3 岩石材料有限元模型建立依据图 1所示力学模型(1 000 m×400 m)和表 1对应的模型参数,采用图 3所示有限元网格建立PHF-LSM法的均质和分层岩石模型.采用ABAQUS软件中的固结分析模块和CPE8P单元实现水力压裂过程的模拟.单元高宽为AR=3.0,网格包含133 000个单元和401 267个节点.垂直和水平方向的应力分别为
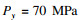
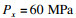
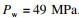
表 1(Table 1)
| 表 1 力学模型参数 Table 1 Parameters of mechanical model |
图 3(Fig. 3)
 | 图 3 有限元网格Fig.3 Finite element mesh |
表 2(Table 2)
| 表 2 岩石材料属性 Table 2 Rock material properties |
2 单裂缝应力阴影效应2.1 基于PHF-LSM法的诱发应力场在图 1的模型中赋予表 2中的产层(Π0)材料属性,建立均质岩石材料模型并计算单一裂缝引起的诱发应力场.模型中心位置施加单点注水速率
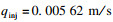
图 4(Fig. 4)
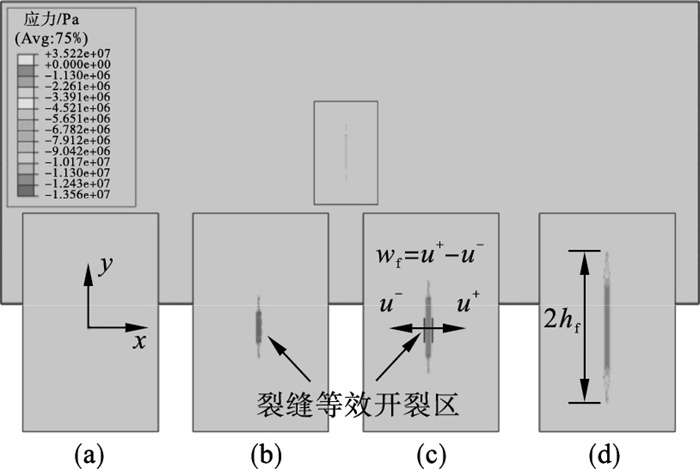 | 图 4 水力裂缝发展过程Fig.4 Development of hydraulic fracture (a)—1.5 s; (b)—69 s; (c)—150 s; (d)—300 s. |
由KGD模型计算的单一水力裂缝的裂缝高度2hf、裂缝开度wf和注水压力Pw随时间变化的理论解[14]分别如式(14)~(16)所示.基于弹性解的起裂压力理论值[15]如式(17)所示.
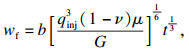 | (14) |
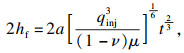 | (15) |
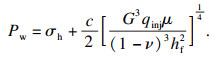 | (16) |
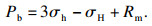 | (17) |
图 5给出了水力裂缝的主要特征参数(等效开度、等效高度和注水压力)随注水时间变化.其中图 5a和5b分别为裂缝等效开度wf与裂缝等效高度2hf随注水时间的变化.该计算结果表明,随着注水时间的增加,裂缝等效高度与等效宽度均增加,且与基于KGD模型的解析解变化一致.基于PHF模型计算的起裂压力和传播压力可由注水点水压力Pw随注水时间的变化曲线得到,见图 5c.该模型对应的起裂压力为127.947 MPa,其值与式(17)计算的理论值117 MPa接近.同时由图 5c可以看出传播压力略高于KGD模型解.图 5d给出了注水点位置的应力路径发展过程,其中平均有效应力p随着注水时间的增加逐渐降低至零(p>0对应受压状态)后变为负值并持续增加(p < 0对应受拉状态);等效剪切应力q先增加后沿着屈服面持续降低至零.
图 5(Fig. 5)
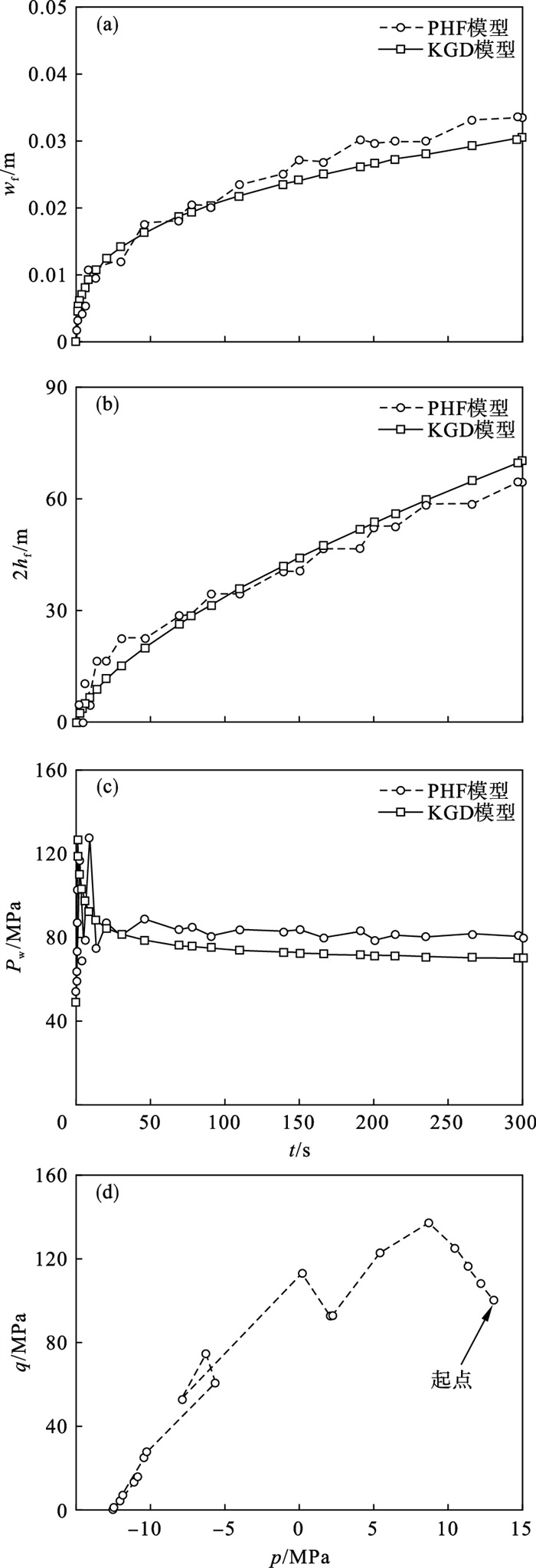 | 图 5 单一水力裂缝特征Fig.5 Characteristics for a single hydraulic fracture (a)—等效裂缝开度;(b)—等效裂缝高度;(c)—注水点水压力;(d)—注水点应力路径. |
多水力裂缝的发展过程受应力阴影效应的影响,因此计算应力场的改变有助于评价裂缝形态发展.已有裂缝产生的应力场主要影响垂直于裂缝方向应力改变,Sneddon等[16]基于弹性理论给出了平面应变条件下二维单一垂直裂缝产生的水平应力场解析解:
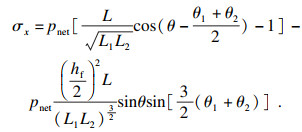 | (18) |
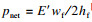
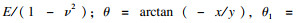
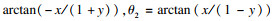
图 6(Fig. 6)
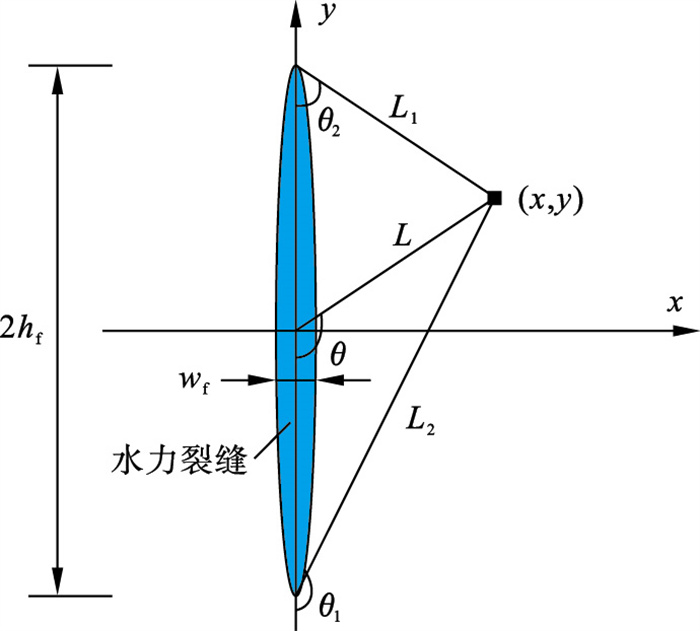 | 图 6 单裂缝坐标示意图Fig.6 Coordinates sketch of single fracture |
采用PHF模型计算的垂直于裂缝方向的诱发应力如图 7所示,数值解峰值及其位置分别用X0和X0表示.由于模型实际并不存在真实裂缝而是使用等效开裂区域(σ′m < 0的区域)模拟裂缝.因此在等效开裂区内与理论解有明显区别;而在等效开裂区域外随着距离的增加,由PHF模型计算的数值解与理论解趋于一致.
图 7(Fig. 7)
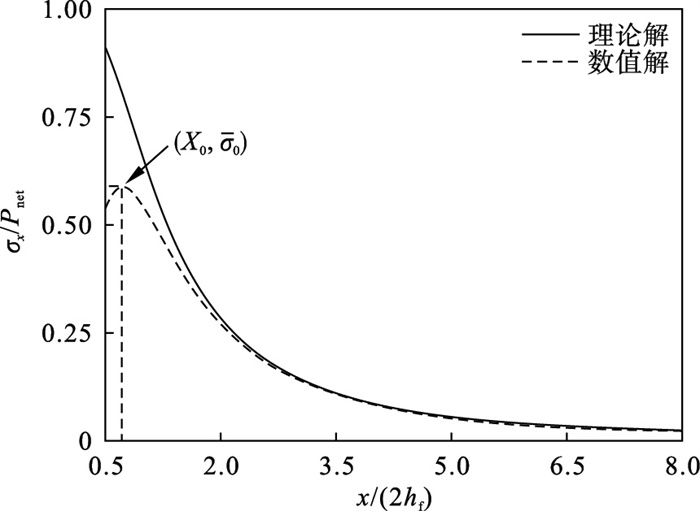 | 图 7 注水点位置垂直裂缝方向诱发应力变化(t=300 s)Fig.7 Induced stress along the path perpendicular to fracture starting from injection point(t=300 s) |
图 8给出了裂缝周围x方向应力场分布,可以看出水平方向的应力随着距离增加而减小.
图 8(Fig. 8)
 | 图 8 基于PHF模型的应力场分布Fig.8 Stress field distribution based on PHF model |
2.2 诱发应力影响因素分析影响裂缝特征及诱发应力场的因素较多,本文重点探讨岩石材料性质和初始地应力的影响,即:弹性模量(E)、泊松比(ν)、渗透系数(K)、孔隙比(e)、抗拉强度(Rm)以及初始水平主应力差(
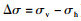
表 3(Table 3)
| 表 3 分析参数取值 Table 3 Analysis parameter value |
为便于分析,对表 3中各参数进行归一化处理.各个因素对裂缝等效开度wf与等效高度hf的影响分别如图 9a与图 9b所示.计算结果表明,wf与孔隙比和抗拉强度呈正相关,与弹性模量、泊松比和水平主应力差呈负相关,而渗透系数与wf相关关系不明显.hf与孔隙比、抗拉强度和渗透系数呈负相关,与弹性模量、泊松比和水平主应力差呈正相关.
图 9(Fig. 9)
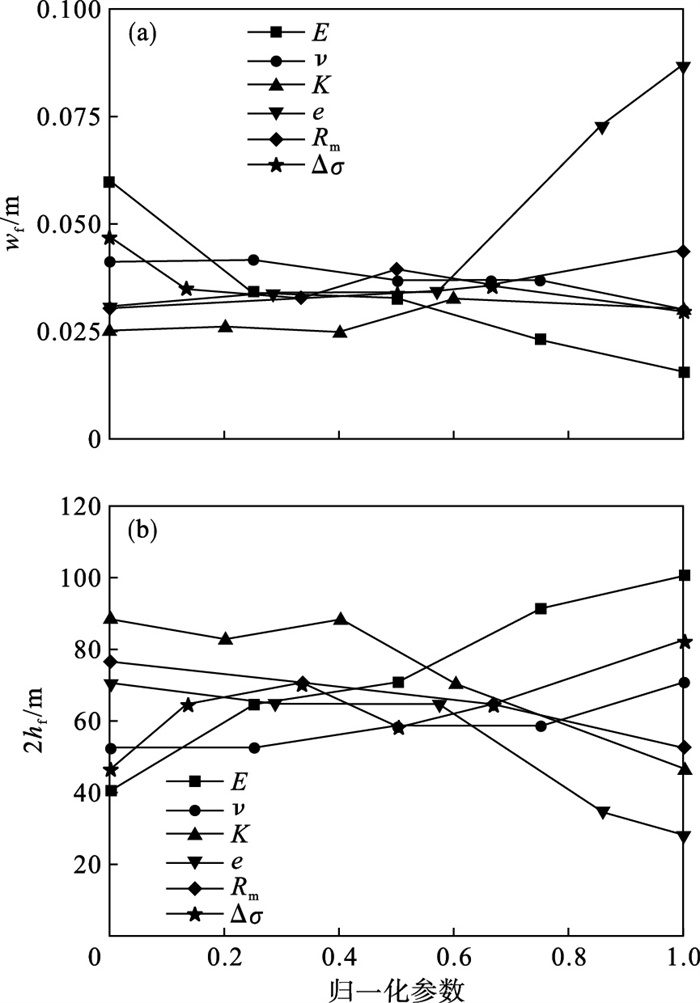 | 图 9 归一化参数对等效裂缝开度与高度的影响Fig.9 Equivalent fracture height and fracture opening influenced by normalized parameters (a)—等效裂缝开度;(b)—等效裂缝高度. |
各参数对裂缝净压力Pnet的影响如图 10所示.该计算结果表明:当弹性模量较小时,与Pnet呈正相关,弹性模量较大时,与Pnet呈负相关;当渗透系数较小时,与Pnet关系不明显,当渗透系数较大时,与Pnet呈负相关;泊松比和水平主应力差与Pnet呈负相关;孔隙比和抗拉强度与Pnet呈正相关.
图 10(Fig. 10)
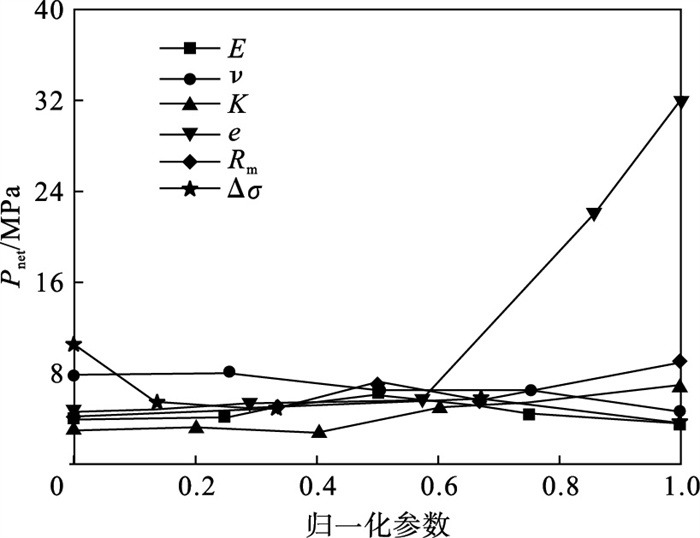 | 图 10 归一化参数对净压力的影响Fig.10 Net pressure influenced by normalized parameters |
图 11给出了各参数对裂缝诱发应力与净压力比值(σx/Pnet)的峰值(σ0)及对应位置(X0)的影响.该计算结果表明:当归一化参数小于0.65时,X0在0.35附近波动;当归一化参数大于0.65时,各参数对X0影响显著;σ0随着归一化参数增加整体呈下降趋势,其中弹性模量、孔隙比和水平主应力差影响显著.
图 11(Fig. 11)
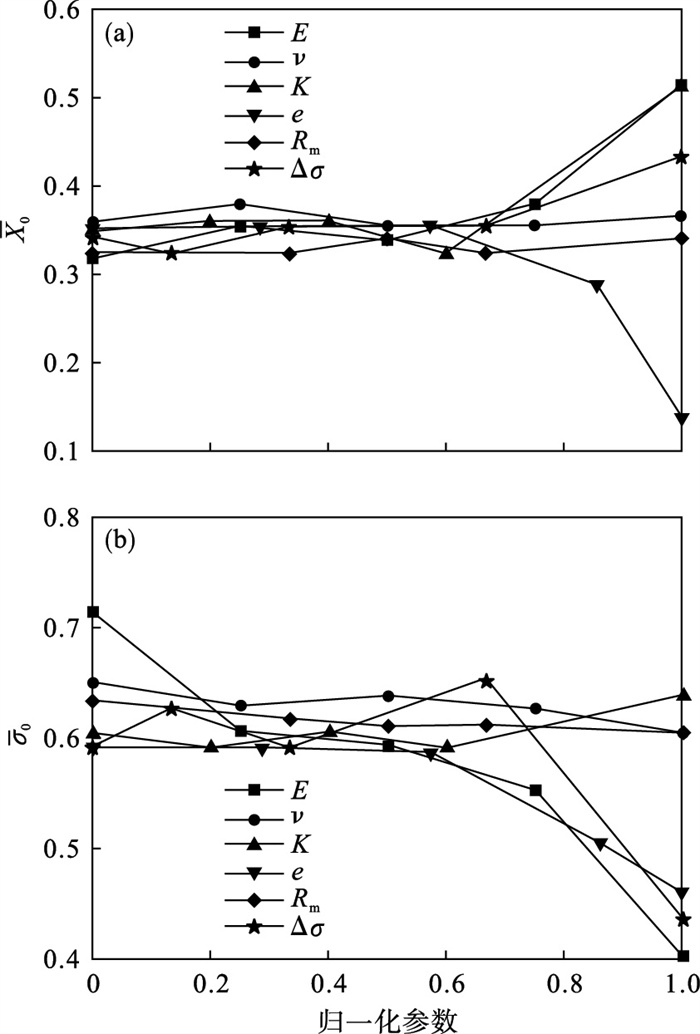 | 图 11 归一化参数对诱发应力峰值及其位置的影响Fig.11 Maximum induced stress and its position influenced by normalized parameters (a)—诱发应力峰值位置;(b)—诱发应力峰值. |
在考虑的单裂缝应力场的6个参数中,弹性模量、泊松比以及水平主应力差的增加会使σ0减小X0增大;渗透系数、孔隙比与抗拉强度的增大会使σ0增大X0减小.
3 均质岩石多裂缝应力阴影效应3.1 射孔间距对水力裂缝特征的影响在均质岩石材料模型(材料参数采用表 2中产层(Π0)的参数)中,采用顺序压裂方式,施加三个大小相同、位置不同的注水荷载.
结合文献[19], 本文计算中考虑注水点间距ls为20,40,60,80和100 m五种情况,注水时间均为300 s.以间距ls=60 m情况为例,采用PHF模型计算的各阶段注水结束后的等效开裂区域如图 12所示.由图 12b中可以看出, 当后一阶段裂缝开始注水,前一阶段裂缝会受其影响在裂缝高度方向继续延伸.由于注水体积一定,前一阶段的裂缝宽度会受到后施加裂缝的影响而降低,同时最后起裂的裂缝受到之前阶段裂缝应力场的影响,裂缝高度发展受到抑制.
图 12(Fig. 12)
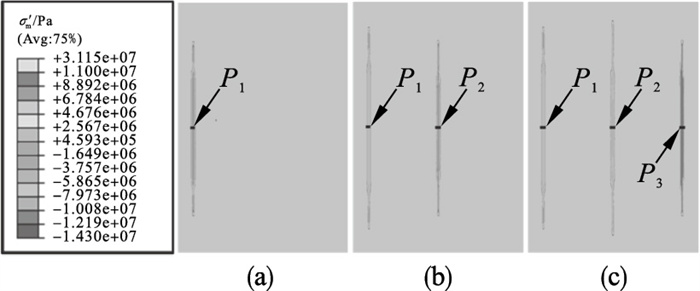 | 图 12 三阶段压裂的等效开裂区域(ls=60 m)Fig.12 Equivalent fracture zone by three-stage injection (a)—一阶段完成;(b)—二阶段完成;(c)—三阶段完成. |
各注水位置的起裂压力Pb随ls变化如图 13所示.由于应力阴影效应的存在,当裂缝间距过近时,后压裂的裂缝Pb大于初始裂缝的Pb;当ls增大时,水力裂缝之间应力阴影效应减弱,即,后压裂裂缝的Pb随ls增加而降低.
图 13(Fig. 13)
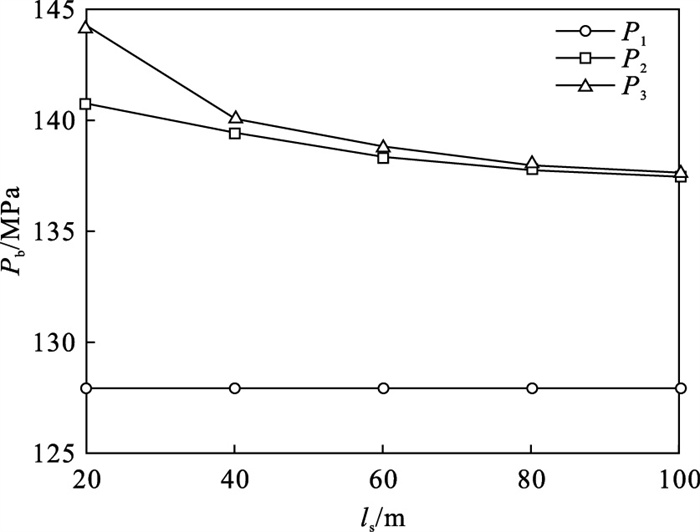 | 图 13 注水点间距对起裂压力影响Fig.13 Breakdown pressure influenced by injection spacing |
图 14给出ls对裂缝等效面积比Ji的影响.等效面积比采用Ji=Ai/A1计算,其中Ai是第i条裂缝的等效面积,A1为第一条裂缝的等效面积.当注水点间距较小时,如ls=20 m,三条裂缝的Ji会逐渐降低,表明下一阶段起裂的裂缝扩展受到了抑制.随着ls的增大,Ji逐渐增加,即ls的增加降低了应力阴影效应对裂缝扩展的影响.
图 14(Fig. 14)
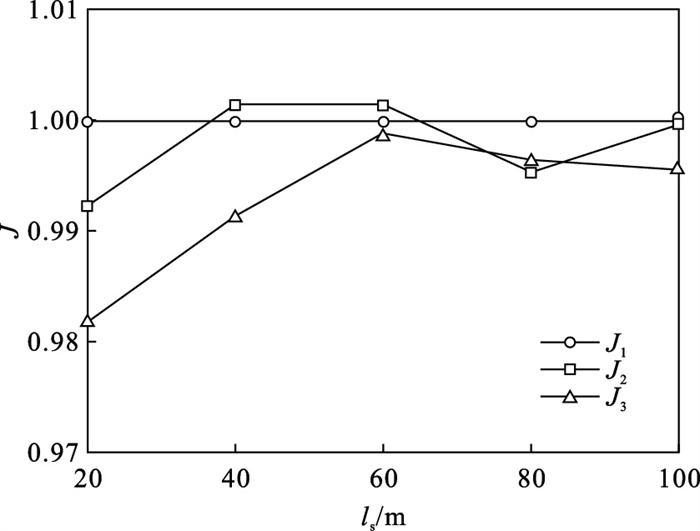 | 图 14 均质岩石材料中注水点间距对等效面积比的影响Fig.14 Equivalent area ratio influenced by injection spacing in homogeneous rock material |
3.2 压裂顺序对水力裂缝特征的影响压裂顺序是改变应力阴影效应的一个有效手段,本文以注水点数量N=3,ls=40 m的工况为例,考虑三种压裂顺序对起裂压力以及裂缝等效面积的影响,即顺序压裂(sequential fracturing,SeF)、同步压裂(synchronous fracturing,SyF)和两步压裂(two-step fracturing,TsF).其中顺序压裂与3.1节相同;同步压裂为对多个注水点同时施加注水荷载;两步压裂为当最外侧注水点压裂完成后再对中间注水点进行压裂.
图 15给出了不同注水位置在压裂顺序改变情况下的裂缝起裂压力.计算结果表明:两步压裂与同步压裂最外侧裂缝的起裂压力基本相同,其中间裂缝具有更高的起裂压力;同步压裂中间裂缝起裂压力略微高于两侧裂缝;顺序压裂的不同注水点的起裂压力依次增加.
图 15(Fig. 15)
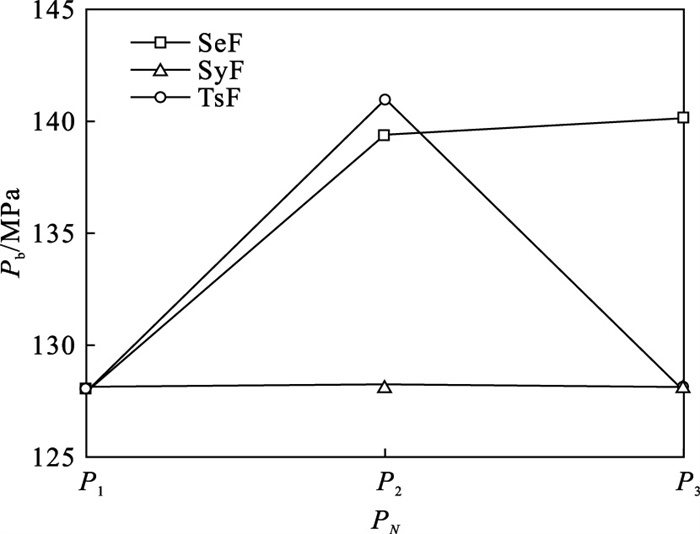 | 图 15 压裂顺序对起裂压力的影响Fig.15 Breakdown pressure influenced by fracturing sequence |
图 16给出了不同压裂顺序下各注水点裂缝等效面积A.计算结果表明:两步压裂与顺序压裂的最外侧裂缝的等效面积基本相同,中部裂缝会受到应力阴影的影响产生不均匀扩展;在顺序压裂情况下,后起裂的裂缝受到应力阴影效应的影响,等效面积A显著降低.两步压裂与顺序压裂产生的有效裂缝面积大于同步压裂,但两步压裂与顺序压裂相比产生更高的起裂压力.
图 16(Fig. 16)
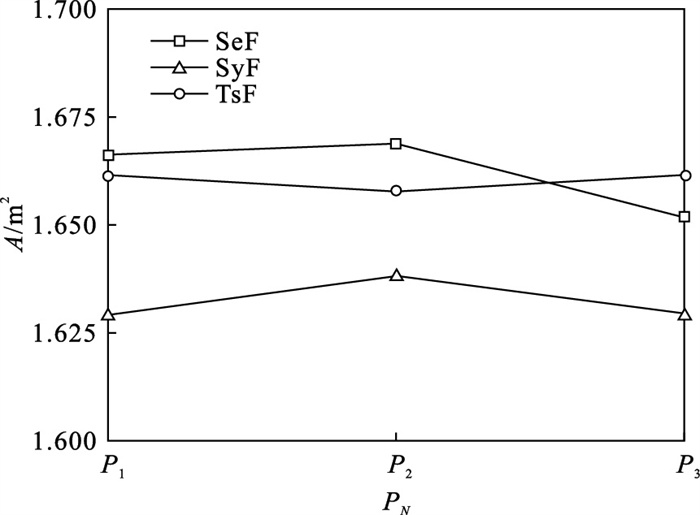 | 图 16 压裂顺序对裂缝等效面积影响Fig.16 Equivalent fracture area influenced by fracturing sequence |
3.3 射孔数量对水力裂缝特征的影响在水平井的分段压裂过程中,当注水点间距ls=50 m时,计算了注水点数量N分别为1, 3, 5和7的顺序压裂过程(压裂顺序为从左到右).N=5时裂缝的等效开裂区域如图 17所示.该结果表明后起裂的裂缝高度明显受到抑制作用.
图 17(Fig. 17)
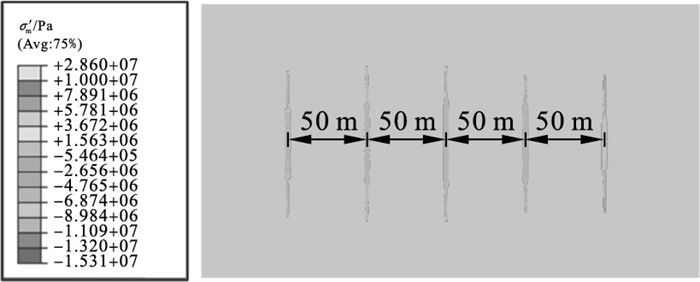 | 图 17 多点压裂等效开裂区域Fig.17 Equvalent fracture zone of multiple points |
注水点数量N对裂缝平均等效面积A和起裂压力Pb的影响如图 18所示.随着N的增大,A呈下降趋势,Pb逐渐增大.由于裂缝产生的水平诱发应力具有可以叠加的性质,在每条裂缝注水时间一定的情况下,后起裂的裂缝所受到的诱发应力场的影响大小由先起裂裂缝的数量与距离的影响,因此随着射孔数量的增加,后起裂裂缝会受到多个裂缝叠加的应力阴影效应.
图 18(Fig. 18)
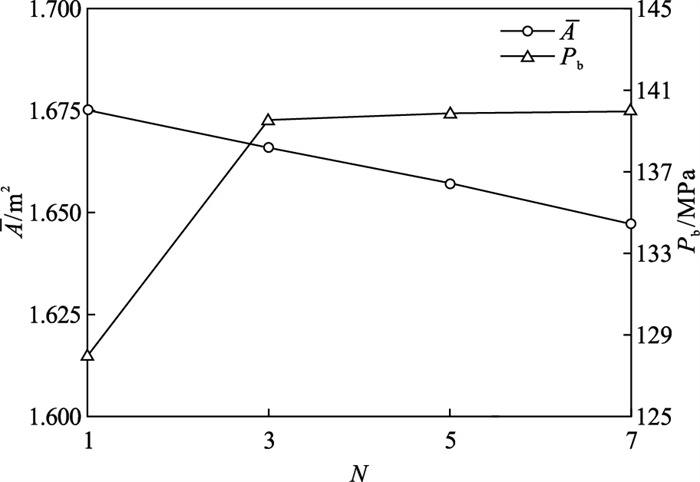 | 图 18 注水点数量对裂缝平均等效面积及起裂压力的影响Fig.18 Average equivalent area and breakdown pressure influenced by the number of injection points |
4 分层岩石多裂缝应力阴影效应4.1 射孔间距的影响实际油层情况可简单看作具有分层特性的岩石材料模型,即:隔层-产层-隔层.建立图 1所示的分层岩石材料模型,材料参数如表 2所示.
在分层岩石材料的多点压裂过程中,本文考虑产层厚度h和注水点间距ls两种因素的影响.当h=80 m,N=3,ls分别取值60,80和100 m时,不同间距下的等效开裂区域如图 19所示.当裂缝间距为60 m时,第二、三条裂缝高度会大于预设置的产层高度,这是由于产层厚度较小,应力阴影效应导致裂缝继续扩展穿过邻近隔层.
图 19(Fig. 19)
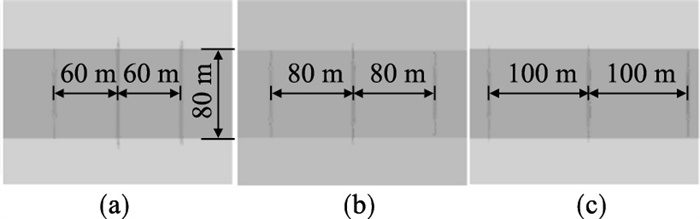 | 图 19 分层岩石等效开裂区域Fig.19 Equivalent fracture zone of layered rock (a)—ls=60 m;(b)—ls=80 m;(c)—ls=100 m. |
图 20给出了ls对裂缝等效面积比值Ji的影响.当ls=60 m时,后两个阶段的裂缝扩展会受到抑制,裂缝等效面积小于初始裂缝等效面积;当间距从60 m扩大到100 m时,后两个阶段裂缝等效面积受到抑制减弱,裂缝间的面积相较于间距60 m时更为均匀.该结果表明:在分层岩石中,扩大间距会显著降低应力阴影效应对裂缝均匀扩展的不利影响.对比图 14中相同间距下的裂缝面积比值发现,分层岩石中的裂缝开裂时,裂缝受到的应力阴影效应会强于均质岩石.图 20结果还表明中部裂缝的裂缝等效面积会小于最后起裂裂缝的等效面积;均质岩石中最后起裂裂缝的等效面积最小.表明分层特性对顺序压裂中的中部裂缝产生更强的抑制作用.
图 20(Fig. 20)
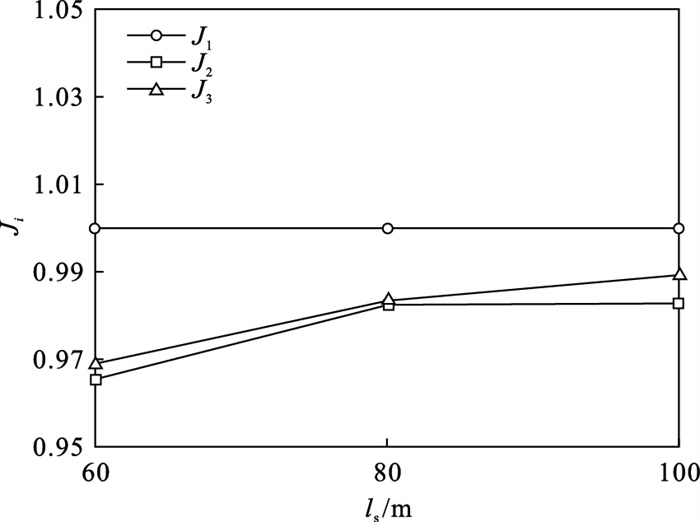 | 图 20 分层岩石中注水点间距对等效面积比的影响Fig.20 Equivalent area ratio influenced by injection spacing in layered rock |
4.2 产层厚度的影响在顺序压裂情况下,注水点间距ls=40 m,N=3,产层厚度h分别为100,120和140 m时,不同产层厚度对应的等效开裂区域如图 21所示.可以看出h的降低限制了水力裂缝沿垂直方向的发展.图 22给出了h改变下各注水位置的裂缝等效面积A与裂缝总等效面积和Asum的影响.该结果表明:由于应力阴影效应的影响,后起裂的裂缝等效面积小于先起裂的裂缝等效面积.当h较小时,其对裂缝的发展起到限制作用,一定程度抑制了应力阴影效应;随着h的增加,裂缝间等效面积差加大,应力阴影效应受到的抑制减弱.
图 21(Fig. 21)
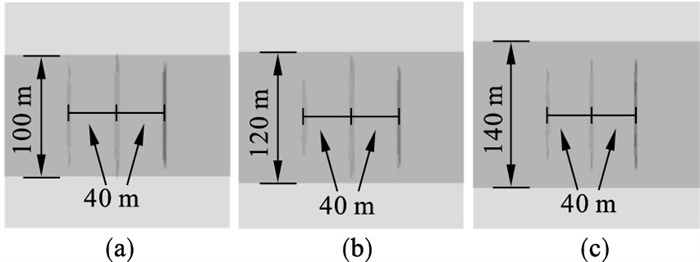 | 图 21 不同产层厚度下的等效开裂区域Fig.21 Equivalent fracture zones influenced by the thickness of pay zone (a)—h=100 m;(b)—h=120 m;(c)—h=140 m. |
图 22(Fig. 22)
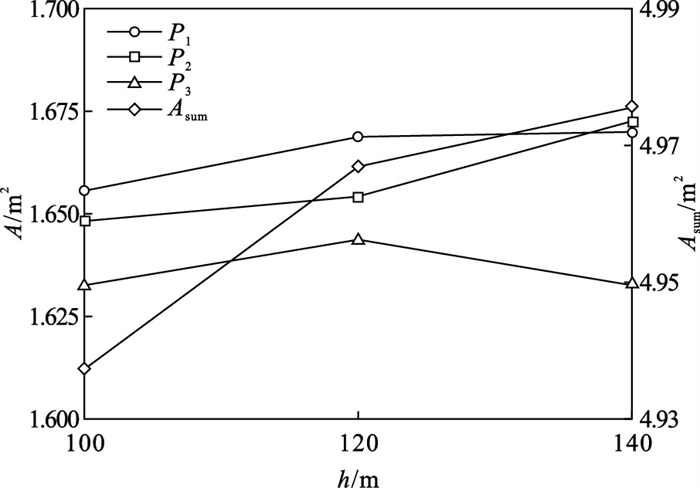 | 图 22 产层厚度对裂缝等效面积及总面积的影响Fig.22 Equivalent fracture area and its sum influenced by the thickness of pay zone |
5 结论1) 诱发应力与净压力比值的峰值和弹性模量、泊松比以及水平主应力差呈负相关,与孔隙比、抗拉强度以及渗透系数呈正相关.
2) 顺序压裂过程中,单井射孔间距会与应力阴影效应呈负相关,促进裂缝均匀发展;随着裂缝间距增加,应力阴影效应减弱,裂缝等效开裂区域的扩展更为均匀.
3) 采用两步压裂与同时压裂时,中部裂缝会受到较大的影响,而顺序压裂情况的最外部裂缝受到影响最大;在应力阴影效应的影响下,两步压裂与顺序压裂的裂缝总面积均大于同时压裂时的面积,但顺序压裂与两步压裂会增大起裂压力.
4) 分段压裂中,压裂总面积不会随着射孔数量呈线性增加,且由于裂缝数量的增加会增加起裂压力.
5) 在分层岩石中,射孔间距与应力阴影效应呈负相关;分层特性的存在会加强应力阴影的效应,较小的产层厚度可以抑制应力阴影效应带来的裂缝不均匀扩展现象,同时也限制裂缝的扩展高度.
参考文献
| [1] | Bunger A P, Zhang X, Jeffrery R G. Parameters affecting the interaction among closely spaced hydraulic fractures[J]. Society of Petroleum Engineers Journal, 2012, 17(1): 292-306. |
| [2] | Green A E, Sneddon I N. The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1950, 46(1): 159-163. DOI:10.1017/S0305004100025585 |
| [3] | 杨正明, 张仲宏, 刘学伟, 等. 低渗/致密油藏分段压裂水平井渗流特征的物理模拟及数值模拟[J]. 石油学报, 2014, 35(1): 85-92. (Yang Zheng-ming, Zhang Zhong-hong, Liu Xue-wei, et al. Physical and numerical simulation of porous flow pattern in multi-stage fractured horizontal wells in low permeability/tight oil reservoirs[J]. Acta Petrolei Sinica, 2014, 35(1): 85-92.) |
| [4] | Bai Q, Liu Z, Zhang C, et al. Geometry nature of hydraulic fracture propagation from oriented perforations and implications for directional hydraulic fracturing[J]. Computers and Geotechnics, 2020, 125: 103682. DOI:10.1016/j.compgeo.2020.103682 |
| [5] | Ju Y, Li Y, Wang Y L, et al. Stress shadow effects and microseismic events during hydrofracturing of multiple vertical wells in tight reservoirs: a three-dimensional numerical model[J]. Journal of Natural Gas Science and Engineering, 2020, 84: 103684. DOI:10.1016/j.jngse.2020.103684 |
| [6] | Yang Z Z, Yi L P, Li X G, et al. Pseudo-three-dimensional numerical model and investigation of multi-cluster fracturing within a stage in a horizontal well[J]. Journal of Petroleum Science and Engineering, 2018, 162: 190-213. DOI:10.1016/j.petrol.2017.12.034 |
| [7] | Zhang H, Sheng J J. Numerical simulation and optimization study of the complex fracture network in naturally fractured reservoirs[J]. Journal of Petroleum Science and Engineering, 2020, 195: 107726. DOI:10.1016/j.petrol.2020.107726 |
| [8] | Liu X, Qu Z, Guo T, et al. Numerical simulation of non-planar fracture propagation in multi-cluster fracturing with natural fractures based on Lattice methods[J]. Engineering Fracture Mechanics, 2019, 220: 106625. DOI:10.1016/j.engfracmech.2019.106625 |
| [9] | Li M, Guo P, Stolle D, et al. Modeling method and hydraulic fracture propagation for jointed rock mass using PHF-LSM method[J]. Journal of Natural Gas Science and Engineering, 2019, 68: 102910. DOI:10.1016/j.jngse.2019.102910 |
| [10] | Li M, Guo P, Stolle D, et al. Development of hydraulic fracture zone in heterogeneous material based on smeared crack method[J]. Journal of Natural Gas Science and Engineering, 2016, 35: 761-774. DOI:10.1016/j.jngse.2016.09.018 |
| [11] | Li M, Guo P, Stolle D, et al. Modeling method for a rock matrix with inclusions distributed and hydraulic fracturing characteristics[J]. Journal of Petroleum Science and Engineering, 2017, 157: 409-421. DOI:10.1016/j.petrol.2017.07.017 |
| [12] | 李明, 郭培军, 李鑫, 等. 基于水平集法的非均质岩石建模及水力压裂传播特性研究[J]. 岩土力学, 2016, 37(12): 3591-3597. (Li Ming, Guo Pei-jun, Li Xin, et al. Modelling method of heterogeneous rock material based on level set method and hydraulic fracture propagation features[J]. Rock and Soil Mechanics, 2016, 37(12): 3591-3597.) |
| [13] | Li M, Guo P J, Stolle D, et al. Heterogeneous rock modeling method and characteristics of multistage hydraulic fracturing based on the PHF-LSM method[J]. Journal of Natural Gas Science and Engineering, 2020, 83: 103518. DOI:10.1016/j.jngse.2020.103518 |
| [14] | Wasantha P L P, Konietzky H, Xu C. Effect of in-situ stress contrast on fracture containment during single- and multi-stage hydraulic fracturing[J]. Engineering Fracture Mechanics, 2019, 205: 175-189. DOI:10.1016/j.engfracmech.2018.11.016 |
| [15] | Medlin W. L.Laboratory investigation of fracture initiation pressure and orientation[J]. Society of Petroleum Engineers Journal, 19(2): 129-144. DOI:10.2118/6087-PA |
| [16] | Sneddon I N, Elliot H A. The opening of a Griffith crack under internal pressure[J]. Quarterly of Applied Mathematics, 1946, 4(3): 262-267. DOI:10.1090/qam/17161 |
| [17] | Rahman M M, Rahman M K. A review of hydraulic fracture models and development of an improved pseudo-3D model for stimulating tight oil/gas sand[J]. Energy Sources, Part A: Recovery, Utilization and Environmental Effects, 2010, 32(15): 1416-1436. DOI:10.1080/15567030903060523 |
| [18] | 才博, 唐邦忠, 丁云宏, 等. 应力阴影效应对水平井压裂的影响[J]. 天然气工业, 2014, 34(7): 55-59. (Cai Bo, Tang Bang-zhong, Ding Yun-hong, et al. Influenc of stress shadow on horizontal well fracturing[J]. Natural Gas Industry, 2014, 34(7): 55-59.) |
| [19] | 尹建, 郭建春, 曾凡辉, 等. 水平井分段压裂射孔间距优化方法[J]. 石油钻探技术, 2012, 40(5): 67-71. (Yin Jian, Guo Jian-chun, Zeng Fan-hui, et al. Perforation spacing optimization for staged fracturing of horizontal well[J]. Petroleum Drilling Techniques, 2012, 40(5): 67-71.) |
