王露, 易平涛, 李伟伟, 董乾坤
东北大学 工商管理学院，辽宁 沈阳 110169
收稿日期：2021-10-19
基金项目：国家自然科学基金资助项目(72171040, 72171041)；中央高校基本科研业务费专项资金资助项目(N2006013, N2006007)。
作者简介：王露(1992-)，女，江西上饶人，东北大学博士后研究人员。

摘要：针对综合评价中混合不确定信息共存、评价信息残缺和评价信息间非独立的评价问题，提出一种多关系混合不确定信息融合集成框架及其求解方法.首先，将混合不确定信息进行分类整合，梳理信息(子)流间的相关关系，构建多关系混合不确定信息集成框架，通过网络分析法(ANP)求解信息(子)流的信息权；其次，将混合信息转化随机数并模拟迭代，充分挖掘信息价值；最后，将被评价对象每次仿真迭代后的结果进行两两比较，获取优胜度矩阵，并通过回归树的方法得到体现概率特征的可能性排序.对混合残缺信息、多关系信息的融合问题进行了探索，降低了评价过程对数据完整性的要求，考虑了信息重叠和信息冗余，得到的相对评价结论对实际问题更具解释力.
关键词：综合评价多关系混合不确定信息集成框架ANP随机模拟可能性排序
Stochastic Simulation Integrated Method for Multi-relational Blended Uncertain Information and Its Applications
WANG Lu, YI Pingtao, LI Weiwei, DONG Qiankun
School of Business Administration, Northeastern University, Shenyang 110169, China
Corresponding author: WANG Lu, E-mail: wanglu1993531@163.com.

Abstract: In view of the problems of the coexistence of multi-source information, incomplete information, and non-independent evaluation questions of evaluation information, an integrated framework for multi-relational blended information and an information aggregation method are proposed. Firstly, the blended uncertain information is classified and integrated, the correlations are explored among information(sub)streams, and the integrated framework for multi-relational blended uncertain information is constructed. Secondly, the blended uncertain information is transformed into random numbers by simulation iterations to fully tap the value of information. Then, through the relationship graph of information(sub)flows, the information weight of information(sub)flows is solved by using the analytic network process(ANP). Finally, by comparing the results of each simulation iteration of the evaluated object, the pairwise priority matrix is obtained, and the probability ranking reflecting the probability characteristics is obtained by the regression tree method. The fusion of blended incomplete information and multi-relational information are explored by constructing the integrated framework for multi-relational blended uncertain information. The requirements for data integrity in the evaluation process are reduced, and information overlapping and information redundancy are considered. The relative conclusion is more explanatory for the practical problems.
Key words: integrated assessmentintegrated framework for multi-relational blended uncertain informationANPstochastic simulationthe most likely ranking
综合评价通常指对以多维信息描述的对象系统地做出客观、公正、全面的评价^[1]，作为管理科学领域的一个重要分支，已被广泛应用于经济发展、社会管理、生态治理等诸多领域，并取得了丰硕的研究成果^[2-3].人类步入信息更迭迅疾的时代，获取信息的方式更加多样，信息内容更加多元，评价者面临的评价环境具有复杂、异质等特征，不确定乃至模糊信息表达方式得到进一步发展，因此利用混合信息对复杂评价问题进行多方面描述是顺应大数据时代综合评价的发展趋势.然而，经典的综合评价模式通常能够处理的数据形式较为单一，如精确值^[4-5]、区间数^[6]、语言信息^[7-11]、模糊信息^[10-13]等，对多源混合评价信息的融合和集成表现出一定的局限性.已有****对此问题开展了研究，多数做法是将不同的数据类型转换成某种同一类型，以便于集结并得到绝对优劣的评价结论^[14-17].然而，不同类型评价信息的统一转换会使得原始数据类型丢失其特征，信息在较大程度上扭曲失真.其次，当评价信息包含来源多样、类别多种的不确定信息时，评价结论的绝对性与不确定信息的模糊特征存在一定的矛盾性，对包含不确定信息评价问题的解释缺乏信服力.
针对通常难以通过一次比较判断给出绝对形式评价结论的相对评价问题，如球队实力、综合能力、发展潜力比较的问题等，易平涛等^[18]将传统评价模式拓展为随机型评价模式，从信息收集、权重方法、集结等环节进行说明，并给出可能性排序的获取方法.文献[19]针对多信息来源、多数据结构的复杂评价问题，将传统评价模式进行了拓展，首次提出了泛综合评价方法，为多源信息的整合及求解提供了方法支撑.文献[20]以传统的评价模式为底层框架，对混合数据、多类型的赋权方法等评价信息进行分类整合，以信息集成框架的形式将所有评价信息囊括其中，通过蒙特卡罗仿真技术求解信息集成框架，得到具有概率特征的相对评价结论.文献[21]针对多方参与的政府绩效评价问题，将各类参与者提供的评价信息进行归类，通过充分的模拟仿真，得到具有概率性质的可能性排序.
上述研究中，被评价对象的评价信息是完整的，但在实际的数据收集过程中，通常会出现缺失信息或片段信息的现象.此外，上述研究均建立在信息(子)流之间独立的假设之上，但实际操作中由于评价环境的复杂性，评价信息之间可能存在一定的相关关系.本文将该问题视为“多关系”混合不确定信息评价问题，并认为“多关系”主要表现为以下两方面：1)信息子流之间存在相关关系；2)信息流之间存在相关关系.为解决上述问题，在已有研究的基础上，分类并整合混合不确定信息，搭建多关系混合不确定信息集成框架，并总结其求解步骤.除此之外，考虑到评价问题的规模及排序结果的稳定性，本研究介绍了基于回归树的可能性排序求解算法，为复杂多关系混合评价信息(包含残缺和片段信息)的融合求解提供一种可行的思路.
1 基本概念和问题界定评价参与者S₁, S₂, …, S_L依据评价流程，给出评价指标的混合信息及其相关关系，情况如下.
1) 评价参与者S_k(k=1, 2, …, L)依据自身知识和经验，给出x_j(j=1, 2, …, m)的指标数据，数据形式根据评价参与者的偏好或表达的精确程度可以为模糊数(实数、区间数、三角模糊数、梯形模糊数、直觉模糊数、区间直觉模糊数、直觉三角模糊数、直觉梯形模糊数)、语言集(语言信息、二元语义信息)、序数等.若评价参与者由于自身知识的限制或领域信息不对称，无法给出某些指标的数据信息，则该指标数据信息视为缺失.
2) 评价参与者S_k就指标数据给出指标赋权方法，一般评价参与者根据实际情况判断、主观意愿或客观数据均可给出赋权方法.
3) 评价参与者S_k依据实际情况和自身偏好提供线性或非线性信息集结方法等.
4) 评价参与者S_k从不同方面描述评价问题，梳理评价信息的相关关系.
综上可知，不同的评价参与者给出的指标信息具有两大特点：一是数据类型多样化；二是信息之间存在相关关系，这无疑加大了评价信息集成的难度.基于此，本研究主要针对多关系、多来源混合不确定信息(包含残缺信息)的集成问题，从评价问题涉及的不同层面对信息进行分类整合，梳理信息(子)流间的关系，构建多关系混合不确定信息集成框架，并进一步探讨其随机聚合求解方法.
2 混合不确定信息的处理和随机数的生成2.1 混合不确定信息的处理对某评价问题，设有L个评价者S₁, S₂, …, S_L给出的n个被评价对象O₁, O₂, …, O_n关于m个指标x₁, x₂, …, x_m的取值为x_ijk(i=1, 2, …, n; j=1, 2, …, m; k=1, 2, …, L)，x_ijk表示原始多源信息.目前数据信息拓展出多种形式，本文对运用广泛且具有代表性的几类信息进行处理.文献[22]介绍了实数、区间数、三角模糊数、直觉模糊数、语言信息、二元语义信息、序数，下面对其他类型的数据进行简单介绍.
设原始评价信息的取值范围为[x_ijk^a, x_ijk^b]，令处理后的评价信息为.其中，精确数、区间数、三角模糊数、直觉模糊数、语言信息、二元语义信息、序数等数据形式的处理参见文献[22]，其他形式数据的处理如下.
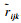
1) 梯形模糊数是一种模糊评价信息，表示为x_ijk=(x_ijk^l, x_ijk^m, x_ijkⁿ, x_ijk^u)∈F(R), 0 < x_ijk^l≤x_ijk^m≤x_ijkⁿ≤x_ijk^u.其中，R为实数集.
令处理后的梯形模糊数为=(r_ijk^l, r_ijk^m, r_ijkⁿ, r_ijk^u)，其中 .其隶属度函数为
2) 直觉梯形模糊数表示为x_ijk= < (x_ijk^l, x_ijk^m, x_ijkⁿ, x_ijk^u); μ_xijk, v_xijk>，处理后的直觉梯形模糊数表示为= < (r_ijk^l, r_ijk^m, r_ijkⁿ, r_ijk^u); >，其中r_ijk^l, r_ijk^m, r_ijkⁿ, r_ijk^u与上述梯形模糊数的处理相同，其隶属度函数为
3) 直觉三角模糊数表示为x_ijk= < (x_ijk^l, x_ijk^m, x_ijk^u); μ_xijk, v_xijk>，令处理后的直觉三角模糊数为= < (r_ijk^l, r_ijk^m, r_ijk^u); >，其中r_ijk^l, r_ijk^m, r_ijk^u的处理参见三角模糊数的处理方法，且隶属度函数为
4) 区间直觉模糊数：，其中.
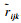
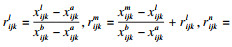
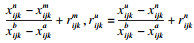
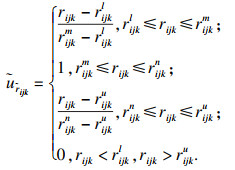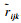
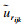
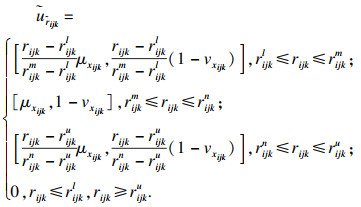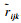
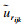
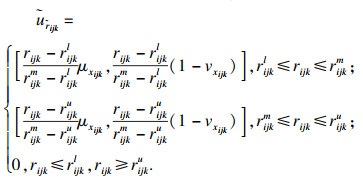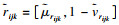
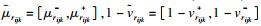
2.2 随机数生成及处理方法x_ijk为评价参与者S_k针对被评价对象o_i关于指标x_j给出的指标值，在2.1节中，将原始混合不确定信息转化至[0, 1]区间内，转化后的数据记为，在区间[r_ijk^l, r_ijk^u]中按特定分布随机生成一组数据，记为[z_ijk]_n×p.
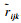
定义1 z_ijk^c表示在[r_ijk^l, r_ijk^u]区间里，运行第c次得到的的随机数，令表示经过处理用于信息集结的随机数值：

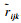
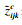
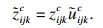(1)

其中，表示z_ijk^c在中的隶属度.
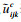
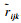
由模糊集的隶属度概念可知，当为实数或区间数时，=1，其余的数据类型可由2.1节中相应的隶属度函数求得.需要指出的是，任何一组随机数均不能表示原始数据的全部信息，只有进行充分的模拟，发生的随机数足够多时，才能尽可能地挖掘出原始信息的全部价值.采用随机模拟仿真生成随机数的方式，既可以避免数据类型之间转化过程中的失真，最大程度地保证每种数据类型本身的特征，又可以充分挖掘信息价值.
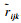
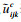
3 多关系混合不确定信息集成框架的构建及求解3.1 多关系混合不确定信息集成框架的构建根据评价问题涉及的不同层面对评价信息进行整合，以经典评价流程(评价数据、数据预处理、属性权重、集结模型)作为信息整合的重要节点.具体思路如下：①评价信息层面划分，按一定标准(如参与者知识领域特征、指标属性)将评价信息进行分类，每一类代表一个评价层；②集成框架构建，按照评价流程对评价信息进行分类和连接处理，即将评价问题层面、参与者、指标属性、数据处理方法、赋权方法、集结方法作为信息节点，将这些节点连起来形成信息流；③确定信息间的相关关系，若信息流和信息子流之间不独立，通过连线箭头反映信息流和信息子流之间的相关性，单向箭头表示单向影响，双向箭头表示相互影响.图 1给出了多关系混合不确定信息集成框架的简单示意图.图 1中，每条信息流可以包含多条信息子流，信息(子)流之间存在一定的相关关系，如图 2所示.
图 1(Fig. 1)

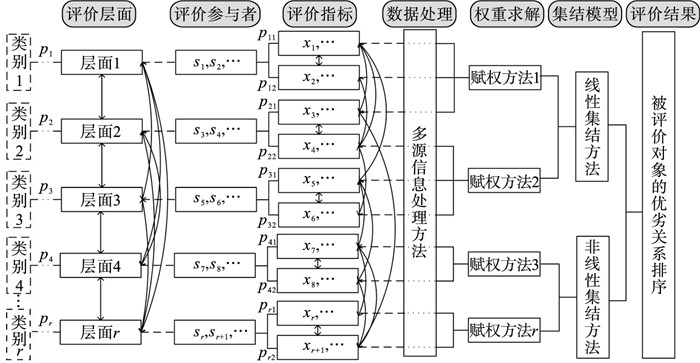图 1 多关系混合不确定信息集成框架Fig.1 Integrated framework for multi-relational blended uncertain information 注：根据评价问题的实际情况，可对集成框架重新调整或设计.

图 2(Fig. 2)

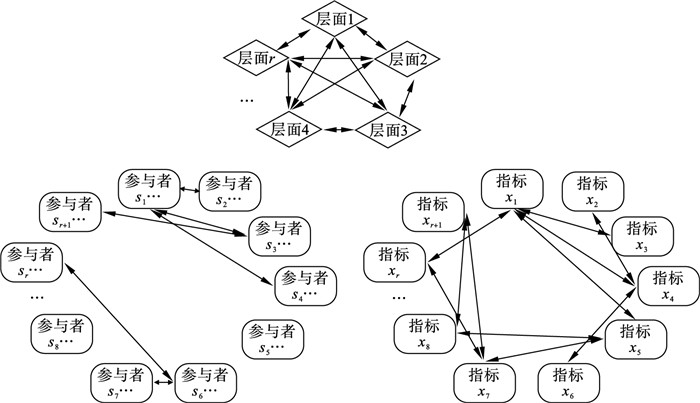图 2 信息(子)流的相关关系示意图Fig.2 Schematic diagram of relationship between information(sub)flows

3.2 多关系混合不确定信息集成框架的求解显然，相比于经典评价流程涉及的数据，本研究构建的信息集成框架中容纳了更多源、更复杂的信息，其求解过程中主要涉及两个关键问题：一是评价信息缺失时，如何求解集成框架；二是信息流和信息子流存在相关关系时，如何确定信息(子)流的信息权.
对问题一，本文并非对优胜度矩阵直接进行处理，而是采用对优胜次数矩阵进行线性整合，再转化为优胜度矩阵的求解思路.
对问题二，采用网络层次分析法(ANP)^[23]绘制信息(子)流的关系图，确定信息(子)流的重要性，即信息权，信息权的获取依据ANP的权重求解方法.
基于上述问题的解决思路，将多关系混合不确定信息集成框架的求解步骤总结如下.
步骤1????构建多关系混合不确定信息集成框架，确定信息(子)流之间的相关关系.根据ANP求解各条信息(子)流的信息权.
步骤2????将原始评价信息按照2.1节的处理方法将所有数值转化至[0, 1]区间内，便于模拟仿真的迭代.
步骤3????对第k条信息流，根据2.2节随机数的生成和处理方法，在对应数据类型的[r_ijk^l, r_ijk^u]区间内按某种分布方式随机提取数据，并按式(1)对其进行处理.根据已构建框架中的数据处理、赋权方法、集结模型等环节，对处理后的随机信息进行集结，得到被评价对象之间绝对优劣的排序结果.
步骤4????重复步骤3，进行充分的仿真，统计两两被评价对象之间的优劣结果的次数，得到优胜次数矩阵.当仿真次数足够大时，优胜次数矩阵达到稳定，则结束程序运行，对下一条信息(子)流进行模拟求解.
步骤5????记第k条信息流对应的第t条信息子流的优胜次数矩阵为H_kt，每条信息(子)流运行的次数为所有信息(子)流中运行的最大次数.则被评价对象经过充分仿真后，即两两之间进行充分比较后，可以得到综合优胜次数矩阵，记为H，则

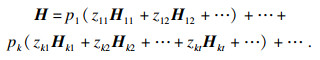(2)

其中：p_k表示第k条信息流的信息权；z_kt表示第k条信息流下的第t条信息子流的信息权.
步骤6????在综合优胜次数矩阵H=[h_ij]_n×n的基础上，由

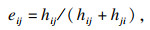(3)

可得优胜度矩阵E=[e_ij]_n×n，e_ij表示被评价对象O_i优于O_j的优胜度概率.
需要说明的是，若信息子流面向的评价信息是残缺的，得到的优胜次数矩阵仅包含非残缺信息的被评价对象的优胜次数结果.当优胜次数矩阵与信息权相乘时，不改变该条信息(子)流随机模拟得到的被评价对象间的优胜度概率.当多条信息(子)流的优胜次数矩阵进行线性整合时，被评价对象的优胜度概率才会发生改变.该方法可以充分利用片段或残缺信息，极大程度降低了数据收集的要求，同时可以在更大程度上实现评价的全面性.
4 基于回归树的可能性排序求解从求解中可以获取被评价对象的优胜度矩阵.显然，当n个对象参与评价问题时，可以得到n阶优胜度矩阵，从中可以导出n！条排序链.基于回归树的方法可以科学快速地导出最优排序链^[24]，需要注意的是，无论是绝对排序还是相对排序，排序的结果应具有保序性，即，则.
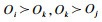
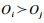
从优胜度概率的意义出发，两两被评价对象比较时被分为优于和劣于两类，当e_ij>0.5，表示O_i优于O_j，当e_ij < 0.5，表示O_i劣于O_j，当e_ij=0.5，表示O_i与O_j相当，而回归树的一项重要功能特征是将一个集合划分为两个具有差异的子集.因此，以优胜度概率0.5作为划分特征将所有被评价对象分为彼此存在差异但又不相交的对象集合，可以快速地筛出相邻被评价对象间优胜度概率大于0.5的排序链.具体思路为：若集合中仅包含1个对象，则该集合节点表示为叶节点；若集合中包含2个及以上的对象，则该集合节点表示为当前空间的根(父)节点.回归树的目标是将所有被评价对象划分至叶节点，然后采用中序遍历，先访问左子树，然后是根节点，最后是右子树.记录访问的节点(被评价对象)顺序，该顺序即为最后的排序结果.依据排序结果，从优胜度矩阵中找出排序链中相邻两者间的优胜度概率，即为所求的最稳定的带有概率特征的可能排序结果.
5 应用算例假设有8位评价参与者(S₁, S₂, …, S₈)对7个地区(O₁, O₂, …, O₇)的开放水平进行独立自主的评价，开放水平的评价涉及11项指标，包括对外贸易依存度(d₁)、净出口贡献率(d₂)、人均实际利用外资额(d₃)、服务业利用外资比(d₄)、外资工业企业产值比(d₅)、单位GDP外商投资活跃度(d₆)、货运活跃度(d₇)、客运活跃度(d₈)、城市化水平(d₉)、运网密度(d₁₀)、国际旅游收入比(d₁₁).评价参与者给出的原始评价信息如表 1所示，其中对外贸易依存度(d₁)中缺失被评价对象O₃, O₅, O₇的数据，城市化水平(d₉)中缺失被评价对象O₃, O₆的数据，国际旅游收入比(d₁₁)中缺失被评价对象O₆的数据.
表 1(Table 1)

表 1 开放水平的混合评价信息Table 1 Blended information for evaluating regional open level O d1 d2 d3 d4 d5 d6 O1 0.726 5 [0.734 5, 0.765 4] (相当, 0.4) (0.5, 0.2) 好 [5.6, 7.8, 8.2] O2 0.378 9 [3.652 6, 3.973 7] (相当, 0.25) (0.4, 0.32) 相当 [6.3, 7.2] O3 [2.414 8, 2.765 7] (好, 0.15) (0.6, 0.2) 很好 [5.9, 6.8] O4 0.780 4 [6.582 0, 6.964 4] (很好, -0.35) (0.45, 0.12) 差 [4.4, 4.9, 5.2] O5 [1.935 6, 3.076 9] (差, -0.15) (0.34, 0.3) 好 [3.2, 4.8, 5.3, 6.0] O6 0.082 4 [4.476 5, 7.008 0] (好, -0.45) (0.76, 0.2) 很差 [2.1, 3.4, 6.7, 8.4] O7 [7.100 2, 8.110 7] (很差, 0.45) (0.54, 0.3) (稍好, 0.2) [2.3, 4.5] O d7 d8 d9 d10 d11 O1 (< 0.3, 0.4, 0.5>, 0.6, 0.3) 1(序数) [3.5, 6] [1.386 3, 1.565 9] O2 (< 0.1, 0.3, 0.4, 0.6>, 0.6, 0.2) 2(序数) [6, 7, 9] [1.628 4, 2.956 9] ([0.567 5, 0.778 7], [0.100 0, 0.221 3]) O3 (< 0.4, 0.5, 0.7>, 0.8, 0.1) 3(序数) [2.512 9, 4.409 6, 5.506 6] ([0.458 8, 0.610 9], [0.210 3, 0.261 7]) O4 (< 0.5, 0.6, 0.8>, 0.6, 0.3) 6(序数) [4.9, 8.7] [1.304 4, 1.719 3, 3.116 7] ([0.634 7, 0.762 8], [0.115 2, 0.168 9]) O5 (< 0.4, 0.5, 0.6, 0.7>, 0.8, 0.1) 7(序数) [2.1, 3.5] [0.386 6, 0.854 7, 11.441 9] ([0.345 2, 0.618 4], [0.103 2, 0.228 0]) O6 (< 0.2, 0.4, 0.5>, 0.6, 0.3) 5(序数) [0.361 9, 0.581 6, 0.999 3, 1.567 8] O7 (< 0.2, 0.3, 0.4, 0.5>, 0.7, 0.1) 4(序数) [1.2, 2.4, 3.8] [0.155 2, 0.386 6, 1.097 7, 1.998 2] ([0.544 8, 0.714 7], [0.168 1, 0.260 3])

表 1 开放水平的混合评价信息 Table 1 Blended information for evaluating regional open level

1) 多关系信息集成框架的构建.开放水平的评价问题从4个层面进行描述: 贸易开放(C₁)、生产开放(C₂)、市场开放(C₃)和区位支撑(C₄).其中指标d₁，d₂，d₃，d₄归类于贸易开放；d₅归类于生产开放；d₆，d₇，d₈归类于市场开放；d₉，d₁₀，d₁₁归类于区位支撑.评价参与者S₁，S₂在贸易开放层面具备更完善的知识结构，给出评价信息；S₃，S₄擅长生产开放层面；S₅，S₆擅长市场开放层面；S₇，S₈擅长区位支撑层面.按照文中介绍的步骤构建多关系混合不确定信息集成框架，如图 3所示，评价参与者给出信息流和信息子流的关系图如图 4所示.
图 3(Fig. 3)

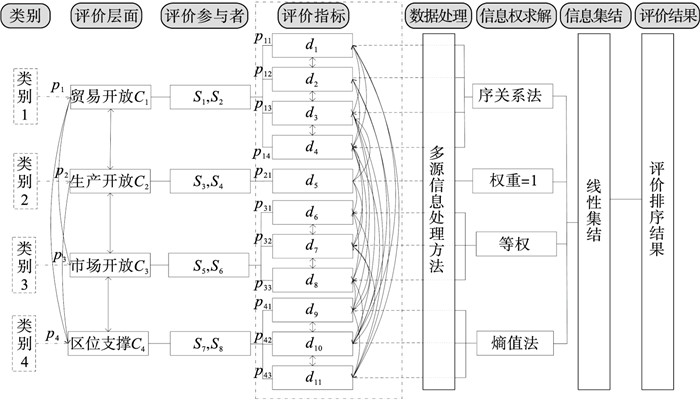图 3 开放水平的多关系混合不确定信息集成框架Fig.3 Integrated framework for multi-relation blended uncertain information of open level

图 4(Fig. 4)

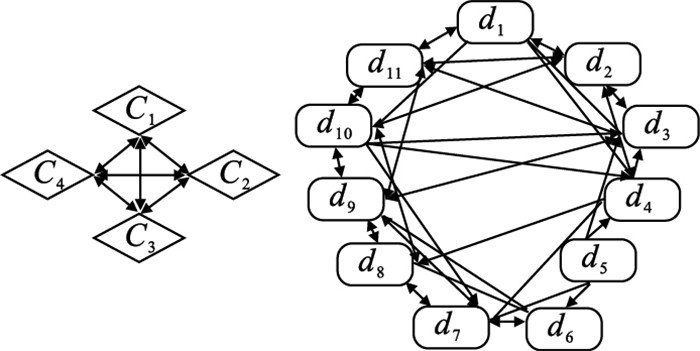图 4 开放水平集成框架信息流和信息子流的关系图Fig.4 Diagram of relationship between information(sub) flows in the integrated framework for open level

2) 信息权的确定.借助Super Decision软件，运用ANP求解信息(子)流的信息权.Super Decision软件给出了多种方式确定判断值输入数据，将所有存在相关关系的元素和元素组进行优势度比较.根据图 4，分别得到4个信息流关系矩阵和11个信息子流关系矩阵，每个关系矩阵都要进行一致性检验.一般地，当平均随机一致性指标小于0.1时，认为判断矩阵的一致性是可以接受的.通过Super Decision软件求得：①信息流的信息权分别为p₁=0.472 9，p₂=0.284 4，p₃=0.072 8，p₄=0.169 9.②不同类别下的信息子流的信息权分别为p₁₁=0.117 6，p₁₂=0.192 7，p₁₃=0.542 3，p₁₄=0.147 4，p₂₁=1，p₃₁=0.558 3，p₃₂=0.297 4，p₃₃=0.144 3，p₄₁=0.454 5，p₄₂=0.144 3，p₄₃=0.401 2.
3) 混合不确定信息的处理.由表 1可见，原始数据的取值范围为[0.065 2, 0.9]，对原始混合不确定信息进行处理，将所有数值转化至[0, 1]区间范围内，便于仿真模拟的迭代，如表 2所示.
表 2(Table 2)

表 2 转化至[0, 1]区间内数据形式的评价信息Table 2 The evaluation information transformed into the range of [0, 1] O d1 d2 d3 d4 d5 d6 O1 0.074 0 [0.074 9, 0.078 4] (0.375, 0.5, 0.725) (0.5, 0.2) (0.625, 0.75, 0.875) [0.619 5, 0.865 7, 0.910 5] O2 0.035 1 [0.401 5, 0.437 4] (0.375, 0.5, 0.688) (0.4, 0.32) (0.375, 0.5, 0.625) [0.697 8, 0.798 5] O3 [0.263 0, 0.302 2] (0.625, 0.75, 0.913) (0.6, 0.2) (0.75, 0.875, 1) [0.653 0, 0.753 8] O4 0.080 0 [0.729 4, 0.772 2] (0.663, 0.875, 1) (0.45, 0.12) (0.125, 0.25, 0.375) [0.485 2, 0.541 1, 0.574 7] O5 [0.209 3, 0.286 8, 0.337 1] (0.087 5, 0.25, 0.375) (0.34, 0.3) (0.625, 0.75, 0.875) [0.350 9, 0.529 9, 0.585 9, 0.664 2] O6 0.001 9 [0.493 7, 0.707 1, 0.777 1] (0.513, 0.75, 0.875) (0.76, 0.2) (0, 0.125, 0.25) [0.227 7, 0.373 2, 0.742 6, 0.932 8] O7 [0.787 4, 0.900 5] (0, 0.125, 0.138) (0.54, 0.3) (0.5, 0.625, 0.8) [0.250 1, 0.496 4] O d7 d8 d9 d10 d11 O1 (< 0.3, 0.4, 0.5>, 0.6, 0.3) (0.875, 1) [0.384 4, 0.664 2] [0.141 9, 0.168 0] O2 (< 0.1, 0.3, 0.4, 0.6>, 0.6, 0.2) (0.75, 0.875) [0.664 2, 0.776 2, 1] [0.175 0, 0.323 6] ([0.567 5, 0.778 7], [0.100 0, 0.221 3]) O3 (< 0.4, 0.5, 0.7>, 0.8, 0.1) (0.625, 0.75) [0.274 0, 0.486 2, 0.609 0] ([0.458 8, 0.610 9], [0.210 3, 0.261 7]) O4 (< 0.5, 0.6, 0.8>, 0.6, 0.3) (0.25, 0.375) [0.541 1, 0.966 4] [0.138 7, 0.185 1, 0.341 5] ([0.634 7, 0.762 8], [0.115 2, 0.168 9]) O5 (< 0.4, 0.5, 0.6, 0.7>, 0.8, 0.1) (0.125, 0.25) [0.227 7, 0.384 4] [0.036 0, 0.088 4, 0.154 1] ([0.345 2, 0.618 4], [0.103 2, 0.228 0]) O6 (< 0.2, 0.4, 0.5>, 0.6, 0.3) (0.375, 0.5) [0.033 2, 0.057 8, 0.104 5, 0.168 2] O7 (< 0.2, 0.3, 0.4, 0.5>, 0.7, 0.1) (0.5, 0.625) [0.127 0, 0.261 3, 0.418 0] [0.010 1, 0.036 0, 0.115 6, 0.216 3] ([0.544 8, 0.714 7], [0.168 1, 0.260 3])

表 2 转化至[0, 1]区间内数据形式的评价信息 Table 2 The evaluation information transformed into the range of [0, 1]

按照均匀分布的方式在各评价指标的取值区间内随机取值，并依据随机模拟仿真步骤和开放水平的多关系混合不确定信息集成框架对随机取值进行集结.
4) 优胜度矩阵.根据式(2)得到综合优胜次数矩阵H为
根据式(3)得到优胜度矩阵E为
5) 基于回归树的可能性排序.基于第4节的方法，求解优胜度矩阵，得到7个地区开放水平的可能性排序.
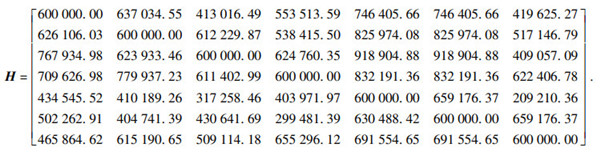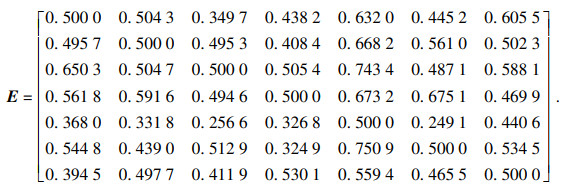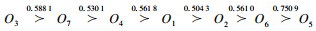
6) 与绝对排序方法的比较.将表 2的评价信息均转化为精确值，区间数取中值，三角模糊数、梯形模糊数取期望值，直觉三角模糊数和直觉梯形模糊数可按(u+v)(x_ijk^l+x_ijk^m+x_ijkⁿ)/3和(u+v)(x_ijk^l+x_ijk^m+x_ijkⁿ+x_ijk^u)/4转化为精确值，直觉模糊数和区间直觉模糊数分别按文献[25]和[26]的精确函数处理.将转化为精确值的信息按极值法进行预处理，并用指标的平均值补足残缺数据.根据复相关系数法^[27]求得非独立指标d₁~d₁₁的权重分别为0.064 47，0.022 65，0.031 73，0.034 75，0.082 69，0.009 94，0.047 40，0.126 76，0.032 17，0.049 64，0.497 79.按线性集结方法求得最后的绝对排序为.
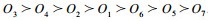
对比可知，虽然绝对排序与上述给出的可能性排序结果之间存在差异，但可将绝对排序看成由优胜度矩阵得到的多种可能性排序中的一种，即，这种带有概率特征的可能性排序对包含不确定信息、复杂关系信息的评价问题的解释更具柔性，如绝对排序和可能性排序中O₆均优于O₅，但可能性排序表示O₆以75.09%的概率优于O₅.绝对排序认为O₂优于O₁，可能性排序中，O₂优于O₁的概率为49.57%，O₂优于O₁发生的概率相对较小，但并非不可能发生.
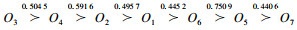
此外，排序链与上述给出的可能性排序的区别在于排序链发生的概率不同，从整条排序链发生概率视角看，本文给出的可能性排序结论更为可取.
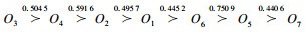
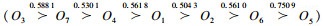
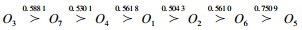
6 结语本文针对混合信息共存、评价信息残缺和评价信息间存在相关关系的评价问题，提出一种多关系信息融合集成框架.求解过程为: 1) 以评价问题涉及的不同层面对信息进行分类整合，梳理信息(子)流之间的相关关系，通过ANP求解信息(子)流的信息权；2) 将混合不确定信息转化为随机数，通过充分的仿真，得到优胜度矩阵；3)基于回归树快速地获取带有概率特征的可能性排序结论.相对评价结论形式提高了对评价问题的解释性，如历史上以少胜多的情形，同时当混合不确定信息共存时，可能性评价结论的概率特征与不确定信息的模糊特征更加呼应，因此更为评价者及被评价对象接受.
所提出的评价方法可以为混合信息提供统一的融合平台，从方法层面上降低对数据完整性的要求，更大程度上实现评价的全面性.在大数据信息时代，信息重叠和信息冗余是普遍存在的现象，文中探讨的方法为处理多关系评价信息提供切实的解决思路，为评价信息不独立且关系复杂的问题提供技术参考.
参考文献

[1]	易平涛, 李伟伟, 郭亚军. 综合评价理论与方法[M]. 2版. 北京: 经济管理出版社, 2019. (Yi Ping-tao, Li Wei-wei, Guo Ya-jun. Theory and method of comprehensive evaluation[M]. 2nd ed. Beijing: Economic Management Press, 2019.)
[2]	Zavadskas E K, Turskis Z. Multiple criteria decision making(MCDM)methods in economics: an overview[J]. Technological and Economic Development of Economy, 2011, 17(2): 397-427. DOI:10.3846/20294913.2011.593291
[3]	Wang X X, Xu Z S, Su S F, et al. A comprehensive bibliometric analysis of uncertain group decision making from 1980 to 2019[J]. Information Sciences, 2021, 547: 328-353. DOI:10.1016/j.ins.2020.08.036
[4]	Ma F M, Guo Y J, Yi P T. Cluster-reliability-induced OWA operators[J]. International Journal of Intelligent Systems, 2012, 27: 823-836. DOI:10.1002/int.21549
[5]	Hsu W C, Liou J J, Lo H W. A group decision-making approach for exploring trends in the development of the healthcare industry in Taiwan[J]. Decision Support Systems, 2021, 141: 113447. DOI:10.1016/j.dss.2020.113447
[6]	Yi P T, Li W W, Zhang D N. On possible outputs of group decision making with interval uncertainties based on simulation techniques[J]. Soft Computing, 2020, 24: 9205-9213. DOI:10.1007/s00500-019-04447-9
[7]	Cabrerizo F J, Alonso S, Herrera-Viedma E. A consensus model for group decision making problems with unbalanced fuzzy linguistic information[J]. International Journal of Information Technology & Decision Making, 2009, 8(1): 109-131.
[8]	Liu P D, Chen S M. Multi-attribute group decision making based on intuitionistic 2-tuple linguistic information[J]. Information Sciences, 2018, 430/431: 599-619. DOI:10.1016/j.ins.2017.11.059
[9]	Wu Q, Wang F, Zhou L, et al. Method of multiple attribute group decision making based on 2-dimension interval type-2 fuzzy aggregation operators with multi-granularity linguistic information[J]. International Journal of Fuzzy Systems, 2017, 19: 1880-1903. DOI:10.1007/s40815-016-0291-9
[10]	Garg H, Kumar K. Linguistic interval-valued Atanassov intuitionistic fuzzy sets and their applications to group decision making problems[J]. IEEE Transactions on Fuzzy Systems, 2019, 27(12): 2302-2311. DOI:10.1109/TFUZZ.2019.2897961
[11]	Garg H. Linguistic pythagorean fuzzy sets and its applications in multi-attribute decision-making process[J]. International Journal of Intelligent Systems, 2018, 33(6): 1234-1263. DOI:10.1002/int.21979
[12]	Mardani A, Nilashi M, Zavadskas E K, et al. Decision making methods based on fuzzy aggregation operators: three decades review from 1986 to 2017[J]. International Journal of Information Technology & Decision Making, 2018, 17(2): 391-466.
[13]	Sirbiladze G, Sikharulidze A. Extensions of probability intuitionistic fuzzy aggregation operators in fuzzy MCDM/MADM[J]. International Journal of Information Technology & Decision Making, 2018, 17(2): 621-655.
[14]	Morente-Molinera J A, Wu X, Morfeq A, et al. A novel multi-criteria group decision-making method for heterogeneous and dynamic contexts using multi-granular fuzzy linguistic modelling and consensus measures[J]. Information Fusion, 2020, 53: 240-250. DOI:10.1016/j.inffus.2019.06.028
[15]	Hasan M M, Jiang D, Ullah A S, et al. Resilient supplier selection in logistics 4.0 with heterogeneous information[J]. Expert Systems with Applications, 2020, 139: 112799. DOI:10.1016/j.eswa.2019.07.016
[16]	Liang Y, Qin J, Martínez L, et al. A heterogeneous QUALIFLEX method with criteria interaction for multi-criteria group decision making[J]. Information Sciences, 2020, 512: 1481-1502. DOI:10.1016/j.ins.2019.10.044
[17]	Yu J, Gu S, Zhang W J. Technology state control based on multi-source heterogeneous data fusion in manufacturing[J]. International Journal of Computational Intelligence Systems, 2020, 13(1): 638-644. DOI:10.2991/ijcis.d.200518.001
[18]	易平涛, 李伟伟, 郭亚军. 随机模拟型综合评价模式及其求解算法[J]. 运筹与管理, 2014, 23(6): 222-228. (Yi Ping-tao, Li Wei-wei, Guo Ya-jun. Stochastic simulation model of comprehensive evaluation and the solution[J]. Operations Research and Management Science, 2014, 23(6): 222-228. DOI:10.3969/j.issn.1007-3221.2014.06.030)
[19]	易平涛, 李伟伟, 郭亚军. 泛综合评价信息集成框架求解算法及应用[J]. 中国管理科学, 2015, 23(10): 131-138. (Yi Ping-tao, Li Wei-wei, Guo Ya-jun. Information integrated framework and its algorithm of generic comprehensive evaluation and the applications[J]. Chinese Journal of Management Science, 2015, 23(10): 131-138.)
[20]	李伟伟, 易平涛, 郭亚军, 等. 模拟视角下广义混合型决策信息的综合集成[J]. 系统工程与电子技术, 2016, 38(6): 1339-1344. (Li Wei-wei, Yi Ping-tao, Guo Ya-jun, et al. Synthetic integration of generalized hybrid decision information under simulation aspect[J]. Systems Engineering and Electronics, 2016, 38(6): 1339-1344.)
[21]	李伟伟, 易平涛, 郭亚军. 多方参与政府绩效评价的模式、方法及求解[J]. 系统工程, 2014, 32(10): 105-111. (Li Wei-wei, Yi Ping-tao, Guo Ya-jun. The evaluation model, method and algorithm of government performance evaluated by multi-participants[J]. Systems Engineering, 2014, 32(10): 105-111. DOI:10.3969/j.issn.1001-2362.2014.10.065)
[22]	李伟伟, 易平涛, 郭亚军. 混合评价信息的随机转化方法和应用[J]. 控制与决策, 2014, 29(4): 753-758. (Li Wei-wei, Yi Ping-tao, Guo Ya-jun. Blended evaluation information random transformation method and its application[J]. Control and Decision, 2014, 29(4): 753-758.)
[23]	Saaty T L. Decision making—the analytic hierarchy and network processes(AHP/ANP)[J]. Journal of Systems Science and Systems Engineering, 2004, 13(1): 1-35. DOI:10.1007/s11518-006-0151-5
[24]	王露, 易平涛, 李伟伟. 多源不确定信息的随机模拟聚合评价方法及应用[J/OL]. 中国管理科学[2022-06-10]. DOI: https://xuebao.neu.edu.cn/natural/article/2022/1005-3026/10.16381/j.cnki.issn1003-207x.2021.0547. (Wang Lu, Yi Ping-tao, Li Wei-wei. Stochastic simulation integrated method for multi-source uncertain information and its application[J/OL]. Chinese Journal of Management Science[2022-06-10]. DOI: https://xuebao.neu.edu.cn/natural/article/2022/1005-3026/10.16381/j.cnki.issn1003-207x.2021.0547. )
[25]	Atanassov K T, Gargov G. Interval-valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1989, 31(3): 343-349. DOI:10.1016/0165-0114(89)90205-4
[26]	龚日朝, 马霖源. 基于区间直觉模糊数得得分函数与精确函数及其应用[J]. 系统工程理论与实践, 2019, 39(2): 463-475. (Gong Ri-chao, Ma Lin-yuan. A new score function and accuracy function of interval-valued intuitionistic fuzzy number and its application[J]. System Engineering Theory and Practice, 2019, 39(2): 463-475.)
[27]	Garg H, Rani D. A robust correlation coefficient measure of complex intuitionistic fuzzy sets and their applications in decision-making[J]. Applied Intelligence, 2019, 49: 496-512. DOI:10.1007/s10489-018-1290-3