
 , 何年, 刘隆兴
, 何年, 刘隆兴 东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004
收稿日期:2021-11-29
基金项目:中央高校基本科研业务费专项资金资助项目(N2023021)。
作者简介:单鹏(1985-),男,河南平舆人,东北大学副教授。
摘要:利用衰减全反射傅里叶变换红外光谱(ATR-FTIR)技术对聚谷氨酸(γ-PGA)发酵批次进行快速识别检测.根据5个批次的γ-PGA发酵液光谱建立了5个偏最小二乘判别分析(PLSDA)分类模型来鉴别每一批次与其他批次,在某些局部评价指标(准确率)上取得了不错的结果.为了提高模型在全体指标(如准确率、精度、灵敏度等)上的整体效果和模型的可解释性,采用子窗口置换分析(SPA)、竞争自适应重加权采样(CARS)以及随机青蛙(RF)三种波数选择算法结合PLSDA提取特征波数,建立PLSDA判别模型.实验结果表明,经波数选择(除CARS)后,PLSDA在各个批次上的各项性能指标均得到提升,而且模型复杂度降低,可解释性增强;ATR-FTIR技术结合SPA-PLSDA或RF-PLSDA方法可实现对γ-PGA发酵批次的快速识别.
关键词:衰减全反射聚谷氨酸偏最小二乘判别分析竞争自适应波数选择
Research on Batch Classification of γ-Polyglutamic-Acid Fermentation Based on ATR-FTIR Spectroscopy
SHAN Peng, WU Zhui

 , HE Nian, LIU Long-xing
, HE Nian, LIU Long-xing School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: WU Zhui, E-mail: ZhuiWu_NEU@163.com.
Abstract: Attenuated total reflection Fourier transform infrared spectroscopy(ATR-FTIR)technology is utilized to quickly identify and detect different fermentation batches for γ-polyglutamic-acid(γ-PGA). Based on partial least squares discriminant analysis(PLSDA), five classification models were established to distinguish each batch from other batches, which performed well on several individual evaluation indicators(e.g., accuracy). In order to improve the model performance on all the indicators(e.g., accuracy, precision, sensitivity, etc.)and the model interpretability, three wavenumber selection methods including subwindow permutation analysis(SPA), competitive adaptive reweighted sampling(CARS)and random frog(RF)were combined with PLSDA to extract key wavenumbers and then established the corresponding classification models. Experimental results show that all the performance indicators of PLSDA combined with wavenumber selection(except CARS-PLSDA)are improved. Additionally, both the model complexity and interpretability are improved. Therefore, ATR-FTIR technology combined with SPA-PLSDA or RF-PLSDA method can realize rapid identification of different γ-PGA fermentation batches.
Key words: attenuated total reflectionγ-polyglutamic-acid (γ-PGA)partial least squares discriminant analysis(PLSDA)competitive adaptivewavenumber selection
聚谷氨酸(γ-polyglatamic-acid, γ-PGA)由于其水溶性、吸附性好等特点,它及其衍生物被广泛应用于食品工业、化妆品行业,以及医疗保健行业[1].γ-PGA作为一种批次发酵的产物,其发酵过程复杂,易受到各种因素的影响,无法严格保证每个批次发酵条件完全相同,使得不同批次生产的γ-PGA产品质量有所差异.通过对γ-PGA发酵批次的鉴别,可以为鉴别γ-PGA产品质量提供关键的信息.传统的CTAB法[2]、HPLC法[3]、GPC法[4]等化学检测方法对γ-PGA发酵过程提供信息十分有限,而且上述分析方法大多相对复杂、耗时长且需要专业技能.此外,通常需要对样品进行预处理,这样不仅进一步增加检测的复杂性和成本,还可能改变γ-PGA发酵有机分子官能团特征.相比之下,衰减全反射傅里叶变换红外光谱(ATR-FTIR)是一种相对简单、快速、廉价且非侵入性的技术[5],无需任何复杂的样品预处理;此外其光谱范围在4 000到400 cm-1之间,能够准确地提供γ-PGA发酵过程中大部分有机分子化学键和官能团信息,非常适用于γ-PGA发酵过程的监测.
由于发酵条件无法保证完全相同,不同批次γ-PGA发酵液光谱存在差异.根据这些光谱差异,可以对γ-PGA产品批次进行鉴别.γ-PGA光谱信息量大,而且变量之间存在多元相关性.传统的判别分析方法,如线性判别分析(linear discriminant analysis, LDA)[6]、二次判别分析(quadratic discriminant analysis, QDA)[7]、K近邻(K-nearest neighbor, KNN)[8]无法处理多元共线性,分类效果很不理想,所以本文采用了适合处理多元共线性问题的偏最小二次判别分析(partial least squares discriminant analysis, PLSDA)[9]方法.PLSDA方法包括了主成分分析、多元线性回归分析、典型相关性分析,对于本文处理γ-PGA发酵光谱的高维度、噪声大、变量间存在相关性的数据十分适用[10-15].
本文采集了5个批次的γ-PGA发酵液ATR-FTIR数据.先利用波数选择的方法挑选出了重要变量,再利用PLSDA建立分类模型,对样品的批次进行定性分析,测试样品的准确率可以达到87 % 以上.实验表明,波数选择结合PLSDA可以对ATR-FTIR采集的γ-PGA发酵液光谱实现快速鉴别分类.
1 实验部分1.1 对菌种进行发酵培养γ-PGA发酵实验选用中国工业微生物菌种保藏管理中心(China Center of Industrial Culture Collection, CICC)枯草芽孢杆菌亚种为菌种(编号20643).菌种是以冻干粉形式储存的,将菌种溶于无菌水恢复活性后,用接种环将菌群接种于固体培养基,再将其置于电热恒温箱培养24~48 h.随后挑选一株长势良好的菌体,接种在种子培养基中,然后在37 ℃和180 r/min的恒温振荡培养箱中(THZ-92A,跃进医疗器械有限公司,中国上海)培养10~16 h.接着将种子培养基中种子液按2 % 接种量接种至发酵培养基中,并将3 L的发酵培养基置于5 L的发酵罐(GRJB-5D,绿色生物工程有限公司,中国镇江)中,在37 ℃恒温和300 r/min搅拌速度的条件下进行发酵.上述三种培养基配置如下,固体培养基:蛋白胨(10 g/L),牛肉膏(5 g/L),氯化钠(5 g/L)以及2 % 琼脂粉;种子培养基:葡萄糖(10 g/L),牛肉膏(5 g/L),蛋白胨(10 g/L),氯化钠(5 g/L);发酵培养基:葡萄糖(35 g/L),酵母膏(5 g/L),谷氨酸钠(30 g/L),氯化铵(2 g/L),磷酸氢二钾(5 g/L)和硫酸镁(0.5 g/L).三种培养基均需在121 ℃下灭菌20 min.
1.2 对发酵液进行光谱采集采用带有水平铂金钻石ATR采样附件的布鲁克Alpha型傅里叶变换红外光谱仪(德国埃特林根)来收集发酵液光谱数据.在35 ℃下,以8 cm-1的分辨率进行了64次扫描,在4 000~600 cm-1的波数范围内测量每个批次的发酵液光谱.在每个批次发酵液测量前,用蒸馏水作为参考获取背景光谱.对于每个样品,都将测量重复两次.在总共进行了48 h的5次发酵实验中,获得了5个批次共151个样品的光谱数据.5个批次样本数分别为14,27,40,40和30,它们的光谱见图 1.γ-PGA特征光谱分别位于1 649~1 902 cm-1和2 698~2 834 cm-1两个波段;1 536~1 596 cm-1是谷氨酸钠的特征光谱范围;葡萄糖的特征光谱范围位于1 326~1 392 cm-1.此外C=C,C=O,C=N等伸缩振动时红外吸收波数范围为1 800~1 500 cm-1,而—CHO等伸缩振动红外吸收波数范围为2 700~3 000 cm-1.这些光谱差异信息可以作为γ-PGA批次分类的鉴别信息.
图 1(Fig. 1)
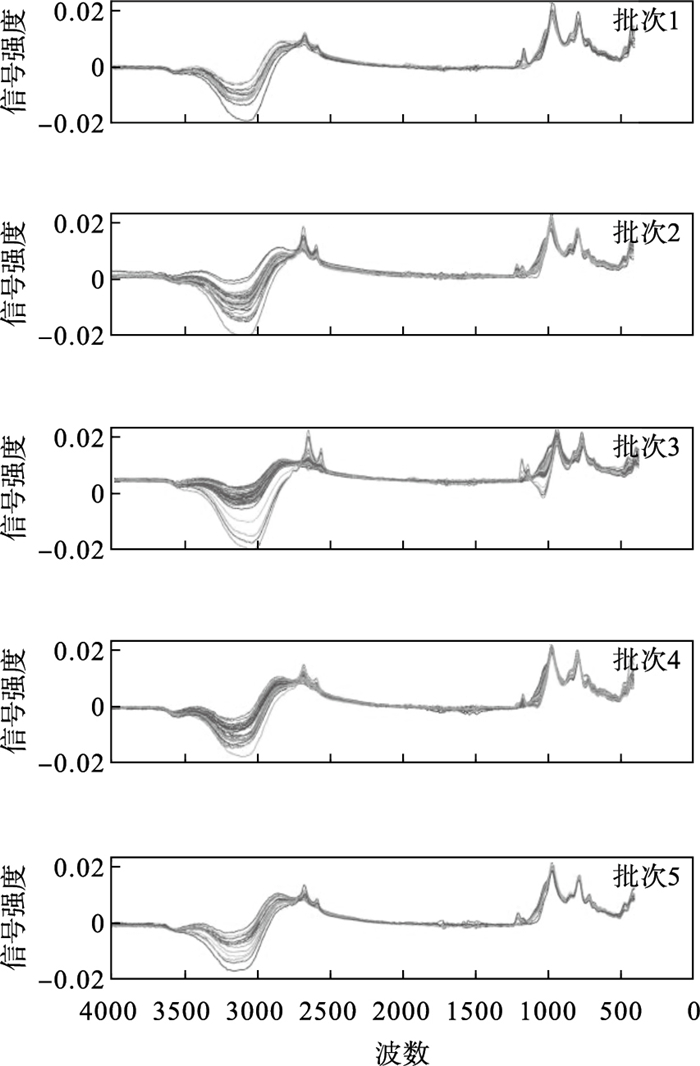 | 图 1 γ-PGA 5个发酵批次的光谱图Fig.1 The spectra for 5 different batches of γ-PGA fermentation |
1.3 模型建立1.3.1 PLSDA原理简介PLSDA是一种有监督的判别分析统计方法[16],该方法被用来建立γ-PGA发酵液样品光谱与发酵批次之间的关系模型,来实现对样品批次的预测.PLSDA是基于LDA基础上的偏最小二乘(partial least squares,PLS),它同时对样本光谱矩阵X∈ Rm×n (m和n分别为样本数和光谱变量数)和类别标签向量y∈Rm×1进行分解,突显类别信息在光谱分解时的作用,以提取出与样本类别最相关的光谱信息,即最大化提取不同类别光谱之间的差异.
PLSDA建立X与y之间的数学模型:
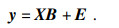 | (1) |
在建立模型(1)之前,先通过PLS对X和y进行双线性分解:
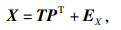 | (2) |
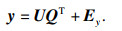 | (3) |
T和U中的得分向量为原始变量的线性组合:
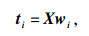 | (4) |
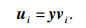 | (5) |
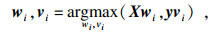 | (6) |
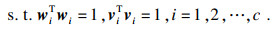 | (7) |
图 2(Fig. 2)
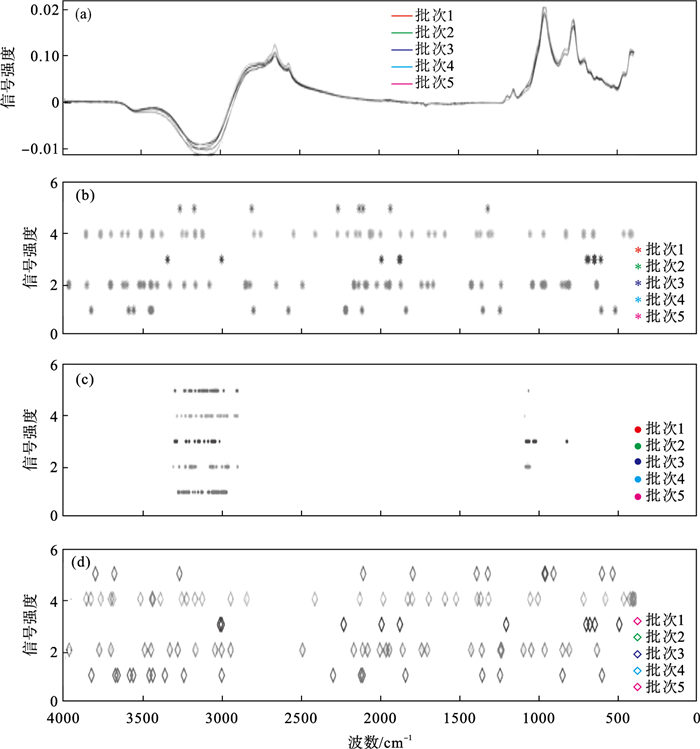 | 图 2 5个批次的平均光谱及不同选择方法挑选的波数Fig.2 Average spectrum of five batches and select wavenumber by different method (a)—平均光谱;(b)—方法RF;(c)—方法SPA;(d)—方法CARS. |
1.3.3 建立模型本文主要关注每个批次与其他批次的分类效果,因此采用二分类分类器,将每个批次作为一个小类,将其余4个批次作为一个大类.为了保证样本划分均衡,对大类和小类同时进行KS(kennard-stone)划分.用KS算法将γ-PGA发酵液光谱数据按照3∶ 1比例划分,其中3份作为训练集,建立模型;一份作为测试集,用来验证模型.用波数选择方法,挑选出重要性高的波数.采用5折交叉验证,对挑选出的变量交叉验证分析,从1~20中选出最佳潜在变量个数.最后利用PLSDA算法对训练集建立模型,用测试集来验证模型精度.所有模型建立之前,光谱数据均进行中心化预处理.
1.3.4 评价指标所得模型根据正确率、准确率、召回率、特异性、F1得分共5个指标来评价,其中真阳性(true positive, TP)、假阳性(false positive, FP)、假阴性(false negative, FN),真阴性(true negative, TN)评价指标计算公式如下:
正确率表示预测正确样本占总样本数比例:
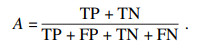 | (8) |
 | (9) |
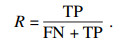 | (10) |
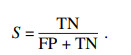 | (11) |
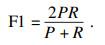 | (12) |
2 结果与讨论2.1 PLSDA(无波数选择)结果分析不进行波数挑选,直接利用PLSDA算法进行5次二分类,5个批次训练集的精度都达到了100 %,测试集精度除了批次3为100 %,其余4个批次也在92.1 % ~94.9 % 之间.具体数据如表 1所示.
表 1(Table 1)
| 表 1 PLSDA方法分类结果 Table 1 Classification results with PLSDA method | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2 不同波数选择结合PLSDA的结果分析2.2.1 SPA-PLSDA结果分析通过1 000次蒙特卡洛实验,SPA挑选出合理的波数,再结合PLSDA对挑选出的波数进行建模,实验结果见表 2.挑选的波数(见图 2c)主要集中在波峰与波谷处,挑选出连续的波数,对应了其移动窗口选择波数的特点.相比于不进行波数选择,SPA-PLSDA模型在5个训练集模型精度都接近100 %,测试集精度4个批次达到了100 %,批次1为97.4 %,而且F1得分、测试集敏感度以及测试集精度上都有显著提升.经过波数选择后,大大降低了模型的复杂度,但预测精度仍然能够保持甚至提升.这些结果都表明了SPA-PLSDA十分适用于γ-PGA发酵批次分类.
表 2(Table 2)
| 表 2 SPA-PLSDA方法分类结果 Table 2 Classification results with SPA-PLSDA method | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2.2 CARS-PLSDA结果分析利用CARS算法进行波数选择,首先构建包含所有变量的模型,接着以迭代方式消除最不重要的变量.每次迭代中要消除的变量数量由指数递减函数和自适应加权采样技术所决定.且在每次迭代中,不是对单个变量重要性评估,而是对变量子集进行评估[21].CARS算法对于变量重要程度判断标准较为严格,挑选的波数(见图 2d)主要集中在波段的前部和中后部;其中批次3虽然只挑选了10个特征波数的组合(279,282,501,569,602,793,937,943,952和996 cm-1),但预测性能与全波段模型性能相当.相比于表 1不进行波数选择情况,尽管训练模型的精度仍然是100 %,但测试集精度显著降低,其中批次1,2和4都降低了5 % ~8 %,降低幅度较大,特别是在测试集批次1中,将所有类别都归为了大类,而仅仅在批次5有一点提升,各项指标也不够理想,具体数据如表 3所示.
表 3(Table 3)
| 表 3 CARS-PLSDA方法分类结果 Table 3 Classification results with CARS-PLSDA method | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2.3 RF-PLSDA结果分析RF通过在模型空间中模拟一条服从稳态分布的马尔科夫链,来计算每个变量的被选概率,然后根据所有变量的排名选择变量[22].挑选的波数见图 2b,整个波数的选择都比较随机,在整个波段中也比较均匀分散.特别是批次3与5分别挑选出10个(951,963,941,952,603,601,938,185,569和282 cm-1)和8个(207,233,336,536,760,529,491和585 cm-1)特征波数组合,仍然取得了测试集100 % 和97.4 % 的准确率.相比直接进行PLSDA分类,经过RF算法挑选波数,训练集准确率仍然为100 %,除了测试集3个批次仍然保持100 % 外,其他几个批次均有2 % ~8 % 左右的提升,测试集准确率均在97.4 % 以上,其余指标如敏感度以及F1得分方面也有明显提升,模型的复杂度经过波数选择后显著降低,具体数据如表 4所示.
表 4(Table 4)
| 表 4 RF-PLSDA方法的分类结果 Table 4 Classification results with RF-PLSDA method | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.3 三种波数选择方法比较将SPA-PLSDA,CARS-PLSDA,RF-PLSDA三种方法进行比较.对于训练集来说经过波数选择后对于鉴别γ-PGA批次准确率都非常高,对于测试集来说CARS-PLSDA方法效果较差,主要是因为CARS-PLSDA将批次1分类中全部归为了大类,导致准确率低.而SPA-PLSDA和RF-PLSDA两种波数选择方法取得的效果相差不大,均能很好地对γ-PGA发酵批次进行判别.其中SPA-PLSDA将批次2,4和5的准确率提升到了100 %,RF-PLSDA将批次2和4的准确率提升到了100 %,将批次5提升了2.5 % 达到97.4 %.具体数据如表 5所示.
表 5(Table 5)
| 表 5 三种波数选择方法比较 Table 5 Comparison of three wave number selection methods? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 结论1) 利用波数选择的方法对ATR-FTIR光谱仪测量的γ-PGA发酵液的5个批次进行快速鉴别,相比于直接应用PLSDA,波数选择方法显著降低了模型复杂度.
2) 在波数选择方法中,CARS算法由于每次迭代中要消除的变量数量由指数递减函数决定,消除变量数太多,尽管大幅降低模型复杂度,但其他指标并不理想.
3) RF和SPA算法都取得了良好的效果,经过SPA和RF波数选择后,批次2,4和5的各项指标都得到了提升.其中SPA-PLSDA方法在批次2~5上的准确率更是达到100 %,批次1达到97.4 %.因此合适的波数选择的方法结合PLSDA可以成功应用到γ-PGA的批次鉴别上.
参考文献
| [1] | 邓星波, 邹水洋, 朱丹, 等. γ-PGA的保湿性研究[J]. 广州化工, 2019, 47(6): 48-50. (Deng Xing-bo, Zou Shui-yang, Zhu Dan, et al. Research on moisturizing properties of γ-PGA[J]. Guangzhou Chemical Industry, 2019, 47(6): 48-50.) |
| [2] | 邹水洋, 张树友, 贾梦影, 等. 一种从发酵液中高效提取γ-PGA的工艺: CN105837815A[P]. 2016. (Zou Shui-yang, Zhang Shu-you, Jia Meng-ying, et al. A process for efficient extraction of γ-PGA from fermentation broth: CN105837815A[P]. 2016. ) |
| [3] | 朱广跃, 杨卫, 吴健, 等. HPLC法定量分析微生物法制备液中产物γ-氨基丁酸和底物L-谷氨酸[J]. 食品科学, 2015(24): 190-194. (Zhu Guang-yue, Yang Wei, Wu Jian, et al. Quantitative analysis of product γ-aminobutyric acid and substrate L-glutamic acid in microbial preparation solution by HPLC[J]. Food Science, 2015(24): 190-194. DOI:10.7506/spkx1002-6630-201524035) |
| [4] | 陈旭升, 李树, 张超, 等. 微生物合成ε-聚赖氨酸的结构鉴定及其抑菌活性的研究[J]. 食品与发酵工业, 2008(9): 54-57. (Chen Xu-sheng, Li Shu, Zhang Chao, et al. Structural identification and antibacterial activity of ε-polylysine synthesized by microorganisms[J]. Food and Fermentation Industry, 2008(9): 54-57.) |
| [5] | 黄红英, 尹齐和. 傅里叶变换衰减全反射红外光谱法(ATR-FTIR)的原理与应用进展[J]. 中山大学研究生学刊(自然科学医学版), 2011, 32(1): 20-31. (Huang Hong-ying, Yin Qi-he. The principle and application progress of Fourier transform attenuated total reflection infrared spectroscopy(ATR-FTIR)[J]. Sun Yat-Sen University Graduate Journal(Natural Science·Medical Edition, 2011, 32(1): 20-31.) |
| [6] | 郭淑霞. 表面增强拉曼光谱信息处理技术的研究与应用[D]. 厦门: 厦门大学, 2014. (Guo Shu-xia. Research and application of surface-enhanced Raman spectroscopy information processing technology[D]. Xiamen: Xiamen University, 2014. ) |
| [7] | Ghosh A, Saharay R, Chakrabarty S, et al. Robust generalised quadratic discriminant analysis[J]. Pattern Recognition, 2021, 117: 107981. DOI:10.1016/j.patcog.2021.107981 |
| [8] | Mitchell H B, Schaefer P A. A "soft" K-nearest neighbor voting scheme[J]. International Journal of Intelligent Systems, 2010, 16(4): 459-468. |
| [9] | Westerhuis J A, Velzen E, Hoefsloot H, et al. Multivariate paired data analysis: multilevel PLSDA versus OPLSDA[J]. Metabolomics, 2010, 6(1): 119-128. DOI:10.1007/s11306-009-0185-z |
| [10] | Brereton R G, Lloyd G R. Partial least squares discriminant analysis: taking the magic away[J]. Journal of Chemometrics, 2014, 28(4): 213-225. DOI:10.1002/cem.2609 |
| [11] | Jiang M, Wang C, Zhang Y, et al. Sparse partial-least-squares discriminant analysis for different geographical origins of Salvia miltiorrhiza by H-NMR-based metabolomics[J]. Phytochemical Analysis, 2014, 25(1): 50-58. DOI:10.1002/pca.2461 |
| [12] | Anne-Laure B, Korbinian S. Partial least squares: a versatile tool for the analysis of high-dimensional genomic data[J]. Briefings in Bioinformatics, 2008(1): 32-44. |
| [13] | Abdi H, Williams L J. Partial least squares methods: partial least squares correlation and partial least square regression[J]. Methods in Molecular Biology, 2013, 930: 549-579. |
| [14] | Westerhuis J A, Hoefsloot H, Smit S, et al. Assessment of PLSDA cross validation[J]. Metabolomics, 2008, 4(1): 81-89. DOI:10.1007/s11306-007-0099-6 |
| [15] | 曲思杨, 张秋菊, 王文佶, 等. 多次交叉验证对PLSDA模型的影响研究[J]. 中国卫生统计, 2017, 34(1): 15-17. (Qu Si-yang, Zhang Qiu-ju, Wang Wen-ji, et al. Research on the influence of multiple cross-validation on the PLSDA model[J]. China Health Statistics, 2017, 34(1): 15-17.) |
| [16] | 郝勇, 商庆园, 饶敏, 等. 木材种类的近红外光谱和模式识别[J]. 光谱学与光谱分析, 2019, 39(3): 705-710. (Hao Yong, Shang Qing-yuan, Rao Min, et al. Near-infrared spectroscopy and pattern recognition of wood species[J]. Spectroscopy and Spectral Analysis, 2019, 39(3): 705-710.) |
| [17] | Li H D, Zeng M M, Tan B B, et al. Recipe for revealing informative metabolites based on model population analysis[J]. Metabolomics, 2010, 6(3): 353-361. |
| [18] | Li H D, Liang Y Z, Xu Q S, et al. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration[J]. Analytica Chimica Acta, 2009, 648(1): 77-84. |
| [19] | 林两魁, 徐晖, 许丹, 等. 基于可逆跳跃马尔可夫链蒙特卡罗方法的空间邻近目标红外像平面分辨[J]. 光学学报, 2011(5): 96-103. (Lin Liang-kui, Xu Hui, Xu Dan, et al. Infrared image plane resolution of spatially adjacent targets based on reversible hopping Markov chain Monte Carlo method[J]. Acta Optics Sinica, 2011(5): 96-103.) |
| [20] | Li H D, Xu Q S, Liang Y Z. Random frog: an efficient reversible jump Markov chain Monte Carlo-like approach for variable selection with applications to gene selection and disease classification[J]. Analytica Chimica Acta, 2012, 740(1): 20-26. |
| [21] | Li H D. LibPLS: an integrated library for partial least squares regression and linear discriminant analysis[J]. Chemometrics & Intelligent Laboratory Systems, 2018, 176: 34-43. |
| [22] | Yun Y H, Li H D, Wood L E, et al. An efficient method of wavelength interval selection based on random frog for multivariate spectral calibration[J]. Spectrochimica Acta Part A: Molecular & Biomolecular Spectroscopy, 2013, 111: 31-36. |
