孙磊, 陈彦峰, 常爽爽, 邓庆绪
东北大学 计算机科学与工程学院, 辽宁 沈阳 110169
收稿日期：2021-10-11
基金项目：兴辽英才计划项目(XLYC1902017)；NSFC-辽宁联合基金重点资助项目(U1908212)。
作者简介：孙磊(1986-)，男，河南南阳人，东北大学博士研究生;
邓庆绪(1970-)，男，河南南阳人，东北大学教授，博士生导师。

摘要：为了缓解电动汽车里程焦虑问题，降低因充电时间过长对日常使用的影响，对家用电动汽车的充电策略进行了研究.针对家用汽车使用场景的离散性，提出弹性充电的方法，利用使用间隙规划充电方案，降低对行程的延误.并提出选择充电站和充电量的最优算法，根据电动汽车自身电池特性和周边充电站的资源竞争情况计算最优的充电决策.通过对真实车型数据和用车场景的模拟，验证了算法的有效性.这表明弹性充电策略能够大幅度节省行程时间，消除用户的里程焦虑.
关键词：电动汽车充电站里程焦虑弹性充电充电调度策略
Research on Elastic Charging Strategy of Electric Vehicles
SUN Lei, CHEN Yan-feng, CHANG Shuang-shuang, DENG Qing-xu
School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: DENG Qing-xu, E-mail: dengqx@mail.neu.edu.cn.

Abstract: In order to alleviate the range anxiety of electric vehicles(EVs)and reduce the impact of long charging time on daily use, the charging strategy of private EVs is studied. Aiming at the discreteness of private EV usage scenarios, an elastic charging method is proposed. It plans charging scheme to reduce delays to trips by taking advantage of usage gaps. An optimal algorithm for selecting the charging station and capacity is proposed, which makes optimal charging decisions according to the characteristics of the EV battery and the resource competition of surrounding charging stations. The effectiveness of the algorithm is verified by simulating real EV data and usage scenarios. It indicates that the elastic charging strategy can significantly save travel time and eliminate range anxiety for EV users.
Key words: electric vehicle(EV)charging stationrange anxietyelastic chargingcharging scheduling strategy
电动汽车在环保和经济方面的优势得到了广泛的认可.然而，由于锂电池的能量密度远不及化石燃料，电动汽车的续航里程与传统燃油汽车相比有很大差距.电动汽车充电通常需要数小时甚至更长的时间.里程焦虑和充电麻烦的问题严重影响电动汽车的使用体验，阻碍了电动汽车的普及.本文提出弹性充电策略，针对家用汽车的使用场景，根据行程需求灵活调整充电时间，从而降低充电过程对行程的影响.在不影响电动汽车正常使用的前提下，通过精确计算，合理选择沿途的充电站并确定最优的充电量，节省通行时间、减少充电次数、提高通行效率.
1 相关工作关于电动汽车的研究很早就开始了，近些年随着新能源、车联网、混合动力等新技术的兴起，电动汽车的研究也向多元化方向发展.由于电动汽车需要较长的充电时间，很多研究针对停车时充电场景(parking and charging)进行研究.文献[1]研究了停车时充电场景下人们对服务价格的敏感性.文献[2]利用电动汽车电池储存电力的能力，将电动汽车停车充电的调度问题看作一个多目标资源分配问题，一方面补偿电网随时间变化的无功功率，另一方面降低车主停车充电的成本.文献[3]根据停车充电的场景，从面向智能电网、面向集合商和面向客户的三个不同的维度研究了协同充电的各种影响因素.文献[4]将光伏能源与停车时充电的场景相结合，论证了基于光伏能源的充电站的可行性.文献[5-6]研究了将新能源引入电动汽车充电领域对智能电网的影响.
电动汽车大规模集中充电对电网造成很大压力.针对有限的电力资源，文献[7-8]从用户满意度的方向研究了充电站内部的资源分配方法.文献[9]在此基础上引入马斯充电曲线，提高充电效率.文献[10]从算法角度总结了充电站和电网的调度策略.文献[11]不仅从用户满意度的角度提出了高效率低复杂度的充电站资源调度算法，还从节省充电成本的角度为电动汽车用户提出了充电站选择算法.文献[12]针对充电站分配不平衡问题提出一种随机平衡算法，缓解某些充电站排队过长而另一些充电站得不到充分利用的问题.
以上文献都是针对单次充电，没有考虑后续的行程和充电计划.本文将停车时充电与行程中充电结合起来，根据充电站的调度策略，计算合适的充电时间和充电量，缩短行程时间.
2 弹性充电策略2.1 弹性充电的思想电动汽车一旦电量用尽，充满电需要较长时间，会严重影响到之后的行程安排.当前我国的充电设施建设还处于起步阶段，即使在充电设施发展较快的大城市，寻找充电桩也是电动汽车用户的一大难题.为了缓解里程焦虑，只要找到可用的充电桩，用户就会把电池充满.这也造成了电动汽车充电难、充电慢的印象.
家用汽车的使用场景是离散的，由一段一段的行程组成，而不像商用车那样需要长时间高强度的持续行驶.例如，图 1a是一辆家用汽车在一天中的行驶状态示例，坐标轴代表时间，区域D1，D2表示汽车在该时间处于行驶状态，空白部分表示汽车处于空闲状态.它在一天中有D1, D2两段行程，其他大量时间处于空闲状态.如果在行程D1中汽车电量不足，需要寻找附近充电站进行充电，那么充电过程会大幅度增加第一段行程的时间，形成图 1b的状态.图 1b中区域C为充电占用的时间，它延长了D1的时间，挤压了其后的空闲时间，甚至会造成后续行程D2的延误，这是电动汽车用户里程焦虑的根本原因.如果在D1之后的空闲时间可以为汽车充电，那么就不必在行程途中占用大量时间把电池充满，而是只补充少量满足当前行程所需的能量，其余能量利用空闲时间补充，如图 1c所示.充电需求被分为两部分，一部分是紧急需求，必须在行程途中停下来充电，即区域C1，否则汽车无法完成行程；另一部分能量需求不紧急，可以在汽车到达目的地后再补充，即区域C2，不占用行程D1的时间.本文把这种利用行程间隙充电的方式称为弹性充电.
图 1(Fig. 1)

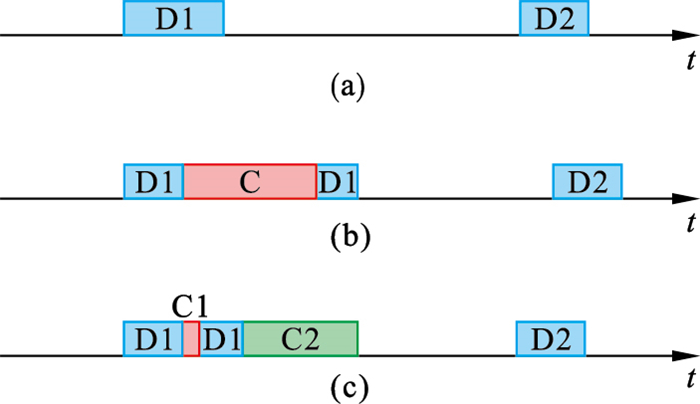图 1 弹性充电策略Fig.1 Elastic charging strategy (a)—行程规划；(b)—非弹性充电策略的时间规划；(c)—弹性充电策略的时间规划.

弹性充电的实现需要完善的充电设施建设.汽车在空闲时间通常停放在目的地附近的停车场或停车位，要利用这段时间充电，就需要对应的停车位提供充电桩.同时还需要普及道路旁快速充电站，以应对行程中电量不足以及行程更改等情况.我国政府已经提早对电动汽车充电设施的强大需求做出了预判和布局.2015年，国务院办公厅印发《关于加快电动汽车充电基础设施建设的指导意见》，要求加快配建充电桩、城市充换电站、城际快充站等设施，新建住宅停车位建设或预留安装充电设施的比例应达到100 %，大型公共建筑物、公共停车场不低于10 %.随着充电设施的逐步完善，当人们开车回家时，以及去往大型商场、写字楼或其他设有充电桩的公共停车场时，只要剩余电量能够行驶到目的地，就可以在到达目的地之后开始充电.当下一段行程开始的时候，汽车已经充入相当一部分电量，即使不足以支撑剩下的全部行程，也可以在中途的充电站快速补足能量缺口，相比于中途停下来全部充满电要节省很多时间.停车场充电和道路旁快速充电站相结合将成为家用电动汽车的主要充电方式.相比于在充电站花费几个小时充满之后再上路，这种方式把充电过程的存在感降到最低，使充电问题不再成为电动汽车使用中的障碍.
弹性充电一方面降低充电过程的存在感，实现无感充电，另一方面把用户的充电需求由充电站转移到停车场的充电桩，把紧急需求变成平缓需求.这不仅缓解了快速充电站的压力，还为均衡电网负载提供了可能.此外，电动汽车采用动力锂电池，没有记忆效应，适合浅充浅放的使用方式，长时间维持高电量反而对电池寿命不利.相对于有机会就充满的使用方式，弹性充电还能延缓电池的衰老.
2.2 电动汽车的充电过程锂电池常采用恒流-恒压的充电方式，在第一阶段以恒定电流充电，当电池电压上升到一定值后转为恒压充电.这种方式实现简单，但是并没有达到最快的充电速度.文献[13]揭示了锂电池所能接受的最大充电电流与充电时间的关系.电池的最大接受电流为

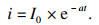(1)

其中：I₀是最大初始电流；a是电池的接受率，是表示电池充电速度衰减率的一个常数；t是充电时间.
锂电池的最大接受电流根据充电时间的变化曲线，称为马斯曲线.按照最大接受电流给锂电池充电，在不损伤电池的前提下可以达到最快的充电速度.
锂电池的初始接受电流一般较大，可能会超出充电桩和线缆的上限.为了保障充电设施的安全，本文采取两阶段充电：第一阶段以恒定电流充电，在此过程中电池的最大接受电流持续下降；当接受电流降低到与恒流充电的电流等同时，转入第二阶段，按照电池的最大接受电流充电.当接受电流下降到趋近于零时，电池充满.充电电流的变化如图 2所示.
图 2(Fig. 2)

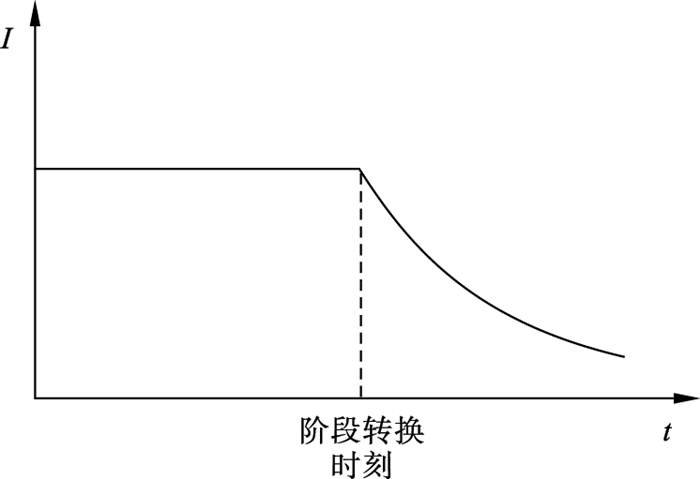图 2 两阶段充电的电流变化Fig.2 Current change of two-stage charging

2.3 充电站的充电策略电动汽车的普及将对我国的电力供应带来巨大压力.电动汽车的电力需求很大，当前主流快充功率在20 kW以上，家用充电桩也在7 kW左右, 这大大超出了普通居民用电需求.电动汽车的普及使大量汽车的燃油需求转变为电力需求，当前的输电网和配电网无法承受这急剧增长的负载, 这一矛盾制约着城市快速充电站的规模.对于一座充电站来说，如果所有车辆都以最大功率满负荷充电，将超出充电站的承载上限.实际上，由于电池的最大接受电流在充电过程中逐渐降低，并不是所有汽车都需要满功率充电.当充电站无法满足所有汽车的功率需求时，根据每辆车的用户满意度来决定功率分配.
****关于用户对电动汽车充电的满意度进行了很多研究，建立了各种模型^[7-11].本文采用文献[9]对用户满意度的量化方法.用户满意度分为两部分，一部分是充电速度对用户满意度的影响，用式(2)表示：

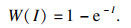(2)

电池在充放电过程中电压变化不大，充电速度取决于充电电流的大小，因此满意度是关于充电电流I的单调递增函数.当充电电流很小时，用户对充电速度的变化很敏感，随着充电速度的提高用户满意度迅速增长；当充电速度达到较高速度时，用户的敏感度降低，再提升充电速度对用户的满意度的影响就很小了.所以式(2)是关于充电电流I的凹函数.其中e是自然常数.
另一部分是电量的增长量对满意度的影响，用式(3)表示：

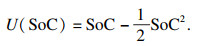(3)

其中，SoC(state of charge)是电池电量，用百分数表示.类似地，用户对充入电量的满意度也是与电量正相关，对电量的敏感性随着电量的增长而降低.因此，式(3)是关于充入电量的单调递增的凹函数.
把这两部分结合起来，就得到用户对充电过程的总体满意度Sa：

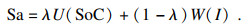(4)

其中，λ为平衡因子，调节充入电量和充电速度所占的权重.
由于充电站内正在充电的汽车的电池容量、接受率、电量以及开始充电的时间等参数各不相同，因此它们对充电功率的敏感度也各有不同.充电站作为基本公共服务的提供方，需要实现总体社会效益的最大化.用户对充电过程的满意度即是充电站社会效益的体现.因此充电站的优化目标是正在充电的所有用户的满意度总和的最大化：

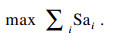(5)

充电桩通过充电线缆与电动汽车相连接.充电线缆不仅能够传输电能，还担负着充电桩与电动汽车信息交互的责任.充电站可以通过充电桩向电动汽车传输控制信号，获取各项参数.采集到所有汽车的充电参数之后，充电站对它们的满意度的增长率进行排序，优先分配功率给满意度增长快的，直到所有汽车的满意度增长率相同，从而保持总体满意度的最大化.
2.4 弹性充电系统模型弹性充电需要精确地掌握汽车的电池性能和充电站的信息.电池会因多种因素造成电量衰减、性能衰退，电动汽车具有功能完善的电池管理系统(battery management system, BMS)，实时监控整个电池组，准确记录电池的实际容量和充放电性能.现在上市的很多电动汽车已经部署了车联网装置，未来将普及到所有车型.通过车联网云平台，汽车可以获取接入云平台的各种配套设施的信息，包括充电站、停车场等.
当行程开始之后，汽车通过车联网与目的地停车场通信，获取目的地充电设施的信息；并且根据当前行程的路径规划和电量信息判断是否需要在中途充电.对于行程途中需要充电的汽车，通过车联网实现与周边的充电站进行信息交互.汽车将充电需求和电池状态发送给附近可以到达的多个充电站.充电站根据电动汽车的需求和充电站正在充电车辆的情况，依据用户满意度最大的策略，计算出能够分配给该电动汽车的充电功率，并反馈给汽车.如图 3所示，虚线圈内为汽车当前电量可以到达的范围.然后汽车根据各个充电站的反馈以及路径因素做出决策，选择最节省时间的充电站进行充电.对于电动汽车来说，要实现弹性充电策略，所要解决的问题是确定充电需求以及选择最合适的充电站.
图 3(Fig. 3)

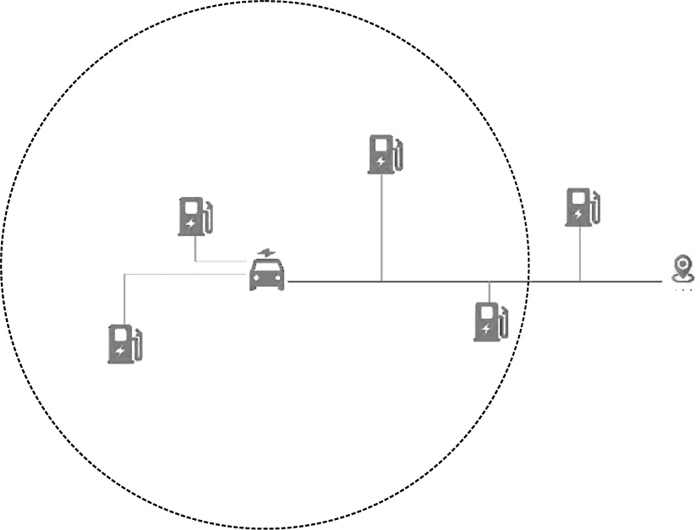图 3 电动汽车在行程中充电时对充电站的选择Fig.3 Choice of charging station during the trip

3 电动汽车的充电需求电动汽车在行驶途中，如果剩余电量不足以行驶到目的地，那么需要在途中的充电站补充能量.如果在充电站充电过多，会花费不必要的时间，拖慢行程.如果充电过少，会导致无法到达目的地或者频繁寻找充电站充电，增加充电次数.因此，精确控制充电量对缩短行程时间、提高通行效率非常重要.
电动汽车可以通过车联网技术与目的地停车场、充电站进行通信，及时获取停车场充电设施的信息，以及周边充电站的空闲资源数据.电动汽车对充电量的需求根据当前行程的终点是否能够停车充电分为两种情况.如果当前行程的目的地可以进行充电，就不用考虑后续行程的影响.如果目的地没有充电设施，无法充电，还要考虑后续行程的电量需求是否能得到保障.
电动汽车能耗不仅取决于行驶里程，还与车辆加减速、道路坡度及车载用电器等因素有关.但是，电动汽车不像燃油车那样怠速时也消耗能量，而且当前主流电动汽车都配备了制动能量回收装置，减少了频繁加减速导致的能量损失.车载用电设备相对于车辆行驶来说功率很小，可以忽略不计.为了便于计算，本文假设电动汽车的能耗与行驶里程成正比.
3.1 行程目的地能够充电情况下的充电需求如果行程终点能够充电，那么中途只需要补充必要的电量.充电站不一定正好在行驶路线上.如果充电站不在路线上，那么到充电站充电就会因为绕路而消耗更多的电量.为保证汽车能顺利完成当前行程，充电量既要满足行驶到终点的需求，还要满足绕路到充电站的需求.此外，为了应对意外状况和保护电池，汽车最后还要保留一部分电量.汽车需要补充的电量为

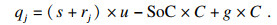(6)

其中：q_j是到第j个充电站充电需求的充电量；s是当前行程的剩余里程；r_j是去往第j个充电站的绕路距离；u是单位里程的耗电量；C是电池容量；g是电池保留电量的比例，该保留电量用于应对行程改变或其他突发状况，保障电动汽车在意外情况下也能够行驶到充电站或有充电条件的地方，不会因电量耗尽而困在途中.
3.2 行程目的地不可充电情况下的充电需求当前行程的目的地不具备充电条件，那么不仅需要考虑当前行程的电量需求，还要满足此后行程的需求.如果电量仅仅能够行驶到当前目的地，到达目的地后得不到补充，那么下一段行程的电量必然不足.所以补充的电量应该额外包含下一段行程所需的用电量：

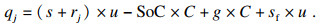(7)

其中，s_f是下一段行程的总里程.
为了保障汽车的续航安全，而把之后行程所需的电量也充满，显然会占用当前行程的时间，拖慢当前行程.只要保证汽车在下次行程开始时，电量足够行驶到最近的充电站，就不至于造成汽车困在半路的后果.因此，式(7)是电动汽车电量需求的上限，本文将它记为q_j^up，下限只要能够满足行驶到距离下一段行程起点的最近充电站即可.充电需求的下限为

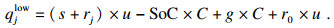(8)

其中，r₀是下一阶段行程从起点到最近充电站的距离.
对于行程终点没有充电条件的汽车来说，电量需求是由式(7)和式(8)构成的一个区间.
4 充电站的选择策略电动汽车的剩余电量如果不足以支撑剩余部分的行程，可以在电量能够到达的范围内选择充电站进行补电.不仅限于行程路线上经过的充电站，偏移路线不远的充电站也同样可以选择.如果充电站不在行驶路线上，会因为绕路而产生额外的行驶距离，消耗额外的电量和时间.偏移越远，额外消耗的电量和时间就越多.此外，由2.3节可知，各个充电站由于功率资源的限制和其他汽车充电需求的竞争，所能提供的充电功率和充电速度也各不相同.因此选择合适的充电站对缩短行程时间有至关重要的意义.本文以缩短行程时间为目标对充电站和充电量的选择进行优化.
车辆行驶时间不仅取决于距离的远近，还受车速和路况的影响.根据交通流随时间变化的状况可以推测出未来路况的变化趋势，从而预测车速和行驶时间.
由此可以得出，如果到第j个充电站充电，那么到达当前行程目的地的总时间为

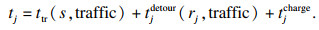(9)

其中：t_tr(s, traffic)为剩余路程s在路况(traffic)下的行驶时间；t_j^detour(r_j, traffic)是因去往第j个充电站而绕路r_j多行驶的时间；t_j^charge为在第j个充电站的充电时间.
4.1 行程目的地可充电情况下的充电站选择策略如果行程目的地能够充电，那么中途需要额外补充的电量可由式(6)得出.采用文献[9]中的充电站功率分配策略，充电速度和充入需求电量的时间都由充电站根据功率资源总量和竞争情况计算出来.进而通过式(9)可以计算出到第j个充电站充电的总的行程时间.对所有充电站的行程时间排序，即可找出行程时间最短的充电站.对此，本文提出行程目的地可充电情况下的充电站选择算法(算法1)，根据每一个充电站的情况计算充电量和行程总时间，选取行程总时间最短的充电站前去充电.
算法1 ??行程目的地可充电情况下的充电站选择算法.
1. for j←1 to m do
2. ????????q_j←(s+r_j)*u-SoC*C+g*C;
3. ????????t_j^charge: =q_j;
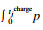
4. ???????????t_j←t_tr(s, traffic)+t_j^detour(r_j, traffic)+t_j^charge;
5. end for
6. find min t_j while j←1 to m
算法中1~5行分别向每一个可以选择的充电站发送请求，根据充电站的资源竞争情况和电动汽车自身的电池状况计算出最优的充电量和充电时间，进而得出行程的总时间.第6行找出其中最短的行程时间和对应的充电站.
4.2 行程目的地不可充电情况下的充电站选择策略如果目的地不能充电，还要增加额外的充电量以保障下一段行程，这会使充电时间变长.多充的这部分电量是用于下一段行程的，相当于节省了下一段行程的时间.为了公平，在计算当前行程时间的时候，应该将这部分多充的电量折算成时间减去.那么当前行程的总耗时应为

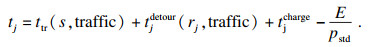(10)

其中：E为多充的电量；p_std是综合当前时刻周边所有可达充电站充电功率的标准充电功率，计算公式为

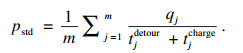(11)

电动汽车可以通过车联网将自己的需求和充电参数发送给周边的充电站，并从充电站获取当前可提供的充电功率，进而计算出当下的标准充电功率.
定理1 ??电动汽车进行额外充电的过程中，如果充电功率高于标准功率p_std，总行程时间减少；如果充电功率低于p_std，总行程时间增加.
证明??由式(10)可知，对于充电站j，总行程时间主要取决于充电时间和额外充电量的折算时间.标准功率p_std是可计算出的，当充电功率高于标准功率p_std时，额外充电量E折算成的时间E/p_std的增长速度大于充电时间t^charge的增长速度，所以总行程时间t_j减少.同样地，当充电功率低于标准功率p_std，E/p_std的增长速度小于充电时间t^charge的增长速度，总行程时间增加.证毕.
当前充电的需求量是一个区间.需求电量并不确定，就无法像上面那样简单地通过充电站的分配策略计算出充电时间.
推论1 ??当充电功率下降到与平均功率相等时停止充电，行程时间最短.
证明??由2.2节可知，充电站对电动汽车采用两阶段充电，充电过程中充电功率是单调递减的.由定理1可知，充电功率下降到与平均功率相等时，总行程时间达到最小值.继续充电则充电功率低于平均功率，行程时间增加.证毕.
根据推论1，可以计算出在第j个充电站充电时最优的充电量，进而得出最优的充电时间和行程时间.对所有充电站对应的行程时间排序，即可找出时间最短的充电站.
本文提出行程目的地不可充电情况下的充电站选择算法(算法2)，先通过周边充电站所能够提供的充电功率计算出标准充电功率作为选择充电量的依据；然后对每一个充电站计算充电量的上下界，并根据标准充电功率确定充电量，进而得出行程总时间；最后选取行程总时间最小的充电站前去充电.
算法2 ??行程目的地不可充电情况下的充电站选择算法.
1. for j←1 to m do
2. ????????q_j←(s+r_j)*u-SoC*C+g*C;
3. ????????t_j^charge: =q_j;
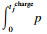
4. end for
5. p_std← ;
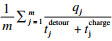
6. for j←1 to m do??z
7. ????????q_j^up←(s+r_j)*u-SoC*C+g*C+s_f*u;
8. ????????q_j^low←(s+r_j)*u-SoC*C+g*C+r₀*u;
9. ????????if p_j≤p_stdthen
10. ???????????q_j←q_j^low;
11. ???????????t_j^charge: =q_j^low;
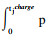
12. ???????????t_j←t_tr(s, traffic)+t_j^detour(r_j, traffic)+t_j^charge;
13. ?????else
14. ???????????t_op←;
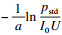
15. ???????????q_op←;
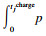
16. ??????????if q_op < q_j^low then
17. ??????????????q_j←q_j^low;
18. ??????????????t_j^charge: =q_j^low;
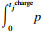
19. ??????????????t_j←t_tr(s, traffic)+t_j^detour(r_j, traffic)+t_j^charge;
20. ??????????else if q_op>q_j^up then
21. ??????????????q_j←q_j^up;
22. ??????????????t_j^charge: =q_j^up;
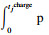
23. ??????????????????t_j←t_tr(s, traffic)+t_j^detour(r_j, traffic)+t_j^charge-;
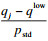
24. ??????????else
25. ??????????????q_j←q_op;
26. ??????????????t_j^charge←t_op;
27. ??????????????????t_j←t_tr(s, traffic)+t_j^detour(r_j, traffic)+ t_j^charge-;
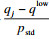
28. ??????????end if
29. ?????end if
30. end for
31. find min t_j while j←1 to m
算法中1~5行通过车联网获取充电站所能提供的充电功率并计算标准充电功率, 6~30行分别计算去各个充电站充电的总行程时间.其中7~8行计算充电量需求的上下界, 9~12行表示充电站提供的功率小于平均功率时，只按照电量需求下限进行充电, 14~15行计算出最优的充电时间和充电量, 16~19行表示当最优充电量小于电量需求下限时，按照需求下限进行充电，20~23行表示当最优充电量大于电量需求上限时，按照需求上限充电, 24~28行按照最优充电量充电，第31行找出其中最短的行程时间和对应的充电站.
5 实验测试当前的城市快速充电站的建设还在发展中，数量和密度都无法满足电动车普及的需求.因此无法以实际场景为基础进行实验测试.本文利用真实电动车的参数来进行模拟实验，测试弹性充电的效果，使实验结果能够正确反映现实情况.
5.1 实验设置本文针对家用车行程分散的特点，提出弹性充电策略以减轻充电过程对行程的影响.为了验证弹性充电的优势，本文分别针对行程目的地可以充电和不可充电这两种情况进行模拟，测试弹性充电策略下的行程时间.作为对比，本文还模拟并测试了在相同情况下采用非弹性充电(电量不足时在附近充电桩充满电再上路)策略下的行程时间.同时，由于采用弹性充电方式的电动汽车需要与充电站进行交互获得充电站的充电速度等信息，本文还模拟了充电站以总体用户满意度最大化为目标的功率分配策略，详见2.3节.
本文根据真实车型的信息和其他文献中的统计规律来生成随机的测试数据.本文的方法是针对普通家用车的使用场景进行优化的，因此本文选取当前的主流电动车车型，以它们真实的电池参数作为测试数据.公共充电站的位置按照平均分布随机生成，每个充电站的资源竞争情况与其位置相关，地段越好的充电站资源竞争越激烈.
5.2 实验结果与分析车辆和行程数据是根据上一节中的规律随机生成的，其中一部分汽车的电量足够行驶到终点，不需要在中途充电.不需充电的车辆不在本文讨论的范围内，因此把这部分数据剔除，仅保留需要充电的车辆行程数据.
1) 按照行程长度和车辆初始SoC服从正态分布随机生成多组汽车电池容量不同的测试数据，分析电池容量对充电时间和行程总时间的影响.取测试结果的平均值，如图 4所示.
图 4(Fig. 4)

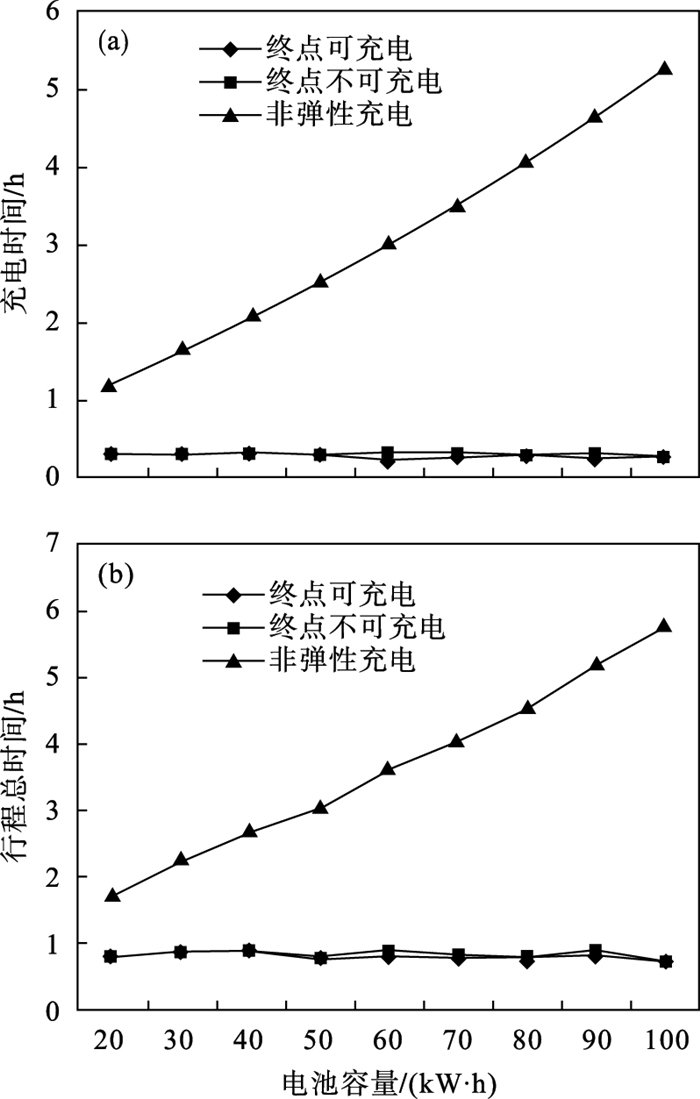图 4 电动汽车电池容量对充电时间和行程时间的影响Fig.4 Influence of EV battery capacity on charging time and trip time (a)—充电时间与电池容量的关系；(b)—行程总时间与电池容量的关系.

由图 4a可以看出，随着电池容量的增加，采用非弹性充电策略的充电时间近似线性增长；而采用弹性充电的车辆充电时间较短，并且基本保持恒定，其中终点不可充电情况下的充电时间略高于终点可充电的情况.图 4b中行程总时间的变化趋势与充电时间相似.
由此可见，电池容量对采用弹性充电的车辆影响不大，不同电池容量下，充电时间和行程总时间变化不大.非弹性充电的车辆，充电时间和行程时间则随电池容量的增加而增加.在不同的电池容量下，弹性充电在充电时间和行程总时间上均有较大优势，而且随着电池容量的增大，优势愈发明显.产生这一结果的原因是弹性充电只需充入当前行程需求的电量，电池总容量远大于这一需求，因此总容量的大小并不会影响到充电决策.而非弹性充电策略要将电池充满，电池容量越大，需要的充电时间就越长，所以充电时间和总行程时间随电池容量的增加而增加.另外，本文测试的充电调度结果显示，弹性充电策略选择绕路较近的充电站多一些，而非弹性充电策略倾向于选择充电速度快的充电站，对其他方面不敏感.原因是非弹性充电车辆的充电时间长，占行程总时间的比重大，充电速度对总时间的影响高于其他因素，如绕路距离等.
2) 初始剩余电量(SoC)对电动汽车的充电决策至关重要.根据行程的统计规律，随机生成不同剩余电量的测试数据，研究SoC对行程的影响.
充电时间和行程总时间如图 5所示.由于不需要中途充电的车辆行程数据被剔除掉了，SoC大于30 % 且需要中途充电的数据较少，不具有代表性，本文只考虑SoC在30 % 以内的.
图 5(Fig. 5)

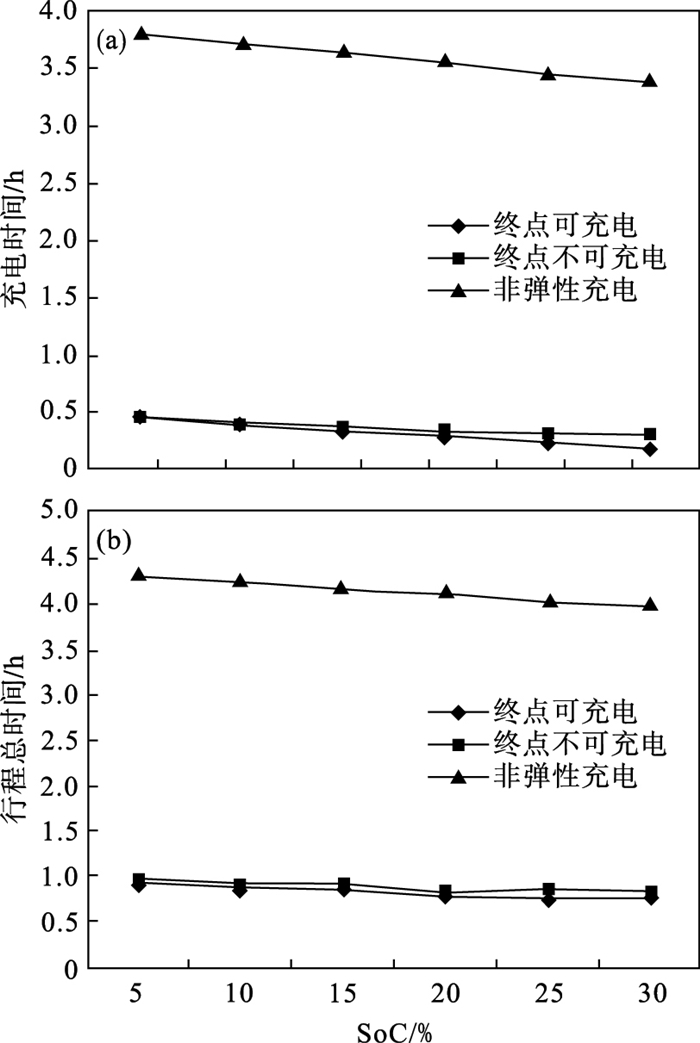图 5 电动汽车初始SoC对充电时间和行程时间的影响Fig.5 Influence of initial SoC on charging time and trip time (a)—充电时间与初始SoC的关系；(b)—行程总时间与初始SoC的关系.

如图 5所示，采用弹性充电策略的车辆无论是充电时间还是行程总时间都远小于采用非弹性充电的车辆.三种情况下的充电时间和行程总时间都随着SoC的增加而减少，但是减少幅度不大.
造成弹性充电在充电时间上巨大优势的原因仍然是弹性充电策略大大降低了充电量，减少了行程途中的充电时间，从而缩短了整个行程的时间.充电时间随着SoC的增加而减少，一方面是因为SoC越多，能够行驶的距离越远，可以在更大范围内选择充电站，车辆会选择充电速度更快或绕路距离更短的充电站以节省时间；另一方面，SoC越多，所需的充电量一般就越少，特别是要将整个电池都充满的非弹性充电策略，因此非弹性充电策略的充电时间随SoC的增加而下降的趋势更明显.
综上所述，在不同电池容量、SoC的情况下，弹性充电策略均能大幅度缩短充电时间和行程总时间，在行程终点可充电情况下比终点不可充电的情况略占优势.
6 结语本文根据家用电动汽车的充电特性和用户需求特征，针对电动汽车充电时间过长的问题，提出弹性充电的解决方案，并对弹性充电中充电站和充电量的选择问题给出优化算法；最后通过实验验证了弹性充电能够大幅度降低电动汽车因充电而造成的行程延长.本文从电动汽车用户的角度优化了行程总时间，没有考虑充电站的负载优化问题，今后将从时间和空间两个维度进行研究，解决充电站在时间上的负载均衡问题和不同充电站之间的需求平衡问题.
参考文献

[1]	Latinopoulos C, Sivakumar A, Polak J W. Response of electric vehicle drivers to dynamic pricing of parking and charging services: risky choice in early reservations[J]. Transportation Research: Part C, 2017, 80: 175-189. DOI:10.1016/j.trc.2017.04.008
[2]	Jiang B, Fei Y. Decentralized scheduling of PEV on-street parking and charging for smart grid reactive power compensation[C]// 2013 IEEE PES Innovative Smart Grid Technologies Conference(ISGT). Washington D C, 2013: 1-6.
[3]	Kong F, Qiao X, Kong L, et al. On-line event-driven scheduling for electric vehicle charging via park-and-charge[C]// 2016 IEEE Real-Time Systems Symposium(RTSS). Porto, 2016: 69-78.
[4]	Tulpule P J, Marano V, Yurkovich S, et al. Economic and environmental impacts of a PV powered workplace parking garage charging station[J]. Applied Energy, 2013, 108: 323-332. DOI:10.1016/j.apenergy.2013.02.068
[5]	Kong F, Liu X. Distributed deadline and renewable aware electric vehicle demand response in the smart grid[C]// Real-Time Systems Symposium(RTSS). San Antonio, 2015: 23-32.
[6]	Liu L, Kong F, Liu X, et al. A review on electric vehicles interacting with renewable energy in smart grid[J]. Renewable & Sustainable Energy Reviews, 2015, 51: 648-661.
[7]	Ardakanian O, Rosenberg C, Keshav S. Distributed control of electric vehicle charging[C]// Proceedings of the Fourth International Conference on Future Energy Systems. New York, 2013: 101-112.
[8]	Rahbari-Asr N, Chow M Y, Yang Z, et al. Network cooperative distributed pricing control system for large-scale optimal charging of PHEVs/PEVs[C]// Conference of the IEEE Industrial Electronics Society. Vienna, 2013: 6148-6153.
[9]	Sun L, Chen Y, Li W, et al. Charging stations oriented electric vehicle charging strategy based on battery characteristics[J]. Software: Practice and Experience, 2021, 51(11): 2168-2184. DOI:10.1002/spe.2980
[10]	Wang Q, Liu X, Du J, et al. Smart charging for electric vehicles: a survey from the algorithmic perspective[J]. IEEE Communications Surveys & Tutorials, 2016, 18(2): 1500-1517.
[11]	Kong F, Liu X, Lee I. Joint rate control and demand balancing for electric vehicle charging[C] // 2018 IEEE/ACM the Third International Conference on Internet-of-Things Design and Implementation(IoTDI). Orlando, 2018: 213-224.
[12]	Hausler F, Crisostomi E, Schlote A, et al. Stochastic park-and-charge balancing for fully electric and plug-in hybrid vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2): 895-901. DOI:10.1109/TITS.2013.2286266
[13]	Mas J A. New charging system controlled by battery acceptance[J]. SAE Journal, 1969, 77(6): 31-33.