
 , 朱文豪, 孙红玉
, 朱文豪, 孙红玉 华北水利水电大学 电力学院,河南 郑州 450011
收稿日期:2021-08-27
基金项目:河南省高等学校青年骨干教师培养计划项目(2018GGJS079); 国家自然科学基金资助项目(U1504622)。
作者简介:周玉(1979-),男, 安徽枞阳人, 华北水利电力大学副教授,博士。
摘要:针对传统的基于密度的局部离群点检测算法对原始数据集没有进行预处理导致该算法在面对未知数据集时检测效果不理想,又由于其需要计算每一个数据点的离群因子,在数据量过多时,计算量大大增加的问题,通过对局部离群点检测算法的分析,提出了一种基于目标函数的局部离群点检测方法FOLOF(FCM objective function-based LOF).首先,使用肘部法则确定数据集的最佳聚类个数;然后,通过FCM的目标函数对数据集进行剪枝,得到离群点候选集;最后,利用加权局部离群因子检测算法计算候选集中每个点的离群程度.利用该方法在人工数据集和UCI数据集上进行了相关实验,并与其他相关方法进行了对比,结果显示,该算法能够提高离群点检测精度,减少计算量,有效提高离群点检测性能.
关键词:离群点检测模糊C均值算法目标函数局部离群因子剪枝
A Local Outlier Detection Method Based on Objective Function
ZHOU Yu

 , ZHU Wen-hao, SUN Hong-yu
, ZHU Wen-hao, SUN Hong-yu School of Electric Power, North China University of Water Resources and Electric Power, Zhengzhou 450011, China
Corresponding author: ZHOU Yu, E-mail: zhouyu_beijing@126.com.
Abstract: The traditional density based local outlier detection algorithm does not preprocess the original data set, which leads to the unsatisfactory detection effect when facing the unknown data set. Moreover, due to the need to calculate the outlier factor of each data point, the amount of calculation increases greatly when the amount of data is too large. Through the analysis of the local outlier detection algorithm, a local outlier detection method based on objective function FOLOF(FCM objective function-based LOF)is proposed. Firstly, the elbow rule is used to determine the optimal number of clusters in the data set.Then, the data set is pruned by the objective function of FCM to obtain the outlier candidate set.Finally, the weighted local outlier factor detection algorithm is used to calculate the outlier degree of each point in the candidate set. The relevant experiments are carried out on the artificial data set and UCI data sets. At the same time, the proposed method is compared with other methods.The results show that the proposed algorithm can improve the outlier detection accuracy, reduce the computational cost, and effectively achieve a better performance.
Key words: outlier detectionfuzzy C-means (FCM) algorithmobjective functionlocal outlier factor(LOF)pruning
离群点是偏离大部分数据较远的点,它常被怀疑由不同的机制产生[1].根据数据对象的数量可以分为单独离群点和集体离群点;根据数据类型可以分为矢量离群点、序列离群点、轨迹离群点和图形离群点等[2].离群点检测在数据处理中占有重要地位,它旨在找出数据集中的偏远数据,是当下研究的热点.其在欺诈检测[3]、入侵检测[4]、公共安全[5]、图像处理[6]和目标跟踪[7]等方面已经有了广泛应用,其检测方法大致为基于统计、基于距离、基于密度和基于聚类等方法[8-9].
Breuing等提出了局部离群因子的概念LOF(local outlier factor)[10-11],这种方法基于密度给离群点赋予了离群因子,定量地描述了离群点的离群程度,其不再将离群点看作一个二值属性.在没有明确数据分布的情况下依然能准确发现离群点,由于其需要逐个查找数据点的邻域,计算数据点的离群因子,这就使得此方法的计算量巨大.随后,在此基础上出现了很多改进的方法,例如文献[12]提出的NLOF(new LOF)算法, 通过聚类算法DBSCAN(density-based spatial clustering of applications with noise)对数据集进行剪枝处理,得到初步的异常数据集,然后利用LOF算法计算初步异常数据集中对象的局部异常程度,提高了离群点检测精度.但此算法中DBSCAN聚类需要人为输入的参数过多且敏感度较大,面对未知数据集时,在参数设置方面存在较大问题.同样,文献[13]也提出了类似的用DBSCAN对数据集进行预处理的检测方法,这种方法分为两个阶段.第一阶段,为了减少参数输入,用k近邻的个数代替Minpts并通过k近邻确定聚类半径,通过改进的DBSCAN对混合数据进行初步筛选,一定程度减小了计算量;然后利用新构造的LAOF(LOF based on the area density)计算筛选后数据的离群程度,为了表征不同属性的贡献度,在距离度量中采用除一化信息熵差对属性加权,并在第二阶段进行二次权重确定,提高了检测精度,但这种方法和NLOF存在同样的问题.文献[14]使用EWT(empirical wavelet transform)方法对原始热工过程时间序列的运行趋势进行去除后,使用LOF算法得到该序列中的异常值点,避免了判断阈值不易直接给出的问题,在动态和稳态过程中均具有适用性,但是,k距离和箱型图截断点系数β的选择对结果的敏感度较大,并且此方法只适用于一维数据的检测.文献[15]从定义出发,提出基于聚类的局部离群点的概念,解释了局部的定义,即小聚类在宏观上可以看作离它最近的大聚类的局部,给出倍数β作为大小聚类的判别.通过新的局部概念,提出了CBLOF(cluster-based local outlier factor)的计算公式,计算得到每一个数据点的局部离群因子来表征离群程度,但这种方法对数据集并未进行预处理,计算复杂度十分高,面对大规模数据集不具备处理能力且用参数β来判别大小聚类并不精确.
针对上述问题,本文提出了一种新的基于目标函数的局部离群点检测方法. ①在进行检测之前,对数据集进行预处理,由于使用FCM(fuzzy C-means),为了有较好的聚类效果,因此使用肘部法则确定最佳聚类个数;②FCM的目标函数是根据距离求和的,拿走一个点,它的值必然会减小,而拿走离聚类中心较远的点,它的值减小幅度就会更大,通过减小的幅度来大概判断一个点的离群可能性,将大部分正常数据去除,剪枝得到初步的离群点集,这是本文最大的贡献,相比于其他剪枝方法更精确;③每一维特征对数据集的贡献度不同,采用属性熵来表征每一维特征的离散程度,熵越大,离散程度越大,此维特征所占的权值越大,用传统的LOF方法得出每一维的异常值得分,加权得到每个数据最终的异常得分,将其顺序排列,值越大的离群程度越大.经过实验对比验证,结果显示该方法能提高检测精度,改善聚类效果,实现有效的离群点检测.
1 预备知识1.1 FCM算法FCM算法属于划分聚类算法,聚类之后相同簇对象之间相似度最大,不同簇对象之间相似度最小是FCM的主要思想[16].FCM已成为聚类分析的主流[17],其在图像处理[18]、海水深度预测[19]、故障诊断[20]等方面有广泛应用.
设有样本集X={x1,x2,…,xn},c为聚类中心个数,m为模糊权重指数,隶属度为uij(i=1,2,…,c;j=1,2, …,n).其中uij∈[0, 1],聚类中心为V ={V1,V2,…, Vc},算法目标函数为
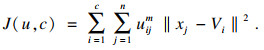 | (1) |
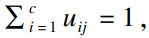
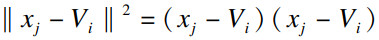
步骤1 ??参数初始化,输入聚类中心个数c(2≤c≤n),停止阈值ε,模糊权重指数m,选取初始聚类中心. V(b)={V1,V2,…,Vc},迭代计数器b=0.
步骤2 ??用式(2)计算并更新划分矩阵U(b):
U (b)=[uij(b)],对于任意i,j,如果存在dij(b)>0,则
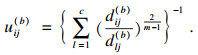 | (2) |
步骤3 ??用式(3)更新聚类中心矩阵V (b+1):
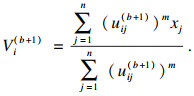 | (3) |
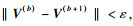
1.2 局部离群点检测算法LOFLOF算法用离群因子定量地描述每一个数据对象的离群程度,其没有全局计算数据点的密度,而是通过k邻域计算得到数据点的局部可达密度,因此其中表征离群程度的量被称为“局部”异常因子[21].传统LOF算法需要明确以下几个定义.
1) d(p, o): 点p与点o之间的距离.
2) 第k距离(k-distance): p的第k距离为p到其周围第k远的点的距离,但不包括p.
3) 第k距离邻域(k-distance neighborhood of p): 与点p的距离不超过其第k距离的所有点,包括第k距离上的点所组成的点集为p的第k距离邻域Nk(p).因此p的第k邻域点的个数Nk(p)≥k.
4) 可达距离(reach-distance): 点o到点p的第k可达距离为
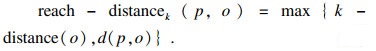 | (4) |
5) 局部可达密度(local reachability density): 点p的局部可达密度表示为
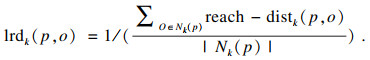 | (5) |
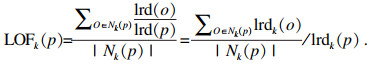 | (6) |
1.3 肘部法则聚类算法对聚类个数c的选取将直接影响算法的聚类效果.肘部法则将不同c值的成本函数值刻画出来,每个簇包含的样本数会随着c值的增大而减少,样本会更靠近其聚类中心,代价函数(式(7))随之减小.但随着c继续增大,代价函数的减小幅度不断下降,直至代价函数曲线趋于平稳.在c值增大过程中,代价函数减小幅度最大的位置就是肘部,使用这个c值一般可以取得很好的效果.
定义代价函数:
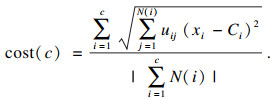 | (7) |
2 基于目标函数的局部离群点检测方法2.1 基于FCM目标函数的剪枝算法在1.1和文献[22]的基础上,提出了一种新的剪枝方法,即基于FCM目标函数的剪枝算法.首先,执行FCM算法,生成一个目标函数和几个簇;然后,将数据个数少于簇平均个数的小簇视为离群簇,将其加入离群候选集;由式(1)得知,从数据集中移除某个点,必然会导致目标函数的减小,若移除的点偏离正常数据较远,也就是离群程度较高的话,目标函数值的减小程度会更大,由此判断数据的离群程度.
基于FCM目标函数的剪枝算法推导过程:
令式(1)中的xj-Vi=dij,表示第j个点到第i个聚类中心的距离,n表示数据集D的样本个数,若移除数据集D中的某个点,样本个数变为n-1,且某个点的移除对整个数据集的聚类中心几乎不产生影响,此时,FCM的目标函数变为
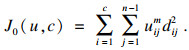 | (8) |
假设:
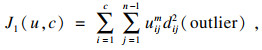 | (9) |
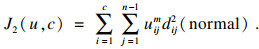 | (10) |
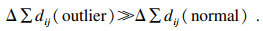 | (11) |
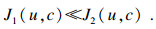 | (12) |
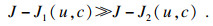 | (13) |
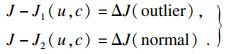 | (14) |
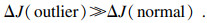 | (15) |
本文提出以下参数来说明上述方法,完整数据集的目标函数值OF,移除第i个点之后数据集的目标函数值OFi,移除第i个点后的目标函数值减少量DOFi=OF-OFi,逐次移除所有点之后的平均减少量
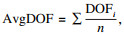
算法1??基于目标函数值剪枝算法.
输入:数据集D;
输出:离群候选集D0.
步骤1??对完整的数据集执行FCM算法,得到OF,并将小簇放入离群候选集;
步骤2??逐次移除剩余的点,得到所有的OFi,计算得到每一个DOFi和平均减少量AvgDOF;
步骤3??比较DOFi和T(AvgDOF),若DOF> T(AvgDOF),则将第i个点放入离群候选集.
2.2 加权LOF算法信息熵常被用于表征数据的离散程度,熵值越大代表变量的离散程度越大,其提供的信息越少;熵值越小代表变量的离散程度越小,其提供的信息越多.因此数据不同维的特征提供的信息量不同,需要相应赋予不同的权值.对于熵大的属性,所占权重应该较高,这样可以将其离散程度更明显地体现出来.
算法2??加权LOF算法.
输入: 数据集D;
输出: 权值集合W={ω1,ω2,…,ωm},每个数据的异常值得分LOFi.
步骤1??对数据集D执行Z-score标准化得到D′,通过式(16)计算得到数据集D′中第i个数据的第j维属性的比重Pij:
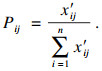 | (16) |
步骤2??用式(17)计算数据集D′中第j维属性的信息熵Ej:
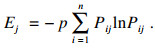 | (17) |
步骤3??用式(18)计算第j维属性的权值ωj:
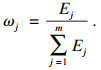 | (18) |
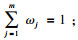
步骤4??利用熵权法对每一维属性赋权之后,再对每一维属性单独执行传统LOF算法,根据式(19)对其加权,获取最终的LOF值作为整体数据的异常得分.
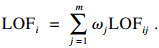 | (19) |
2.3 基于目标函数的局部离群点检测算法描述算法3??基于目标函数的局部离群点检测算法.
输入: 数据集D,邻域查询个数k,剪枝阈值T,离群点个数p;
输出: Top p个离群点.
步骤1??运用肘部法则确定数据集D的最佳聚类个数c;
步骤2??输入参数c,使用FCM算法对数据集D聚类,列出每一个数据移除后的目标函数值变化量并进行对比,依据剪枝阈值T(AvgDOFi),对数据集D剪枝得到离群候选集D0;
步骤3??在离群候选集D0中,利用式(16)~式(18)对每一维属性进行加权,之后用式(19)计算得到每一个数据的异常值得分LOF;
步骤4??将每个数据的LOF值按从大到小的顺序排列,输出前p个数据对象,组成数据集D的离群点集合.
传统的LOF算法在面对未知数据集,即不知道其数据分布,聚类个数等特征时检测效果十分不理想,并且由于其必须计算每一个数据点的离群程度,这又导致算法的计算量大大增加,FOLOF算法在这两方面做出了一定的改进.
3 实验对比在人工数据集和UCI数据库中选取Iris,Wine,Yeast和User Knowledge Modeling四个数据集,从聚类效果(CH指数,Dunn指数,I指数,S指数)[23]、准确度、误检率[24]等方面来验证所提出算法的可行性.前面部分提到的所有参数在下面实验中统一设置,剪枝时用到的阈值T取1,LOF算法和FOLOF算法中的邻域个数k取5.
3.1 人工数据集为了可视化离群点检测的整个过程,首先利用人工数据集Dataset1来进行实验.该数据集共有70个数据点,包含10个离群点,分别是第6,7,19,30,40,45,52,58,69,70等点,如图 1所示.先使用肘部法则确定最佳聚类个数,再剪枝得到离群候选集,运行加权LOF算法,将得出的离群值顺序排列.
图 1(Fig. 1)
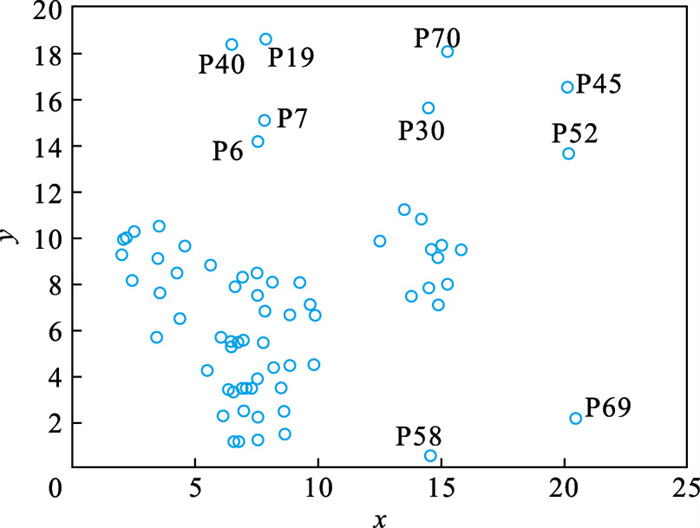 | 图 1 Dataset1数据集Fig.1 Dataset1 dataset |
如图 2所示,当聚类个数从3变到4时,代价函数逐渐趋于平缓,所以最佳聚类个数c为3,运行剪枝算法,得到OF的值为568.317,Avg(DOFi)的值为8.431,将每一个DOFi都列于表 1中,图 3为移除第i个点后的目标函数值图,图 4为移除第i个点后的目标函数值变化量针状图,与Avg(DOFi) 进行对比,最终剪枝剩下第6,7,8,19,30,40,45,52,58,60,69,70等12个点将其放入离群候选集,候选集中包含所有离群点,剪枝精度为100 %,运行加权LOF算法,将各点离群因子列于表 2中,输出离群值最大的前10个点,分别为第8,58,69,60,6,7,52,30,19,40等10个点,其中有8个为真实离群点,移除所检测出来的离群点后,重新对数据集进行聚类,聚类效果提升,如表 3所示.
图 2(Fig. 2)
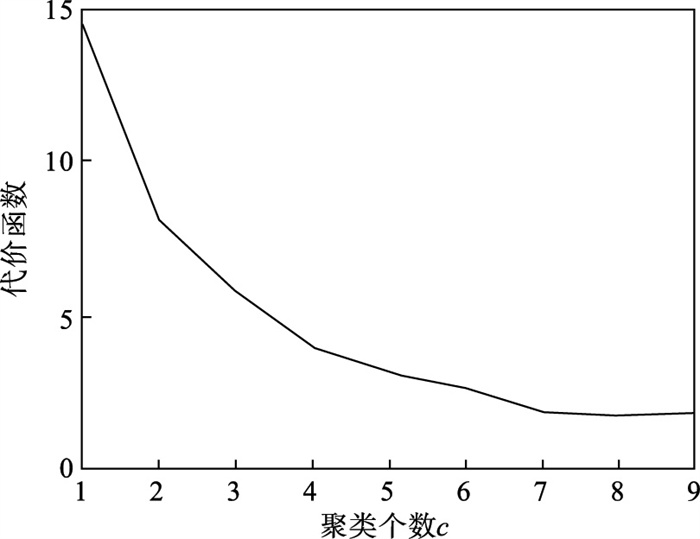 | 图 2 代价函数衰减Fig.2 Cost function attenuation |
表 1(Table 1)
| 表 1 目标函数值减少量对比 Table 1 Comparison of value reduction of objective function |
图 3(Fig. 3)
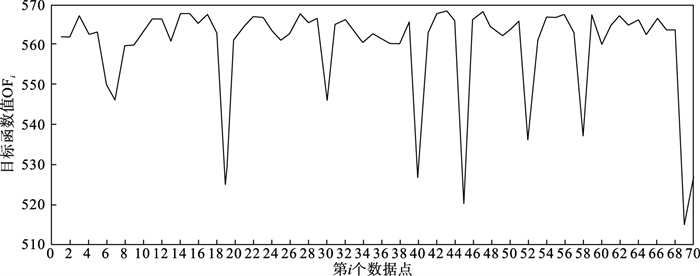 | 图 3 移除第i个点后的目标函数值Fig.3 Objective function value after removing the i point |
图 4(Fig. 4)
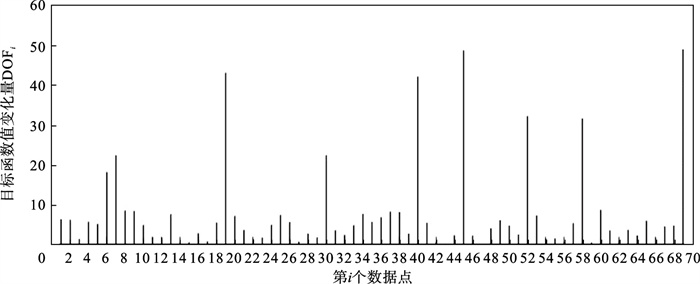 | 图 4 移除第i个点后的目标函数值变化量Fig.4 Variation of objective function value after removing the i point |
表 2(Table 2)
| 表 2 Dataset1离群候选集中各点离群因子(降序排列) Table 2 Outlier factors of each point in Dataset1 outlier candidate set (in descending order) |
表 3(Table 3)
| 表 3 Dataset1聚类指标对比 Table 3 Comparison of Dataset1 clustering indicators |
为了评估离群点检测的性能,采用准确度(precision,Pr)和误检率(noise factor,Nf)两个指标,分别用Pr和Nf表示.用TP表示算法检测到的真实离群点数量,用FP表示算法错将真实数据检测为离群点的数量,则
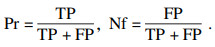 | (20) |
3.2 UCI数据集通过对比本文算法和LOF离群点检测算法在实际数据集中的运行结果来验证本文算法的性能,实验数据集如表 4所示.
表 4(Table 4)
| 表 4 实验数据统计 Table 4 Experimental data statistics |
对每个数据集运行肘部法则确定最佳聚类个数,分别是3,3,10,4,最佳聚类个数与实际分类个数基本一致,提出的方法对未知数据集具有可行性.
Iris数据集选取前两类数据作为正常数据,第三类中取10个数据作为离群数据.选取Wine数据集的前两类共130个数据点作为正常数据,第三类中随机选取8个数据作为离群数据.对于Yeast数据集,没有必要用到全部数据,选取CYT,NUC和MIT三个大类共1 136个数据作为正常数据,选取POX类共20个数据作为离群数据,另外,由于其第6维属性含有0值,在运行属性赋权算法计算比重时,不允许有0值的存在,则删除第6维属性,剩下其余7维属性进行离群点检测.对于UKM数据集,由于very_low中含有0值,则选取High,Middle两类共224个数据做为正常数据,Low中随机选取5个数据作为离群数据.
由剪枝精度,即剪枝后得到的离群候选集中真实离群点数量与整个数据集中的离群点数量的比值与剪枝后剩余数据量对比,结果证明FCM剪枝方法相比于DBSCAN剪枝方法、PMLDOF剪枝[25]方法具有比较明显的优势,如表 5和表 6所示.
表 5(Table 5)
| 表 5 剪枝精度对比 Table 5 Comparison of pruning accuracy |
表 6(Table 6)
| 表 6 剪枝后剩余数据量对比 Table 6 Comparison of remaining data after pruning |
通过对比检测结果和移除所检测出的离群点之后的聚类效果,证明所提出的方法相比于LOF算法具有优势,实验结果如表 7和表 8所示,运行时间为t,单位s.算法采用MatlabR2016a编写,实验环境为:酷睿i5 2.90 GHz CPU,8.00 GB内存,Windows7操作系统.
表 7(Table 7)
| 表 7 四种数据集检测结果对比 Table 7 Comparison of test results of four datasets | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 8(Table 8)
| 表 8 四种数据集去除离群点前后聚类效果对比 Table 8 Comparison of clustering effects of four datasets before and after removing outliers | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
经过仿真实验验证,本文提出的算法对未知数据集具有一定的处理能力,与传统的LOF算法相比在检测结果方面有明显提升.去除所检测出来的离群点后,重新对数据集聚类,聚类效果有明显改善,在进行检测之前先通过FCM进行了数据剪枝,减少了很大一部分计算量,相比于LOF算法,运行时间明显减少.
3.3 分析讨论1) FOLOF算法通过肘部法则确定数据集的最佳聚类个数以达到最好的聚类效果,这使得其在面对未知数据集时具备更好的处理能力,而LOF算法在面对所有数据集时的处理方法全部一致即逐个计算离群因子,对不同的数据集缺乏针对性.
2) FOLOF算法通过FCM的目标函数变化量对数据集进行剪枝,得到初步的离群点集,这就在数据量方面大大降低了计算复杂度,而LOF算法并未对数据集进行预处理,会导致较大的计算量和较长的运行时间.
3) 在输入参数方面,FOLOF算法只需要人为输入邻域查询个数k,剪枝阈值T和需要输出的离群点个数p,并且这些参数的设定不需要经过繁琐的实验过程,一般都采用经验值就能得到不错的检测效果.
4) 在检测精度方面,FOLOF算法的检测精度高于LOF算法,其综合检测性能得到了提高.
4 结语本文提出一种基于目标函数的离群点检测方法FOLOF,首先,根据肘部法则确定最佳聚类个数;然后,利用目标函数对数据集进行剪枝;最后,采用加权LOF算法确定数据点的离群程度.相比于传统的LOF离群点检测算法,本文所提的方法在检测精度、检测效果以及检测速度等方面的性能均有明显提升.然而,该方法还需要在以下2个方面进行深入研究:阈值T的敏感度分析以及基于阈值T的离群点分类的研究,即研究出相应的方法实现强弱离群点的辨别;在FCM算法之外,其他聚类算法的目标函数是否可以用于剪枝及对剪枝结果有何种影响.
参考文献
| [1] | Hawkins D. Identification of outliers[M]. Londen: Chapman and Hall, 1980. |
| [2] | Ji Z. Advancements of outlier detection: a survey[J]. ICST Transactions on Scalable Information Systems, 2013, 13(1): 1-24. DOI:10.4108/trans.sis.2013.01-03.e1 |
| [3] | Vijayakumar V, Sri N, Sarojini P. Isolation forest and local outlier factor for credit card fraud detection system[J]. International Journal of Engineering and Advanced Technology, 2020, 4(9): 261-265. |
| [4] | Wang F, Wei Z, Zuo X. Anomaly IoT node detection based on local outlier factor and time series[J]. Computers, Materials & Continua, 2020, 2(64): 1063-1073. |
| [5] | Yuan X, Li J, Bai J. A local outlier factor-based detection of copy number variations from NGS data[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2019(99): 1-1. |
| [6] | 吴强, 张锐. 基于局部异常因子的近地全天时星图小波去噪[J]. 光学学报, 2020, 40(8): 46-54. (Wu Qiang, Zhang Rui. Wavelet denoising of near earth all sky time star map based on local anomaly factor[J]. Journal of Optics, 2020, 40(8): 46-54.) |
| [7] | Liu X, Cheung Y M, Peng S J, et al. Automatic mitral valve leaflet tracking in Echocardiography via constrained outlier pursuit and region-scalable active contours[J]. Neurocomputing, 2014(144): 47-57. |
| [8] | 周玉, 朱文豪, 房倩, 等. 基于聚类的离群点检测方法研究综述[J]. 计算机工程与应用, 2021, 57(12): 37-45. (Zhou Yu, Zhu Wen-hao, Fang Qian, et al. Research review of outlier detection methods based on clustering[J]. Computer Engineering and Application, 2021, 57(12): 37-45. DOI:10.3778/j.issn.1002-8331.2102-0167) |
| [9] | 梅林, 张凤荔, 高强. 离群点检测技术综述[J]. 计算机应用研究, 2020, 37(2): 3521-3527. (Mei Lin, Zhang Feng-li, Gao Qiang. Overview of outlier detection technology[J]. Computer Application Research, 2020, 37(2): 3521-3527.) |
| [10] | Breuning M, Krigegel H P, Ng R, et al. LOF: identifying density based local outliers[C]//Proceeding of the ACM SIGMOD International Conference on Management of Data. Dallas, 2000: 93-104. |
| [11] | Li L, Huang L, Yang W. Privacy-preserving LOF outlier detection[J]. Knowledge and Information Systems, 2015, 42(3): 579-597. DOI:10.1007/s10115-013-0692-0 |
| [12] | 王敬华, 赵新想, 张国燕, 等. NLOF: 一种新的基于密度的局部离群点检测算法[J]. 计算机科学, 2013, 40(8): 181-185. (Wang Jing-hua, Zhao Xin-xiang, Zhang Guo-yan, et al. NLOF: a new density based local outlier detection algorithm[J]. Computer Science, 2013, 40(8): 181-185.) |
| [13] | 石鸿雁, 马晓娟. 改进的DBSCAN聚类和LAOF两阶段混合数据离群点检测方法[J]. 小型微型计算机系统, 2018, 39(1): 74-77. (Shi Hong-yan, Ma Xiao-juan. Improved DBSCAN clustering and LAOF two-stage mixed data outlier detection method[J]. Small Microcomputer System, 2018, 39(1): 74-77.) |
| [14] | 董泽, 贾昊. 基于EWT-LOF的热工过程数据异常值检测方法[J]. 仪器仪表学报, 2020, 41(2): 126-134. (Dong Ze, Jia Hao. Abnormal value detection method of thermal process data based on ewt-lof[J]. Journal of Instrumentation, 2020, 41(2): 126-134.) |
| [15] | He Z Y, Xu X F, Deng S C. Discovering cluster-based local outliers[J]. Pattern Recognition Letters, 2003, 9(24): 1641-1650. |
| [16] | Li Q, Zhang J P, Feng G S. An outlier detection method based on fuzzy c-means clustering[J]. Key Engineering Materials, 2010, 419/420: 165-168. |
| [17] | Subramaniam M, Kathirvel A, Sabitha E, et al. Modified firefly algorithm and fuzzy c-means clustering based semantic information retrieval[J]. Journal of Web Engineering, 2021, 1(20): 33-52. |
| [18] | 徐金东, 赵甜雨, 冯国政, 等. 基于上下文模糊C均值聚类的图像分割算法[J]. 电子与信息学报, 2021, 43(7): 2079-2086. (Xu Jin-dong, Zhao Tian-yu, Feng Guo-zheng, et al. Image segmentation algorithm based on context fuzzy c-means clustering[J]. Journal of Electronics and Information, 2021, 43(7): 2079-2086.) |
| [19] | Kamolov A A, Park S. Prediction of depth of seawater using fuzzy c-means clustering algorithm of crowdsourced sonar data[J]. Sustainability, 2021, 13(11): 5823-5823. |
| [20] | Zhou Y, Ren Q C. Fuzzy c-means clustering algorithm for performance improvement of ENN[J]. Cluster Computing, 2019, 22(5): 11163-11174. |
| [21] | 王立英, 石磊, 伊静, 等. NLOF: 基于网格过滤的两阶段离群点检测算法[J]. 计算机应用研究, 2020, 37(24): 990-993. (Wang Li-ying, Shi Lei, Yi Jing, et al. NLOF: two-stage outlier detection algorithm based on grid filtering[J]. Computer Application Research, 2020, 37(24): 990-993.) |
| [22] | Moh D, Bela L, Zoubi A L, et al. New outlier detection method based on fuzzy clustering[J]. WSEAS Transactions on Information Science and Applications, 2010, 7(4/5/6): 681-690. |
| [23] | Gan G J, Kwok-Po M. K-means clustering with outlier removal[J]. Pattern Recognition Letters, 2017, 90(15): 8-14. |
| [24] | Feng G, Li Z, Zhou W, et al. Entropy-based outlier detection using spark[J]. Cluster Computing, 2020(23): 409-419. |
| [25] | 古平, 刘海波, 罗志恒. 一种基于多重聚类的离群点检测算法[J]. 计算机应用研究, 2013, 30(3): 751-753. (Gu Ping, Liu Hai-bo, Luo Zhi-heng. An outlier detection algorithm based on multi clustering[J]. Computer Application Research, 2013, 30(3): 751-753.) |
