
 , 王述红, 李友明
, 王述红, 李友明 东北大学 资源与土木工程学院,辽宁 沈阳 110819
收稿日期:2021-09-29
基金项目:国家自然科学基金资助项目(52004052);中央高校基本科研业务费专项资金资助项目(N2101027)。
作者简介:赵永(1991-),男,山东临沂人,东北大学讲师;
王述红(1969-),男,江苏泰州人,东北大学教授,博士生导师。
摘要:随着国家对深部工程开发的需求增大,深部高岩温条件下断层黏滑失稳过程的演化规律和形成机制亟待研究.为此,本文借助离散元数值模拟手段,构建热力耦合数值模型,对6种不同温度场条件下的断层黏滑力学行为进行了详细研究,探究了不同温度场对断层黏滑失稳过程的影响机制.结果表明:随着温度场的不断上升,断层黏滑的破坏形态以及破坏模式均发生改变;断层黏滑次数、启滑应力以及启滑应力降整体上随温度上升,呈现不断下降的变化趋势;断层黏滑能量耗散以摩擦滑动为主;断层启滑时,总应变能与温度呈正相关,耗散能与温度呈负相关.
关键词:断层黏滑温度场离散元裂隙演化
Simulation of Fault Stick-Slip Instability Processes Under Different Temperature Fields
ZHAO Yong, ZHAO Qian-bai

 , WANG Shu-hong, LI You-ming
, WANG Shu-hong, LI You-ming School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: ZHAO Qian-bai, E-mail: 2538440998@qq.com.
Abstract: With the development of deep engineering in China, the evolution law and formation mechanism of fault stick-slip instability process in the deep area and high rock temperature need to be studied. Therefore, a numerical thermo-mechanical coupling model is constructed with discrete element code, the mechanical behavior of fault stick-slip under six different temperature fields was studied in detail, and the influence mechanism of different temperature fields on the process of fault stick-slip instability was explored. The results show that the failure patterns and failure modes of fault stick-slip change with the increase of temperature. The number of stick slip, initiation slip stress and initiation slip stress drop show an overall decreasing trend with increasing temperature. The energy dissipation of fault stick-slip is dominated by frictional sliding. When the fault starts sliding, the total strain energy is positively correlated with temperature, and the dissipated energy is negatively correlated with temperature.
Key words: fault stick-sliptemperature fieldsdiscrete elementsfracture evolution
自然界中,岩体往往会受到构造应力的作用而形成节理、破裂面及断层等不同类型的结构面与结构体,继而对岩体的力学性质产生影响[1].在天然岩体中,节理的一种地质延伸和扩展的结果即为断层,其相对于节理的组织结构而言,更为复杂,规模和影响也大得多.Goodman[2]将断层作为地质隐患评价的首位影响因子.断层黏滑是岩石摩擦滑动的基本形式之一,是一种不稳定的滑动.此类断层的摩擦滑动形式往往会对隧洞、采矿、地下洞室以及地表建筑物等工程项目造成严重的危害,给社会造成巨大的经济损失.因此,详细研究断层黏滑失稳过程的演化规律和形成机制有着重要的科学意义与工程价值.
目前,国内外诸多****对断层黏滑失稳过程开展了许多有意义的研究.赵扬锋等[3]联合微震和电荷感应监测方法,研究了不同断层倾角下断层黏滑失稳过程的微震与电荷信号时序特征.Khazaei等[4]建立了断层黏滑离散元模型,并开发了断层黏滑失稳过程微震事件的模拟算法,研究了法向应力、断层摩擦系数、断层刚度等不同因素对黏滑行为的影响.Yta等[5]在毫米级的滑动界面粗糙度的前提下,建立了不同粗糙度下花岗岩的三轴黏滑数值模型,再现了黏滑物理实验中的关键力学特征.Kettermann等[6]采用沙盒试验与离散元相结合的方式,研究了岩盐对膨胀性断层运动的影响,分析了含韧性材料断层带的黏滑行为.然而,由于工程岩体开挖深度的不断增大,断层所处地层深度增大,围岩温度随之不断上升.高温作用下,断层结构面摩擦力以及断层两侧岩体强度下降.常温条件下的研究结果,并不完全适用于高温条件下的断层黏滑力学特性的描述.因此,温度对断层黏滑失稳行为的影响不容忽略.
当前许多****对岩石热损伤及温度作用下的岩石力学特性展开了研究. Zhao[7]建立了花岗岩离散元的热力耦合模型,揭示了热致微裂纹演化与模型边界条件、加热路径的内在联系,论述了温度致使岩石力学性质演变的机理.Tian等[8]以PFC中的Cluster模型为基础建立了花岗岩试样的数值模型,研究了热处理后花岗岩的裂纹演化规律和力学特性.贾蓬等[9]利用超声波无损检测、XRD衍射和偏光显微镜等观测手段,研究了高温岩体水冷却后的力学特性及微观破裂特征.温度的升高导致岩体内部强度与黏滞系数普遍降低,岩体结构面的摩擦系数下降.温度场作用下的岩体力学特性的研究多以物理试验为主要的研究手段. 通过数值模拟方法揭示岩体力学行为特性的研究,多以不同温度下岩体的破坏力学行为特性为主,缺少对不同温度下岩体结构面力学行为特性分析.
综上,本文通过建立断层黏滑的离散元数值模型,对不同温度场下花岗岩的断层黏滑失稳过程进行模拟研究.从微观角度出发,分析了断层黏滑失稳过程的裂纹演化、能量演化及应力演化特性,得到不同温度场下断层黏滑过程的力学行为模式,有助于进一步认识深部高温条件下的断层黏滑失稳过程的演化规律和形成机制.
1 断层黏滑模型构建及模拟工况1.1 断层黏滑模型构建颗粒流离散元法是基于力-位移定律和牛顿第二运动定律,采用显式有限差分方法进行循环迭代求解,通过模拟刚性颗粒集合体的运动与相互作用,继而有效体现介质破裂损伤、裂纹扩展等现象[10].颗粒之间的接触模型是表征颗粒集合体力学特性的基本单元, PFC中内置了多种类型的接触模型以表征不同力学特性的颗粒集合体.因此,本文利用PFC中的平行黏结模型模拟岩体基质,光滑节理模型模拟断层结构面.基于赵扬锋等[3]室内双轴压缩试验岩体预处理与加载条件;基于文献[7]数值模拟中的岩体组分、尺寸与接触参数,建立断层黏滑的二维数值模型,进行双轴压缩试验,具体步骤如下:
1) 由试样尺寸50 mm×50 mm设定合适的计算区域,生成岩体模型的边界,并进行5 mm×5 mm的倒角处理.以31 % 的石英、27 % 的钾长石、38 % 的斜长石以及4 % 的云母为颗粒分组依据,生成均匀的指定孔隙率的颗粒集合体[7](试样模拟模型,见图 1).
图 1(Fig. 1)
 | 图 1 断层黏滑模拟模型Fig.1 Simulation model of the fault stick-slip (a)—完整岩体;(b)—含45°断层岩体. |
2) 编写FISH函数对8面墙体进行伺服控制,调整颗粒间的内应力,以此使数值模型达到平衡稳定的状态.
3) 按表 1花岗岩的微观参数[7]添加平行黏结接触模型,以此模拟完整岩体的力学特性.
表 1(Table 1)
| 表 1 花岗岩的微观参数[7] Table 1 Microscopic parameters of granite[7] |
4) 添加倾斜角度为45°的断层,并将断层颗粒的接触由平行黏结模型更改为光滑节理模型,循环模型至静态平衡状态.
5) 对含断层的花岗岩数值模型进行伺服控制,分别在X与Y方向上施加20 MPa的围压.
6) 保持X方向的伺服控制,关闭Y方向的伺服.选择0.05 s-1应变率进行加载.加载直至Y方向的应变达到1 %,停止加载,完成断层黏滑失稳过程的数值模拟.
1.2 不同温度场工况构建在构建含45°断层岩体的数值模型基础上,进一步研究不同温度场作用下断层黏滑失稳过程的演化规律及形成机制.利用热模块构建热力耦合数值模型.热模块中,颗粒作为储热器,颗粒与颗粒之间的接触作为热管,二者共同形成了热网络,以反映瞬态热传导的过程[8].由于颗粒集合体中存在“悬浮颗粒”,该颗粒与周围颗粒之间并未生成接触,而热流量以颗粒间的接触作为传导的媒介.因此,当墙体或颗粒作为加热源对模型进行热传导时,颗粒与墙体或颗粒之间无接触的位置易出现“热泄漏”的现象.以图 2为例,温度无法正常地从加热源向内部传导,也易造成“热冲击”的现象发生.采用墙体或颗粒作为加热源[7]的计算效率较低,即数值模型中颗粒数量达到万级以上,模拟时间将大幅上升;无法使岩体模型整体均匀升温至指定温度.因此,这种计算模型不适合模拟不同温度场下的断层黏滑失稳问题.综上所述,本文热力耦合计算模型更适用不同温度场下断层黏滑失稳的工况, 计算效率更高, 有效避免“热冲击”与“热泄漏”现象.
图 2(Fig. 2)
 | 图 2 瞬态热传导的“热泄漏”Fig.2 "Heat leakage"of transient heat conduction |
热力耦合的实现通过温度变化使得颗粒产生膨胀或收缩,引起了热应变,颗粒热膨胀的表达式为
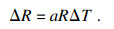 | (1) |
热膨胀导致颗粒之间的法向黏结力发生变化,其表达式为
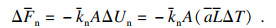 | (2) |
为了能够准确表征含断层岩体因温度场作用下的热行为,对构成花岗岩的组分赋予不同的热膨胀系数[7]:斜长石为14.1×10-6 K-1,钾长石为8.7×10-6 K-1,云母为3.0×10-6 K-1,石英为24.3×10-6 K-1.各组分颗粒的比热容统一取为1 015 J · kg-1 K-1,颗粒之间热管的热阻取值由宏观热导率3.5 W · m-1 K-1及定义的计算公式得到,其公式为
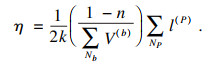 | (3) |
为了分析6种不同温度场下断层黏滑失稳过程中的力学特性,设定颗粒集合体的初始温度场为20 ℃,并逐渐加热到5种不同峰值温度:100,200,300,400和500 ℃,随后进行双轴压缩试验.为了避免热力耦合过程中瞬态热传导产生“热冲击”效应,温度场程序的编写采用Deltemp(自上一次力模块计算以来的温度增量)关键命令语句,并通过以下3个步骤进行热力耦合的模拟:①模型循环至静态平衡状态,该状态由设定平衡极限比Mech-aratio值为0.000 01所控制;②模型以每个循环上升10 ℃进行缓慢升温,由初始温度均匀变化至指定的峰值温度;③重新循环至静态平衡状态. 图 3为不同温度场下岩体模型的微裂纹演化,图 4为裂纹数量随温度的变化趋势.
图 3(Fig. 3)
 | 图 3 不同温度场下岩体微裂纹分布Fig.3 Distribution of microcracks in the rock at different temperature fields (a)—20 ℃; (b)—100 ℃; (c)—200 ℃; (d)—300 ℃; (e)—400 ℃; (f)—500 ℃. |
图 4(Fig. 4)
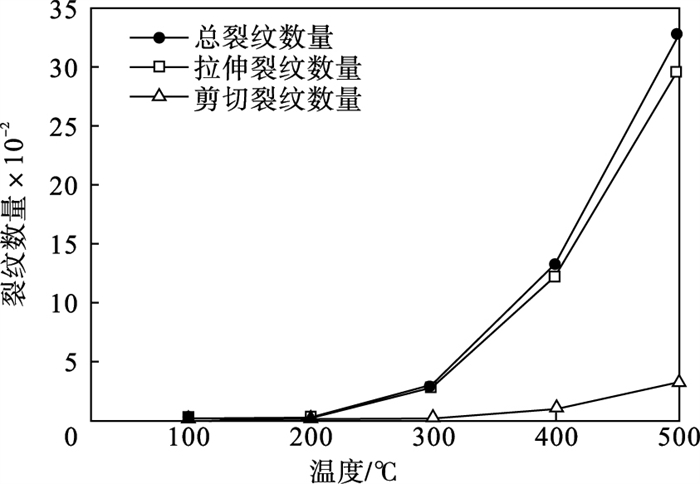 | 图 4 裂纹数量随温度的变化趋势Fig.4 Trend of the numbers of crack with temperature |
从图 3、图 4可知,花岗岩各组分线膨胀系数与颗粒半径的差异性导致了颗粒变形不同,继而产生热应力,当平行黏结模型中的法向或切向强度不足以抵抗温度变化所产生的热应力时,就会发生拉伸或剪切破坏.加热过程中裂纹种类以及数量的变化趋势中:初始温度25 ℃到100 ℃之间并没有微裂纹的产生,此时的热应力未达到颗粒之间接触模型发生拉伸或剪切破坏的临界值;100 ℃到200 ℃之间产生少量的微裂纹,随着温度的不断上升,直至500 ℃,微裂纹以指数函数的发展趋势不断增加.这些微裂纹在岩石内部随机分布,彼此之间并未形成宏观裂纹.其中,剪切裂纹占据总裂纹的百分比远远小于拉伸裂纹.由此可知,花岗岩的热破裂主要以拉伸破坏为主.
2 断层黏滑过程力学特性分析2.1 断层黏滑过程应力-应变曲线演化分析对不同温度场下含断层的岩体模型进行双轴压缩试验,其最终的应力-应变曲线如图 5所示.断层黏滑失稳过程可划分为4个阶段:
图 5(Fig. 5)
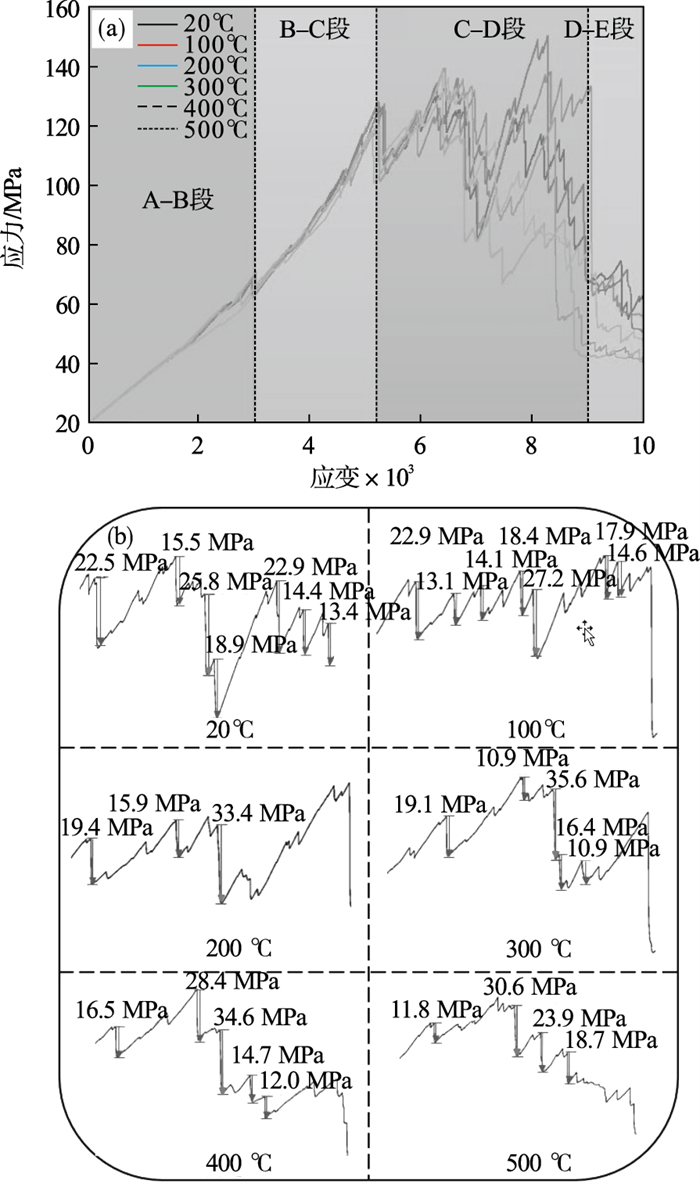 | 图 5 不同温度场下断层黏滑应力-应变曲线Fig.5 Stress-strain curves of the fault stick-slip at different temperature fields (a)—应力-应变全过程演化曲线;(b)—应力-应变局部演化曲线(C-D段). |
1) A-B压缩阶段.含断层岩体模型承受不断增大的轴向应力,但尚未达到产生断层黏滑的临界值,断层结构面两侧的岩石未发生相对错动,呈现一种免“自锁”现象.此时,可将含断层的岩体模型近似看作完整岩体受压,发生弹性形变,岩体模型内部各区域未出现微裂纹.
2) B-C黏滑前阶段.随着上下墙体施加的应力不断增加,断层结构面两端的倒角区域出现少量微裂纹,并不断向着加载方向发展.断层结构面出现微量的微裂纹,应力增长速率缓慢上升.
3) C-D黏滑阶段.随着岩体模型所受的轴向应力增大,直至达到断层黏滑临界值,断层结构面的剪应力超过了摩擦阻力,岩体模型的上盘与下盘发生了相对错动,积累的应变能迅速释放,产生应力突降(启滑).同时,黏滑失稳现象导致断层结构面两侧一定范围内岩体微裂纹的形成.随后,断层结构面两侧的岩体又将呈现“自锁”现象,应力重新开始增加,达到一定临界值后,岩体上下盘再次出现错动,如此反复,形成了多次黏滑运动.
4) D-E黏滑后阶段.断层黏滑失稳造成了断层两侧岩体严重的损伤,应力出现大幅度的突降.此时可视为岩体发生了失稳破坏.
通过上述断层黏滑失稳过程的应力-应变曲线表现出不同的黏滑力学特征分析以及图 6曲线的变化趋势可知,随着温度的不断上升,岩体内部热损伤逐渐增大,断层两侧岩体的强度不断持续下降,导致断层黏滑过程次数不断下降.最大应力降量值在不同温度场下呈现出上升-下降的变化规律.原因在于温度增量较小时,岩体内部损伤较小,强度的变化较小,每次断层黏滑失稳对岩体破坏程度较小,小损伤不断积累直至达到阈值.因此,应力-应变曲线出现“断崖”式下降,最大应力降在该阶段呈现上升的趋势.当温度增量达到一定量值之后,断层两侧岩体强度下降较大,应力-应变曲线产生大幅度应力降前,断层两侧岩体不断产生若干个小幅度应力降,不断释放积累的应变能,每一次大幅度断层黏滑失稳对岩体破坏程度较大,断层两侧岩体“自锁”程度减弱.因此,最大应力降量值下降.而随着温度的不断上升,断层结构面的损伤程度增大,静摩擦力逐渐下降,导致启滑应力整体呈现下降趋势.断层黏滑的启滑应力降整体表现出下降的趋势,原因在于温度增量导致断层结构面颗粒半径产生膨胀,颗粒之间的接触面积增大,动摩擦阻力上升,故启滑应力降不断随温度的上升而下降.
图 6(Fig. 6)
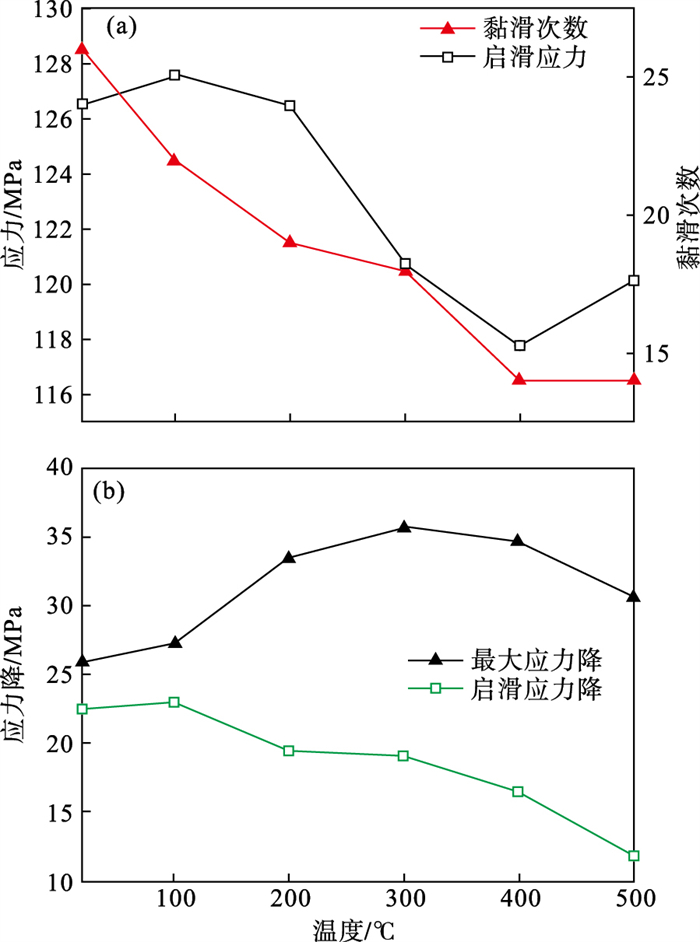 | 图 6 断层黏滑过程机械特性的变化Fig.6 Evolution of the mechanical characteristics of fault stick-slip processes (a)—启滑应力与黏滑次数的变化趋势;(b)—最大应力降与启滑应力降的变化趋势. |
2.2 断层黏滑过程裂纹空间演化分析断层黏滑过程裂纹的空间演化一定程度上反映了黏滑过程的演化规律和形成机制,不同的破坏形态反映出不同温度场下断层黏滑的破坏模式, 如图 7所示.
图 7(Fig. 7)
 | 图 7 不同温度场下岩体破坏形态Fig.7 Damage patterns of rock masses under different temperature fields (a)—20 ℃; (b)—100 ℃; (c)—200 ℃; (d)—300 ℃; (e)—400 ℃; (f)—500 ℃. |
从不同温度场下含断层岩体模型的破坏形态可知:随着轴向应力的不断增大,导致断层结构面附近出现应力集中,剪应力随之增大,当断层结构面的剪应力超过摩擦阻力时,断层两侧的岩石发生相对错动,产生黏滑现象.
由图 7可知,温度的改变并未使其破坏形态发生根本性质的改变.大量的裂纹出现在断层两侧临近的部分,较多的微裂纹形成于断层结构面的中心位置,而距断层较远的岩体部位未产生微裂纹, 多数微裂纹形成于岩石的上盘,微裂纹之间形成贯通的宏观裂隙.
20,100,200与300 ℃的破坏形态更为接近,随着断层黏滑失稳现象的产生,微裂纹导致了宏观裂隙的出现,并形成了块状破碎,同时部分宏观裂隙与断层结构面形成一定的夹角,并向远离断层结构面的两侧不断发展,但最终未贯穿整个岩体模型.
400与500 ℃的破坏形态表现得极为相似,相对于低温度场出现的纵向裂隙破坏形态而言,这二种高温条件下的断层黏滑所产生的微裂纹表现出聚集的形态.大量裂纹集中于断层结构面的中心偏上部的位置,造成断层结构面邻近的岩体产生了块状破碎.随着黏滑的多次发生,断层结构面产生了一定的损伤,而断层面的损伤又将影响着下一次黏滑的产生.二者之间存在着相互协同、互相影响的关系.
由图 8a可知,随着温度的不断上升,裂纹数量整体呈现一种缓慢上升、快速下降又快速上升的趋势.导致该现象的原因在于:20~200 ℃区间,温度对岩体损伤程度较小,断层结构面强度下降,有利于黏滑现象的产生,裂纹数量在该阶段呈现缓慢上升;200~400 ℃区间,温度对岩体损伤程度较大,断层两侧岩体承受相对于前三种工况更少黏滑次数后即发生失稳破坏,因此裂纹数量下降;400~500 ℃区间,岩体所受到损伤大幅上升,达到阈值,断层两侧岩体虽然承受黏滑次数下降,但是每一次的黏滑失稳均对两侧岩体造成更大的破坏,故裂纹再次呈现出上升的趋势.断层两侧岩体产生黏滑失稳时,产生了反方向的错动滑移,断层结构面邻近区域颗粒之间的位移存在着非一致性,导致断层结构面附近的岩体微裂纹破坏模式以拉伸破坏为主导.其中6种温度下拉伸裂纹占总裂纹的百分比分别为92.8 %,91.2 %,92.6 %,93.3 %,94.0 %,95.3 %.可见,拉伸裂纹数量随着温度的不断升高,占据总裂纹的百分比整体也呈现不断上升的趋势,而剪切裂纹仅占据总裂纹的小部分.由此可知,断层黏滑所产生的微裂纹破坏形态以拉伸破坏为主导.
图 8(Fig. 8)
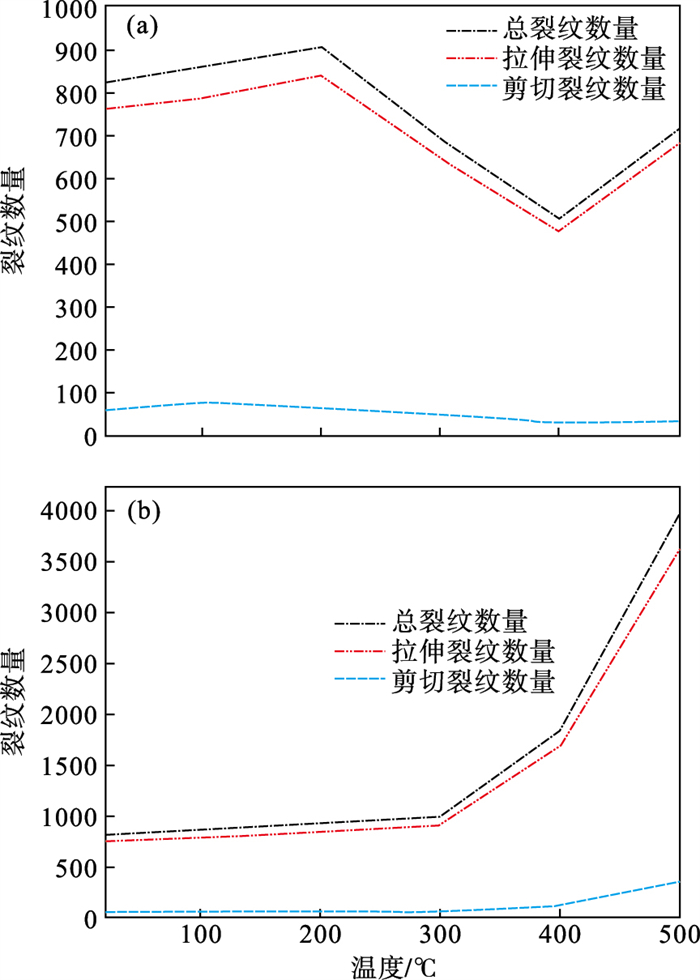 | 图 8 不同温度场下裂纹演化曲线Fig.8 Crack evolution curves at different temperature fields (a)—不包含热损伤;(b)—包含热损伤以及断层黏滑失稳. |
由图 8b可知,对断层黏滑失稳全过程以及热损伤全过程的裂纹数量统计, 总裂纹数量在400~500 ℃区间内呈现大幅上升的趋势,热损伤程度越大,断层黏滑失稳后对断层两侧岩体的累计损伤越大.因此,该裂纹演化曲线整体呈现出上升的趋势.
2.3 断层黏滑过程力链演化及能量演化分析力链是颗粒集合体在应力加载作用下,颗粒之间彼此相互挤压形成的接触网络.对不同温度场下断层黏滑失稳过程的力链演化进行分析,有助于进一步认识黏滑失稳的演化规律和形成机制.
图 9为不同温度场下断层黏滑失稳过程的力链演化图,其中黑色代表受压区域,浅色代表拉伸区域.由此可见:20 ℃时,岩体模型的拉伸区域主要分布在断层附近以及垂直断层中心线附近,形成一个集中化十字交叉的区域.随着温度的不断上升,岩体模型内部的拉伸区域逐渐开始向集中化十字交叉区域外围发展,100与200 ℃的拉伸区域离散化程度相近;300 ℃的拉伸区域离散化主要分布在岩石的下盘,上盘的拉伸区域明显减少;400与500 ℃的拉伸区域有了显著的增加,且呈现明显的离散化,分布在岩石上下盘的内部.
图 9(Fig. 9)
 | 图 9 不同温度场下岩体拉压区域空间分布状态Fig.9 Spatial distribution of tension and compression zones in rock under different temperature fields (a)—20 ℃; (b)—100 ℃; (c)—200 ℃; (d)—300 ℃; (e)—400 ℃; (f)—500 ℃. |
断层黏滑失稳过程力学特征变化的内在本质是能量转换.因此,通过能量追踪命令,编写能量监测程序,以每20时步为间隔,实时记录断层黏滑失稳过程中的各类能量变化数值.为深入了解黏滑失稳过程的能量演化机制,以温度场为20 ℃工况下的断层黏滑作为研究对象进行分析.
图 10为断层黏滑过程能量演化曲线,由图可知,整个能量演化过程可分为4个阶段.其中断层黏滑过程中应力降常伴随着颗粒动能的突增,动能幅值的大小与应力降的大小呈现出正相关的趋势.但从图 10b可知,断层黏滑过程中边界能转换为动能的数值极小.因此,在断层黏滑过程中颗粒几乎不产生大幅运动,与准静态加载的原则具有一致性.与其他类型的能量幅值对比,双方不在同一数量级,可将其视为不变量.因此,动能演化在断层黏滑过程的4个阶段中不做能量演化机制的研究对象.
图 10(Fig. 10)
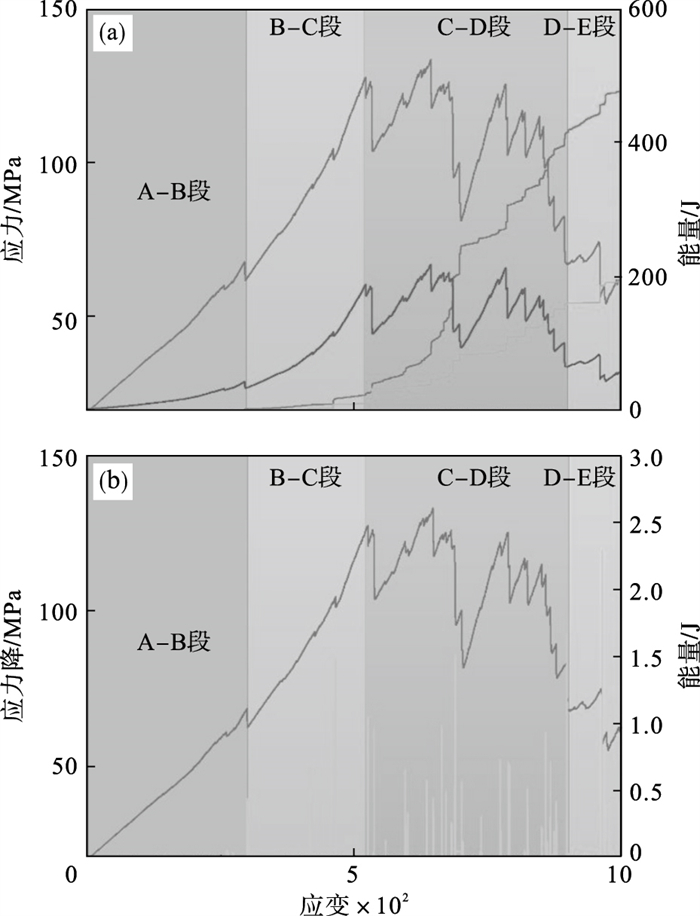 | 图 10 断层黏滑过程能量演化(20 ℃)Fig.10 Energy evolution of the fault stick-slip process(20 ℃) (a)—能量演化曲线;(b)—动能演化曲线. |
1) A-B压缩阶段.随着上下墙体以恒定速度对模型加载做功,岩体模型内部的阻尼能和摩擦能均为0,保持不变.这说明,边界能全部转化为颗粒线性与平行黏结弹簧部分的应变能,并且由于颗粒之间的接触不断加强,总应变能保持一定的增长速率持续上升.断层两侧岩体呈现“自锁”的形态,未产生黏滑失稳现象.因此,岩体内部应变能并未转化为胶结破坏能,即无微裂纹产生.
2) B-C黏滑前阶段.随着上下墙体所施加应力的不断上升,部分边界能转化为阻尼能和耗散能,断层两侧岩体呈现出相互错动的趋势.岩体内部总应变能转化为胶结破坏能,能量的释放导致岩体部分区域接触发生断裂,出现少量微裂纹.该阶段仅产生少量的小幅值黏滑现象.因此,岩体内部的摩擦能和阻尼能以一种缓慢趋势持续上升,而总应变能以不断增加的增长速率持续上升.
3) C-D黏滑阶段.在该阶段过程中,断层两侧岩体不断发生错动,产生黏滑失稳现象,导致颗粒间积累的大量应变能得到了释放,造成微裂纹数量的迅速发展.每一次黏滑失稳过程中,总应变能下降的量值与应力降的量值具有正相关性.断层两侧岩体出现大量微裂纹,形成裂纹带.同时,由于断层两侧岩体抵抗摩擦做功而耗散的能量呈现快速上升的趋势.随着黏滑次数的不断增大,边界能转化为摩擦能的量值逐渐超过颗粒间积累的应变能,而阻尼能增长速率以及增长量值均小于摩擦能.
由此可见,黏滑岩体模型系统内部的能量耗散方式以摩擦滑动为主导.摩擦能量值大小同样与应力降量值大小呈现正相关的趋势,即应力降的量值越大,断层之间所要克服摩擦做功越大,总应变能转化为胶结破坏能越多,对断层两侧岩体内部产生的损伤越大.
4) D-E黏滑后阶段.岩体内部颗粒间接触断裂数量与损伤程度已积累到一定量值,颗粒无法储存更多的总应变能.因此,总应变能曲线演化已不再呈现上升趋势,仍伴随着黏滑失稳而产生正相关性的下降.摩擦能与阻尼能的增长量值主要是由于颗粒摩擦及运动所导致.因此,随着断层黏滑现象逐渐消失,二者增长趋势逐渐趋向于平稳.
断层面应力达到启滑阈值时产生黏滑失稳,在此应力特征点下,分析岩体模型内部总应变能与耗散能随温度变化关系,见图 11.
图 11(Fig. 11)
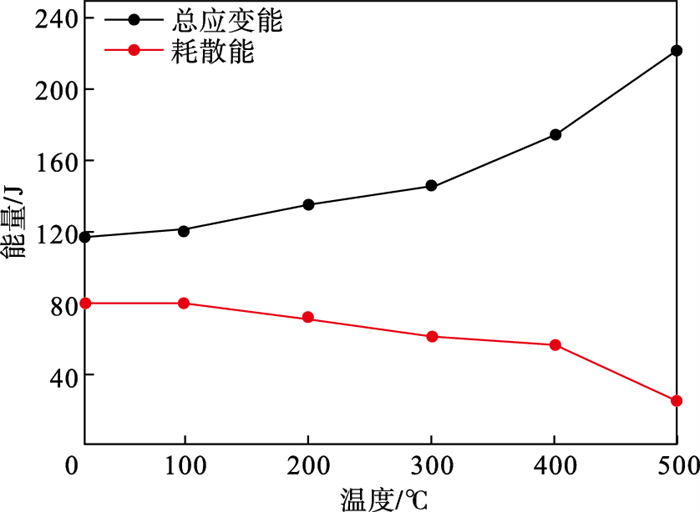 | 图 11 断层黏滑过程能量与温度关系Fig.11 Relationship between energy released during fault stick-slip and temperature |
由图 11可知,相同断层倾角条件下,应力-应变曲线产生启滑应力降时,随着温度不断上升,岩体内部颗粒间弱接触已在热应力作用下发生断裂,而强接触承担着外荷载对岩体模型系统做功.岩体模型系统的能量主要来自上下墙体加载而不断输入的能量(边界能).断层两侧岩体受到热应力的破坏程度较大,岩体内部损伤程度上升,造成启滑时,断层结构面因摩擦消耗较少的能量即可产生黏滑现象.因此,耗散能与温度呈负相关关系.岩体模型系统满足能量守恒定律,且不以摩擦生热的方式对外耗散.因此,边界能更多部分以应变能的方式储存在颗粒接触之间,总应变能与温度呈现正相关关系.
3 结论1) 通过离散元法建立了断层黏滑过程的双轴压缩试验模型,并编写程序建立了岩体的热力耦合损伤计算模型,实现了对不同温度场下断层黏滑过程的模拟.
2) 黏滑微观破坏形态的微裂纹主要分布在断层结构面的两侧,以拉伸裂纹为主导,且随着温度的不断上升,拉伸裂纹所占总裂纹的百分比不断上升,黏滑的拉伸区域逐渐由集中化的十字交叉转变为离散化.黏滑的宏观破坏模式由断层结构面的纵向裂隙与块体破碎二者并存形态,逐渐转变为块体破碎的单一形态.
3) 伴随着温度的不断上升,20 ℃至500 ℃之间,断层两侧岩体产生黏滑失稳的启滑应力、启滑应力降与黏滑次数整体上呈现不断下降的趋势.温度的改变既改变了断层两侧岩体的力学性质,又对断层面的力学性质产生了影响.
4) 断层黏滑过程中能量耗散方式以摩擦滑动为主,总应变能的变化趋势与应力-应变曲线具有一致性.断层启滑时,随着温度的升高,总应变能呈上升趋势,耗散能呈下降趋势,即高岩温下断层消耗较少的能量,便会发生黏滑.
参考文献
| [1] | Zhou X P, Shou Y D, Yang L H, et al. Stick-slip failure in heterogeneous sheared fault with a variety of fault roughness[J]. Physics of the Earth and Planetary Interiors, 2020, 309: 106587. DOI:10.1016/j.pepi.2020.106587 |
| [2] | Goodman R E. Introduction to rock mechanics[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1981, 18(6): 109-114. |
| [3] | 赵扬锋, 荆刚, 樊艺, 等. 断层黏滑失稳过程微震与电荷信号时频特征研究[J]. 岩石力学与工程学报, 2020, 39(7): 1385-1395. (Zhao Yang-feng, Jing Gang, Fan Yi, et al. Time-frequency characteristics of microseismic and charge signals during fault viscous slip destabilization[J]. Journal of Rock Mechanics and Engineering, 2020, 39(7): 1385-1395.) |
| [4] | Khazaei C, Hazzard J, Chalaturnyk R. Discrete element modeling of stick-slip instability and induced microseismicity[J]. Pure and Applied Geophysics, 2016, 173(3): 775-794. DOI:10.1007/s00024-015-1036-7 |
| [5] | Yta B, Tgc D, Jpa A. Experimental and modeling study of the effect of fault roughness on dynamic frictional sliding[J]. Earth and Planetary Science Letters, 2020, 536: 116133. DOI:10.1016/j.epsl.2020.116133 |
| [6] | Kettermann M, Steffen A, Alexander F R, et al. The effect of salt in dilatant faults on rates and magnitudes of induced seismicity-first results building on the geological setting of the Groningen Rotliegend reservoirs[J]. Netherlands Journal of Geosciences, 2018, 96(5): 87-104. |
| [7] | Zhao Z H. Thermal influence on mechanical properties of granite: a microcracking perspective[J]. Rock Mechanics and Rock Engineering, 2016, 49(3): 747-762. DOI:10.1007/s00603-015-0767-1 |
| [8] | Tian W L, Yang S Q, Huang Y H. Macro and micro mechanics behavior of granite after heat treatment by cluster model in particle flow code[J]. Acta Mechanica Sinica, 2018, 34(1): 175-186. |
| [9] | 贾蓬, 杨其要, 刘冬桥, 等. 高温花岗岩水冷却后物理力学特性及微观破裂特征[J]. 岩土力学, 2021, 42(6): 1568-1578. (Jia Peng, Yang Qi-yao, Liu Dong-qiao, et al. Physical and mechanical properties and microscopic fracture characteristics of high-temperature granite after water cooling[J]. Geotechnics, 2021, 42(6): 1568-1578.) |
| [10] | Itasca Consulting Group. PFC2D(particle flow code in 2 dimensions)user's guide[R]. Minneapolis: Itasca Consulting Group, 2008. |
