张路路¹, 范俊¹, 金光¹, 张昆²
1. 国防科技大学 系统工程学院, 湖南 长沙 410073;
2. 国防科技大学 文理学院, 湖南 长沙 410073
收稿日期：2021-07-20
基金项目：湖南省研究生科研创新资助项目(CX20200079)。
作者简介：张路路(1988-)，男，山东德州人，国防科技大学博士研究生;
金光(1973-)，男，河北抚宁人，国防科技大学教授，博士生导师。

摘要：受地面试验条件限制，无法进行航天器抗多组源X射线地面模拟试验，提出了一种单组源X射线数值模拟等效试验方法.针对期望提高方法构建的等效试验模型在等效试验搜索过程中存在“过度贪婪”问题，构建了层次期望提高等效试验模型，并在此基础上对提高函数进行了二次方处理，进一步改善层次期望等效试验模型的全局搜索能力.以碳纤维增强树脂(carbon fiber reinforced polymer, CFRP)材料的抗X射线辐射数值模拟试验为对象，利用层次期望提高等效试验模型进行等效试验输入值搜索.结果表明层次期望提高等效试验模型具有更高的搜索精度.
关键词：层次期望提高等效试验高斯过程模型X射线辐射CFRP材料
Equivalent Test Method of Spacecraft Anti-radiation Based on Hierarchical Expected Improvement
ZHANG Lu-lu¹, FAN Jun¹, JIN Guang¹, ZHANG Kun²
1. College of Systems Engineering, National University of Defense Technology, Changsha 410073, China;
2. College of Science, National University of Defense Technology, Changsha 410073, China
Corresponding author: FAN Jun, E-mail: fanjun891009@163.com.

Abstract: Restricted by test conditions, performing spacecraft anti-multi-source X-ray ground simulation test is generally difficult. A single source X-ray numerical simulation equivalent test method is proposed. To overcome the "excessive greedy" phenomenon of the expected improvement(EI)method in the equivalent test points searching, a hierarchical EI equivalent test model is established. On this basis, by introducing quadratic terms into the improvement function, the model's global searching ability is further improved. The anti-X-ray radiation numerical simulation test of CFRP material is subject to the object, and the hierarchical EI equivalent test model is used for equivalent test input value search. The results indicate that the hierarchical EI equivalent test model has higher search accuracy.
Key words: hierarchical expected improvementequivalent testGaussian process modelX-ray radiationCFRP material
空间辐射环境中的高能带电粒子、中子、电磁波、射线等作用于航天器时，会对航天器不同部件造成损伤^[1-2].X射线照射到航天器上时，会立即完成能量转换，而能量的积攒将对航天器产生严重威胁，例如引起航天器外保护材料的烧蚀、汽化、层裂等破坏性行为，严重影响航天器的正常工作及寿命^[3-4].因此，研究空间飞行航天器抗X射线照射性能具有重要意义.
空间环境中的X射线主要由太阳耀斑产生，尤其是在太阳活动剧烈的环境下，将产生大量高能量的X射线.针对太空中有目的的改变小行星飞行轨道，清除航天器发射中遗留到低轨道中的各种太空垃圾等问题，一种有效的建议是进行有限的太空核爆炸，而空间环境中的核爆炸也会产生高能密度的X射线辐射.针对航天器抗X射线辐射飞行试验的研究极为有限，主要采取数值模拟和地面模拟试验方法进行研究^[5-9].相比于数值模拟试验，地面模拟试验的试验精度更高，试验响应更真实.受地面试验条件限制，当前仍无法进行多组源X射线辐照地面模拟试验.相比于地面试验, 数值模拟试验成本较低, 可模拟多组源试验环境, 是地面模拟试验的重要补充.
基于X射线辐照因子材料的热-力学响应特性，可用单组源X射线辐照试验等效多组源X射线辐照试验响应.针对当前地面模拟试验中CFRP材料多组源X射线辐照无法进行的局限性，利用数值模拟试验在使用中具有灵活与低成本的优点，构建了一种基于数值模拟试验的等效试验设计方法，用于指导地面模拟等效试验的进行.
1 数值模拟试验数据融合建模在数值模拟试验中，x=[x₁, …, x_k]表示X射线源的输入变量，f_mul表示多组源X射线输入条件下的目标响应输出值，z=[z₁, …, z_n]^T表示已完成的单组源等效数值模拟响应值，对应的初始样本输入为X=[x₁, …, x_n]^T，y_i=|z_i-f_mul|为单组源等效数值模拟响应值与目标响应的差值，Y=[y₁, …, y_n]^T为响应差值向量，k为X射线组源的数量，n为数值模拟试验次数.不失一般性，首先利用正交试验设计方法^[10]，在数值模拟试验空间内随机抽取数量为n的初始样本，作为后续建模的训练样本.
利用层次高斯随机过程模型构建等效数值模拟试验差值数据模型：

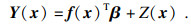(1)

式中：f(x)=[f₁(x), …, f_q(x)]^T，为已知均值函数向量; β为未知回归系数向量; Z(x)~GP(0, σ_l², Φ_l)表示均值为0，相关参数为Φ_l，方差参数为σ_l²的高斯过程.
设x₁，x₂为任意两次X射线数值模拟试验的输入矢量，协方差cov(y(x₁), y(x₂))= σ_l²R(x₁, x₂)，R(x₁, x₂)为输入的相关函数：

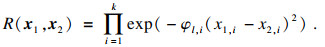(2)

式中，φ_{l, i}≥0.
为了便于后续计算推导，设未知参数β, σ_l²和Φ_l满足共轭先验：
p(β|σ_l²)~N(u, vI_q×qσ_l²)，p(σ_l²)~IG(α, γ)，p(φ_{l, i})~IG(a, b).式中，I_q×q为q×q的单位矩阵.
进一步可推导出未知输入x₀条件下数值模拟输出响应满足非中心t分布^[11]：

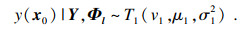(3)

式中：v₁=n+v₀，表示非中心t分布函数的自由度; μ₁=f^T(x)μ+rR^-1(Y-Fμ)，表示非中心t分布函数的均值; ，表示非中心t分布函数的方差; F=[f(x₁), …, f(x_n)]^T，表示均值函数的向量矩阵; v₀=2α; = .
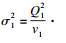
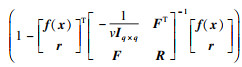
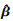
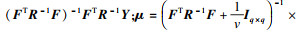
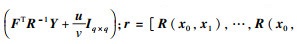
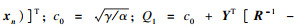
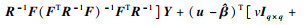
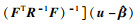
非中心t分布T₁(v₁, μ₁, σ₁²)的密度函数为

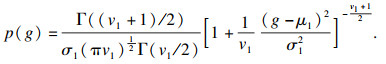(4)

基于初始样本构建X射线数值模拟试验数据预测模型，对未知输入条件下的数值模拟试验结果进行预测.由于初始试验样本的数量极为有限，且极有可能未给出试验样本空间中的关键位置点，致使构建的预测模型过于“粗糙”，预测结果的可信度较低，无法准确搜索到等效试验的有效位置.如何在尽可能少的补充试验样本的条件下，提高等效试验搜索精度，成为解决上述问题的关键.
2 数值模拟等效试验建模以等效试验输出为目标，结合上述层次高斯过程模型，构建层次期望提高搜索等效试验模型，并在此基础上对层次提高函数进行二次方处理，提升层次期望提高^[12]搜索模型的全局优化搜索能力.
基于期望提高方法，构建层次提高函数：

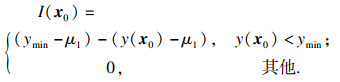(5)

式中，y_min=min(y₁, …, y_n)为等效试验响应差值的最小值; y(x₀)为未知输入x₀条件下的等效试验响应差值.
由式(5)层次提高函数可知，在未知输入x₀及其对应响应y(x₀)的条件下，y_min的提高量随层次提高函数乘方数的增加而增加，增加了后续期望函数搜索的不确定性.为进一步提高模型的全局搜索能力，避免出现局部最优收敛，对层次提高函数进行二次方处理，再求取层次提高函数的期望值：

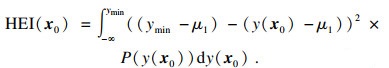(6)

式中，P(y(x₀))为y(x₀)的概率分布密度函数，满足式(4)中的非中心t分布.
为便于后续求解，对式(6)进行如下处理：

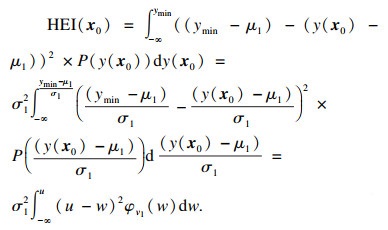(7)

式中：是自由度为v₁的非中心t分布的概率密度函数.
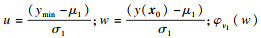
对式(7)进行求解：

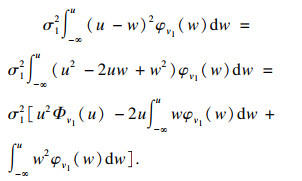(8)

式中，Φ_v1(u)是自由度为v₁的非中心t分布的累计密度函数.由式(8)可知，和的求解是关键.
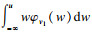
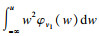
对式进行求解：

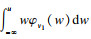
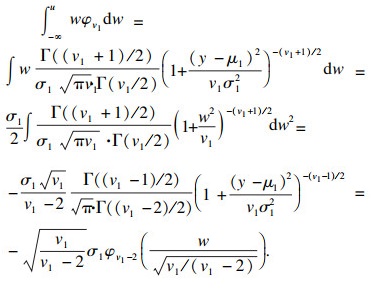(9)

对进行求解, 利用分部积分可得，
结合式(9)，可得

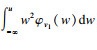
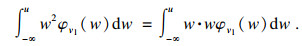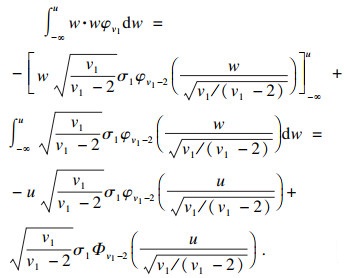(10)

将式(9)、式(10)代入式(8)，可得

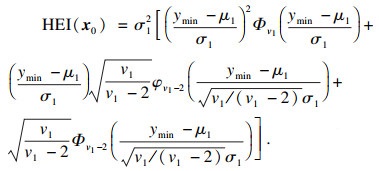(11)

通过数据处理，等效试验点搜索问题可轻松转换为求极小值的问题，在搜索空间C_k内求HEI(x₀)的极大值，实现对极小值y(x₀)所对应的输入变量x₀的搜索：
经上述不断搜索，期望结果趋于稳定，数值模拟试验次数由n增加到n₁.
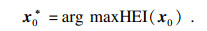3 数值算例为验证层次期望提高等效试验方法的有效性，引入两个数值算例^[13]：
算例1：f(x)=(6x-2)²sin(12x-4)，x∈[0, 1];
算例2：f(x)=4x₁²-2.1x₁⁴+x₁x₂-4x₂²+4x₂⁴，x₁，x₂∈[-2, 2].
与算例1相比，算例2的输入维度更高，复杂度也更高.
设等效试验点为函数的极小值点，利用拉丁超立方试验设计方法分别从上述两个算例中筛选出3个和10个样本; 利用层次期望提高等效试验方法与EI^[14]等效试验方法对上述算例进行搜索，对应的等效试验搜索结果和等效试验搜索精度如图 1~图 4所示.
图 1(Fig. 1)

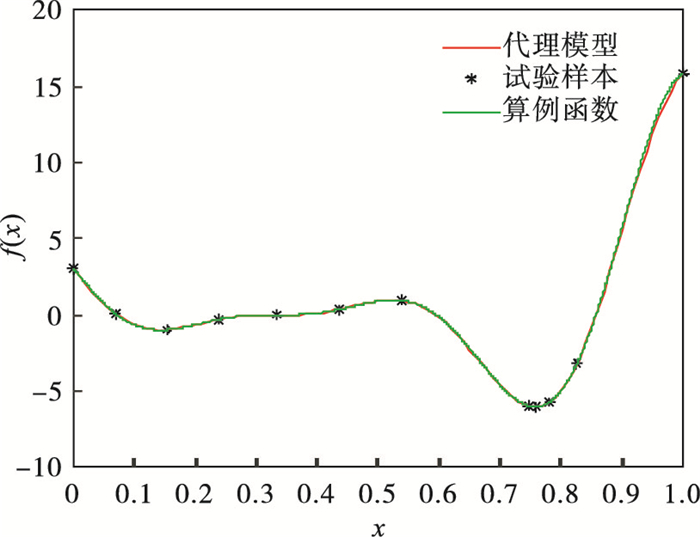图 1 算例1的等效试验搜索结果Fig.1 Equivalent test search results for case 1

图 2(Fig. 2)

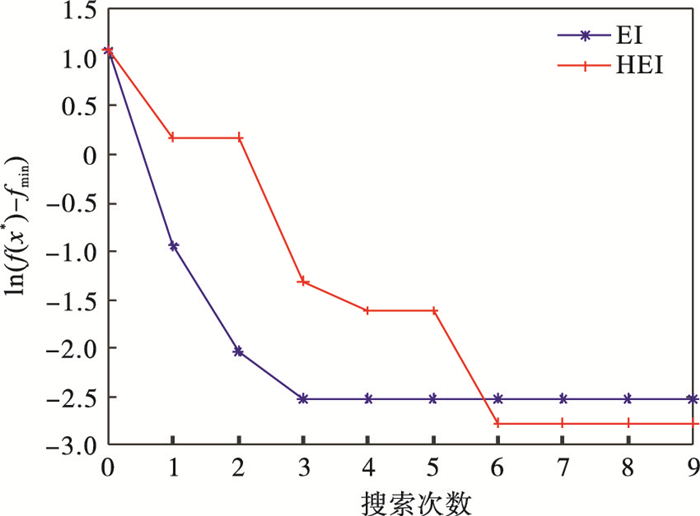图 2 算例1的等效试验搜索精度Fig.2 Equivalent test search accuracy for case 1

图 3(Fig. 3)

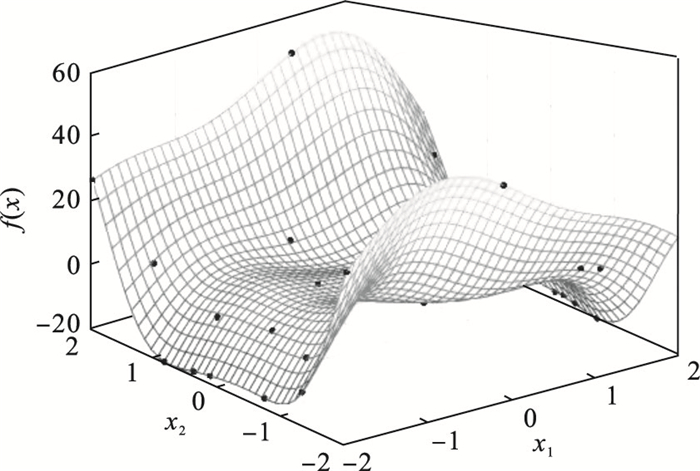图 3 算例2的等效试验搜索结果Fig.3 Equivalent test search results for case

图 4(Fig. 4)

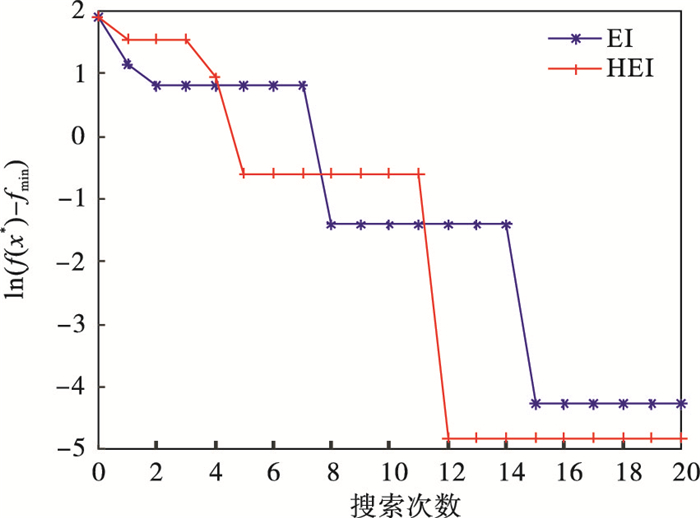图 4 算例2的等效试验搜索精度Fig.4 Equivalent test search accuracy for case 2

由图 1~图 4的搜索结果可知，对于复杂度较低的数值算例(算例1)，文献[14]中的EI方法搜索速度较快，搜索精度却明显不足; 随数值算例复杂度的提高(算例2)，HEI等效试验方法在搜索速度与精度方面的优势愈加明显.由此可知，HEI等效试验方法具有更强的全局搜索能力，尤其是在应对复杂度较高的测试函数时，对等效试验最优值的搜索精度更高，可有效避免局部最优值对全局搜索的影响.
4 实验结果分析以X射线辐照引起的材料热-力学响应为研究对象，采用有限元方法^[3](FEM)对材料特性进行分析.选择两个X射线源作为数值模拟试验的输入源，两个X射线源的黑体谱温度分别为1，3 keV，入射X射线的能通量Φ为输入变量，碳纤维增强树脂(carbon fiber reinforced polymer，CFRP)复合材料为靶板材料，输出响应为单位面积气体动量.在具体的数据获取上，采用气体动量直接读取的方法，并进行动量守恒监测，保证了数据的可信度^[15].
由于X射线源黑体谱温度不同，它们的软硬存在较大差异，作用于CFRP材料时，造成材料的失效机理更为复杂，因此，多组源X射线辐射响应值并不是单组源X射线源辐射响应的简单叠加.假设，飞行试验中黑体谱温度和射线能通量分别为1 keV和400 J/cm²的X射线源，黑体谱温度和射线能通量分别为3 keV和3 400 J/cm²的X射线源，同时辐照CFRP材料，需要求得CFRP材料单位面积气体动量响应值.首先，进行数值模拟试验，获得该条件下数值模拟试验的单位面积气体动量响应值为744.39 Pa · s，即此处的多组源X射线等效试验的目标响应值f_mul=744.39，将其作为单组源X射线等效试验搜索的目标响应.由当前地面模拟试验条件可知，实验室设备能够提供的黑体谱温度范围为1~10 keV，能通量范围为100~5 000 J/cm²，以此作为数值模拟试验输入的边界条件，利用层次期望提高等效试验方法，搜索数值模拟试验中等效单组源X射线辐射的黑体谱温度和射线能通量取值，并将迭代搜索后得到的最优解作为地面模拟的目标输入进行地面模拟试验，用于等效实现上述多组源X射线地面模拟试验的辐射响应.
经20次等效试验迭代搜索可知，利用HEI方法搜索到的最优解为x₀=(1.511 8，1 835.986 3)，响应值为z(x₀)=721.024 Pa · s，精度差值为f(x₀)=|z(x₀)-f_mul|=23.366 Pa · s.利用文献[14]中EI构建的等效试验方法搜索到最优解x₀=(1.213 2, 1 601.986 3)，响应值为z(x₀)=772.564 Pa · s，精度差值f(x₀)=|z(x₀)- f_mul|=28.174 Pa · s.由此可知，本文方法的搜索精度更高.HEI方法与文献[14]中的EI方法的搜索精度如图 5所示.
图 5(Fig. 5)

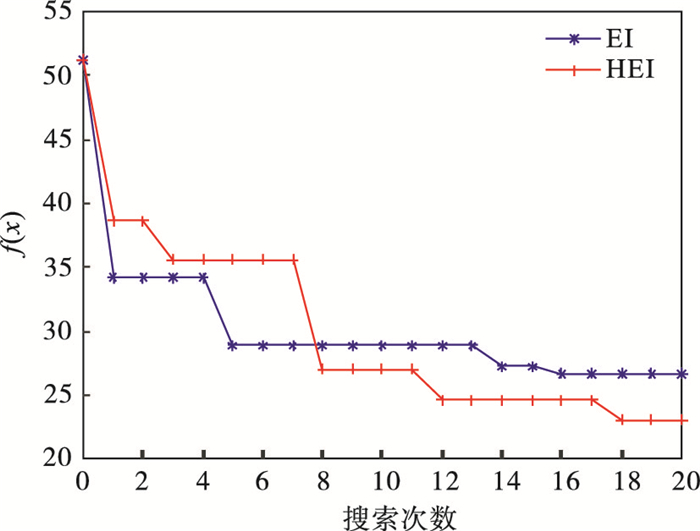图 5 等效试验搜索精度Fig.5 Equivalent test search accuracy

由图 5可知，初期搜索中EI搜索速率更快，但很快陷入了局部最优，随搜索样本数量的增加，HEI等效试验方法的搜索精度优于EI方法的搜索精度.由于文中采用的数值模拟试验为有限元分析，试验本身存在一定误差，因此，应记录多个最优搜索输入，并将其用于后续单组源X射线地面模拟等效试验，以提高单组源X射线地面模拟等效试验的精度.
5 拓展由上述研究可知，对层次提高函数进行二次方处理后，层次期望提高等效试验模型的全局搜索能力得到改善.为了应对更为复杂、多维、多峰的黑箱函数，对层次提高函数进行更高次方处理，进一步提高等效试验模型的全局搜索能力.
引入平衡参数g，用平衡层次期望提高等效试验模型的局部-全局搜索能力构建层次提高函数：

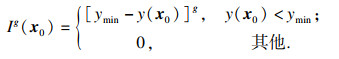(12)

求层次提高函数的期望：

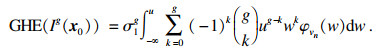(13)

式中：，为预测值y(x₀)的标准化; ，为样本最小值y_min的标准化; v_n=n+2α，为自由度.
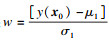
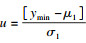
式(13)显式表达式的求取成为层次期望提高模型构建的关键，是进行后续研究的关键内容.
6 结论1) 为了构建X射线抗辐照等效试验模型，借助贝叶斯优化理论在搜索黑箱模型全局最优中的优势，构建了层次期望提高等效试验模型，搭建了解决等效试验问题的理论框架.
2) 通过算例分析，验证了层次期望提高等效试验模型的搜索精度更高.将构建的等效试验模型用于解决X射线抗辐照数值模拟等效试验问题，效果良好，为后续地面模拟试验的进行提供理论支撑.
参考文献

[1]	沈自才. 空间辐射环境工程[M]. 北京: 中国宇航出版社, 2013: 1-30. (Shen Zi-cai. Space radiation environment engineering[M]. Beijing: China Astronautic Publishing House, 2013: 1-30.)
[2]	赵元富, 王亮, 岳素格, 等. 纳米级CMOS集成电路的单粒子效应及其加固技术[J]. 电子学报, 2018, 46(10): 2511-2518. (Zhao Yuan-fu, Wang Liang, Yue Su-ge, et al. Single event effect and its hardening technique in nano-scale CMOS integrated circuits[J]. Acta Electronic Sinica, 2018, 46(10): 2511-2518. DOI:10.3969/j.issn.0372-2112.2018.10.027)
[3]	Zhang K, Tang W, Fu K. Modeling of dynamic behavior of carbon fiber-reinforced polymer(CFRP)composite under X-ray radiation[J]. Materials, 2018, 11(1): 143. DOI:10.3390/ma11010143
[4]	Sollfrey W. Effects of propagation on the high-frequency electromagnetic radiation from low-altitude nuclear explosions[J]. Proceedings of IEEE, 1965, 53(12): 2035-2042. DOI:10.1109/PROC.1965.4480
[5]	Turley W D, Stevens G D, Hixson R S, et al. Explosive-induced shock damage in copper and recompression of the damaged region[J]. Journal of Applied Physics, 2016, 120(8): 1321-1328.
[6]	Remo J L, Furnish M D, Lawrence R J. Plasma-driven Z-pinch X-ray loading and momentum coupling in meteorite and planetary materials[J]. Journal of Plasma Physics, 2013, 79(2): 121-141. DOI:10.1017/S0022377812000712
[7]	Lawrence R J, Furnish M D, Remo J L. Analytic models for pulsed X-ray impulse coupling[C]//7th Biennial Conference of the American-Physical-Society-Topical-Group on Shock Compression of Condensed Matter. New York: 2012: 883-886.
[8]	Remo J L, Furnish M D. Analysis of Z-pinch shock wave experiments on meteorite and planetary materials[J]. International Journal of Impact Engineering, 2008, 35(12): 1516-1521. DOI:10.1016/j.ijimpeng.2008.07.075
[9]	Remo J L, Lawrence R J, Jacobsen S B, et al. High energy density soft X-ray momentum coupling to comet analogs for Neo mitigation[J]. Acta Astronautica, 2016, 129: 384-388. DOI:10.1016/j.actaastro.2016.09.026
[10]	李传锋, 徐宇, 宋娟娟, 等. 基于正交设计的风力机翼型尾缘襟翼参数分析[J]. 工程热物理学报, 2012, 33(8): 1322-1325. (Li Chuan-feng, Xu Yu, Song Juan-juan, et al. Parameter analysis on wind turbine airfoil wit trailing edge flap based on orthogonal design method[J]. Journal of Engineering Thermophysics, 2012, 33(8): 1322-1325.)
[11]	Santner T J, Williams B J, Notz W, et al. The design and analysis of computer experiments[M]. New York: Springer, 2018: 30-80.
[12]	Zhang L L, Jin G, Liu T Y, et al. Generalized hierarchical expected improvement method based on black-box functions of adaptive search strategy[J]. Applied Mathematical Modelling, 2022, 106: 30-44. DOI:10.1016/j.apm.2021.12.041
[13]	Shu L S, Jiang P, Wang Y. A multi-fidelity Bayesian optimization approach based on the expected further improvement[J]. Structural and Multidisciplinary Optimization, 2021, 63: 1709-1719. DOI:10.1007/s00158-020-02772-4
[14]	Jones D R, Schoulau M, Welch W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492. DOI:10.1023/A:1008306431147
[15]	张昆. 各向异性复合材料的本构关系及其在X射线辐照下动力学响应的三维有限元模拟[D]. 长沙: 国防科技大学, 2018. (Zhang Kun. Constitutive relationship of anisotropic composites and its application in a FEM simulation of the dynamic response within the X-ray radiation in 3D condition[D]. Changsha: National University of Defence Technology, 2018. )