
 , 黎明
, 黎明 东北大学 机械工程与自动化学院,辽宁 沈阳 110819
收稿日期:2021-09-18
基金项目:中央高校基本科研业务费专项资金资助项目(N180312012)。
作者简介:刘钺(1996-),男,辽宁鞍山人,东北大学硕士研究生;
孙伟(1975-),男,辽宁营口人,东北大学教授,博士生导师。
摘要:为了有效实施压电分流阻尼减振,创建一个能预估其减振效果的动力学分析模型以指导减振设计.根据压电分流薄板结构,提出了一种将基体结构和分流电路分别建模并通过压电片将二者耦合起来的分步耦合建模方法.在ANSYS软件平台上,详细描述了面向压电分流薄板结构采用分步耦合法的建模流程.实验验证了建模方法的合理性,压电分流阻尼对结构具有较好的减振效果,降低共振响应幅度可达50%以上.分析了电感值、压电片贴敷位置、压电片面积等参数对薄板振动响应的影响.结果表明:对于电阻-电感串联及并联分流电路,存在一个最优的电感值可使薄板减振效果最优;压电片贴在变形较大的区域及增大压电片尺寸对减振有利.
关键词:分步耦合压电分流薄板结构减振分析ANSYS仿真
Dynamic Modeling and Analysis of Piezoelectric Shunt Thin Plates Based on Step-by-Step Coupling
LIU Yue, SUN Wei

 , LI Ming
, LI Ming School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: SUN Wei, E-mail: weisun@mail.neu.edu.cn.
Abstract: In order to effectively implement piezoelectric shunt damping vibration, a dynamic analysis model which can estimate the vibration reduction effect is created to guide the vibration reduction design. A step-by-step coupling modeling method for piezoelectric shunt thin plate structures is proposed, in which the substrate structure and shunt circuit are modeled separately and the two are coupled by piezoelectric patches. Based on the ANSYS software platform, the modeling process of piezoelectric shunt thin plates with step-by-step coupling is described in detail. The experiment verifies the rationality of the modeling method, and the piezoelectric shunt damping has a good vibration reduction effect, which reduces the resonance response by more than 50%. The influence of inductance values, piezoelectric patch position and area on the vibration response of the thin plate is analyzed. The results show that for resistance-inductors in series and parallel shunt circuits, there is an optimal inductance value to optimize the vibration reduction effects of thin plates. The piezoelectric patch is attached to a larger region and increases the piezoelectric sheet size to vibration reduction.
Key words: step-by-step couplingpiezoelectric shuntthin plate structurevibration reduction analysisANSYS simulation
以航空发动机叶片为代表的类薄板结构,在惯性力、气动力、基础激振力等多场载荷作用下易产生振动超标,进而发生振动疲劳破坏.对这类薄板结构的减振越来越关注,常用的减振方法包括硬涂层[1]、黏弹性阻尼层[2-3]、摩擦阻尼减振[4]等.近年来,在薄板结构上贴敷压电分流阻尼片[5]对结构过大振动进行控制.
压电分流阻尼减振是一种利用压电片的正压电效应,将结构的振动能量转换为电能,通过分流电路耗散实现对结构过大的振动进行控制[6].分流电路包括电阻分流、电阻-电感串联、电阻-电感并联及更加复杂的分流电路.压电分流是一种被动减振方式,比压电主动减振更加稳定、可靠.压电分流减振已在航空发动机叶片[7]、整体叶盘[8]、鼓盘[9]等结构上应用,取得了较好的减振效果.
为了在薄板结构上有效实施压电分流阻尼减振,创建可以有效再现及预测压电分流阻尼减振效果的动力学分析模型至关重要.基于压电分流阻尼减振机理,创建模型需要能够模拟压电片与薄板结构的正压电效应以及分流电路对能量的耗散.这里包含了两种耦合:一是压电片与基体结构之间的机电耦合;二是分流电路与压电片之间的耦合.目前,研究者针对包含压电分流阻尼结构系统动力学建模已开展了大量研究,其中借助于工程有限元软件ANSYS执行相关建模与分析是一种重要的手段.Becker等[10]将电阻分流电路和压电贴片模型集成为一个超单元进行建模与分析,这是一种直接耦合的建模方式,该超单元被贴敷在基体结构的多个位置上,利用ANSYS对整体结构进行模态和响应分析.Nguyen等[11]利用公共节点电压相同的原则,将连接在两个有源节点的电阻和电感分别进行各自的电压值计算,将该电压值直接耦合到公共节点中进行谐响应分析.Zhao等[12]利用ANSYS软件对压电板进行建模并提取包含压电耦合的刚度、质量矩阵,建立分流电路矩阵与组集,最终得到了压电板的振动响应.
由文献可知,将分流电路电子元件、压电片与基体结构直接耦合的方法是在ANSYS软件中分析压电分流电路的普遍方式.由于多电子元件分流电路公共节点较多导致电压耦合难以设定,这种直接耦合方式通常适用于仅包含单一电子元件(如仅有电阻、电感、电容单元件)的电路,对于相对复杂的电路,例如多电子元件串、并联电路,这种直接耦合建模通常无法实现.
为了解决直接耦合建模对复杂电路存在的问题,提出了一种基于ANSYS软件的分步耦合求解方法,其原理是将机械结构和压电分流电路分别建模与分析.详细描述了分步耦合求解的原理及面向压电分流阻尼薄板结构的求解流程.最后,进行了实例研究,用实验校验了分步耦合建模与求解的合理性,同时基于所创建的模型分析了压电片位置、面积及电感值对薄板结构减振效果的影响.
1 压电分流阻尼结构分步耦合求解原理在对比直接耦合求解原理的基础上,详细描述了利用分步耦合求解贴敷压电分流阻尼片结构动力学特性的基本原理.
1.1 直接耦合求解直接耦合是将压电片产生的电压作为分流电路的电源,同时考虑分流电路及基体结构进行动力学求解过程,直接耦合求解原理示意图如图 1所示.
图 1(Fig. 1)
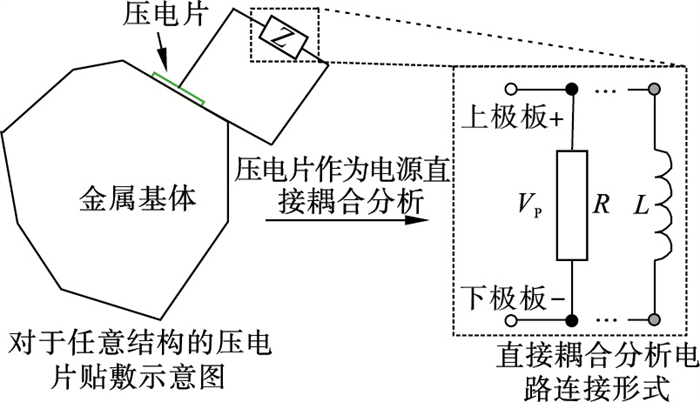 | 图 1 直接耦合求解示意图Fig.1 Direct coupling solving schematic |
在ANSYS软件中,对压电分流阻尼结构进行直接耦合求解的过程可描述为:分别创建基体结构、压电片及分流电路的有限元模型;分流电路元件两端引出两个公共节点,将这两个公共节点与压电片上、下极板的两个主节点分别相连,相当于电路结构和基体结构进行直接连接;直接进行求解,将电路部分的参数整体耦合到压电片中,进而完成整个结构系统振动特性的求解,如图 2所示.
图 2(Fig. 2)
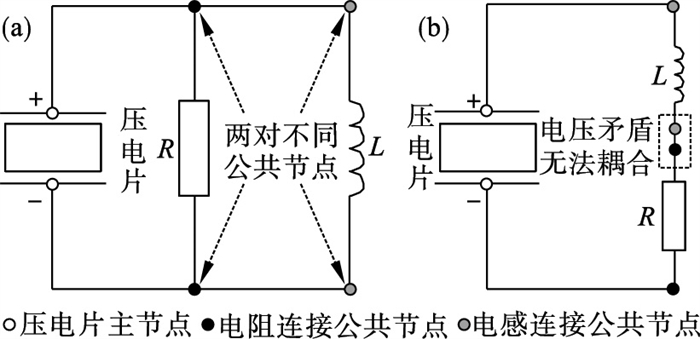 | 图 2 分流电路各节点关系图Fig.2 Relationship diagram of each node of shunt circuits (a)—并联电路;(b)—串联电路. |
1.2 分步耦合求解ANSYS在电路单元模块中能够针对复杂电路进行有效建模与分析.在结构分析模块中,很容易完成包含压电片机电耦合的结构系统动力学建模与分析.提出面向压电分流阻尼结构先进行电路分析再进行结构分析的方法.该方法以压电片为衔接单元,先将压电片与待减振的结构进行节点耦合,以接受压电片的电参数作用;将压电片与分流电路进行电压耦合,引入分流电路,这种先节点耦合后电压耦合的方法定义为分步耦合法,分步压电耦合求解方式如图 3所示.
图 3(Fig. 3)
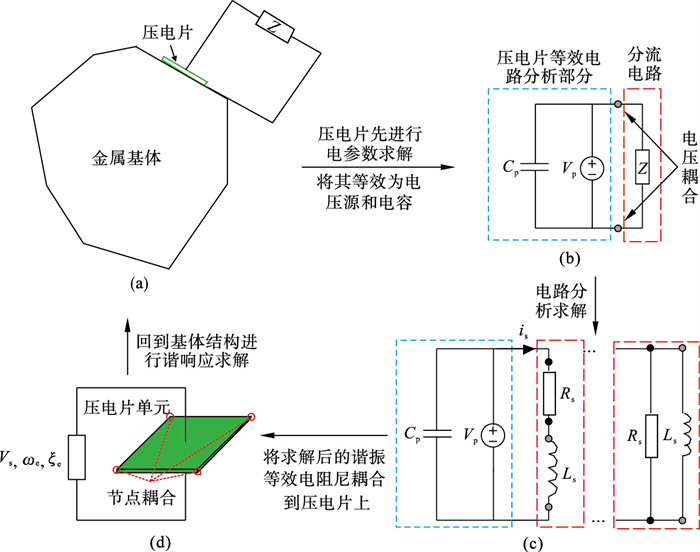 | 图 3 分步压电耦合求解方式Fig.3 Solution method of stepwise piezoelectric coupling (a)—分流电路减振结构示意图; (b)—电压耦合示意图; (c)—具体形式分流分路求解; (d)—压电片与基体结构进行节点耦合. |
在电路分析部分,执行压电片与电路电压耦合,将压电片作为电容来处理,压电片的电压值由实验获得.使用万用表测量压电片上、下极板得到压电片间的电压.由于ANSYS对于电路分析没有公共节点耦合的设置问题,可针对任意复杂电路求解出等效电频率、电阻尼及分流电路作用后施加到压电片的电压值等参数.
在结构分析部分,可执行压电片与基体结构之间的节点耦合,引入电路分析部分求解出的电频率、电阻尼等参数.在实际操作中,节点耦合可在结构建模中先于电压耦合完成相关设定.进一步执行结构分析,可计算出包含分流电路参数的结构系统动力学特性,实现对压电分流减振效果进行准确预估.
2 基于分步耦合的压电分流薄板结构分析流程以贴敷压电分流阻尼片薄板结构为例,详细描述在ANSYS软件中基于分步耦合求解理念对复合薄板进行动力学求解的流程.
1) 分流电路建模:压电分流电路需要在电场模块下进行建模,在ANSYS中电路电子元件建模可使用CIRCU94单元.通过特征值KEYOPT可以设定该单元的电学参数,KEYOPT值分别取0,1,2,4时对应的电子元件依次为电阻、电感、电容、电压源.在电路建模环境下,对于电阻、电感、电容元件,只需要设定两端的连接节点即可,对于电压源需要额外设定一个节点用于电流矢量ik的接入.通过上述电子元件单元可以按需要对串、并联压电分流或更加复杂的分流电路完成建模,串联电路建模如图 4所示.
图 4(Fig. 4)
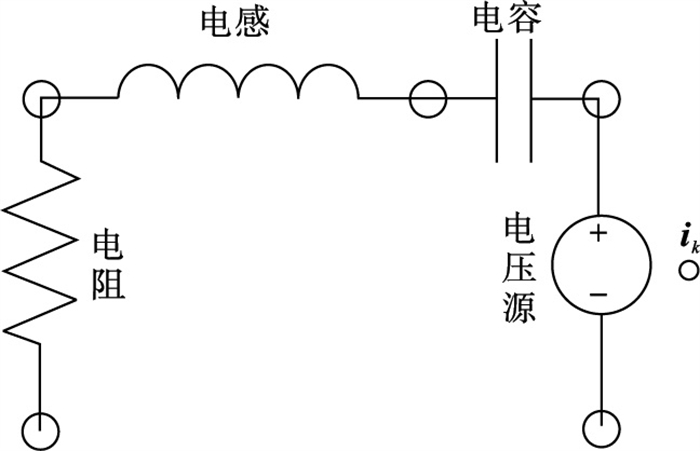 | 图 4 串联电路建模Fig.4 Series circuit modeling |
2) 节点耦合:压电片通过节点耦合与薄板结构联系起来,在ANSYS中执行节点耦合的命令为NUMMRG.NUMCMP耦合命令会对整个结构的节点编号进行重新排列,压电片与薄板结构节点的相对关系如图 5所示.节点耦合后,压电片与薄板的耦合节点相互作用,便于后续执行压电分流阻尼减振预估.
图 5(Fig. 5)
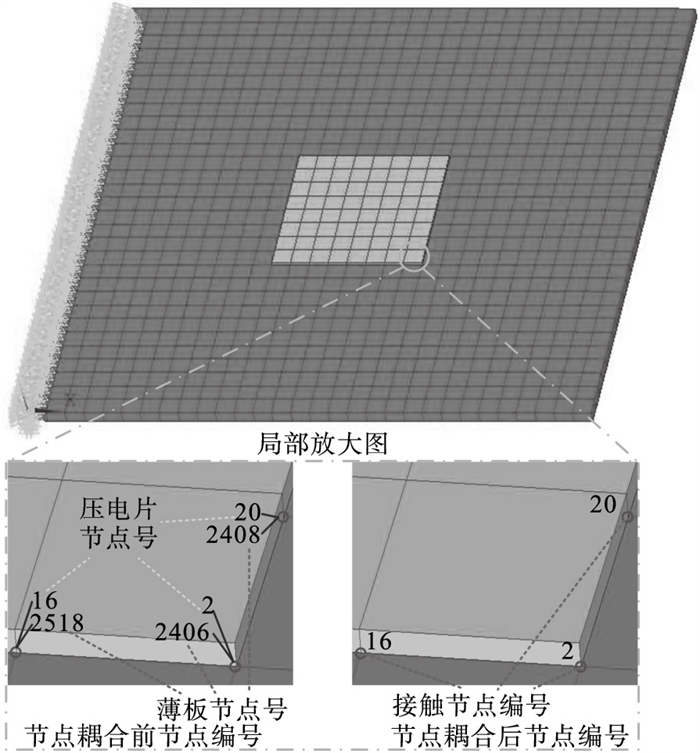 | 图 5 压电片与薄板结构节点的相对关系Fig.5 Relative relationship between piezoelectric sheets and thin plate structure nodes |
3) 电路分析:执行电路分析需将分流电路与压电片进行电压耦合,进而求解电路频率、阻尼及耦合作用后的电压值等参数.通过静态求解激活电路分析与求解模块,激活命令为ANTYPE,STATIC.激活后利用*GET指定压电片上表面进行节点选取,并通过Cp=abs(Qp)进行电荷绝对值计算.静态求解前忽略压电片电压值,将其作为电容元件接入回路中,进行压电片电容值求解并将电容值赋值到电容元件中:
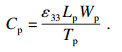 | (1) |
压电片在薄板结构上,而分流电路在薄板结构外,需执行电压耦合将两者联系起来,具体操作描述如下:针对压电片,使用D命令设定上极板N_top与下极板N_bot所有节点电压,并将其设定为在板弯曲方向上进行极化;利用*GET命令将极化电压面所有节点耦合到一个主节点中;通过CP命令耦合压电片主节点与分流电路两端端点电压.电压耦合后薄板结构上的压电片就与分流电路建立起联系,如图 6所示.可认为这里的电压耦合也是一个隐含求解的过程,执行耦合后会将求得的电频率、电阻尼及耦合后的电压值等作用到压电片上.
图 6(Fig. 6)
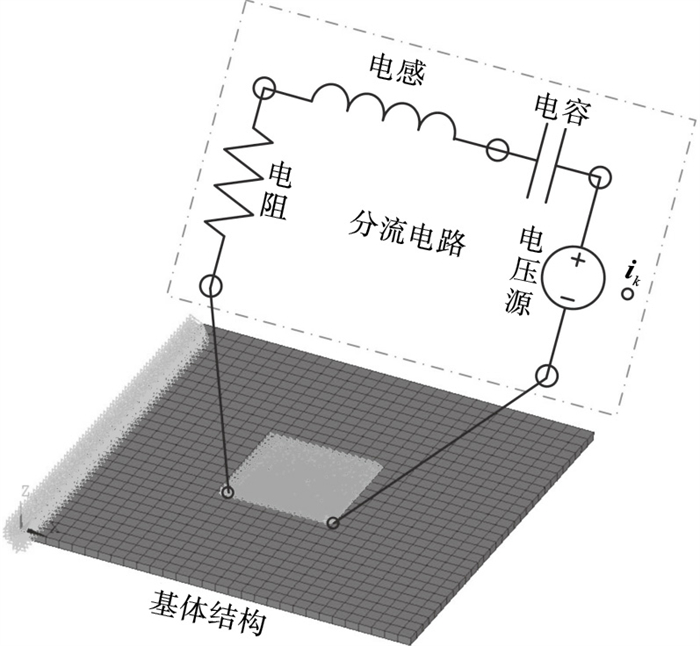 | 图 6 含压电分流薄板结构的完整分析模型Fig.6 Complete analysis model of piezoelectric shunt thin plate structures |
4) 结构分析:因为已建立了分流电路与薄板上压电片的耦合,在结构分析部分可以正常求解,例如执行谐响应分析.整个分析是个动态过程,结构运动产生的电压值作用到分流电路,分流电路会将这个电压源消耗又反作用到压电片,进而完成含压电分流薄板的结构分析,输出振动响应结果.
3 实例以一个具体的含压电分流阻尼片薄板为例,用所提出的基于分步耦合方法对其进行动力学建模,并用实验校验了模型的合理性.在此基础上,讨论了压电片贴敷位置、大小及分流电路中的电感参数对复合结构振动特性的影响.
3.1 实验系统及减振特性测试所选定的薄板为处于悬臂状态的铝板,尺寸为150 mm×150 mm×3 mm,在其中间上面贴敷PZT-5H压电片, 尺寸为40 mm×40 mm×0.5 mm,如图 7所示.
图 7(Fig. 7)
 | 图 7 贴敷压电分流阻尼片的铝板Fig.7 Aluminum plate pasted with a piezoelectric shunt damping piece |
铝板的材料参数为:密度2 740 kg/m3、杨氏模量7.2×1010 Pa,压电片的材料参数见表 1.压电片外接的分流电路包括3种:仅有电阻(R电路)、电阻-电感串联(串联RL电路)和电阻尼-电感并联(并联RL电路).
表 1(Table 1)
| 表 1 PZT-5H型压电片材料参数 Table 1 Material parameters of PZT-5H piezoelectric sheet |
贴敷压电分流阻尼片的铝板通过夹具悬臂固定,螺栓拧紧力矩为50 N·m.铝板由联能JZK-2柔性杆激振器对其进行激励,具体激振点位置如图 7所示.激励的大小可由PCB 208C04型力传感器进行测量.振动的拾取用B&K4517轻质加速度传感器,拾振点的位置见图 7.铝板的压电分流阻尼减振实验如图 8所示.分流电路由电感线圈、可调电阻、可调电容及若干导线组成,这些电路元件可分别组建成仅有电阻、电阻-电感串联和电阻-电感并联的分流电路.数据采集用LMS16通道数据采集仪来完成.为了快速获取铝板的固有频率,实验系统还配有PCB模态力锤.基于上述实验系统可对含压电分流铝板进行扫频响应和模态测试,而这些测试结果可用于校验本文所提出的分步耦合建模方法的合理性.
图 8(Fig. 8)
 | 图 8 实验装置连接图Fig.8 Connection diagram of the experimental equipment |
用模态力锤敲击铝板获得频响函数,由频响函数的峰值获得复合板的固有频率.由于分流电路的接通与否并不影响复合板的固有频率,因而仅需测试开路状态下的固有频率值.由柔性杆激振器产生简谐激振力,设定力的幅值为0.02 N,分别对连接前三种分流电路及开路状态的复合板进行扫频响应测试,频率范围为880~900 Hz.各分流电路的设置参数为:对于R电路设定6 000 Ω电阻,对于串联RL电路设定2 000 Ω电阻与0.17 H电感,对于并联RL电路设定6 000 Ω电阻与0.37 H电感.需要说明的是上述使用的电阻与电感参数并不一定是最优值,仅是在可调整的分辨率下能达到较好减振效果的一组电阻和电感值.所设定的扫频范围(880~900 Hz)针对的是压电薄板第4阶共振响应区.由于包含电感的压电分流电路只能面向高频实施减振(如果针对低频需要很大的电感值,当前试验条件不具备),为了
统一比较各分流的减振效果,以第4阶共振区扫频响应来研究压电分流阻尼对薄板的减振效果.所有的测试结果均用于后面与仿真结果的比较.
3.2 含压电阻尼片薄板动力学建模按照分析流程中所描述的分步耦合建模方法对该压电分流结构进行动力学建模与分析.薄板被划分为900个单元和6 603个节点,压电片被划分为64个单元和531个节点,并且每个压电单元节点与基体单元节点一一对应,以保证能实施有效的节点耦合.使用CIRCU94单元分别组建仅有电阻、电阻-电感串联和电阻-电感并联的分流电路,并完成与压电片的电压耦合.由于实验系统中使用的是柔性杆激励,必然会引入附加刚度,因而需要在力传感器接触处的5个节点上施加弹簧单元来模拟此附加刚度.利用创建的有限元模型求解压电分流薄板的固有频率及在第4阶共振区的谐响应,相关结果分别见表 2和图 9.需要说明的是,这里的各阶固有频率比较是在同一振型下进行的.
表 2(Table 2)
| 表 2 实验与仿真获得的薄板固有频率比较 Table 2 Comparison of natural frequencies of thin plates obtained by experiment and simulation | ||||||||||
图 9(Fig. 9)
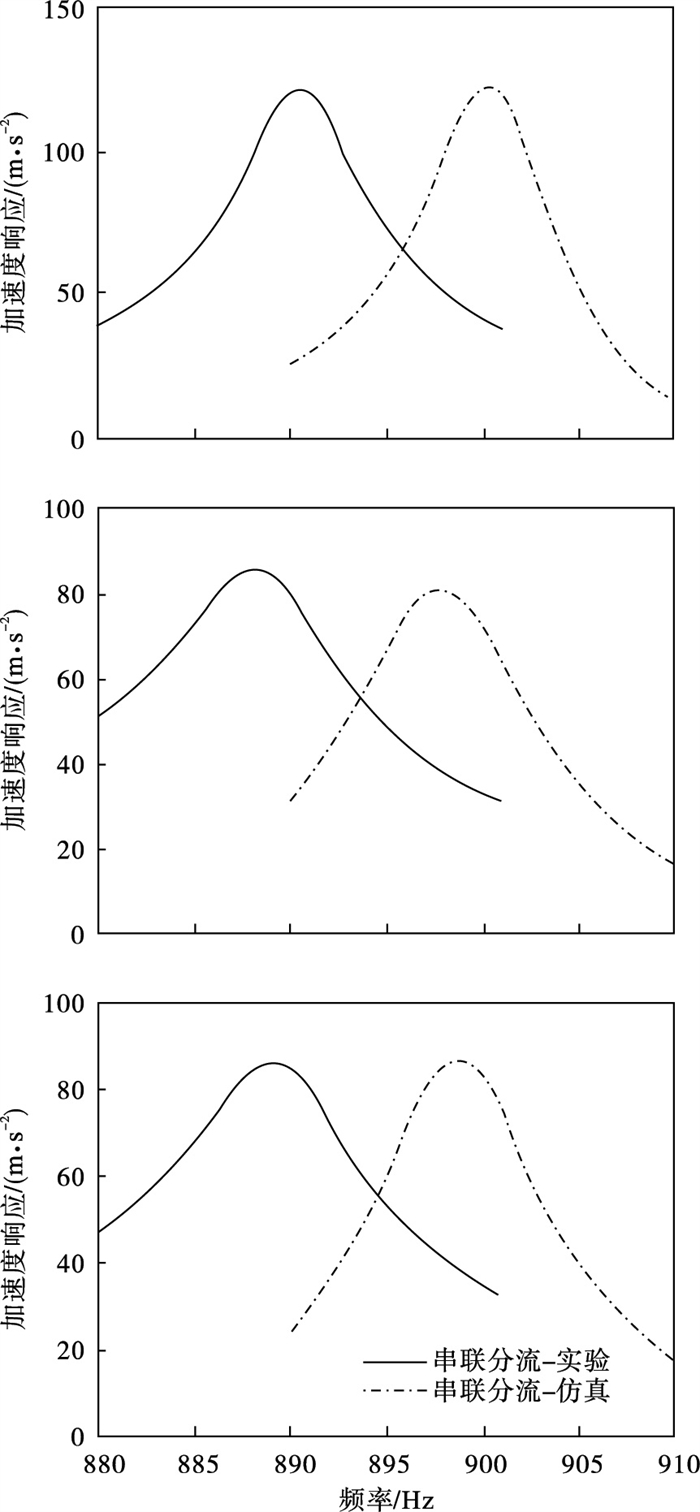 | 图 9 不同分流电路实验-仿真分析获得的扫频响应对比Fig.9 Comparison of sweep response obtained from the experiment-simulation analysis for different shunt circuits (a)—仅有电阻分流电路;(b)—并联分流电路;(c)—串联分流电路. |
由表 2可知,用有限元法获得的前4阶固有频率与实验值相比最大偏差低于5%,证明了所创建的压电片与薄板结构部分有限元建模的合理性.而从针对第4阶共振区的扫频响应对比来看,无论是仅有电阻还是电阻-电感串、并联分流电路,仿真获得的结果与实测值均较为接近,从而证明了所提出的用分步耦合建模模拟压电分流薄板振动行为的合理性.
将开路状态下的扫频响应与图 9中三种分流电路后的扫频响应进行对比,以检验分流电路对薄板结构的减振效果,具体如图 10所示(需要说明的是由于实验及仿真结果很接近,这里仅列出了仿真结果的对比).从中可以看出,仅有电阻电路的减振效果可以达到52%左右,串联与并联电路减振效果相对于仅有电阻电路减振性能进一步增强,可以达到69%左右.
图 10(Fig. 10)
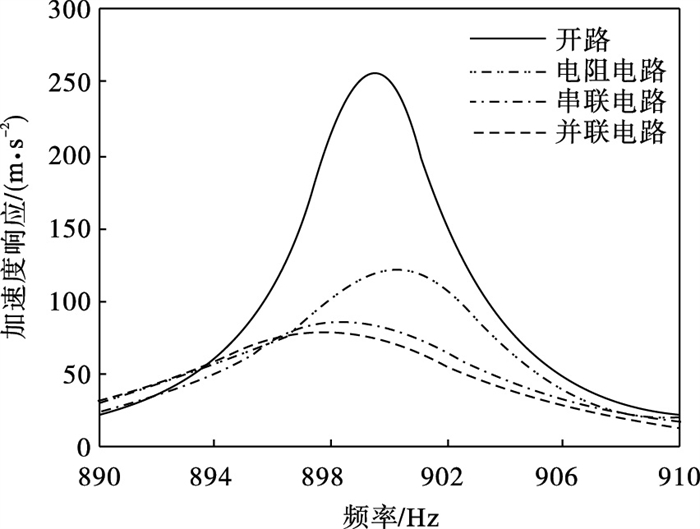 | 图 10 开路及接通不同分流电路后薄板振动响应的对比Fig.10 Comparison of vibration response of thin plates after opening and connecting different shunt circuits |
3.3 参数影响分析以下选择薄板连接并联RL分流电路的情况,分析电感、压电贴敷位置、压电片面积等参数对薄板振动响应的影响.以位移量来描述振动响应值,并将激振力幅设定为5 N.
1) 电感的影响:电感在分流电路中主要起调谐作用,因而其具体值对分流电路的减振效果有重要影响.电感分别为0.2,0.37,0.5 H时,求解压电分流板在第4阶共振区的扫频响应,如图 11所示.随电感值的增大,共振响应值先减小再增大,说明在压电分流减振中,存在一个最优的电感值使减振效果最优.
图 11(Fig. 11)
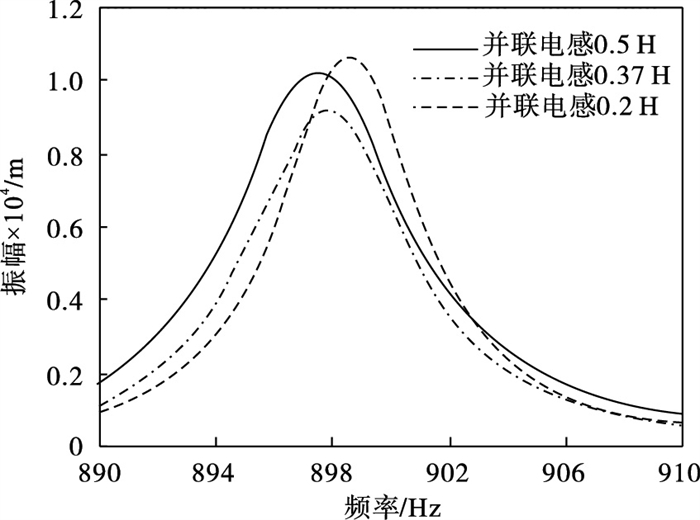 | 图 11 最优电感与任意电感值的响应对比Fig.11 Response comparison between optimal inductance and arbitrary inductance value |
2) 压电片位置的影响:将压电片沿薄板的中轴线分别放置在自由端、中部和约束端,如图 12所示.考核压电位置对薄板振动特性的影响.为了突显位置影响,选择第3阶共振区执行此影响分析.第3阶的振型如图 13所示,可知变形最大的区域在板的中部.具体对应不同贴敷位置的振动响应分析结果如14所示.可知压电贴在中部,为变形最大的区域,共振响应最小,说明压电片贴敷在变形相对大的区域对减振有利.
图 12(Fig. 12)
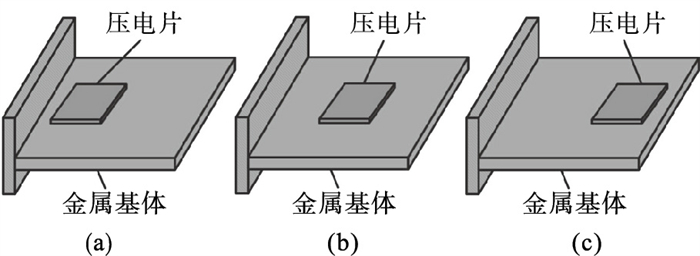 | 图 12 压电片贴敷位置示意图Fig.12 Schematic diagram of the piezoelectric sheet placemens (a)—约束端贴敷; (b)—中部贴敷; (c)—自由端贴敷. |
图 13(Fig. 13)
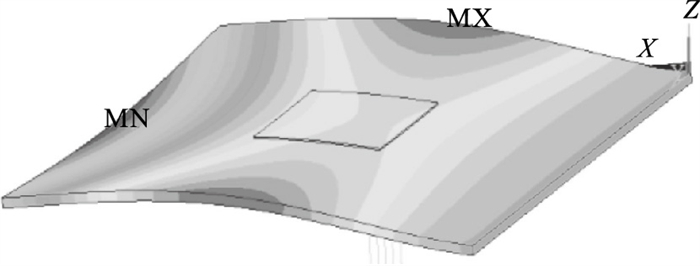 | 图 13 第3阶频率下的板结构模态振型Fig.13 Mode shapes of plate structures at the third frequency |
3) 压电片面积的影响:将压电片的尺寸分别设定为30 mm×30 mm×0.5 mm,40 mm×40 mm×0.5 mm,60 mm×60 mm×0.5 mm,贴敷位置在薄板中部.仍以第3阶共振区为例,分析压电片面积的改变对薄板振动响应的影响,相关结果如图 15所示.可知,随压电尺寸的增大,薄板的共振响应降低,说明压电片尺寸增大对减振有利.
图 14(Fig. 14)
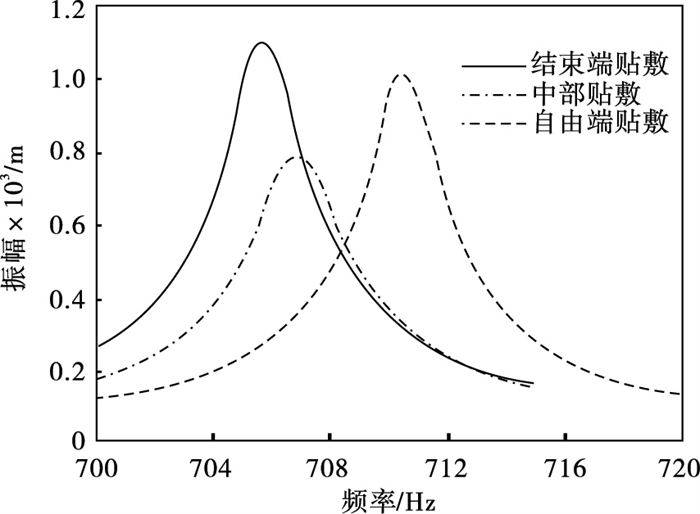 | 图 14 压电片不同贴敷位置的频率响应对比Fig.14 Comparison of frequency response of the piezoelectric sheet at different placements |
图 15(Fig. 15)
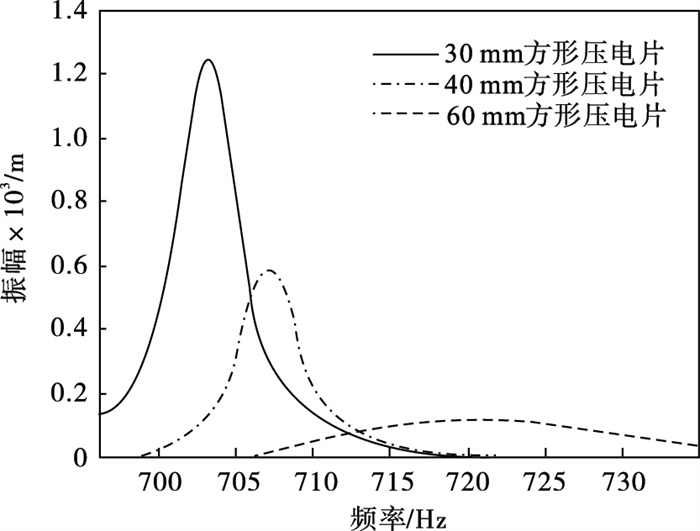 | 图 15 不同压电片的减振幅度对比Fig.15 Comparison of the amplitude of vibration reduction of different piezoelectric sheets |
4 结论1) 面向压电分流阻尼结构先进行电路分析再进行结构分析的方法定义为分步耦合法,这种分步耦合法可以针对任意复杂分流电路完成复合结构的建模与分析.针对压电分流薄板结构的实例研究显示,无论是仅有电阻还是电阻-电感串、并联分流电路,仿真结果与实测值均较为接近.
2) 试验和仿真研究表明,薄板上贴敷压电分流阻尼片具有很好的减振效果.与开路状态相比,仅有电阻电路的减振效果可达52%左右,串联与并联电路减振效果相对于仅有电阻电路减振性能进一步增强,可达69%左右.
3) 通过执行电感参数对薄板振动响应的影响分析可知:对于电阻-电感串联及并联分流电路减振,存在一个最优的电感值可使薄板减振效果最优.
参考文献
| [1] | Christopher B, Anthony P, George T J, et al. The evaluation of the damping characteristics of a hard coating on titanium[J]. Shock and Vibration, 2007, 14(1): 37-51. DOI:10.1155/2007/260183 |
| [2] | 荣万崇, 周娜, 张体南, 等. 悬臂边界下带粘弹性层的纤维增强复合薄板固有特性研究[J]. 哈尔滨工程大学学报, 2019, 40(11): 1911-1916. (Rong Wan-chong, Zhou Na, Zhang Ti-nan, et al. Inherent characteristics of fiber-reinforced composite thin plate with viscoelastic layer under cantilever boundary condition[J]. Journal of Harbin Engineering University, 2019, 40(11): 1911-1916.) |
| [3] | Madeira J F A, Araújo A L, Mota S C M, et al. Multiobjective optimization for vibration reduction in composite plate structures using constrained layer damping[J]. Computers and Structures, 2020, 232: 105810. DOI:10.1016/j.compstruc.2017.07.012 |
| [4] | 陈俊杰, 臧朝平, 周标, 等. 带干摩擦接触的叶根模态阻尼分析方法[J]. 振动与冲击, 2020, 39(20): 281-285, 294. (Chen Jun-jie, Zang Chao-ping, Zhou Biao, et al. Modal damping analysis method for blade root with dry friction contact[J]. Journal of Vibration and Shock, 2020, 39(20): 281-285, 294.) |
| [5] | Gardonio P, Casagrande D. Shunted piezoelectric patch vibration absorber on two-dimensional thin structures: tuning considerations[J]. Journal of Sound and Vibration, 2017, 395: 26-47. DOI:10.1016/j.jsv.2017.02.019 |
| [6] | Gripp J A B, Rade D A. Vibration and noise control using shunted piezoelectric transducers: a review[J]. Mechanical Systems and Signal Processing, 2018, 112: 359-383. DOI:10.1016/j.ymssp.2018.04.041 |
| [7] | Cross C J, Fleeter S. Shunted piezoelectrics for passive control of turbo machine blading flow-induced vibrations[J]. Smart Materials and Structures, 2002, 11(2): 239. DOI:10.1088/0964-1726/11/2/307 |
| [8] | Zhou B, Thouverez F, Lenoir D. Vibration reduction of mistuned bladed disks by passive piezoelectric shunt damping techniques[J]. AIAA Journal, 2014, 52(6): 1194-1206. DOI:10.2514/1.J052202 |
| [9] | Mokrani B, Bastaits R, Horodinca M, et al. Parallel piezoelectric shunt damping of rotationally periodic structures[J]. Advances in Materials Science and Engineering, 2015, 2015(1): 162782. |
| [10] | Becker J, Fein O, Maess M, et al. Finite element-based analysis of shunted piezoelectric structures for vibration damping[J]. Computers and Structures, 2006, 84(31): 2340-2350. |
| [11] | Nguyen C H, Pietrzko S J. FE analysis of a PZT-actuated adaptive beam with vibration damping using a parallel R-L shunt circuit[J]. Finite Elements in Analysis and Design, 2006, 42(14): 1231-1239. |
| [12] | Zhao Y. Vibration suppression of a quadrilateral plate using hybrid piezoelectric circuits[J]. Journal of Vibration and Control, 2010, 16(5): 701-720. DOI:10.1177/1077546309106529 |



