张春雷, 李鹤, 董茂林, 张圣杰
东北大学 机械工程与自动化学院，辽宁 沈阳 110819
收稿日期：2021-09-16
基金项目：国家自然科学基金资助项目(51675091)。
作者简介：张春雷(1994-)，男，黑龙江佳木斯人，东北大学博士研究生;
李鹤(1975-)，男，河南方城人，东北大学教授，博士生导师。

摘要：聚合物电解质膜燃料电池(polymer electrolyte membrane fuel cell, PEMFC)空气供应系统易受参数不确定性和外部干扰的负面影响，难以实现高精度数学建模和鲁棒控制.设计了一种自适应神经网络滑模控制器，用于将PEMFC空气供应系统过氧比调节至其最优参考值，以维持最大系统输出净功率并避免氧饥饿.利用径向基函数神经网络在线逼近系统的未建模动态，而无需对外部干扰与模型参数摄动的界的先验信息.由Lyapunov理论分别推导出神经网络权值和滑模增益的自适应律，以保证闭环系统稳定性.仿真结果表明，所设计的控制器不仅改善了过氧比控制的动态行为，还有效减弱了控制输入的大幅超调和抖振.
关键词：聚合物电解质膜燃料电池过氧比径向基函数神经网络滑模控制自适应律
Adaptive Neural Network Sliding Mode Control for the Fuel Cell Air Supply System
ZHANG Chun-lei, LI He, DONG Mao-lin, ZHANG Sheng-jie
School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: LI He, E-mail: hli@mail.neu.edu.cn.

Abstract: The air supply system of polymer electrolyte membrane fuel cell(PEMFC) is vulnerable to the negative impact of parameter uncertainties and external disturbances, and it is difficult to achieve high-precision mathematical modeling and robust control. An adaptive neural network sliding mode controller is designed to adjust the oxygen excess ratio of PEMFC air supply system to its optimal reference value so as to maintain the maximum system output net power and avoid oxygen starvation. The radial basis function(RBF) neural network is employed to approximate the dynamics of the unmodeled system online without prior information of the boundary of external disturbances and model parameter perturbations. To ensure the stability of the closed-loop system, the adaptive laws of neural network weights and sliding mode gains are derived by Lyapunov theory. The numerical simulation results demonstrate that the designed controller not only improves the dynamic behavior of the oxygen excess ratio control, but also effectively alleviates the large overshoot and chattering of the control input.
Key words: polymer electrolyte membrane fuel cell(PEMFC)oxygen excess ratioradial basis function(RBF)neural networksliding mode controladaptive law
当前全球环境污染和化石能源短缺问题愈发严峻，清洁新能源的开发与利用受全球瞩目^[1]，进而促进了氢燃料电池的研究与发展.聚合物电解质膜燃料电池(polymer electrolyte membrane fuel cell, PEMFC)作为一种将氢气和氧气的化学能直接转化为电能的电化学装置，凭借运行温度低、功率密度高、效率高、耐腐蚀、噪声小及反应副产物无污染等优点，在新能源汽车和固定式发电领域展现出巨大潜力^[2].为满足实际输出电压需求，通常要将多个PEMFC堆叠在一起组成电堆，并依靠各外围辅助子系统的协调配合为电堆提供燃料和氧化剂，以及必要的反应条件(温度、压力和流量等).目前，PEMFC系统的大规模商业化和广泛普及仍面临许多技术挑战.其中，空气供应子系统的控制策略是影响PEMFC系统输出性能和电堆使用寿命的重要因素^[3].作为空气供应子系统的核心工作部件，空压机需在不同工况下向电堆阴极内注入适量空气.当外部负载发生瞬变时，如果因供气量不足而发生氧饥饿现象，则会导致电堆输出电压陡降，并使聚合物电解质膜表面产生局部热点甚至被烧毁.若补充过量空气，则会增加空压机的运行负荷，在电堆输出总功率无明显提升的情况下使寄生功率大幅增加，导致系统输出净功率降低.将进入电堆阴极内的氧气流量与电化学反应消耗的氧气流量之比(即过氧比)准确并快速控制在理想范围内，是解决上述矛盾的可行有效方案^[4].
众多国内外****围绕PEMFC空气供应子系统的过氧比控制问题开展了相关研究.Pukrushpan等^[4]分析并研究了基于反应机理的PEMFC系统集总参数建模与控制问题，并设计了一种基于状态反馈的线性二次型最优控制器来调节过氧比.Taij等^[5]根据给定平衡点处的线性逼近模型提出一种无源性鲁棒PI控制方法.Abdullah等^[6]提出一种有约束的模型预测控制策略，避免了空压机的喘振和阻流.Chen等^[7]开发了一种用于厢式空压机的反馈线性化控制器跟踪最佳过氧比，以保持系统净功率最大.然而，上述方法的设计通常需要依赖高精度系统模型或在预定义系统工作点处近似线性模型，对不可预测的外部干扰和由设备引起的模型参数误差较为敏感，实际工作点也会随工况条件的变化而变化.PEMFC空气供应系统是一个具有强非线性的多变量耦合系统，其数学模型必然存在未建模动态与参数不确定性，必须综合考虑系统特性和上述关键实际因素设计更有效的过氧比控制方案^[8].
滑模控制作为一类实用且有效的非线性控制方案，具有精度高、有限时间快速收敛、对外部干扰与系统参数摄动的敏感度低等优点^[9].其中，一阶滑模控制^[10]、基于超扭转算法的二阶滑模控制^[11-12]、次优二阶滑模控制^[13]和高阶滑模控制^[14]等控制方案已被应用于过氧比控制问题的研究中.然而，仍存在两个主要的应用限制：1)对复杂性较高的PEMFC空气供应系统进行建模所需的准备工作繁琐且周期较长，某些物理参数信息无法获得，难以建立面向控制应用的高精度数学模型；2)系统参数摄动与外部干扰的边界是未知的，先验信息也难以在实际中准确获得，导致滑模增益的选取通常过于保守.近年来，神经网络与控制算法的融合进一步拓展了对具有不确定性和外部干扰的非线性系统的建模与控制研究.其中，径向基函数(radial basis function, RBF)神经网络结构简单、易于实时计算和编程实现，能以任意精度快速逼近未知的非线性函数^[15].Wang等^[16]利用RBF神经网络逼近PEMFC空气供应系统模型中的未建模动态，据此设计了一种鲁棒自适应神经网络控制器，跟踪电堆阴极入口氧气流量，并通过硬件在环测试验证了该方案的可行性.然而，该控制器在实时响应速度方面要慢于在以往文献中报道的滑模类控制器.
本文提出一种将滑模控制方法与神经网络逼近技术相结合的控制策略，使过氧比在具有外部干扰和系统参数摄动的情况下快速准确跟踪其最佳参考值.该控制策略的设计无需依靠精确的系统数学模型，而是利用RBF神经网络在线自适应逼近未建模系统动态，并通过自适应滑模控制实现对复合干扰项的补偿，避免了复杂的分析和大量计算过程.神经网络权值和滑模增益的自适应律均根据Lyapunov理论推导，以保证闭环系统的稳定性.通过数值仿真验证了所提方法的可行性、有效性和优越性.
1 系统模型与控制目标PEMFC系统的基本配置如图 1所示，其主要由电堆和辅助系统(包括空气供应子系统、供氢子系统、水管理子系统和温度管理子系统)组成.为独立研究空气供应系统，需对其他子系统进行合理假设：1)进入电堆阳极的氢气完全参加反应；2)电堆阳极压力能快速跟踪阴极压力的变化；3)电堆内温度和湿度均可由专用控制器快速调节至其理想值.
图 1(Fig. 1)

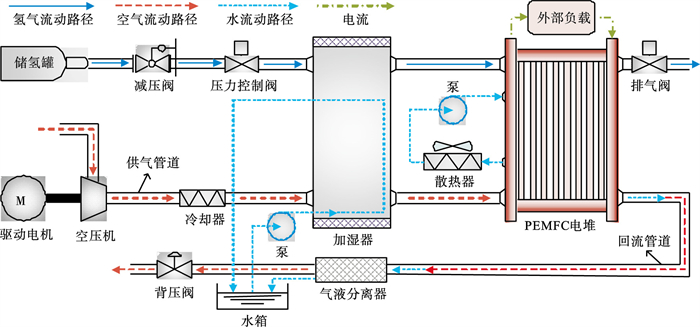图 1 PEMFC系统的基本配置Fig.1 Basic configuration of the PEMFC system

为便于分析说明，本文采用PEMFC空气供应系统的简化三阶动态模型^[17]，其状态空间方程为

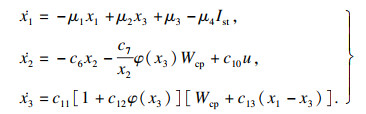(1)

式中：φ(x₃)=[(x₃/c₈)^c₉-1];W_cp=c₁₅x₂; x₁，x₂和x₃分别为电堆阴极压力、空压机转速和供气管道压力；W_cp为空压机出口流量；I_st为电堆电流，被视为一种可测量的外部干扰；u为系统唯一的控制输入，即空压机驱动电机的二次电流，0 < u≤U_m.
过氧比和输出净功率是PEMFC系统的两个关键性能变量.假设PEMFC系统的寄生功耗全部来自空压机，可得到系统输出净功率的表达式：

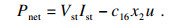(2)

式中：V_st为电堆电压.
过氧比的表达式为

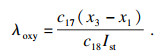(3)

文献[13]针对过氧比与系统输出净功率的稳态关系可知，在不同电堆电流下，PEMFC系统的输出净功率总存在一个最大值，与之对应的过氧比称为最优过氧比λ_{oxy, opt}，其拟合后的表达式为

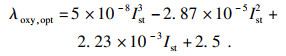(4)

本文的主要控制目标是使实际过氧比λ_oxy准确、快速跟踪其最优参考值λ_{oxy, opt}，从而在不同工况下均能保证PEMFC系统避免氧饥饿现象并取得最大输出净功率.PEMFC系统模型与实际系统存在差异，通常存在未建模动态和未知的模型参数不确定性，实际系统性能还会受到电堆电流瞬变等外部干扰的负面影响，因此，所设计的控制器必须保证对这些干扰因素具有良好的适应性和鲁棒性.
根据文献[12]提出的假设，当空气湿度控制效果十分理想时，过氧比的控制问题可被间接转化为空压机流量的控制问题.空压机出口流量的最优值仅依赖于电堆电流，其表达式为

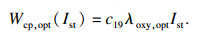(5)

2 自适应神经网络滑模控制器设计本文设计一种自适应径向基函数神经网络滑模(adaptive radial basis function neural network sliding mode, ARBFNNSM)控制器，其实现原理如图 2所示.
图 2(Fig. 2)

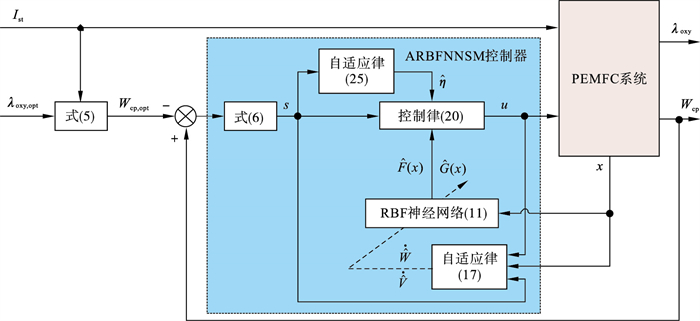图 2 自适应径向基函数神经网络滑模控制器原理图Fig.2 Schematic diagram of the adaptive radial basis function neural network sliding mode controller

定义滑模变量s为

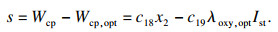(6)

考虑到系统式(1)中存在不确定性，可得

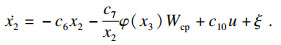(7)

式中：ξ表示由未建模动态和模型参数不确定性所组成的复合不确定项.
取滑模变量s的一阶导数：

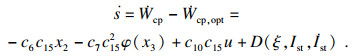(8)

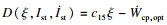
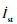
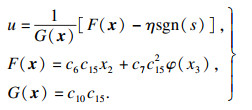式中：, 代表由复合不确定项和外部负载干扰所组成的复合干扰项，结合实际情况可知，电堆电流I_st、变化率及ξ均是有界的，因此复合干扰项式(9)必然是有界的，且满足0 < |D|≤D_max.若PEMFC系统模型的结构参数完全已知，理想的滑模控制律为

(9)

式中：x=[x₁, x₂, x₃]^T为状态向量；滑模增益η是一个正数，且满足η≥ D_max；F(x)和G(x)为连续且充分光滑的系统动态，均为恒大于0的有界函数.F(x)和G(x)在实际应用中是未知的且难以精确建模，所以理想控制律式(9)无法保证期望的控制性能.
RBF神经网络能以任意精度逼近未知非线性函数，便于实时计算，且具备很强的泛化能力^[18].因此，本文采用RBF神经网络在线估计控制律式(9)中未知的有界函数F(x)和G(x).RBF神经网络的结构如图 3所示，其输入到输出的算法为
图 3(Fig. 3)

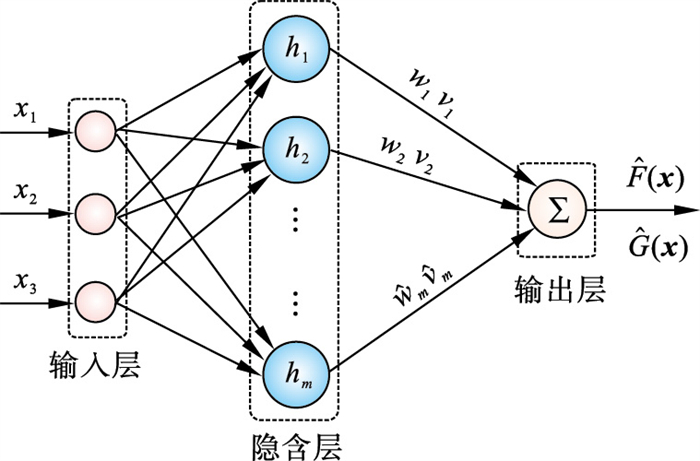图 3 RBF神经网络结构Fig.3 RBF neural network structure

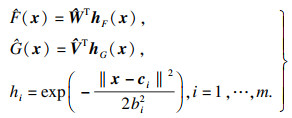(10)

式中：x=[x₁, x₂, x₃]^T为网络输入；F(x)和G(x)的估计值和为网络输出；m为隐含层神经元数量；h(x)=[h₁, h₂, …, h_m]^T为高斯基函数的输出；b_i和c_i分别为高斯基函数h_i的宽度和中心; 分别为估计和所对应的网络权值向量.
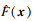
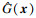
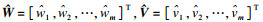
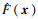
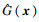
将式(10)代入式(9)，得到如下控制律：

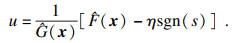(11)

式中：，由此可保证控制律式(11)的非奇异性和有界性，且有0 < u≤U_m.
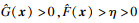
将式(11)代入式(8)可得

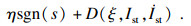(12)

式中：；W和V分别为逼近F(x)和G(x)的理想网络权值向量；且有

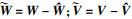
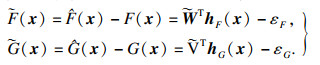(13)

其中，ε_F和ε_G为神经网络逼近误差，且满足|ε_F|≤ε_MF，|ε_G|≤ε_MG.
定义Lyapunov函数L₁为

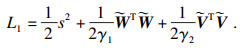(14)

式中：γ₁> 0，γ₂> 0，且满足L₁>0.
结合式(12)，得到L₁的一阶导数为

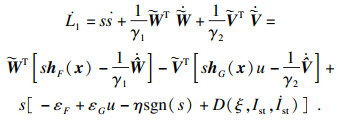(15)

RBF神经网络权值向量的自适应律为

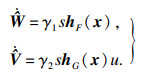(16)

则有

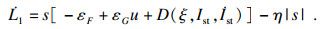(17)

取η≥ε_MF+ε_MGU_m+D_max+σ，且σ>0，则有

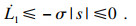(18)

当时，s≡0，根据LaSalle不变集原理可知，当t→∞时，s→0.由此证明包含控制律式(12)的闭环控制系统具有稳定性^[19].
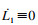
为保证控制器具备良好的抗扰性，滑模增益η不能小于由外部干扰、系统参数不确定性与神经网络估计误差所组成的总干扰项的上界值，但关于该上界值的先验信息难以在实际应用中准确获取.出于保守考虑，滑模增益通常会选取较大的数值以实现抗扰，但过大滑模增益又会增强控制输入和滑模变量的抖振作用.本文利用自适应技术^[19-20]在线调整滑模增益，并基于控制律式(12)构建自适应RBF神经网络滑模控制律：

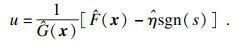(19)

式中：为理想滑模增益η的估计值.
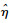
构造Lyapunov函数：

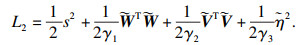(20)

式中：.
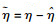
取L₂的一阶导数：

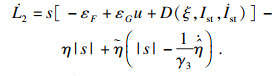(21)

滑模增益的自适应律为

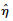
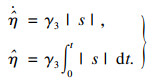(22)

则有

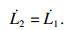(23)

与式(17)和式(18)的分析过程同理，易知当t→∞时，s→0，即采用控制律式(19)的闭环系统是稳定的.
注2：在实际应用中，由于系统会受到测量噪声和切换延迟等因素的限制，|s|只能无限趋近于零，而无法精确收敛到零.因此，即使在滑模变量趋近于零时，式(22)中自适应滑模增益也将一直缓慢增加，造成控制输入发生抖振.本文采用死区方法^[21]改进自适应律式(22)，即

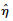
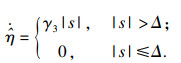(24)

式中：Δ是一个很小的正实数，对控制器性能具有重要影响.若Δ太小以致于恒小于|s|，则式(24)与式(22)的作用完全相同，此时并未起到改善作用；若Δ太大，则易导致滑模增益始终不变，从而降低控制品质.因此，Δ需结合控制输入、控制精度和响应速度的相关要求进行协调选取.
3 仿真结果与分析基于MATLAB/Simulink数值仿真平台，验证本文所设计的ARBFNNSM控制器同时针对大范围电堆电流变化和模型参数摄动情况的有效性，并将其与PID控制器和恒增益滑模(constant gain sliding mode, CGSM)控制器进行对比分析.
3.1 仿真条件设置在仿真环境中搭建文献[4]中提出的75 kW电堆模型.在PEMFC系统模型中关键物理参数名义值的基础之上添加不确定性，得到仿真中采用的参数值，如表 1所示.系统状态变量的初始值设置为x₁(0)=1.4×10⁵ Pa，x₂(0)=400 rad/s，x₃(0)=1.5 ×10⁵ Pa.电堆电流的变化规律如图 4所示.
表 1(Table 1)

表 1 PEMFC系统模型的不确定性参数Table 1 Uncertain parameters of the PEMFC system model 物理参数 名义值 仿真值 大气温度/K 298.15 328 电堆温度/K 353.15 388 供气管道容积/m3 0.02 0.018 电堆阴极流场容积/m3 0.01 0.009 空压机转动惯量/(kg·m2) 671.9 ×10-5 739.1 ×10-5

表 1 PEMFC系统模型的不确定性参数 Table 1 Uncertain parameters of the PEMFC system model

图 4(Fig. 4)

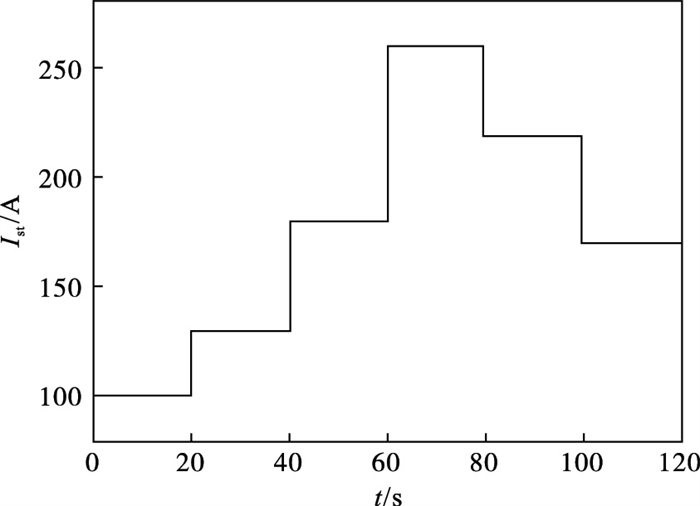图 4 时变的电堆电流Fig.4 Time-varying stack current

ARBFNNSM控制器的参数取值为：m=5，b_i=0.5，c₁=[0 0 0]^T，c₂=[0.25 0.25 0.25]^T，c₃=[0.5 0.5 0.5]^T，c₄=[0.75 0.75 0.75]^T，c₅=[1 1 1]^T，γ₁=0.05，γ₂=0.05，γ₃=2，Δ=5×10^-4.CGSM控制器的滑模增益η=0.02；PID控制器的比例系数、积分时间常数和微分时间常数分别为600，500和8.
3.2 结果分析ARBFNNSM控制器、PID控制器和CGSM控制器对过氧比的控制效果如图 5所示，与之对应的控制输入信号(即电机二次电流)如图 6所示.
图 5(Fig. 5)

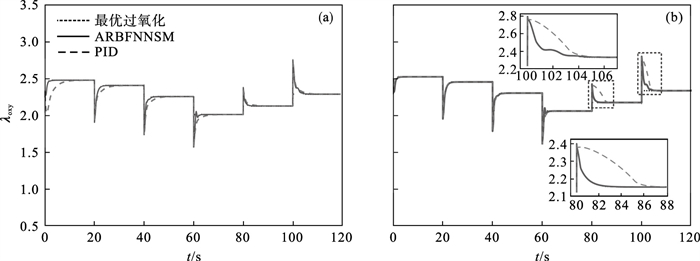图 5 不同控制器的过氧比Fig.5 Oxygen excess ratio of different controllers (a)—ARBFNNSM控制器与PID控制器的控制效果对比；(b)—ARBFNNSM控制器与CGSM控制器的控制效果对比.

图 6(Fig. 6)

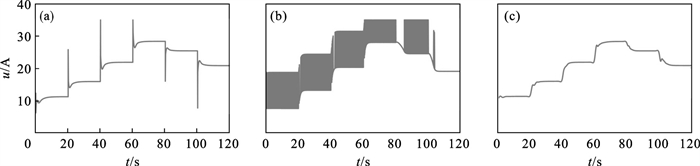图 6 不同控制器的控制输入Fig.6 Control input for different controllers (a)—PID；(b)—CGSM; (c)—ARBFNNSM.

由图 5可知，上述三种控制器均能在有限时间内将实际过氧比调节至最优参考值，然而，它们的动态响应性能明显不同.图 5a表明ARBFNNSM控制器的响应速度总体上快于PID控制器，这一特点在t=0~80 s时尤为明显.图 5b表明，t=0~80 s，ARBFNNSM控制器与CGSM控制器的响应速度基本一致.t=80 s，ARBFNNSM控制器展现出比CGSM控制器更快的动态响应速度.
由图 6可知，与PID控制器和CGSM控制器对应的控制输入信号中分别发生较大幅度的瞬时跳变和较强抖振，这不仅会额外增加PEMFC系统的寄生功耗，致使系统输出净功率降低，还极易造成执行器故障，从而对电堆的使用寿命和耐久性产生不利影响.相比之下，采用ARBFNNSM控制器获得的控制输入信号更平稳平滑，无明显跳变和抖振，并在此基础上取得了良好的过氧比控制效果，这进一步证明了本文所提方法的有效性和优越性.
4 结论1) 针对PEMFC空气供应系统的过氧比控制问题提出了一种ARBFNNSM控制器，该控制器能避免复杂分析建模与大量计算过程，并在参数不确定性和外部负载瞬变干扰的情况下仍能使实际过氧比准确、快速跟踪最优参考值，从而保证了PEMFC系统取得最大输出净功率并避免氧饥饿.
2) 与PID和CGSM控制器相比，ARBFNNSM控制器能提升对过氧比控制的响应速度，有效减弱了控制输入的跳变和抖振，因此更具实际应用潜力.
参考文献

[1]	Abbaker A M O, Wang H, Tian Y. Adaptive integral type-terminal sliding mode control for PEMFC air supply system using time delay estimation algorithm[J]. Asian Journal of Control, 2022, 24(1): 217-226. DOI:10.1002/asjc.2451
[2]	Deng H, Li Q, Cui Y, et al. Nonlinear controller design based on cascade adaptive sliding mode control for PEM fuel cell air supply systems[J]. International Journal of Hydrogen Energy, 2019, 44(35): 19357-19369. DOI:10.1016/j.ijhydene.2018.10.180
[3]	Ou K, Wang Y X, Li Z Z, et al. Feed forward fuzzy-PID control for air flow regulation of PEM fuel cell system[J]. International Journal of Hydrogen Energy, 2015, 40(35): 11686-11695. DOI:10.1016/j.ijhydene.2015.04.080
[4]	Pukrushpan J T, Stefanopoulou A G, Peng H. Control of fuel cell breathing[J]. IEEE Control Systems, 2004, 2(24): 30-46.
[5]	Talj R J, Ortega R, Astolfi A. Passivity and robust PI control of the air supply system of a PEM fuel cell model[J]. Automatica, 2011, 47(12): 2554-2561. DOI:10.1016/j.automatica.2011.08.028
[6]	Abdullah M, Idres M. Constrained model predictive control of proton exchange membrane fuel cell[J]. Journal of Mechanical Science and Technology, 2014, 28(9): 3855-3862. DOI:10.1007/s12206-014-0849-0
[7]	Chen J, Liu Z Y, Wang F, et al. Optimal oxygen excess ratio control for PEM fuel cells[J]. IEEE Transactions on Control Systems Technology, 2018, 26(5): 1711-1721. DOI:10.1109/TCST.2017.2723343
[8]	Baroud Z, Benmiloud M, Benalia A, et al. Novel hybrid fuzzy-PID control scheme for air supply in PEM fuel-cell-based systems[J]. International Journal of Hydrogen Energy, 2017, 42(15): 10435-10447. DOI:10.1016/j.ijhydene.2017.01.014
[9]	Ahmed S, Wang H P, Tian Y. Model-free control using time delay estimation and fractional-order nonsingular fast terminal sliding mode for uncertain lower-limb exoskeleton[J]. Journal of Vibration and Control, 2018, 24(22): 5273-5290. DOI:10.1177/1077546317750978
[10]	Javaid U, Mehmood A, Arshad A, et al. Operational efficiency improvement of PEM fuel cell—a sliding mode based modern control approach[J]. IEEE Access, 2020, 8: 95823-95831. DOI:10.1109/ACCESS.2020.2995895
[11]	Naghmeh M, Mehdi R S, Mahmood G. Robust control design for air breathing proton exchange membrane fuel cell system via variable gain second-order sliding mode[J]. Energy Science & Engineering, 2018, 6(3): 126-143.
[12]	Kunusch C, Puleston P F, Mayosky M A, et al. Sliding mode strategy for PEM fuel cells stacks breathing control using a super-twisting algorithm[J]. IEEE Transactions on Control Systems Technology, 2009, 17(1): 167-174. DOI:10.1109/TCST.2008.922504
[13]	Matraji I, Laghrouche S, Jemei S, et al. Robust control of the PEM fuel cell air-feed system via sub-optimal second order sliding mode[J]. Applied Energy, 2013, 104: 945-957. DOI:10.1016/j.apenergy.2012.12.012
[14]	Pilloni A, Pisano A, Usai E. Observer-based air excess ratio control of a PEM fuel cell system via high-order sliding mode[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 5236-5246. DOI:10.1109/TIE.2015.2412520
[15]	Wang J, Liu Y, Cao G, et al. Design of RBF adaptive sliding mode controller for a super cavitating vehicle[J]. IEEE Access, 2021, 9: 39873-39883. DOI:10.1109/ACCESS.2021.3063192
[16]	Wang Y L, Wang Y F, Chen G. Robust composite adaptive neural network control for air management system of PEM fuel cell based on high-gain observer[J]. Neural Computing and Applications, 2020, 32(14): 10229-10243. DOI:10.1007/s00521-019-04561-7
[17]	Talj R J, Hissel D, Ortega R, et al. Experimental validation of a PEM fuel cell reduced order model and a moto-compressor higher order sliding mode control[J]. IEEE Transactions on Industrial Electronics, 2010, 57(6): 1906-1913. DOI:10.1109/TIE.2009.2029588
[18]	Li T, Duan S, Liu J, et al. An improved design of RBF neural network control algorithm based on spintronic memristor crossbar array[J]. Neural Computing & Applications, 2016, 30: 1939-1946.
[19]	Wang H, He P, Yu M, et al. Adaptive neural network sliding mode control for steer-by-wire-based vehicle stability control[J]. Journal of Intelligent & Fuzzy Systems, 2016, 31(2): 885-902.
[20]	Nasiri A, Nguang S K, Swain A. Adaptive sliding mode control for a class of MIMO nonlinear systems with uncertainties[J]. Journal of the Franklin Institute, 2014, 351(4): 2048-2061. DOI:10.1016/j.jfranklin.2012.12.019
[21]	Qin H D, Yu X, Zhu Z B, et al. An expectation-maximization based single-beacon underwater navigation method with unknown ESV[J]. Neurocomputing, 2019, 378: 295-303.