张伟健¹, 巩亚东¹, 赵旭², 赵显力¹
1. 东北大学 机械工程与自动化学院，辽宁 沈阳 110819;
2. 辽宁科技大学 机械工程与自动化学院，辽宁 鞍山 114051
收稿日期：2021-09-19
基金项目：国家自然科学基金资助项目(U1908230)；中央高校基本科研业务费专项资金资助项目(N2203005，N2203015)。
作者简介：张伟健(1993 -)，男，辽宁大连人，东北大学博士研究生;
巩亚东(1958-), 男, 辽宁本溪人, 东北大学教授, 博士生导师。

摘要：采用非接触测量方法对锆刚玉砂带(P120，P320)与陶瓷氧化铝砂带(P120)三维形貌进行测量与评价.结果表明：锆刚玉砂带和陶瓷氧化铝砂带磨粒凸出高度分别呈正态分布、右偏态分布.锆刚玉砂带和陶瓷氧化铝砂带磨粒凸出面积均呈右偏态分布.磨粒凸出高度和凸出面积随磨料粒度的减小而减小，陶瓷氧化铝砂带磨粒凸出高度和凸出面积均小于同粒度锆刚玉砂带.砂带磨粒几何外形均近似呈球顶圆锥体.磨料粒度对磨粒球顶半径影响显著，即粒度越小，球顶半径越小，但对锥顶角影响不明显.同粒度的两种磨料砂带的磨粒球顶半径及锥顶角差异较大.
关键词：砂带形貌非接触测量磨粒粒度外形参数
Investigation on the Measurement and Evaluation of Abrasive Belt Surface Morphology
ZHANG Wei-jian¹, GONG Ya-dong¹, ZHAO Xu², ZHAO Xian-li¹
1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. School of Mechanical Engineering & Automation, University of Science and Technology Liaoning, Anshan 114051, China
Corresponding author: GONG Ya-dong, E-mail: gongyd@mail.neu.edu.cn.

Abstract: The non-contact measurement method is used to measure and evaluate the three-dimensional morphology of zirconia abrasive belts(P120, P320)and ceramic alumina belt(P120). The results show that the protrusion height of the zirconia abrasive belt and ceramic alumina belt is in the normal distribution and right-skewness distribution respectively. The protrusion area of the zirconia abrasive belt and ceramic alumina belt is both in the right polarized distribution. The protrusion height and area of abrasive grains decrease with the decrease of grain size. The protrusion height and area of abrasive grains in the ceramic alumina belt are smaller than those in the zirconia abrasive belt. The geometric shapes of the abrasive grains of the abrasive belts are similar to the spherical-top cone. The grain size has a significant effect on the spherical-top radius, i.e., the smaller the grain size, the smaller the spherical-top radius, but the effect on the cone apex angle is not significant. There are great differences in the spherical-top radius and cone apex angle of the two abrasive belts with the same particle size.
Key words: abrasive belt morphologynon-contact measurementabrasive graingrain sizeprofile parameter
机器人磨抛技术具有自由度高、通用性强、一致性好等优点，在叶片加工领域受到高度重视.由于具有优异的综合性能，砂带常作为机器人磨抛加工的主要磨具.磨粒通常以静电植砂的方式植入到砂带表面，保证磨粒小端朝外，提高砂带锋利性^[1].此外，砂带磨抛系统中还包含了接触轮等弹性构件，使砂带较砂轮具有更优异的磨削性能.
磨粒在砂带表面的排布和外形决定了砂带形貌特征，而砂带形貌往往是建立砂带磨抛理论模型、仿真模型及研究工艺优化的基础和前提.许多研究人员针对砂带与砂轮形貌的测量和建模开展了一系列研究.文献[2]运用球形探针接触测量金刚石砂轮表面三维坐标数据，并提出了微米级砂轮凸出形貌图形化评价方法.与接触测量相比，非接触测量利用光学检测或显微镜成像技术不仅检测精度更高，而且可以获取更为全面的三维形貌信息，因而在精确表征砂带和砂轮形貌上被广泛运用.文献[3-14]运用光学检测或扫描电镜获取砂带或砂轮表面形貌信息，并提出相应的量化特征参数，对砂带和砂轮表面进行定量评价与仿真建模.从现有文献来看，针对砂带表面形貌测量与评价的相关研究相对较少，而砂带形貌对于砂带磨抛工艺理论研究尤为重要.针对机器人磨抛航发叶片的锆刚玉砂带及陶瓷氧化铝砂带，利用3D测量激光显微镜开展非接触检测，对砂带表面磨粒凸出高度、凸出面积及几何形状参数进行测量与评价，为砂带磨抛工艺理论研究奠定基础.
1 实验条件与测量方法1.1 实验条件航空发动机叶片材料通常为高温合金和钛合金，这两类材料在复杂多变的高温环境中具有优异的力学性能和稳定性.两类材料在磨削加工过程中由于硬度高和易黏附表现出“硬黏特性”，是典型的难加工材料.锆刚玉和陶瓷氧化铝磨料具有良好的强度和耐磨性，在加工叶片材料上表现出优越的磨削性能，选用德国VSM公司所生产的这两种磨料砂带作为研究对象，砂带的型号、规格等参数如表 1所示.
表 1(Table 1)

表 1 砂带及主要参数Table 1 Abrasive belts and main parameters 型号 磨料 图片 规格 粒度 接头方式 ZK713X 锆刚玉 宽：5 mm 周长：330 mm P120 平接 ZK713X 锆刚玉 宽：5 mm 周长：330 mm P320 平接 XK870X 陶瓷氧化铝 宽：5 mm 周长：330 mm P120 平接

表 1 砂带及主要参数 Table 1 Abrasive belts and main parameters

1.2 测量方法3D测量激光显微镜(OLS4100)可实现非接触测量，通过沿Z轴方向多次扫描获取砂带截面的二维图像，实现砂带表面微纳米尺度的三维形貌测量与分析.
使用3D激光显微镜测量砂带形貌的具体方法如图 1所示.
图 1(Fig. 1)

图 1 测量过程Fig.1 Measurement process (a)—样品制备；(b)—数据获取；(c)—数据处理；(d)—测量分析.

1) 样品制备：为了便于观察，将首尾相接的闭环砂带裁剪成25 mm左右长的条形样片，并将样片黏结于平面载物块上，避免因为样片翘曲而影响测量结果.
2) 数据获取：将载有样片的载物块置于激光显微镜下观察和测量，每条样片均选取两个不同区域(粗粒度砂带：10x镜头；细粒度砂带：20x镜头)进行测量，获取不同放大倍率下的三维形貌数据.
3) 数据处理：使用激光显微镜自有测量功能，对砂带形貌源文件进行预处理操作；考虑到所获取的砂带三维形貌数据中除了磨粒的相关数据外，还包含了大量的砂面黏结剂等高频噪声，利用滤波功能排除这些噪声的干扰；对测量表面进行校正，完成原始数据的预处理.
4) 测量分析：在砂带磨削过程中，实际起到切削作用的是从基体中凸出的磨粒切刃，因此在测量分析时仅考虑这些磨粒；把砂带形貌切换到二维显示状态，由于凸出磨粒与周围黏接剂颜色差异显著，因此直接将二者的分界线作为测量基准；磨粒顶点到底部基准的竖直距离即为磨粒凸出高度，而分界线所围成的区域面积即为磨粒凸出面积；在测量磨粒凸出高度时，测量横向剖面、纵向剖面两个方向的凸出高度，求取均值以消除由于不同方向凸出高度不均而引起的误差，并将均值结果作为最终的磨粒凸出高度；对砂带凸出磨粒的球顶半径与锥顶角在横、纵剖面进行了测量，并将两个方向的测量结果取均值.
2 实验结果与讨论2.1 磨粒凸出高度将三条样片上所测量的磨粒凸出高度值分别进行整合，磨粒凸出高度的频率分布直方图如图 2所示.基于磨粒凸出高度频率分布直方图，特征选取合理的拟合函数对分布频率进行拟合，依次采用高斯函数和对数正态分布函数对锆刚玉砂带和陶瓷氧化铝砂带的磨粒凸出高度频率分布直方图进行拟合：
图 2(Fig. 2)

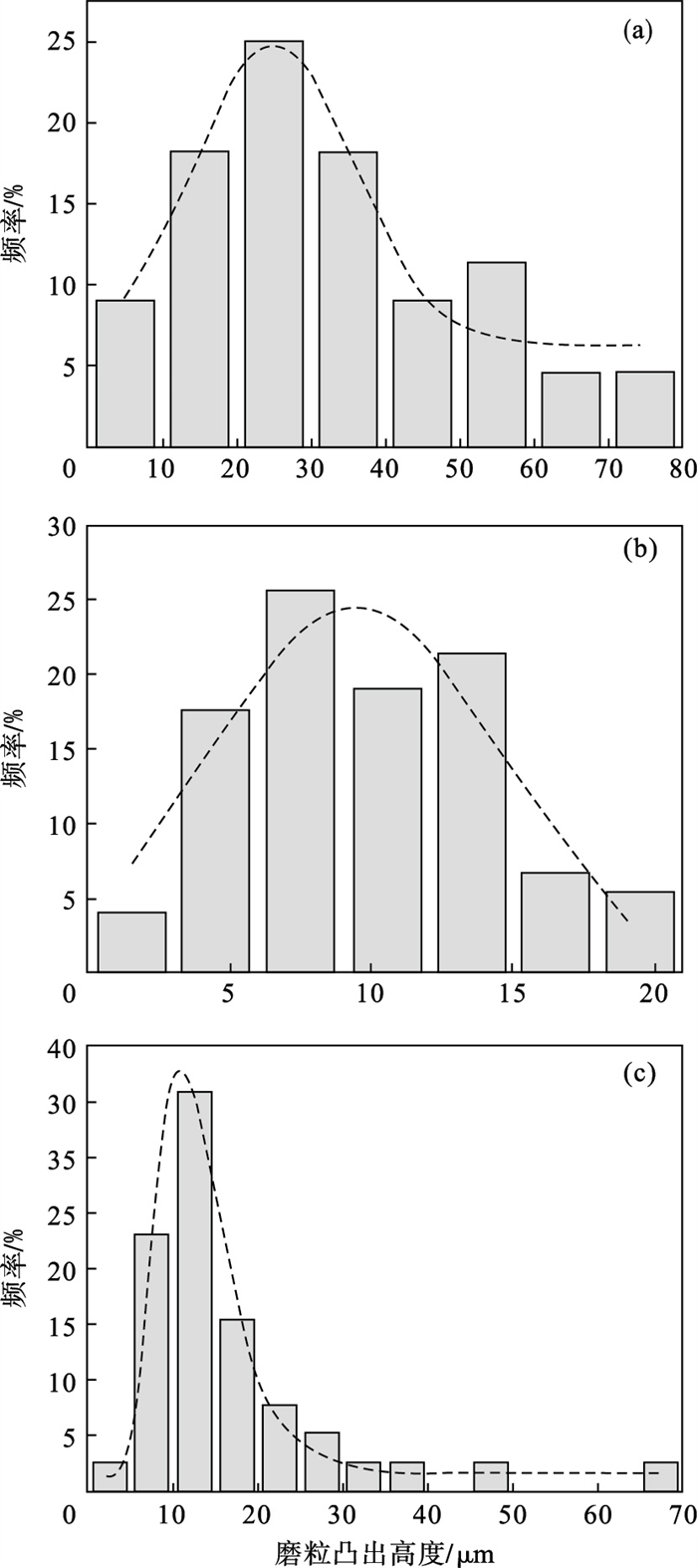图 2 磨粒凸出高度分布频率直方图Fig.2 Frequency histogram of abrasive grain protrusion height distribution (a)—锆刚玉砂带(P120)；(b)—锆刚玉砂带(P320)；(c)—陶瓷氧化铝砂带(P120).

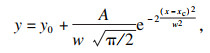(1)

(2)

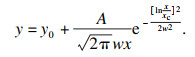式中：y₀为偏移量；x_c为均值；w为标准差；A为幅值.每条拟合曲线所对应的参数值见表 2.
表 2(Table 2)

表 2 磨粒凸出高度频率分布拟合曲线参数值Table 2 Parameters of frequency distribution fitting curve of abrasive grain protrusion height ? μm 砂带 y0 xc w A 锆刚玉(P120) 6.359 25.154 21.427 494.943 锆刚玉(P320) -1.240 9.394 5.325 25.725 陶瓷氧化铝(P120) 1.588 12.404 0.365 385.309

表 2 磨粒凸出高度频率分布拟合曲线参数值 Table 2 Parameters of frequency distribution fitting curve of abrasive grain protrusion height ?

可知图 2中的三条非线性拟合曲线均和相应的频率分布直方图拟合较好，可进一步确定砂带磨粒凸出高度的分布特性.不同粒度的锆刚玉砂带磨粒凸出高度均呈正态分布特征，粗粒度(P120)锆刚玉磨粒凸出高度分布主要集中于15~35 μm，细粒度(P320)砂带磨粒凸出高度分布主要集中于6~12 μm.与锆刚玉砂带磨粒凸出高度相对称的分布特征有所不同的是陶瓷氧化铝砂带(P120)的磨粒凸出高度并非对称分布，频率分布拟合曲线偏向右侧拓展，呈右偏态分布特征，磨粒凸出高度主要分布于5~20 μm.
经计算，三条砂带磨粒凸出高度的均值分别为：锆刚玉(P120)32.40 μm，锆刚玉(P320)10.12 μm，陶瓷氧化铝(P120)17.05 μm.由于不同粒度磨粒的平均粒径差别较大(P120：144.6 μm；P320：47.6 μm)，因此，磨料粒度对磨粒凸出高度大小及分布范围影响显著.磨粒凸出高度越大，磨粒可切入工件材料的最大深度越大，砂带磨削去除率越高、比磨削能越小，使得粗粒度砂带适用于高效砂带磨削，而细粒度砂带适用于精密砂带磨削.
陶瓷氧化铝砂带磨粒凸出高度小于同粒度的锆刚玉砂带(差值-15.35 μm)，表明多数陶瓷氧化铝磨粒嵌入砂面黏结剂的深度更大.一方面，这对于增大磨粒把持力、防止磨粒脱落更为有利; 但另一方面，砂带的磨削效率可能会由于磨粒切深减小而降低.
2.2 磨粒凸出面积将三条样片上所测量的磨粒凸出面积分别进行整合，由此绘制出磨粒凸出面积的频率分布直方图，如图 3所示.
图 3(Fig. 3)

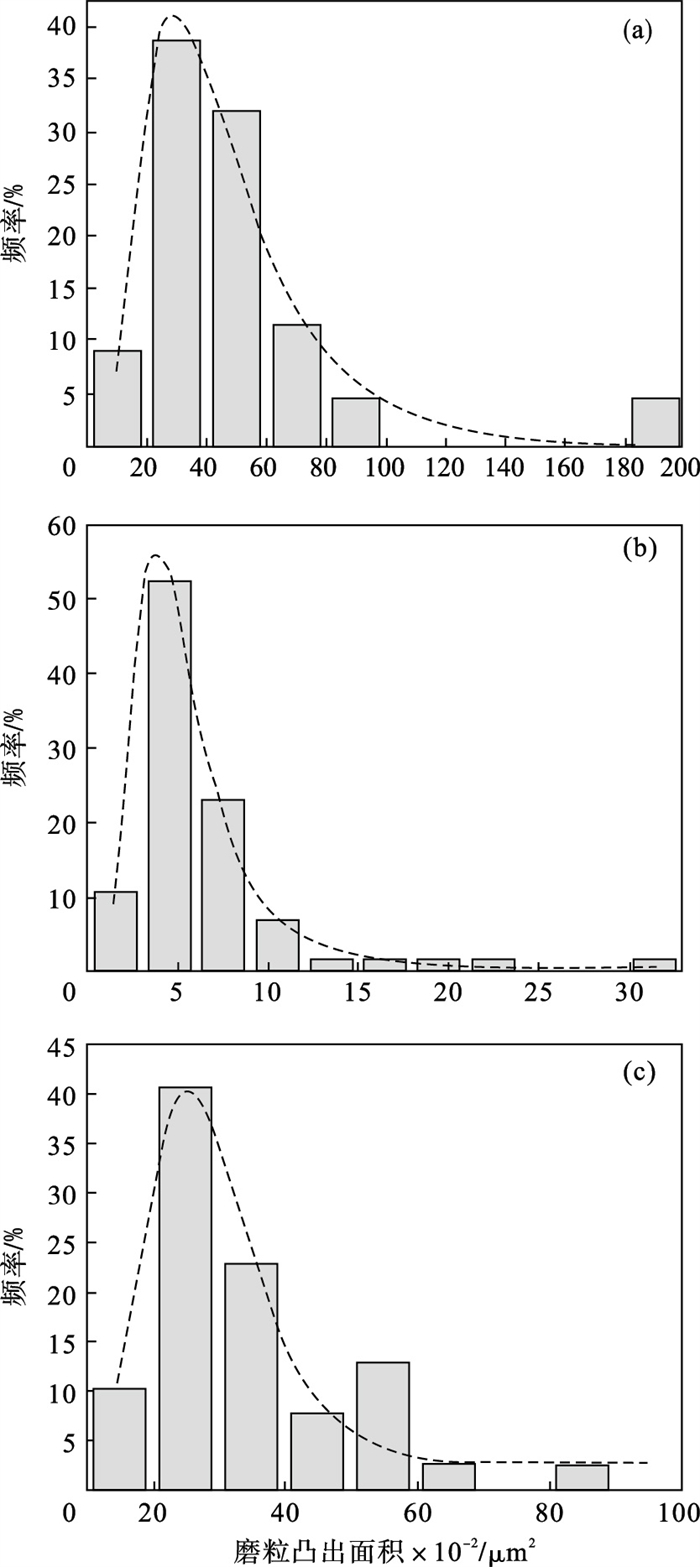图 3 磨粒凸出面积分布频率直方图Fig.3 Frequency histogram of abrasive grain protrusion area distribution (a)—锆刚玉砂带(P120)；(b)—锆刚玉砂带(P320)；(c)—陶瓷氧化铝砂带(P120).

基于磨粒凸出面积频率分布的直方图特征选取合理的拟合函数对分布频率进行拟合.采用对数正态分布函数式(2)对锆刚玉砂带和陶瓷氧化铝砂带的磨粒凸出高度频率分布直方图进行拟合，每条拟合曲线所对应的参数值见表 3.
表 3(Table 3)

表 3 磨粒凸出面积频率分布拟合曲线参数值Table 3 Parameters of frequency distribution fitting curve of abrasive grain protrusion area ? μm2 砂带 y0 xc w A 锆刚玉(P120) -0.178 4 131.113 0.580 208 804.617 锆刚玉(P320) 0.500 0 484.890 0.500 29 897.453 陶瓷氧化铝(P120) 2.702 2 783.269 0.304 76 119.770

表 3 磨粒凸出面积频率分布拟合曲线参数值 Table 3 Parameters of frequency distribution fitting curve of abrasive grain protrusion area ?

图 3中的三条非线性拟合曲线均与相应频率分布直方图拟合较好，可进一步确定砂带磨粒凸出面积的分布特性.与图 2中频率分布直方图及相应的拟合曲线对比发现，三条砂带磨粒凸出面积均非对称分布，频率分布拟合曲线均偏向右侧拓展更为明显，呈右偏态分布特征.粗粒度(P120)锆刚玉砂带磨粒凸出面积主要分布于2 000~6 000 μm²，细粒度(P320)锆刚玉砂带磨粒凸出面积主要分布于300~900 μm²，陶瓷氧化铝砂带(P120)磨粒凸出面积主要分布于2 000~4 000 μm².
经计算，三条砂带磨粒凸出面积的均值分别为：锆刚玉(P120)4 908.90 μm²，锆刚玉(P320)627.33 μm²，陶瓷氧化铝(P120)3 404.23 μm².可知，磨料粒度不同的磨粒粒径尺寸差异较大，导致磨料粒度对磨粒凸出面积的大小和分布影响显著.相比之下，细粒度砂带单位面积内有效磨粒数多于粗粒度砂带，单颗磨粒受力减小，从而减小磨损.由于陶瓷氧化铝砂带磨粒整体凸出高度较小，磨粒凸出面积小于同粒度的锆刚玉砂带(差值为-1 504.67 μm²)，因而有效磨粒的密度相对较大.
2.3 磨粒几何外形磨粒的几何外形通常不规则，而在磨削机理的理论研究中常把磨粒的几何外形适当简化，常见的有球体、圆锥体、棱锥体、圆台和棱台等简单模型.图 4为3D测量激光显微镜拍摄的锆刚玉砂带(P320)和陶瓷氧化铝砂带(P120)的局部形貌，为了更为清楚地显示单颗磨粒的外形特征，在图中选定磨粒并将其放大，并将放大图置于原图中.
图 4(Fig. 4)

图 4 磨粒形貌Fig.4 Abrasive grain morphology (a)—锆刚玉磨粒；(b)—陶瓷氧化铝磨粒.

砂带普遍采用静电植砂的方法排布磨粒，在保证磨粒分布均匀性的同时使得磨粒尖端朝外，确保砂面磨削锋利.从图中同样可以看到，砂带表面上磨粒排布较为均匀，并且磨粒大端嵌入砂带基体中，小端(尖端)朝外，从而保证砂带的磨削效率.
从几何外观来看，磨粒外形均近似于圆锥体与球体的组合体，即球顶圆锥体.将两类磨粒几何外形简化为规则几何体，如图 5所示.图中：H为磨粒凸出高度，μm；h为磨粒圆锥体部分高度，μm；r为球顶半径，μm；2θ为锥顶角，(°)；R为磨粒底部半径，μm.
图 5(Fig. 5)

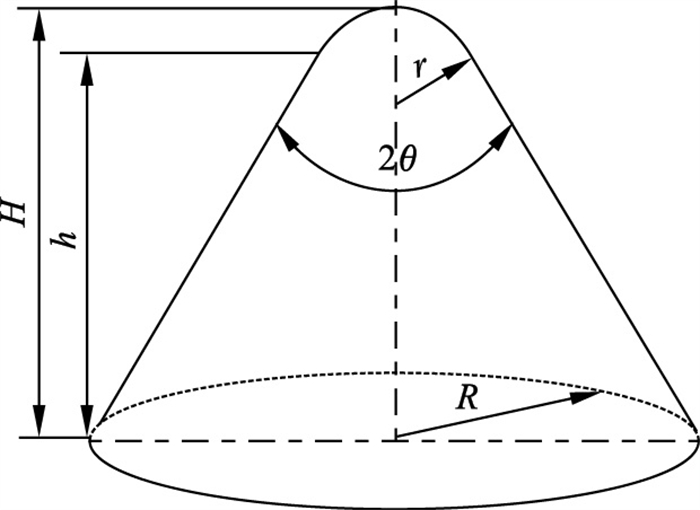图 5 磨粒简化模型Fig.5 Simplified model of abrasive grains

将三条样片上所测量的磨粒球顶半径r与锥顶角2θ数据分别进行整合并取平均值，最终结果如表 4所示.砂带各磨粒几何参数对比情况如图 6所示.在球顶半径r的大小关系上，锆刚玉(P120)>陶瓷氧化铝(P120)>锆刚玉(P320).由于磨料粒度小的磨粒平均粒径更小，锆刚玉磨粒(P320)球顶半径更小，说明磨料粒度对磨粒球顶半径有显著影响.陶瓷氧化铝磨粒球顶半径比同粒度的锆刚玉磨粒更小(差值-10.55 μm).磨粒球顶半径越小，其前角越大，切刃越锋利，磨粒对工件的挤压作用减弱、切削作用增强，从而提高砂带磨削性能.
表 4(Table 4)

表 4 磨粒几何参数计算结果Table 4 Calculation results of abrasive grain geometric parameters 磨料 H/μm 2θ/(°) r/μm h/μm R/μm 锆刚玉(P120) 32.40 67.99 23.12 22.21 34.15 锆刚玉(P320) 10.12 60.65 6.02 7.14 9.37 陶瓷氧化铝(P120) 17.05 83.47 12.57 12.85 20.84

表 4 磨粒几何参数计算结果 Table 4 Calculation results of abrasive grain geometric parameters

图 6(Fig. 6)

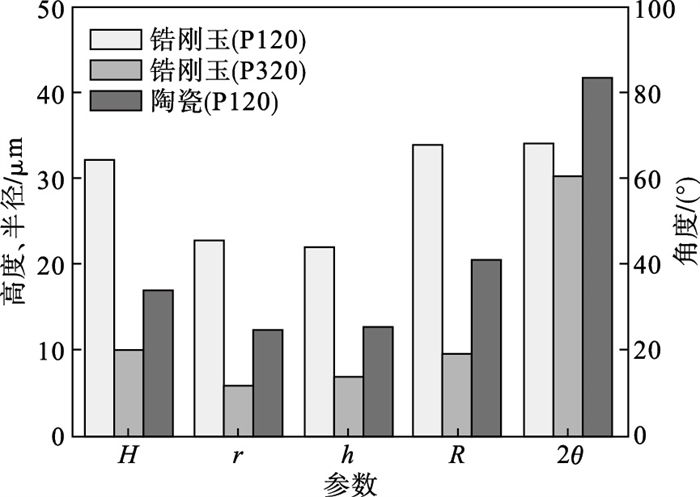图 6 磨粒几何参数Fig.6 Geometric parameters of abrasive grains

在锥顶角2θ的大小关系上，陶瓷氧化铝(P120)>锆刚玉(P120)>锆刚玉(P320)，陶瓷氧化铝磨粒锥顶角最大，而磨料粒度对锆刚玉砂带磨粒锥顶角的影响并不显著.
在磨粒几何参数H，2θ，r确定后，其他两个参数可以通过几何关系式(3)与式(4)确定：

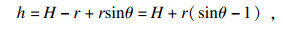(3)

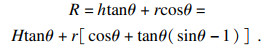(4)

参数h和R的计算结果如表 4所示.三组砂带磨粒在h，R的大小关系上与H，r相同，即锆刚玉(P120)>陶瓷氧化铝(P120)>锆刚玉(P320).
3 结论1) 锆刚玉砂带和陶瓷氧化铝砂带磨粒凸出高度分别呈正态分布、右偏态分布；锆刚玉砂带与陶瓷氧化铝砂带磨粒凸出面积均呈右偏态分布.
2) 磨料粒度对磨粒凸出高度和凸出面积影响显著，二者均随磨料粒度的减小而减小，粗粒度砂带适用于高效磨削，细粒度砂带则适用于精密磨削.陶瓷氧化铝砂带磨粒凸出高度和凸出面积均小于锆刚玉砂带(差值-15.35 μm，-1504.67 μm²)，在提高磨粒把持力的同时可能会降低磨削效率.
3) 锆刚玉砂带与陶瓷氧化铝砂带磨粒几何外形均近似为球顶圆锥体.磨料粒度对磨粒球顶半径影响显著(粒度越小，球顶半径越小)，而对磨粒锥顶角影响不明显.陶瓷氧化铝砂带磨粒球顶半径及锥顶角较同粒度锆刚玉砂带差异较大(差值-10.55 μm，15.48°).
参考文献

[1]	黄云, 黄智. 现代砂带磨削技术及工程应用[M]. 重庆: 重庆大学出版社, 2009: 57-60. (Huang Yun, Huang Zhi. Modern belt grinding technology and engineering application[M]. Chongqing: Chongqing University Press, 2009: 57-60.)
[2]	Xie J, Xu J, Tang Y, et al. 3D graphical evaluation of micron-scale protrusion topography of diamond grinding wheel[J]. International Journal of Machine Tools & Manufacture, 2008, 48(11): 1254-1260.
[3]	Nguyen A T, Butler D L. Correlation of grinding wheel topography and grinding performance: a study from a viewpoint of three-dimensional surface characterization[J]. Journal of Materials Processing Technology, 2008, 208(1/2/3): 14-23.
[4]	Darafon A, Warkentin A, Bauer R. Characterization of grinding wheel topography using a white chromatic sensor[J]. International Journal of Machine Tools & Manufacture, 2013, 70: 22-31.
[5]	Kap?onek W, Nadolny K. Assessment of the grinding wheel active surface condition using SEM and image analysis techniques[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2013, 35(3): 207-215. DOI:10.1007/s40430-013-0018-x
[6]	McDonald A, Bauer R, Warkentin A. Design and validation of a grinding wheel optical scanner system to repeatedly measure and characterize wheel surface topography[J]. Measurement, 2016, 93: 541-551. DOI:10.1016/j.measurement.2016.07.061
[7]	王文玺, 李建勇, 樊文刚, 等. 砂带三维表面形貌特征量化评价方法[J]. 华南理工大学学报(自然科学版), 2016, 44(12): 14-22. (Wang Wen-xi, Li Jian-yong, Fan Wen-gang, et al. Quantitative evaluation method for 3D surface topography of abrasive belt[J]. Journal of South China University of Technology(Natural Science Edition), 2016, 44(12): 14-22. DOI:10.3969/j.issn.1000-565X.2016.12.003)
[8]	何喆, 李建勇, 刘月明, 等. 砂带虚拟形貌的建模[J]. 华南理工大学学报(自然科学版), 2017, 45(12): 85-91, 105. (He Zhe, Li Jian-yong, Liu Yue-ming, et al. Modeling of virtual topography of abrasive belt[J]. Journal of South China University of Technology(Natural Science Edition), 2017, 45(12): 85-91, 105. DOI:10.3969/j.issn.1000-565X.2017.12.013)
[9]	刘伟, 商圆圆, 邓朝晖, 等. 砂轮表面形貌定量评价及修整效果研究[J]. 中国机械工程, 2018, 29(19): 2277-2283. (Liu Wei, Shang Yuan-yuan, Deng Zhao-hui, et al. Study on quantitative evaluations and dressing effectiveness for surface topography of grinding wheels[J]. China Mechanical Engineering, 2018, 29(19): 2277-2283. DOI:10.3969/j.issn.1004-132X.2018.19.002)
[10]	Pang Z J, Wu C J, Wang Q X, et al. Modeling of grinding wheel topography based on a joint method of 3D microscopic observation and embedded grindable thermocouple technique[J]. International Journal of Advanced Manufacturing Technology, 2018, 97(1/2/3/4): 25-37.
[11]	Tang J J, Qiu Z J, Li T Y. A novel measurement method and application for grinding wheel surface topography based on shape from focus[J]. Measurement, 2019, 133: 495-507. DOI:10.1016/j.measurement.2018.10.006
[12]	Liu W, Deng Z H, Shang Y Y, et al. Parametric evaluation and three-dimensional modelling for surface topography of grinding wheel[J]. International Journal of Mechanical Sciences, 2019, 155: 334-342. DOI:10.1016/j.ijmecsci.2019.03.006
[13]	Kang M X, Zhang L, Tang W C. Study on three-dimensional topography modeling of the grinding wheel with image processing techniques[J]. International Journal of Mechanical Sciences, 2020, 167: 237-242.
[14]	Godino L, Pombo I, Sanchez J A, et al. Characterization of vitrified alumina grinding wheel topography using 3D roughness parameters: influence of the crystalline structure of abrasive grains[J]. International Journal of Advanced Manufacturing Technology, 2021, 113(5/6): 1673-1684.