

1. 东北大学 医学与生物信息工程学院,辽宁 沈阳 110169;
2. 中国医科大学 生物医学工程系,辽宁 沈阳 110122;
3. 沈阳东软智能医疗科技研究院有限公司,辽宁 沈阳 110167
收稿日期:2021-09-14
基金项目:国家自然科学基金资助项目(61773110);沈阳市科学技术计划项目(20-201-4-10);中央高校基本科研业务费专项资金资助项目(N2119008);沈阳东软智能医疗科技研究院有限公司会员课题基金资助项目(MCMP062002)。
作者简介:柳军(1981-),男,山东烟台人,东北大学博士研究生;
徐礼胜(1975-),男,安徽安庆人,东北大学教授,博士生导师。
摘要:针对模型估计左心室压力波形的临床个性化需求和大量参数优化计算复杂情况,提出基于灵敏度分析的模型参数子集选择策略.以左心室压力波形特征作为体循环模型的输出,通过自适应稀疏多项式混沌展开算法构建原始模型的元模型,改进索贝尔灵敏度指标计算,选出模型中对左心室压力波形特征有重要影响的参数作为参数子集.本文提出的选择策略可以为左心室压力波形估计中的模型参数临床个性化提供参考依据;参数子集中模型参数数量的减少,可以降低优化空间和参数求解的复杂度.实验结果表明,采用参数子集的左心室压力波形及特征估计与模型的全体参数估计具有很高的一致性.
关键词:灵敏度分析参数子集选择左心室压力波形估计自适应稀疏多项式混沌展开算法索贝尔法
A Method of Model Parameters Subset Selection for Left Ventricle Pressure Waveform Individual Estimation
LIU Jun1,2, HAO Li-ling1, HE Guang-yu3, XU Li-sheng1,3


1. College of Medicine and Biological Information Engineering, Northeastern University, Shenyang 110169, China;
2. Department of Biomedical Engineering, China Medical University, Shenyang 110122, China;
3. Neusoft Research of Intelligent Healthcare Technology Co., Ltd., Shenyang 110167, China
Corresponding author: XU Li-sheng, E-mail: xuls@bmie.neu.edu.cn.
Abstract: Since the left ventricle pressure waveform(LVPW)estimation is based on the model with numerous patient specific parameters, there is a great need to reduce the computation cost. A parameter subset selection strategy based on sensitivity analysis is proposed to solve these problems. LVPW features are chosen as outputs of a systemic circulation model. The meta model is created by adaptive sparse polynomial chaos expansion algorithm, and then Sobol sensitivity index is computed. Finally, the parameters which have large impact on LVPW features are selected as parameter subset. The parameter subset selection proposed in this paper can provide help for applying model to patient specific situations in clinical applications. Meantime, the results indicate that the reducing size of parameter subset can decrease the complex computation of parameter optimization significantly. Furthermore, LVPW estimation based on the proposed method has high correlation with that based on full model parameters.
Key words: sensitivity analysisparameter subset selectionleft ventricle pressure waveform(LVPW)estimationadaptive sparse polynomial chaos expansion algorithmSobol method
心脏中左心室压力波形(left ventricle pressure waveform, LVPW)直接反映了左心室的血流动力学特征,在临床压力容积环指标中是不可或缺的[1],对于主动脉瓣狭窄等临床病症有重要的诊断和治疗意义[2].
目前LVPW的测量主要是有创测量和无创模型估计两种方法.有创测量是在临床中通过导管介入手术实现,但是病人需要承受一定的创伤和风险,并且医疗成本较高.无创测量的方法主要是通过各种特定背景下的心血管模型估计[3-4],同时可以适当结合患者的外周无创测量信息.模型估计方法由于无需手术、患者没有创伤成为目前的一个研究方向[5].而针对每个不同病人,模型参数个性化成为近年来的研究热点[6].
通常一个模型中有很多参数,在临床应用中不可能对模型中所有参数进行个性化取值,因为有的模型参数可能无法测量或者临床中的医疗成本过高,所以应当挑选出模型中对LVPW有较大影响的参数进行个性化取值.灵敏度分析(sensitivity analysis, SA)方法近年来逐渐应用于心血管模型参数个性化选择中[7].
本文以一个体循环模型估计LVPW作为实例,采用自适应稀疏多项式混沌展开(adaptive sparse polynomial chaos expansion, asPCE)算法构建出原始模型的元模型(meta model),采用索贝尔法(Sobol method)进行灵敏度指标计算,最后遴选出对LVPW有较大影响的模型参数作为参数子集.
1 体循环模型本文以一个体循环模型作为估计LVPW的例子,在最近的研究中也有类似的模型用于估计LVPW[8],模型的具体原理公式的推导在文献[9]中有详细的介绍,本文不再赘述.总体结构上模型由一个左心室单纤维模型作为驱动,外周血管由Windkessel模型构成,主动脉瓣和二尖瓣由二极管模型模拟.体循环模型构成原理图如图 1所示.
图 1(Fig. 1)
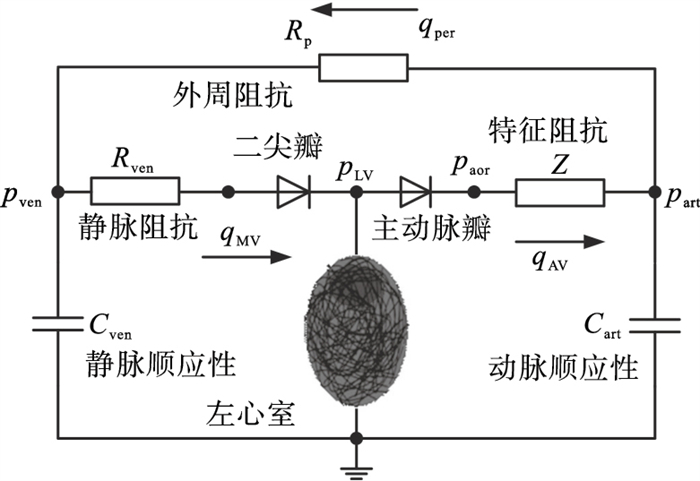 | 图 1 体循环模型构成原理图Fig.1 Schematic diagram of systemic circulation model |
模型的输出为LVPW以及4个波形特征,在本文中4个波形特征分别定义为一个心动周期内LVPW的平均压pMB,收缩压pSB,从二尖瓣关闭时刻到收缩压pSB的时间间隔tr,从收缩压pSB时刻到二尖瓣打开时刻的时间间隔td,具体波形特征在LVPW中的含义如图 2所示.
图 2(Fig. 2)
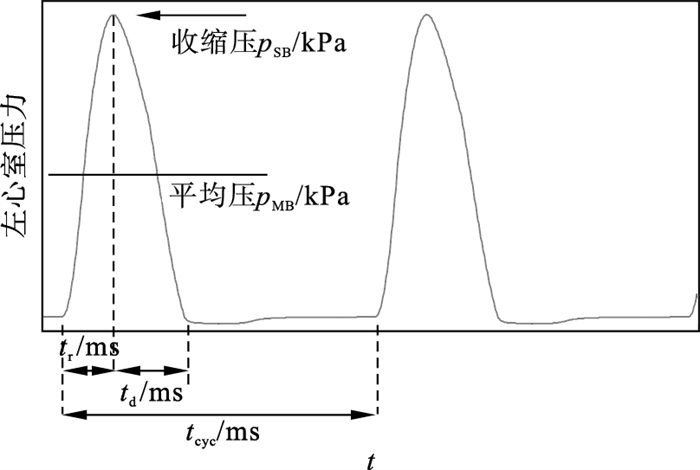 | 图 2 左心室压力波形特征Fig.2 Features of LVPW |
本文体循环模型中涉及的模型参数分为三类:生理类参数,Windkessel外周模型参数,单纤维模型心肌纤维参数.表 1~表 3分别给出模型中各个参数的单位、描述及其范围.
表 1(Table 1)
| 表 1 体循环模型中的生理类参数 Table 1 Physiological parameters of systemic circulation model |
表 2(Table 2)
| 表 2 体循环模型中的外周参数 Table 2 Peripheral parameters of systemic circulation model |
表 3(Table 3)
| 表 3 体循环模型中的心肌纤维参数 Table 3 Myocardial fiber parameters of systemic circulation model |
2 模型参数灵敏度计算2.1 灵敏度指标本文灵敏度分析采用Sobol法进行计算.该方法是基于方差分解[10]的思想,用模型输出的方差来衡量输出不确定性,输出的方差可以分解成偏方差的组合.这些偏方差可以表示每个输入参数或者多个输入参数相互影响的不确定性对输出的影响.
假设模型输出输入关系为
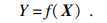 | (1) |
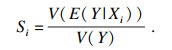 | (2) |
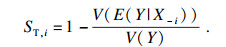 | (3) |
2.2 元模型构建和灵敏度指标计算2.2.1 元模型构成及灵敏度计算各个参数的索贝尔灵敏度指标最初是由蒙特卡洛统计学方法[11]求出,由于蒙特卡洛方法需要进行大量的模型样本运算,计算量巨大,后来有****[12]提出了采用多项式混沌展开来替代原始模型,根据展开式的系数来计算索贝尔灵敏度指标.本文采用自适应稀疏多项式混沌展开算法进行元模型的构建[13],然后根据多项式系数计算主灵敏度和总灵敏度两个灵敏度指标.
模型的输出可以表示为输入参数的一系列截断后的有限项正交多项式的组合,本文采用勒让德正交多项式,输入参数需要转换到[-1, +1]的范围内,以满足勒让德正交多项式的要求.模型的输出输入关系为
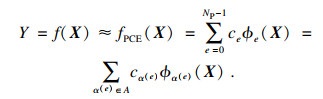 | (4) |
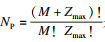
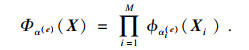 | (5) |
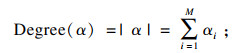 | (6) |
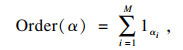 | (7) |
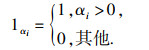 | (8) |
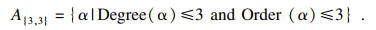 | (9) |
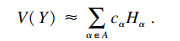 | (10) |
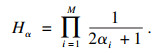 | (11) |
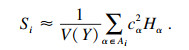 | (12) |
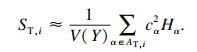 | (13) |
2.2.2 asPCE算法构建元模型在构建元模型和求解多项式系数的过程中,本文采用asPCE的算法.该算法的优点是可以减少模型运算样本数量.在构建元模型的过程中,有选择地挑选多项式组合中对输出结果有较大影响的项,作为最终元模型多项式组合的组成部分.在算法的迭代过程中,将重复进行两步重要多项式的挑选操作:前向选择和后向选择.在前向选择中,从零开始逐渐增加多项式的最高阶次和互相阶次,挑选出可以显著提高元模型准确度的部分,构成前向选择的多项式组合;在构建完前向选择的多项式组合后,再进行后向选择,在后向选择中,去掉那些前向选择中留下的似乎重要但是并没有显著提高元模型准确度的部分.多项式的最高阶次和互相阶次从零开始逐渐增大到设定值,在此过程中,算法需要的模型运算样本点数量将逐渐增加,前向选择和后向选择的操作在不断地迭代进行,直到最后确定元模型所包括的多项式组合.
在asPCE算法中,需要设置若干参数值.本文的参数设置情况借鉴了以前****的研究[13],设最高多项式阶次Zmax=3,最高互相阶次jmax=3,表征元模型与真实模型的接近程度的参数设为Qtgt2=0.99,前向选择中的阈值设为T_F=0.001,后向选择中的阈值设为T_B=0.001.前向选择和后向选择过程中构建的元模型与真实模型的接近程度可以用决定系数R2来衡量,定义如下:
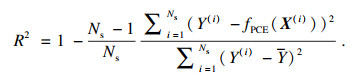 | (14) |
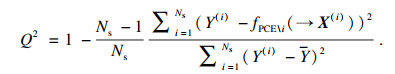 | (15) |
本文迭代停止的条件设置为两个,满足其中一个迭代过程立刻停止.其中一个停止条件是当多项式的阶次增大到最大预设值Zmax; 另外一个停止条件是当元模型的质量系数Q2达到预设值Qtgt2.整个asPCE算法的迭代过程和灵敏度计算如图 3所示.
图 3(Fig. 3)
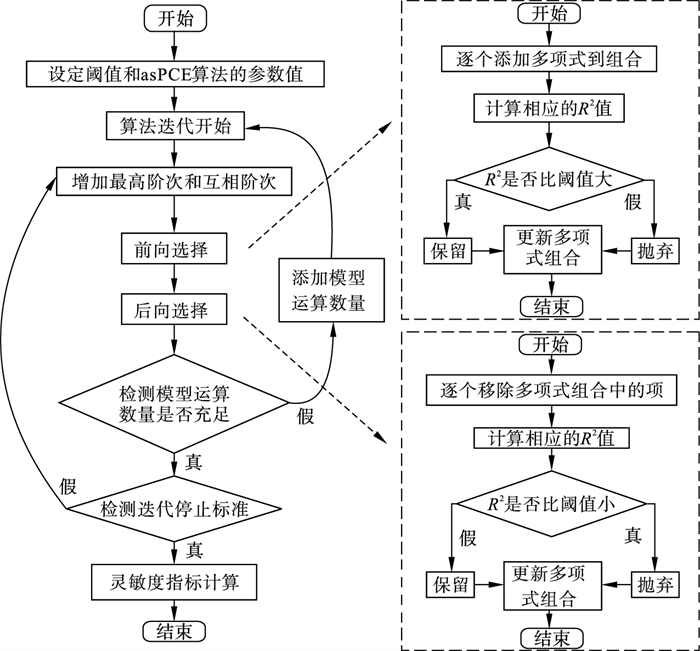 | 图 3 asPCE算法流程与灵敏度计算Fig.3 Schematic flowchart of asPCE algorithm and sensitivity analysis calculation |
2.3 模型样本运算由于asPCE算法中,求解多项式系数需要用到线性回归方法,因此需要提前进行模型样本的运算.在通用的多项式混沌展开(general polynomial chaos expansion, gPCE)方法中,至少需要NP次模型运算样本.而在asPCE算法中,模型运算样本的数量可以大大减少,本文按照gPCE方法进行了NP=4060次模型运算,但是实际asPCE算法迭代中只是用到了其中一部分.
在进行模型运算之前,模型的输入参数需要进行随机取值.本文采用Sobol序列准随机数生成方法[14],该方法以2为底数来形成更精细的单位间隔,并且可以生成输入参数的基于均匀分布的随机序列.
由于模型的输入参数是高维随机序列生成,在模型运算中,模型输出值有很多情况是不符合实际人体的生理数据,因此,要把这些不正确的模型输出值排除在最后元模型的构建过程中.本文根据健康人群和各种心血管病人群的特点以及文献[15]的相关类似设置,设置了以下的模型输出过滤规则:
1) 模型输出的计算是基于连续多个心动周期逐渐收敛稳定,因此设定相邻两个周期的2范数阈值为0.05,当超过15个心动周期并且相邻2个心动周期波形的2范数小于0.05,就认为模型输出波形达到收敛; 2) 左心室压力波形的平均值范围为1~10kPa; 3) 左心室压力波形的收缩压范围为5~24kPa; 4) 左心室压力波形在舒张期内的压力范围为0.3~3kPa; 5) 左心室压力波形中收缩期时长与舒张期时长的比值范围为0.5~1.2.
3 灵敏度指标结果及元模型与真实模型输出对比本文模型有27个输入参数和4个左心室压力波形特征输出指标,经过以上主灵敏度和总灵敏度指标的计算,所有输入参数的灵敏度指标计算结果如图 4所示.从最后的主灵敏度和总灵敏度结果可以看出,4个左心室压力波形特征分别对应的重要的输入参数有所区别.取4个波形特征所对应的所有重要参数的并集作为最后模型输出左心室压力波形的重要参数子集,共计12个参数,并在表 4给出了每个参数对应的4个波形特征的主灵敏度最大值和总灵敏度最大值.
图 4(Fig. 4)
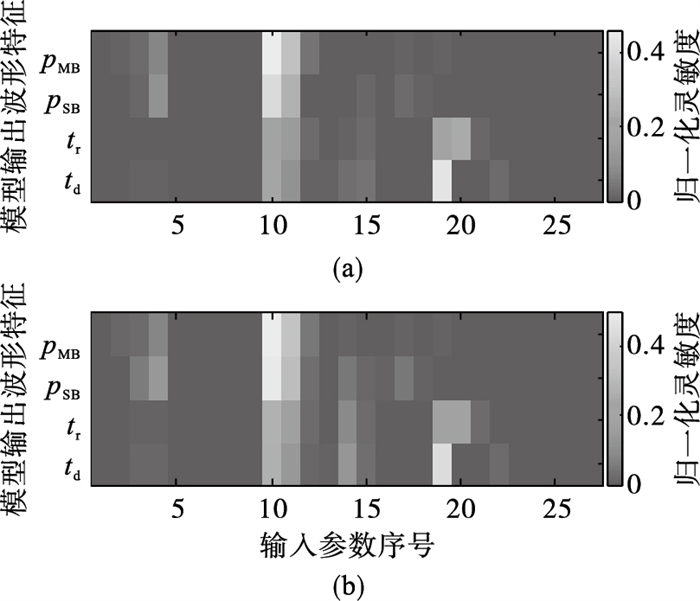 | 图 4 灵敏度分析结果Fig.4 Results of sensitivity analysis (a)—主灵敏度;(b)—总灵敏度. |
表 4(Table 4)
| 表 4 对应左心室压力波形特征的重要输入参数 Table 4 Important parameters corresponding to the features of LVPW |
为了检验元模型与真实模型的逼近程度,本文进行了左心室压力波形特征的对比,在输入参数相同的情况下,比较从真实模型和元模型输出的左心室压力波形的4个特征,具体对比结果如图 5所示.其中所有相关性图中,r=0.99, P < 0.001.并且4个特征分别对应的两组数据没有显著差异(P>0.05).从上面的LVPW的波形特征相关性曲线和一致性结果图中,可以清楚地看到元模型与真实模型具有很好的相关性和一致性.
图 5(Fig. 5)
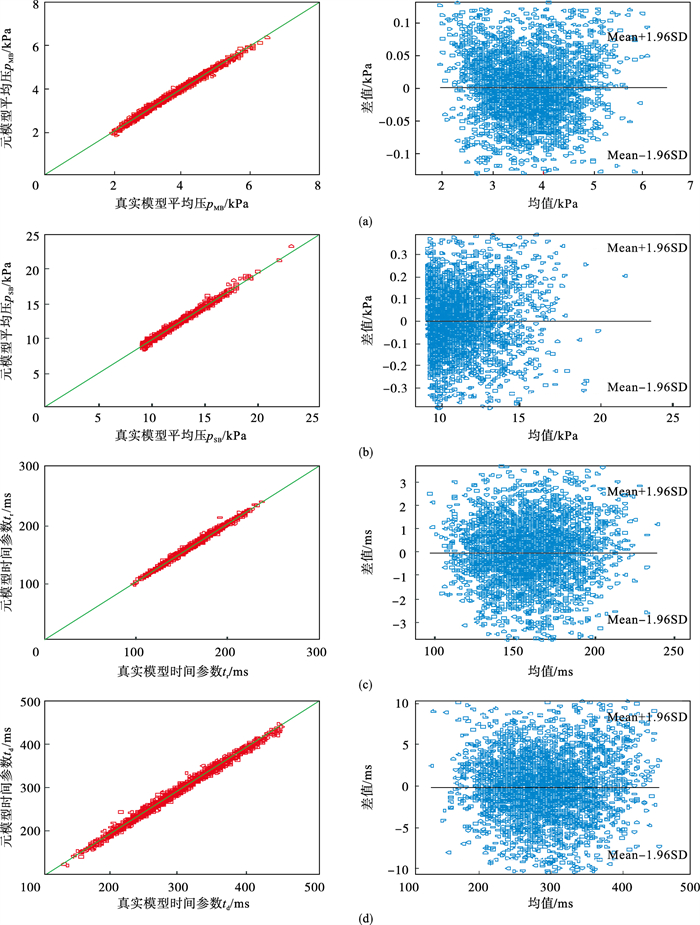 | 图 5 真实模型和元模型输出的波形特征相关性曲线和对应的Bland-Altman图Fig.5 Correlation and Bland-Altman plots of LVPW features for true model versus meta model (a)—平均压;(b)—收缩压;(c)—时间常数tr;(d)—时间参数td. |
4 模型输出LVPW对比及灵敏度计算方法对比为了验证当模型中不重要参数取值固定(经验值或平均值)时,模型输出的左心室压力波形情况,进行了左心室压力波形和波形特征的对比.把模型的参数分成两个部分,重要参数和非重要参数.重要参数取值相同(随机取值),非重要参数一种情况随机取值,另外一种情况固定取值(经验值).在这两种情况下,对真实模型输出的左心室压力波形和波形特征进行对比,结果如图 6和图 7所示,其中所有的相关性曲线中,r=0.99, P < 0.001.
图 6(Fig. 6)
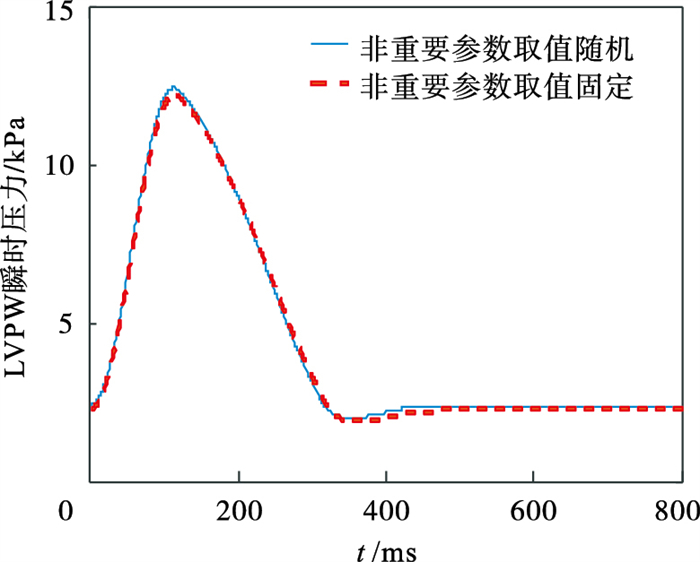 | 图 6 不同参数取值情况下模型输出LVPW对比Fig.6 Comparison of LVPW with different input parameters |
图 7(Fig. 7)
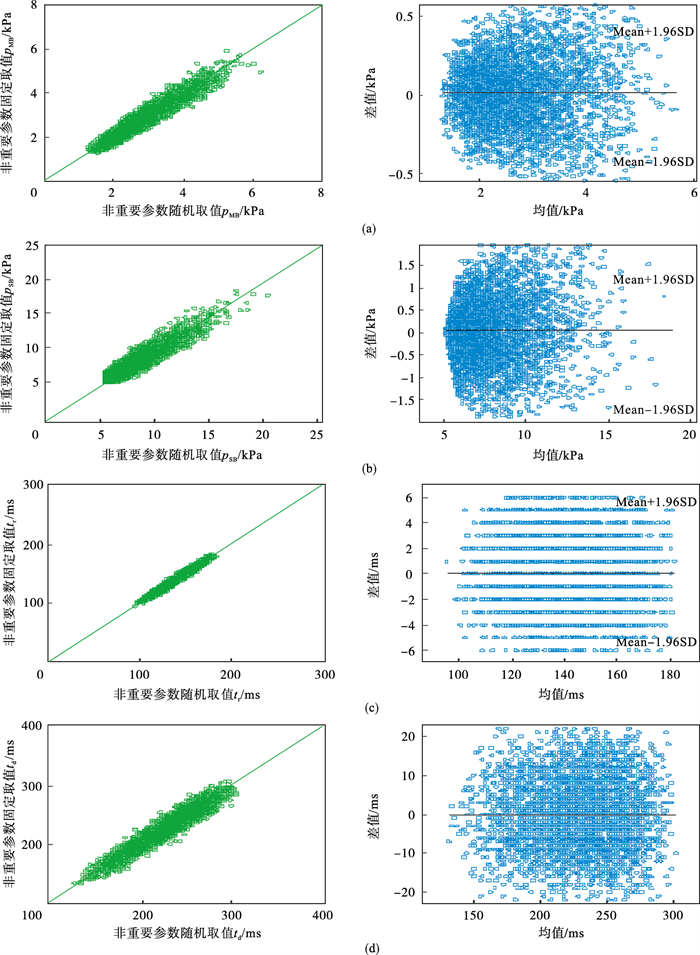 | 图 7 不同参数取值情况下模型输出波形特征的相关性分析和Bland-Altman分析Fig.7 Correlation and Bland-Altman plots of LVPW features with different input parameters (a)—平均压;(b)—收缩压;(c)—时间参数tr;(d)—时间参数td. |
LVPW和波形特征在两种情况下没有显著差异(P>0.05).本文进行了3431次实验,随机取其中一例波形对比图如图 6所示.经过灵敏度选择后,重要参数子集的数量比全部参数数量显著减少,从对比结果图中可以看出,在重要参数取值相同,非重要参数取值固定与取值随机两种情况下,最后输出的左心室压力波形和波形特征都具有很好的一致性.经过灵敏度选择后,重要参数作为重点关注的参数子集,非重要参数取值固定对LVPW波形的估计几乎没有重大影响.
传统的灵敏度计算经常采用蒙特卡洛方法,其劣势在于需要巨量的模型计算样本,计算量大,特别对于参数数量较多的模型,计算量呈几何数量级增长.采用asPCE算法构建原始模型的元模型进行灵敏度指标的计算,一方面可以对不了解原始模型内部原理的研究者提供一个简单的多项式组合的元模型,另一方面,基于此算法进行灵敏度指标的计算,可以显著降低模型计算样本数量的需求,对模型参数较多的情况,效果更加明显.本文模型有27个参数,多项式的最高阶次为3,假定蒙特卡洛样本数量10000的情况下,蒙特卡洛算法,gPCE算法和本文提出的asPCE算法所需要的模型运算样本数量依次是290000, 4060和2582.
5 结语当临床所用心血管模型参数很多时,LVPW估计的个性化和参数优化计算工作将会很复杂.本文提出基于灵敏度分析的方法对模型中的参数进行重要参数子集选择,最终选出对LVPW有较大影响的参数子集,这样的参数子集可为临床患者的LVPW个性化估计提供参考,临床中可以重点关注这些灵敏度指标较高的参数.参数子集中的参数数量减少,可以明显降低模型参数优化计算的复杂度.实验结果表明,基于灵敏度选择的参数子集的LVPW估计,与模型全参数估计具有很高的一致性.
参考文献
| [1] | Bastos M B, Burkhoff D, Maly J, et al. Invasive left ventricle pressure-volume analysis: overview and practical clinical implications[J]. European Heart Journal, 2020, 41(12): 1286-1297. DOI:10.1093/eurheartj/ehz552 |
| [2] | Gotzmann M, Hauptmann S, Hogeweg M, et al. Hemodynamics of paradoxical severe aortic stenosis: insight from a pressure-volume loop analysis[J]. Clinical Research in Cardiology, 2019, 108(8): 931-939. DOI:10.1007/s00392-019-01423-z |
| [3] | Seemann F, Arvidsson P, Nordlund D, et al. Noninvasive quantification of pressure-volume loops from brachial pressure and cardiovascular magnetic resonance[J]. Circulation Cardiovascular Imaging, 2019, 12(1): e008493. |
| [4] | Davidson S, Pretty C, Kamoi S, et al. Beat-by-beat estimation of the left ventricular pressure-volume loop under clinical conditions[J]. Annals of Biomedical Engineering, 2018, 46(1): 171-185. DOI:10.1007/s10439-017-1947-9 |
| [5] | Owashi K P, Hubert A, Galli E, et al. Model-based estimation of left ventricular pressure and myocardial work in aortic stenosis[J]. PloS One, 2020, 15(3): e0229609. DOI:10.1371/journal.pone.0229609 |
| [6] | Bonfanti M, Franzetti G, Maritati G, et al. Patient-specific haemodynamic simulations of complex aortic dissections informed by commonly available clinical datasets[J]. Medical Engineering & Physics, 2019, 71: 45-55. |
| [7] | Olsen C H, Ottesen J T, Smith R C, et al. Parameter subset selection techniques for problems in mathematical biology[J]. Biological Cybernetics, 2019, 113(1): 121-138. |
| [8] | Meiburg R, Huberts W, Rutten M C M, et al. Uncertainty in model-based treatment decision support: applied to aortic valve stenosis[J]. International Journal for Numerical Methods in Biomedical Engineering, 2020, 36(10): e3388. |
| [9] | Rondanina E, Bovendeerd P H M. Stimulus-effect relations for left ventricular growth obtained with a simple multi-scale model: the influence of hemodynamic feedback[J]. Biomechanics and Modeling in Mechanobiology, 2020, 19(6): 2111-2126. DOI:10.1007/s10237-020-01327-2 |
| [10] | IM S. Sensitivity estimates for nonlinear mathematical models[J]. Mathematical Modeling and Computational Experiment, 1993, 1(4): 407-414. |
| [11] | Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1/2/3): 271-280. |
| [12] | Sudret B. Global sensitivity analysis using polynomial chaos expansions[J]. Reliability Engineering & System Safety, 2008, 93(7): 964-979. |
| [13] | Quicken S, Donders W P, van Disseldorp E M J, et al. Application of an adaptive polynomial chaos expansion on computationally expensive three-dimensional cardiovascular models for uncertainty quantification and sensitivity analysis[J]. Journal of Biomechanical Engineering, 2016, 138(12): 121010. |
| [14] | Bratley P, Fox B L. Implementing Sobols quasirandom sequence generator(algorithm 659)[J]. ACM Transactions on Mathematical Software, 2003, 29(1): 49-57. |
| [15] | Willemet M, Chowienczyk P, Alastruey J. A database of virtual healthy subjects to assess the accuracy of foot-to-foot pulse wave velocities for estimation of aortic stiffness[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2015, 309(4): H663-H675. |
