李杰, 贾长旺, 成林海, 赵旗
吉林大学 汽车仿真与控制国家重点实验室，吉林 长春 130025
收稿日期：2021-07-09
基金项目：汽车仿真与控制国家重点实验室自由探索项目(ASCL-Zytsxm-202001)；吉林省省校共建项目(SXGJSF2017-2-1-1)；国家自然科学基金国际(地区)合作与交流重点项目(61520106008)。
作者简介：李杰(1964-)，男，吉林双辽人，吉林大学教授，博士生导师;
赵旗(1967-)，女，吉林长春人，吉林大学研究员。

摘要：为了分析轮毂电机偏心对电动汽车平顺性的影响，建立了考虑轮毂电机质量和轮毂电机激励的电动汽车平面4自由度振动模型，推导出相应的状态方程和输出向量表示，确定了平顺性评价指标.采用滤波白噪声方法建立了随机路面前轮激励，将Laplace变换和4阶对称Pade逼近相结合获得了随机路面后轮激励与随机路面前轮激励的关系，给出了典型的四相8/6极开关磁阻电机整体垂向激励的表示.实现了随机路面激励和轮毂电机激励的仿真，在B级路面上进行了4种工况的随机路面平顺性仿真和比较.结果表明，轮毂电机偏心对随机路面下电动汽车平顺性有着不可忽视的影响，设计电动汽车时需要考虑轮毂电机偏心引入的负效应.
关键词：纯电动汽车平顺性随机路面轮毂电机电机偏心
Influence of In-Wheel Motors' Eccentricity on Ride Comfort of Electric Vehicles on Random Roads
LI Jie, JIA Chang-wang, CHENG Lin-hai, ZHAO Qi
State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130025, China
Corresponding author: LI Jie, E-mail: lj@jlu.edu.cn.

Abstract: To analyze the influence of in-wheel motors' eccentricity on the ride comfort of electric vehicles, a four degree-of-freedom vibration model of electric vehicles was established to consider the mass and excitation of in-wheel motors. The corresponding state equation and output vector expression were derived, and the ride comfort evaluation index was determined. The random road excitation of the front wheel was established by using the filtered white noise method. The random road excitation relationship between the rear wheel and the front wheel was obtained by combining the Laplace transformation and the fourth-order symmetric Pade approximation. The whole vertical excitation of a typical four-phase 8/6-pole switched reluctance motor was presented. The simulation of random road excitation and in-wheel motor excitation was realized, and the ride comfort simulation and comparison of four working conditions were carried out on a B-grade road. The results showed that in-wheel motors' eccentricity has an important influence on the ride comfort of electric vehicles on random roads, and the negative effect of in-wheel motors' eccentricity should be considered in the design of electric vehicles.
Key words: battery electric vehicleride comfortrandom roadin-wheel motormotors' eccentricity
随着国内外对于新能源汽车的重视，加之大数据、智能网联、5G通信、辅助驾驶和车用传感器技术的快速发展，汽车行业迎来巨大的变革.电动汽车作为以上技术发展连接点和重要一环，引起了传统汽车厂商、新型造车势力、互联网技术公司和消费群体的广泛关注^[1-4].
轮毂电机电动汽车具有节能高效、环境友好、结构紧凑和对单个车轮可以独立控制等优点，正在成为新能源汽车的一个研究热点^[5-7].
相较于传统汽车和集中驱动电动汽车，轮毂电机电动汽车直接将电机集成于车轮内，使得非簧载质量增加，对电动汽车平顺性造成直接影响.为了改善轮毂电机对电动汽车平顺性造成的影响，在不改变悬架构型的情况下，已经从电机轻量化^[8]和引入动力吸振结构^[9]等方面开展了相应的研究工作.
然而，以往研究较少考虑轮毂电机偏心对电动汽车平顺性的影响.事实上，制造或者装配都可能造成轮毂电机偏心，即使在制造或装配过程不存在电机偏心，轮毂电机使用磨损也会造成电机偏心.因此，研究电机偏心对轮毂电机电动汽车平顺性的影响具有理论研究价值和实际应用意义.
针对上述问题，在前人研究的基础上，本文开展轮毂电机电动汽车振动模型、路面激励和轮毂电机激励、轮毂电机偏心对平顺性影响的研究，完成从理论分析、程序开发到仿真实现的全部过程，为轮毂电机电动汽车平顺性的改善、优化和控制奠定前期工作基础.
1 轮毂电机电动汽车振动模型1.1 模型描述在传统汽车平面4自由度振动模型基础上^[10]，在前后轴非簧载质量中引入轮毂电机质量，增加电机激励，建立轮毂电机电动汽车平面4自由度振动模型，如图 1所示.
图 1(Fig. 1)

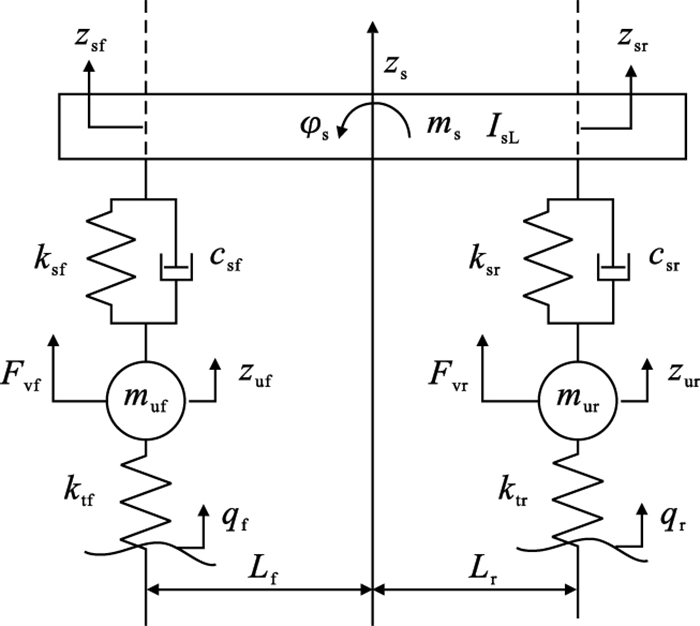图 1 轮毂电机电动汽车平面4自由度振动模型Fig.1 Four degree-of-freedom vibration model of in-wheel motor electric vehicles

在图 1中，m_s和I_sL为车身质量和车身俯仰转动惯量，kg和kg·m²；m_uf和m_ur为包含轮毂电机的前轴和后轴的非簧载质量，kg；k_sf和k_sr为前轴和后轴的悬架刚度，N/m；k_tf和k_tr为前轴和后轴的轮胎刚度，N/m；c_sf和c_sr为前轴和后轴的悬架阻尼，N·s/m；L_f和L_r为车身质心与前轴和后轴的距离，m；F_vf和F_vr为前轴和后轴的轮毂电机激励，N；q_f和q_r为前轮和后轮的路面激励，m；z_s和φ_s为车身的垂向位移和俯仰角位移，m和rad；z_sf和z_sr为前轴和后轴的悬架与车身连接点垂向位移，m；z_uf和z_ur为前轴和后轴的非簧载质量垂向位移，m.
1.2 状态方程基于Lagrange方程，针对z_sf，z_sr，z_uf和z_ur分别建立如下微分方程：

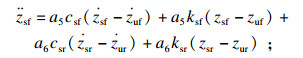(1)

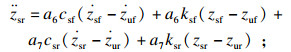(2)

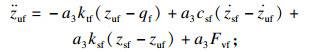(3)

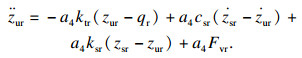(4)

其中：
联立式(1)~式(4)，得到状态方程:

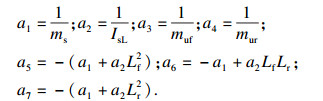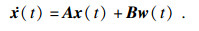(5)

其中：
1.3 输出向量取前悬架动行程z_sf-z_uf、后悬架动行程z_sr-z_ur、前轮动行程z_uf-q_f、后轮动行程z_ur-q_r、车身垂向加速度和车身俯仰角加速度组成输出向量y(t)，其与状态向量x(t)的关系为

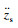
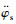
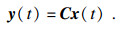(6)

其中:
前轮胎和后轮胎的动载荷F_df和F_dr为

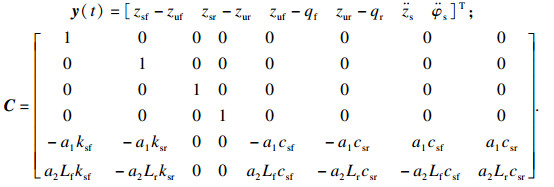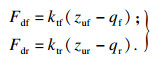(7)

由静态平衡关系可知，前轮胎和后轮胎的静载荷G_f和G_r为

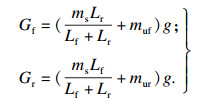(8)

式中，g为重力加速度，m/s².
1.4 评价指标为了保证电动汽车平顺性，取如下响应作为振动响应量：
1) 车身的垂向加速度和俯仰角加速度；
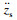
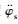
2) 前悬架动行程z_uf-q_f和后悬架动行程z_ur-q_r；
3) 前轮胎相对动载F_df/G_f和后轮胎相对动载F_dr/G_r.
在随机路面下，平顺性评价指标由各个振动响应量的均方根值表示^[11]，即

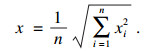(9)

式中：x为振动响应量的均方根值；x_i为振动响应量各个时刻的值；n为采样点个数.
2 随机路面激励和轮毂电机激励2.1 随机路面前轮激励由滤波白噪声方法建立随机路面前轮激励q_f(t)为^[12]

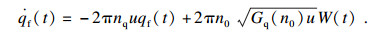(10)

式中：W(t)为理想单位白噪声，其均值为0和功率密度为1；u为车速，m/s；n_q=0.000 1为截止空间频率，m^-1；n₀=0.1为参考空间频率，m^-1；G_q(n₀)为空间参考频率n₀的路面不平度系数，值由路面标准决定^[11].
2.2 随机路面后轮激励当车辆在道路上直线行驶时，假设随机路面前后轮激励输入是相同的^[11]，并且随机路面后轮激励与随机路面前轮激励只是存在一个时间的滞后τ，即

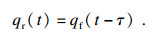(11)

式中，q_r(t)为随机路面后轮激励，m.
滞后时间τ为车辆轴距L与车速u的比值：

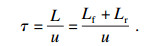(12)

对式(11)进行Laplace变换，有

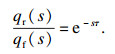(13)

式中：q_f(s)为随机路面前轮激励q_f(t)的Laplace变换，m；q_r(s)为随机路面后轮激励q_r(t)的Laplace变换，m.
对式(13)的右端项，采用4阶对称Pade逼近，再通过Laplace逆变换得到q_r(t)和q_f(t)的关系^[13]，有

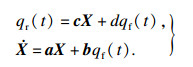(14)

其中：
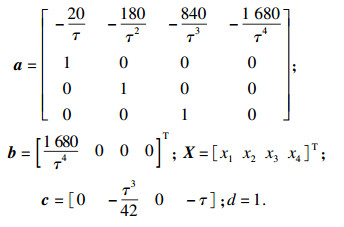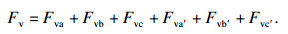2.3 轮毂电机激励轮毂电机主要有永磁同步电机、开关磁阻电机、异步电机和横向磁场电机等^[14].开关磁阻电机具有简单可靠、运行效率高等优点，但其转矩波动较大、振动噪声大.因此，选择开关磁阻电机作为研究对象^[15].典型的四相8/6极开关磁阻电机及其一组开关电路，如图 2所示.在对电机进行一定的假设条件下，某一时刻下电机整体垂向激励为单相转子垂向力之和^[16]，即

(15)

图 2(Fig. 2)

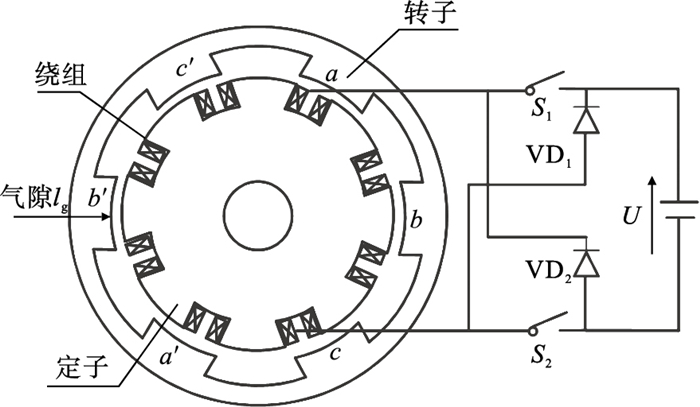图 2 四相8/6极开关磁阻电机结构Fig.2 Four-phase 8/6 pole switched reluctance motor construction

式中：F_va，F_va′，F_vb，F_vb′，F_vc和F_vc′分别为单相转子的垂向力，N；a和a′，b和b′，c和c′为轮毂电机中对应的转子.
单相转子的垂向力为^[13]

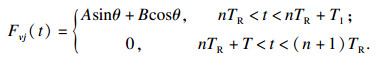(16)

其中：j=a, b, c, a′, b′, c′;
式中：i为电机电流，A；L_min为最小电感，H；b为电机气隙，m；e为定子和转子的偏心距, m；K为电感上升斜率，H/rad；R为转子内半径，m；r为定子外半径，m；T_R为单相转子转动周期，s；ω为电机转动角速度，rad/s；θ_int为各相转子初始位置，rad；φ为各定子绕组的相位角，rad.
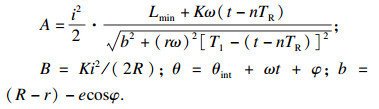3 轮毂电机偏心对平顺性的影响3.1 随机路面激励仿真基于随机路面激励的描述，开发了随机路面前轮和后轮的激励Matlab/Simulink仿真模型.其中，白噪声序列使用Simulink的【Band-Limited White Noise】模块生成，采用Runge-Kutta方法求解式(10)和式(14).
选取路面等级为B级路面，取所研究电动汽车的轴距为2.76 m，车速为40 km/h，仿真时间为20 s，步长为0.001 s.随机路面前轮和后轮的激励，如图 3所示.
图 3(Fig. 3)

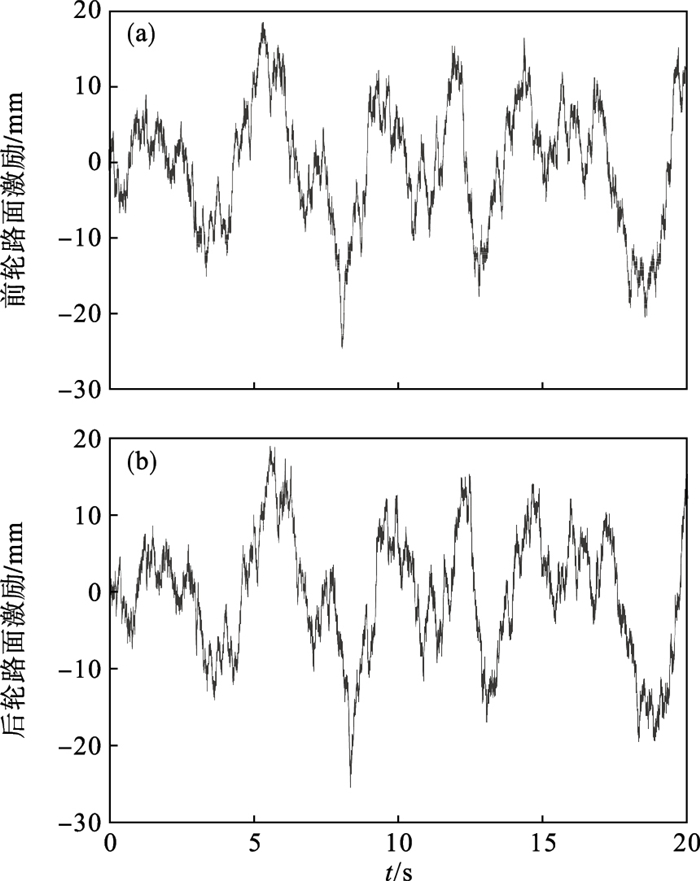图 3 B级路面前轮和后轮的激励Fig.3 B-grade road excitation of the front and rear wheels (a)—前轮路面激励；(b)—后轮路面激励.

由图 3可知，本文所建立的前轮和后轮的B级随机路面激励是随机变化的，符合随机路面激励变化规律.
3.2 轮毂电机激励仿真基于轮毂电机激励的描述，开发了开关磁阻电机激励Matlab/Simulink仿真模型.
设偏心距e=(R-r)·e_r，其中e_r是以百分率表示的偏心率.分别取e_r=0和e_r=10%两种情况，前者对应于电机无偏心情况，后者对应于电机偏心情况，取某开关磁阻电机参数^[13]，两种情况的电机偏心激励，如图 4所示.
图 4(Fig. 4)

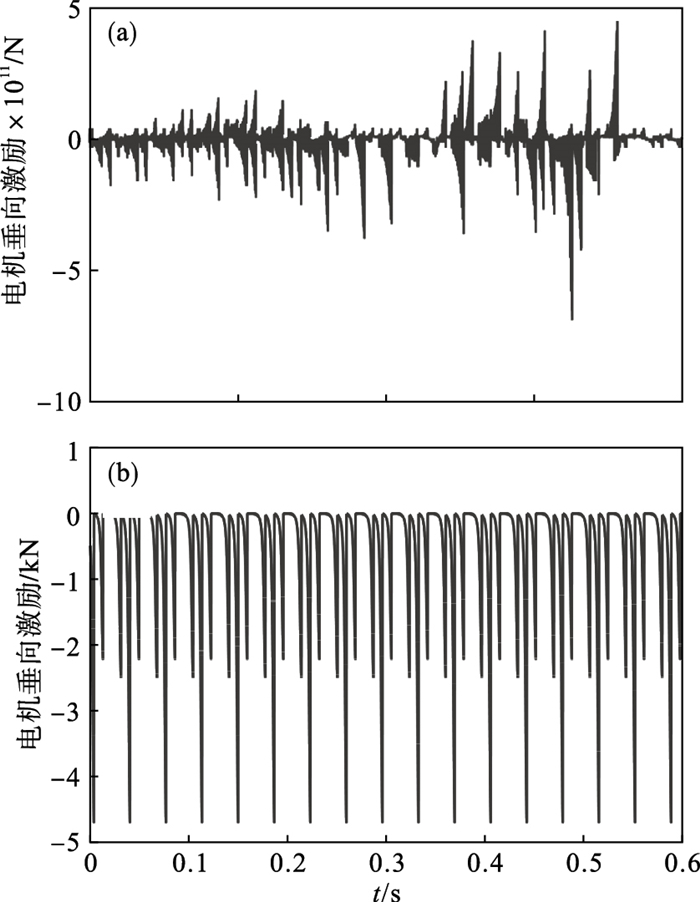图 4 两种情况的轮毂电机偏心激励Fig.4 Eccentric excitation of in-wheel motors in two cases (a)—无偏心；(b)—偏心率10%.

由图 4可知，当电机不存在偏心时，由于各处气隙相同，电机垂向激励几乎为零，即电机不存在垂向激励；当电机转子和定子存在偏心时，由于各处气隙不同，电机产生单一方向的垂向激励.所以，在理想情况下，电机定子和转子圆心重合不存在偏心，即e=0.在电机使用过程中，由于磨损等原因，使得定子和转子产生偏心，即e≠0，造成气隙变化，导致电机产生不平衡的电机垂向激励.
3.3 平顺性仿真基于轮毂电机电动汽车振动模型，开发了轮毂电机电动汽车平顺性Matlab/Simulink仿真模型.
在B级路面上，采用某轮毂电机电动汽车参数，设定如下4种情况：
1) 前后轮无偏心，简称无偏心；
2) 前轮偏心而后轮无偏心，简称前轮偏心；
3) 前轮无偏心而后轮偏心，简称后轮偏心；
4) 前后轮偏心，简称双轮偏心.
在车速60 km/h时，针对上述4种情况进行仿真，可得到4种情况的车身垂向加速度、车身俯仰角加速度、前悬架动行程、后悬架动行程、前轮胎相对动载和后轮胎相对动载的时间历程.车身垂向加速度、前悬架动行程和前轮胎相对动载的无偏心与双轮偏心的结果对比，车身俯仰角加速度、后悬架动行程和后轮胎相对动载的前轮偏心与后轮偏心的结果对比，如图 5所示.
图 5(Fig. 5)

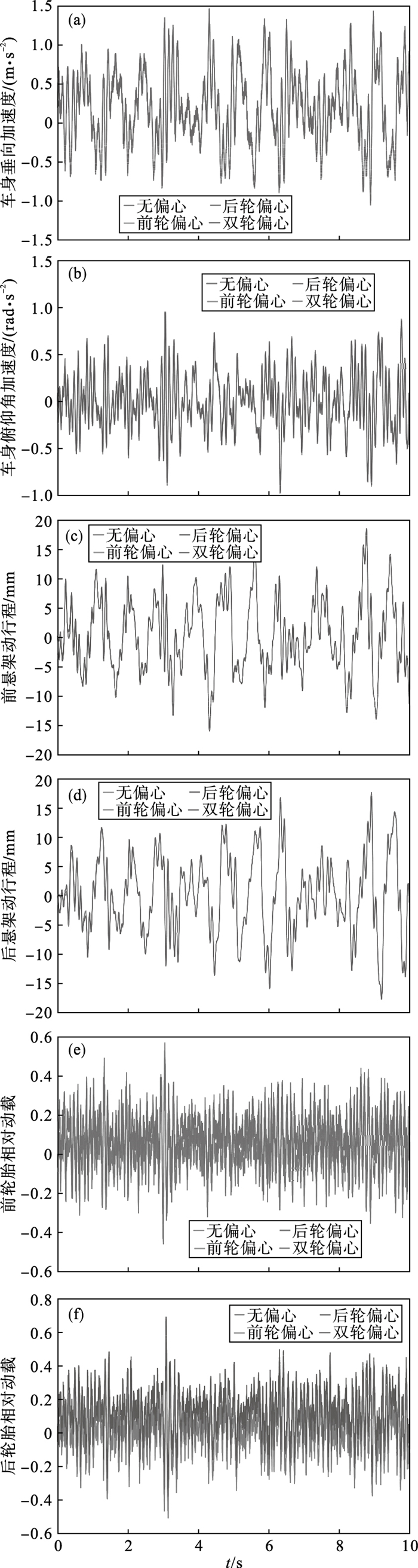图 5 B级路面60 km/h时4种情况的振动响应量Fig.5 Vibration responses of the B-grade road under four conditions at 60 km/h (a)—车身垂向加速度；(b)—车身俯仰角加速度；(c)—前悬架动行程；(d)—后悬架动行程；(e)—前轮胎相对动载；(f)—后轮胎相对动载.

由图 5可知，4种情况的各个振动响应量都随着时间变化而变化.
以1 km/h为增量，使车速由1 km/h变化到80 km/h，上述4种情况的评价指标与车速的变化关系，即振动响应量均方根值与车速的变化关系，如图 6所示.
图 6(Fig. 6)

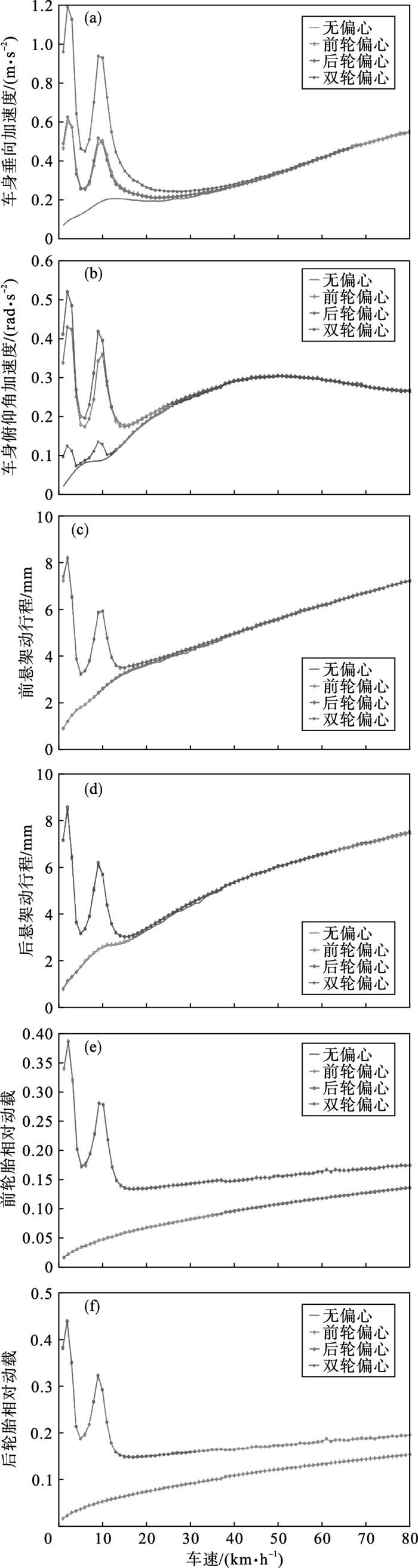图 6 B级路面不同速度时4种情况的评价指标Fig.6 Evaluation indexes of the B-grade road under four conditions at different speeds (a)—车身垂向加速度；(b)—车身俯仰角加速度；(c)—前悬架动行程；(d)—后悬架动行程；(e)—前轮胎相对动载；(f)—后轮胎相对动载.

由图 6可知，在B级路面和不同速度下，轮毂电机电动汽车不同位置的电机偏心对评价指标有着不同的影响.
1) 不同的电机偏心对车身垂向加速度都有影响，在速度4 km/h和10 km/h左右时有峰值；在速度小于35 km/h时，不同的电机偏心都使车身垂向加速度增大，其中双轮同时偏心影响最大；在速度大于35 km/h时，近似于无偏心.
2) 不同的电机偏心对车身俯仰角加速度都有影响，在速度4 km/h和10 km/h左右时有峰值，其中前轮偏心和后轮偏心影响较大；在速度小于20 km/h时，相较于正常悬架增大；在速度大于20 km/h时，近似于无偏心.
3) 前轮偏心和双轮偏心对前悬架动行程有影响，在速度4 km/h和10 km/h左右时有峰值；在速度小于20 km/h时，前轮偏心和双轮偏心时大于无偏心；在速度大于20 km/h时，近似于无偏心；后轮偏心对前悬架动行程影响较小.
4) 后轮偏心和双轮同时偏心对后悬架动行程有影响，在速度4 km/h和10 km/h左右时有峰值；在速度小于20 km/h时，后轮偏心和双轮偏心大于无偏心；在速度大于20 km/h时，近似于无偏心；前轮偏心对后悬架动行程影响较小.
5) 前轮偏心和双轮偏心对前轮胎相对动载有影响，在速度4 km/h和10 km/h左右时有峰值；其他速度范围内大于无偏心；后轮偏心时，对前轮相对动载影响较小.
6) 后轮偏心和双轮偏心对后轮胎相对动载有影响，在速度4 km/h和10 km/h左右时有峰值；其他速度范围内大于无偏心；前轮偏心对后轮胎相对动载影响较小.
4 结语建立了轮毂电机电动汽车平面4自由度振动模型，可用于分析电机质量、电机偏心和路面对电动汽车平顺性的影响.采用Matlab/Simulink分别开发了相应的轮毂电机电动汽车平顺性仿真模型，可以实现前轮和后轮的随机路面激励、轮毂电机激励和轮毂电机电动汽车随机路面平顺性仿真.结果表明，电机偏心对轮毂电机电动汽车振动性能有着不可忽视的影响，也体现了轮毂电机电动汽车与传统汽车的平顺性不同.
参考文献

[1]	马建, 刘晓东, 陈轶嵩, 等. 中国新能源汽车产业与技术发展现状及对策[J]. 中国公路学报, 2018, 31(8): 1-19. (Ma Jian, Liu Xiao-dong, Chen Yi-song, et al. Current status and counter measures for China's new energy automobile industry and technology development[J]. China Journal of Highway and Transportation, 2018, 31(8): 1-19. DOI:10.3969/j.issn.1001-7372.2018.08.001)
[2]	万钢. 新时代推进我国新能源汽车发展的新思考[J]. 汽车工程学报, 2018, 8(4): 235-238. (Wan Gang. New thoughts on promoting the development of China's new energy vehicles in the new era[J]. Chinese Journal of Automotive Engineering, 2018, 8(4): 235-238. DOI:10.3969/j.issn.2095-1469.2018.04.01)
[3]	李琳辉, 张鑫亮, 连静, 等. 多因素影响下的纯电动汽车电耗算法优化[J]. 东北大学学报(自然科学版), 2022, 43(2): 228-235. (Li Lin-hui, Zhang Xin-liang, Lian Jing, et al. Optimization of power consumption algorithm for pure electric vehicle under the influence of multiple factors[J]. Journal of Northeastern University(Natural Science), 2022, 43(2): 228-235.)
[4]	纪东, 吕鸣松, 王义. 工作场所光伏电动汽车充电站可行性研究[J]. 东北大学学报(自然科学版), 2019, 40(6): 783-788. (Ji Dong, Lyu Ming-song, Wang Yi. Feasibility study on photovoltaic electric vehicle charging station for workplace[J]. Journal of Northeastern University(Natural Science), 2019, 40(6): 783-788.)
[5]	丁晓林, 王震坡, 张雷. 四轮轮毂电机驱动电动汽车驱动系统参数多目标优化匹配[J]. 机械工程学报, 2021, 57(8): 195-204. (Ding Xiao-lin, Wang Zhen-po, Zhang Lei. Powertrain sizing for four-wheel-independent-actuated electric vehicles based on multi-objective optimization[J]. Journal of Mechanical Engineering, 2021, 57(8): 195-204.)
[6]	王军年, 刘鹏, 杨钫, 等. 轮毂电机驱动电动汽车双横臂前悬架运动学优化[J]. 汽车工程, 2021, 43(3): 305-312. (Wang Jun-nian, Liu Peng, Yang Fang, et al. Kinematics optimization of double wishbone front suspension for in-wheel-motor-driven electric vehicles[J]. Automotive Engineering, 2021, 43(3): 305-312.)
[7]	成林海, 周淑辉, 郑玲玲, 等. 轮毂电机驱动电动汽车3种构型的平顺性分析[J]. 汽车工程学报, 2021, 11(3): 171-177. (Cheng Lin-hai, Zhou Shu-hui, Zheng Ling-ling, et al. Ride comfort analysis of three configurations of electric vehicles driven by in-wheel motors[J]. Chinese Journal of Automotive Engineering, 2021, 11(3): 171-177. DOI:10.3969/j.issn.2095-1469.2021.03.03)
[8]	韩以伦, 李国珊, 王强, 等. 基于垂向振动负效应的新型轮毂电机电动汽车平顺性影响[J]. 科学技术与工程, 2019, 19(16): 363-369. (Han Yi-lun, Li Guo-shan, Wang Qiang, et al. Ride comfort of a new in-wheel motor driving electric vehicle based on the negative effect of vertical vibration[J]. Science Technology and Engineering, 2019, 19(16): 363-369. DOI:10.3969/j.issn.1671-1815.2019.16.057)
[9]	Nagaya G. Development of an in-wheel drive with advanced dynamic-damper mechanism[J]. JSAE Review, 2003, 24(4): 477-481. DOI:10.1016/S0389-4304(03)00077-8
[10]	林逸, 俞凡. 汽车系统动力学[M]. 北京: 机械工业出版社, 2016. (Lin Yi, Yu Fan. Vehicle system dynamics[M]. Beijing: China Machine Press, 2016.)
[11]	余志生. 汽车理论[M]. 北京: 机械工业出版社, 2009. (Yu Zhi-sheng. Automobile theory[M]. Beijing: China Mechine Press, 2009.)
[12]	赵旗, 王培德, 罗兰, 等. 路面激励Simulink模型的建立及其应用[J]. 科学技术与工程, 2018, 18(1): 128-132. (Zhao Qi, Wang Pei-de, Luo Lan, et al. Establishment of Simulink model for road excitation and its application[J]. Science Technology and Engineering, 2018, 18(1): 128-132.)
[13]	陈少帅. 基于磁流变减振器逆模型的轮毂电机式电动汽车悬架控制研究[D]. 长春: 吉林大学, 2019. (Chen Shao-shuai. Research on suspension control of electric vehicle with in-wheel motor based on magnetorheological damper inverse model[D]. Changchun: Jilin University, 2019. )
[14]	李勇, 徐兴, 孙晓东, 等. 轮毂电机驱动技术研究概况及发展综述[J]. 电机与控制应用, 2017, 44(6): 1-7. (Li Yong, Xu Xing, Sun Xiao-dong, et al. Review and future development of in-wheel-motor drive technology[J]. Electric Machines & Control Application, 2017, 44(6): 1-7. DOI:10.3969/j.issn.1673-6540.2017.06.001)
[15]	高雄. 轮边电机驱动中巴客车平顺性分析与多目标优化[D]. 长春: 吉林大学, 2019. (Gao Xiong. Analysis and multi-objective optimization of ride comfort for wheel-side motor drived medium bud[D]. Changchun: Jilin University, 2019. )
[16]	李杰, 高雄, 王培德, 等. 路面和开关磁阻电机作用下电动汽车振动分析[J]. 湖南大学学报(自然科学版), 2018, 45(8): 7-14. (Li Jie, Gao Xiong, Wang Pei-de, et al. Vibration analysis of electric vehicle under the action of road and switched reluctance motor[J]. Journal of Hunan University(Natural Science), 2018, 45(8): 7-14.)