张旭¹, 吕建起¹, 李伟², 李小彭³
1. 天津工业大学 天津市现代机电装备技术重点实验室，天津 300387;
2. 天津城建大学 能源与安全工程学院，天津 300384;
3. 东北大学 机械工程与自动化学院，辽宁 沈阳 110819
收稿日期：2021-06-22
基金项目：国家自然科学基金资助项目(51805369); 天津市科技计划项目(20YDTPJC00820)。
作者简介：张旭(1978-), 女, 河北安平人, 天津工业大学教授;
李小彭(1976-), 男, 江西宁都人, 东北大学教授, 博士生导师。

摘要：为了准确识别复合材料损伤的位置和程度，提出一种以模态曲率差幂函数为损伤指标的新检测方法.基于ANSYS的APDL语言，应用Shell181单元建立简支层合板模型，并通过Camanho损伤准则构建层内纤维失效模型.利用模态分析获得层合板的固有频率及网格节点模态位移，应用差分法得到曲面的高斯曲率，研究损伤前后高斯曲率差随损伤位置和程度的变化规律.采用高斯曲率差的平方增加峰值与其他区域的差距，将其定义为模态位移不平整系数并进行层内损伤位置和程度检测.结果表明：模态位移不平整系数使损伤位置检测的准确性提高，且随损伤程度的增加而增大.研究结论为改进复合材料层合板层内损伤的无损检测方法提供指导.
关键词：复合材料层内损伤模态分析高斯曲率不平整系数
An Unevenness Coefficient Method of Modal Displacements for Intra-laminar Damage Detection in Composite Laminates
ZHANG Xu¹, LYU Jian-qi¹, LI Wei², LI Xiao-peng³
1. Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology, Tiangong University, Tianjin 300387, China;
2. School of Energy and Safety Engineering, Tianjin Chengjian University, Tianjin 300384, China;
3. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: LI Wei, E-mail: anplw@126.com.

Abstract: A new detection method using the power function of modal curvature differences as damage index was proposed to accurately identify the location and extent of composite material damage. Based on the APDL language of ANSYS, the Shell181 element was used to establish the simply supported laminate model, and the intra-laminar fiber failure model was constructed according to the Camanho damage criterion. The natural frequency of the laminate and the modal displacement of mesh nodes were obtained by modal analysis. The Gaussian curvature of the surface was obtained by the difference method, and the change of the Gaussian curvature difference before and after damage with the damage location and extent was studied. The square of the Gaussian curvature difference was used to increase the gap between the peak value and that of the other regions, which was defined as the modal displacement unevenness coefficient to detect the intra-laminar damage location and extent. The results show that the modal displacement unevenness coefficient improves the accuracy of the damage location detection, and it increases with the rise of the damage extent. The research conclusions provide guidance for improving the non-destructive testing methods for the intra-laminar damage of composite laminates.
Key words: composite materialintra-laminar damagemodal analysisGaussian curvatureunevenness coefficient
复合材料层合板在高速冲击载荷作用下，容易发生层内损伤和层间分层，导致强度和刚度明显降低，使用寿命减少^[1-2].通过X光射线、超声波、模态等分析方法，可以实现对复合材料的无损检测^[3].X光射线对于不透射线液体无法渗透到的区域难以进行损伤检测，超声波由于不能提供足够宽的反射表面，难以识别垂直于表面的损伤.鉴于层合板损伤后几何形状均会发生改变，模态分析可将几何外形与材料性能的耦合变换到模态空间进行解耦，可用其识别前面两种方法不能检测的损伤.当层合板仅发生单层或双层损伤时，直接利用模态参数很难准确确定损伤的位置和程度.因此，构建具有高精确性的模态特征损伤检测指标，对完善层合板损伤的无损检测方法具有重要的理论意义和工程应用价值.
国内外****针对模态方法检测复合材料损伤开展了一系列研究.Santos等^[4]、Qiao等^[5]以层合板损伤前后的模态位移差作为损伤指标，研究其随损伤位置的变化规律.Lestari等^[6]采用模态实验提取梁的模态位移，分析损伤前后的曲率差与损伤位置的关系.Hu等^[7]通过分离单元节点的位置建立含裂纹的层合板模型，并以出现裂纹前后的应变能比值为指标进行损伤检测.Hui等^[8]改变层合板的局部刚度，建立基体失效和纤维失效的模型，利用模态曲率检测损伤.Zhang等^[9]应用固有频率检测层间分层梁的损伤位置和程度.Roy等^[10]针对悬臂剪切梁，研究模态振型与损伤程度的关系.Dessi等^[11]采用折减局部刚度建立损伤的欧拉- 伯努利梁，分析固有频率和损伤前后的模态曲率差随损伤位置变化的规律.Montalvao等^[12]对通过降低杨氏模量建立的损伤层合板进行模态分析，探究阻尼比、总刚度随损伤程度的变化趋势.Chandrashekhar等^[13]应用无剪切变形的壳单元建立4个不同损伤程度的层合板，并分析损伤程度对固有频率和模态位移的影响.Govindasamy等^[14]利用模态位移计算层合板的模态曲率，并用其检测含有不同长度和深度裂纹的层合板.上述研究多是利用固有频率、模态位移和模态曲率的变化量进行损伤检测，但固有频率仅能反映是否发生损伤且模态位移及其曲率的改变也只能检测几何外形或弹性模量变化较大的损伤.
鉴于此，本文提出一种以模态位移不平整系数检测损伤程度较小层合板的新方法.利用Camanho损伤准则，建立层内纤维失效的简支层合板模型；基于模态分析，提取层合板的模态位移，通过差分法得到曲面的高斯曲率；定义损伤前后高斯曲率差的平方为损伤指标，检测层合板的纤维失效.
1 层合板层内损伤模型建立1.1 层合板建模层合板的有限元模型如图 1所示.基于ANSYS的APDL语言，建立0.4 m×0.1 m×0.002 m的层合板几何模型，如图 1a所示.利用Shell181单元划分网格，采用碳/环氧预浸料(T700/M21)依次进行纤维角度为0°，90°，0°，90°，90°，0°，90°，0°的铺层，约束层合板四边的法向自由度U_Z和切向自由度U_X/U_Y，如图 1b所示.各铺层厚度为0.000 25 m，预浸料属性^[15]如表 1所示.
图 1(Fig. 1)

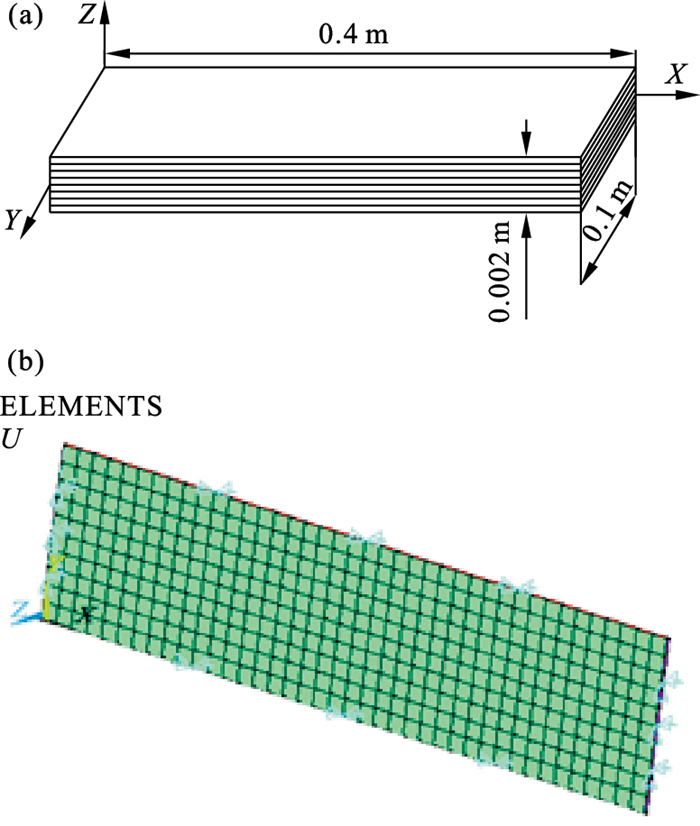图 1 层合板的有限元模型Fig.1 Finite element model of the laminates (a)—几何模型；(b)—有限元模型.

表 1(Table 1)

表 1 T700/M21的材料属性Table 1 Material properties of T700/M21 材料属性 数值 每层厚度/m 0.000 25 弹性模量/MPa EX=130 324，EY=7 680，EZ=7 680 泊松比 υXY=0.33，υXZ=0.33，υYZ=0.4 剪切模量/MPa GXY=4 750，GXZ=4 750，GYZ=2 742 密度/(kg·m-3) 1 550

表 1 T700/M21的材料属性 Table 1 Material properties of T700/M21

应用上述有限元建模方法，采用与文献[16]相同的几何尺寸、预浸料、铺层方式、网格大小和边界约束，进行无损板的模态分析，结果如表 2所示.由于层合板在低阶频率容易发生共振，故选取模态阶次的扩展数为6.可知，计算所得固有频率虽与文献[16]存在一定误差，但均小于0.95%.造成误差的原因是本文选用四节点壳单元，而文献采用实体单元，单元不同导致网格划分后的节点分布不同，以至于位移矩阵排布出现微小差异.壳单元适用于分层结构的细长薄板，且无剪切变形的壳截面可减少模态位移提取的不确定性，因此本文采用的单元更合适.
表 2(Table 2)

表 2 本文和文献[16]给出的无损板固有频率Table 2 Natural frequencies of the non-destructive laminates in this paper and Ref.[16] 阶次 固有频率/Hz 误差/% 本文结果 文献[16]结果 一阶 49.981 50.03 0.098 二阶 100.78 101.42 0.63 三阶 133.33 134.61 0.95 四阶 142.80 143.55 0.52 五阶 166.20 166.83 0.37 六阶 264.11 265.87 0.66

表 2 本文和文献[16]给出的无损板固有频率 Table 2 Natural frequencies of the non-destructive laminates in this paper and Ref.[16]

1.2 层合板层内损伤模型建立依据Camanho损伤准则^[2]，层合板发生纤维拉伸和压缩失效后的弹性模量E₁₁^S和E₁₁^C分别折减为

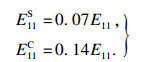(1)

简支层合板的一阶、二阶振型如图 2所示.将前两层、第一层纤维分别设置为拉伸、压缩失效，损伤位于以前两阶振型极点或非振型极点为中心且边长为0.02 m的正方形区域内，如图 3所示.层合板层内损伤工况如表 3所示.
图 2(Fig. 2)

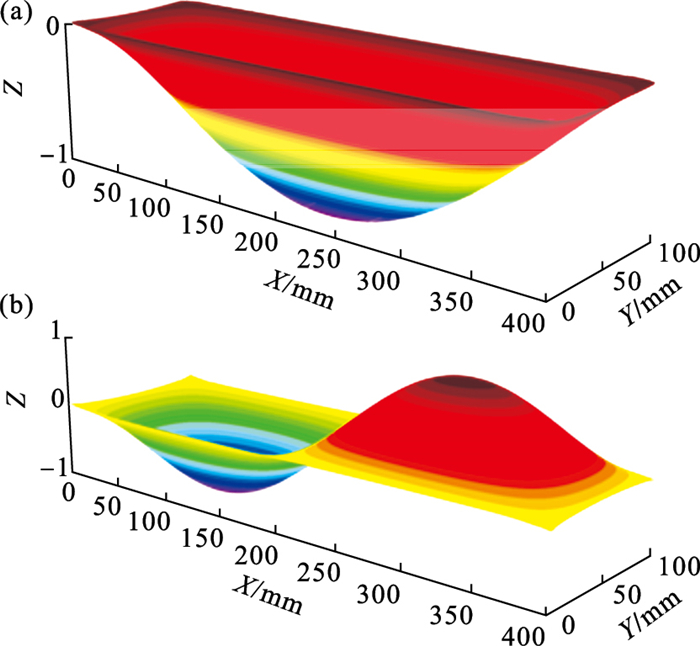图 2 简支层合板的前两阶振型Fig.2 First two modes of simply supported laminate (a)—一阶振型；(b)—二阶振型.

图 3(Fig. 3)

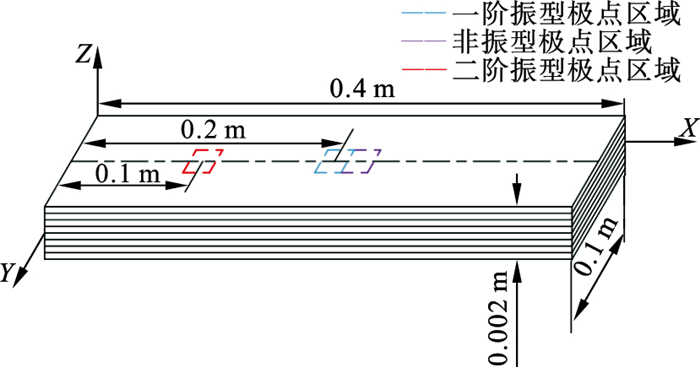图 3 层合板纤维失效位置Fig.3 Fiber failure location of the laminates

表 3(Table 3)

表 3 层合板层内损伤工况Table 3 Intra-laminar damage condition of the laminates 损伤工况 损伤位置 损伤层 弹性模量 工况1 {(X1，Y1)| 0.19≤X1≤0.21，0.04≤Y1≤0.06} 第1，2层 E11S=0.07E11 工况2 {(X2，Y2)| 0.21≤X2≤0.23，0.04≤Y2≤0.06} 第1，2层 E11S=0.07E11 工况3 {(X3，Y3)| 0.09≤X3≤0.11，0.04≤Y3≤0.06} 第1，2层 E11S=0.07E11 工况4 {(X4，Y4)| 0.19≤X4≤0.21，0.04≤Y4≤0.06} 第1层 E11C=0.14E11 工况5 {(X5，Y5)| 0.21≤X5≤0.23，0.04≤Y5≤0.06} 第1层 E11C=0.14E11 工况6 {(X6，Y6)| 0.09≤X6≤0.11，0.04≤Y6≤0.06} 第1层 E11C=0.14E11

表 3 层合板层内损伤工况 Table 3 Intra-laminar damage condition of the laminates

1.3 网格敏感性分析与损伤边界处理方式为分析网格大小对固有频率的影响，分别以0.005，0.01，0.015，0.02，0.025，0.03，0.035，0.04 m为边长进行未损伤层合板的网格划分，如图 4所示.可以看出，固有频率在网格边长为0.005 ~0.015 m时趋于稳定，故选用边长为0.01 m的四边形网格.
图 4(Fig. 4)

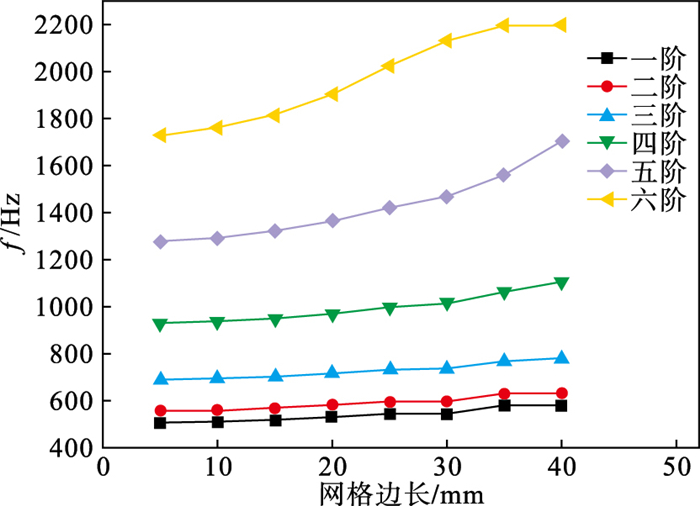图 4 不同网格边长下的固有频率Fig.4 Natural frequencies for different mesh sizes

以黏接和工作平面切分图素两种方式分别进行层合板损伤区域的边界处理，不同损伤边界处理方式下层合板的固有频率如图 5所示.
图 5(Fig. 5)

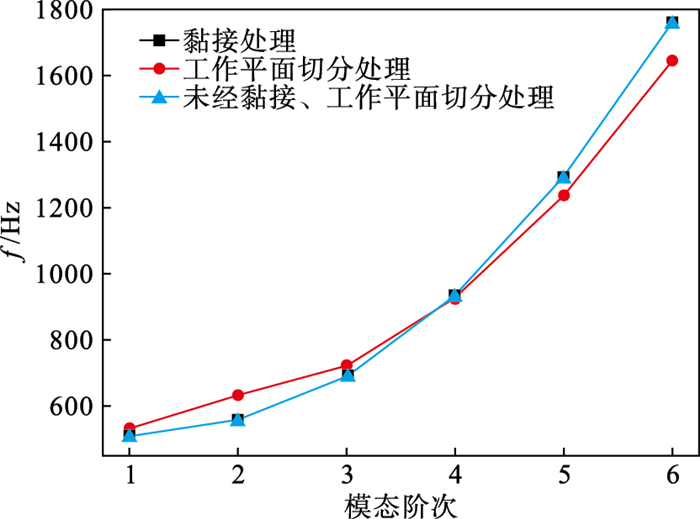图 5 不同损伤边界处理方式下层合板的固有频率Fig.5 Natural frequencies of the laminates for different damage boundary treatments

黏接方式的结果与原简支层合板的前六阶固有频率相同，依次均为510.05，559.36，691.66，935.55，1 293.7，1 760.6 Hz.表明此方式处理损伤边界接触不会改变模态结果，故选用黏接的处理方式.
2 模态位移曲率分析2.1 固有频率与模态位移分析对具有不同损伤位置和程度的层合板进行模态分析，不同损伤工况下层合板的固有频率如表 4所示.可知，对于具有相同损伤位置的工况，固有频率随损伤程度的增加而减少；对于具有相同损伤程度的工况，固有频率在同一阶次随损伤位置的改变并不明显，变化率均小于1.09%.
表 4(Table 4)

表 4 不同损伤工况下层合板的固有频率Table 4 Natural frequencies of the laminates under different damage conditions 损伤工况 固有频率/Hz 一阶 二阶 三阶 四阶 五阶 六阶 无损板 510.05 559.36 691.66 935.55 1 293.7 1 760.6 工况1 504.51 559.32 685.13 935.25 1 281.5 1 759.3 工况2 504.53 559.19 685.47 934.44 1 283.2 1 756.1 工况3 507.00 553.95 688.43 935.25 1 287.1 1 744.1 工况4 510.04 559.35 689.47 935.37 1 284.9 1 759.6 工况5 510.04 559.34 689.59 934.90 1 286.1 1 757.1 工况6 510.04 558.83 690.55 935.37 1 289.0 1 747.5

表 4 不同损伤工况下层合板的固有频率 Table 4 Natural frequencies of the laminates under different damage conditions

归一化处理模态位移，并将损伤前后的差值拟合成三维曲面.由于高阶振型很难被激励起来，故图 6只给出一阶、二阶时的结果.可以看出，仅工况3，6在一阶模态和工况5，6在二阶模态检测出实际损伤的位置，且对于损伤位置相同的工况3，6，一阶模态位移差随损伤程度的降低而减小.该指标峰值与损伤位置的重合性较低且无规律性.
图 6(Fig. 6)

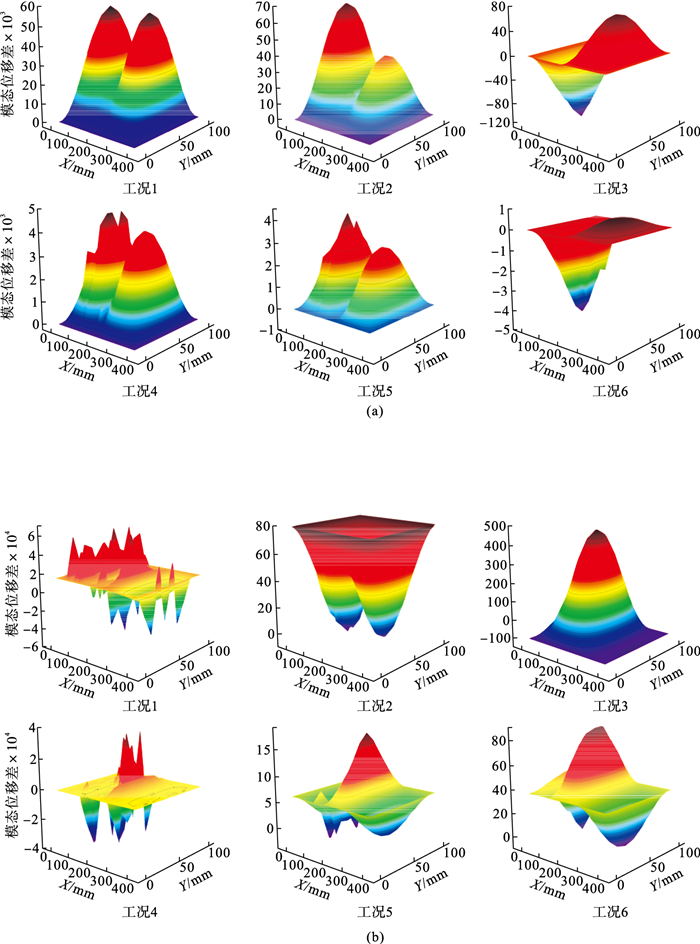图 6 不同损伤工况下的模态位移差Fig.6 Modal displacement differences under different damage conditions (a)—一阶模态位移差；(b)—二阶模态位移差.

2.2 高斯曲率分析鉴于模态位移差检测层合板损伤的准确性较低，故构建损伤前后模态位移高斯曲率差为检测指标并进行效果分析.采用中心差分法求得三维曲面的高斯曲率K为

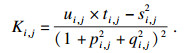(2)

式中：p_{i, j}, q_{i, j}, u_{i, j}, s_{i, j}, t_{i, j}为网格节点模态位移的一阶、二阶偏导数，, w_i，j为节点(i，j)归一化后的模态位移，Δx，Δy分别为网格的长度和宽度.
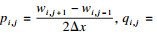
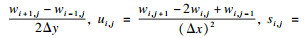
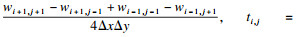
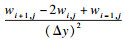
计算层合板一阶、二阶模态位移的高斯曲率，并将损伤前后的差值拟合为等势图，如图 7所示.可知，工况1，2，4，5在一阶模态和工况3，6在二阶模态的高斯曲率差的峰值与实际损伤位置的重合性较高；对于损伤位置相同的层合板，高斯曲率差的峰值在一阶、二阶振型时均随损伤程度的降低而降低.由于工况1，2，4，5的等势图在损伤位置等势线不集中，工况3，6在另一个二阶振型极点(未发生损伤)也存在峰值，干扰了损伤区域的准确识别.
图 7(Fig. 7)

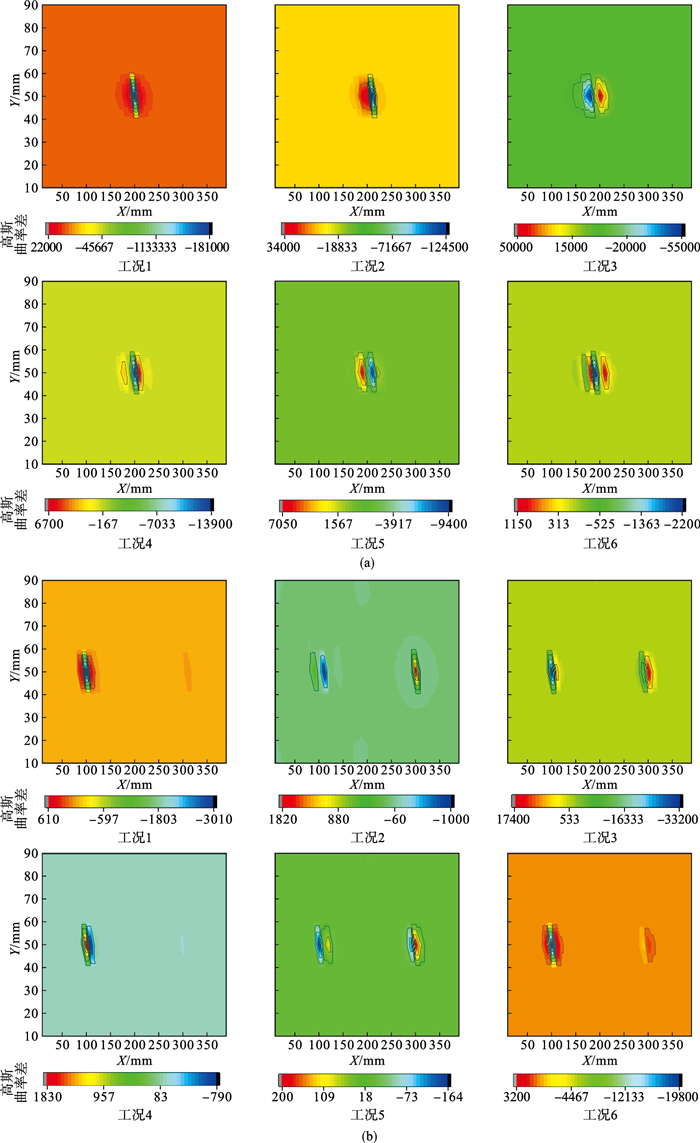图 7 不同损伤工况下的高斯曲率差Fig.7 Gaussian curvature differences under different damage conditions (a)—一阶模态高斯曲率差；(b)—二阶模态高斯曲率差.

3 模态位移不平整系数检测损伤3.1 模态位移不平整系数建立为减小模态位移高斯曲率差等势图中损伤位置周围等势线发散以及其他略小峰值的干扰，构建高斯曲率差的幂函数使峰值与其他区域的差距更为明显.定义层合板损伤前后模态位移高斯曲率差的平方为不平整系数V_i，j：

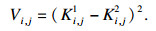(3)

式中，K_i，j¹，K_i，j²分别为损伤前后模态位移的高斯曲率.
3.2 模态位移不平整系数分析计算工况1，2，4，5在一阶模态和工况3，6在二阶模态的模态位移不平整系数，并绘制图 8所示的等势图.可以看出，工况1，2，4在一阶模态和工况6在二阶模态的模态位移不平整系数的峰值与实际损伤位置完全重合，工况5，3的等势图分别在一阶振型极点和另一个二阶振型极点(未发生损伤)周围均存在较小峰值，但损伤识别的干扰却减弱了.模态位移不平整系数随损伤程度的增加而增大.
图 8(Fig. 8)

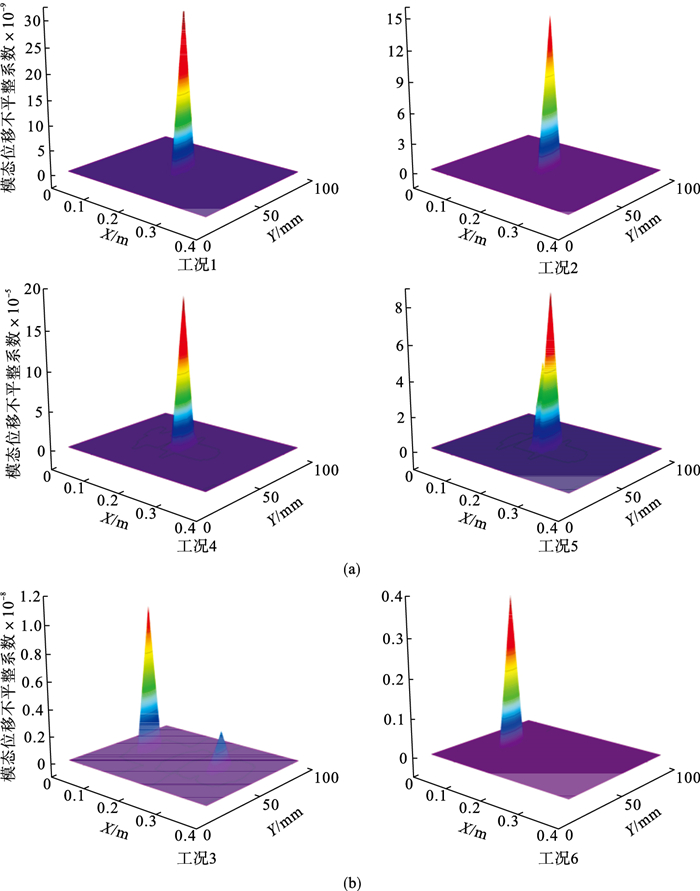图 8 不同损伤工况下的模态位移不平整系数Fig.8 Unevenness coefficients of modal displacements under different damage conditions (a)—一阶模态位移不平整系数；(b)—二阶模态位移不平整系数.

4 结论1) 利用固有频率的变化仅能判断层合板是否发生损伤，但通过模态位移差可以部分识别层合板损伤的位置和程度.
2) 高斯曲率差可以在某阶模态检测出位于该阶振型极点附近的损伤，且随损伤程度的降低而降低，但受到等势线发散和未损伤位置出现峰值的干扰.
3) 利用模态位移不平整系数提高了层合板损伤位置的识别准确性，且该检测指标随损伤程度的增加而增大.
参考文献

[1]	Zhao Y, Noori M, Altabey W A, et al. A fatigue damage model for FRP composite laminate systems based on stiffness reduction[J]. Structural Durability and Health Monitoring, 2019, 13(1): 85-103. DOI:10.32604/sdhm.2019.04695
[2]	Camanho P P, Matthews F L. A progressive damage model for mechanically fastened joints in composite laminates[J]. Journal of Composite Materials, 1999, 33(24): 2248-2280. DOI:10.1177/002199839903302402
[3]	Aymerich F, Meili S. Ultrasonic evaluation of matrix damage in impacted composite laminates[J]. Composites Part B: Engineering, 2000, 31(1): 1-6. DOI:10.1016/S1359-8368(99)00067-0
[4]	Santos J V A, Lopes H M R, Vaz M, et al. Damage localization in laminated composite plates using mode shapes measured by pulsed TV holography[J]. Composite Structures, 2006, 76(3): 272-281. DOI:10.1016/j.compstruct.2006.06.034
[5]	Qiao P Z, Kan L, Lestari W, et al. Curvature mode shape-based damage detection in composite laminated plates[J]. Steel Construction, 2006, 80(3): 409-428.
[6]	Lestari W, Qiao P Z, Hanagud S. Curvature mode shape-based damage assessment of carbon/epoxy composite beams[J]. Journal of Intelligent Material Systems & Structures, 2007, 18(3): 189-208.
[7]	Hu H W, Wang J M. Damage detection of a woven fabric composite laminate using a modal strain energy method[J]. Engineering Structures, 2009, 31(5): 1042-1055. DOI:10.1016/j.engstruct.2008.12.015
[8]	Hui J, Wan X P, Zhao M Y. Damage modes detection of composite laminates using improved modal strain energy method[J]. Advanced Materials Research, 2011, 338: 375-379. DOI:10.4028/www.scientific.net/AMR.338.375
[9]	Zhang Z F, Shankar K, Ray T, et al. Vibration-based inverse algorithms for detection of delamination in composites[J]. Composite Structures, 2013, 102(8): 226-236.
[10]	Roy K, Ray-Chaudhuri S. Fundamental mode shape and its derivatives in structural damage localization[J]. Journal of Sound & Vibration, 2013, 332(21): 5584-5593.
[11]	Dessi D, Camerlengo G. Damage identification techniques via modal curvature analysis: overview and comparison[J]. Mechanical Systems and Signal Processing, 2015, 52.
[12]	Montalvao D, Karanatsis D, Ribeiro A M, et al. An experimental study on the evolution of modal damping with damage in carbon fiber laminates[J]. Journal of Composite Materials, 2015, 49(19): 2403-2413. DOI:10.1177/0021998314547526
[13]	Chandrashekhar M, Ganguli R. Damage assessment of composite plate structures with material and measurement uncertainty[J]. Mechanical Systems & Signal Processing, 2016, 75: 75-93.
[14]	Govindasamy M, Kamalakannan G, Kesavan C, et al. Damage detection in glass/epoxy laminated composite plates using modal curvature for structural health monitoring applications[J]. Journal of Composites Science, 2020, 4(185): 1-27.
[15]	Selva P, Cherrier O, Budinger V, et al. Smart monitoring of aeronautical composites plates based on electromechanical impedance measurements and artificial neural networks[J]. Engineering Structures, 2013, 56: 794-804.
[16]	Ullah I, Sinha J K. A novel method for delamination detection in composites[J]. International Journal of Innovation and Applied Studies, 2013, 2(1): 34-42.