
 , 周广磊2, 勒治华1
, 周广磊2, 勒治华1 1. 东北大学 资源与土木工程学院,辽宁 沈阳 110819;
2. 山东科技大学 能源与矿业工程学院,山东 青岛 266590
收稿日期:2021-05-01
基金项目:国家自然科学基金资助项目(51974062, 42172312); “十三五”国家重点研发计划项目(2017YFC1503101)。
作者简介:袁阳(1993-),男,江西新余人,东北大学博士研究生;
徐涛(1975-),男,湖北随州人,东北大学教授,博士生导师。
摘要:为解决有限元计算在模拟脆性岩石损伤过程方面的网格依赖性问题,本文基于微平面模型和正则化方法建立了改进的微平面损伤模型,将单轴压缩条件下的岩石实验结果与数值模型进行了对比.引入不同非均质系数对三点弯曲岩石试样的损伤发展进行模拟,结果表明非均质系数越高损伤区域越集中.此外,通过引入高阶梯度正则化方法对不同特征长度的三点弯曲实验进行数值模拟.特征长度为1 mm时,在不同网格尺寸下的正则化微平面模型的损伤演化结果基本相同,而没有采用正则化方法的微平面损伤模型在不同网格尺寸下出现明显的网格依赖性.最后,通过对比普通模型和正则化模型的载荷-位移曲线,发现网格密度对采用高阶梯度正则化后的微平面损伤模型损伤演化影响较低.
关键词:微平面模型非均质损伤演化正则化数值模拟
Simulation Method of Damage and Fracture for Brittle Rock Based on Microplane Model and Regularization
YUAN Yang1, XU Tao1

 , ZHOU Guang-lei2, LE Zhi-hua1
, ZHOU Guang-lei2, LE Zhi-hua1 1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China;
2. College of Energy and Mining Engineering, Shandong University of Science and Technology, Qingdao 266590, China
Corresponding author: XU Tao, E-mail: xutao@mail.neu.edu.cn.
Abstract: To solve the mesh dependence of finite element method in simulating the failure of brittle rock, an improved microplane damage model was built based on the microplane model and regularization method. And the numerical simulations were compared with the experimental results under uniaxial compression test. Heterogeneous indexes were introduced for the damage process simulation of three points bending tests. The results showed that the damage area was more concentrated at the high heterogeneous index. In addition, the three points bending tests with different characteristic length were simulated by regularization based on higher-order deformation gradients. The results showed that the damage evolution of microplane damage models with regularization are analogous when the characteristic length is 1 mm, while the microplane damage model without regularization has a significant mesh-dependence at different mesh size. Finally, the load-displacement relationship of normal model and regularization model was contrasted. Mesh density has little effect on the microplane damage model based on regularization with higher-order deformation gradients.
Key words: microplane modelheterogeneousdamage evolutionregularizationnumerical simulation
在外力和环境的作用下,由于细观结构缺陷(如微裂纹、微孔洞等)引起的材料或结构的劣化过程称为损伤.根据所采用的损伤力学理论,岩石损伤本构模型可分为宏观损伤模型和细观损伤模型[1].针对岩石、混凝土等准脆性材料非弹性力学行为与微裂纹张开、闭合、摩擦滑移等细观力学损伤机制,Bazant等对塑性滑移理论[2]进行拓展,建立了微平面模型(microplane model)[3-4],其基本思想是直接以应力和应变的矢量而不是张量建立本构关系.经过不断发展,微平面模型已经成功用于混凝土、土和岩石的本构模型中[5].微平面是指在宏观连续介质体内任何一点的无穷小区域内垂直于任意方向的平面.与传统方法采用宏观连续介质应力、应变张量及其不变性来表达材料的本构模型不同,微平面模型通过在给定的材料点上作用于所有可能取向的单个微平面上的应力和应变矢量来描述材料在宏观尺度上的行为.这种从微观到宏观的分析方法为描述岩石的力学本构行为提供了新思路[6].
数值模拟方法在岩石破坏机理研究中获得广泛应用,而采用连续介质损伤力学方法在模拟岩石类材料破坏时会导致局部化也已成为共识[7-8],这意味着有限元模拟分析中使用应变软化模型时会严重依赖于离散化网格的尺寸[9].Mondal等[10]认为这种全局响应对空间离散化表现出很强的依赖性的原因是当应用网格细化连续介质时,渐进损伤破坏区域的解不能收敛.崔焕平等[11]将损伤判定的极限拉应变值替换成与网格尺寸相关的函数来解决网格尺寸效应.Bazant等[12]将非局部理论用于分析准脆性材料损伤问题,初步发展了非局部损伤力学方法,并对积分型非局部模型进行了综述[13].基于准脆性材料在压缩和剪切状态下拉伸开裂和非线性三轴响应的微平面模型,Bazant等[14]提出了一种能够反映材料损伤和结构尺寸效应的非局部微平面模型.文献[15-16]基于ABAQUS有限元软件二次开发平台将非局部理论[17]嵌入M7微平面模型[18]中,对混凝土应变局部化的有限元网格敏感性进行了分析.但目前提出的微平面模型及其损伤均是通过在每个微平面上添加指数函数来表征微平面应力到达阈值后产生的应力软化从而影响宏观应力[16].
本文提出了一种基于有效应力概念的微平面损伤模型,通过引入非均质细观模型的思想[19],摒弃了微平面中采用的应力边界假设,大大减少所需的力学参数.基于有限元软件COMSOL及MATLAB二次开发平台,将微平面非线性本构关系所采用的PDE(partial differential equation)形式嵌入程序中,编写了定义微平面损伤的相关程序,并在数值模型中引入高阶梯度正则化方法,通过在方程中定义材料的内部特征长度来防止局部化问题,模型中节点处的应力或应变状态不仅受到该点历史应力应变状态影响,而且还受到邻近节点状态的影响,一定程度上解决了有限元计算中的网格依赖性问题.
1 数值模型与方法1.1 微平面模型微平面模型通过应力率和应变率之间的关系构建微平面上本构关系来描述宏观应力应变与时间之间的变化关系.其基本假设有静态约束和动态约束,动态约束指微平面上的应变等于宏观应变张量εij的投影分量,其宏观应变张量与微平面上的应变分量直接相关,而静态约束则是指微平面上的应力等于宏观应力张量σi, j的投影分量,其宏观应力张量与微平面上的应力分量直接相关[20].本文采用的动态约束适用于描述微平面应变沿各方向连续变化,而微平面应力沿各方向变化不连续的情况,微平面上法向、切向应变分量与宏观应变张量之间的关系可表示为
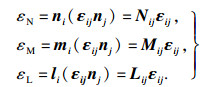 | (1) |
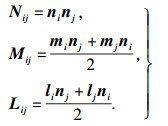 | (2) |
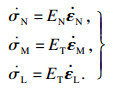 | (3) |
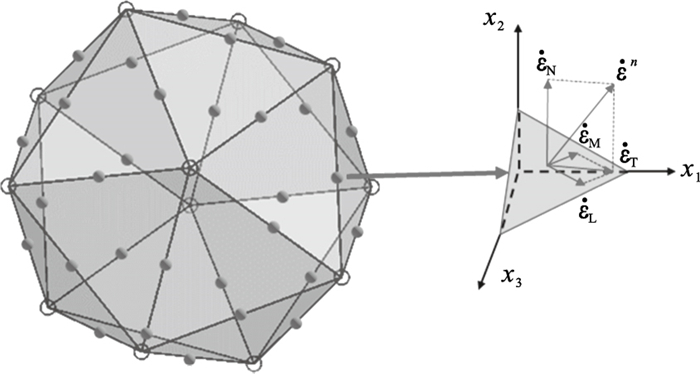 | 图 1 微平面上应变率矢量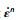 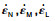 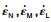 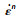 |
其中,EN, ET分别为法向和切向弹性常数,其与单元的弹性模量关系为
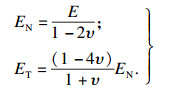 | (4) |
宏观应力张量为微平面应力在各积分点上不同方向进行积分求值之和,为在程序中更好地进行计算,宏观应力张量与微平面应力矢量通过不同方向积分后的近似关系如式(5)所示,其积分点的空间位置及权重详细论述可见文献[6].
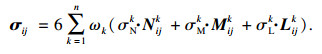 | (5) |
1.2 微平面损伤模型基于应变等效假设[23]的损伤在细观损伤力学模型中已得到广泛的应用[24-26],其基本思想是将无损材料中的名义应力以有损材料的有效应力代替建立的损伤本构关系.有损材料的弹性模量定义为
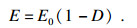 | (6) |
本文提出的微平面损伤模型的应力状态基于屈服准则判定.首先,对于处于拉应力状态时的节点,即法向应力为正(σN> 0)的情况采用最大拉应力准则,认为某个微平面上的最大法向应力超过阈值时,该微平面系统对应的节点即发生损伤,可表示为
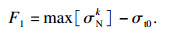 | (7) |
当单元处于压缩状态(σN≤0)时,采用Mohr- Coulomb(MC)屈服准则.在微平面系统中可以理解为当单元的某个微平面上的正应力和剪应力满足该条件时发生剪切破坏,可表示为
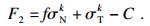 | (8) |
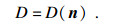 | (9) |
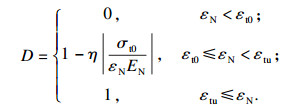 | (10) |
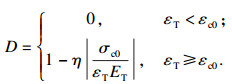 | (11) |
1.3 正则化方法引入正则化方法认为,材料点上的应力不仅依赖于该点处的应变,而且与该点一定范围内的应变场有关.其思想是通过一个平滑的非局部变量来代替局部变量,与单元网格相关的损伤变量取决于相邻网格单元之间的平均应变,其中损伤准则和损伤演化保持不变,即在弹性损伤模型中,意味着在x点处损伤不再受此处局部应变的控制,而是取决于在以点x处为中心,半径为l的球体上的应变平均值.但这意味着在三维有限元计算中,针对任意一个单元都需要与模型中其他所有单元的相对距离与特征长度进行判断和修正,会占用大量计算资源,因此需要将其进行简化.这里采用高阶梯度正则化方法来替换局部应变[10].局部应变
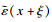
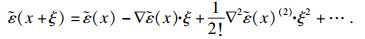 | (12) |
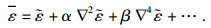 | (13) |
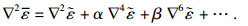 | (14) |
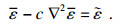 | (15) |
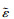
1.4 岩石的非均质表征岩石由各种晶粒、胶结物和孔隙组成,为表征其非均质特性,假设其内部细观参数服从Weibull分布:
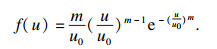 | (16) |
图 2(Fig. 2)
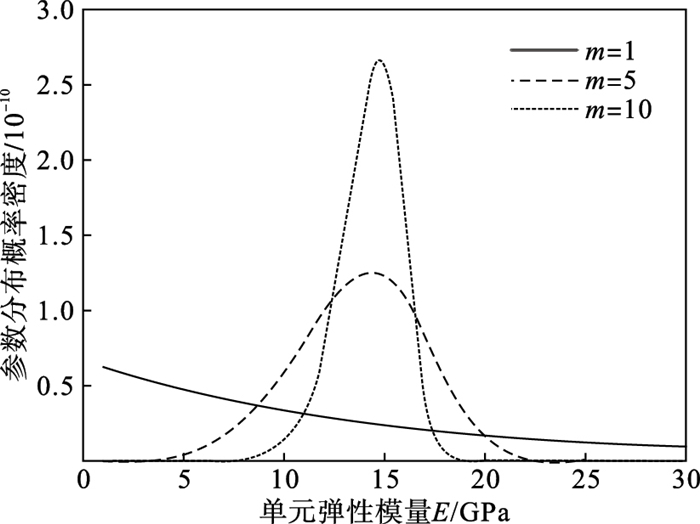 | 图 2 非均质系数m对应的概率密度分布(弹性模量)Fig.2 Probability density distribution with heterogeneous index m(elastic modulus) |
2 模型在COMSOL中的实现及验证微平面模型需要针对每一个微平面构建本构关系,本文模型基于COMSOL Multiphysics 5.2和MATLAB平台进行二次开发.
2.1 模型在COMSOL平台实现过程通过在COMSOL中建立微平面损伤模型,在MATLAB平台中加入循环函数以实现岩石参数(弹性模量、强度、内聚力和损伤)的每一步求解后的更新迭代.具体流程(见图 3)为,先对每一个方向上的微平面本构关系在COMSOL界面中通过添加PDE物理场以建立微平面上的应力-应变随时间变化的关系,如需建立2×21个积分点的微平面模型,则需要建立21个物理场,每个物理场中包含3个偏微分方程对应式(3),对于本文中的数值模型,表征微平面模型共建立63个偏微分方程.计算流程为首先对每个单元节点上的局部宏观应变增量根据式(1)进行分解,即微平面k上的微平面法向应变矢量为非局部应变张量与法向投影张量的乘积(动态约束).对于每一个应变分量,可以建立Helmholtz方程通过式(15)进行局部应变和非局部应变之间的替换.值得注意的是,本文中采用正则化模型对三点弯曲实验进行模拟,该实验预制裂缝处主要为拉伸破坏.因此为减少计算量,本文只对微平面法向应变进行非局部变量的替换,而切向应变则不替换.得到微平面非局部应变矢量分量后,根据微平面本构关系式(3)进行微平面应力的计算,继而根据微平面上的损伤状态进行判断是否需要对单元的弹性模量进行折减,最后通过高斯公式进行数值积分得到该加载步下的宏观应力张量.
图 3(Fig. 3)
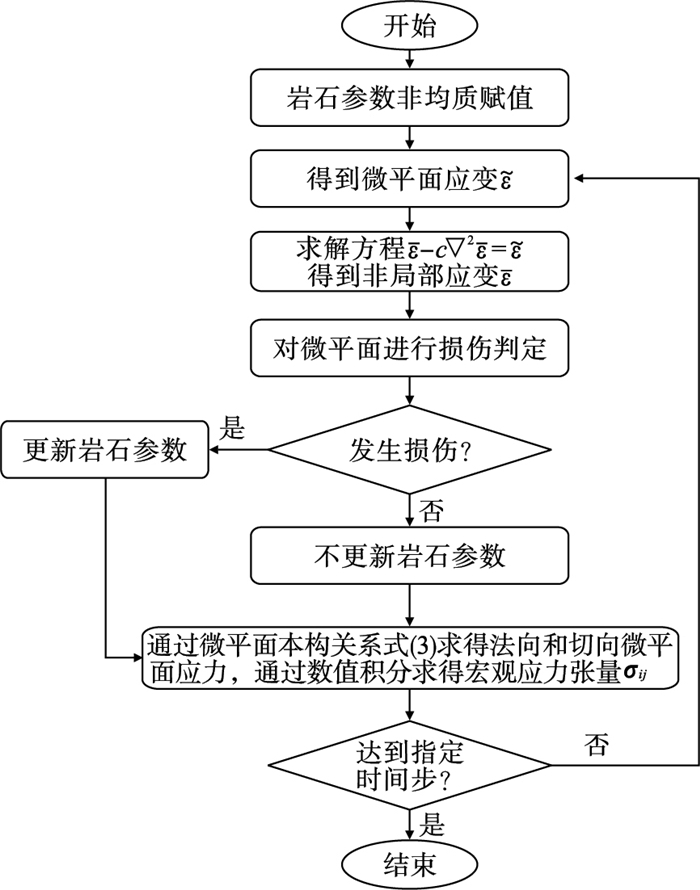 | 图 3 基于微平面损伤模型的正则化方法计算流程图Fig.3 Flow chart of regularization based on microplane damage model |
2.2 模型验证根据上述步骤,编写基于微平面损伤模型的MATLAB程序,为节省计算资源,选取单位球面积分点数目为2×21.实验建立了单轴压缩模型,试件尺寸为直径25 mm,高62.5 mm.数值模型和花岗岩参数如表 1所示.值得注意的是,数值模拟的弹性模量和强度是单元的平均值[27],而实验中的弹性模量和强度是实验结果.
表 1(Table 1)
| 表 1 单轴压缩实验和模拟的材料参数 Table 1 Parameters of simulation and experiment under uniaxial compression |
图 4绘制了数值模型和实验的应力-应变曲线,实验开始加载阶段为孔隙压密阶段,后线性部分为弹性阶段,接近峰值时出现非线性阶段,试件达到峰值强度162.3 MPa后破坏,由于实验过程的应变通过应变片来采集,故不能显示峰后阶段.
图 4(Fig. 4)
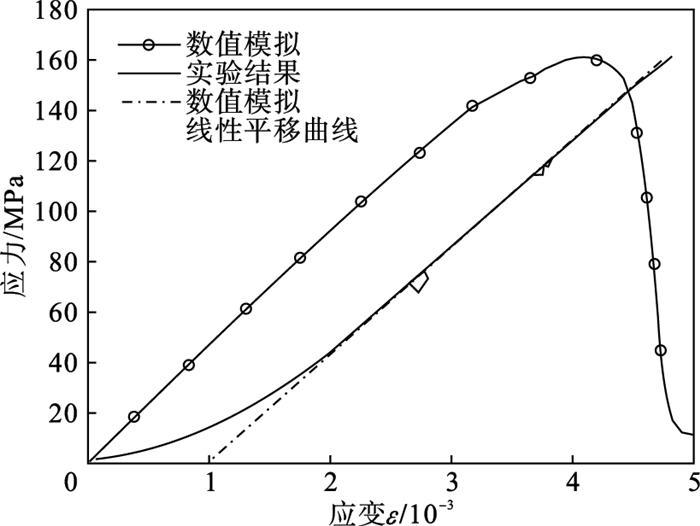 | 图 4 单轴压缩数值模拟和实验结果应力-应变曲线Fig.4 Stress-strain relationship between the numerical simulation and experimental results of uniaxial compression |
本文提出的微平面损伤模型并未假设孔隙压密阶段,因此不能表征这一阶段.图 4中的点划线为数值模拟线性阶段平移曲线,可知对于弹性阶段和接近峰值的非线性阶段以及峰值强度,数值结果与实验结果较为吻合.
限于篇幅,图 5只给出了单轴压缩数值模拟结果的部分损伤演化过程图,图例中不同数值代表损伤值的种类和大小.根据1.2节定义正值为压缩状态下的剪切损伤,负值为拉伸损伤,绝对值越大代表该种损伤越大.在开始加载阶段,模型损伤为零.随着加载步增大,试件随机出现了剪切和拉伸损伤,在短时间内,这些损伤逐渐汇聚贯通,最后与单轴压缩实验中的试件相同形成剪切带.而数值模拟在第66~68步恰好为峰值强度后出现应力跌落.结果表明,模型能够较好地反映岩石在应力加载条件下的损伤演化过程.
图 5(Fig. 5)
 | 图 5 单轴压缩数值模拟和实验破坏结果对比Fig.5 Comparisons between the numerical simulation and experimental results of uniaxial compression |
3 正则化模型分析采用微平面损伤模型(本文称之为普通模型)得到的宏观变形、应力及损伤发展依赖于有限元网格尺寸和数量.本文采用三点弯曲试件进行正则化方法分析,试件尺寸如图 6所示,底部2个支座固定,试件跨度为70 mm,试件长度为90 mm,试件高度为30 mm,宽度为10 mm,预制裂缝a为宽1 mm,高4 mm.在数值模拟中,倘若常采用圆柱作为上下支点,其与试件为线接触,在进行损伤迭代计算时,易于在支点处产生应力集中发生破坏,与实际情况不符.为获得良好的计算结果,本文将圆柱体与试件接触改为宽2 mm,长10 mm的矩形接触面,加载速率为1×10-6 m/s.
图 6(Fig. 6)
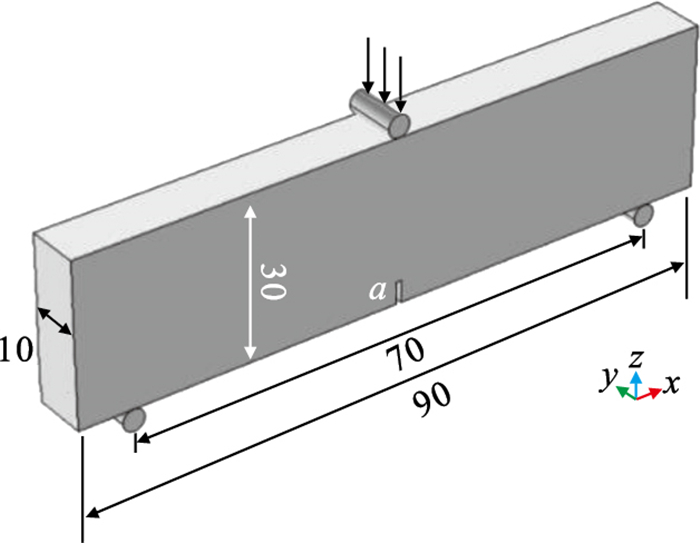 | 图 6 三点弯曲实验试件尺寸(单位:mm)Fig.6 Sample size of three-point bending test(unit: mm) |
3.1 非均质系数对损伤的影响首先对不同非均质系数(1,5和10)的微平面损伤普通模型在不同时间加载步下的破坏模式进行对比分析.除加载速率外数值模型参数见表 1.为提高模型计算速度并防止网格收敛性问题,模型网格划分采用COMSOL默认的四面体网格(Mesh1),最大单元尺寸为3.15×10-3m,最小单元尺寸为1.35×10-4m,最大单元增长率为1.35,单元总数为70 109个.图 7给出了不同非均质系数m的试件损伤演化.由图 7可见,非均质系数对试件的损伤破坏影响明显,非均质系数低(m=1)时,岩样中损伤在预置裂缝周围弥散分布;非均质系数高(5,10)时,岩样中损伤集中于预置裂缝尖端,形成明显的局部化损伤区域.非均质系数为1时,损伤区域虽然在预制裂缝处较多,但是在试件其他区域也有大量损伤区域存在,与实际情况不符.对于岩石材料而言,非均质系数为5左右时结果较为合理[25-27].
图 7(Fig. 7)
 | 图 7 不同非均质系数的试件损伤演化Fig.7 Damage evolution of sample with heterogeneous index (a)—m=1;(b)—m=5;(c)—m=10. |
3.2 特征长度对损伤影响根据有限元模型网格尺寸(1.35×10-4~3.15×10-3 m),采用特征长度分别为0.3,0.4,0.5,1,2 mm进行数值模拟,数值模型非均质系数均为5,网格划分方式(Mesh1)是由COMSOL根据物理场自动生成的四面体形式.图 8为具有不同特征长度的数值模型的损伤云图(时步为50),图例中的数值其意义与2.2节中相同.从图 8可知,采用相同网格划分方式,正则化模型与普通模型的破坏模式大致相同.因此正则化模型可以看作是对普通微平面损伤模型中某些变量(如应变)的修正,并不会导致结果产生巨大差异.并且,在相同网格划分下,特征长度越小,越接近最小网格尺寸,损伤效果越好;特征长度为0.4 mm和0.3 mm时损伤位置和损伤发展方向准确,但最终损伤效果与特征长度为0.5 mm的结果相近,因此模型单元尺寸与特征长度相近时,可认为对损伤结果影响较小.特征长度(l=2 mm)过大时,由于特征长度大于大部分网格尺寸,导致损伤面积过大而不符合实际情况.由此可见,在相同网格划分条件下,存在一个最优特征长度值,可以得到最好的裂纹扩展效果.在可预见的范围内,对相同尺寸的数值模型而言,随着网格密度增大,最小单元尺寸减小,最优特征长度值也会随之减小.
图 8(Fig. 8)
 | 图 8 不同特征长度的损伤演化Fig.8 Damage evolution of different characteristic lengths |
3.3 网格敏感性分析采用第二种较稀疏的网格(Mesh2)进行数值模拟,均质度为5.图 9为普通和正则化模型三点弯曲数值模型在两种网格情况下第50步时局部损伤云图,图中Mesh1网格的最大单元为3.15×10-3m,最小单元为1.35×10-4m,总单元数量为70 109个,Mesh2网格的最大单元尺寸为7.2×10-3m,最小单元尺寸为9×10-4m,总单元数量为10 772个.图中正则化模型采用的特征长度为1 mm.可以得知,在改变网格密度后,在相同加载步数下,普通微平面模型的破坏模式发生了较大的改变,损伤区域长度变短,并且与裂缝平行的相邻单元也发生了损伤.而对于正则化模型而言,改变网格密度后,其破坏区域大小和方向基本保持不变,说明引入正则化方法后,模型损伤结果对网格依赖性较小.
图 9(Fig. 9)
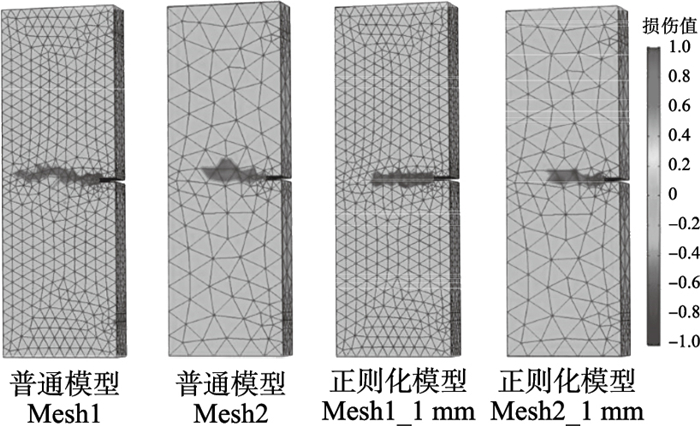 | 图 9 普通模型和正则化模型两种网格密度损伤演化Fig.9 Damage evolution under two meshing densities of normal and regularization model |
对两种网格划分Mesh1和Mesh2的载荷-位移曲线进行普通模型和正则化模型的对比分析.载荷为施加在试件上部区域的z方向反力,位移为施加载荷的区域z方向位移.图 10为普通和正则化模型在两种不同网格密度下对三点弯曲试件进行数值模拟,其中正则化模型的特征长度为1 mm,非均质系数为5.由图 10可知,随着网格密度减小(网格尺寸增大),普通模型模拟的强度发生了明显变化,此为有限元计算过程中出现的相同模型由于网格尺寸大小、密度不同产生的尺寸效应.总体而言,模型在引入正则化方法后,试件的整体强度和应变峰值增大,但不同网格密度大小对正则化模型的载荷-位移曲线影响较小,二者趋势在第40计算步之前基本一致,这是由于正则化微平面损伤模型可以考虑单元与有限范围内单元之间的影响,这样减少了由于损伤局部化引起的单元网格敏感性,保证了数值模拟结果的客观性.而在峰后阶段(第40计算步后)载荷-位移曲线相差较大,其原因可能是本文提出的损伤模型不涉及峰后阶段的岩石力学行为,该部分工作将于今后开展.
图 10(Fig. 10)
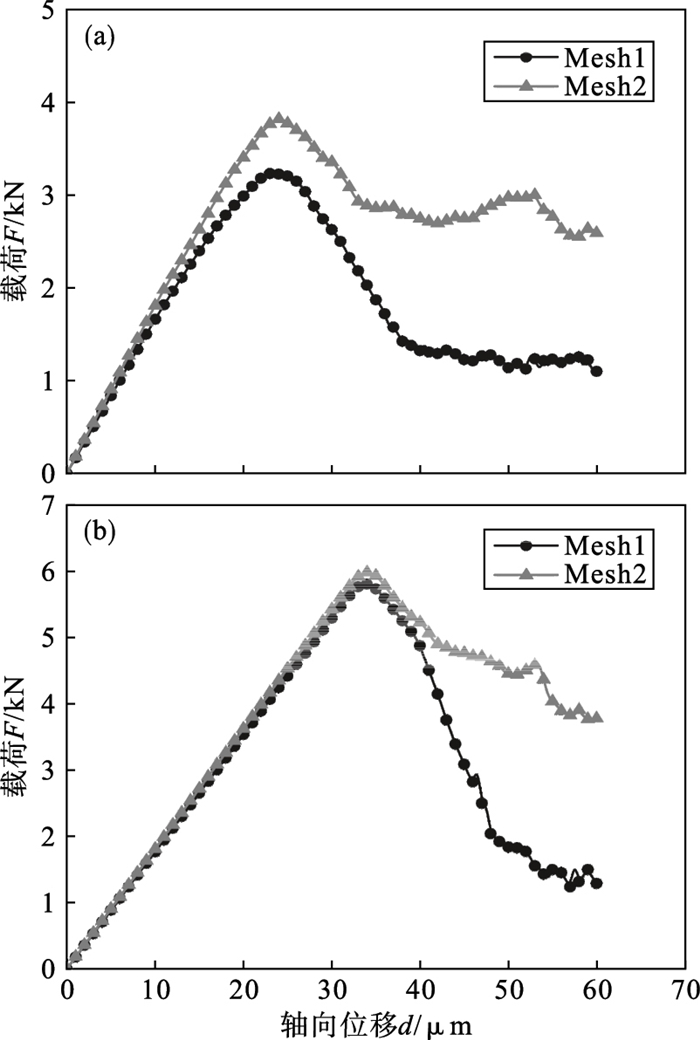 | 图 10 普通和正则化三点弯曲模型的载荷-位移曲线Fig.10 Load versus displacement curves of normal and regularized three points bending test model (a)—普通模型;(b)—正则化模型. |
4 结论1) 对于普通微平面损伤模型,材料越均匀,其损伤区域越集中,裂纹扩展模式越稳定.
2) 普通微平面损伤模型和正则化模型的损伤模式基本一致,但正则化模型通过引入不同特征长度来表征损伤程度,对于给定的数值模型,存在一个最优的特征长度来得到较好的损伤效果.一般而言,特征长度与模型网格长度相近时损伤效果较好.
3) 正则化方法一定程度上消除了局部损伤模型的网格尺寸效应.该方法通过考虑特征长度范围内的积分点的非局部效应,对网格敏感性进行限制,保证了数值模拟结果的客观性.
参考文献
| [1] | 冯西桥. 脆性材料的细观损伤理论和损伤结构的安定分析[D]. 北京: 清华大学, 1995. (Feng Xi-qiao. Micro-failure theory for brittle materials and shakedown analysis of structures with damage[D]. Beijing: Tsinghua University, 1995. ) |
| [2] | Batdorf S B, Budiansky B. A mathematical theory of plasticity based on the concept of slip[J]. Soviet Applied Mechanics, 1949, 12(12): 1102-1112. |
| [3] | Bazant Z, Caner F, Carol I, et al. Microplane model M4 for concrete Ⅰ: formulation with work-conjugate deviatoric stress[J]. Journal of Engineering Mechanics, 2000, 126(9): 944-953. DOI:10.1061/(ASCE)0733-9399(2000)126:9(944) |
| [4] | Caner F, Bazant Z. Microplane model M7 for plain concrete Ⅰ: formulation[J]. Journal of Engineering Mechanics, 2013, 139(12): 1714-1723. DOI:10.1061/(ASCE)EM.1943-7889.0000570 |
| [5] | Carol I, Bazant Z. Damage and plasticity in microplane theory[J]. International Journal of Solids and Structures, 1997, 34(29): 3807-3835. DOI:10.1016/S0020-7683(96)00238-7 |
| [6] | 陈新, 杨强, 李德建. 岩体裂隙网络各向异性损伤力学效应研究[M]. 北京: 科学出版社, 2016. (Chen Xin, Yang Qiang, Li De-jian. Study on anisotropic damage mechanics effect of fracture network in rock mass[M]. Beijing: Science Press, 2016.) |
| [7] | Murakami S, Liu Y. Mesh-dependence in local approach to creep fracture[J]. International Journal of Damage Mechanics, 1995, 4: 230-250. DOI:10.1177/105678959500400303 |
| [8] | Liu Y, Murakami S, Yamada T, et al. Mesh dependence in local approach to creep fracture analysis of perforated plate[J]. Transactions of the Japan Society of Mechanical Engineers, 1995, 61: 2030-2036. DOI:10.1299/kikaia.61.2030 |
| [9] | Borst R, Sluys L J, Muhlhaus H, et al. Fundamental issues in finite element analysis of localization of deformation[J]. Engineering Computations, 1993, 10(2): 99-121. DOI:10.1108/eb023897 |
| [10] | Mondal S, Olsen-Kettle L, Gross L. Regularization of continuum damage mechanics models for 3-D brittle materials using implicit gradient enhancement[J]. Computers and Geotechnics, 2020, 122: 103505. DOI:10.1016/j.compgeo.2020.103505 |
| [11] | 崔焕平, 崔燕平, 王宗敏. 混凝土非线性有限元分析中的网格尺寸效应[J]. 混凝土, 2007(6): 27-29. (Cui Huan-ping, Cui Yan-ping, Wang Zong-min. Mesh size effect in nonlinear finite element analysis of concrete[J]. Concrete, 2007(6): 27-29. DOI:10.3969/j.issn.1002-3550.2007.06.009) |
| [12] | Bazant Z, Pijaudier-Cabot G. Nonlocal continuum damage, localization instability and convergence[J]. Journal of Applied Mechanics, 1988, 55(2): 287-293. DOI:10.1115/1.3173674 |
| [13] | Bazant Z, Jirásek M. Nonlocal integral formulations of plasticity and damage: survey of progress[J]. Journal of Engineering Mechanics, 2002, 128(11): 1129-1239. |
| [14] | Bazant Z, O?bolt J. Nonlocal microplane model for fracture, damage, and size effect in structures[J]. Journal of Engineering Mechanics, 1990, 116(11): 2485-2505. DOI:10.1061/(ASCE)0733-9399(1990)116:11(2485) |
| [15] | 崔溦, 杨娜娜, 宋慧芳. 基于非局部微平面模型M7的混凝土非线性有限元分析[J]. 建筑结构学报, 2017, 38(2): 126-133. (Cui Wei, Yang Na-na, Song Hui-fang. Nonlinear finite element analysis of concrete structure based on nonlocal microplane model M7[J]. Journal of Building Structures, 2017, 38(2): 126-133.) |
| [16] | 杨娜娜. 基于非局部理论的混凝土M7微平面本构模型研究及应用[D]. 天津: 天津大学, 2016. (Yang Na-na. Research and application of microplane constitutive model M7 based on nonlocal theory for plain concrete[D]. Tianjin: Tianjin University, 2016. ) |
| [17] | Bazant Z, Di L G. Nonlocal microplane model with strain-softening yield limits[J]. International Journal of Solids and Structures, 2004, 41(24/25): 7209-7240. |
| [18] | Caner F, Bazant Z. Microplane model M7 for plain concrete Ⅱ: calibration and verification[J]. Journal of Engineering Mechanics, 2013, 139(12): 1724-1735. DOI:10.1061/(ASCE)EM.1943-7889.0000571 |
| [19] | Xu T, Tang C A, Zhao J, et al. Modelling the time-dependent rheological behaviour of heterogeneous brittle rocks[J]. Geophysical Journal International, 2012, 189(3): 1781-1796. DOI:10.1111/j.1365-246X.2012.05460.x |
| [20] | Chen X, Bazant Z. Microplane damage model for jointed rock masses[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(14): 1431-1452. DOI:10.1002/nag.2257 |
| [21] | Bazant Z, Oh B. Microplane model for progressive fracture of concrete and rock[J]. Journal of Engineering Mechanics, 1985, 111(4): 559-582. DOI:10.1061/(ASCE)0733-9399(1985)111:4(559) |
| [22] | Bazant Z, Xiang Y, Prat P. Microplane model for concrete Ⅰ: stress-strain boundaries and finite strain[J]. Journal of Engineering Mechanics, 1996, 122(3): 245-254. DOI:10.1061/(ASCE)0733-9399(1996)122:3(245) |
| [23] | Kachanov L M. Rupture time under creep conditions[J]. International Journal of Fracture, 1999, 97(1/2/3/4): 11-18. |
| [24] | 朱万成, 唐春安, 杨天鸿, 等. 岩石破裂过程分析用(RFPA~(2D))系统的细观单元本构关系及验证[J]. 岩石力学与工程学报, 2003, 22(1): 24-29. (Zhu Wan-cheng, Tang Chun-an, Yang Tian-hong, et al. Constitutive relationship of mesoscopic elements used in RFPA~2D and its validations[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 24-29.) |
| [25] | 梁正召. 三维条件下的岩石破裂过程分析及其数值试验方法研究[D]. 沈阳: 东北大学, 2005. (Liang Zheng-zhao. Three-dimensional failure process analysis of rock and associated numerical tests[D]. Shenyang: Norteastern University, 2005. ) |
| [26] | Xu T, Yuan Y, Heap M J, et al. Microwave-assisted damage and fracturing of hard rocks and its implications for effective mineral resources recovery[J]. Minerals Engineering, 2021, 160: 106663. |
| [27] | Yuan Y, Xu T, Heap M J, et al. A three-dimensional mesoscale model for progressive time-dependent deformation and fracturing of brittle rock with application to slope stability[J]. Computers and Geotechnics, 2021, 135: 104160. DOI:10.1016/j.compgeo.2021.104160 |
