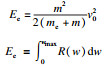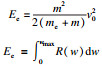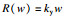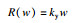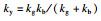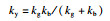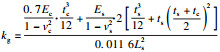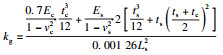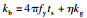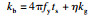安国青, 王蕊, 赵晖, 李铁英
太原理工大学 土木工程学院，山西 太原 030024
收稿日期：2021-06-28
基金项目：国家自然科学基金资助项目(52108162)；山西省基础研究项目(20210302124208)。
作者简介：安国青(1992-)，男，山西大同人，太原理工大学博士研究生;
王蕊(1979-)，女，山西太原人，太原理工大学教授，博士生导师;
李铁英(1968-)，男，山西太原人，太原理工大学教授，博士生导师。

摘要：为研究双钢板混凝土组合(SC)板的抗撞性能，本文采用ABAQUS建立了SC板在落锤撞击下的有限元模型，并通过已有SC板落锤撞击试验结果验证了数值模型的准确性.基于此，重点研究了构件钢板含钢率、撞击高度、材料强度、边界条件与撞击物形状等参数对该类构件动力响应的影响；最后利用简化能量守恒法计算了SC板跨中最大挠度.结果表明：在本研究参数分析范围内，钢板含钢率、撞击高度、撞击物形状与边界条件对该类构件动力响应影响较大，且当钢板含钢率大于4%时影响更加明显.建议的简化能量守恒法可有效预测SC板在撞击荷载作用下的跨中最大挠度.
关键词：双钢板混凝土组合板撞击有限元分析动力响应理论计算
Dynamic Response of Double-Skin Steel-Concrete Composite Panel Under Impact Loading
AN Guo-qing, WANG Rui, ZHAO Hui, LI Tie-ying
School of Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, China
Corresponding author: ZHAO Hui, E-mail: zhaohui01@tyut.edu.cn.

Abstract: In order to study the impact-resistant performance of double-skin steel-concrete composite(SC)panel, the ABAQUS software was utilized to establish the finite element(FE)models of SC panel subjected to drop hammer impact. The accuracy of numerical models was verified by comparing the FE simulations with the test results. Based on the validated models, the influences of steel plate ratio, impact height, material strength, boundary condition and indenter shape on the dynamic responses of SC specimen were revealed. Finally, the energy method was employed to calculate the maximum mid-span deflection of SC panel. The results indicate that steel plate ratio, impact height, indenter shape and boundary condition present significant effects on the dynamic response within the parameter range of this work, and the effects are more obvious when the steel plate ratio exceeds 4%. The theoretical calculation method used in this study can reasonably predict the maximum mid-span deflection of SC panel under impact loading.
Key words: double-skin steel-concrete composite panelimpactfinite element analysisdynamic responsetheoretical calculation
双钢板混凝土组合(double-skin steel-concrete composite, SC)板主要由外侧钢板、夹层混凝土与抗剪连接件组成.由于具有承载力高、刚度大、密封性好与施工便捷等突出特点，SC板目前已广泛应用于核电站、房屋建筑、海洋平台与防护结构中^[1-2].该类构件在其全生命周期内除了要承受静力荷载外，还可能会遭受撞击、爆炸等偶然荷载的作用，例如海堤与海洋平台易遭受浮冰的撞击、核电站与高层建筑易遭受飞行物的撞击、防护墙板易遭受车辆撞击等.
针对钢-混凝土组合结构与钢结构的抗撞性能，作者所在课题组成员进行了相关试验与理论研究工作，包括实心钢管混凝土^[3]、中空夹层钢管混凝土^[4-5]、钢管混凝土叠合柱^[6]、H型钢以及格构式钢柱^[7-8]等.研究发现，相比于静力加载，结构构件在撞击作用下呈现出明显不同的变形与破坏模式.针对SC板抗撞击性能，Remennikov等^[9-10]对轴向约束的非组合SC板进行了落锤撞击试验.结果表明轴向约束可以有效发挥钢板的膜力效应，但是由于缺乏抗剪连接件，钢板与夹层混凝土容易分离.Sohel等^[11]对采用J形钩连接件的SC板进行了撞击试验，并基于弹塑性分析提出了SC构件在落锤撞击下动力响应的计算方法模型.Zhao等^[12]对采用拉筋连接件的SC板进行了撞击试验，在验证数值模型的基础上通过参数分析给出了试验试件的临界轴压比.Yan等^[13]通过试验研究了采用螺栓连接件的曲面SC板撞击力学性能.
综上，目前对SC板撞击动力响应的研究相对较少且影响参数分析范围仅局限于试验试件.为进一步明晰SC板的抗撞性能，亟需对该类构件的撞击动力响应进行深入研究.
基于此，本文采用ABAQUS建立碳素钢-混凝土-碳素钢组合板侧向撞击数值计算模型，重点研究钢板含钢率、撞击高度、材料强度、边界条件等参数对构件动力响应的影响，最后通过理论公式计算不同边界条件下SC板跨中最大挠度，为其防撞设计提供参考.
1 有限元模型建立与验证1.1 试验参数设计本文根据相关设计规范^[14-15]共设计了40个SC构件，图 1给出了该类构件示意图.重点分析了钢板含钢率(α=2%~8%)、落锤撞击高度(H=2~6 m)、落锤撞击物形状(方形200 mm×200 mm、半球形r=100 mm)、钢板屈服强度(f_y=235~420 MPa)与边界条件(四边简支、四边固支)对该类构件动力响应的影响规律.
图 1(Fig. 1)

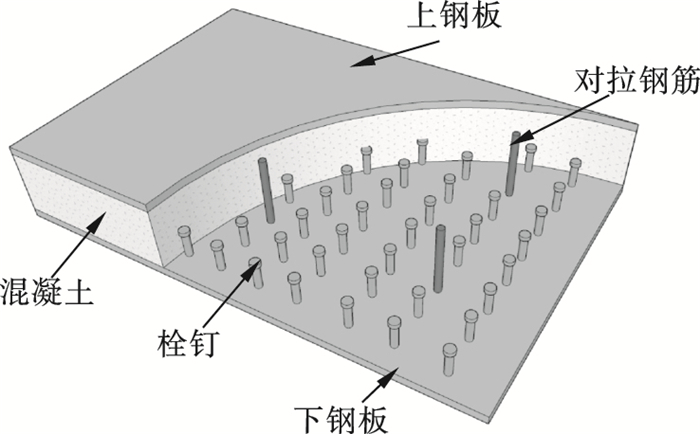图 1 SC构件示意图Fig.1 Diagram of SC components

构件尺寸均为1 800 mm×1 800 mm×130 mm(长×宽×高)；栓钉长度为30 mm，直径与间距分别为5 mm与100 mm；对拉钢筋直径与间距分别为10 mm与200 mm.表 1给出了部分构件的详细参数，其中h为构件截面高度；t_s为钢板厚度；ρ_s为钢板含钢率(单位宽度钢板截面积与单位宽度试件截面积之比^[14])；f_cu为混凝土立方体抗压强度；f_y为钢板屈服强度；m为落锤质量；H为落锤撞击高度.
表 1(Table 1)

表 1 构件详细参数Table 1 Detailed parameters of specimen 组别 构件编号 h/mm ts/mm ρs/% fcu/MPa fy/MPa m/kg H/m 边界条件 撞击物形状 A A2 130 1.28 2.0 30 235 180 2 四边简支 方形 A4 130 2.50 4.0 30 235 180 2 四边简支 方形 A6 130 3.70 6.0 30 235 180 2 四边简支 方形 A8 130 4.80 8.0 30 235 180 2 四边简支 方形 B B2 130 1.28 2.0 30 235 180 4 四边简支 方形 B4 130 2.50 4.0 30 235 180 4 四边简支 方形 B6 130 3.70 6.0 30 235 180 4 四边简支 方形 B8 130 4.80 8.0 30 235 180 4 四边简支 方形 C C2 130 1.28 2.0 30 235 180 2 四边简支 半球形 C4 130 2.50 4.0 30 235 180 2 四边简支 半球形 C6 130 3.70 6.0 30 235 180 2 四边简支 半球形

表 1 构件详细参数 Table 1 Detailed parameters of specimen

1.2 有限元模型建立1.2.1 材料模型低碳钢采用韩林海^[16]建议的五阶段弹塑性模型. 钢板在撞击荷载作用下可能发生受拉破坏，因此在本构关系中需引入断裂准则.通过在材料属性中设置延性损伤进行模拟，包括设置断裂应变、应力三轴度与应变率等材料失效参数^[17]，本文中钢板断裂应变、应力三轴度与应变率分别设置为0.3，0.9与26.8 s^-1，最后通过设置单元删除将失效单元去除.钢材在撞击作用下需考虑材料的应变率效应，本文钢板、栓钉与对拉钢筋均为低碳钢，采用Cowper-Symonds模型进行计算，见式(1)：

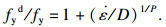(1)

式中：f_y^d与f_y分别表示应变率为时的动态屈服强度与静态屈服强度；为应变率，s^-1；D，P分别为6 844 s^-1，3.91^[5].
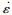
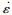
夹层混凝土采用塑性损伤模型(CDP模型)进行模拟.其单轴受压与受拉应力-应变关系采用文献[18]建议的模型，并分别采用CEB-FIP规范^[19]与文献[20]中建议的公式考虑混凝土受压与受拉应变率效应，分别如式(2)与式(3)所示：

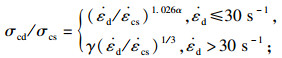(2)

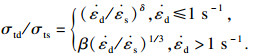(3)

式中：σ_cd与σ_td分别表示混凝土在撞击作用下(应变率为_d)的抗压强度与抗拉强度；σ_cs为混凝土在静力作用下(应变率为_cs)的抗压强度；σ_ts为混凝土在静力作用下(应变率为_s)的抗拉强度; _cs=-30×10^-6s^-1；α=1/(5+9σ_c/σ_c0)，lgγ=6.156α-2，σ_c0=10 MPa，σ_c=f_ck+8，f_ck为混凝土轴心抗压强度标准值. _s=10^-6s^-1，δ=1/(1+8σ_c/σ_c0)，lg β=6δ-2.
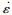
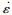
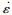
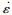
1.2.2 单元类型、边界条件夹层混凝土、外层钢板、栓钉与落锤采用实体单元C3D8R；对拉钢筋采用梁单元B31.在落锤内部设置参考点，并为其设置刚体约束.试件的边界条件施加在四边端面的钢板与混凝土上，且通过约束端面自由度实现边界条件的设置.对于落锤，除撞击方向外，其他所有方向自由度均受约束.
1.2.3 网格划分与界面接触图 2给出了典型SC板精细化有限元模型示意图.落锤撞击区域网格局部加密，加密区网格尺寸是未加密区域网格尺寸的一半.首先通过网格敏感性分析确定了当未加密区网格尺寸为35 mm，加密区网格尺寸为17.5 mm时，可获得较好的模拟精度.将落锤放置于构件跨中正上方0.02 mm处，撞击荷载是通过在预定义场中为落锤施加初速度来定义，落锤的初速度与质量都通过其内部的参考点施加.为模拟实际中试件受到的重力作用，整个模型施加重力加速度.
图 2(Fig. 2)

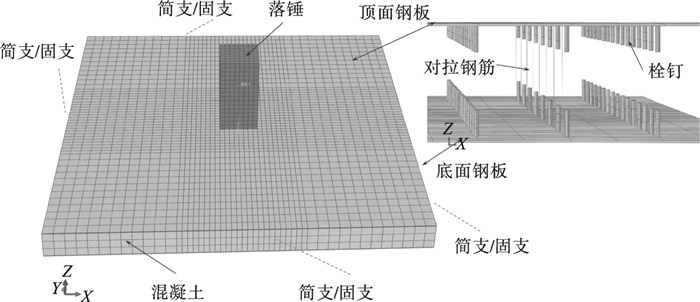图 2 SC板有限元模型示意图Fig.2 Diagram of finite element model of SC panel

钢板内表面、栓钉表面、对拉钢筋表面与混凝土接触面法向采用硬接触，切向接触采用库仑摩擦模型，摩擦系数取0.6^[5]；落锤与试件之间的摩擦系数取0^[5].所有栓钉以及对拉钢筋通过“Tie”约束与钢板内表面绑定，实现对实际焊接的模拟.
1.3 有限元模型验证文献[12]采用课题组自主研发的DHR9401型落锤冲击试验机进行撞击试验，试验装置高达13.47 m，最大撞击高度为12.60 m，可实现低速撞击对不同能量的要求.落锤总质量为233.5 kg，锤头为直径80 mm的半球形刚体，配重与撞击头之间设置力传感器，用于记录撞击力时程曲线，通过在板底布置动态位移传感器记录跨中挠度时程曲线.所有试件长1 000 mm，宽800 mm，内填混凝土厚度为75 mm；栓钉间距和对拉钢筋间距分别为75 mm和150 mm.
为验证所建模型的准确性，本文对文献[12]的撞击试验结果进行了验证，内容包括撞击力时程曲线、跨中挠度时程曲线和典型试件破坏形态.表 2为所验证的算例及其计算结果，其中H表示撞击高度，N为轴力，F_p为撞击力惯性峰值，F_m为撞击力膜力峰值，w_max表示跨中最大挠度，w_res为跨中残余挠度，FE表示有限元计算结果，Test表示试验结果.图 3给出了部分典型试件撞击力时程与跨中挠度时程曲线有限元计算结果与试验结果的对比，可以发现有限元模拟曲线形状与试验曲线趋势符合良好.在撞击力惯性阶段，当落锤与试件发生接触后，撞击力迅速上升达到峰值，试件获得较大动能，试件速度相应增大.当应力波在试件中不断传播并来回反射多次后，支座反力开始作用，试件整体变形增加.由于试件变形消耗了撞击能量，速度减小并与落锤重新接触.落锤与试件之间重复的分离与接触使撞击力减小的过程中出现较大震荡.图 4进一步给出了典型试件T03H75落锤撞击损伤与数值模拟损伤的对比，由图 4b可见落锤撞击区域钢板断裂后失效单元被删除，内部混凝土裸露.综上，有限元结果可较好预测试件的破坏形态.
表 2(Table 2)

表 2 验证算例与计算结果Table 2 Verification example and calculation results 试件编号 H/m N/kN Fp/kN FE Fm/kN FE wmax/mm FE wres/mm FE FE Test Test FE Test Test FE Test Test FE Test Test T03H15 1.5 0 228 238 0.96 175 180 0.97 19.6 20.3 0.97 15.2 14.2 1.07 T03H30 3.0 0 299 324 0.92 251 250 1.00 30.0 32.0 0.94 23.6 24.3 0.97 T03H45 4.5 0 322 335 0.96 312 282 1.10 37.8 41.4 0.91 29.9 32.0 0.93 T03H60 6.0 0 350 414 0.85 322 296 1.09 42.2 47.6 0.89 34.4 36.6 0.94 T03H75 7.5 0 421 484 0.87 — 289 — 48.8 53.1 0.92 40.5 43.5 0.93 T03H15N 1.5 197 249 274 0.91 199 208 0.96 17.0 19.1 0.89 14.9 13.4 1.11 T03H45N 4.5 197 441 486 0.91 307 277 1.11 36.3 37.6 0.97 30.6 29.3 1.04 T03H75N 7.5 197 678 725 0.94 — 247 — 50.0 52.7 0.95 43.8 40.4 1.08 平均值μ 0.92 1.04 0.93 1.01 方差δ 0.001 0.004 0.001 0.005

表 2 验证算例与计算结果 Table 2 Verification example and calculation results

图 3(Fig. 3)

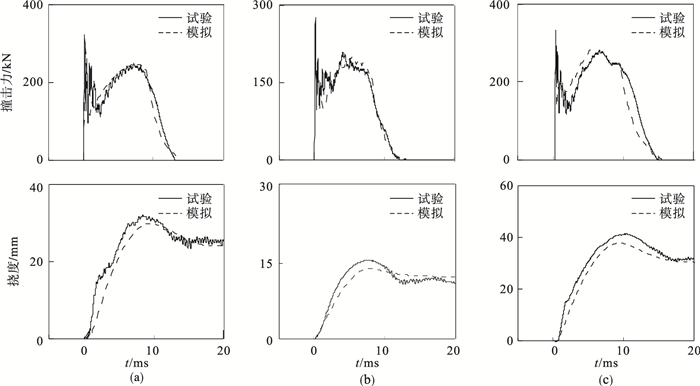图 3 试验与数值模拟结果对比Fig.3 Comparison of test and FE results (a)—T03H30；(b)—T03H15N；(c)—T03H45.

图 4(Fig. 4)

图 4 撞击区域损伤对比Fig.4 Comparison of damage at impact area (a)—试验(T03H75)[12]；(b)—有限元(T03H75).

1.4 能量变化分析图 5给出了典型SC板T03H30(源自文献[12])在撞击过程中各部件内能时程曲线以及落锤动能时程曲线，各部件内能与落锤动能变化曲线均取自有限元计算结果.可见，撞击过程开始后，落锤动能开始迅速下降，损耗的落锤动能转化为构件各部件的内能，其中混凝土内能增长最快且占比最多.研究结果表明，撞击荷载作用下，夹层混凝土是主要的耗能部件.当试件达到最大挠度时，落锤动能降为0，各部件内能达到峰值.然后，随着试件发生回弹，构件的少部分内能转化为落锤的动能，试件各部件的内能变化趋于平稳.
图 5(Fig. 5)

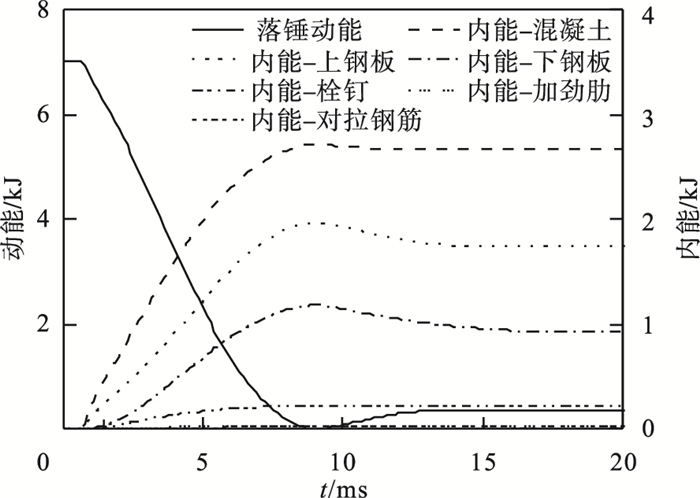图 5 落锤动能与SC板各构件内能时程曲线Fig.5 Time interval curves of kinetic energy of drop hammer and internal energy of each component of SC panel

2 参数分析2.1 钢板含钢率的影响在构件截面高度一定时，钢板含钢率对SC板撞击力时程(F-t)与跨中挠度时程(w-t)曲线的影响如图 6所示.其中混凝土强度、钢板屈服强度、落锤质量、撞击高度、边界条件与撞击物形状分别为30 MPa、235 MPa、180 kg、2 m、四边简支与方形.
图 6(Fig. 6)

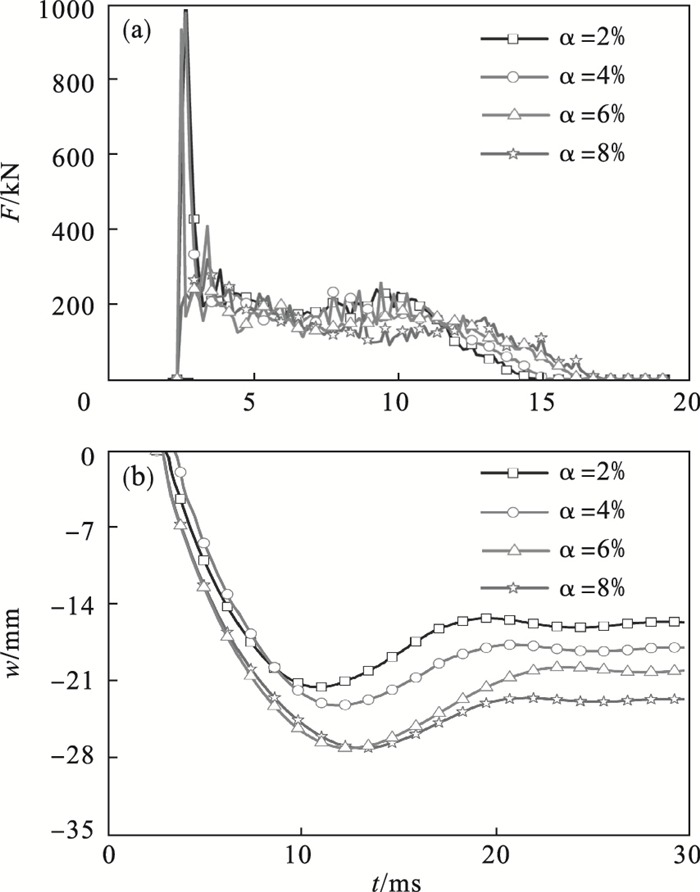图 6 钢板含钢率的影响Fig.6 Effect of steel plate ratio (a)—撞击力时程曲线；(b)—跨中挠度时程曲线.

可见，当α从2%增大到4%时，在撞击作用下SC板的膜力峰值变化不大；而当α从4%增大到8%时，SC板膜力峰值明显降低，跨中挠度明显增大，可能由于混凝土厚度的减少对构件整体刚度的削弱作用，构件产生了更大变形.综上，在本文参数研究的范围内，当α大于4%时，钢板含钢率对SC板动力响应影响显著.
2.2 钢板屈服强度的影响图 7给出了钢板屈服强度(f_y)对SC板撞击力时程(F-t)与跨中挠度时程(w-t)曲线的影响，其中混凝土强度、钢板含钢率、落锤质量、撞击高度、边界条件与撞击物形状分别为30 MPa、4%、180 kg、2 m、四边简支与方形.
图 7(Fig. 7)

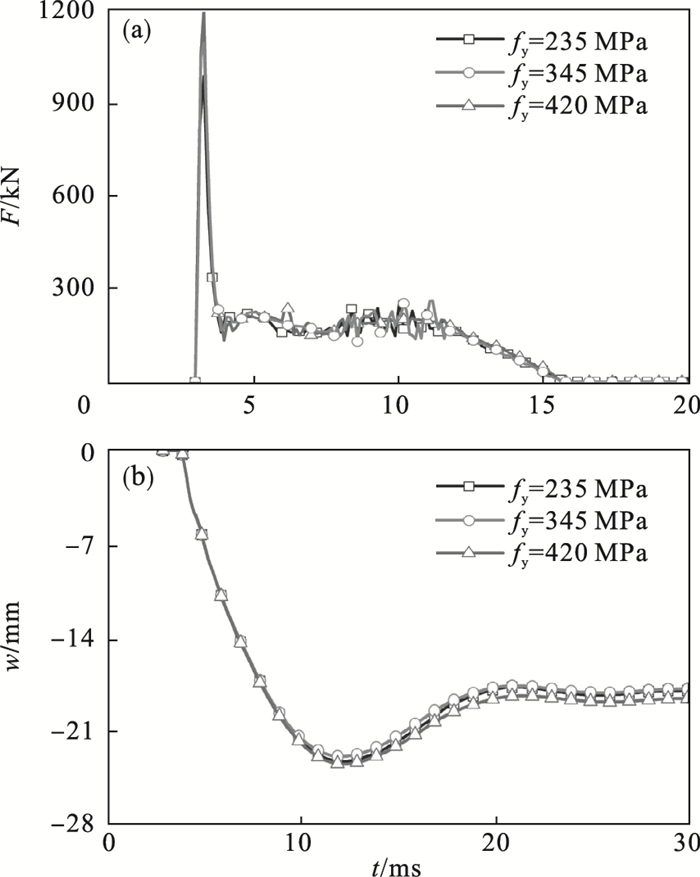图 7 钢板屈服强度的影响Fig.7 Effect of steel plate yield strength (a)—撞击力时程曲线；(b)—跨中挠度时程曲线.

可以发现，钢板屈服强度对构件撞击力惯性峰值有一定的影响，随着钢板屈服强度提高，构件撞击力惯性峰值有所增大，主要是f_y的增大使得接触刚度提高所致.钢板屈服强度的增大对构件撞击力膜力峰值与跨中挠度几乎没有影响，主要是由于钢板屈服强度的提高对构件抗弯刚度几乎没有影响.综上，钢板屈服强度对SC板动力响应影响较小.
2.3 撞击高度的影响图 8给出了落锤撞击高度对SC板撞击力时程(F-t)与跨中挠度时程(w-t)曲线的影响，其中混凝土强度、钢板含钢率、落锤质量、钢板屈服强度、边界条件与撞击物形状分别为30 MPa、4%、180 kg、235 MPa、四边简支与方形.
图 8(Fig. 8)

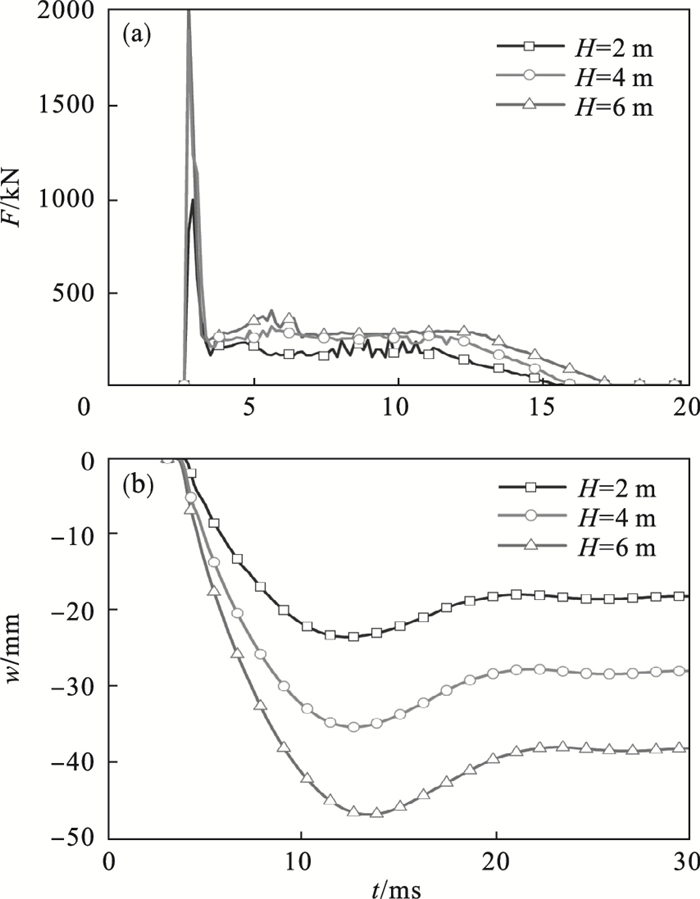图 8 撞击高度的影响Fig.8 Effect of impact height (a)—撞击力时程曲线；(b)—跨中挠度时程曲线.

可见，撞击高度的增大使得构件撞击力惯性峰值、撞击力持时与撞击膜力峰值明显提高，是因为撞击力惯性峰值主要和撞击速度(高度)、接触刚度与接触质量有关，撞击力膜力峰值主要与构件的抗弯刚度有关.撞击高度的增大增加了落锤的撞击速度，致使材料应变率效应明显，构件抗弯刚度提高.
此外，构件需要通过产生更大的塑性变形消耗撞击能量，撞击力持时明显增加.如图 8b所示，当撞击高度从2 m增加到4 m时，构件跨中残余变形增加了54%；当撞击高度从4 m增加到6 m时，构件跨中残余变形增加了36%.综上，撞击高度对SC板的动力响应影响显著.
2.4 撞击物形状的影响图 9为撞击物形状对SC板撞击力时程(F-t)与跨中挠度时程(w-t)曲线的影响.其中，混凝土强度、钢板含钢率、落锤质量、钢板屈服强度、边界条件与撞击高度分别为30 MPa、4%、180 kg、235 MPa、四边简支与2 m.
图 9(Fig. 9)

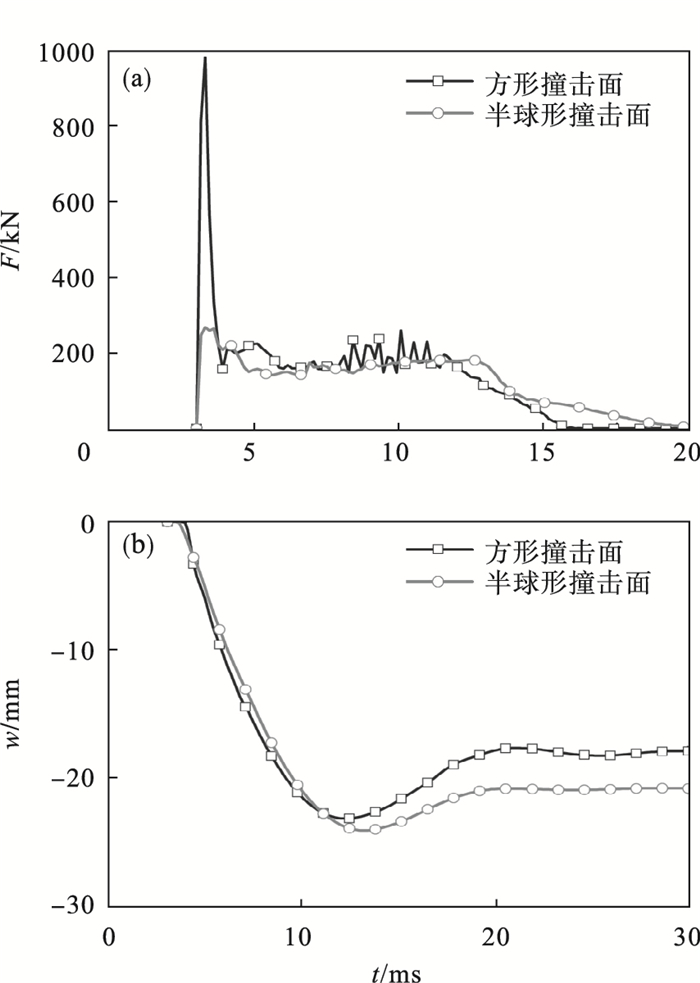图 9 撞击物形状的影响Fig.9 Effect of indenter shape (a)—撞击力时程曲线；(b)—跨中挠度时程曲线.

可以发现，方形撞击面造成的撞击力惯性峰值明显高于半球形，撞击过程持时与跨中挠度明显小于半球形，表明方形撞击面作用下构件的抗撞性能较好.这是因为不同形状的冲击头与构件的接触面积不同，使得冲击头与构件接触刚度发生变化.撞击过程中撞击力惯性峰值与接触刚度相关，平头落锤撞击下锤头与试件的接触刚度更大，加速更快，因此会产生更大的撞击力惯性峰值^[21].此外，方形撞击面撞击后对受撞区域的混凝土造成的冲切锥体面积较大，通过混凝土破碎吸收的能量比较多，钢板变形较小.
图 10进一步给出了方形与半球形撞击物作用下SC板上层钢板Mises应力云图.可见，半球形撞击物作用下撞击区域最大应力约是方形撞击面的1.35倍，半球形撞击物对构件会造成更加严重的损伤.综上，撞击物形状对构件动力响应影响明显，在对SC板的抗撞设计中应予以考虑.
图 10(Fig. 10)

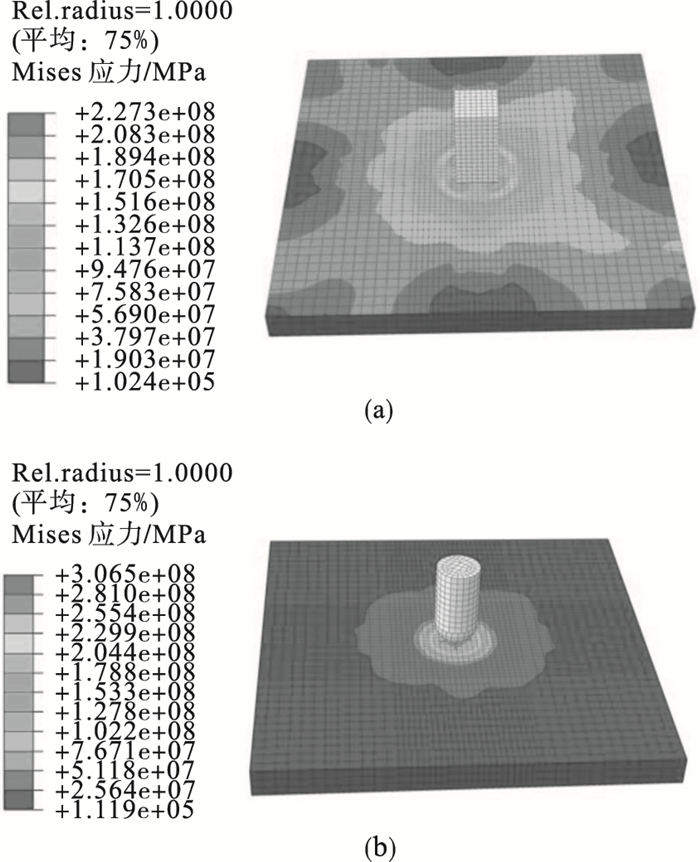图 10 上层钢板Mises应力云图Fig.10 Mises stress nephogram of top steel faceplate (a)—方形撞击物；(b)—半球形撞击物.

2.5 边界条件的影响图 11为不同边界条件对SC板撞击动力响应的影响.其中混凝土强度、钢板含钢率、落锤质量、钢板屈服强度、撞击物形状与撞击高度分别为30 MPa、6%、180 kg、235 MPa、方形与2 m.
图 11(Fig. 11)

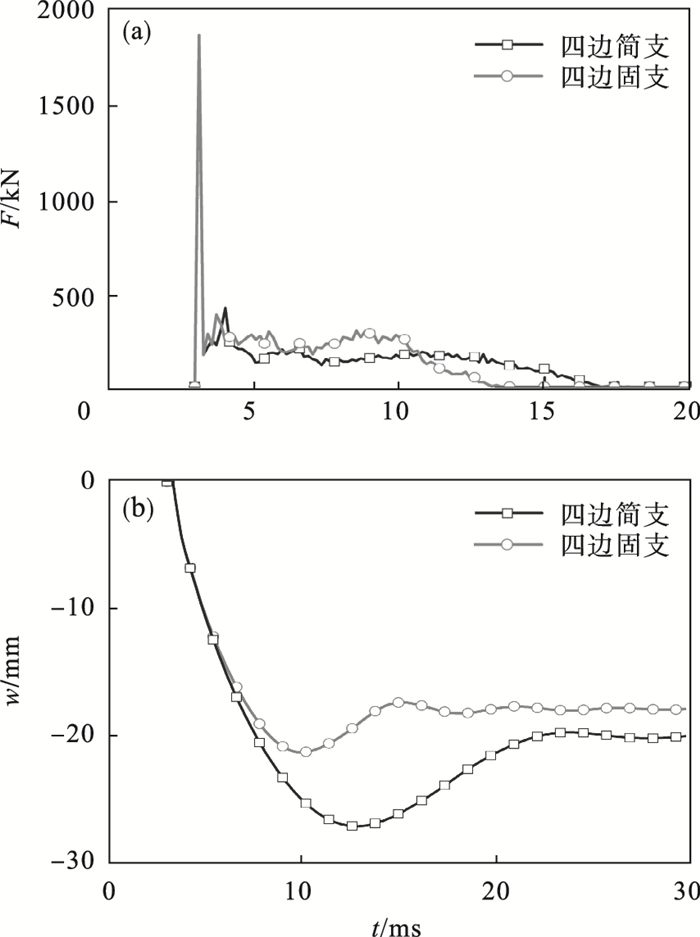图 11 边界条件的影响Fig.11 Effect of boundary conditions (a)—撞击力时程曲线；(b)—跨中挠度时程曲线.

可以发现，随着边界条件的增强，构件撞击力惯性峰值与膜力峰值显著提高，撞击力持时与跨中挠度明显减小.主要是由于边界条件增强，构件的抗弯刚度得到大幅提升，提高了构件的耐撞击性能.综上，边界条件对构件动力响应影响显著.
3 动力响应计算撞击作用下结构构件的最大挠度是工程设计所关注的，本文根据文献[11]提到的能量守恒法(energy method, EM)，并基于板壳理论^[22]计算SC板在撞击荷载作用下的跨中最大挠度(w_max).
图 12给出了简化计算模型(EM模型)示意图，关键输入参数与相关计算公式分别见表 3与表 4.其中：E_e为等效初始动能；R(w)为抗力；k_y为屈服点割线刚度；k_g为整体变形刚度，根据板壳理论^[22]建议的公式进行计算；k_b为局部变形刚度(考虑对拉钢筋的影响0 < η < 1)，即随着冲切变形的发展SC板内部混凝土发生开裂，并将荷载传递至底部钢板使其发生局部鼓起变形，文中SC板中设置了对拉钢筋，底部钢板局部鼓起变形减小，刚度有所提高，在k_b中引入整体刚度的η倍(0 < η < 1)以表征对拉钢筋的影响；m表示撞击物质量；v₀为撞击速度；m_s为SC板的质量；L_s为构件跨度；w(t)为下钢板板底中心挠度；m_e为SC板等效质量，依据文献[23]取值0.2 m_s；n_t为单侧钢板栓钉数量；n_ah为撞击区域对拉钢筋数量；c为撞击区域宽度.
图 12(Fig. 12)

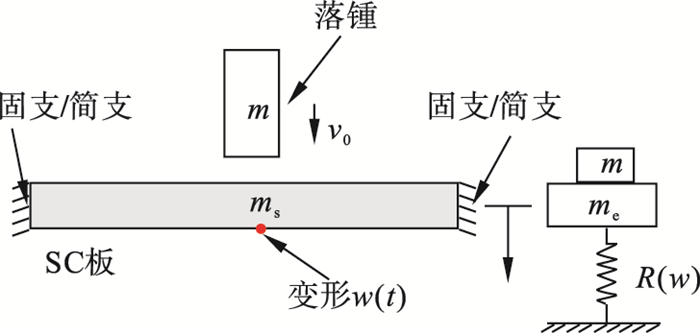图 12 简化计算模型示意图Fig.12 Diagram of EM model

表 3(Table 3)

表 3 简化模型需要的关键参数Table 3 Key parameters required for the model 试件来源 m/kg Ls/mm nt nah c/mm 本文试件 180 1 800 256 8 200 文献[12] 233.5 750 65 5 80

表 3 简化模型需要的关键参数 Table 3 Key parameters required for the model

表 4(Table 4)

表 4 不同边界条件下的相关计算公式Table 4 Calculation formulas under different boundary conditions 变量 四边简支 四边固支 Ee R(w) ky kg kb

表 4 不同边界条件下的相关计算公式 Table 4 Calculation formulas under different boundary conditions

图 13为利用EM法计算得到的构件跨中最大挠度值与本文有限元计算和文献[12]中试验结果值的对比.可以发现，在参数研究范围内公式可较好预测不同边界SC板在撞击作用下的跨中最大挠度，便于SC板的防撞设计.
图 13(Fig. 13)

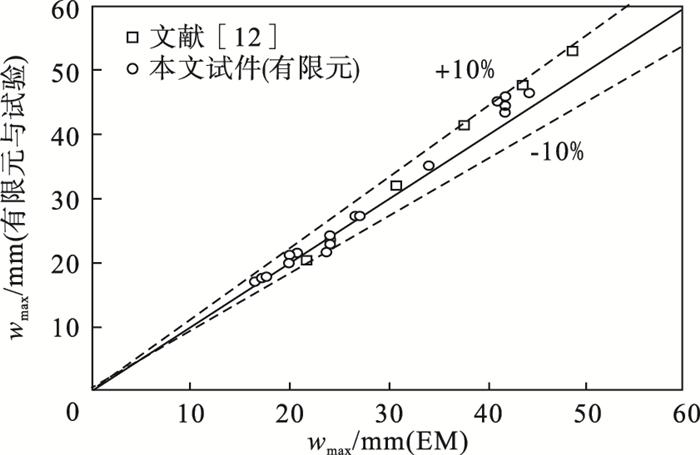图 13 由公式预测与有限元计算、试验得出的wmax值的比较(三条线表示相对误差)Fig.13 wmaxvalues obtained from equation, FE and test

4 结论1) 本文采用ABAQUS建立的有限元模型可以有效预测SC板在落锤撞击作用下的撞击力、挠度以及破坏模式.
2) 钢板含钢率、撞击高度、撞击物形状与边界条件对构件撞击力与跨中挠度影响较大，且当钢板含钢率大于4%时，钢板含钢率的影响更加显著，而钢板屈服强度对构件动力响应的影响较小.
3) 简化能量守恒法可有效预测不同边界SC板在撞击荷载作用下的跨中最大挠度，为该类构件在撞击荷载作用下损伤评估与抗撞性能研究提供参考.
参考文献

[1]	Hilo S J, Badaruzzaman W H W, Osman S A, et al. A state-of-the-art review on double-skinned composite wall systems[J]. Thin-Walled Structures, 2015, 97: 74-100. DOI:10.1016/j.tws.2015.09.007
[2]	Liew J Y R, Yan J B, Huang Z Y. Steel-concrete-steel sandwich composite structures—recent innovations[J]. Journal of Constructional Steel Research, 2017, 130: 202-221. DOI:10.1016/j.jcsr.2016.12.007
[3]	Wang R, Han L H, Hou C C. Behavior of concrete filled steel tubular(CFST)members under lateral impact: experiment and FEA model[J]. Journal of Constructional Steel Research, 2013, 80: 188-201. DOI:10.1016/j.jcsr.2012.09.003
[4]	Wang R, Han L H, Zhao X L, et al. Experimental behavior of concrete filled double steel tubular(CFDST)members under low velocity drop weight impact[J]. Thin-Walled Structures, 2015, 97: 279-295. DOI:10.1016/j.tws.2015.09.009
[5]	安国青, 赵晖, 王蕊, 等. 外包不锈钢圆中空夹层钢管混凝土柱抗撞计算方法研究[J]. 工程力学, 2021, 38(6): 227-236. (An Guo-qing, Zhao Hui, Wang Rui, et al. Calculation method for impact resistance of circular concrete-filled double-skin tubular columns with external stainless steel tube[J]. Engineering Mechanics, 2021, 38(6): 227-236.)
[6]	Zhao H, Wang R, Hou C C, et al. Experimental behaviour of hollow reinforced concrete members with inner octagonal steel tube under lateral impact[J]. Advances in Structural Engineering, 2019, 22(15): 3328-3340. DOI:10.1177/1369433219858700
[7]	Zhao H, Wang R, Li Q M, et al. Experimental and numerical investigation on impact and post-impact behaviours of H-shaped steel members[J]. Engineering Structures, 2020, 216: 110750. DOI:10.1016/j.engstruct.2020.110750
[8]	Cui J L, Wang R, Zhao H, et al. Built-up battened steel columns under impact loading: experimental and numerical analysis[J]. Journal of Constructional Steel Research, 2021, 179: 106515. DOI:10.1016/j.jcsr.2020.106515
[9]	Remennikov A M, Kong S Y. Numerical simulation and validation of impact response of axially-restrained steel-concrete-steel sandwich panels[J]. Composite Structures, 2012, 94(12): 3546-3555. DOI:10.1016/j.compstruct.2012.05.011
[10]	Remennikov A M, Kong S Y, Uy B. The response of axially restrained non-composite steel-concrete-steel sandwich panels due to large impact loading[J]. Engineering Structures, 2013, 49: 806-818. DOI:10.1016/j.engstruct.2012.11.014
[11]	Sohel K M A, Liew J Y R. Behavior of steel-concrete-steel sandwich slabs subject to impact load[J]. Journal of Constructional Steel Research, 2014, 100: 163-175. DOI:10.1016/j.jcsr.2014.04.018
[12]	Zhao W Y, Guo Q Q, Dou X Q, et al. Impact response of steel-concrete composite panels: experiments and FE analyses[J]. Steel and Composite Structures, 2018, 26(3): 255-263.
[13]	Yan C, Wang Y H, Zhai X M. Low velocity impact performance of curved steel-concrete-steel sandwich shells with bolt connectors[J]. Thin-Walled Structures, 2020, 150: 106672. DOI:10.1016/j.tws.2020.106672
[14]	中华人民共和国住房和城乡建设部. 核电站钢板混凝土结构技术标准: GB/T 51340—2018[S]. 北京: 中国计划出版社, 2018. (Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical standard for steel plate concrete structures of nuclear power plants : GB/T 51340-2018[S]. Beijing: China Plan Press, 2018. )
[15]	Japan Electric Association. Technical guidelines for aseismic design of steel plate reinforced concrete structures buildings and structures: JEAG 4618—2005[S]. Tokyo: Japan Electric Association Nuclear Standards Committee, 2005.
[16]	韩林海. 钢管混凝土结构——理论与实践[M]. 北京: 科学出版社, 2016. (Han Lin-hai. Concrete filled steel tubular structures—theory and practice[M]. Beijing: Science Press, 2016.)
[17]	Al-Thairy H, Wang Y C. A numerical study of the behaviour and failure modes of axially compressed steel columns subjected to transverse impact[J]. International Journal of Impact Engineering, 2011, 38: 732-744. DOI:10.1016/j.ijimpeng.2011.03.005
[18]	Xiang S, Zeng L, Liu Y H, et al. Experimental study on the dynamic behavior of T-shaped steel reinforced concrete columns under impact loading[J]. Engineering Structures, 2020, 208: 110307.
[19]	Comite Euro-International du Beton. CEB-FIP model code 1990[M]. Trowbridge, Wiltshire: Redwood Books, 1993: 48-51.
[20]	Malvar L J, Ross C A. Review of strain rate effects for concrete in tension[J]. ACI Materials Journal, 1998, 95(6): 735-739.
[21]	Hao H, Tran T T, Li H W, et al. On the accuracy, reliability and controllability of impact tests of RC beams[J]. International Journal of Impact Engineering, 2021, 157: 103979.
[22]	Timoshenko S, Woinowsky-Krieger S. Theory of plates and shells[M]. New York: McGraw-hill, 1959.
[23]	Bruhl J C, Varma A H, Kim J M. Static resistance function for steel-plate composite(SC)walls subject to impactive loading[J]. Nuclear Engineering and Design, 2015, 295: 843-859.