付兴¹, 杜文龙¹, 郑帅², 李宏男^1,3
1. 大连理工大学 建设工程学部，辽宁 大连 116024;
2. 中国建筑第八工程局有限公司 东北分公司，辽宁 大连 116021;
3. 沈阳建筑大学 土木工程学院，辽宁 沈阳 110168
收稿日期：2021-06-28
基金项目：国家自然科学基金资助项目(52078104)；大连市高层次人才创新支持计划项目(2020RQ056)；中央高校基本科研业务费专项资金资助项目(DUT21JC07)。
作者简介：付兴(1988-)，男，辽宁葫芦岛人，大连理工大学副教授;
李宏男(1957-)，男，辽宁沈阳人，大连理工大学********，博士生导师。

摘要：为研究良态风与台风作用下的输电线路风振系数，以广东省国古线一铁塔为原型建立了有限元模型，采用谐波叠加法模拟了台风风场，并开展了动力分析.首先，对比了5种国内外设计规范的风振系数计算方法，发现各规范均未单独考虑台风的强脉动特性；然后，基于惯性力法获取了铁塔风振系数并揭示了塔线耦联效应的影响.最后，利用生死单元法定量评估了两种风场下输电线路的抗风性能.结果表明：台风的高湍流特性导致顺风向风振系数大于良态风对应值；导线可增大铁塔横风向基频，并使铁塔振型由单塔的弯曲型变为塔线体系的弯剪型，塔线体系横担处风振系数大于单塔；湍流度从0.14提高至0.20，临界倒塌风荷载降低约11%.因此，台风多发地区的输电塔设计应适当提高湍流度取值，必要时还应考虑塔线耦联效应.
关键词：输电线路风振系数台风塔线耦联效应抗风性能评估
Research on Gust Response Factor and Wind-Resistance Performance of Transmission Lines Under Typhoon
FU Xing¹, DU Wen-long¹, ZHENG Shuai², LI Hong-nan^1,3
1. Faculty of Infrastructures Engineering, Dalian University of Technology, Dalian 116024, China;
2. The Northeast Branch, China Construction Eighth Engineering Bureau Co., Ltd., Dalian 116021, China;
3. School of Civil Engineering, Shenyang Jianzhu University, Shenyang 110168, China
Corresponding author: FU Xing, E-mail: fuxing@dlut.edu.cn.

Abstract: To study the gust response factors(GRF) of transmission lines under normal wind and typhoon, a finite element model is established based on a steel tower of the Guogu line in Guangdong Province. The typhoon wind field is simulated via a harmonic superposition method, and the dynamic analysis is carried out. First, the GRF methods in five design codes at home and abroad are compared. It turns out that none of them considers the strong fluctuating characteristics of typhoon. Then, the GRF is obtained based on the inertia force method, and the tower-line coupling effect on GRF is studied. Finally, the wind-resistance performance of the transmission line under the two wind fields is quantitatively evaluated by the method of birth to death element. The results showed that the high turbulence characteristics of typhoons lead GRF to be greater than that of normal wind and the conductor can increase the natural frequency of the tower in the cross-wind direction, changing the mode from the bending type of a single tower to the bending-shear type of the tower-line system, whose GRF at the cross arm is greater than that of a single tower. The critical collapse wind load will decrease by 11% if the turbulence intensity increases from 0.14 to 0.20. Thus, the design of transmission towers in typhoon-prone areas should properly increase the turbulence intensity and take into account the tower-line coupling effect when necessary.
Key words: transmission linegust response factortyphoontower-line coupling effectwind-resistance performance evaluation
输电线路具有刚柔耦合、跨越距离大和塔体高等典型特征，对风荷载异常敏感，在风荷载作用下极易出现疲劳损伤及屈曲倒塌^[1-2].据统计，逾70%的电力中断由架空输电线路造成，其中台风、飓风等造成的灾害最为严重.中国东部为全球热带气旋多发区，频繁登陆的台风造成了大量的电力中断事故，以2015年超强台风“彩虹”为例，登陆期间共造成220 kV输电线路倒塔46基.强台风具有风速大、高湍流和非平稳等明显特点，可使线路因巨大的惯性力^[3]而发生强烈振动.目前，国内外通常采用风振系数法来考虑结构的顺风向风振响应.
Davenport等^[4]首先根据随机振动理论提出了阵风响应因子(即风振系数)的概念，并根据近百次的强风观测记录提出了顺风向的脉动风速谱.Simiu等^[5]改进了Davenport的阵风响应因子理论，并被许多国家的设计规范所采纳，但是该理论仅能较为准确地估计位移响应.为克服该方法的局限性，Kareem等^[6]提出通过基底弯矩来计算风振系数.Piccardo等^[7]提出一种计算结构非耦合顺风向荷载、横风向荷载和扭转荷载的闭合解，它可计算柔性结构在湍流抖振或旋涡脱落作用下引起的响应，其三维风振系数计算方法被一般化为经典顺风向风振系数理论.目前，风振系数的实测研究相对较少，其中Harikrishna等^[8]在一座52 m高的格构式塔架上进行了全尺度的现场实测，分别获取了基于基底弯矩和塔顶位移响应的风振系数，其中位移风振系数明显小于各类规范的推荐值，而基底弯矩风振系数则与各类规范推荐值基本相当.上述研究都是基于良态风模型开展的，因此对台风作用下的输电线路风振系数还需开展进一步的研究.
现有风振系数理论均采用单塔计算模型，未考虑导线影响.随着输电工程的不断发展，跨越距离数千米的特高压输电线路得到了广泛应用，导线的影响也逐渐变得不可忽视.李正良等^[9]基于风洞试验和数值仿真研究了塔线体系与单塔风振系数的差异，并作了风攻角的参数分析，研究表明塔线体系横风向风振系数明显大于单塔；谢强等^[10]基于三塔两线体系开展了风洞试验，指出高风速下输电塔和导线响应的功率谱密度会出现能量交叉，塔线耦合效应大大增强.现有研究大多把塔线体系风振系数与单塔之间的差异归因于导线增大了铁塔局部质量和受风面积，而未从模态着手开展相关研究.
本文对比了5种国内外设计规范的风振系数计算方法，进而模拟了台风的三维风场，分析了台风作用下的加速度风振系数，从导线对铁塔模态的影响出发，揭示了风振系数的塔线耦联效应；最后，建立了输电线路的抗风性能评估框架，定量分析了湍流度和水平档距对抗风性能的影响.
1 各国规范对比研究1.1 建筑结构荷载规范(GB 50009—2012)^[11]结构i点处的风振系数β_zi可按下列公式计算：

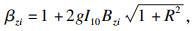(1)

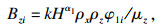(2)

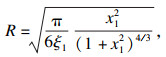(3)

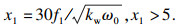(4)

式中：I₁₀为10 m高度处的名义湍流度；g为峰值因子，中国规范取2.5；B_zi和R分别为背景响应因子和共振响应因子；k和α₁均为与地面粗糙度相关的系数；φ_1i为i点处的一阶振型系数；H为结构总高度；ρ_x和ρ_z分别为水平及竖直方向相关系数；μ_z为风压高度变化系数；ξ₁为结构阻尼比；f₁为一阶频率；k_w为地面粗糙度相关系数；ω₀为基本风压.
GB 50009—2012仅适用于质量和外形沿高度连续变化的结构，而输电塔沿高度一般分布有若干横担，直接采用该规范计算风振系数误差较大.
1.2 架空输电线路荷载规范(DL/T 5551—2018)^[12]考虑到输电塔的结构特点，DL/T 5551—2018对GB 50009—2012中的背景响应进行了修正，采用该规范计算杆塔风振系数时应对杆塔分段，即简化为“糖葫芦串”模型.风振系数按下述公式计算：

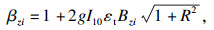(5)

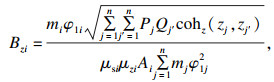(6)

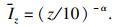(7)

式中：n为输电塔的分段数目；ε_t为铁塔风荷载脉动折减系数；m_i为第i分段质量；μ_si为风载体型系数；P_j=μ_sjμ_zjφ_1jI_zjA_j，Q_j^'=μ_sj^'μ_zj^'φ_1j^'I_zj^'A_j^'，其中μ_s，μ_z，φ₁，I_z和A分别为风载体型系数、风压高度变化系数、一阶振型系数、湍流度函数和受风面积，下标j和j^'分别代表分段的编号；A_i为第i分段的受风面积；μ_zi为风压高度变化系数；z为计算点处高度；α为地面粗糙度幂指数；coh_z(z_j，z_j^')为竖向相干函数，其值取.
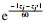
旧规范DL/T 5551—2012规定，若输电塔的高度低于60 m，则各高度处的风振系数取相同值，超过60 m后则采用GB 50009—2012推荐的方法计算.DL/T 5551—2012直接将建筑结构领域的风振系数理论引入到输电线路领域，而未考虑输电塔的外形和质量在高度方向上有显著突变的特点，因此新规范DL/T 5551—2018对GB 50009—2012中的背景分量因子作了优化，以修正横担的影响.
1.3 美国规范(ASCE No. 74—2009)^[13]格构式桁架结构风振系数的计算公式为

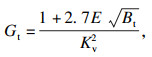(8)

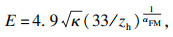(9)

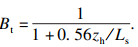(10)

式中：z_h为输电塔总高度的2/3(单位：英尺，1英尺=0.304 8 m)；K_v为3 s阵风风速与10 min平均风速之比；κ，α_FM和L_s等参数取值见规范.
ASCE No. 74—2009认为，现阶段的输电塔高度一般不会超过60 m，结构的一阶频率一般在2.0~4.0 Hz，导线及地线巨大的气动阻尼会降低体系的共振响应，故该规范忽略了共振响应.
1.4 国际电工委员会规范(IEC 60826—2017)^[14]该规范采用与地形有关的风速关联因子G_t来考虑脉动风影响.A类地形为大范围逆风水域及平坦的沿海地区，B类地形为开阔地，C类地形为有低矮障碍物的地区，D类地形为有高大障碍物的郊区或城镇.G_t在4类地形中的拟合公式如下：

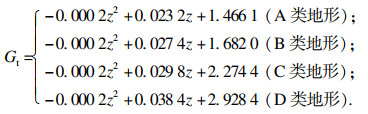(11)

G_t仅考虑了高度和地形的影响，风场的影响被隐藏在地形之中，因而G_t=μ_zβ_z.若将风振系数从风速关联因子G_t中分离出来，则有

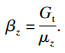(12)

该规范的风振系数表达式仅考虑了地形的影响，而忽略了结构自身的效应.
1.5 欧洲规范(BS EN 50341-1:2012)^[15]BS EN 50341-1:2012并未单独考虑脉动风的影响，也未给出风振系数的概念，但对比中国规范的风荷载计算方法可知，其风振系数表达式为

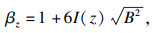(13)

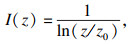(14)

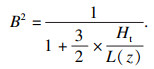(15)

式中：H_t为塔身的总高度；L(z)为高度z处的湍流积分尺度；z₀为粗糙长度.
该规范的风振系数包含高度、地面粗糙度和结构尺寸等参数，考虑的因素较为全面.
1.6 算例分析以广东省国古线一角钢塔Tower 1为例(下文所有算例均采用该塔)，分别计算了上述5种规范的风振系数推荐值.该塔总高度68.5 m，自振频率2.00 Hz，基本风速为25 m/s，10 m高度处名义湍流度为0.14，位于中国规范和IEC 60826—2017的B类地形、ASCE No. 74—2009的C类地形，以及BS EN 50341-1:2012的Ⅱ类地形^[11].将该输电塔简化为12个离散的计算点，如图 1所示.
图 1(Fig. 1)

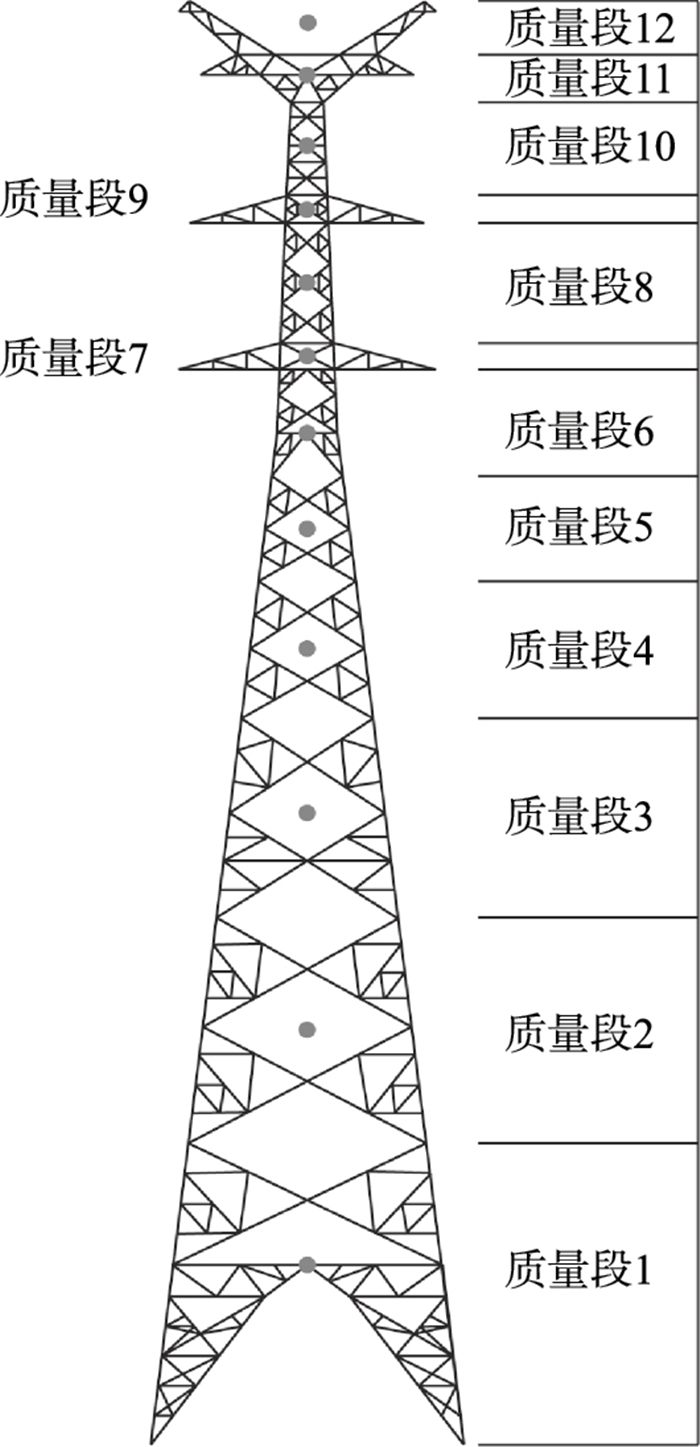图 1 计算点Fig.1 Calculation points

图 2绘制了上述5种规范风振系数沿塔高度的分布，中国规范风振系数推荐值均随高度的增加而增大，IEC 60826—2017和BS EN 50341-1:2012的推荐值则随高度的增加而减小，ASCE No. 74—2009的风振系数推荐值则始终为常数.各国规范均未单独考虑台风的特殊性，亦未考虑导线的影响.
图 2(Fig. 2)

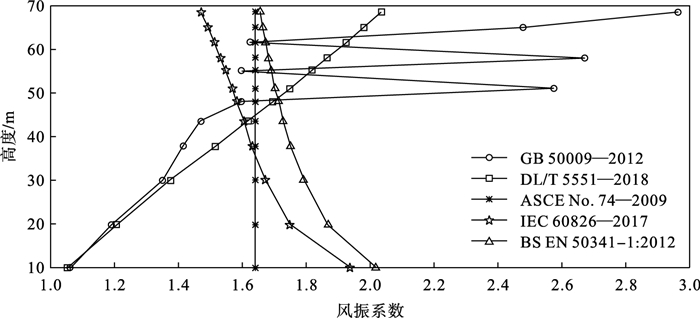图 2 各规范风振系数值沿塔高度的分布Fig.2 Distribution of gust response factor along the height of tower based on various codes

Fu等^[16]根据实测研究指出，台风具有较高的湍流度，随着风速的提高，湍流度会逐渐稳定在0.20左右，而中国规范取值仅为0.14.分别取10 m处名义湍流度为0.14和0.20，中国规范风振系数沿高度的分布如图 3所示.湍流度从0.14提高到0.20，风振系数有显著增大.图中最高点为地线挂点，此处风振系数DL/T 5551—2018推荐值从2.96提高到3.80，提高了28.4%；GB 50009—2012推荐值从2.08提高到2.46，提高了18.2%.表明DL/T 5551—2018的风振系数计算方法对湍流度更敏感.
图 3(Fig. 3)

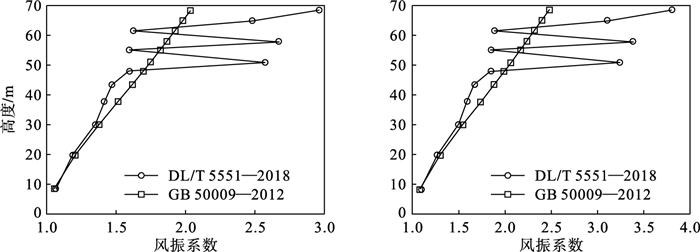图 3 不同湍流度对应的风振系数Fig.3 GRFs with different turbulence intensities (a)—湍流度取0.14；(b)—湍流度取0.20.

2 台风风振系数2.1 风场模拟与下击暴流或龙卷风等小尺度风暴相比，短时间内的台风风速序列相对平稳.台风平均风速与良态风类似，沿高度呈对数增长，可用如下的指数函数予以描述，风剖面幂指数可按表 1取值^[17].

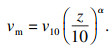(16)

式中：v_m为平均风速；v₁₀为10 m高度处的基本风速；z为模拟点的高度；α为风剖面幂指数.
表 1(Table 1)

表 1 风剖面幂指数Table 1 Power-law exponents of wind profile 地面粗糙类别 描述 中国规范 台风 A1 直接暴露在风中的平坦地区 0.12 0.10 B1 有分散障碍物的郊区 0.15 0.14 C1 有密集建筑物的城市地区 0.22 0.22

表 1 风剖面幂指数 Table 1 Power-law exponents of wind profile

目前，脉动风速时程的模拟方法主要有谐波叠加法、线性滤波法和小波逆变换法等.本文采用谐波叠加法对台风脉动风场进行模拟，具体模拟流程见文献[18]，本文不再赘述.
采用石沅谱模拟台风脉动风速，该谱为不随高度变化的台风水平风速经验谱，由石沅等^[19]在对上海地区的台风进行实测后拟合得出：

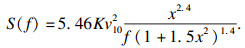(17)

式中：S(f)为风速谱；f为脉动风频率；K为阻力系数，取值为1.682×α^3.937+0.004251，α为风剖面幂指数；x取1200f/v₁₀.
脉动风速的参数如下：1) 地面粗糙度类别为B类；2) 总时间为600 s，时间步长为0.1 s；3) 截止频率为5 Hz；4) 基本风速为40 m/s.
生成了Tower 1各计算点处的风速时程，其中塔顶处的脉动风速时程如图 4所示.
图 4(Fig. 4)

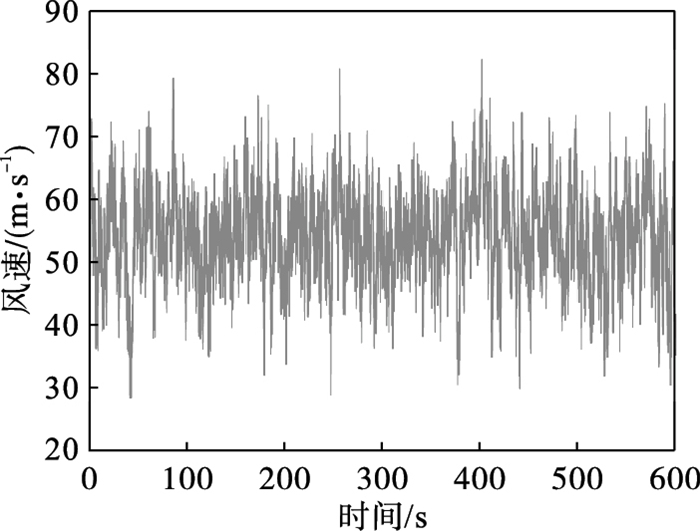图 4 塔顶处的脉动风速Fig.4 Fluctuating wind speed at the tower tip

模拟谱在目标谱附近波动，总体趋势一致，由图 5可以看出，说明模拟程序具有足够的精度.
图 5(Fig. 5)

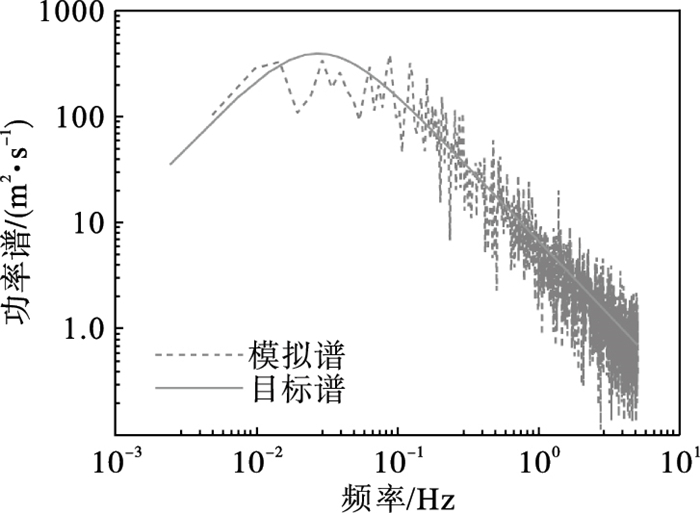图 5 风谱对比Fig.5 The comparison of wind spectrums

表征风场特性的参数除了风速之外还有湍流度，它反映了脉动风相对强度，常用脉动风速均方根与时均速度(时距10 min)之比来表示.模拟的台风湍流度值为0.19，远大于中国规范的推荐值0.14，表明台风脉动强度明显大于良态风.由准稳态理论，总风荷载计算式为

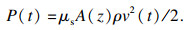(18)

式中：μ_s为风载体型系数；v(t)为总风速，代表平均风速与脉动风速之和；ρ为空气的密度(1.25 kg/m³)；A(z)为结构承受风荷载的投影面积.
2.2 风振系数计算基于ANSYS软件建立了Tower 1的有限元模型，如图 6所示.采用Beam 188单元模拟主材及辅材，单元划分数量为3.风荷载时程施加在与计算点同高的4根主材上.
图 6(Fig. 6)

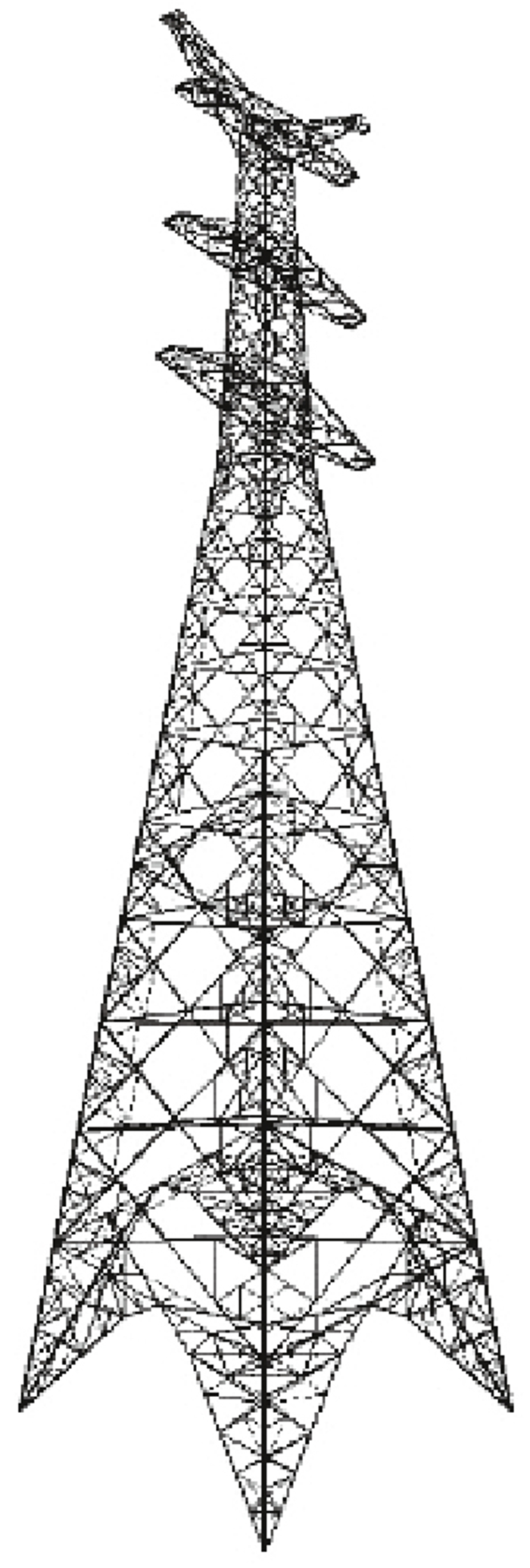图 6 Tower 1的有限元模型Fig.6 The FEM of Tower 1

对Tower 1进行了动力分析，提取了铁塔各计算点处主材的加速度时程，并根据惯性力法(推导过程见文献[17])计算台风风振系数β_z：

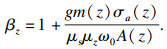(19)

式中：m(z)为高度z处的质量；σ_a(z)为高度z处加速度均方根；μ_z为风压高度变化系数.
将模拟台风风振系数同《架空输电线路荷载规范》(DL/T 5551—2018)的推荐值进行了对比，二者沿高度的趋势一致，如图 7所示.当湍流度取0.19时，模拟台风风振系数与规范推荐值基本重合；若湍流度取0.14，则模拟台风风振系数明显大于规范推荐值，说明现行中国规范低估了该塔在台风作用下的风振系数，其中对湍流度的低估是主要原因.
图 7(Fig. 7)

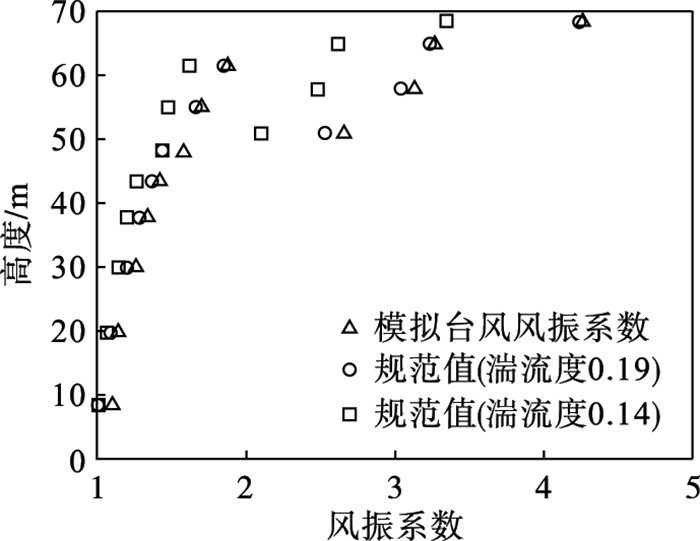图 7 模拟台风风振系数与中国规范推荐值对比Fig.7 The comparison of GRFs between the simulation results under typhoon and Chinese code

2.3 塔线耦联效应为了探究风振系数的塔线耦联效应，本节在Tower 1单塔有限元模型的基础上，分别建立了塔线体系的有限元模型，其水平档距分别为200，400和600 m，如图 8所示.分别采用Link 10单元和Link 8单元模拟导线和绝缘子.采用循环找形方法建立了单线模型，其中杆单元初应变取3.3×10^-6，运行张力取拉断力的25%.导线和地线直径分别为34和16 mm，单位长度质量分别为2.007和0.639 kg/m.与铁塔的简化方法类似，将导线等距简化为20个计算点，并在计算点上施加风荷载.
图 8(Fig. 8)

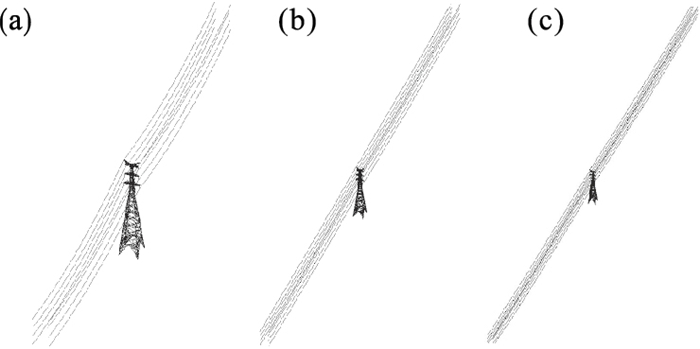图 8 不同档距塔线体系的有限元模型Fig.8 FEMs of tower-line system with different spans (a)—200 m；(b)—400 m；(c)—600 m.

首先，识别了单塔及塔线体系的频率.分别对4组模型进行了模态分析，单塔基频为2.00 Hz.塔线体系前5阶模态均为导线模态，第6阶模态为铁塔横风向的整体变形，对应200，400和600 m档距塔线体系的铁塔基频分别为2.63，2.61和2.60 Hz，说明导线增大了铁塔横风向的基频.铁塔基频随水平档距的增大而减小，主要原因是该塔较柔，导线提供的附加侧向刚度大于附加质量的影响.
进而，提取了4组模型中铁塔的基本振型，如图 9所示.导线使得铁塔的振型从弯曲型变为弯剪型，且剪切变形随水平档距的减小而增大.现有理论计算风振系数时均采用弯曲型的单塔振型，这显然并不合理.塔线体系之间横风向的频率和振型区别不大，但塔线体系与单塔之间有显著差别.
图 9(Fig. 9)

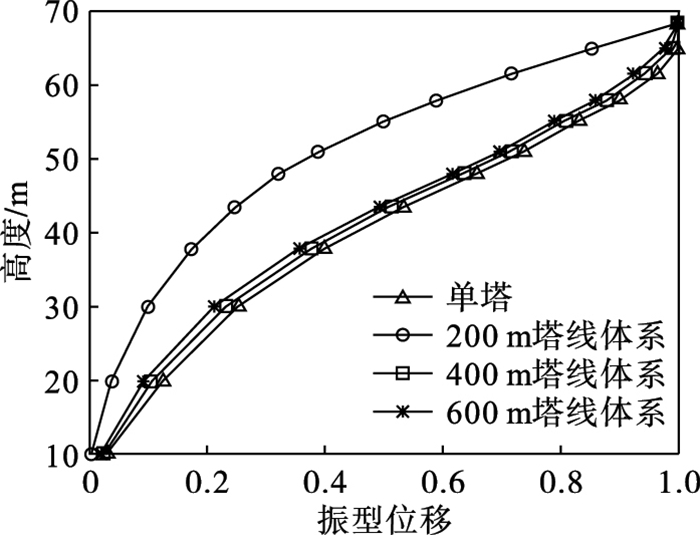图 9 不同档距塔线体系及单塔的振型Fig.9 Mode shapes of tower-line systems with different spans and the single tower

对塔线体系的台风风场开展了动力分析，获取了4组模型的加速度风振系数.图 10表明，塔线体系横担处风振系数明显大于单塔，但塔线体系之间的风振系数差异较小，这与频率和振型方面的规律十分相似，说明导线对铁塔频率及振型的影响是导致塔线体系和单塔风振系数差异的重要因素.因此，在计算风振系数时，应根据塔线体系的动力分析来获取铁塔基频和振型.
图 10(Fig. 10)

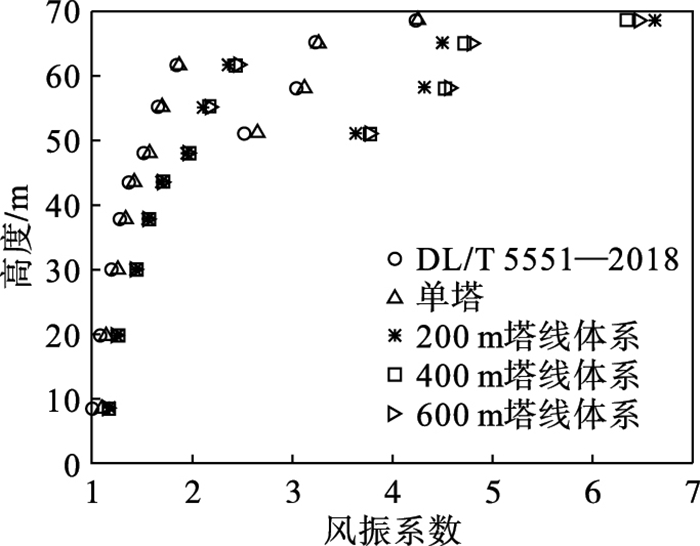图 10 塔线体系和单塔风振系数对比Fig.10 The comparison of GRFs between tower-line system and single tower

3 台风作用下输电线路风振系数3.1 湍流度为定量分析湍流度对输电线路抗风性能的影响，本文基于一致缺陷模态法和生死单元法^[20]提出了如图 11所示的抗风性能评估框架.
图 11(Fig. 11)

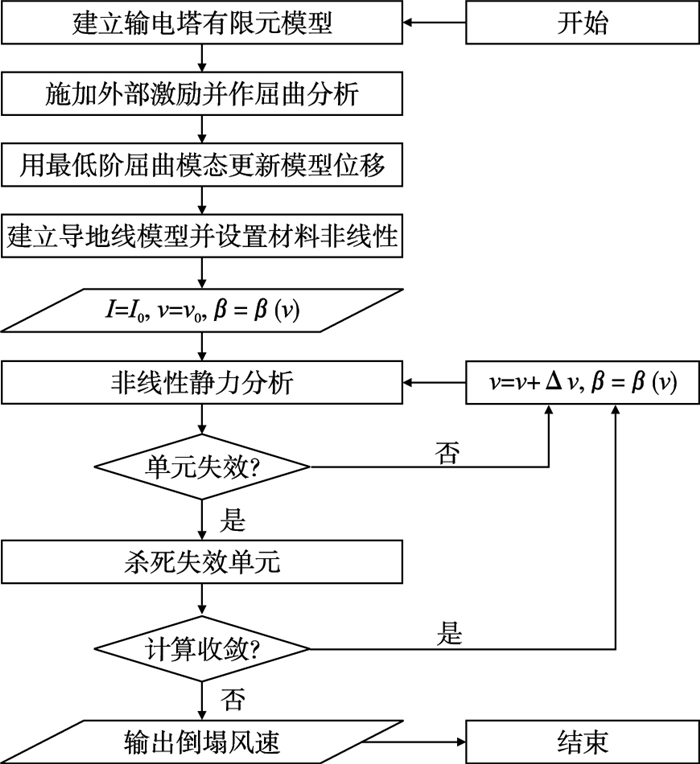图 11 输电线路抗风性能评估框架Fig.11 The evaluation framework of the wind-resistance performance of a transmission line

输电塔风振系数基于《架空输电线路荷载规范》(DL/T 5551—2018)和《建筑结构荷载规范》(GB 50009—2012)，导线风振系数基于《架空输电线路荷载规范》(DL/T 5551—2018).湍流度取值从0.10到0.40，步长为0.02.由于风振系数与基本风速相关，因此每完成一个荷载步要根据基本风速更新风振系数，直至计算发散即可获得临界倒塌风速.
基于图 11所示的计算流程，分别绘制了不同湍流度对应的推覆曲线以及湍流度与倒塌风速之间的关系，分别如图 12和图 13所示.随着湍流度不断提高，输电线路临界倒塌风速逐渐减小.DL/T 5551—2018对应的倒塌风速比GB 50009—2012小，说明考虑横担处质量的不均匀分布之后，前者风振系数明显大于后者.
图 12(Fig. 12)

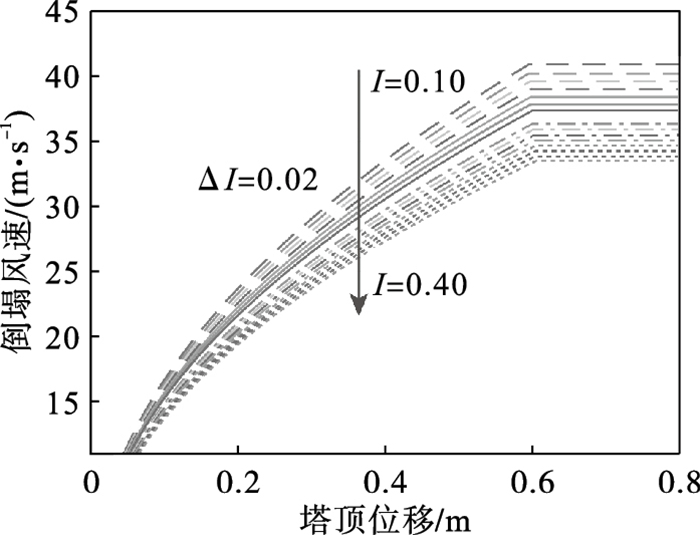图 12 不同湍流度的推覆曲线Fig.12 Pushover curves with various turbulence intensities

图 13(Fig. 13)

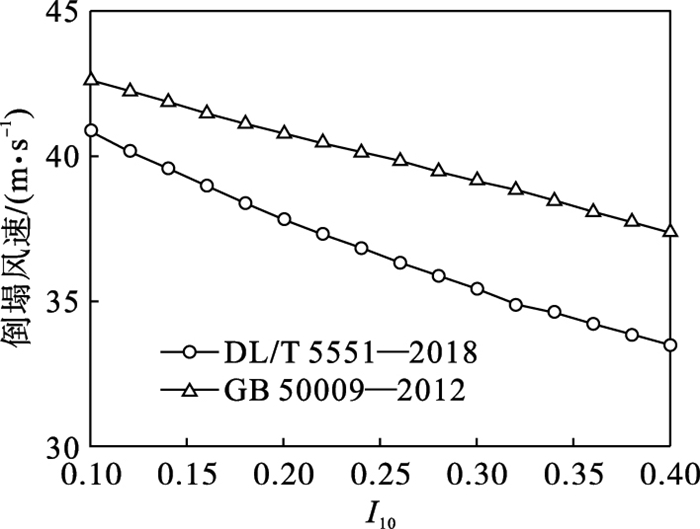图 13 两种规范对应的湍流度与倒塌风速关系Fig.13 Relationship between turbulence intensities and collapse wind speeds based on two codes

根据Sharma等^[21]的研究，台风湍流度约为良态风的1.48倍，DL/T 5551—2018推荐的湍流度取值为0.14，因此台风湍流度取值约为0.20.湍流度取0.14和0.20时对应的临界倒塌风速分别为39.6和37.65 m/s，二者相差1.95 m/s.风荷载与风速之间为平方关系，见式(18)，因而二者临界倒塌风荷载相差11%，说明提高湍流度会显著降低输电线路的临界倒塌风速.
3.2 水平档距以1.6节中的单塔及塔线体系为研究对象，基于前述的分析框架探讨了水平档距对线路抗风性能的影响.图 14和图 15分别为不同水平档距输电线路的推覆曲线，以及水平档距和倒塌风速两者间的关系.水平档距从200 m增加至600 m，输电线路的临界倒塌风速从52.65 m/s迅速降低至39.85 m/s，主要是因为水平档距的增加显著增大了导线通过绝缘子传递给铁塔的风荷载.因而，当水平档距较大时导线风荷载会起到控制作用.
图 14(Fig. 14)

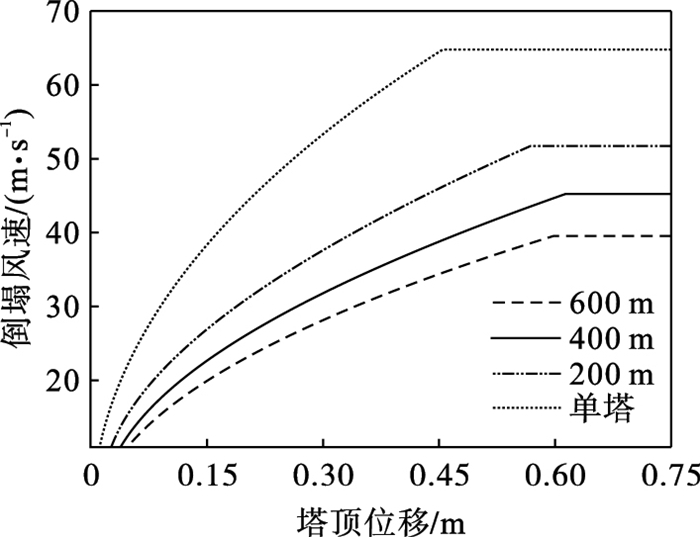图 14 不同水平档距的推覆曲线Fig.14 Pushover curves with various horizontal spans

图 15(Fig. 15)

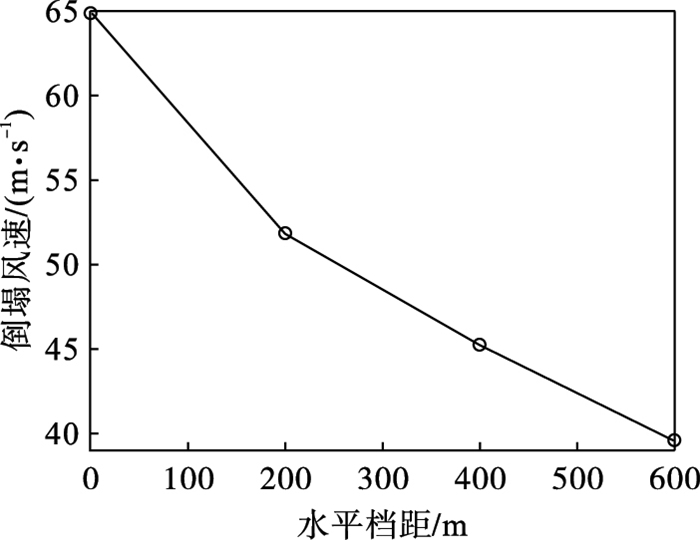图 15 水平档距和倒塌风速关系Fig.15 Relationship between horizontal spans and collapse wind speeds

4 结论1) 现行的各类规范均未考虑台风的强脉动特性，计算模型均为单塔，不考虑塔线耦联效应.
2) 台风湍流度(约为0.19至0.20)和风振系数均明显大于现行中国规范推荐值.
3) 导线会使铁塔横风向的一阶自振频率大于单塔，此影响随水平档距的增大而减小，振型由单塔的弯曲型变为塔线体系的弯剪型，并使塔线体系横担处的风振系数显著大于单塔.
4) 湍流度从0.14提高至0.20，倒塌风荷载降低约11%；水平档距从200 m增加至600 m，倒塌风速从52.65 m/s降低至39.85 m/s.建议设计台风多发区输电线路时应适当提高湍流度取值.
参考文献

[1]	Fu X, Jiang Y, Du W L, et al. A new radial spoiler for suppressing vortex-induced vibration of a tubular tower and its practical design method[J]. Shock and Vibration, 2021, 2021: 6971178.
[2]	Wang J, Li H N, Fu X, et al. Geometric imperfections and ultimate capacity analysis of a steel lattice transmission tower[J]. Journal of Constructional Steel Research, 2021, 183: 106734. DOI:10.1016/j.jcsr.2021.106734
[3]	马涌泉, 邱洪兴. 输电塔-线体系风致响应的鲁棒半主动控制[J]. 东北大学学报(自然科学版), 2016, 37(2): 279-284. (Ma Yong-quan, Qiu Hong-xing. Wind-induced response suppression of transmission tower-line system using a robust and semi-active controller[J]. Journal of Northeastern University(Natural Science), 2016, 37(2): 279-284.)
[4]	Davenport A G, Sparling B F. Dynamic gust response factors for guyed towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(1/2/3): 2237-2248.
[5]	Simiu E, Scanlan R H. Wind effects on structures: fundamentals and applications to design[M]. New York: Wiley, 1996.
[6]	Kareem A, Zhou Y. Gust loading factor—past, present and future[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(12/13/14/15): 1301-1328.
[7]	Piccardo G, Solari G. 3D wind-excited response of slender structures: closed-form solution[J]. Journal of Structural Engineering, 2000, 126(8): 936-943. DOI:10.1061/(ASCE)0733-9445(2000)126:8(936)
[8]	Harikrishna P, Shanmugasundaram J, Gomathinayagam S, et al. Analytical and experimental studies on the gust response of a 52 m tall steel lattice tower under wind loading[J]. Computers & Structures, 1999, 70(2): 149-160.
[9]	李正良, 罗熙越, 蔡青青. 考虑塔-线耦合作用的输电塔体系风振系数研究[J]. 建筑钢结构进展, 2021, 23(3): 119-128. (Li Zheng-liang, Luo Xi-yue, Cai Qing-qing. A study on the wind vibration coefficient of transmission tower system considering tower-line coupling effect[J]. Progress in Steel Building Structures, 2021, 23(3): 119-128.)
[10]	谢强, 杨洁. 输电塔线耦联体系风洞试验及数值模拟研究[J]. 电网技术, 2013, 37(5): 1237-1243. (Xie Qiang, Yang Jie. Wind tunnel test and numerical simulation on transmission tower-line coupling system[J]. Power System Technology, 2013, 37(5): 1237-1243.)
[11]	中华人民共和国住房和城乡建设部. 建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012. (Ministry of Housing and Urban-Rural Development of the People's Republic of China. Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Architecture & Building Press, 2012. )
[12]	中华人民共和国国家能源局. 架空输电线路荷载规范: DL/T 5551—2018[S]. 北京: 中国计划出版社, 2018. (National Energy Administration of the People's Republic of China. Load code for the design of overhead transmission line: DL/T 5551—2018[S]. Beijing: China Planning Press, 2018. )
[13]	American Society of Civil Engineers. Guidelines for electrical transmission line structural loading: ASCE No. 74—2009[S]. Reston: American Society of Civil Engineers, 2010.
[14]	International Electrotechnical Commission. Design criteria of overhead transmission lines: IEC 60826—2017[S]. Geneva: International Electrotechnical Commission, 2017.
[15]	British Standards Institution. Overhead electrical lines exceeding AC 1 kV. Part 1: general requirements-common specifications: BS EN 50341-1: 2012[S]. Brussels: British Standards Institution, 2012.
[16]	Fu X, Du W L, Li H N, et al. On-site measured gust response factors of transmission towers based on SHM system[J]. Journal of Aerospace Engineering, 2021, 34(1): 04020104. DOI:10.1061/(ASCE)AS.1943-5525.0001218
[17]	Fu X, Du W L, Li H N, et al. Gust response factor of a transmission tower under typhoon[J]. International Journal of Structural Stability and Dynamics, 2021, 21(1): 2150001. DOI:10.1142/S0219455421500012
[18]	Fu X, Zhang X H, Li H N, et al. A high-efficiency simulation method of wind field and its application on transmission line[J]. Wind and Structures, 2021, 33(4): 277-288.
[19]	石沅, 陆威, 钟严. 上海地区台风结构特征研究[C]//第二届全国结构风效应学术会议论文集. 上海: 同济大学, 1988: 106-112. (Shi Yuan, Lu Wei, Zhong Yan. Study on the structural characteristics of typhoon in Shanghai[C]//Proceedings of the 2nd National Conference on Structural Wind Effect. Shanghai: Tongji University, 1988: 106-112. )
[20]	Fu X, Du W L, Li H N, et al. Stress state and failure path of a tension tower in a transmission line under multiple loading conditions[J]. Thin-Walled Structures, 2020, 157: 107012.
[21]	Sharma R N, Richards P J. A re-examination of the characteristics of tropical cyclone winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 83: 21-33.