
 , 方成1, 陈善平1, 阎爽2
, 方成1, 陈善平1, 阎爽2 1. 东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004;
2. 京能秦皇岛热电有限公司,河北 秦皇岛 066004
收稿日期:2021-09-06
基金项目:国家自然科学基金资助项目(61973262,51405068);河北省自然科学基金资助项目(E2019203146,E2020501013);中央高校基本科研业务费专项资金资助项目(N2023023)。
作者简介:侯东晓(1982-),男,山西平遥人,东北大学副教授。
摘要:考虑板带轧机垂直振动对液压压下系统中四通伺服电磁阀非线性流量的影响,推导出非线性流量变化下的液压缸的非对称分段弹簧力,并建立了板带轧机液压压下-垂直振动动力学方程.运用平均法求解出该轧机振动系统的幅频响应方程,并利用奇异性理论求解了轧机在动态轧制过程的分岔特性,得到4组不同的转迁集及其对应的分岔图,分析了开折参数对轧机分岔特性的影响.最后以实际轧机参数为例,通过仿真发现系统幅频曲线在分段处出现拐弯特性,调整伺服阀响应时间可降低系统振幅不稳定频率区域,通过调整外激励幅值与阻尼比等参数可有效改善系统共振情况,为进一步抑制轧机辊系振动提供理论参考.
关键词:液压压下-垂直振动板带轧机非线性流量非对称分段弹簧力分岔
Research on Hydraulic Screw down-Vertical Vibration Characteristics of Strip Rolling Mill
HOU Dong-xiao1

 , FANG Cheng1, CHEN Shan-ping1, YAN Shuang2
, FANG Cheng1, CHEN Shan-ping1, YAN Shuang2 1. School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China;
2. Jingneng Qinhuangdao Thermal Power Co., Ltd., Qinhuangdao 066004, China
Corresponding author: HOU Dong-xiao, E-mail:houdongxiao1982@163.com.
Abstract: Considering the effect of the vertical vibration of the strip mill on the non-linear flow rate of the four-way servo solenoid valve in the hydraulic system, the asymmetric segmented spring force of the hydraulic screw down cylinder under the non-linear flow rate change is derived. The dynamic equations of hydraulic screw down-vertical coupling vibration of the strip mill are established. The averaging method is used to solve the amplitude-frequency response equation of the coupled vibration system of the rolling mill, and the bifurcation characteristics of the rolling mill in the dynamic rolling process are solved using the singularity theory. Four different transition sets and their corresponding bifurcation diagrams are obtained. The effect of the unfolding parameters on the bifurcation characteristics of the rolling mill are analyzed. Finally, based on the actual rolling mill parameters, it is found through simulation that the amplitude-frequency curve of the system has turning characteristics at the section. Adjusting the response time of the servo valve can reduce the unstable frequency area of the coupling system. By adjusting the external excitation amplitude and damping ratio and other parameters, the resonance of the coupled system can be effectively improved. This can provide a theoretical reference for further suppressing the vibration of the roll system of the rolling mill.
Key words: hydraulic screw down-vertical vibrationstrip rolling millnon-linear flow rateasymmetrical segmented spring forcebifurcation
板带轧机中的辊系振动问题一直是影响钢铁企业正常轧制生产的技术难题,辊系异常振动的发生不仅影响着轧制产品的精度与表面质量,严重时还可能引发钢带断裂并损坏设备[1-3].
针对轧机振动问题,****们从不同的角度进行了研究[4-8].Yun等[9]和Hu等[10-11]考虑轧制角与咬入角对轧制稳定性的影响,建立了水平-垂直-扭转耦合模型.Johnson等[12]考虑了接触非线性对工作辊-支承辊界面动态特性的影响,指出接触非线性会产生高频谐波振动.Swiatoniowski等[13-14]考虑轧件变形的非线性弹性力和参激振动,研究了轧机辊系垂直振动特性.侯东晓等[15]考虑压下缸和平衡缸多个缸体间结构弹性约束影响,建立了分段非线性弹性约束下轧机振动模型,并研究了该模型的分岔特性.****们在此基础上进一步考虑多个液压缸的弹性约束影响:刘浩然等[16]研究了多非线性弹性约束下的轧机振动;刘飞等[17]进一步研究了液压缸在分段弹性力与非线性摩擦力共同作用下的轧机振动特性;刘彬等[18]针对含液压缸非线性弹簧力的轧机振动模型,通过设计相应的吸振器控制轧机辊系振动行为.
目前轧机液压系统非线性因素主要考虑了液压缸结构中缸体弹性刚度的非线性,液压缸在轧制过程的工作状态也较为复杂,除了缸体机械结构非线性因素影响外,缸体中液压油流量的非线性也可能对轧机振动造成影响,目前对该问题还尚未有较为深入的研究.
因此本文考虑液压压下缸中液压缸伺服电磁阀非线性流量影响,首先建立了非线性流量影响下液压缸的分段非线性刚度,然后建立了板带轧机液压压下-垂直振动的非线性动力学模型.通过求解得到该非线性系统的幅频方程,并研究了轧机振动系统在不同开折参数下的分岔行为.最后以实际轧机参数为例,研究了不同参数对轧机幅频特性的影响,为进一步抑制轧机振动提供理论参考.
1 非线性流量下分段非线性弹性力在轧制过程中,板带轧机液压压下装置主要负责调节和保持辊缝大小,减小偶然冲击对轧件表面质量的影响,液压压下系统结构示意图如图 1所示.
图 1(Fig. 1)
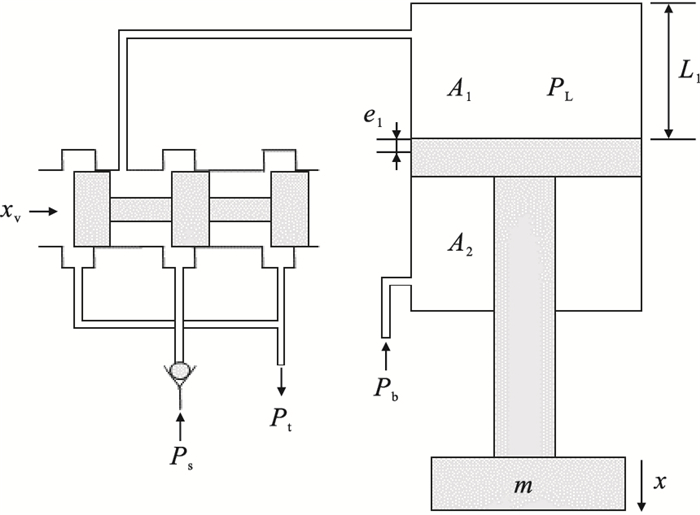 | 图 1 轧机液压系统示意图Fig.1 Schematic diagram of the rolling mill hydraulic system |
为了避免轧机在工作过程中产生的振动使液压缸无杆腔内压力油回流,一般在四通伺服电磁阀前设置单向阀来阻止此现象的发生.当活塞杆向下移动时单向阀打开,油液进入无杆腔;活塞杆向上移动时单向阀关闭,防止油液流出.此时油液流量将表现为不同的运动状态.液压压下缸的等效刚度可视作由活塞杆刚度与液压油刚度串联构成,在上述非线性流量的影响下液压压下缸的等效刚度可表示为
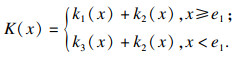 | (1) |
在轧制过程中,液压缸中的液压油始终受力,产生形变.液压油体积变化情况可以通过体积模量表示,液压油受到的压力与体积变化关系可以表示为
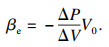 | (2) |
当活塞杆产生向下位移x时,无杆腔内的压力变化有
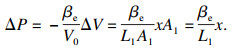 | (3) |
采用如下的四通阀非线性流量方程[19]:
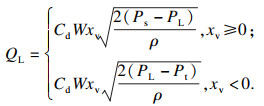 | (4) |
压下缸在工作过程中由缸内压力油提供轧制力,故阀芯位移xv≥0.考虑到管路压力损失对液压缸刚度影响较小[20],可将其忽略,并考虑电磁阀响应速度,可得在响应时间内无杆腔内流入的液压油体积为
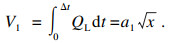 | (5) |
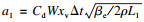
当活塞杆产生向下位移x时,可得由非线性流量产生的位移变化Δx与压力变化ΔPn:
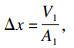 | (6) |
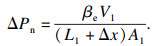 | (7) |
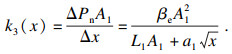 | (8) |
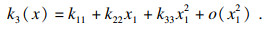 | (9) |
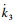
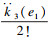
此时可得非线性弹性力
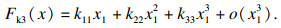 | (10) |
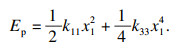 | (11) |
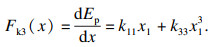 | (12) |
同理有
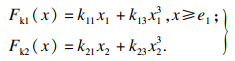 | (13) |
此时可得到非线性流量影响下液压压下缸的分段非线性弹性力为
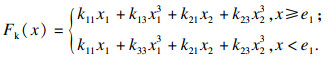 | (14) |
图 2(Fig. 2)
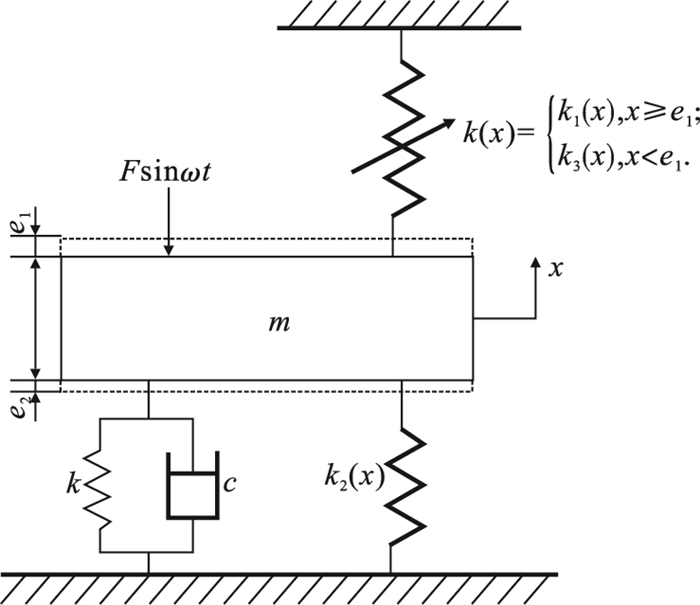 | 图 2 轧机辊系分段动力学模型Fig.2 Piecewise dynamic model of the rolling mill roll system |
由于支承辊质量远大于工作辊质量,可将其简化为等效质量m[22],k与c分别是轧件的等效线性刚度与阻尼,k2(x)为轧机液压压下缸有杆腔的等效刚度,k(x)为考虑非线性流量影响下液压压下缸分段非线性刚度,e1和e2分别为稳态轧制时液压压下缸内无杆腔与有杆腔内液体的初始弹性变形(e1>0,e2 < 0),F(t)为周期性外扰力.
此时可得轧机辊系分段非线性动力学方程为
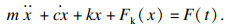 | (15) |
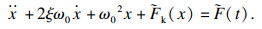 | (16) |
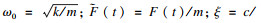
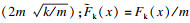
此时的分段非线性弹簧力可写为
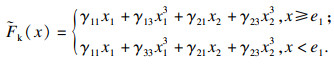 | (17) |
3 轧机辊系的幅频特性方程假设轧机辊系受到周期性外部扰动,该扰动为F(t)=Fsinωt.将系统中非线性影响因素考虑为弱非线性项,引入小参数ε,令ω2=(1+εσ)·ω02.式(16)可写为
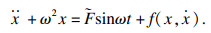 | (18) |
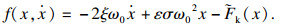 | (19) |
采用平均法,设式(18)有如下形式的解:
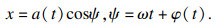 | (20) |
将式(20)代入式(18)中,可得出
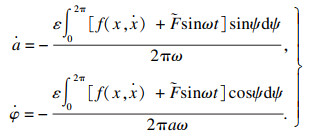 | (21) |
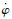
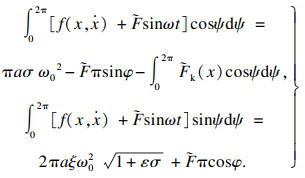 | (22) |
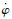
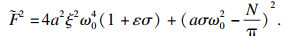 | (23) |
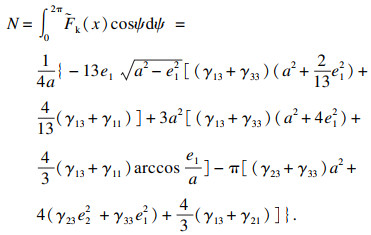 |
4 轧机辊系分岔特性分析由于板带轧机模型参数或多或少会存在一定的误差,模型参数的轻微变化有可能使得轧机表现出不同的分岔特性.而分岔现象往往与轧机失稳状态密切相关,如果失稳状态不及时加以控制,将导致轧机辊系出现不可预测的振动,从而导致产品质量降低,严重时甚至会破坏轧机结构的稳定性.因此可采用奇异性理论研究轧机振动系统参数变化对轧机辊系振动状态的影响.
将式(23)在a=a0处进行泰勒展开,并略去高次项后可得
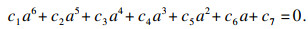 | (24) |
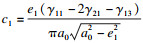
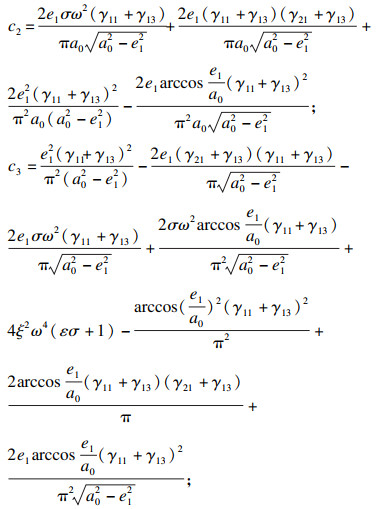 |
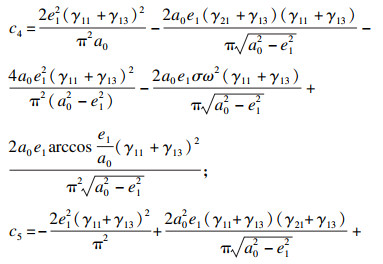 |
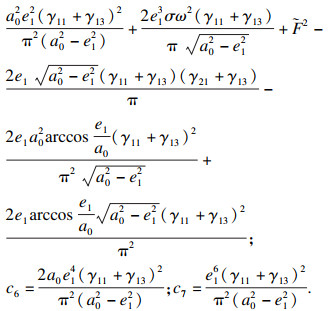 |
本文通过将余维为4的4-参数分岔方程的参数分别为零,得到了4个三维转迁集,并在转迁集分隔成的空间内分别讨论其分岔图.避免了多个参数同时为零时结果与原分岔方程差异较大的情况发生.
4.2 分岔方程计算令
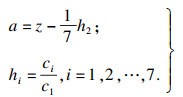 | (25) |
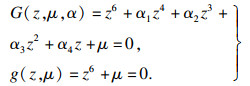 | (26) |
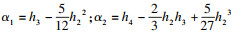
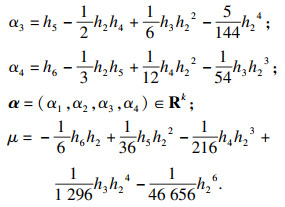 |
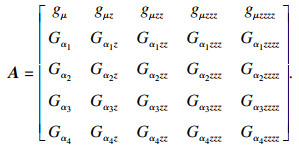 | (27) |
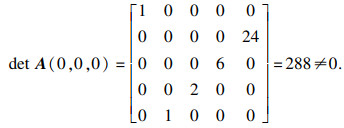 |
分岔集B={α∈Rk|,存在(x,μ)使得在(x,μ,α)处有G=Gα=Gμ=0}.
滞后点集H={α∈Rk|,存在(x,μ)使得在(x,μ,α)处有G=Gx=Gxx=0}.
双极限点集D={α∈Rk|,存在(xi,μ)(i=1,2),x1≠x2,使得在(xi,μ,α)处有G=Gx=0}.
1) 当α1=0时.
分岔集为
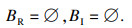 |
滞后点集为
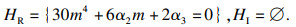 |
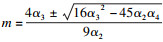
双极限点集为
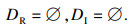 |
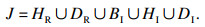 |
图 3(Fig. 3)
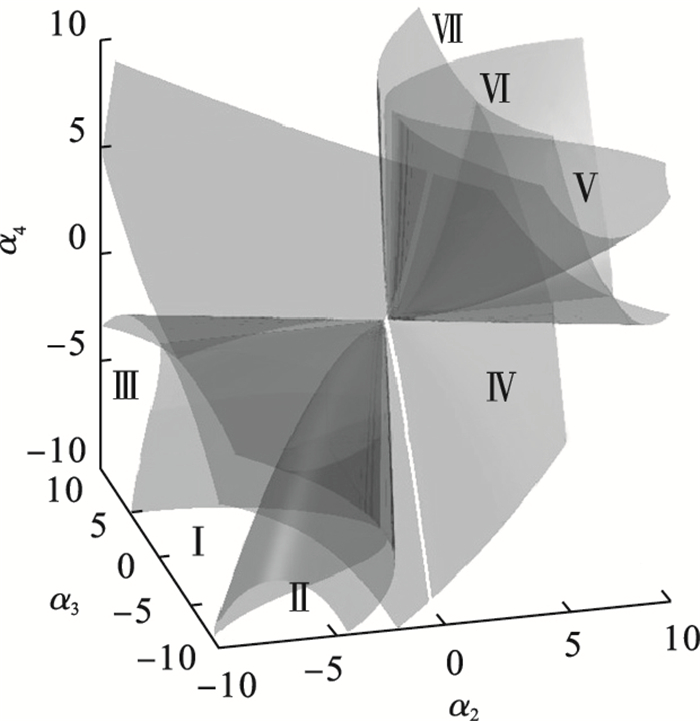 | 图 3 α1=0时轧机振动系统的转迁集Fig.3 Transition set of the rolling mill vibration system when α1=0 |
图 4(Fig. 4)
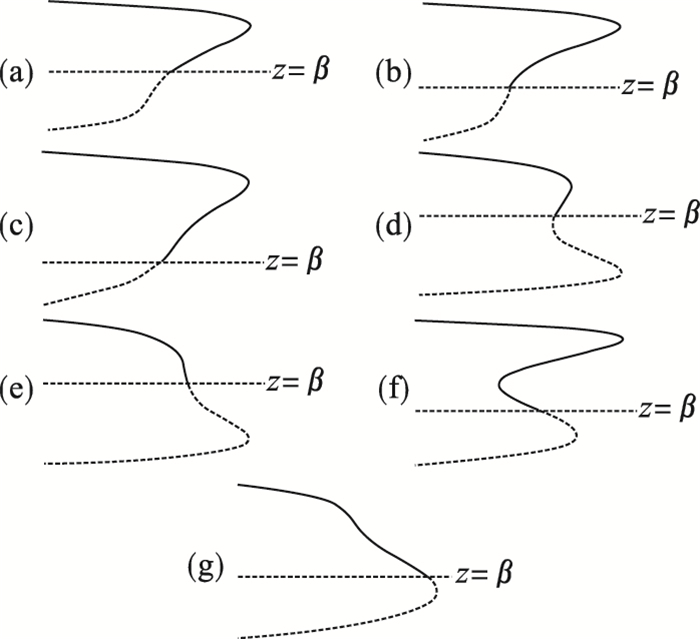 | 图 4 α1=0时图 3中不同区域内分岔图Fig.4 Bifurcation diagram in Fig. 3 when α1=0. (a)—Ⅰ区;(b)—Ⅱ区;(c)—Ⅲ区;(d)—Ⅳ区;(e)—Ⅴ区;(f)—Ⅵ区;(g)—Ⅶ区. |
由图 3与图 4可知,转迁集将轧辊系统的振动情况分隔成7个空间,在不同的区域内轧辊振动的分岔图曲线拓扑性质不同.因为轧辊的振幅总是一个大于零的值,即a≥0,在分岔方程中的约束条件为z≥β,β=h2/7.当轧机振动系统的参数在转迁集所分隔的区域内时,分岔图的拓扑性质不发生变化.
2) 当α2=0时.
分岔集为
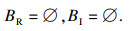 |
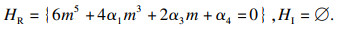 |
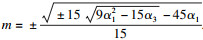
双极限点集为
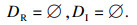 |
图 5(Fig. 5)
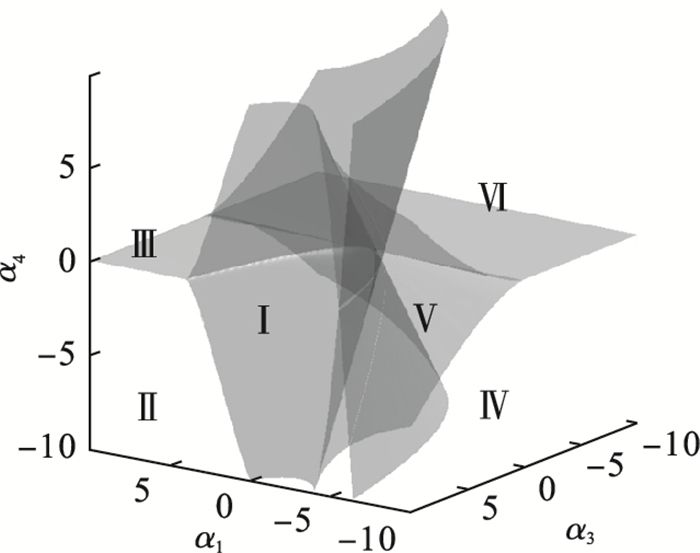 | 图 5 α2=0时轧机振动系统的转迁集Fig.5 Transition set of the rolling mill vibration system when α2=0 |
图 6(Fig. 6)
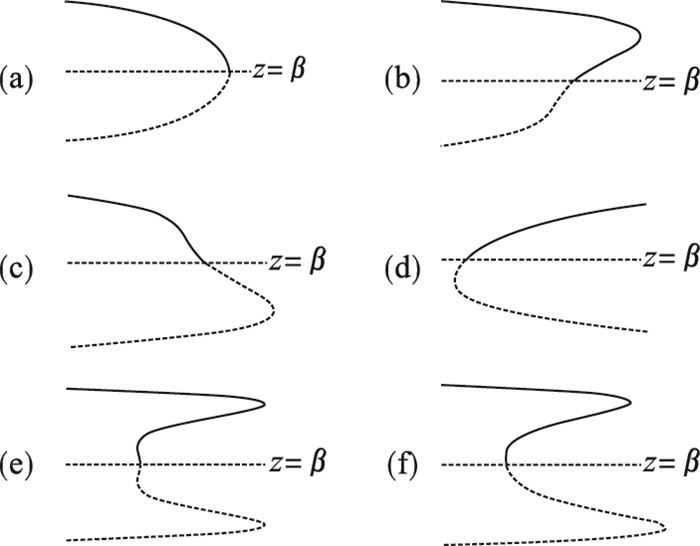 | 图 6 α2=0时图 5中不同区域内分岔图Fig.6 Bifurcation diagram in Fig. 5 when α2=0 (a)—Ⅰ区;(b)—Ⅱ区;(c)—Ⅲ区;(d)—Ⅳ区;(e)—Ⅴ区;(f)—Ⅵ区. |
3) 当α3=0时.
分岔集为
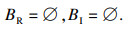 |
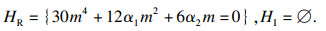 |
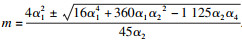
双极限点集为
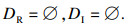 |
图 7(Fig. 7)
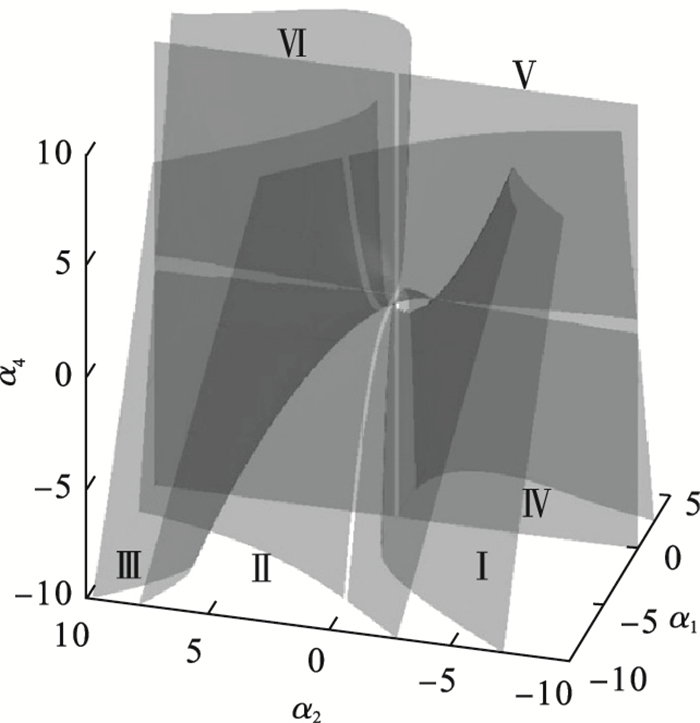 | 图 7 α3=0时轧机振动系统的转迁集Fig.7 Transition set of the rolling mill vibration system when α3=0 |
图 8(Fig. 8)
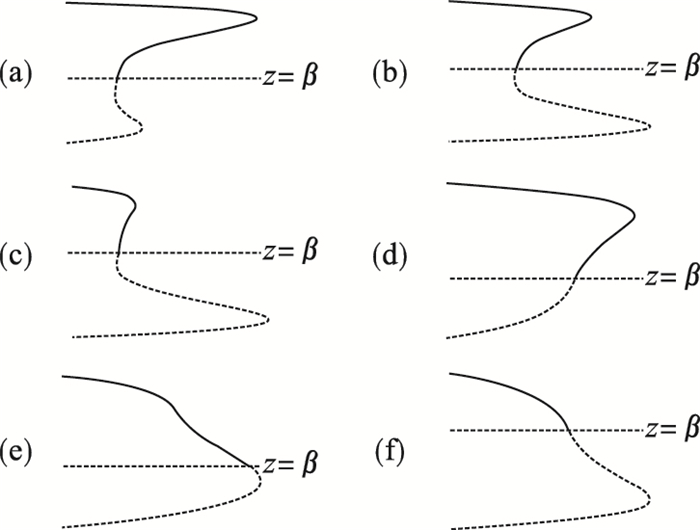 | 图 8 α3=0时图 7中不同区域内分岔图Fig.8 Bifurcation diagram in Fig. 7 when α3=0 (a)—Ⅰ区;(b)—Ⅱ区;(c)—Ⅲ区;(d)—Ⅳ区;(e)—Ⅴ区;(f)—Ⅵ区. |
4) 当α4=0时.
分岔集为
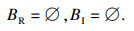 |
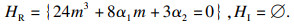 |
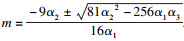
双极限点集为
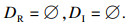 |
图 9(Fig. 9)
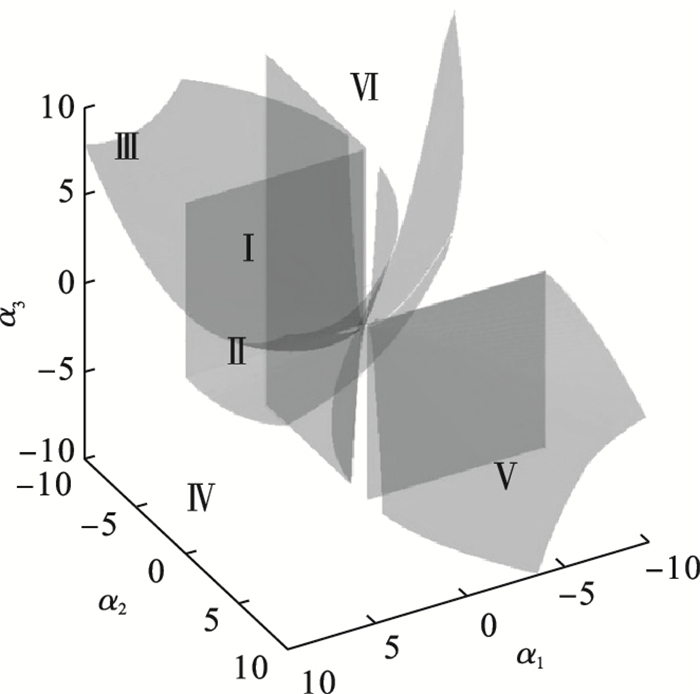 | 图 9 α4=0时轧机振动系统的转迁集Fig.9 Transition set of the rolling mill vibration system when α4=0 |
图 10(Fig. 10)
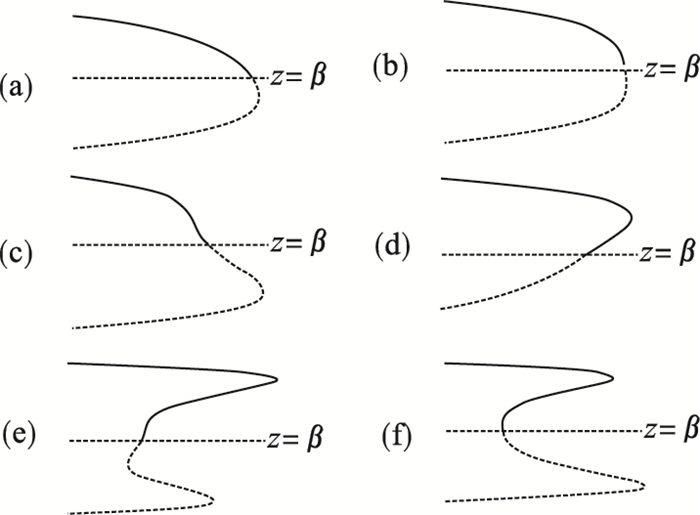 | 图 10 α4=0时图 9中不同区域内分岔图Fig.10 Bifurcation diagram in Fig. 9 set when α4=0 (a)—Ⅰ区;(b)—Ⅱ区;(c)—Ⅲ区;(d)—Ⅳ区;(e)—Ⅴ区;(f)—Ⅵ区. |
通过上述四种情况可以看出,转迁集将轧机振动系统分成若干个子空间,在同一子空间内任意选择点振动系统的分岔图均有着相同的拓扑性质,在不同的子空间内取点轧机振动系统分岔图的拓扑性质不同.当轧机振动系统不同参数发生变化时会出现不同的分岔行为,通过研究分岔行为可以避免轧机振动系统进入不稳定的参数区域.同时可以得出,改变分岔参数μ可使轧机辊系处于不同的振动状态,通过调整分岔参数可让轧辊的振动处于稳定状态,这能够为降低轧机辊系的垂直振动提供理论参考.
5 仿真研究根据某厂1780热连轧机图纸数据进行仿真,取轧机的实际结构参数以及液压压下系统参数如表 1所示.
表 1(Table 1)
| 表 1 1780热连轧机参数 Table 1 Parameters of 1780 hot rolling mill |
由式(23)中的幅频方程可以得到如图 11所示的板带轧机液压压下-垂直振动系统的幅频曲线,从图中可以看出,当外扰力频率增加时,轧机辊系的振幅出现了非线性系统中特有的“跳跃”与“滞后”现象,当外扰频率从曲线左侧开始增大时,振幅沿曲线从点A经过点B,C移动至点D,达到最大振幅,随着外扰力频率继续增加超过点D时,辊系的振幅突然降至点F,随后经过点G,轧辊的振幅在点D出现了跳跃现象;当外扰频率从右侧开始减小时,轧辊振幅沿曲线从点G经过点F到达点E,当频率继续降低小于点E时,轧辊振幅升至点C并沿着CB方向运动经过点A.因此当外扰力频率经过DE段时,系统的振幅是不稳定的,在实际工作中需要避免.
图 11(Fig. 11)
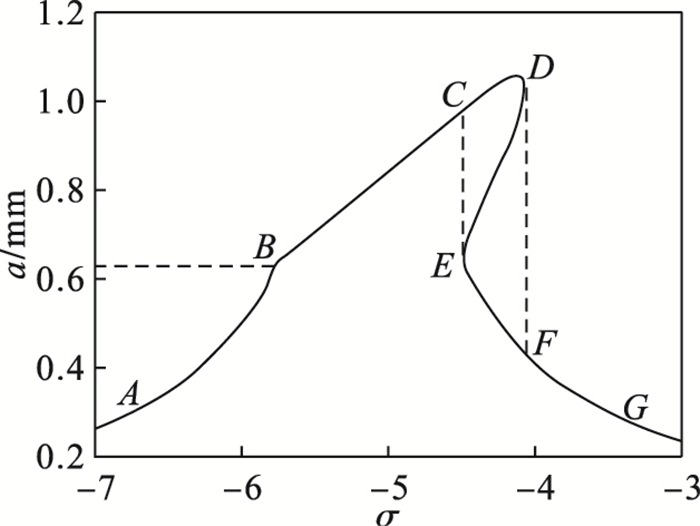 | 图 11 振动系统幅频响应曲线Fig.11 Amplitude frequency response curve of the vibration system |
同时可以发现,由于液压压下系统的分段非线性弹簧力,当外扰频率到点B时,振动系统的非线性刚度发生改变,幅频曲线出现拐弯.这种现象说明,在不同的振幅区段,由于振动系统非线性刚度变化会导致轧辊处于不同的振动状态.
图 12为伺服电磁阀不同响应时间下的系统幅频曲线.从图中可以看出,随着电磁阀响应时间变小,幅频曲线的拐弯特性变弱,在拐弯点附近的非线性刚度变化变小,轧机辊系的不稳定振幅频率区域变小;当电磁阀的响应时间变长,轧辊的不稳定振幅频率区域变大,幅频曲线的滞后现象明显.
图 12(Fig. 12)
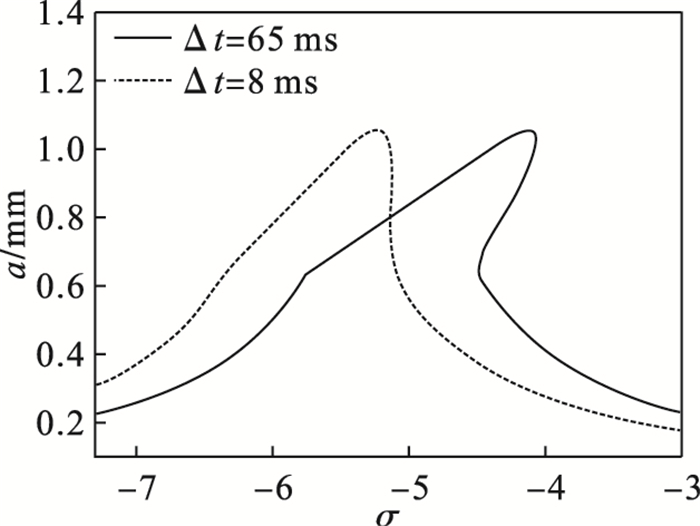 | 图 12 响应时间对幅频特性的影响Fig.12 Influence of response time on amplitude frequency characteristics |
图 13为不同外激励下振动系统幅频曲线的变化情况.从图中可以看出,随着外激励增加,在同一扰动频率下的轧辊振幅将变大,共振频率范围也将变宽.当外激励使振幅低于e1时,幅频曲线中的拐弯特性消失,轧辊处于稳定状态.
图 13(Fig. 13)
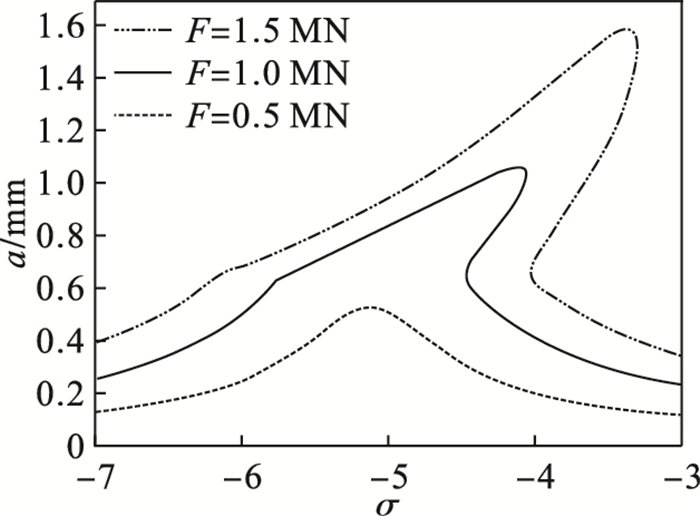 | 图 13 外激励对系统幅频特性的影响Fig.13 Effect of external excitation on amplitude frequency characteristics of the system |
图 14为不同阻尼比下轧机振动系统的幅频曲线.可以看出,随着阻尼比的增加,轧辊的振动幅值降低,当阻尼比增加到一定程度时,轧机振动系统的幅频曲线拐弯现象消失,因此可通过增加轧机系统的阻尼比降低轧辊振动.
图 14(Fig. 14)
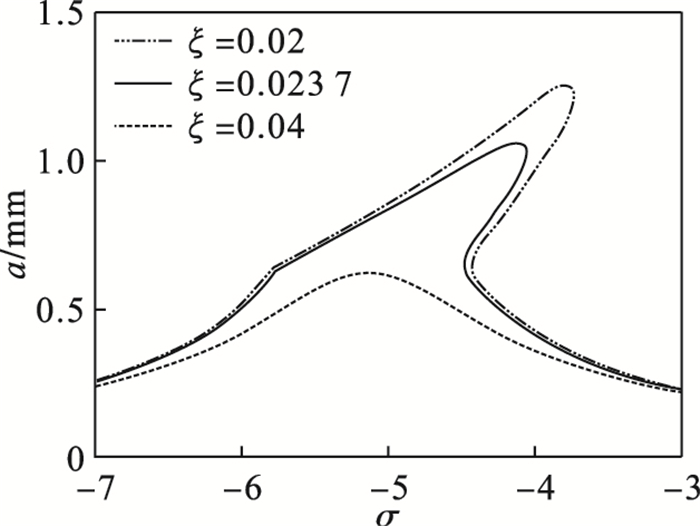 | 图 14 阻尼比对系统幅频特性的影响Fig.14 Effect of damping ratio on amplitude frequency characteristics of the system |
由图 11~图 14可以看出,伺服阀响应速度、外激励与阻尼比的变化均会对振动系统的幅频曲线产生影响,通过改变参数(如提高系统的阻尼比和降低外激励幅值,提高伺服电磁阀响应速度等)可以使轧机辊系的振动减弱,避免在工作中出现共振现象.
6 结论1) 依据四辊轧机辊系机械的特点和液压系统非线性特性,考虑板带轧机液压系统电磁伺服阀非线性流量对垂直振动的影响,推导出液压系统非线性流量与液压压下缸非线性弹簧力的关系,建立了板带轧机液压压下-垂直振动动力学模型,为研究非线性因素对轧机辊系振动影响提供了一种新的模型依据.
2) 分析了轧机振动系统在不同参数下的分岔拓扑结构,得到4组不同的转迁集与分岔图.可以看出,随着分岔参数m取值的变化,分岔图呈现出不同的拓扑结构,导致轧机辊系处于不同的振动状态.因此可通过调整工艺参数以及分岔参数m避免轧机处于发生振动的频率区.
3) 研究系统参数对板带轧机液压压下-垂直振动系统幅频特性中的拐弯与跳跃现象的影响,提高伺服电磁阀的响应速度可以有效减小非线性系统的跳跃现象,减小振幅不稳定频率区域.并且通过提高系统阻尼和降低外激励幅值可以有效降低系统振幅,避免轧机出现共振现象,从而可以提高轧机辊系工作的稳定性.
参考文献
| [1] | Yang X, Tong C N, Yue G F, et al. Coupling dynamic model of chatter for cold rolling[J]. Journal of Iron and Steel Research International, 2010, 17(12): 30-34. DOI:10.1016/S1006-706X(10)60193-8 |
| [2] | Krot P. Nonlinear vibrations and backlashes diagnostics in the rolling mills drive trains[C]//Proceedings of 6th EUROMECH Nonlinear Dynamics Conference. Saint Petersburg, 2008: 26-30. |
| [3] | Tang H P, Wang D Y, Zhong J. Investigation into the electromechanical coupling unstability of a rolling mill[J]. Journal of Materials Processing Technology, 2002, 129(1): 294-298. |
| [4] | Paton D L, Critchley S. Tandem mill vibration: its cause and control[J]. Iron and Steel Making, 1985, 12(3): 37-43. |
| [5] | Zhu Y, Tang S, Wang C, et al. Bifurcation characteristic research on the load vertical vibration of a hydraulic automatic gauge control system[J]. Processes, 2019, 7(10): 718-727. DOI:10.3390/pr7100718 |
| [6] | Zhao H Y, Ehmann K F. Stability analysis of chatter in tandem rolling mills single-and multi-stand negative damping effect[J]. Journal of Manufacturing Science and Engineering, 2013, 135(3): 1-19. |
| [7] | Gao Z Y, Zang Y, Wu D P. HOPF bifurcation and feedback control of self-excited torsion vibration in the drive system[J]. Noise & Vibration Worldwide, 2011, 2(10): 68-74. |
| [8] | Heidari A, Forouzan M R. Optimization of cold rolling process parameters in order to increasing rolling speed limited by chatter vibrations[J]. Journal of Advanced Research, 2013, 4(1): 27-34. DOI:10.1016/j.jare.2011.12.001 |
| [9] | Yun I S, Wilson W R D, Ehmann K F. Review of chatter studies in cold rolling[J]. International Journal of Machine Tools and Manufacture, 1998, 38(12): 1499-1530. DOI:10.1016/S0890-6955(97)00133-8 |
| [10] | Hu P H, Ehmann K F. A dynamic model of the rolling process.Part Ⅰ: homogeneous model[J]. International Journal of Machine Tools and Manufacture, 2000, 40(1): 1-19. DOI:10.1016/S0890-6955(99)00049-8 |
| [11] | Hu P H, Ehmann K F. A dynamic model of the rolling process.Part Ⅱ: inhomogeneous model[J]. International Journal of Machine Tools and Manufacture, 2000, 40(1): 21-31. DOI:10.1016/S0890-6955(99)00050-4 |
| [12] | Johnson R, Qi Q. Chatter dynamics in sheet rolling[J]. International Journal of Mechanical Sciences, 1994, 6(7): 617-630. |
| [13] | Swiatoniowski A, Bar O. Mathematical modeling of the high frequency vibrations during cold rolling process[J]. Archives of Metallurgy and Materials, 2013, 58(4): 1085-1091. DOI:10.2478/amm-2013-0130 |
| [14] | Swiatoniowski A, Bar A. Parametrical excitement vibration in tandem mills-mathematical model and its analysis[J]. Journal of Materials Processing Technology, 2003, 134(2): 214-224. DOI:10.1016/S0924-0136(02)01037-3 |
| [15] | 侯东晓, 刘彬, 时培明, 等. 分段非线性轧机辊系系统的分岔行为研究[J]. 振动与冲击, 2010, 29(12): 138-141. (Hou Dong-xiao, Liu Bin, Shi Pei-ming, et al. Research on the bifurcation behavior of the piecewise nonlinear rolling mill roll system[J]. Shock and Vibration, 2010, 29(12): 138-141.) |
| [16] | 刘浩然, 刘飞, 侯东晓, 等. 多非线性弹性约束下轧机辊系振动特性[J]. 机械工程学报, 2012, 48(9): 89-94. (Liu Hao-ran, Liu Fei, Hou Dong-xiao, et al. Vibration characteristics of mill rolls under multi-segment nonlinear elastic constraints[J]. Journal of Mechanical Engineering, 2012, 48(9): 89-94.) |
| [17] | 刘飞, 刘彬, 时培明, 等. 液压缸非线性约束下的轧机辊系振动行为[J]. 机械工程学报, 2014, 50(24): 59-65. (Liu Fei, Liu Bin, Shi Pei-ming, et al. Vibration behavior of roll system under nonlinear constraints of the hydraulic cylinder[J]. Journal of Mechanical Engineering, 2014, 50(24): 59-65.) |
| [18] | 刘彬, 潘贵翔, 李鹏, 等. 液压缸非线性弹簧力下的轧机特性及控制[J]. 中国机械工程, 2018, 29(24): 2925-2932. (Liu Bin, Pan Gui-xiang, Li Peng, et al. Rolling mill characteristics and control under nonlinear spring force of hydraulic cylinder[J]. China Mechanical Engineering, 2018, 29(24): 2925-2932. DOI:10.3969/j.issn.1004-132X.2018.24.005) |
| [19] | 张永顺, 姜万录, 李振宝. 轧机液压压下系统非线性振动诱因分析[J]. 钢铁, 2020, 55(4): 106-112. (Zhang Yong-shun, Jiang Wan-lu, Li Zhen-bao. Analysis of nonlinear vibration inducements of rolling mill hydraulic reduction system[J]. Iron & Steel, 2020, 55(4): 106-112.) |
| [20] | Feng H, Du Q G, Huang Y X, et al. Modelling study on stiffness characteristics of hydraulic cylinder under multi-factors[J]. Journal of Mechanical Engineering, 2017, 63(7): 447-456. |
| [21] | 郜志英, 臧勇, 曾令强. 轧机颤振建模及理论研究进展[J]. 机械工程学报, 2015, 51(16): 87-105. (Gao Zhi-ying, Zang Yong, Zeng Ling-qiang. Review of modelling and theoretical studies on chatter in the rolling mills[J]. Journal of Mechanical Engineering, 2015, 51(16): 87-105.) |
| [22] | Tamiya T, Furui K, Lida H. Analysis of chattering phenomenon in cold rolling[C]//Proceedings of Science and Technology of Flat Rolled Products. Tokyo: International Conference on Steel Rolling, 1980: 1191-1202. |
| [23] | 彭荣荣, 巩长芬. 分段对称非线性刚度作用下的轧机辊系分岔与混沌行为分析[J]. 锻压技术, 2019, 44(5): 99-104. (Peng Rong-rong, Gong Chang-fen. Analysis on bifurcation and chaos behavior of mill rolls under piecewise symmetric nonlinear stiffness[J]. Forging and Stamping Technology, 2019, 44(5): 99-104.) |
