

1. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819;
2. 东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004
收稿日期:2021-09-06
基金项目:国家自然科学基金资助项目(52075088);中央高校基本科研业务费专项资金资助项目(N182303034,N150306001);沈阳市科技创新平台项目(18006001)。
作者简介:王振宇(1989-),男,辽宁沈阳人,东北大学博士研究生;
于天彪(1968-),男,吉林榆树人,东北大学教授,博士生导师。
摘要:针对圆柱直齿轮的多轴铣削精加工,提出一种无干涉刀具路径规划方法. 首先,建立齿轮包络铣削运动模型,准确描述铣刀和工件之间的运动关系;其次,在齿轮齿廓精确模型描述的基础上,通过残留高度曲线与刀具圆弧的求交,计算出残留高度点;根据残留高度点到刀具圆弧中心之间的距离等于刀具半径,计算出刀具路径曲线上的下一刀位点;依次递推计算出等残留高度进给下的所有刀位点;再次,以等残留高度刀位点计算结果为基础,残留高度约束下,计算出等弧长进给和等径向进给的刀位点;然后,通过距离法判断刀具与工件是否存在全局干涉,给出刀具不同刀位点对应的刀偏角,局部干涉通过调整刀具半径来避免;最后,通过仿真计算实例验证所提出方法的可行性和有效性.
关键词:齿轮铣削无干涉等残留高度刀位点刀具路径规划
Interference-Free Tool Path Generation for Milling of Spur Gears
WANG Zhen-yu1, ZHANG Rong-chuang2, YU Tian-biao1


1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: YU Tian-biao, E-mail: yutianbiao_neu@163.com.
Abstract: Regarding the finish machining of multi-axis milling, an interference-free tool path generating method for milling of spur gears was proposed. The kinematics model of gear enveloping was established to precisely describe the kinematic relation between the milling tool and workpiece. Based on the accurate model of gear tooth profiles, the scallop point is determined by intersection calculation between the circle of the cutter radius and scallop curve. According to the way that the tool radius is equal to the distance between the scallop point and center point of the cutter arc, the next cutter location(CL) point is identified on the tool path curve. All CL points are determined by the iterative method. On the basis of the CL points on the scallop curve, CL points of the equal radial feeding strategy and equal arc-length feeding strategy were calculated under the constraint of scallop height. The occurrence of global interference was judged by calculating the minimum distance between the milling tool and workpiece. Then the cutting edge angles corresponding to different CL points were given. The occurrence of local over-cut interference was avoided by adjusting the cutter radius. The simulation results showed the proposed method was feasible and effective.
Key words: gear millinginterference-freeconstant scallop heightcutter location pointtool path generation
随着数控技术的发展,通用铣刀多轴加工,因其在齿轮加工过程中具有的高度柔性化,已成为一种重要的齿轮加工方法[1-4]. 相对于传统的滚齿等加工方法,铣削加工在新式齿轮的快速原型制造、大型齿轮的单件生产以及齿轮的修复等方面具有明显的优势. 由于采用多轴铣削加工,合理地规划刀具路径是保证齿轮加工精度和加工效率的关键.
齿轮铣削刀具路径规划主要有以下两种方法.一是渐开线包络法. 齿轮齿廓既可通过立铣刀的侧刃,类似于滚刀直线刃包络出渐开线,也可以通过球头铣刀圆弧刃包络出渐开线,两种方式在工业中都有广泛应用. ?zel采用径向铣齿加工齿轮,根据渐开线方程推导出切削路径和齿廓偏差,分析加工参数和齿轮参数对二者的影响[5-6]. Guo等提出一种渐开线圆柱齿轮立铣刀包络铣削加工方法,通过所建立的数学模型分析齿面精度和刀具路径之间的关系,实现铣刀具路径规划与齿面精度特性优化匹配[7].郭二廓等推导出立铣刀侧铣加工齿轮的齿廓误差模型,研究了刀具进给策略、齿轮几何参数对齿廓误差的影响[8]. Shi等研究了粗糙度一致性约束下的圆柱齿轮铣削路径规划方法,通过渐开线的等距线确定出刀位点[9-10].二是自由曲面包络法.即将齿廓曲面拟合成自由曲面,根据自由曲面的多轴加工方法来铣削齿轮.Kawasaki等将锥齿轮设计齿廓点导入到CAM软件中,进行光顺后形成NURBS曲面,进而利用CAM软件中自由曲面铣削功能实现齿廓铣削加工的刀具路径规划[11]. Bouquet等在CAD/CAM软件中对圆柱齿轮铣削进行刀具路径规划,将切削过程分为立铣刀齿坯加工、立铣刀齿槽粗加工、立铣刀齿面粗加工,以及保证齿廓精度的球头铣刀精加工四个步骤[1]. álvarez等基于CAM软件在多任务五轴机床大型螺旋锥齿轮铣削加工中制定不同的加工策略和刀具路径,通过误差分析优化刀具路径[12]. Staudt等对圆柱齿轮自由铣削加工过程进行详细论述,包括CAX过程链确定、刀具选择以及加工策略选择等[3]. 相对于自由曲面包络法,渐开线包络法可以根据齿廓的几何特性、齿廓精度要求,准确地计算出刀具路径.上述研究成果中,刀具路径规划主要集中于刀位点的计算,算法较少涉及铣刀与齿廓之间的全局干涉以及刀具半径过大造成局部干涉问题的处理.
基于此,以球头铣刀圆弧刃铣削圆柱直齿轮保证齿廓精度的精加工为对象,利用渐开线包络法确定出铣刀圆弧刃包络齿廓的刀位点,通过干涉判断计算出无干涉条件下刀具偏角范围,提出一种无干涉圆柱齿轮球头铣削刀具路径规划方法,通过仿真实例验证该方法的可行性和有效性.
1 齿轮铣削加工数学模型1.1 铣削运动模型铣削运动如图 1所示,采用四轴数控机床进行齿轮包络铣削加工,工件固定在B轴上,跟随B轴旋转实现间歇分度运动;球头铣刀固定在回转主轴S轴上,通过x,y,z轴直线进给定位,完成工件材料去除加工.
图 1(Fig. 1)
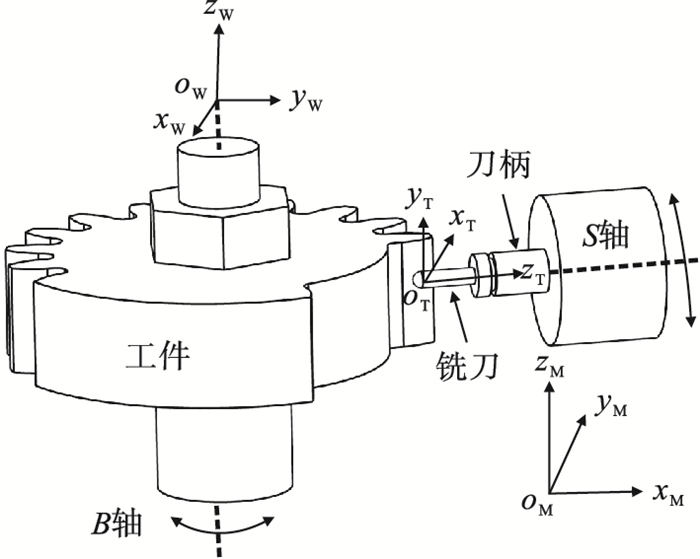 | 图 1 齿轮铣削运动示意图Fig.1 Basic kinematics of gear milling |
图 2所示为齿轮铣削坐标系统. 机床坐标系oM-xMyMzM与机床床身固定连接,定义为坐标系统的绝对坐标系,zM轴与齿轮回转轴线重合;坐标系oW-xWyWzW与工件固定连接,坐标轴yW与齿廓中心线重合,围绕机床坐标系的zM轴作间歇回转分度运动,φ表示工件回转的角度;坐标系oT-xTyTzT为球头铣刀坐标系,坐标原点oT位于球头铣刀的球心,坐标轴zT与机床主轴轴线一致;oG-xGyGzG为描述轮齿齿廓数学模型的齿廓坐标系,其轴线yG与齿廓中心线重合;?为与工件坐标系之间的夹角,当?=0时,与工件坐标系相重合.
图 2(Fig. 2)
 | 图 2 齿轮铣削坐标系统Fig.2 Coordinate system of gear milling |
齿廓坐标系与工件坐标系之间的变换矩阵为
 | (1) |
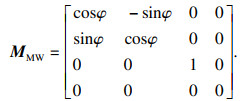 | (2) |
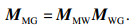 | (3) |
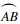
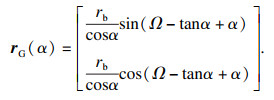 | (4) |
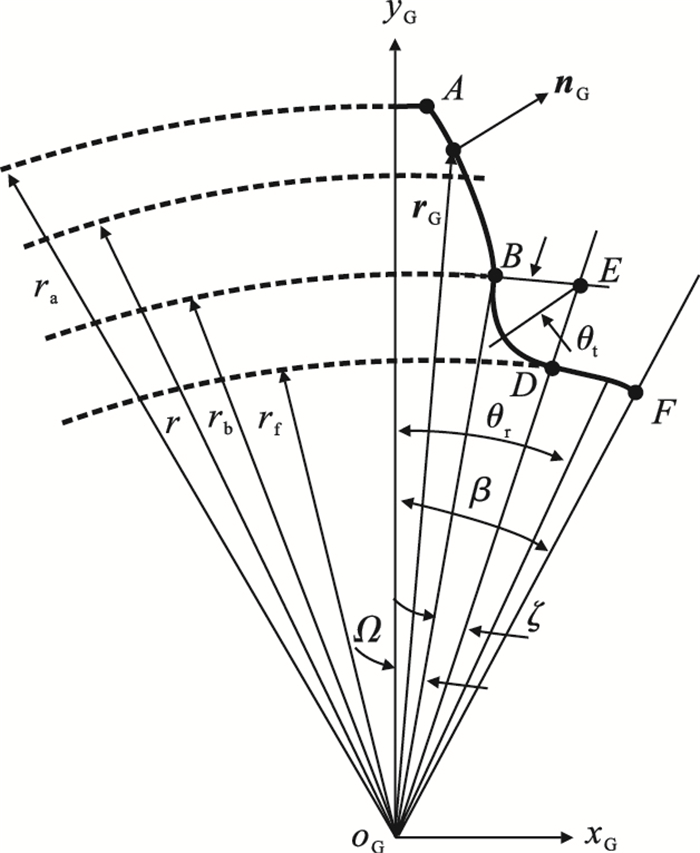 | 图 3 直齿轮齿廓几何模型Fig.3 Geometric model of the spur gear tooth profile |
式中:压力角α取值为0≤α≤arccos
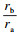
过渡曲线
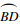
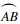
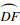
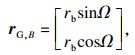 | (5) |
 | (6) |
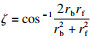
过渡曲线
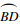
 | (7) |
齿根圆弧上
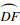
 | (8) |
渐开线齿廓
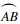
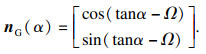 | (9) |
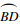
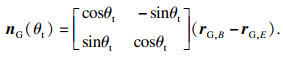 | (10) |
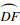
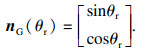 | (11) |
2.1 刀位点计算2.1.1 渐开线齿廓刀位点计算渐开线齿廓刀位点的确定取决于齿廓铣削的刀具进给策略;进给策略主要有等残留高度、等弧长、等径向三种,等残留高度刀位点计算是其余进给策略刀位点计算的基础.
1) 等残留高度进给策略刀位点计算.
图 4所示为渐开线齿廓刀位点计算示意图.理论齿廓曲线ε1是不同刀位点刀具圆弧的包络线;CG,K,LG,K分别为已知的刀触点和刀位点,对应的渐开线压力角为αK,LG,K+1为需要求取的刀位点. ε2为等残留高度曲线,ε3为刀具路径曲线;GK为等残留高度点,位于ε2上,到ε1的距离为残留高度h,同时也是相邻两个刀位点刀具圆弧的交点.
图 4(Fig. 4)
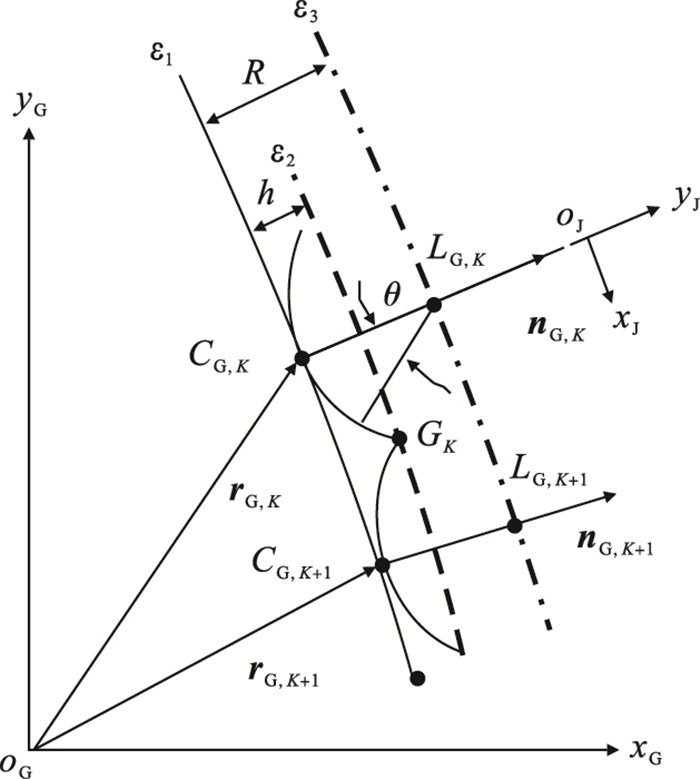 | 图 4 渐开线齿廓刀位点计算Fig.4 Cutter location point calculation for the involute tooth profile |
ε2表示为
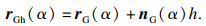 | (12) |
 | (13) |
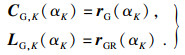 | (14) |
 | (15) |
 | (16) |
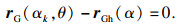 | (17) |
① rG(αk,θ)在ε2上的投影点;
② 求取θh,满足|rG(αk,θh)-rGh(α)|=0.
rG(αk,θ)在ε2上的投影点对应最短距离,定义距离平方函数为
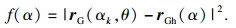 | (18) |
Newton-Raphson迭代法需要确定θ的初值,定义rG(αk,θ)到ε2的距离函数为
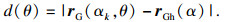 | (19) |
求出等残留高度点GK后,刀具路径上下一个刀位点LG,K+1通过下面几何关系进行求解:LG,K+1位于刀具路径曲线ε3上;GK点到LG,K+1点的距离由刀具半径R确定.LG,K+1点的具体计算方法与GK点求取类似.
2) 等弧长、等径向进给策略刀位点计算.
图 5所示为等弧长和等径向进给示意图.图 5a中ΔS为常量,图 5b中Δy为常量,刀位点计算以等残留高度计算结果为基础.图 6所示为等残留高度计算出的刀触点CG,K,CG,K+1之间的弧长ΔSK与径向间距ΔyK,计算公式如下:
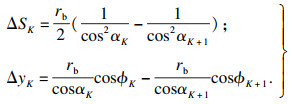 | (20) |
 | 图 5 等弧长、等径向进给策略Fig.5 Feeding strategies of equal arc length and equal radial direction (a)—等弧长进给;(b)—等径向进给. |
图 6(Fig. 6)
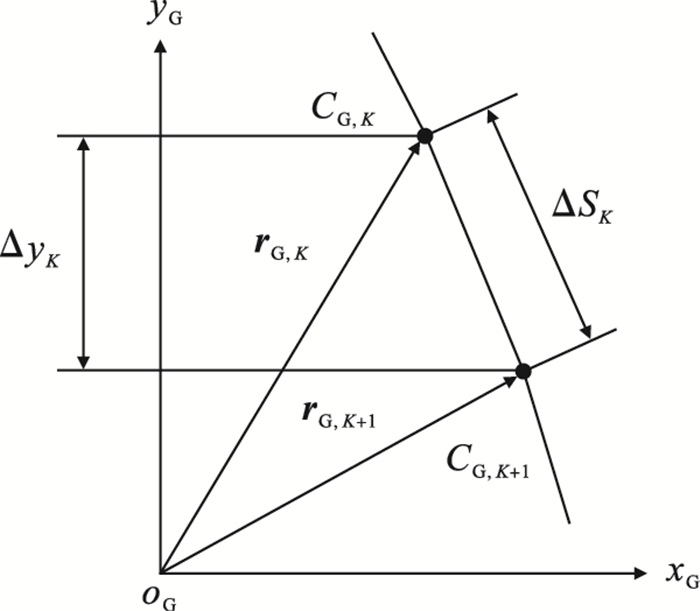 | 图 6 ΔSK和ΔyK计算Fig.6 Calculation for ΔSK and ΔyK |
式中,
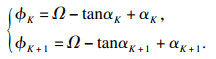 |
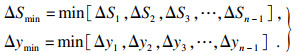 | (21) |
以ΔSmin为相邻刀位点计算的离散弧长,计算出LG,K+1点对应的等弧长进给下的压力角αK+1为
 | (22) |
以Δymin为相邻刀位点在径向上进给的离散间距,通过数值计算得到LG,K+1点对应的压力角αK+1为
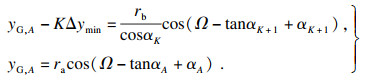 | (23) |
根据式(22)和式(23)求出αK+1之后,将其代入到式(14),计算出对应的LG,K+1点的位置.
2.1.2 过渡曲线和齿根曲线刀位点计算过渡齿廓和齿根齿廓均为圆弧曲线,本文中采用等残留高度进给策略进行铣削. 通过解析法进行求解. 如图 7所示,过渡齿廓为凹圆弧,过渡圆弧的半径为rt=|rG,E-rG,B|,则相邻刀位点之间的间隔角δ1表示为
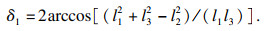 | (24) |
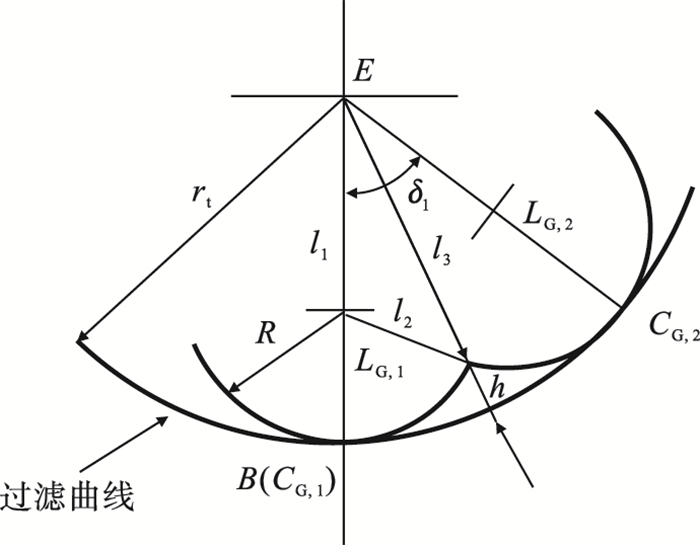 | 图 7 过渡曲线刀位点计算Fig.7 Cutter location point calculation for the transition curve |
式中:l1=rt-R;l2=R;l3=rt-h.
LG,K+1点的位置表示为
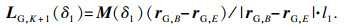 | (25) |
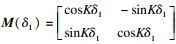
如图 8所示,齿根圆为凸圆弧,与过渡曲线刀位点计算相似,则δ2表示为
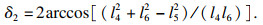 | (26) |
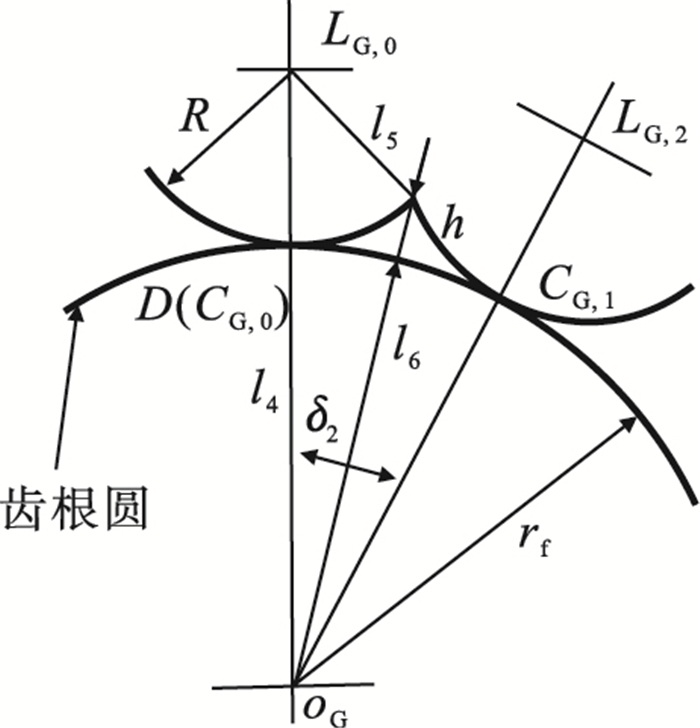 | 图 8 齿根圆刀位点计算Fig.8 Cutter location point calculation for the root circle |
式中:l4=rf+R;l5=R;l6=rf+h.
LG,K+1点的位置表示为
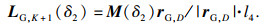 | (27) |
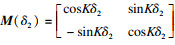
由图 2可知,机床坐标系下的刀位点计算,应先确定工件回转角φ. 图 9所示,定义齿廓法向量nW,K和刀轴矢量tW,λ之间的夹角λ为刀具偏角,相对于nW,K旋转逆时针为正,顺时针为负,其范围为[-π/2,π/2].
图 9(Fig. 9)
 | 图 9 工件回转角φFig.9 Rotation angles φ of workpiece |
tW,λ表示为
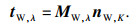 | (28) |
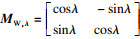
主轴S矢量T=[0 0 1],与tW,λ之间的夹角φ即为工件的回转角,计算公式为
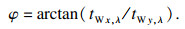 | (29) |
1) 干涉类型.齿轮铣削过程中主要有两种干涉状况,分别为局部干涉和全局干涉.局部干涉通常指采用过大的刀具半径时导致齿根产生过切干涉,可以通过改变刀具半径大小来避免,如图 10所示;全局干涉通常指刀具整体与工件的渐开线齿廓相碰撞,可以通过改变铣刀刀轴方向来避免,如图 11所示.
图 10(Fig. 10)
 | 图 10 局部过切干涉与避免Fig.10 Local over-cut interference and its avoidance |
图 11(Fig. 11)
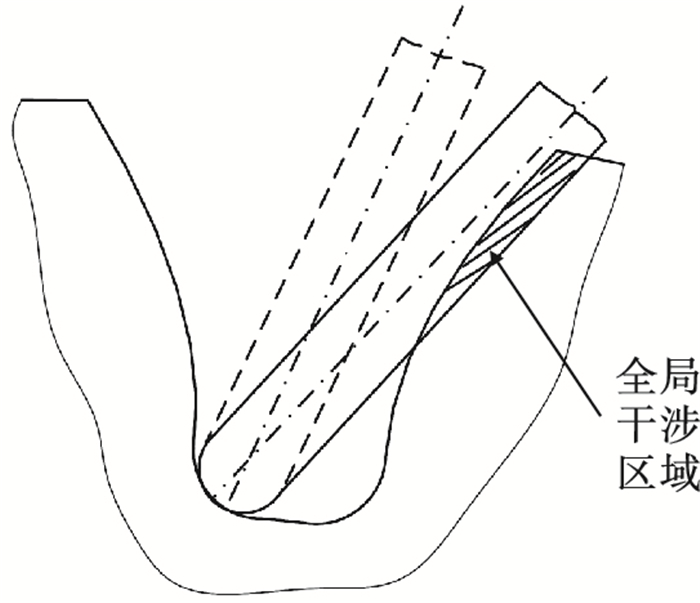 | 图 11 全局干涉与避免Fig.11 Global interference and its avoidance |
2) 局部干涉产生和避免.齿轮齿廓中渐开线齿廓和齿根圆齿廓为凸面,不能够产生局部过切干涉;而过渡曲面为凹曲面容易产生局部过切干涉.
不产生干涉的条件为
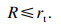 | (30) |
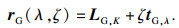 | (31) |
 | 图 12 全局干涉判断Fig.12 Global interferemce detection |
式中:0≤ζ≤L;LG,K表示点LG,K的位置矢量.
铣刀轴上任意一点到齿廓的距离表示为
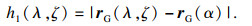 | (32) |
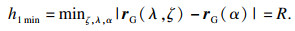 | (33) |
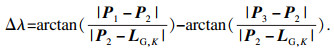 | (34) |
3 仿真实例表 1所示为仿真实例采用的齿轮几何参数,球头铣刀半径R=2,进给策略采用等残留高度进给. 图 13所示为不产生全局干涉的刀具偏角变化范围,渐开线齿廓部分刀具偏角可行域范围明显大于齿根过渡曲线和齿根圆部分.图 14所示为基于CAD实体法齿轮铣削加工中刀具和工件之间的相对位置,刀具始终位于切削齿槽内,没有产生干涉现象. 图 15所示为实体法仿真后的齿廓偏差,渐开线齿廓刀具偏角λ=60°,过渡曲线和齿根圆刀具偏角λ=-20°,相邻刀位点之间的齿廓偏差一致,均小于等于残留高度h.图 16所示为基于VERICUT的齿轮铣削过程仿真.机床采用图 16a中Makino a77四轴卧式加工中心,图 16b中齿根圆铣削设置刀具偏角λ=-20°时,铣刀和齿廓之间没有发生全局干涉现象,然而图 16c中λ=-25.71°时,则产生明显的全局干涉. 上述仿真结果验证了刀具路径规划方法的可行性和有效性.
表 1(Table 1)
| 表 1 齿轮几何参数 Table 1 Geometry of the spur gear tooth |
图 13(Fig. 13)
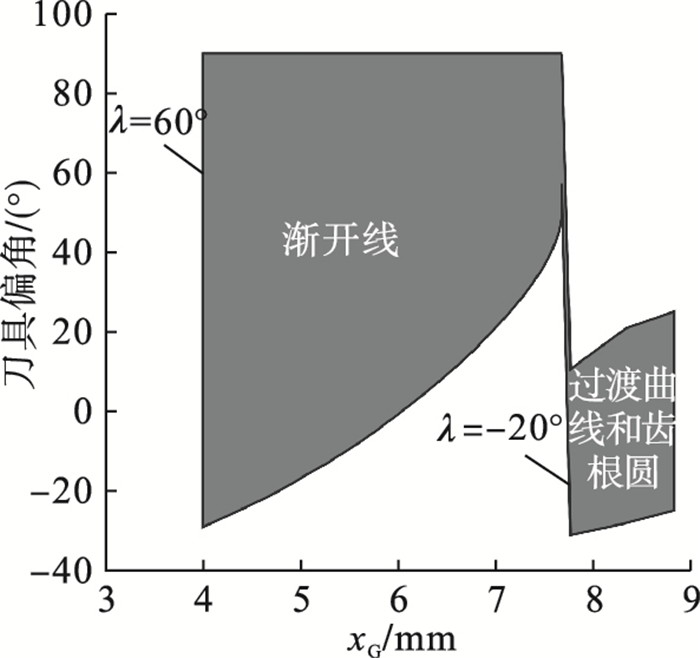 | 图 13 无全局干涉刀具偏角Fig.13 Feasible region of cutter orientation to avoid collision interference |
图 14(Fig. 14)
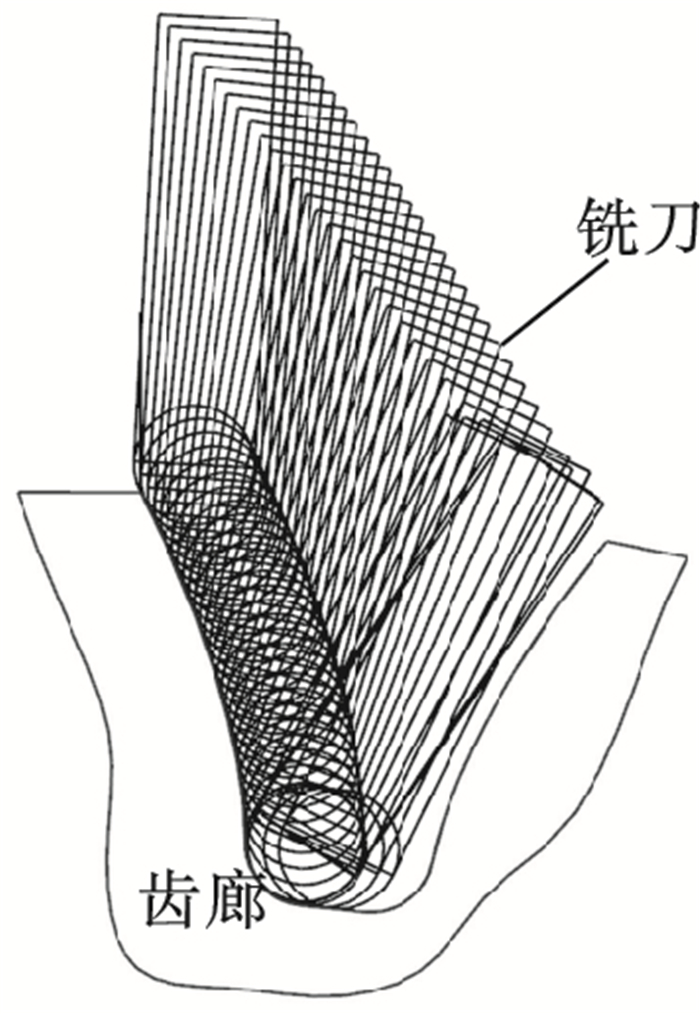 | 图 14 铣刀与工件的相对位置Fig.14 Relative positions of the tool and workpiece |
图 15(Fig. 15)
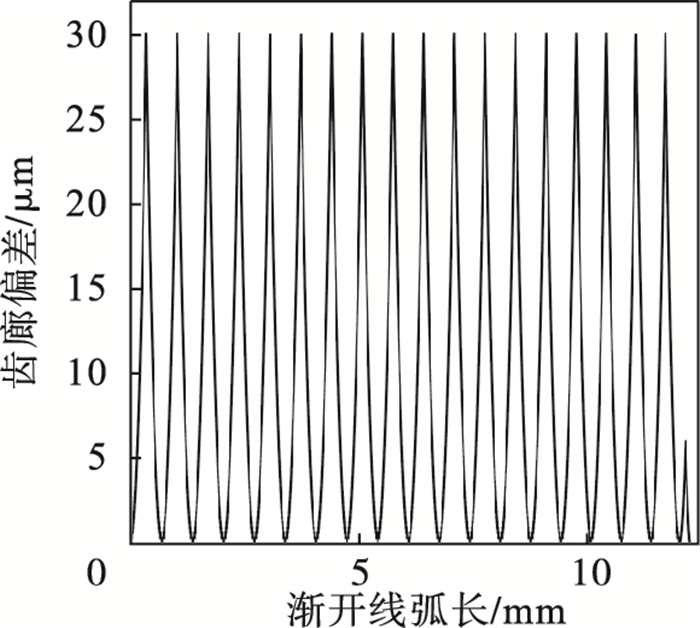 | 图 15 齿廓偏差Fig.15 Tooth profile deviation |
图 16(Fig. 16)
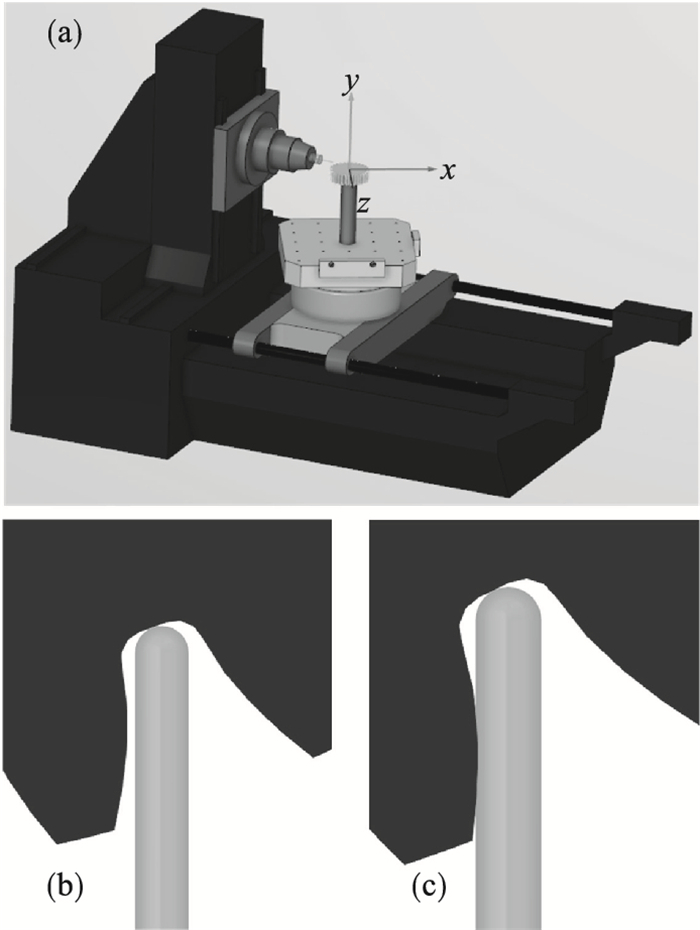 | 图 16 全局干涉仿真Fig.16 Global interference simulation (a)—Makino a77机床;(b)—λ=-20°;(c)—λ=-25.71°. |
4 结论1) 建立齿轮包络铣削运动模型,分析渐开线齿轮齿廓的几何特性,研究等残留高度下的球头铣刀包络齿廓的刀位点计算方法.
2) 以等残留高度计算刀位点为基础,残留高度约束下,给出了等弧长、等径向进给的刀位点计算方法.
3) 针对刀具干涉情况,通过选择小于过渡曲线圆弧的刀具半径来避免;全局干涉采用距离法来确定是否干涉,给出刀具无干涉情况下的刀具偏角范围.
4) 在仿真实例的齿廓偏差曲线中,不同刀位点处的偏差一致,等于残留高度,仿真加工过程有效地避免刀具干涉. 仿真结果验证了本文所采用方法的可行性和有效性.
参考文献
| [1] | Bouquet J, Hensgen L, Klink A, et al. Fast production of gear prototypes—a comparison of technologies[J]. Procedia CIRP, 2014, 14: 77-82. DOI:10.1016/j.procir.2014.03.066 |
| [2] | Klocke F, Brumm M, Staudt J. Quality and surface of gears manufactured by free form milling with standard tools[C]//Proceedings of the International Gear Conference. Lyon: Chandos Publishing, 2014: 506-515. |
| [3] | L?penhaus C, Klocke F, Staudt J. Performance of gears manufactured by 5-axis milling[J]. Gear Technology, 2017, 34(3): 58-65. |
| [4] | Yu Y, Lin C, Hu Y. Study on simulation and experiment of non-circular gear surface topography in ball end milling[J]. The International Journal of Advanced Manufacturing Technology, 2021, 114(7): 1913-1923. |
| [5] | ?zel C. Research of production times and cutting of the spur gears by end mill in CNC milling machine[J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(1/2/3/4): 203-213. |
| [6] | ?zel C. A study on cutting errors in the tooth profiles of the spur gears manufactured in CNC milling machine[J]. The International Journal of Advanced Manufacturing Technology, 2012, 59(1/2/3/4): 243-251. |
| [7] | Guo E, Ren N, Liu Z, et al. Study on tooth profile error of cylindrical gears manufactured by flexible free-form milling[J]. The International Journal of Advanced Manufacturing Technology, 2019, 103(9): 4443-4451. |
| [8] | 郭二廓, 任乃飞, 任旭东, 等. 考虑齿面精度特性的渐开线圆柱齿轮包络铣削加工[J]. 计算机集成制造系统, 2020, 26(11): 3011-3019. (Guo Er-kuo, Ren Nai-fei, Ren Xu-dong, et al. Free-form milling of involute cylindrical gears considering tooth surface accuracy characteristics[J]. Computer Integrated Manufacturing Systems, 2020, 26(11): 3011-3019.) |
| [9] | Shi Z, Feng Z, Wang P. Study on path planning of involute tooth surface milling with general cutting tool[C]//ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Anaheim: American Society of Mechanical Engineers, 2019: 97156. |
| [10] | Shi Z, Feng Z, Lin S, et al. Milling path planning for helical surface copper electrodes[J]. The International Journal of Advanced Manufacturing Technology, 2021, 114(3): 1031-1048. |
| [11] | Kawasaki K, Tsuji I, Abe Y, et al. Manufacturing method of large-sized spiral bevel gears in cyclo-palloid system using multi-axis control and multi-tasking machine tool[J]. Gear Technology, 2011, 8: 56-61. |
| [12] | álvarez á, Calleja A, Ortega N, et al. Five-axis milling of large spiral bevel gears: toolpath definition, finishing, and shape errors[J]. Metals-Open Access Metallurgy Journal, 2018, 8(5): 8050353. |
| [13] | Spitas V, Costopoulos T, Spitas C. Increasing the strength of standard involute gear teeth with novel circular root fillet design[J]. American Journal of Applied Sciences, 2005, 2(6): 1058-1064. DOI:10.3844/ajassp.2005.1058.1064 |
| [14] | Zou T, Shaker M, Angeles J, et al. An innovative tooth root profile for spur gears and its effect on service life[J]. Mechanica, 2017, 52(8): 1825-1841. DOI:10.1007/s11012-016-0519-7 |
| [15] | Feng H Y, Li H. Constant scallop-height tool path generation for three-axis sculptured surface machining[J]. Computer-Aided Design, 2002, 34(9): 647-654. DOI:10.1016/S0010-4485(01)00136-1 |
| [16] | Luo S, Liao L, Wang J, et al. Study on inspection and avoidance of interferences in five-axis end milling of cycloidal gears[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(9): 3307-3314. |
