孙浩^1,2, 朱东风^1,2, 金爱兵^1,2, 陈帅军^1,2
1. 北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京 100083;
2. 北京科技大学 土木与资源工程学院，北京 100083
收稿日期：2021-10-14
基金项目：国家自然科学基金资助项目(52174106，52004017)；中央高校基本科研业务费专项资金资助项目(FRF-TP-19-026A1，FRF-IDRY-20-021)。
作者简介：孙浩(1992-)，男，安徽阜阳人，北京科技大学讲师，博士;
金爱兵(1974-)，男，江苏兴化人，北京科技大学教授，博士生导师。

摘要：为研究硬岩卸荷阶段速率非线性变化时的破坏特性，利用室内三轴压缩试验和颗粒流数值模拟开展余弦型、直线型和指数型三种卸荷速率变化方式的硬岩破坏研究.结果表明：指数型卸荷的硬岩首先失稳破坏，余弦型卸荷的硬岩则不易发生破坏，前期较快的卸荷速率对整个卸荷过程的损伤积累影响更大；硬岩卸载过程中的承载强度受初始围压和卸荷方式的共同影响，且围压愈高则卸荷方式影响愈显著；根据Mogi-Coulomb准则，指数型卸荷通过内摩擦角影响硬岩强度，而直线型和余弦型卸荷的硬岩强度主要受黏聚力影响；指数型卸荷因前期快速卸荷易在端部产生部分破碎，直线型卸荷随围压升高由陡倾角剪切破裂带过渡多个“V”型剪切破坏，余弦型卸荷随围压增大呈塑性破坏特征趋势.
关键词：硬岩非线性卸荷速率破坏特性裂纹演化颗粒流
Failure Characteristics and Crack Evolution Laws of Hard Rock Under Nonlinear Unloading Rates
SUN Hao^1,2, ZHU Dong-feng^1,2, JIN Ai-bing^1,2, CHEN Shuai-jun^1,2
1. Key Laboratory of Ministry of Education for Efficient Mining and Safety of Metal Mines, University of Science and Technology Beijing, Beijing 100083, China;
2. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China
Corresponding author: JIN Ai-bing, E-mail: jinaibing@ustb.edu.cn.

Abstract: In order to study the failure characteristics of hard rock with nonlinear velocity variety in unloading phase, three unloading rate variety modes of cosine, linear and exponent were used to study the damage and failure of the hard rock by using the indoor triaxial compression tests and particle flow numerical simulation. The results show that the hard rock with exponential unloading rate first fails to stabilize, while the hard rock with cosine unloading rate is less likely to fail. The faster unloading rate in the early stage has a greater impact on the damage accumulation in the whole unloading process. The bearing strength of hard rock in unloading process is affected by both initial confining pressures and unloading modes, and the higher the confining pressure is, the more significant the influence of unloading mode is. According to the Mogi-Coulomb strength criterion, exponential unloading affects hard rock strength through internal friction angle, while the strength of hard rock under linear and cosine unloading mode is mainly affected by cohesion. Exponential unloading is easy to cause partial breakage at the end due to rapid unloading at the early stage. With the increase of confining pressure, linear unloading leads to multiple "V-shaped" shear failures from the steep dip shear fracture zone. Cosine unloading presents a plastic failure characteristic trend with the increase of confining pressure.
Key words: hard rocknonlinear unloading ratesfailure characteristicscrack evolutionsparticle flow
地下隧(巷)道、硐室等工程开挖破坏岩体完整性，平衡打破致使原岩应力重分布，表现为某个或几个方向的应力释放.由于开挖改变附近岩体赋存环境，不同卸荷速率变化方式的力学过程导致其应力变化过程更加复杂，会对地下工程开挖的稳定性产生显著影响.因此，岩体工程开挖卸荷一直是岩石力学及其工程应用相关领域的焦点问题^[1-3].
国内外****利用室内试验和数值模拟等手段，针对岩体卸荷问题开展了一系列研究.在室内试验研究方面，Chen等^[4]针对砂岩开展不同初始围压作用下的卸荷试验研究，发现围压增大导致裂纹体积应变减小，且较高卸荷速率则容易引起冲击地压.Wang等^[5]通过研究英安岩的卸荷破坏特征，认为卸荷破坏是拉应力通过裂纹分支传递、微裂纹相交而形成一个或多个宏观裂纹的过程.许文松等^[6]通过真三轴扰动卸荷岩石测试系统，分析不同应力路径的能量积聚型和应力集中型物理模型，发现在同一围压下岩体卸荷比加载更容易导致模型试件破坏，且破坏强度仅是加载时的80%.
室内试验存在操作复杂、重复性差等弊端，因而越来越多****利用数值模拟手段开展更复杂条件下硬岩宏-细观破坏特性研究.数值模拟主要有连续方法和离散单元法，但连续方法只能间接表示破裂，而离散单元法可直观再现岩样的破裂过程^[7].Cundall等^[8]基于离散单元法提出颗粒流PFC模拟软件，在岩土工程和地质工程等领域得到了广泛应用.Li等^[9]模拟裂隙岩体的卸荷过程，结果表明：卸荷破坏强度随裂纹倾角的增加而增大，卸载速率越快，则会产生更多的劈裂裂纹.Shi等^[10]基于离散元模拟岩石卸荷发现加轴压卸围压过程剪胀程度最大.李江腾等^[11]采用PFC软件建立数值模型模拟发现卸载时各类裂纹数量快速增加，且剪切裂纹数相比加载时有所降低.赵怡晴等^[12]采用PFC软件分析非贯通节理岩体加卸荷条件下破坏特性，研究发现在卸荷过程中，节理两侧剪应力最大，岩桥中心次之，节理面的剪应力最小.
目前，已有的硬岩卸荷问题研究多集中于恒轴压卸围压、加轴压卸围压、轴压与围压等量和不等量减少等不同应力路径，亦或是针对不同卸荷点进行不同卸荷速率的岩石卸荷特性研究，且研究中一般保持卸荷速率不变，而实际岩体工程开挖中难以保证施工速度一定、卸荷速率不变^[13-14].因此，本文在现有恒定卸荷速率研究的基础上，分析不同卸荷阶段的卸荷速率变化对硬岩破坏的影响，采用余弦型、直线型和指数型等典型卸荷速率变化方式，基于室内试验和数值模拟手段从硬岩强度及其特征参数、裂纹演化和破裂特征等方面探究硬岩在不同卸荷速率变化方式下的破坏特性与裂纹演化规律.研究结果对硬岩岩体工程的稳定性分析和施工进度调整等具有指导意义.
1 数值模型构建与模拟方案开展花岗岩室内三轴压缩试验，获取岩样宏观参数，在此基础上利用PFC软件构建岩样数值模型，确定其细观力学参数，并采用以余弦型、直线型和指数型为代表的卸荷速率变化方式进行卸荷模拟.
1.1 宏-细观参数匹配本次室内试验所用试样是取自山东省泗水县的典型硬质岩石——花岗岩，主要成分为角闪石、石英、长石、黑云母等，并加工成如图 1所示的直径50 mm、高100 mm圆柱型岩样.
图 1(Fig. 1)

图 1 室内试验所用花岗岩试样Fig.1 Granite samples used in laboratory tests

采用TAW-2000型电液伺服岩石三轴试验机对花岗岩试样进行常规三轴压缩室内试验(图 2)：首先以0.2 MPa/s加载速度增加围压至5或10 MPa；然后保持围压不变，以0.01 mm/min位移控制速率增加轴向压力，直至岩样完全破坏^[15].通过上述室内试验获取其应力-应变曲线以及峰值强度等宏观力学参数.
图 2(Fig. 2)

图 2 常规三轴压缩室内试验Fig.2 Conventional triaxial compression laboratory tests

PFC模拟选用的颗粒接触黏结模型为平节理模型(flat-joint model，FJM)，具有増强颗粒自锁、旋转阻抗适当、可预制裂纹和剪切强度随应力变化等特点，相比平行黏结模型(parallel-bond model，PBM)更适用于模拟花岗岩等硬质岩石^[16].
数值模型与室内试验所用花岗岩试样尺寸一致，即高100 mm，高径比为2∶1，进行多次三轴压缩模拟，通过宏-细观参数匹配研究，得到如图 3所示应力-应变对比曲线.图 3中的室内试验应力-应变数据是同一围压下三组岩样的平均值，可为数值模型细观力学参数优选提供数据支持.由于室内试验的岩样内部存在微孔隙，故室内试验加载初期的应力-应变曲线会出现一段凹陷，即存在孔隙压密阶段，而数值模拟中的颗粒在组成岩样模型时已达平衡状态，不存在可以压密的微孔隙，因此数值试验曲线在加载初期阶段呈直线状态.模拟结果与室内试验应力-应变曲线趋势基本一致(图 3)，最终确定选用表 1所示的硬岩数值模型细观参数组合.
图 3(Fig. 3)

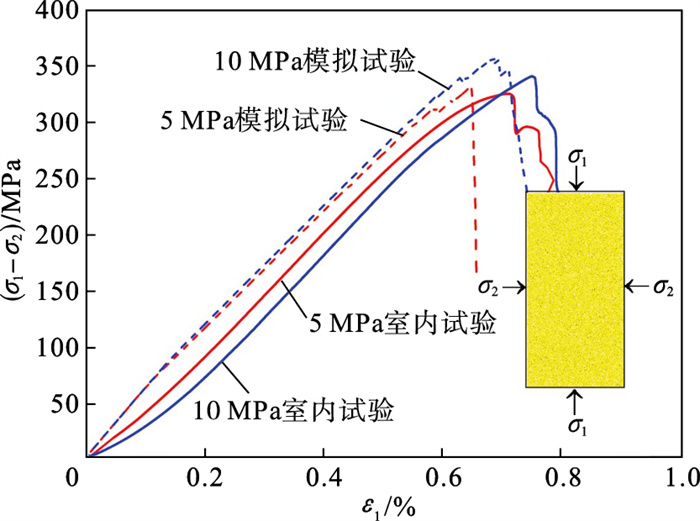图 3 三轴压缩试验与模拟所得应力-应变曲线Fig.3 Experimental and numerical stress-strain curves of rock in triaxial compression

表 1(Table 1)

表 1 硬岩数值模型细观参数Table 1 Microscopic parameters of numerical model for hard rock 密度 最小晶粒直径/mm 最大与最小晶粒直径比 安装间距 径向单元个数 刚度比 摩擦角 有效模量 黏结张拉力和标准差 黏结内聚力和标准差 kg·m-3 mm (°) GPa MPa MPa 2 700 0.9 1.66 0.4 4 3.5 10 48 15±1.5 120±12

表 1 硬岩数值模型细观参数 Table 1 Microscopic parameters of numerical model for hard rock

在此基础上为确定卸荷点，首先进行三轴压缩模拟，获得不同围压下岩样峰值应力，并以峰值应力的80%作为卸荷点^[17].进行10，20和30 MPa三种围压下的常规三轴压缩模拟，得到如图 4所示不同围压条件下的应力-应变曲线及卸荷点应力.
图 4(Fig. 4)

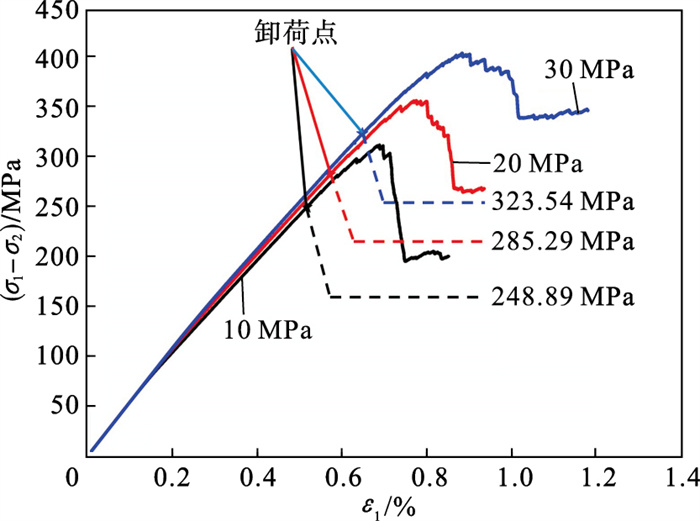图 4 三轴压缩数值模拟应力-应变曲线及卸荷点Fig.4 Numerical stress-strain curves and unloading points in triaxial compression

1.2 卸荷数值模拟方案针对隧道掘进、地下采矿等地下岩体工程开挖，其围岩、矿柱受力一般表现为轴向应力增加而径向应力减小.岩体开挖中保持卸荷速率恒定势必会增加工程难度，实际不同施工阶段的卸荷速率往往是不断变化的.因此，采用加轴压卸围压应力路径，选取余弦型(卸荷速率由慢转快)、直线型(卸荷速率恒定)和指数型(卸荷速率由快转慢)等典型卸荷速率变化方式^[13-14]探究不同卸荷阶段的速率变化对硬岩破坏的影响.
卸荷模拟前期应力加载与常规三轴压缩试验施加步骤一致，当岩样以2.5 mm/s移动上下墙体增加轴向应力至图 4所示卸荷点应力值后，将围压按照图 5所示不同卸荷速率变化方式进行加轴压卸围压，其中u处即为卸荷点.余弦型卸荷、直线型卸荷和指数型卸荷的表达式分别为

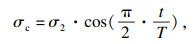(1)

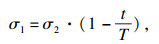(2)

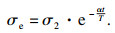(3)

图 5(Fig. 5)

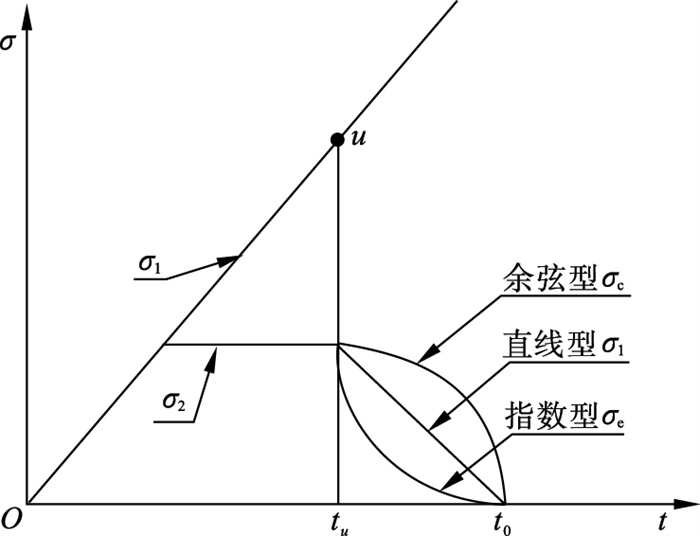图 5 卸荷应力路径示意图Fig.5 Schematic diagram of unloading stress path

式中：σ₂为初始围压；t为时间；α为指数衰减系数；T为卸荷总时间，即t₀-t_u.
以往采用PFC软件进行岩石力学数值模拟研究中通常忽略时间步长波动对模拟结果产生的误差^[9-12]，因而本次卸荷模拟过程中采取如下优化方式：
① 在轴向应力达到卸荷点后将径向应力按照式(4)围压函数关系进行卸载，同时监测时间步长在整个卸荷过程中的数值变化；
② 选取时步在卸围压计算过程中最小步长值作为后续卸荷过程中固定的时步值；
③ 固定时间步长后再次依据式(4)进行卸荷，以此得到固定时步条件下卸荷的总时间T，供图 5中不同卸荷方式的函数使用.

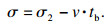(4)

式中：v为线性卸载速率；t_b为时步.
2 硬岩破坏特性与裂纹演化规律根据数值模拟结果，对比分析三种初始围压和不同卸荷速率变化方式对硬岩强度及其特征参数的影响，探究非线性卸荷过程中硬岩裂纹的总数量和增量随轴向应变的演化规律，揭示硬岩在不同卸荷速率变化方式下的破坏特性和裂纹演化规律.
2.1 初始围压和卸荷方式对硬岩强度的影响在同一初始围压条件下，岩样所受轴向应力达到卸荷点前，三种卸荷方式下的应力-应变变化曲线一致，故以卸荷点作为起始点，监测岩样在三种围压下进行卸荷数值模拟所得应力-应变曲线如图 6所示.
图 6(Fig. 6)

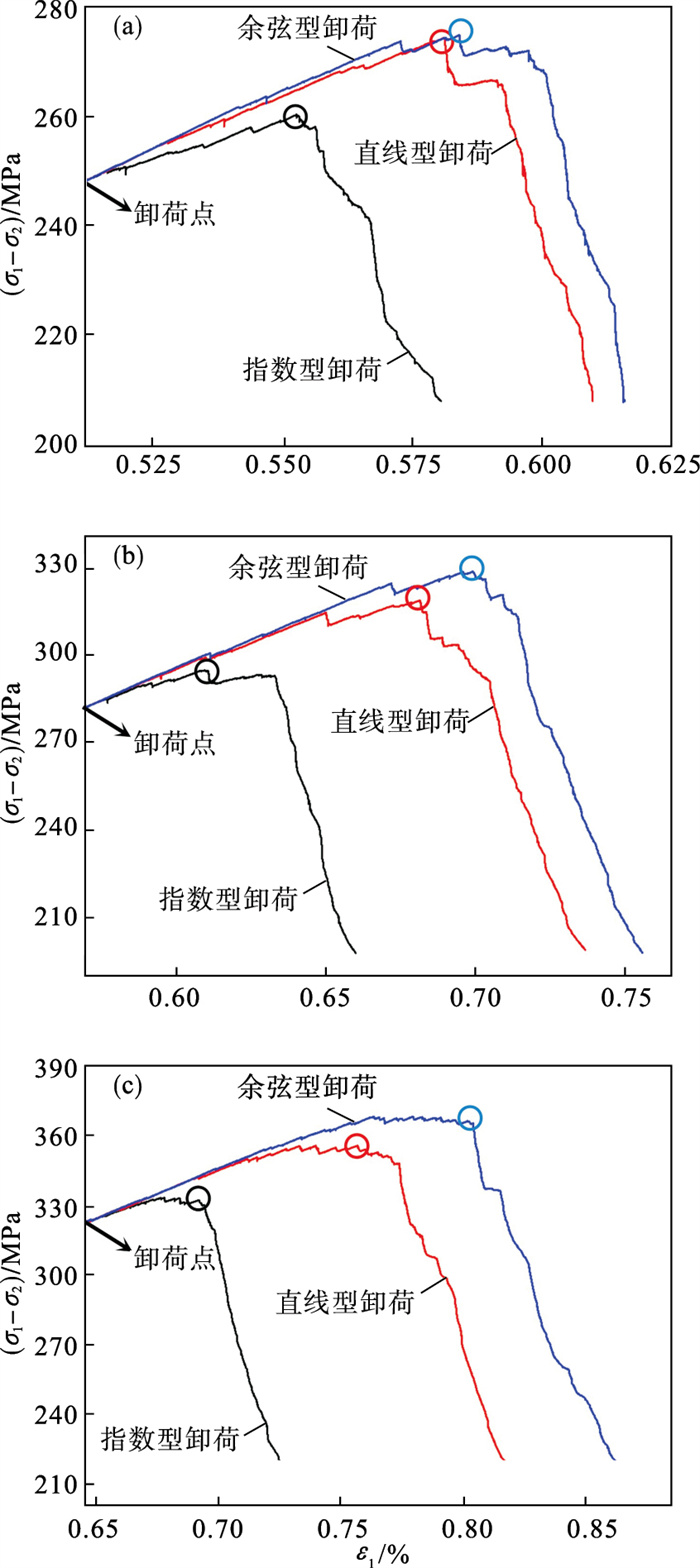图 6 不同初始围压和卸荷方式下的应力-应变曲线Fig.6 Stress-strain curves under different initial confining pressures and unloading modes (a)—10 MPa; (b)—20 MPa; (c)—30 MPa.

由图 6中的余弦型、直线型和指数型卸荷曲线对比可知，指数型卸荷岩样首先发生破坏，直线型和余弦型均迟于指数型屈服破坏且余弦型卸荷岩样峰值强度最高.岩样卸荷是一个连续过程，期间卸荷速率变化势必会对其破坏结果造成不同程度的影响.围压快速卸载导致岩样径向抑制能力急剧减弱，偏应力单位时间内变化大，裂纹迅速扩展，岩样损伤积累激增造成破坏.本文研究的指数型卸荷方式下岩样极限承载力最低，说明前期较快卸荷速率在整个开挖过程中对岩样稳定产生显著的扰动作用，卸荷前期阶段的损伤积累较为活跃，且影响程度大于后期速率的影响. 因此，针对隧道掘进、地下采矿等实际岩体卸荷工程，在保证总体施工进度的前提下，采用前慢后快的卸荷施工方案，即适当控制前期开挖速率有利于保持实际施工中矿柱和围岩的稳定性.后续将细化卸荷速率变化梯度，进而探究前期卸荷影响硬岩稳定的速率阈值.
针对不同初始围压环境下岩样卸荷模拟所得峰值应力进行统计分析，得到如图 7所示的峰值应力和初始围压及卸荷速率变化方式的关系示意图.
图 7(Fig. 7)

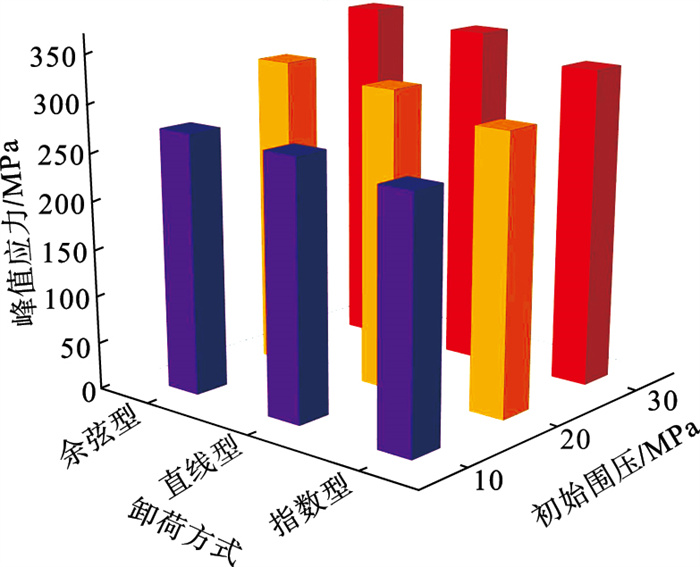图 7 卸荷方式与初始围压共同作用下的硬岩峰值应力Fig.7 Peak stress of hard rock under the coupling of unloading modes and initial confining pressures

由图 7分析可知，卸荷速率变化方式和初始围压对岩样强度均会产生不同程度的影响：
① 当岩样所处环境径向受力较小时(σ₂=10 MPa)，三种卸荷速率变化方式下的峰值强度相近，即表明低围压下不同卸荷方式对岩样承载力影响较小.
② 随着初始围压增加，抑制岩样径向变形以增大其承载力，三种卸荷速率变化方式下的岩样峰值强度均有所增加，而同一初始围压下不同卸荷方式所得的岩样峰值应力之差从14.51 MPa逐渐增大到35.19 MPa，增加的比例分别为5.57%和10.55%，围压增加使得同一围压下不同卸荷方式造成的应力差增大近一倍.
③ 对于相邻围压梯度，如10 MPa余弦型卸荷与20 MPa指数型卸荷的峰值应力相差18.69 MPa，而20 MPa余弦型卸荷和30 MPa指数型卸荷的峰值应力仅差5.36 MPa.相邻围压不同卸荷方式的应力差比值从6.79%缩减到1.63%，表明初始围压越大，卸荷速率变化方式对岩样强度的影响愈加显著.
综上，硬岩在卸荷过程的承载力受初始围压和卸荷速率变化方式两种因素的共同影响，围压越高则其抵抗变形破坏的能力越强，进而提升围岩整体承载能力；岩体在较高围压环境下的变形受卸荷速率变化方式的影响更加显著，因而卸荷方式对高围压岩体承载强度具有显著影响.深部高围压岩体具有较强抵抗变形能力，但当前期卸载速率较快时，应及时做好支护等安全措施.
2.2 硬岩卸荷强度参数分析强度准则是岩石力学理论的重要组成部分，反映岩石破坏时应力与强度参数关系.Mogi^[18]在Mohr-Coulomb强度准则基础上进行改进提出了Mogi-Coulomb强度准则，能够更准确地表征岩石破坏强度参数变化^[19]，广泛应用于岩石加卸载破坏特征分析^[20].为进一步研究硬岩破坏强度参数，采用Mogi-Coulomb强度准则，分析三轴加载和不同卸荷速率变化方式的硬岩强度参数变化，具体应力关系如下：

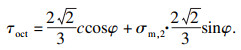(5)

式中：τ_oct为八面体剪应力；σ_{m, 2}为有效中间主应力；c为黏聚力；φ为内摩擦角.
根据岩样在不同围压下进行三轴加卸载的试验数据，应用Mogi-Coulomb准则可拟合得到如图 8所示τ_oct和σ_{m, 2}的关系曲线，τ_oct和σ_{m, 2}拟合相关系数R²均大于0.99，因此Mogi-Coulomb强度准则能够很好地表征常规三轴加载和不同卸荷速率变化方式下的硬岩破坏强度特征参数变化.
图 8(Fig. 8)

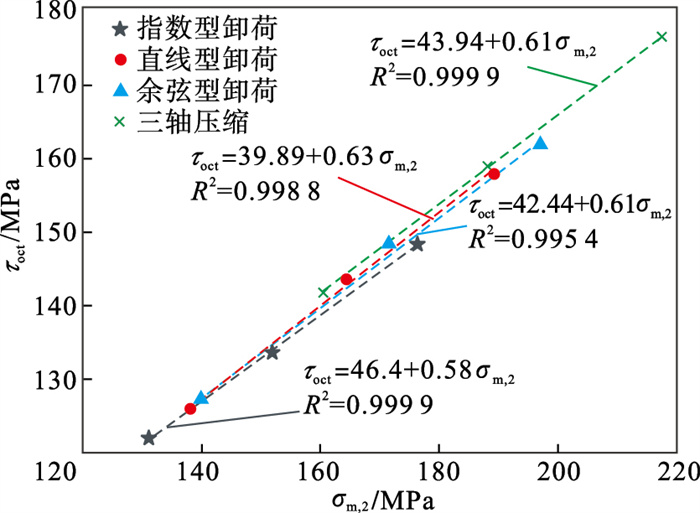图 8 基于Mogi-Coulomb准则的τoct和σm, 2拟合曲线Fig.8 τoct and σm, 2 fitting curves based on the Mogi-Coulomb criterion

综合比较岩样在不同加卸载条件下的强度参数，将岩样在不同卸荷速率变化方式下的拟合结果与三轴压缩进行对比，可得强度参数变化关系如图 9所示.由于不同卸荷方式仅是改变试验条件，并未改变试样，故参数变化量最大为7.28%，与李江腾等^[11]强度参数研究变化范围相似.与常规三轴压缩相比，指数型卸荷内摩擦角减小6.4%，前期卸荷速率较快会造成岩样局部变形严重，显著减弱岩样内部颗粒摩擦，因此指数型卸荷主要通过内摩擦角影响硬岩强度；而直线型卸荷黏聚力减小7.28%，余弦型卸荷黏聚力减小3.45%，卸荷后期保持速率不变(直线型)或增加卸荷速率(余弦型)则会因前期卸荷速率缓慢而充分发育损伤，劣化黏聚强度，因而直线型和余弦型卸荷方式下影响硬岩强度的关键因素是黏聚力.
图 9(Fig. 9)

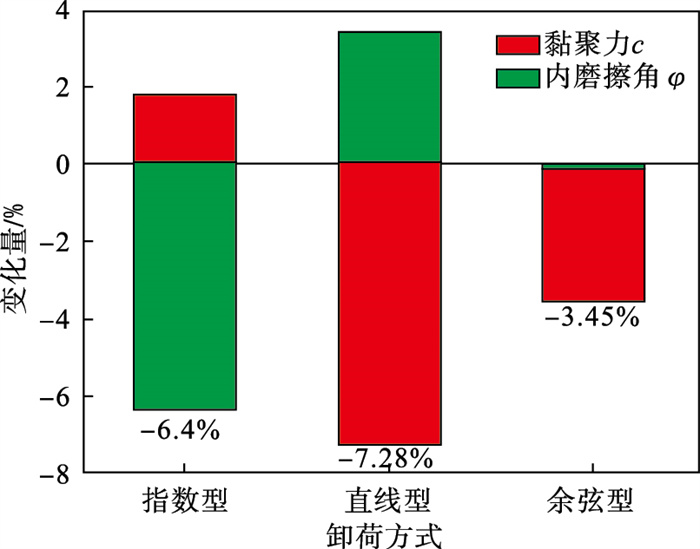图 9 不同卸荷方式下的强度参数变化关系Fig.9 The variation of strength parameters under different unloading modes

2.3 硬岩裂纹演化规律分析岩样在加轴压卸围压模拟中产生大量微裂纹并逐渐贯通形成宏观破裂，为研究不同卸荷速率变化方式下岩样裂纹演化规律，在PFC模拟中自卸荷点开始监测岩样裂纹随轴向应变的总数量和增量演化过程(图 10).
图 10(Fig. 10)

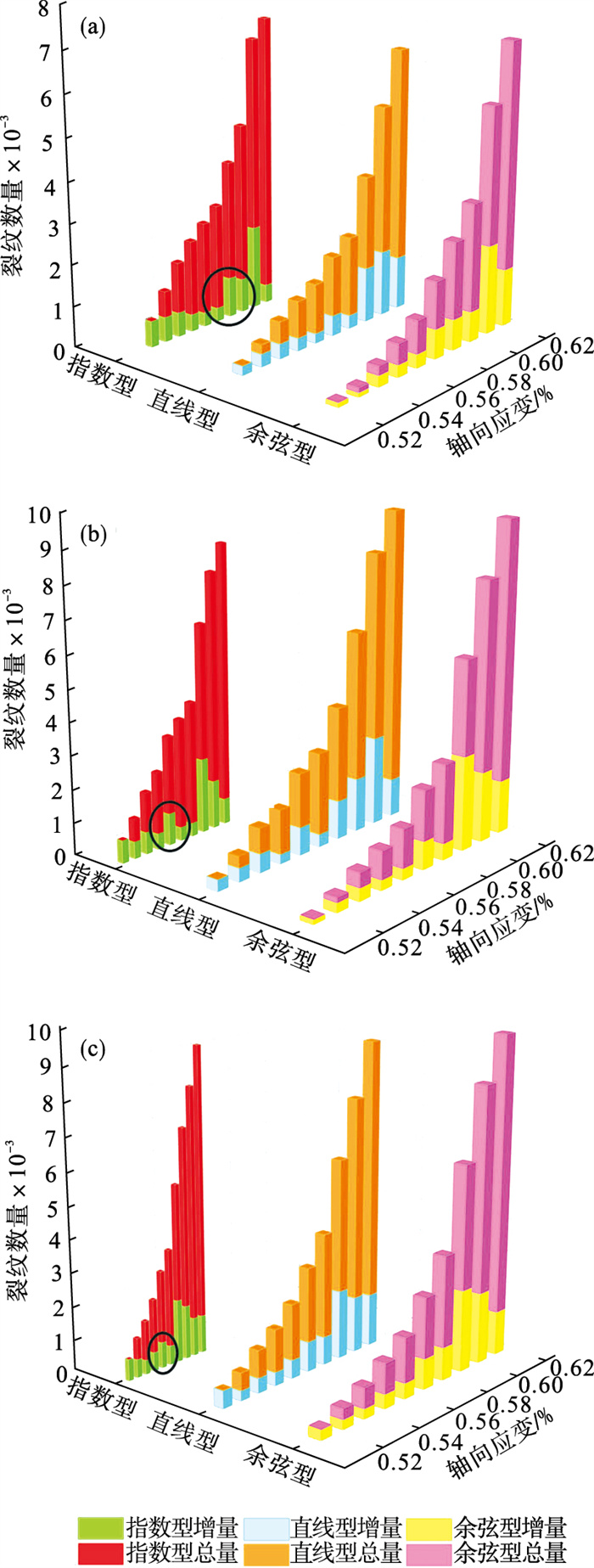图 10 不同初始围压和卸荷方式下裂纹总数量和增量的演化过程Fig.10 The variation of the total number and increment of cracks under different initial confining pressures and unloading modes (a)—10 MPa; (b)—20 MPa; (c)—30 MPa.

图 10中的红色、橙色和洋红色柱状图表示不同初始围压和卸荷速率变化方式下岩样产生裂纹总数量随轴向应变的演化过程，由此可以看出，岩样在加轴压卸围压过程中，线性和非线性卸荷速率变化方式下破裂产生的裂纹总数量均呈非线性增长趋势.
由图 10的绿色柱状图可知，岩样进行指数型非线性卸荷的裂纹增量总体呈现由多转少再激增的趋势.这是由于其卸荷速率变化特征所致，前期卸荷速率较快，相应偏应力变化迅速，对岩样内部裂纹的产生与扩展有促进作用而导致裂纹增量大，而后卸荷速率减慢导致裂纹增量渐缓；岩样裂纹增量由多转少过渡不平滑，破坏前呈现裂纹增量突增而后下降的现象(图 10黑色圆框内绿色柱体)，与其发生破坏前的裂纹增量高峰相差甚远.这是由于卸荷过程轴向应力仍在增加，裂纹增量却持续降低，岩样内部损伤积累到一定程度需通过裂纹激增释放耗散能.其余两种卸荷方式前期卸荷速率较低，卸荷过程的裂纹增量并不比卸荷点低，内部损伤耗散能由裂纹发育得到有效释放，故而没有裂纹增量突增现象.
由图 10的青色柱状图变化分析可知，直线型卸荷方式下岩样的裂纹增量在破坏前大致处于相近水平，初始围压较小时裂纹增量则会出现小幅波动(图 10a和10b).这是由于岩样在加轴压过程的卸围压速率线性不变，低围压径向抑制作用较小使得岩样易发生损伤，即产生裂纹，而后间隔一段应变积累损伤后再次增大裂纹增量，故而发生裂纹增量小范围波动，直至由于岩样破坏致使裂纹增量变大.
分析图 10的黄色柱状图走势可知，余弦型非线性卸荷的岩样前期卸载缓慢，对裂纹产生起抑制作用，故裂纹增量相较其余两种卸荷方式最小，而后期由于卸荷速率加快，裂纹才得以逐渐扩展，岩样裂纹发育缓慢不易破坏，与2.1节中所得硬岩在该卸荷方式下是最稳定、强度最高的结论相吻合，裂纹增量仅在屈服破坏阶段才显著增加.
综上，对比图 10中的绿色、青色和黄色柱状图所示不同卸荷速率变化方式下岩样裂纹增量演化过程可知，不同初始围压和改变卸荷速率变化方式均会致使硬岩裂纹萌生演化过程差异明显，进而显著影响硬岩的损伤积累与完整性：①指数型卸荷的裂纹增量在破坏前由多转少过渡不平滑，呈现在卸荷后期突增而再下降.故实际采用该卸荷方式进行硬岩卸载时，注意区分裂纹增量突增与岩体破坏裂纹增量高峰；②直线型卸荷的裂纹增量在破坏前处于相近平缓状态，当硬岩环境围压较低时，裂纹增量表现小范围波动，实际工程中采用匀速卸载时硬岩裂纹增量发育平稳即表明岩体稳定；③余弦型卸荷的硬岩在前期裂纹增量最少，随着卸荷进行裂纹增量缓慢升高，故实际采掘开挖硬岩岩体时使用该卸荷方式的可在相同变形情况下产生最少裂隙，从而保持岩体稳定.
2.4 硬岩破裂特征分析不同卸荷速率变化方式会导致岩样产生不同的破裂特征，岩样在不同初始围压及卸荷速率变化方式下的裂纹分布和破坏特征分析如表 2所示，其中红色短线表示剪切裂纹产生位置.因PFC模拟中平节理模型颗粒之间是由多个抽象单元组成的接触面，产生的裂隙可能仅是其接触面上某个抽象单元断裂，在平节理接触中就会出现拉伸裂纹，当产生剪切裂纹时，接触面则会完全断开，因此岩样在不同初始围压和不同卸荷方式下的破坏伴随着拉伸裂纹和剪切裂纹的集中分布.考虑该模型接触面多单元破裂特征，为保证岩样破坏特征分析的准确性，故隐去岩样表面密布的拉伸裂纹，针对剪切裂纹集中分布产生的破坏进行对比分析.
表 2(Table 2)

表 2 不同卸荷方式和初始围压下的岩样破裂特征Table 2 Failure characteristics of rock samples under different unloading modes and initial confining pressures 围压/MPa 指数型卸荷 直线型卸荷 余弦型卸荷 破裂特征分析 10 初始围压为10 MPa时，不同卸荷方式下岩样主要破裂面均为对角贯通陡倾剪切破裂面，次要破坏面因卸荷方式不同而略有区别.其中，指数型卸荷型岩样除主要破裂面外，还产生由于前期卸荷速率过快而导致端部存在部分碎裂；直线型卸荷岩样仅有一个主剪切破裂带伴有部分剪切裂纹，属于典型的剪切破坏模式；余弦型卸荷型岩样破坏产生两条非贯通剪切破坏面.因此，初始围压较小时卸荷速率变化对岩样破坏特征影响较小. 20 初始围压增加到20 MPa时，指数型卸荷由于初期卸荷速率大，岩样端部亦存在部分破碎，并产生多条劈裂破坏；而直线型卸荷的岩样由贯通裂隙形成一条主要剪切破坏面，并且比低围压时多出一些局部剪切裂隙；余弦型卸荷因初期卸荷速率最小，产生的裂纹呈现向端部扩展破坏. 30 初始围压为30 MPa时的破坏发展为众多裂隙贯通多处“V”型剪切面，围压增大致使径向应变受限，因而指数型卸荷的端部碎裂现象有所缓和；直线型卸荷由低围压时的陡倾角剪切面过渡成多个“V”型剪切破裂形式；余弦型卸荷产生多个宏观破裂面，且集中分布在两端，呈塑性破坏特征趋势，这是前期卸荷速率低和初始围压高两因素共同作用所致.

表 2 不同卸荷方式和初始围压下的岩样破裂特征 Table 2 Failure characteristics of rock samples under different unloading modes and initial confining pressures

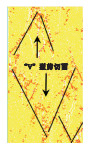
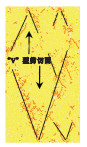
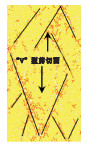
由表 2综合分析可得，低围压时的硬岩主要破裂面均为对角贯通陡倾剪切破裂面，指数型卸荷因前期卸荷速率大而易在端部产生部分碎裂，随着初始围压升高，指数型卸荷的硬岩端部部分破碎现象逐渐消失(当围压达到30 MPa时)；直线型卸荷下的硬岩由陡倾角剪切破裂带过渡成多个“V”型剪切破坏；余弦型卸荷硬岩承载能力大，产生较多宏观裂隙，且随初始围压升高逐渐呈现塑性破坏特征趋势.
3 结论1) 三种卸荷速率变化方式中，指数型卸荷的硬岩首先失稳破坏，而余弦型卸荷的硬岩则不易发生破坏，表明前期较快的卸荷速率对整个卸荷过程的损伤积累影响更大.针对难以保证全程匀速开挖掘进的复杂工况，合理控制前期开挖速率更有利于维持硬岩稳定性.
2) 硬岩极限承载强度受到初始围压和卸荷速率变化方式的共同影响，且随着围压升高，卸荷方式对硬岩破坏的影响程度愈加显著.因此，高围压卸荷环境下更应及时支护开挖掘进面.
3) 硬岩在三种卸荷速率变化方式下的破坏强度特征均符合Mogi-Coulomb强度准则.与常规三轴压缩相比，指数型卸荷主要通过硬岩内摩擦角影响其强度，直线型和余弦型卸荷方式影响硬岩强度的关键因素是黏聚力.
4) 硬岩卸荷过程的裂纹增量与卸荷速率变化方式密切相关：指数型卸荷的裂纹增量在破坏前由多转少过渡不平滑，呈现在卸荷后期突增而再下降；直线型卸荷的裂纹增量在破坏前处于相近水平，初始围压较低时，裂纹增量表现小范围波动；余弦型卸荷的硬岩在前期裂纹增量最少，随着卸荷进行裂纹数量缓慢增加.
5) 不同卸荷速率变化方式导致硬岩呈现不同的破坏形态：指数型卸荷因前期快速卸荷易在端部产生部分破碎；直线型卸荷随围压升高，由陡倾角剪切破裂带过渡成多个“V”型剪切破坏；余弦型卸荷硬岩承载能力大，产生宏观裂隙多，且随围压增大呈塑性破坏特征趋势.
参考文献

[1]	Zhu Z N, Tian H, Kempka T, et al. Mechanical behaviors of granite after thermal treatment under loading and unloading conditions[J]. Natural Resources Research, 2021, 30(3): 2733-2752. DOI:10.1007/s11053-021-09815-7
[2]	Jiang Q, Zhang M Z, Yan F, et al. Effect of initial minimum principal stress and unloading rate on the spalling and rockburst of marble: a true triaxial experiment investigation[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(2): 1617-1634. DOI:10.1007/s10064-020-01995-5
[3]	Zhao H G, Song Z L, Zhang D M, et al. True triaxial experimental study on mechanical characteristics and energy evolution of sandstone under various loading and unloading rates[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 2021, 7(1): 1-17. DOI:10.1007/s40948-020-00190-w
[4]	Chen Y, Zuo J P, Li Z H, et al. Experimental investigation on the crack propagation behaviors of sandstone under different loading and unloading conditions[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 130: 104310. DOI:10.1016/j.ijrmms.2020.104310
[5]	Wang S S, Xu W Y, Yan L, et al. Experimental investigation and failure mechanism analysis for dacite under true triaxial unloading conditions[J]. Engineering Geology, 2020, 264: 105407. DOI:10.1016/j.enggeo.2019.105407
[6]	许文松, 赵光明, 孟祥瑞, 等. 大理岩真三轴单面卸荷条件下加卸载试验研究[J]. 西南交通大学学报, 2019, 54(3): 526-534. (Xu Wen-song, Zhao Guang-ming, Meng Xiang-rui, et al. Test study on true-triaxial loading and unloading for marble with unloaded single face[J]. Journal of Southwest Jiaotong University, 2019, 54(3): 526-534.)
[7]	Potyondy D O, Cundall P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364. DOI:10.1016/j.ijrmms.2004.09.011
[8]	Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47
[9]	Li X B, Chen Z H, Weng L, et al. Unloading responses of pre-flawed rock specimens under different unloading rates[J]. Transactions of Nonferrous Metals Society of China, 2019, 29(7): 1516-1526. DOI:10.1016/S1003-6326(19)65059-4
[10]	Shi C, Yang J X, Chu W J, et al. Macro-and micromechanical behaviors and energy variation of sandstone under different unloading stress paths with DEM[J]. International Journal of Geomechanics, 2021, 21(8): 04021127. DOI:10.1061/(ASCE)GM.1943-5622.0002106
[11]	李江腾, 刘双飞, 赵远, 等. 不同应力路径下砂岩真三轴试验及数值模拟[J]. 中南大学学报(自然科学版), 2021, 52(3): 693-700. (Li Jiang-teng, Liu Shuang-fei, Zhao Yuan, et al. True triaxial test and numerical simulation of sandstone in different stress paths[J]. Journal of Central South University(Science and Technology), 2021, 52(3): 693-700.)
[12]	赵怡晴, 刘佳伟, 金爱兵, 等. 加卸荷条件下非贯通节理岩体破坏特性研究[J]. 中南大学学报(自然科学版), 2020, 51(7): 1893-1901. (Zhao Yi-qing, Liu Jia-wei, Jin Ai-bing, et al. Study on failure characteristics of intermittent jointed rock mass under loading and unloading condition[J]. Journal of Central South University(Science and Technology), 2020, 51(7): 1893-1901.)
[13]	Cao W Z, Li X B, Tao M, et al. Vibrations induced by high initial stress release during underground excavations[J]. Tunnelling and Underground Space Technology, 2016, 53: 78-95. DOI:10.1016/j.tust.2016.01.017
[14]	Li X B, Cao W Z, Zhou Z L, et al. Influence of stress path on excavation unloading response[J]. Tunnelling and Underground Space Technology, 2014, 42: 237-246. DOI:10.1016/j.tust.2014.03.002
[15]	朱杰兵. 高应力下岩石卸荷及其流变特性研究[D]. 武汉: 中国科学院(武汉岩土力学研究所), 2009. (Zhu Jie-bing. Study on unloading mechanics and its rheological properties of rock under high stress[D]. Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, 2009. )
[16]	Potyondy D O. A flat-jointed bonded-particle material for hard rock[EB/OL]. (2012-06-24)[2019-10-10]. http://onepetro.org/ARMAUSRMS/proceedings-abstract/ARMA12/All-ARMA12/ARMA-2012-501/120762.
[17]	赵军, 郭广涛, 徐鼎平, 等. 三轴及循环加卸载应力路径下深埋硬岩变形破坏特征试验研究[J]. 岩土力学, 2020, 41(5): 1521-1530. (Zhao Jun, Guo Guang-tao, Xu Ding-ping, et al. Experimental study on deformation and failure characteristics of deeply-buried hard rock under triaxial and cyclic loading and unloading stress paths[J]. Rock and Soil Mechanics, 2020, 41(5): 1521-1530.)
[18]	Moji K. Fracture and flow of rocks under high triaxial compression[J]. Journal of Geophysical Research, 1971, 76(5): 1255-1269. DOI:10.1029/JB076i005p01255
[19]	Al-Ajmi A M, Zimmerman R W. Relation between the Mogi and the Coulomb failure criteria[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(3): 431-439. DOI:10.1016/j.ijrmms.2004.11.004
[20]	Feng F, Chen S, Wang Y, et al. Cracking mechanism and strength criteria evaluation of granite affected by intermediate principal stresses subjected to unloading stress state[J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 143: 104783.