
 , 张陈龙1, 白海文1, 马少坤1,2
, 张陈龙1, 白海文1, 马少坤1,2 1. 广西大学 土木建筑工程学院,广西 南宁 530004;
2. 广西大学 工程防灾与结构安全教育部重点实验室,广西 南宁 530004
收稿日期:2021-05-24
基金项目:国家自然科学基金资助项目(51678166);广西研究生教育创新计划项目(JGY2021014)。
作者简介:黄震(1989-),男,湖南长沙人,广西大学讲师,博士。
摘要:设计了一种应用于装配式矩形隧道的卯榫接头,探究了卯榫接头装配式隧道静力行为和内爆作用下的抗爆性能,建立了反映接头非线性力学特征的三维精细化数值模型,利用流固耦合分析实现了TNT爆炸模拟,对比评价了卯榫接头与现浇接头在不同围压荷载作用下的抗压弯承载能力、抗爆性及混凝土损伤特性.结果表明:新型接头抗压弯承载能力略高于现浇接头矩形隧道;在相同当量TNT炸药下,新型接头装配式矩形隧道抗爆能力整体上优于现浇接头矩形隧道;新型接头装配式矩形隧道损伤破坏主要发生在钢柱和顶板-墙结点区域.研究结果为装配式矩形隧道结构设计及防灾减灾提供理论支撑.
关键词:装配式隧道接头静力行为抗爆性损伤特性
Static Behavior and Blast Resistance Analysis for New Joint Assembled Rectangular Tunnel
HUANG Zhen1,2

 , ZHANG Chen-long1, BAI Hai-wen1, MA Shao-kun1,2
, ZHANG Chen-long1, BAI Hai-wen1, MA Shao-kun1,2 1. School of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China;
2. Key Laboratory of Engineering Disaster Prevention and Structural Safety of the Ministry of Education, Guangxi University, Nanning 530004, China
Corresponding author: HUANG Zhen, E-mail: hzcslg@163.com.
Abstract: A mortise and tenon joint applied to prefabricated rectangular tunnel is designed, and the static behavior and explosion resistance of prefabricated tunnel with this mortise and tenon joint are studied. A three-dimensional refined numerical model reflecting the nonlinear mechanical characteristics of the joint is established, and the TNT explosion simulation is realized by fluid-solid coupling analysis. The compressive bending capacity, explosion resistance and concrete damage characteristics of mortise joint and cast-in-situ joint under different confining pressures are compared and evaluated. The results show that the bending capacity of the new joint is slightly higher than that of the cast-in-situ joint rectangular tunnel. Under the same equivalent TNT explosive, the anti-explosion capacity of the new joint assembled rectangular tunnel is better than that of the cast-in-situ joint rectangular tunnel as a whole. The damage and failure of the new joint assembled rectangular tunnel mainly occurs in the steel column and roof wall joint area. The research results provide theoretical support for the structural design of prefabricated rectangular tunnel and disaster prevention and mitigation.
Key words: assembled tunneljointstatic behaviorblast resistancedamage characteristics
矩形装配式隧道因具有空间利用率高、速度快和质量易控制等优点,在市政隧道、地铁隧道、管廊等地下工程中应用越来越广泛.这类装配式矩形隧道衬砌通过各类接头连接而成,其结构属于一个非连续体,使得隧道的受力机理非常复杂.接头是矩形隧道建设和运营阶段最为薄弱的部位,其设计不合理和力学性能不佳均影响整个隧道的结构安全.此外,装配式矩形隧道通常位于人口密集区,容易受到汽车爆炸、可燃气或液体泄漏爆炸以及恐怖爆炸袭击等威胁,导致人员伤亡和结构破坏.因此,矩形装配式隧道接头在具备良好承载性能的同时,还需要考虑其在爆炸荷载作用下的抗灾能力.
近年来,国内外****采用试验方法和数值模拟方法对装配式隧道接头的力学行为和抗爆性开展了系列研究.在试验方面,Li等[1]对盾构隧道分段衬砌纵向接头进行了抗弯破坏试验,认为纵向接头的弯矩可分为下垂弯矩和拱起弯矩;黄大维等[2]通过缩尺试验确定了盾构隧道管片纵缝接头设计方法;Meng等[3]利用全尺寸试验研究隧道结构构件对爆炸荷载的响应,发现高性能混凝土能更好地抵抗爆炸荷载作用;Wang等[4]通过试验对瓦斯爆炸进行了研究,确定了超压和气流速度在发生爆炸后呈先增大后减小的趋势;Yu等[5]通过爆炸试验对混凝土板的破坏过程进行研究,认为纤维增强钢筋可以提高混凝土板抗爆性能.上述试验方法是研究隧道接头力学性能最直接的方法,但足尺模型的试验成本昂贵、周期长;缩尺试验虽然能降低成本,但难以还原试件真实受力状态与力学性能;此外,隧道接头抗爆性评价的试验具有危险性,且实施程序复杂.
数值方法在解决隧道结构复杂力学非线性问题上具有很好的优势,因而被众多****采用.如Osinov等[6]基于数值方法建立了隧道与地层耦合模型,发现地表爆炸会引起周围土体和隧道衬砌的大变形,衬砌变形程度取决于土壤的力学性质、水力条件以及爆炸当量等因素;张稳军等[7]研究了隧道复合材料接头的抗剪性能,提出了一定轴力条件下不同破坏形式对应的接头布置范围及最佳布置方式;赵德博等[8]对既有隧道在内爆炸作用下进行数值模拟,发现偏心爆炸工况的冲击波在爆炸远区产生较长时间汇集,此区域受爆炸影响较大;高盟等[9]采用三维有限元模型研究了内源爆炸作用下隧道衬砌的动力响应,发现隧道动力响应随时间而迅速减小,动力响应在隧道径向和轴向上呈指数衰减.
综上,隧道接头力学行为和抗爆性研究已取得丰硕成果,但在接头力学行为方面,研究的接头结构多属于盾构隧道接头,且大多以单一接头构件为研究载体;抗爆性研究中均视隧道衬砌为整体结构,未考虑隧道接头效应的影响;此外关于装配式矩形隧道抗爆性评价研究甚少.基于此,设计一种针对装配式矩形隧道的接头,采用混凝土塑性损伤模型,建立反映新型接头装配式矩形隧道非线性力学特征的三维精细化数值模型,并利用流固耦合分析实现TNT爆炸模拟.通过与现浇接头矩形隧道进行对比分析,评价新型接头隧道的抗压弯承载能力和抗爆性,揭示静力荷载和爆炸荷载作用下新型接头隧道结构损伤演化规律.
1 装配式矩形隧道接头设计与分析1.1 现有接头构造图 1为现有的4种装配式隧道接头(卯榫式、直缝式、现浇和钢箱)构造形式,其中,卯榫式和直缝式接头主要应用于盾构隧道,具有较高的拼装精度和较快的拼装速度等优点,同时可实现荷载有效传递并保证隧道的整体刚度[10].目前装配式矩形隧道建设过程中多数采用现浇和钢箱接头连接,现浇接头有利于隧道装配式构件的分块预制和运输,且预制成型后隧道的整体性强.钢箱接头具有较好的抗剪能力,施工效率高.
图 1(Fig. 1)
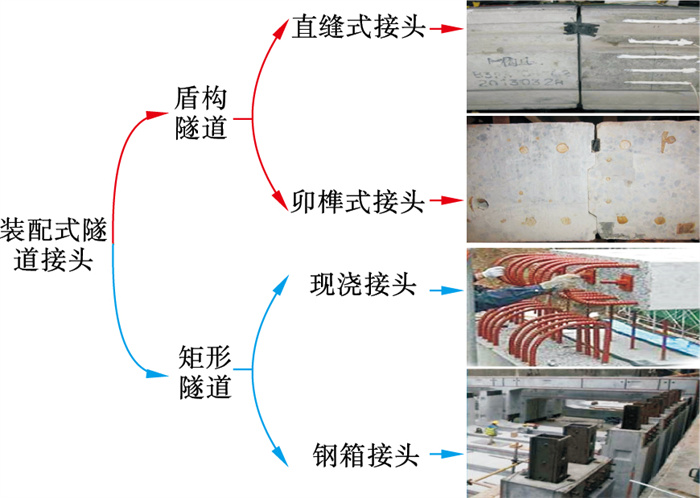 | 图 1 装配式隧道已有的接头类型Fig.1 Existing joint types of assembly tunnel |
1.2 接头设计与分析结合装配式矩形隧道的施工特性,设计了一种用于装配式矩形隧道的新型卯榫式接头(以下简称本文接头),几何构造如图 2所示.隧道在起重设备的作用下,通过钢柱实现上下卯榫连接,上段钢柱采用圆柱形,锚固在隧道上部,下端钢柱采用类圆锥形结构,同时在隧道下部预制了类圆锥形结构对应的凹槽.从结构形式来看,本文接头结构能更好地限制隧道纵向位移,具有一定抗剪切能力;与现浇接头和钢箱接头相比,该种结构形式拼装工序少、工作量低,且对周边环境影响小.但本文接头结构在静力荷载和爆破荷载作用下,其具体力学行为、抗爆性和损伤规律需深入探讨.
图 2(Fig. 2)
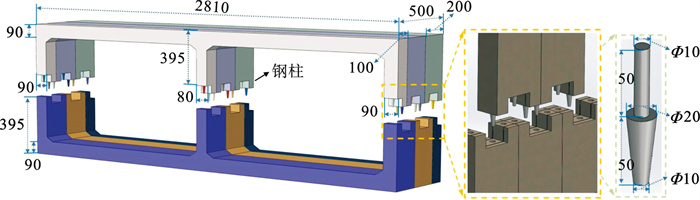 | 图 2 接头铆合方式及尺寸(单位:cm)Fig.2 Joint riveting method and dimension(unit: cm) |
2 数值模拟现浇接头是目前应用最为广泛的装配式矩形隧道接头类型,在接头处预留钢筋并现场浇筑混凝土,其隧道整体性和结构受力性能较好,因此选定现浇接头作为本文接头的比较对象.此外,本文着重考虑围压荷载和爆炸荷载,采用静力加载的方式模拟围压荷载,采用动力加载的方式模拟爆炸荷载.
2.1 本构模型2.1.1 本构方程选取数值模拟采用ABAQUS有限元软件进行非线性分析.合理的本构模型能准确反映材料应力与应变关系,且本构模型的选择既要考虑模型的非线性特征,又要兼顾计算效率和收敛性.本文将采用塑性损伤本构模型模拟接头混凝土材料;钢筋和钢柱采用弹塑性本构模型来模拟;底部支座采用刚性体,模拟地层支撑作用.装配式隧道相关材料属性见表 1.
表 1(Table 1)
| 表 1 材料属性 Table 1 Material properties |
塑性损伤本构模型是基于各向同性弹性损伤和各向同性拉伸与压缩塑性理论来反映材料的非弹性变形,表征损伤带来的刚度退化,通过引入损伤变量d来量化混凝土损伤演化与塑性滑移之间的相互作用[11]. 《混凝土结构设计规范》(GB50010—2010)中给定了混凝土单轴损伤本构方程.
混凝土单轴受压本构方程:
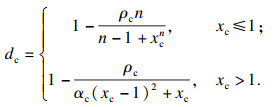 | (1) |
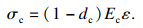 | (2) |
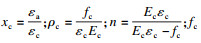
混凝土单轴受拉本构方程:
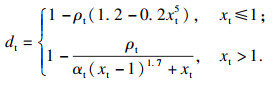 | (3) |
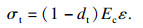 | (4) |
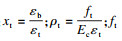
2.1.2 状态方程选取选择TNT炸药爆炸作用作为矩形隧道爆炸荷载.为准确反映爆炸荷载对不同接头形式装配式矩形隧道的动力响应,利用ABAQUS中流体(空气)-固体(隧道)耦合分析方法.相比静力荷载,爆炸荷载需设置欧拉域来实现对空气和TNT炸药的仿真,因此需要确定气体和TNT炸药的本构方程(即状态方程).参考秦文瑾等[12]和陈晨等[13]研究成果,确定了理想气体的状态方程为
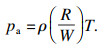 | (5) |
借鉴陈华等[14]、Lee等[15]和Wescott等[16]研究成果,确定了TNT炸药的JWL(Jones-Wilkins-Lee)状态方程为
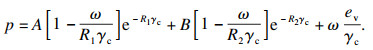 | (6) |
表 2(Table 2)
| 表 2 状态方程输入参数 Table 2 Input parameters of equation of state |
2.2 加载方式按照《公路隧道设计规范》(JTG 3370.1—2018)中规定浅埋隧道围岩压力计算方法,确定围岩压力为
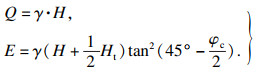 | (7) |
数值模拟中施加的竖向压力q和侧向压力e满足式(7),即竖向压力q=Q时,对应的侧向压力e=E.TNT爆炸位置处于隧道断面中心.本文接头和现浇接头除了接头结构有区别外,两者所承受的荷载大小、方向、位置、边界条件以及材料属性均一致.底部支座完全固定,以此模拟实际施工过程中隧道底板混凝土或基岩对隧道的支撑作用;动力学分析中,设置欧拉域的边界条件为无反射,以此避免反射波接触欧拉边界后来回震荡造成计算结果失稳[18].本文接头隧道数值模型的荷载及边界条件如图 3所示.
图 3(Fig. 3)
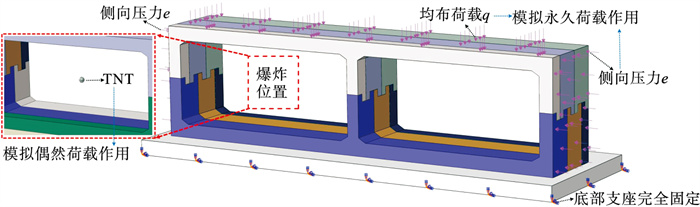 | 图 3 加载模式及边界条件Fig.3 Loading mode and boundary conditions |
为评价本文接头隧道的承载性能及抗爆性能,将静力荷载和爆炸荷载分开施加,荷载施加工况如图 4所示.竖向压力q从25 kPa递增至225 kPa,TNT当量考虑为10,20,30,40 kg共4个级别.
图 4(Fig. 4)
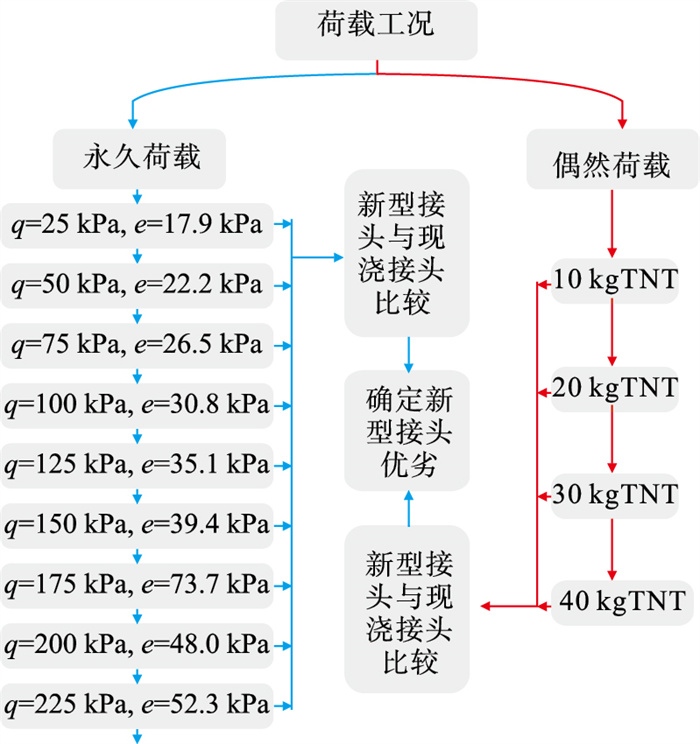 | 图 4 荷载施加工况Fig.4 Load application conditions |
2.3 接触及网格划分由于矩形隧道接头构造形式不同,接触设置方式不同.嵌固混凝土中的钢柱尾端和现浇接头的现浇面设定为绑定接触;混凝土与混凝土之间、混凝土和钢柱非紧固区域之间以及混凝土和支座间采用可相对滑移接触.依据已有文献研究成果,混凝土之间的摩擦系数设定为0.55[19],混凝土和钢铁之间的摩擦系数设定为0.45[20].钢筋和混凝土之间的接触关系设定为嵌入接触,装配钢筋笼时考虑到结构的受力特性和计算结果的准确性,以及计算效率和收敛性,仅考虑主筋,主筋直径为28 mm,以133 mm为间隔进行装配,混凝土保护层厚度设置为50 mm,并满足《公路隧道设计规范》(JTG 3370.1—2018)中对配筋率不低于0.6%的要求.同时基于工程实际,在现浇接头区域中心位置内置直径为28 mm的纵向钢筋来实现隧道构件之间的连接.
结合隧道几何尺寸,采用ABAQUS软件构建三维精细化数值模型.在数值模型的单元类型中,8节点六面体减缩积分单元(C3D8R)对位移求解比较精确,在网格变形时分析精度不会受到影响;2节点线性杆单元(T3D2)能够有效地反映单元轴向应力的变化,适合模拟钢筋;4节点三维双线性刚性单元(R3D4)能够有效模拟混凝土板和基岩对隧道的支撑作用.综上,本文将采用C3D8R模拟接头混凝土和钢柱部件,利用T3D2模拟钢筋,利用R3D4模拟刚体支座.在模拟爆炸时,将隧道置于长、宽、高为50 m×20 m×40 m的欧拉域正中心,实现流固耦合模拟,单元类型选择为8节点线性欧拉六面体单元(EC3D8R),EC3D8R单元能有效模拟出气体变形及TNT爆炸波的传递.隧道模型接触关系及网格划分如图 5所示.
图 5(Fig. 5)
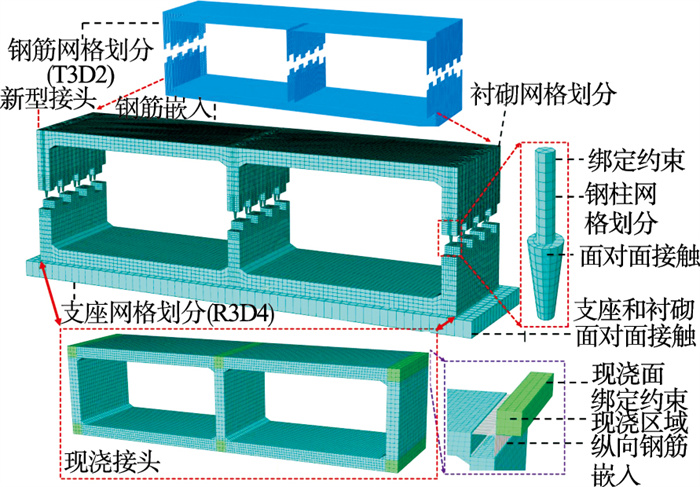 | 图 5 接触关系及网格划分Fig.5 Contact relationship and meshing |
3 模型验证分析3.1 静力学验证为验证采用矩形隧道接头数值模型的准确性和适用性,以Gong等[21]开展的隧道接头足尺试验为基础,采用与足尺试验相同的模型尺寸和边界条件进行计算.选取足尺试验中编号为SJ3的试验工况进行模拟验证.整个接头部件的尺寸见表 3.
表 3(Table 3)
| 表 3 接头部件尺寸 Table 3 Dimensions of joint parts |
采用本文建模方法,建立足尺试验的数值模型,其建模过程中的单元选择、本构关系、接触关系等与本文模型保持一致.由于试验不同,装配钢筋笼时仅考虑直径28 mm的主筋,即分别在接头结构受拉和受压侧各设立7根主筋,混凝土保护层厚度为50 mm.足尺试验的数值模型将下部支座设定为完全固定,整个模型装配过程及接触关系如图 6所示.
图 6(Fig. 6)
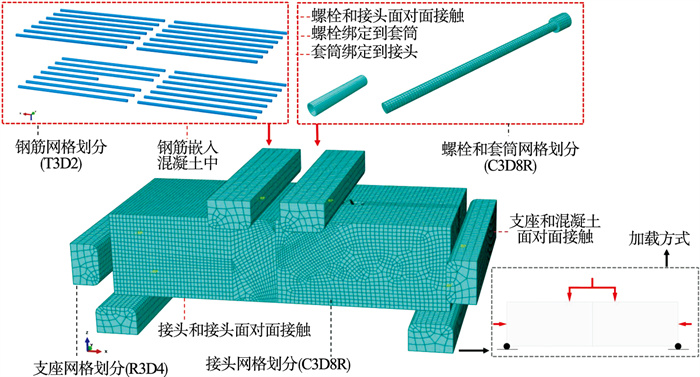 | 图 6 接头数值模型装配关系及加载方式Fig.6 Assembly relationship and loading mode of joint numerical model |
混凝土材料按照足尺试验要求选定为C60混凝土;螺栓选择强度等级为6.8的M36型螺栓,屈服强度为480 MPa;主筋直径28 mm,箍筋直径10 mm,按照足尺试验要求分别赋值屈服强度475和421 MPa;其余材料属性与表 1保持一致.
将本文方法构建的数值模型和足尺试验进行比较,选定能够反映接头变形特征的挠度和接头转角值,得到接头挠度随竖向荷载和接头转角随弯矩的变化曲线,如图 7所示.接头转角定义如下:
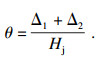 | (8) |
 | 图 7 接头变形对比Fig.7 Comparisons between experimental and numerical joint deformation (a)—接头挠度-竖向荷载关系曲线;(b)—接头转角-弯矩关系曲线. |
式中:Δ1为接头张开量,mm;Δ2为接头压缩量,mm;Hj为接头厚度,mm.
从图 7中可看出,竖向荷载-挠度关系与弯矩-接头转角关系的模拟结果和试验结果整体变化规律一致,但数值上仍然存在一定差异,数值模拟的结果较足尺试验值偏大.
为进一步验证本文本构模型的合理性,将接头破坏和变形云图进行对比,如图 8所示.从图 8中可看出,足尺试验中螺栓、螺栓孔、手孔等细部结构的破坏变形与数值模拟中模型的细部结构损伤部位一致,进一步说明本文数值建模方法能有效反映足尺试验的损伤破坏特征.
图 8(Fig. 8)
 | 图 8 接头损伤特征对比Fig.8 Comparisons between experimental and numerical joint damage characteristics |
3.2 动力学验证结合Yu等[5]钢筋混凝土板的接触爆炸试验,验证本文装配式矩形隧道爆炸动力数值计算可靠性.数值模型尺寸与足尺试验的尺寸相同,数值模型中材料属性与足尺试验一致.采用本文动力数值建模方法,建立足尺试验的数值模型,其建模过程中的单元选择、本构模型、接触及网格划分等与矩形隧道模型保持一致.选取1.9 kg TNT当量爆炸荷载作为计算工况.数值模型与足尺试验模型如图 9所示.
图 9(Fig. 9)
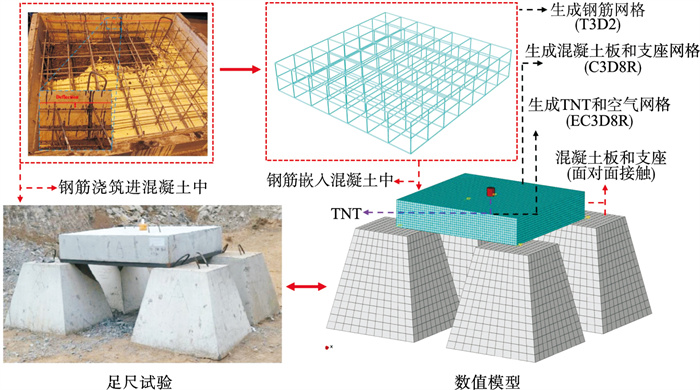 | 图 9 数值模型与足尺试验模型Fig.9 Numerical model and full-scale experimental model |
图 10为爆炸荷载作用后混凝土板损伤数值模拟和足尺试验结果的比较.从图中可看出,数值模拟中混凝土板的破坏特征与足尺试验是一致的,混凝土板各个侧面的破坏形状与足尺试验吻合度很高,说明本文数值建模方法能有效反映足尺试验的损伤破坏特征.
图 10(Fig. 10)
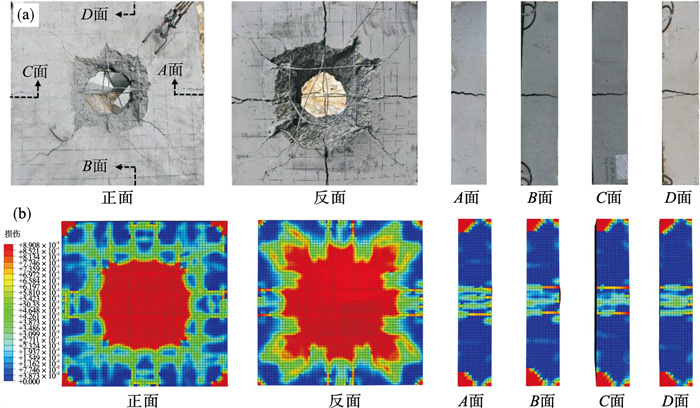 | 图 10 数值模拟和足尺试验模型的损伤特征对比结果Fig.10 Comparison results of damage characteristics between numerical simulation and full-scale experimental model (a)—足尺试验;(b)—数值模拟. |
为量化损伤范围,测量了数值模型中混凝土板正反面剥落直径尺寸,并与足尺试验结果进行对比,结果见表 4.在ФC1和ФS1中,符号Ф表示剥落直径,下标C和S代表混凝土板剥落的正面和反面,数字1—4表示剥落表面的4个方向,ФC和ФS表示混凝土板剥落的正面和反面4个方向剥落直径的平均值.由表 4可知,数值模拟和足尺试验结果剥落直径尺寸存在一定差异,模拟结果整体偏大,但4个方向大小趋势基本一致.模拟结果偏大的原因在于足尺试验测量的混凝土板表面的真实剥落直径不包括裂隙,而数值模型测量的损伤直径不仅包括剥落区域,还包含裂隙损伤区域等,因此,数值模拟结果得到的剥落直径偏大.综上,从损伤特征和剥落直径变化情况来看,动力数值建模过程是合理和可靠的.
表 4(Table 4)
| 表 4 混凝土剥落尺寸对比结果 Table 4 Comparison results of concrete spalling ? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 结果与分析4.1 隧道静力力学行为按照前文静力加载工况,分析本文接头和现浇接头矩形隧道抗压弯力学行为,得到了隧道挠度随压力的关系曲线,如图 11所示,其中竖向挠度是竖向压力q产生的最大挠度,侧向挠度是侧向压力e产生的最大挠度.
图 11(Fig. 11)
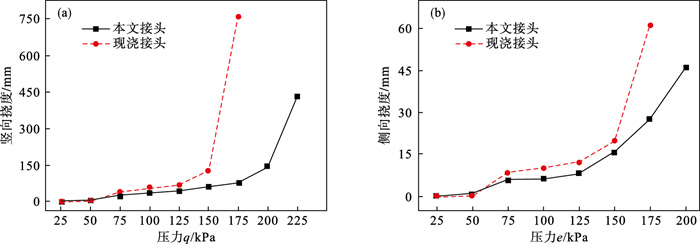 | 图 11 挠度-压力关系曲线Fig.11 Deflection-pressure curves (a)—竖向挠度;(b)—侧向挠度. |
本文接头和现浇接头矩形隧道结构变形特征存在显著差异.从图 11a中可看出,在压力相同情况下,现浇接头隧道竖向挠度大于本文接头隧道竖向挠度.在压力q小于50 kPa时,现浇接头隧道竖向挠度和本文接头的数值大小相近;当压力q超过50 kPa时,本文接头隧道竖向挠度开始明显小于现浇接头,且现浇接头的非线性行为越发明显;当压力q达到225 kPa和175 kPa时,本文接头隧道和现浇接头隧道分别达到最大承载力,本文接头隧道最大承载力略大于现浇接头隧道.
从图 11b中可知,采用本文接头的矩形隧道因在边墙中部利用钢柱实现卯榫连接,相比较整体预制的上板-墙结点,此处更为薄弱,易产生较大的侧向挠度;采用现浇接头的矩形隧道相比较预制的边墙,现浇的上板-墙结点位置结构刚度更低,易产生较大侧向挠度.此外,本文接头的隧道侧向挠度整体小于现浇接头隧道侧向挠度,本文接头和现浇接头隧道在侧向压力e达到150 kPa时都开始加速变形.
综上,在相同压力下,本文接头隧道竖向挠度和侧向挠度均小于现浇接头隧道.原因可能是现浇接头着重考虑整环的横向连接,但环与环之间的纵向连接大多靠螺栓或钢筋完成,造成了隧道整体刚度相对较低.而本文接头同时考虑了整环隧道横向与纵向的卯榫连接,其整体结构刚度高于现浇接头隧道.此外,在隧道板墙结点部位中,本文接头在此位置用预制方式连接梁柱,其刚度高于现浇接头.因此,本文接头隧道侧向挠度小于现浇接头.
Mises应力是一种等效应力,用应力等值线来表示模型内部应力分布情况,其考虑了第一、第二、第三主应力,可用来对疲劳和破坏等结构构件进行性能评价[22].考虑到钢筋作为杆单元只能反映拉压的S11方向应力,因此提取隧道模型Mises应力最大值和钢筋S11应力最大值,得到应力随竖向压力q关系曲线,如图 12所示.
图 12(Fig. 12)
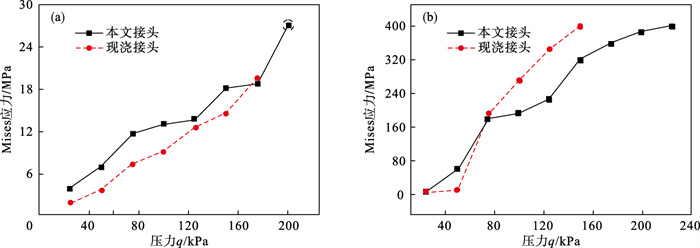 | 图 12 应力与压力q关系曲线Fig.12 Relationship between stress and pressure q (a)—混凝土;(b)—钢筋S11. |
从图 12 a中可看出,本文接头隧道Mises应力整体要大于现浇接头隧道,但随着压力q不断增加,两种隧道Mises应力不断接近,当压力q为175 kPa时,现浇接头隧道Mises应力大于本文接头隧道.本文接头隧道Mises应力较高的原因是由于钢柱构件的存在,导致在隧道卯榫钢柱位置易产生应力集中,Mises应力过高,但随着现浇接头隧道的变形不断增大,导致其Mises应力超过本文接头隧道.从图 12b中可看出,当压力q小于75 kPa时,现浇接头隧道的钢筋应力小于本文接头隧道,但随着压力q的不断增加,现浇接头隧道的钢筋应力大于本文接头隧道,这与接头变形特征保持一致.
4.2 静力荷载下裂缝损伤规律为分析不同接头隧道衬砌混凝土裂缝损伤规律,用拉伸损伤DAMAGET参数来评估裂缝的发展.静力荷载下不同接头装配式矩形隧道的损伤发展如图 13、图 14所示.两种接头隧道衬砌混凝土的裂缝发展规律可描述为以下3个阶段.
图 13(Fig. 13)
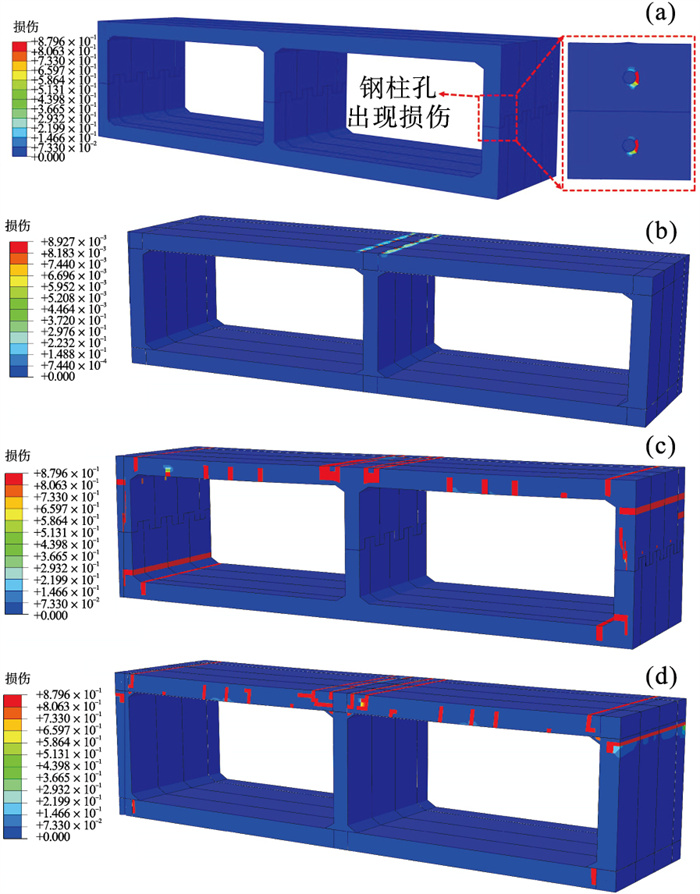 | 图 13 拉伸损伤阶段ⅡFig.13 Tensile damage stage Ⅱ (a)—q=5.88 kPa,本文接头;(b)—q=38.24 kPa,现浇接头;(c)—q=150 kPa,本文接头;(d)—q=100 kPa,现浇接头. |
图 14(Fig. 14)
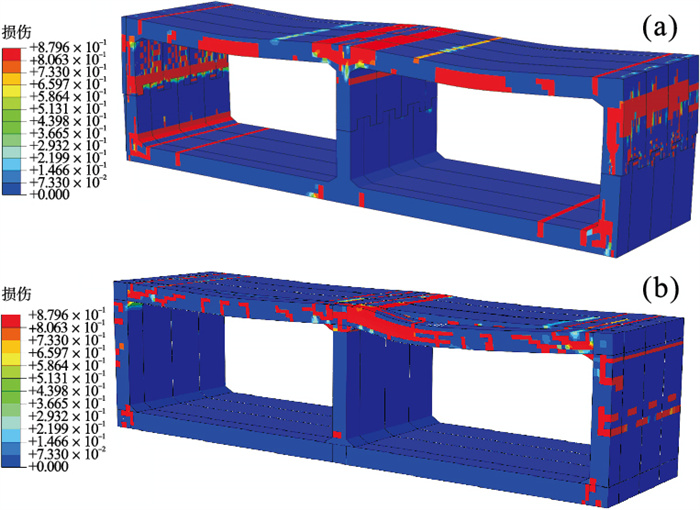 | 图 14 拉伸损伤阶段ⅢFig.14 Tensile damage stage Ⅲ (a)—q=225 kPa,本文接头;(b)—q=175 kPa,现浇接头. |
阶段Ⅰ:属于无裂缝阶段.在这一过程中,本文接头隧道和现浇接头隧道中混凝土和钢筋等材料都处于弹性阶段,混凝土并没有裂缝的产生.随着压力q的不断施加,混凝土拉应变不断增长.
阶段Ⅱ:属于裂缝出现和发展阶段.混凝土开始进入塑性阶段,钢筋应力大幅度增加.当竖向压力q分别达到5.88 kPa和38.24 kPa时,本文接头隧道和现浇接头隧道中混凝土拉应变将达到极限,混凝土中产生裂缝.从图 13a, 13b中可看出,本文接头隧道拉伸损伤最先出现在钢柱卯榫位置,此处产生了明显的应力集中;现浇接头隧道拉伸损伤最先出现在中墙的梁柱结点位置.
随着压力q的增加,混凝土裂缝在隧道中不断增加和扩展.当压力q分别达到150 kPa和100 kPa时,本文接头隧道和现浇接头隧道分别达到允许挠度极限,隧道表面裂缝数量增加,在本文接头隧道和现浇接头隧道中的边墙和中墙梁柱结点位置、上板中部位置、边墙中部位置产生大量拉伸损伤,如图 13c,13d所示.
阶段Ⅲ:属于大量裂缝贯穿性发展阶段.当本文接头和现浇接头隧道超过允许挠度后,随着压力q增加,混凝土裂缝宽度和深度迅速发展,隧道变形加速,如图 14所示.当压力q分别施加到225 kPa和175 kPa时,本文接头隧道和现浇接头隧道开始失效.
4.3 爆炸荷载下衬砌变形特征图 15为本文接头隧道在40 kg TNT爆炸后隧道位移时变结果.在t=0 ms时,爆炸开始,此时冲击波尚未接触到隧道接头,其压力主要分布在爆炸产生的气体周边,隧道未变形;随冲击波的传递,在t=2 ms时,冲击波开始接触隧道结构衬砌上下侧,因下侧存在刚性支座,隧道衬砌变形主要发生在隧道衬砌上侧;在t=4 ms时,冲击波接触到隧道结构的边墙和中墙,此时爆炸源两端的衬砌变形未有显著差异,隧道结构内侧完全受到冲击波的影响;在t=16 ms时,冲击波基本传递完成,隧道衬砌结构变形显著.
图 15(Fig. 15)
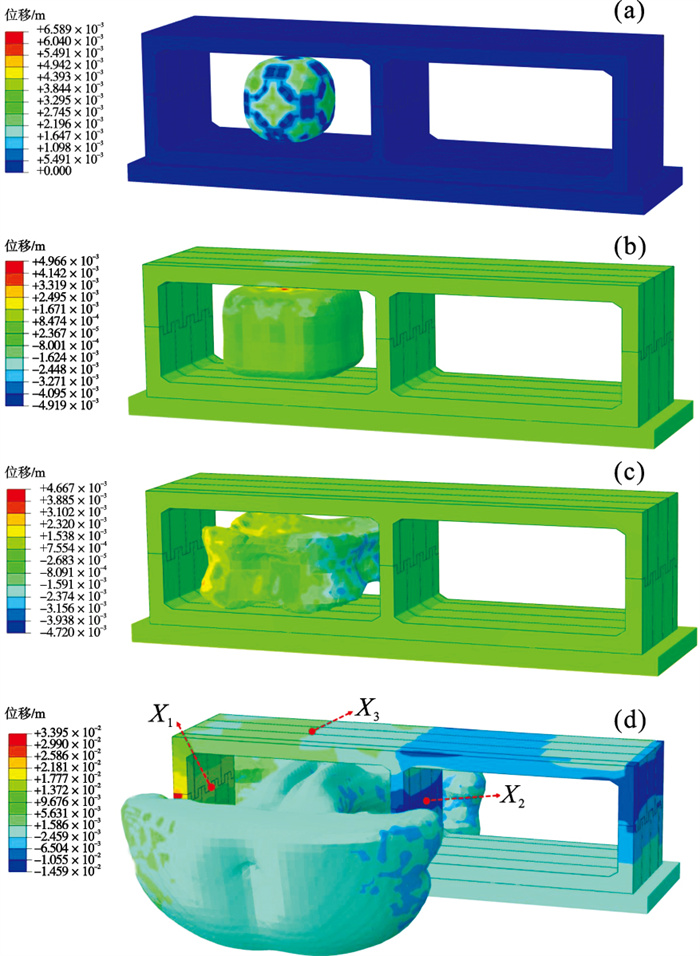 | 图 15 爆炸后隧道位移云图Fig.15 Cloud chart of tunnel displacement after explosion (a)—t=0 ms;(b)—t=2 ms;(c)—t=4 ms;(d)—t=16 ms. |
为揭示本文接头隧道变形演化规律,同时比较现浇接头和本文接头在爆炸荷载作用下的抗变形能力,分别在本文接头隧道和现浇接头隧道爆炸源的左右边墙及顶板位置取X1,X2和X3三点,如图 15所示.获取X1,X2和X3三点位移时程曲线如图 16所示.
图 16(Fig. 16)
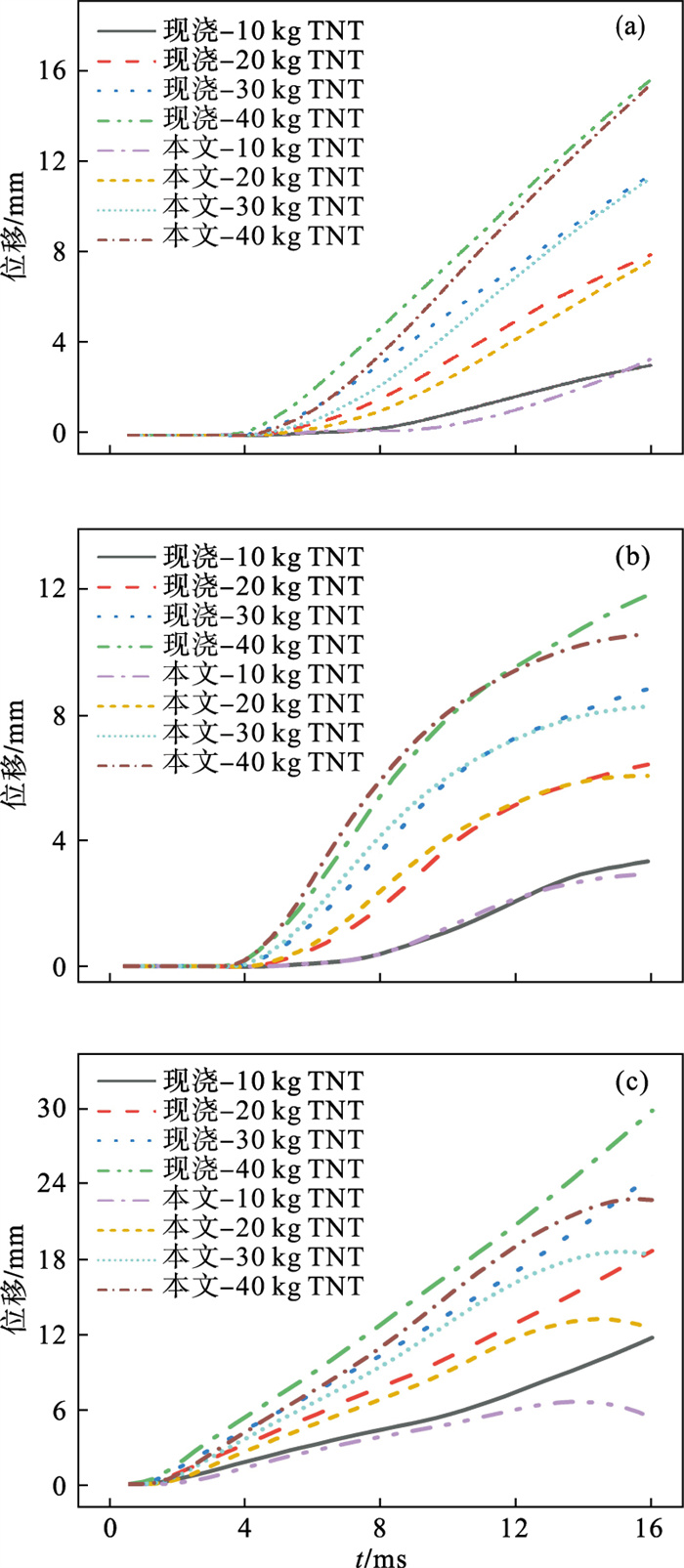 | 图 16 不同部位的时间-位移关系曲线Fig.16 Time-displacement curves at different positions (a)—X1位置;(b)—X2位置;(c)—X3位置. |
从图 16中可看出,随着TNT当量增加,X1,X2和X3位移增大;相同TNT当量作用下,本文接头隧道在X2点位移较大,而现浇接头隧道在X1点位移较大,两者数值大小差异不大;本文接头和现浇接头隧道在X3点位移存在显著差异,现浇接头隧道在X3点的位移明显大于本文接头隧道;综上,本文接头隧道的抗爆变形能力较现浇接头有一定优势.此外,爆炸源左右边墙的位移方向相反,X1点向左位移值较X2点向右位移值略大.但在实际的地层环境中,左侧边墙会因土体存在,其位移会受到约束,而X2点为隧道中隔墙,则在工程实际中需要加强抗爆防护能力.
4.4 爆炸荷载下隧道动力响应图 17为在40 kg TNT爆炸后不同时间的本文接头隧道损伤变化结果.当t=0 ms时爆炸开始,冲击压力主要分布在爆炸产生的气体周边,此时隧道结构未产生损伤;随着冲击波的传递,在t=2 ms时,冲击波接触到隧道结构的衬砌上下侧,在隧道衬砌上下侧出现塑性损伤;当t=4 ms时,冲击波接触到隧道结构的边墙和中墙,边墙和中墙位置开始出现塑性损伤,衬砌上下侧产生明显的拉伸损伤,并伴随裂缝出现;在t=16 ms时,冲击波基本传递完成,在顶板-墙连接处、钢柱区域产生明显的拉伸损伤,裂缝发展成贯穿性裂缝.
图 17(Fig. 17)
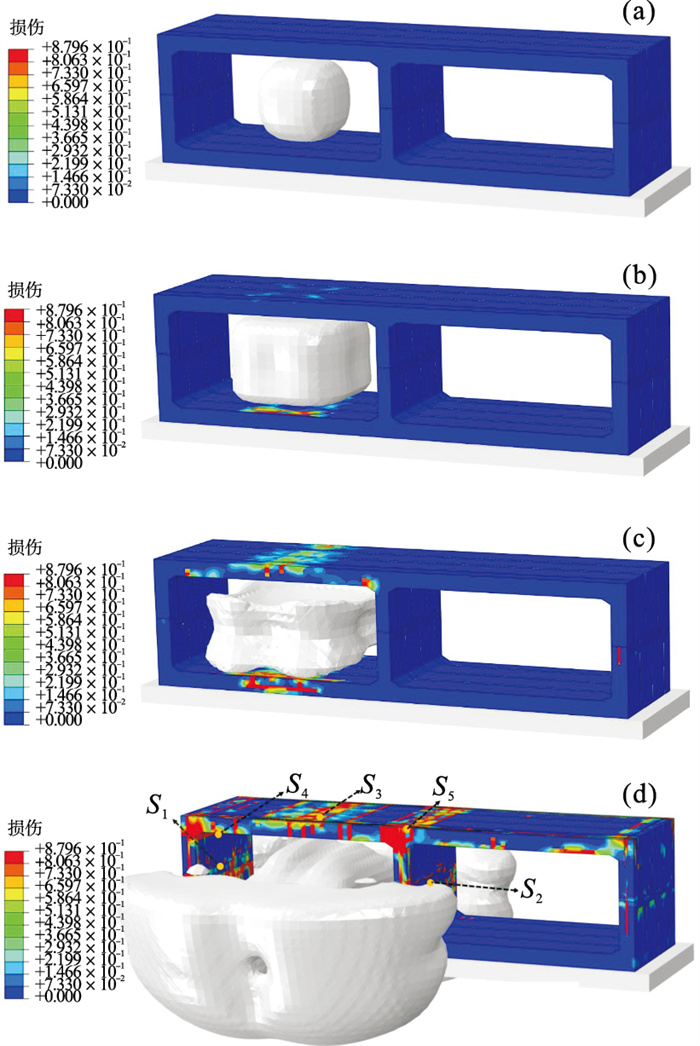 | 图 17 爆炸后本文接头隧道损伤演化规律Fig.17 Damage evolution law of the joint tunnel in this paper after explosion (a)—t=0 ms;(b)—t=2 ms;(c)—t=4 ms;(d)—t=16 ms. |
为探究现浇接头和本文接头隧道在爆炸荷载作用下的动力响应差异性,分别在本文接头隧道和现浇接头隧道爆炸源的左右边墙、顶板中部及顶板拐角部位取S1,S2,S3,S4和S5五个Mises应力监测点,如图 17所示.得到S1,S2,S3,S4和S5的Mises应力时程曲线如图 18所示.
图 18(Fig. 18)
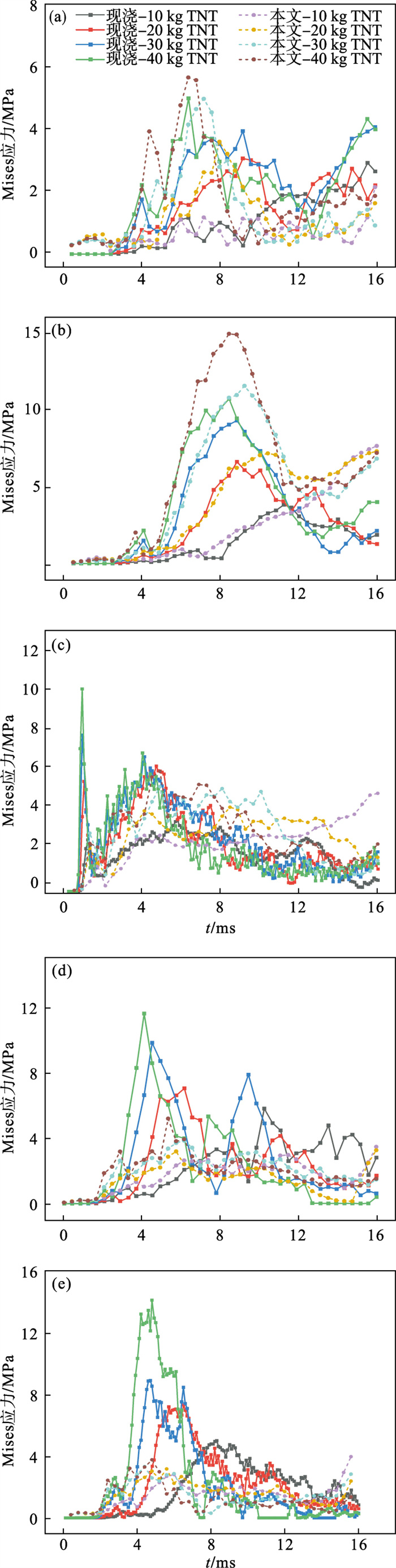 | 图 18 不同部位Mises应力时程曲线Fig.18 Mises stress time-history curves at different positions (a)—S1位置;(b)—S2位置;(c)—S3位置;(d)—S4位置;(e)—S5位置. |
从图 18中可看出,随着TNT当量增加,S1,S2,S4和S5的应力都存在不同幅度的增加;在爆炸源左右边墙中部S1和S2点位置,本文接头隧道也会因为钢柱构件导致应力集中现象,因此本文接头隧道Mises应力大于现浇接头隧道Mises应力;在爆炸源的左右边墙的顶板拐角位置的S4和S5点位置,现浇接头隧道Mises应力大于本文接头隧道Mises应力;在顶板中部的S3点位置,现浇接头隧道Mises峰值应力显著大于本文接头隧道Mises峰值应力;因此,本文接头隧道在爆炸荷载作用下的抗爆性能略强.
为揭示本文接头矩形隧道在爆炸荷载作用下局部结构破坏特征,提取40 kg TNT爆炸后隧道损伤及应力结果,如图 19所示.从图 19中可看出,本文接头隧道在爆炸荷载作用下,在接头部位出现明显损伤,损伤大都集中在钢柱周围,混凝土破损程度较为严重,钢柱应力也超过了300 MPa;此外,从钢筋应力和顶部衬砌损伤可看出,顶板-墙连接部位产生了损伤破坏.因此,本文接头在实际工程应用中,仍需采取措施来改善钢柱部位的应力集中现象,降低顶板-墙连接部位的损伤程度.
图 19(Fig. 19)
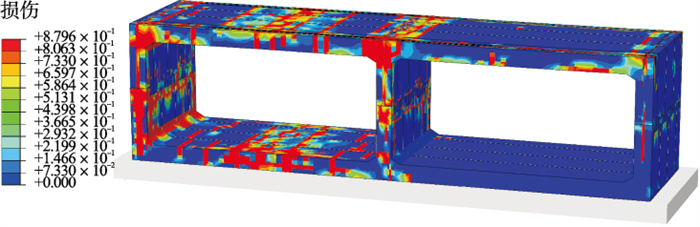 | 图 19 矩形隧道破坏特征Fig.19 Failure characteristics of rectangular tunnel |
5 结论1) 利用桁架和三维实体单元精细化模拟了钢筋和钢柱构件与混凝土的相互作用,用塑性损伤本构模型模拟了混凝土的损伤破坏过程,并通过足尺试验验证了数值建模可靠性.选定合理参数所构建的数值模型,为装配式隧道力学行为和抗爆性研究提供了一种实用方法.
2) 静力荷载作用下本文接头装配式隧道的裂缝发展过程可分为3个阶段:无裂缝阶段、裂缝出现与发展阶段、大量裂缝贯穿性发展阶段.
3) 受静力荷载作用时,在相同竖向压力q下,本文接头隧道的抗压弯能力略高于现浇接头隧道,但混凝土易在钢柱区域产生应力集中现象;受爆炸荷载作用时,在相同当量TNT炸药下,本文接头隧道抗爆性能整体优于现浇接头隧道.
4) 新型接头隧道损伤破坏主要发生在钢柱和顶板-墙结点区域,现浇接头隧道损伤破坏主要发生在顶板-墙结点区域.新型接头隧道在实际工程应用中,还需对钢柱和顶板-墙结点区域进行优化设计或采取技术措施加以改善.
参考文献
| [1] | Li X J, Yan Z G, Wang Z, et al. A progressive model to simulate the full mechanical behavior of concrete segmental lining longitudinal joints[J]. Engineering Structures, 2015, 93: 97-113. DOI:10.1016/j.engstruct.2015.03.011 |
| [2] | 黄大维, 周顺华, 王秀志, 等. 模型盾构隧道管片纵缝接头设计方法[J]. 岩土工程学报, 2015, 37(6): 1068-1076. (Huang Da-wei, Zhou Shun-hua, Wang Xiu-zhi, et al. Design method for longitudinal segment joints of shield tunnel model[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(6): 1068-1076.) |
| [3] | Meng Q F, Wu C Q, Wu P T, et al. A study of pressure characteristics of methane explosion in a 20 m buried tunnel and influence on structural behaviour of concrete elements[J]. Engineering Failure Analysis, 2021, 122: 105273. DOI:10.1016/j.engfailanal.2021.105273 |
| [4] | Wang C, Zhao Y Y, Addai E K. Investigation on propagation mechanism of large scale mine gas explosions[J]. Journal of Loss Prevention in the Process Industries, 2017, 49: 342-347. DOI:10.1016/j.jlp.2017.07.011 |
| [5] | Yu X, Zhou B K, Hu F, et al. Experimental investigation of basalt fiber-reinforced polymer(BFRP) bar reinforced concrete slabs under contact explosions[J]. International Journal of Impact Engineering, 2020, 144: 103632. DOI:10.1016/j.ijimpeng.2020.103632 |
| [6] | Osinov V A, Chrisopoulos S, Triantafyllidis T. Numerical analysis of the tunnel-soil interaction caused by an explosion in the tunnel[J]. Soil Dynamics and Earthquake Engineering, 2019, 122: 318-326. DOI:10.1016/j.soildyn.2018.09.010 |
| [7] | 张稳军, 张高乐, 雷华阳. 基于塑性损伤的盾构隧道FRP-Key接头抗剪性能及布置方式合理性研究[J]. 中国公路学报, 2017, 30(8): 38-48. (Zhang Wen-jun, Zhang Gao-le, Lei Hua-yang. Research on shear performance of FRP-Key joint for shield tunnel and rationality of arrangement based on plastic-damage model[J]. China Journal of Highway and Transport, 2017, 30(8): 38-48. DOI:10.3969/j.issn.1001-7372.2017.08.004) |
| [8] | 赵德博, 储程, 苏栋. 内爆炸作用下隧道衬砌结构动力响应数值分析[J]. 土木工程学报, 2020, 53(增刊1): 265-271. (Zhao De-bo, Chu Cheng, Su Dong. Dynamic responses of tunnel lining structure under internal blasts[J]. China Civil Engineering Journal, 2020, 53(sup1): 265-271.) |
| [9] | 高盟, 张继严, 王滢, 等. 内源爆炸荷载作用下饱和土中圆形衬砌隧道的瞬态响应解答[J]. 岩土工程学报, 2017, 39(12): 2304-2311. (Gao Meng, Zhang Ji-yan, Wang Ying, et al. Exact solutions for dynamic responses of a cylindrical lined tunnel in saturated soil to internal blast loads[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(12): 2304-2311. DOI:10.11779/CJGE201712020) |
| [10] | Liu X, Dong Z B, Song W, et al. Investigation of the structural effect induced by stagger joints in segmental tunnel linings: direct insight from mechanical behaviors of longitudinal and circumferential joints[J]. Tunnelling and Underground Space Technology, 2018, 71: 271-291. DOI:10.1016/j.tust.2017.08.030 |
| [11] | Lee J H, Fenves G L. Plastic-damage model for cyclic loading of concrete structures[J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900. DOI:10.1061/(ASCE)0733-9399(1998)124:8(892) |
| [12] | 秦文瑾, 卢登标, 刘浩. 气体状态方程对正十二烷射流燃烧的影响[J]. 航空动力学报, 2020, 35(1): 66-74. (Qin Wen-jin, Lu Deng-biao, Liu Hao. Effects of gas state equation on n-dodecane jet combustion[J]. Journal of Aerospace Power, 2020, 35(1): 66-74.) |
| [13] | 陈晨, 魏英杰, 王聪, 等. 射弹跨声速入水初期阶段多相流场特性数值研究[J]. 振动与冲击, 2019, 38(6): 46-53, 61. (Chen Chen, Wei Ying-jie, Wang Cong, et al. Numerical analysis of the multiphase flow characteristics in the initial period of water-entry of a projectile at transonic speed[J]. Journal of Vibration and Shock, 2019, 38(6): 46-53, 61.) |
| [14] | 陈华, 周海兵, 刘国昭, 等. 圆筒试验JWL状态方程参数的贝叶斯标定[J]. 爆炸与冲击, 2017, 37(4): 585-590. (Chen Hua, Zhou Hai-bing, Liu Guo-zhao, et al. Bayesian calibration for parameters of JWL equation of state in cylinder test[J]. Explosion and Shock Waves, 2017, 37(4): 585-590.) |
| [15] | Lee E L, Tarver C M. Phenomenological model of shock initiation in heterogeneous explosives[J]. Physics of Fluids, 1980, 23(12): 2362-2372. DOI:10.1063/1.862940 |
| [16] | Wescott B L, Stewart D S, Davis W C. Equation of state and reaction rate for condensed-phase explosives[J]. Journal of Applied Physics, 2005, 98(5): 053514. |
| [17] | Wojciech M. Blast wave propagation in the air and action on rigid obstacles[D]. Poznań: Poznań University of Technology, 2011. |
| [18] | Qian H M, Zong Z H, Wu C Q, et al. Numerical study on the behavior of utility tunnel subjected to ground surface explosion[J]. Thin-Walled Structures, 2021, 161: 107422. DOI:10.1016/j.tws.2020.107422 |
| [19] | 张力, 封坤, 何川, 等. 盾构隧道管片接头三维精细化数值模拟研究[J]. 隧道建设, 2020, 40(8): 1169-1175. (Zhang Li, Feng Kun, He Chuan, et al. Three-dimensional refined numerical simulation of segmental joint of shield tunnel[J]. Tunnel Construction, 2020, 40(8): 1169-1175.) |
| [20] | Liu X P, Bradford M A, Chen Q J, et al. Finite element modelling of steel-concrete composite beams with high-strength friction-grip bolt shear connectors[J]. Finite Elements in Analysis and Design, 2016, 108: 54-65. |
| [21] | Gong C J, Ding W Q, Mosala K M, et al. Comparison of the structural behavior of reinforced concrete and steel fiber reinforced concrete tunnel segmental joints[J]. Tunnelling and Underground Space Technology, 2017, 68: 38-57. |
| [22] | 陈明祥. 弹塑性力学[M]. 北京: 科学出版社, 2010. (Chen Ming-xiang. Elastoplastic mechanics[M]. Beijing: Science Press, 2010.) |
