王海芳, 崔阳阳, 李鸣飞, 李广宇
东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004
收稿日期：2021-09-22
基金项目：国家自然科学基金资助项目(51905080)。
作者简介：王海芳(1976-), 男, 山西高平人, 东北大学副教授。

摘要：针对复杂环境下移动机器人的全局最优路径规划，提出一种基于目标偏置扩展和贝塞尔(Bezier)插值方法的改进RRT*FN路径规划算法.改进算法在未找到初始路径时采用一定概率进行随机点的目标偏置选择，确定初始路径后使用启发式采样方法，使随机采样点围绕初始路径进行迭代选择，提高路径规划的导向性.当改进算法还未找到初始路径时，删除树中远离目标点并且没有子节点的节点; 当改进算法找到初始路径时，删除树中远离最优路径且没有子节点的节点，保留高性能节点，提高算法收敛到最优路径的效率.利用贝塞尔(Bezier)插值方法平滑路径.在MATLAB仿真平台和ROS机器人仿真平台分别进行2D和3D的对比实验，结果验证了所提算法的有效性和优越性.
关键词：快速探索随机树全局路径规划目标偏置选择贝塞尔插值ROS机器人仿真平台
Mobile Robot Path Planning Algorithm Based on Improved RRT*FN
WANG Hai-fang, CUI Yang-yang, LI Ming-fei, LI Guang-yu
School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: WANG Hai-fang, E-mail: hfwang@neuq.edu.cn.

Abstract: Aiming at the global optimal path planning of mobile robots in complex environments, an improved RRT*FN path planning algorithm based on target bias extension and Bezier interpolation method is proposed. The improved algorithm adopts a certain probability to select the target bias of random points when the initial path is not found. After determining the initial path, the heuristic sampling method is used to make random sampling points iteratively select around the initial path, which improves the guidance of path planning. When the improved algorithm has not found the initial path, the nodes far from the target point and no child nodes in the tree are deleted. When the improved algorithm finds the initial path, the nodes far from the optimal path and without child nodes in the tree are deleted, and the high-performance nodes are reserved to improve the efficiency of algorithm convergence to the optimal path. The path is smoothed by Bezier interpolation. 2D and 3D comparative experiments were carried out on MATLAB simulation platform and ROS robot simulation platform respectively. The effectiveness and superiority of the proposed algorithm are verified.
Key words: rapid-exploration random treesglobal path planningtarget bias selectionBezier interpolationROS robot simulation platform
路径规划是指在包含障碍物的给定区域内搜索到一条从初始起点到目标终点的安全无碰撞、可行的路径^[1].基于采样的路径规划算法是目前广泛应用于机器人路径规划的算法之一^[2]，在基于采样的算法中，应用最广泛的是渐进最优快速扩展随机树(rapidly-exploring random trees star, RRT*)算法，该采样算法无需在工作空间中明确表示障碍物信息，通过碰撞检测方法连接一组没有碰撞的节点来获得可行路径.但要获得最优路径，RRT*算法需要不断地增加采样节点数量，花费大量计算时间获得最优路径，从计算角度看，这给计算机在高维空间下的内存增加了很大的负担.针对RRT*算法收敛到最优值效率低的局限性，Nasir等 ^[3]提出了一种RRT*-smart算法，该算法通过启发式函数的方式实现随机点的智能采样，提高了最优路径的收敛速度.在此基础上，杨国田等 ^[4]提出一种改进的RRT*FN算法，该算法有较快的搜索速度，对内存有限的嵌入式飞行机器人有较好的适用性和可行性.文献[5]提出将RRT*FN算法扩展到动态场景，使用两个贪婪启发式路径运动优化方案，在较短时间内找到求解路径，减少收敛时间，提高路径整体收敛效率.Luo等 ^[6]提出了一种Informed-RRT*的变体，利用目标偏置引导策略搜索目标点，利用椭球形子集细化路径，从而找到最优路径.
传统RRT*FN算法通过限制树中节点数量解决这一问题，当树中节点数量超过给定阈值时，随机删除待删除的无子节点的候选节点.在多复杂障碍物和狭窄的二维静态环境下，传统的RRT*FN算法收敛到最优路径会出现效率低的问题，本文结合目标偏向、启发采样策略、删除远离目标点和路径中无子节点的方法对基本RRT*FN算法加以改进，并对生成路径进行优化处理，从而提高算法效率和路径质量.
1 算法基本原理1.1 问题描述令X?Rⁿ表示规划问题的状态空间，X_obs?X表示障碍区域，X_free?X\X_obs表示可行使区域，给定初始节点x_start∈X_free，目标节点x_goal∈X_free.机器人可行路径由连续函数表示s: [0, 1]→ Rⁿ，Σ表示所有的可行路径集合，给定代价函数s: Σ→ R≥0，则寻找最优路径规划问题可以表示为

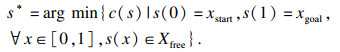(1)

式中：s^*为代价函数值最小的路径集合; R≥0表示非负实数集合.
1.2 基本RRT*FN算法^[7]RRT*FN算法是在RRT*算法的基础上发展而来的.基本的RRT*FN算法同RRT*采样策略相同，通过在状态空间中均匀采样获得随机节点的方式不断扩展树的内存：首先在可行区域随机采样到一个节点x_rand，接着在当前树中找到与随机点的最近邻节点x_nearest，然后连接这两个节点，获得单位向量，并从x_nearest出发以一定的步长ρ生成新节点：

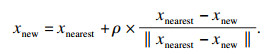(2)

如果最近邻节点与新节点之间的路径与障碍物穿过障碍物区域，即与障碍物发生碰撞，那么删除新节点重新进行采样，否则将新节点加入树中，完成一次树的生长.
RRT*算法对父节点的选择和邻近区域的节点重连作出了改进^[8]：在确定随机点位置后，对新加入搜索树的新节点进行重选父节点和重新布线操作，节点标号表示树中节点产生的顺序，如图 1所示.节点1表示初始节点，节点8，即新节点表示新加入的节点，邻近节点表示与随机点距离最近的树中已有节点，默认为新节点的父节点，节点与节点之间连接线上的数字表示两节点之间的路径代价.重置父节点就是找到一条从初始节点1到节点8的路径代价值最小的可行路径，在图 1a中，以新节点为中心，给定阈值范围内的节点为待选节点，找到各个待选节点与新节点相连接后节点代价值最低的待选节点作为父节点，重置新节点的父节点，待选节点分别为节点4和节点7，原来的路径为1—5—8，路径代价为10+2=12.备选节点与新节点组成的路径为1—2—4—8，1—5—7—8，路径代价分别为2+5+3=10，10+3+2=15，因此将节点8的父节点改为节点4，完成父节点重置.图 1b是重新生成的随机树; 为进一步使随机树节点间连接的代价尽量小，对随机树进行重新布线.重布线的过程可以表述为：如果待选节点的父节点改为新节点可以减小路径代价，则进行更改.图 1c中的待选节点为节点5和节点7，节点5的父节点是节点1，路径是1—5，路径代价为10，如果将节点5的父节点重置为节点8，那么到达节点的路径为1—2—4—8—5，代价为2+5+3+2=12，大于原始的路径代价，不对节点5进行重布线操作，同理，将节点7的父节点由节点5更改为节点8后，更改后的路径为1—2—4—8—7，路径代价为2+5+3+2=12，小于原始路径1—5—7的路径代价，即10+3=13，因此，将节点7的父节点重置为节点8，图 1d是重布线后的随机树.
图 1(Fig. 1)

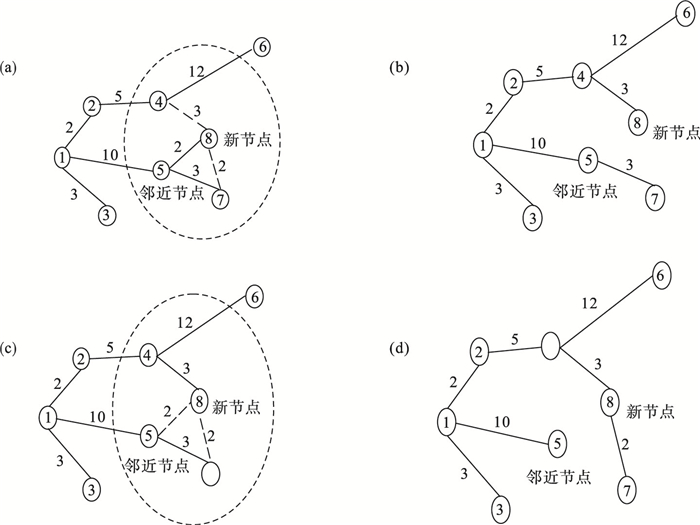图 1 RRT*算法的搜索过程Fig.1 RRT * algorithm search process (a)—父节点重置; (b)—重置后更新随机树; (c)—再次父节点重置; (d)—重置后更新随机树.

RRT*FN算法是在RRT*的基础上，固定树中节点数，并且当树中节点数达到给定的预设值时，删除树中的叶子节点，使算法在路径搜索过程中只使用给定的固定内存空间.RRT*FN不仅节省了内存空间，还保留了RRT*原有算法的优势，概率完备性和渐进最优性^[9]，即只要路径探索迭代的次数足够多，得到的最终路径就可以是较为接近最短的可行路径.
1.3 概率完备性分析文献[2, 9]对RRT相关算法进行了概率完备性和收敛性的证明：对于任何可行的路径规划问题，随迭代次数的不断增加，节点扩展数逐渐趋近于正无穷大时，算法找到可行路径的概率为1.本文算法在进行路径搜索时，预设N为固定节点数，当N为无穷大时，如果此时还未找到初始路径，那么相当于在进行RRT*算法搜索，算法具备概率完备性.在实际搜索过程中，N通常是考虑机器人所拥有的内存空间大小、计算能力及实际的工作环境共同进行设定的.文献[10]对RRT*FN算法进行分析时指出，如果当前节点数已到达最大节点预设值但还未找到初始路径时，则需要重新开始，因此算法的概率完备性和收敛性受到给定固定节点N的影响，具体的N值在仿真实验中进行了分析.
2 改进RRT*FN算法介绍2.1 采样策略与RRT*算法搜索方式相似，本文算法搜索以初始起点作为搜索树的根开始，在每次迭代中，算法都会在配置空间中生成一个随机点，搜索树中最近的点，步长为一个量级.为了克服搜索盲目性，在未搜索到初始路径时，以一定的概率偏向于朝着目标点方向探索.当搜索到一条可行路径时，以可行路径中的节点为最近节点进行采样计算，围绕可行路径产生随机点，减少算法收敛到最优解的计算时间.将产生的一个新的随机点进行碰撞检测，并将与障碍物无碰撞的点扩展到搜索随机树中，当最新搜索节点到达目标点时，算法搜索到一条可行路径.RRT*搜索与目标偏置探索如图 2所示.
图 2(Fig. 2)

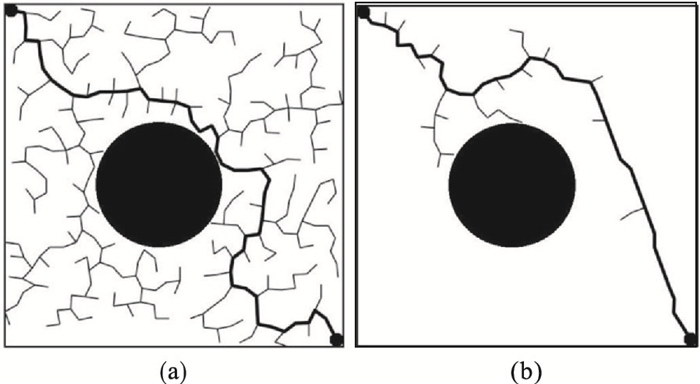图 2 RRT*搜索与目标偏置搜索Fig.2 RRT* search with target bias search (a)—传统RRT*搜索; (b)—目标偏置搜索.

左上角为起点，右下角为终点，黑色折线段为搜索到的一条可行路径.可以看出本文算法的改进策略减少了随机采样的次数，提高了算法效率.
2.2 节点删除当树中的节点到达给定预设值N时，基本的RRT*FN算法对树中的节点采取随机删除节点的方法.考虑到不同路径状态下，节点的影响不同，将本文算法的删除策略分为两种情况：一是当前采样节点数已超过给定内存范围，但还未搜索到初始路径; 二是当前采样节点数超过给定内存范围并已搜索到一条可行路径.
当改进算法还未找到初始路径时，考虑到目标节点周围的节点对找到初始路径贡献可能大于其他节点，并尽量减少不必要的父节点重连与重布线过程，所以选择随机删除树中远离目标点并且没有子节点的节点.当改进算法已经找到一条可行路径时，考虑到可行路径周围的节点可能对最优路径有更大影响，因此保留可行路径一定范围内的节点，删除树中远离最优路径且没有子节点的节点，保留高性能节点.令T表示算法树中的节点集合，goal为目标节点，radius为预保留的节点区域范围长度，PathNodes为可行路径集合，TemTree为临时的待选节点集合，ChildlessNodes为T中无子节点的节点集合，节点删除的伪代码由表 1给出.
表 1(Table 1)

表 1 NodeRemove伪代码Table 1 Pseudo code of NodeRemove 算法 T ← NodeRemove(T, qgoal, radius) 1 If Length(T)>maxNode&InitialPathFound=false 2 TemTree←ExcepGoalRegion(T, goal, radius) 3 ChildlessNodes←FindChildlessNodes(TemTree) 4 T←RangRemove(ChildlessNodes) 5 Else if Length(T)maxNodes&&InitialPathFound=true 6 PathNodes←FindPath(T, goal) 7 TemTree←BesidesPathRegion(T, PathNodes, radius) 8 ChildlessNodes←FindChildlessNodes(TemTree\T) 9 T←RangRemove(ChildlessNodes) 10 return T

表 1 NodeRemove伪代码 Table 1 Pseudo code of NodeRemove

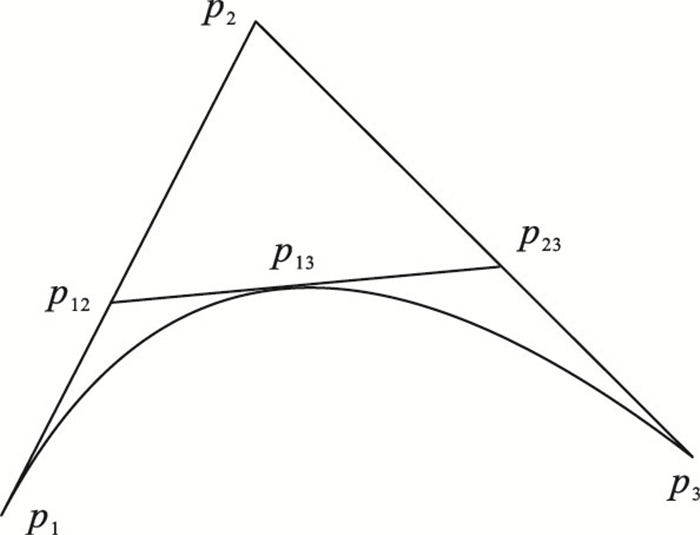
2.3 路径平滑经过本文算法规划出的原始路径是由一些离散点组合成的折线段，不仅有不能满足机器人转弯曲率要求的可能，还会导致机器人在转弯途中增加不必要的转弯时间，不适合直接应用于机器人路径规划中.为了让最后的路径变得光滑，需要对路径进行平滑处理^[11]，使节点保持连续性的同时避免碰撞.常见的平滑处理技巧有B样条曲线插值^[12]、二次贝塞尔曲线插值^[9]、五次多项式插值^[13]和Cantmull-Rom曲线插值^[14].贝塞尔曲线依据伯恩斯坦多项式发展而来，因其控制简便，图像描述能力强的特点被广泛应用于工业和计算机图形学领域.贝塞尔曲线通过选取控制点将折线段通过公式拟合成连续光滑的曲线，最终得到的曲线逼近折线段.改进算法采用二次Bezier曲线进行最终的路径拟合，如图 3所示.
图 3(Fig. 3)

图 3 二次贝塞尔曲线拟合图Fig.3 Quadratic Bezier curve fitting graph

设p₁, p₁₃, p₃依次是一条抛物线上的三个不同点，其中经过点p₁和p₃与抛物线相切的两条切线相交于点p₂，经过点p₁₃与抛物线相切的切线与p₁p₂相交于点p₁₂，与p₂p₃相交于点p₂₃.根据抛物线的三切线定理，有如下比例等式：

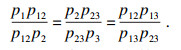(3)

固定p₁, p₃引入参数t，令等式(3)的比值为t: (1-t)，即有

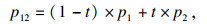(4)

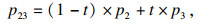(5)

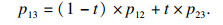(6)

将式(4)和式(5)代入式(6)得

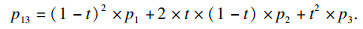(7)

当t从0变到1时，式(7)表示的曲线是由三个固定的点p₁, p₂, p₃定义的一条二次Bezier曲线.
不同的插值方法示意图如图 4所示，其中黑色圆圈表示给定的控制节点，将各个节点用黑色直线连接形成初始路径.从图中可以看出，使用B样条曲线平滑后的路径曲率较大，且不再经过原有节点，五次多项式插值带来了较大的拐点浮动，不适用狭窄环境下的路径，相比于前两种方法，使用二次贝塞尔曲线和Cantmull-Rom插值后的曲线更接近原始路径.本文提出一种更优的局部Bezier曲线进行路径平滑，图 4中的红色虚、实曲线与原始路径更为接近，局部贝塞尔曲线优化策略是：①选择待优化拐点的左、右两条线段，以两条线段的中点作为待优化的起点和终点，其余部分保持原状态，不进行插值优化，缩短待优化的线段长度; ②只对原始路径中出现拐点的路径进行插值处理，其他非拐点处的路径保持不变，处理结果如图 4中的红色虚实曲线，可以看出，优化后的曲线具有更小的曲率半径，与原有的折线段也最为接近.
图 4(Fig. 4)

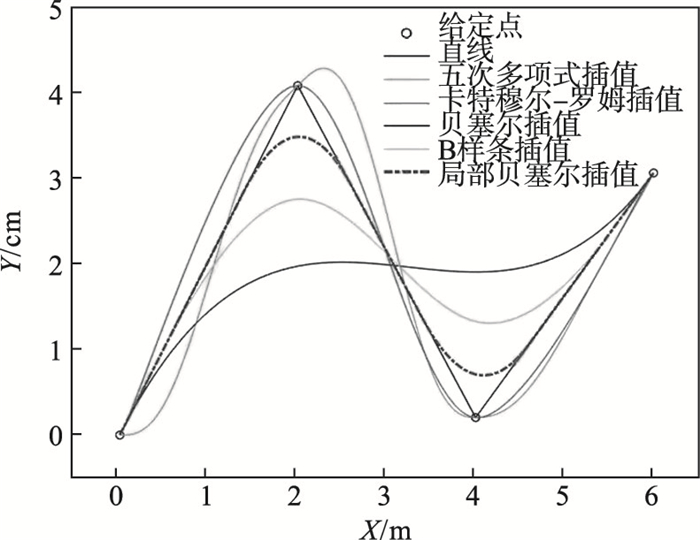图 4 局部Bezier插值曲线示意图Fig.4 Schematic diagram of local Bezier interpolation curves

3 MATLAB仿真实验为了验证本文算法的性能，在MATLAB仿真平台上分别设置了稠密障碍物环境、唯一可行路径的狭窄通道环境及“U”型障碍物三种障碍环境地图，对应地图 1~3，并进行了100次仿真模拟.在地图 1，2中将机器人视为质点运动，同时地图 3选择圆形机器人模型进行仿真模拟，设置本文算法的最大固定节点数为5 000，最大迭代次数为10 000.采用的轨迹规划方案包括：原始地图的大小为40 mm×40 mm; 固定初始点和目标点.将本文算法的仿真结果与文献[7]中所提算法、RRT*及基本RRT*FN进行对比分析，验证本文算法的优越性和正确性.
地图 1为稠密障碍物的复杂环境，用于验证算法在包含多障碍物时的搜索能力，设置的初始点坐标为[1, 1]，目标点坐标为[38, 38].地图 1的规划结果如图 5所示.图 5a中绿色部分表示算法生成树的节点分布情况，红色线段连接成初始路径，可以看出树中随机节点在初始路径附近分布较为集中，这也反映出本文所提采样策略和节点删除策略的有效性.图 5b是对图 5a中生成的初始路径进行了局部贝塞尔曲线优化，并只对原始路径中出现拐点的路径局部优化.将本文实验数据与文献[7]的实验数据整理见表 2.
图 5(Fig. 5)

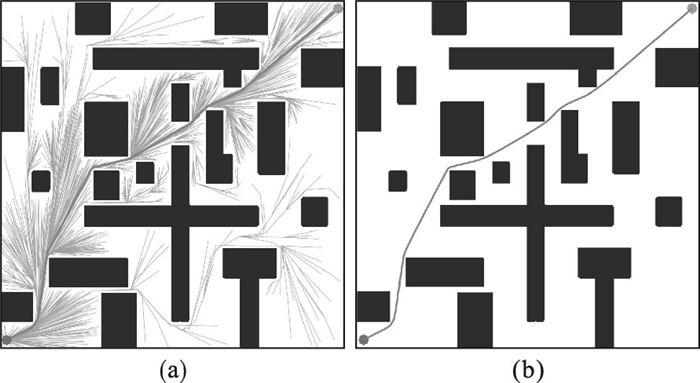图 5 地图 1规划结果Fig.5 Map 1 planning results (a)—初始生成路径及树的结点分布; (b)—初始路径局部优化.

表 2(Table 2)

表 2 地图 1仿真环境下的实验数据Table 2 Experimental data in map 1 simulation environment 算法 平均路径长度/mm 平均运行时间/s RRT* 56.47 49.59 基本RRT*FN 56.48 47.63 改进RRT*FN 55.65 52.18 本文算法 55.55 50.64

表 2 地图 1仿真环境下的实验数据 Table 2 Experimental data in map 1 simulation environment

在地图 1环境下，4种算法路径收敛情况对比如图 6所示.由表 2和图 6可知，RRT*和基本的RRT*FN算法可以在较短时间内获得可行路径，但路径的长度较长，文献[7]所提的改进算法可以获得较短的路径长度，但以牺牲运行时间为代价.
图 6(Fig. 6)

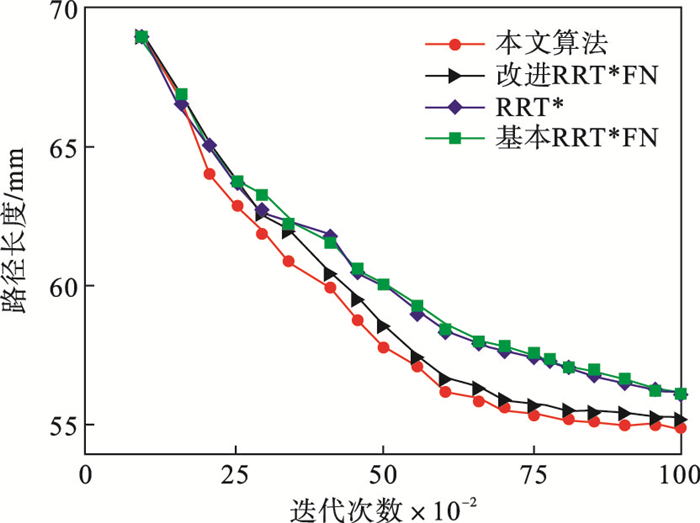图 6 4种算法路径收敛情况对比Fig.6 Comparison of path convergence of four algorithms

相比表 2中的前3种算法，本文算法利用目标偏置策略可以更快找到1条初始路径，当树中结点达到固定节点预设值时，删除无子节点且对最终路径影响较低，即远离初始路径的节点，使随机采样点围绕初始路径进行迭代，迭代精度与文献[7]所提算法接近.从表 2可以得到本文算法比文献[7]所提算法平均路径缩短了0.18 %，在平均收敛时间上少用时2.95 %，因此本文算法可以在相对较短的时间内加快收敛速度，提高收敛效率，获得较短路径.
地图 2为仅存在唯一可行路径的狭窄通道环境，用于验证算法对狭窄通道的搜索能力，设置的初始点坐标为[1, 1]，目标点坐标为[38, 38]，增加了算法采样与路径平滑的难度，实验结果如图 7所示.
图 7(Fig. 7)

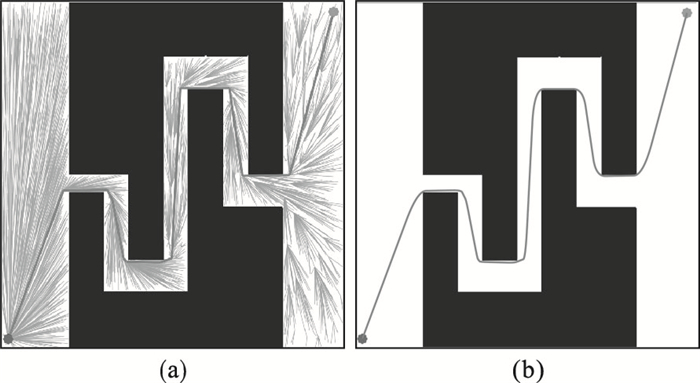图 7 地图 2规划结果Fig.7 Map 2 planning results (a)—初始生成路径及树的结点分布; (b)—初始路径局部优化.

图 7a绿色部分表示算法生成树的节点分布情况，连接的红色线段为初始路径; 图 7b对图 7a中生成的初始路径中出现拐点的路径进行了局部贝塞尔优化.
将本文实验数据与文献[7]的实验数据整理见表 3，地图 1环境下4种算法路径收敛情况对比如图 8所示.
表 3(Table 3)

表 3 地图 2仿真环境下的实验数据Table 3 Experimental data in map 2 simulation environment 算法 平均路径长度 平均运行时间 mm s RRT* 97.08 40.43 基本RRT*FN 97.97 40.47 改进RRT*FN 95.77 37.51 本文算法 93.60 38.21

表 3 地图 2仿真环境下的实验数据 Table 3 Experimental data in map 2 simulation environment

图 8(Fig. 8)

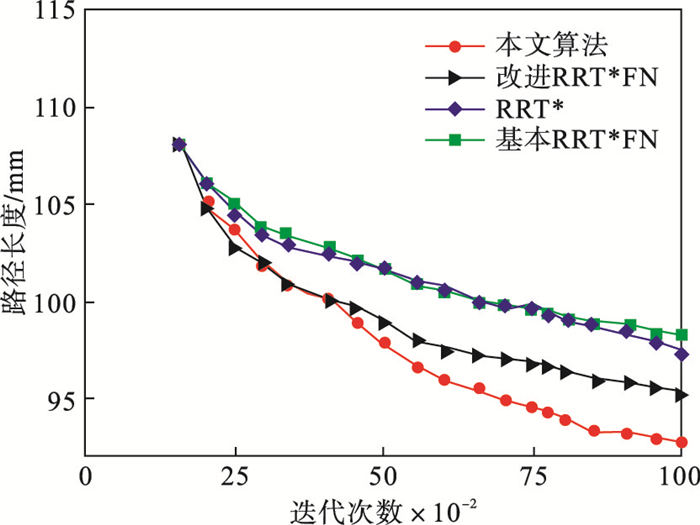图 8 4种算法路径收敛情况对比Fig.8 Comparison of path convergence of four algorithms

地图 3为“U”型障碍物的地图环境，用于验证算法对特定形状障碍物的搜索能力，设置的初始点坐标为[14, 24]，目标点坐标为[26, 16]，将机器人当作质点运动的仿真实验如图 9所示.
图 9(Fig. 9)

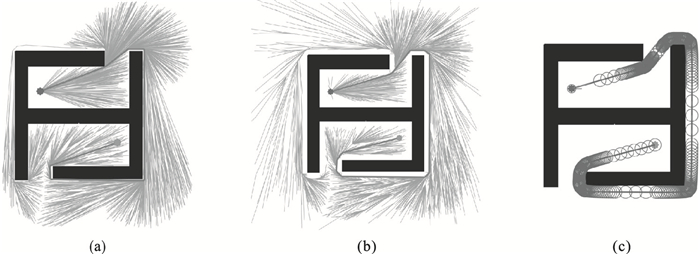图 9 地图 3规划结果Fig.9 Map 3 planning results (a)—初始生成路径及生成树节点分布; (b)—Bezier优化后的路径; (c)—机器人运动情况.

图 9a中绿色部分表示算法生成树的节点分布情况，红色线段连接成初始路径，可以看出树中随机节点在初始路径附近分布较为集中，这也反映出本文所提采样策略和节点删除策略的有效性.对图 9b中生成的初始路径中出现拐点的路径进行了局部Bezier优化，绿色部分为Bezier优化后的随机树节点分布情况，红色曲线表示对初始路径最终优化后的路径效果.图 9c将机器人设置为占有一定空间的蓝色圆圈，同时对障碍物进行膨胀处理，保证机器人在行驶过程中不会与障碍物发生碰撞.本文设置的机器人直径为2 mm，膨胀长度则取机器人的半径1 mm.
将机器人的运动视为通过旋转和平移的方式从1点至另1不同点的运动，机器人从初始点到目标点对规划好的路径进行跟踪的结果如图 9c所示，其中机器人圆圈中突出的蓝色线段指向了机器人的旋转方向.机器人在拐弯处行驶相对缓慢，蓝色圆形显示相对集中，在直线部分行驶相对顺畅，蓝色圆形显示相对稀疏，机器人在不与障碍物发生碰撞的前提下，沿规划好的路径作曲线运动.将本文实验数据和文献[7]的实验数据整理汇总见表 4，图 10是地图 3环境下4种算法路径收敛情况对比.
表 4(Table 4)

表 4 地图 3仿真环境下的实验数据Table 4 Experimental data in map 3 simulation environment 算法 平均路径长度/mm 平均运行时间/s RRT* 69.42 24.59 基本RRT*FN 70.21 27.15 改进RRT*FN 66.14 24.45 本文算法 65.95 20.96

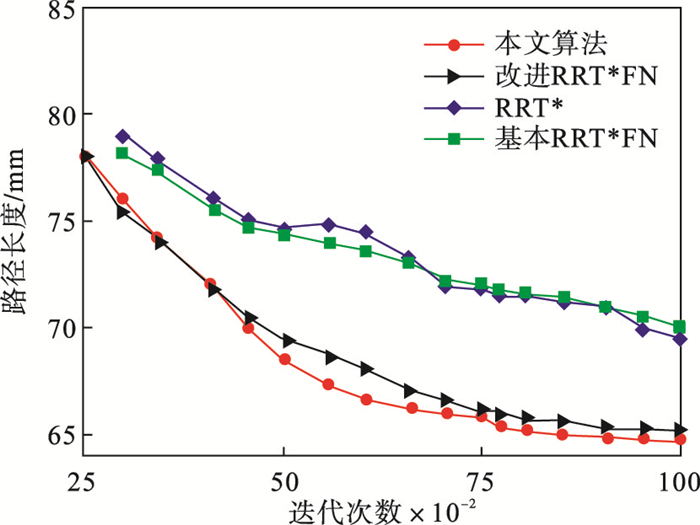
表 4 地图 3仿真环境下的实验数据 Table 4 Experimental data in map 3 simulation environment

图 10(Fig. 10)

图 10 4种算法路径收敛情况对比Fig.10 Comparison of path convergence among four algorithms

由表 4分析可知，在地图 3环境中，相比于RRT*和基本的RRT*FN算法，文献[7]所提的改进RRT*FN算法和本文算法可以在较短的时间内获得较短的路径长度，平均路径缩短了0.29 %，在平均收敛的时间上少用时14.27 %.从图 10可以看出，本文算法和文献[7]所提算法收敛效果较为接近，但改进RRT*FN算法可以在更短的时间内获得较短路径，总体提高了收敛效率，获得较短路径.
4 实际场景测试为了验证实际场景下本文算法的性能，计算机配置为Ubuntu16.04LTS，处理器为Intel I5-6500, 主频为3.2 Hz，运行内存为16 GB，选择第3代TurtleBot3双轮差分驱动机器人为实验对象，实物如图 11所示.利用开源机器人软件系统ROS，室内10 m×5 m的狭窄通道作为实验环境，如图 12所示.纸箱代表环境中的障碍物，规划的路径如图 13所示.图中绿色箭头表示目标点的位置，图 13a表示机器人在初始点的状态; 图 13b~图 13d是机器人根据算法规划的路径躲避障碍物的过程.可以看出，机器人在不碰撞障碍物的前提下沿规划路径行驶，成功避障; 图 13e是机器人成功到达目标点的状态.移动机器人从初始点出发，沿规划好的路径进行导航规划，成功到达目标点，实验验证了所提算法的可行性和有效性.
图 11(Fig. 11)

图 11 Turtlebot burger移动机器人实物Fig.11 Real object of Turtlebot burger mobile robot

图 12(Fig. 12)

图 12 实验整体环境Fig.12 Overall context of the experiment

图 13(Fig. 13)

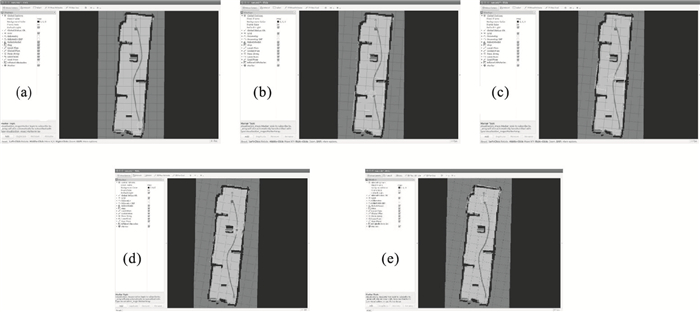图 13 实物路径规划过程Fig.13 Physical path planning process (a)—机器人在初始点; (b)—机器人在避障; (c)—机器人在避障; (d)—机器人在避障; (e)—机器人到达目标点.

5 结论1) 以RRT*算法为基础，结合实际机器人避障模型的应用场景，提出基于改进的RRT*FN路径规划算法.利用状态空间障碍物膨胀处理避免机器人在路径上发生碰撞，在未找到初始路径时利用目标偏置采样的方式提高搜索速度，找到初始路径后使随机采样点围绕初始路径进行选择，提升算法效率.
2) 在路径迭代过程中，如果树中的节点已超过固定节点最大值，但还未找到初始路径时，删除树中远离目标点并且没有子节点的节点，如果是已找到初始路径，删除树中远离最优路径且没有子节点的节点，保留高性能节点，提高算法收敛到最优路径的效率.
3) 采用局部贝塞尔(Bezier)插值对折线段路径进行平滑处理，通过改进算法满足初始位置和目标位置的方向限制，在不同地图环境中进行仿真.结果表明改进后的算法在路径收敛效率、路径长度、运行时间及平滑性上相较于其他算法具有明显优势.在实际环境下的实验验证了所提算法的可行性和有效性.
参考文献

[1]	Gasparetto A, Boscariol P, Lanzutti A, et al. Path planning and trajectory planning algorithms: a general overview[J]. Motion and Operation Planning of Robotic Systems, Mechanisms and Machine Science, 2015, 29(1): 3-27.
[2]	Sertac K, Emilio F. Sampling-based algorithms for optimal motion planning[J]. The International Journal of Robotics Research, 2011, 30(7): 846-894. DOI:10.1177/0278364911406761
[3]	Nasir J, Islam F, Malik U, et al. RRT*-smart: a rapid convergence implementation of RRT*[J]. International Journal of Advanced Robotic Systems, 2013, 10(7): 991-996.
[4]	杨国田, 苏荣强, 吴华, 等. 飞行机器人的电力杆塔巡检路径规划[J]. 华中科技大学学报(自然科学版), 2015, 43(sup1): 324-327. (Yang Guo-tian, Su Rong-qiang, Wu Hua, et al. Electric Pole and tower patrol path planning for flying robot[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2015, 43(sup1): 324-327.)
[5]	Adiyatov O, Varol H A. A novel RRT*-based algorithm for motion planning in dynamic environments[C]//International Conference on Mechatronics and Automation. Takamatsu, 2017: 1416-1421.
[6]	Luo S, Liu S, Zhang B, et al. Path planning algorithm based on Gb informed RRT* with heuristic bias[C]// Chinese Control Conference. Dalian: IEEE, 2017: 297-302.
[7]	谭建豪, 潘豹, 王耀南, 等. 基于改进RRT*FN算法的机器人路径规划[J]. 控制与决策, 2021, 36(08): 1834-1840. (Tan Jian-hao, Pan Bao, Wang Yao-nan, et al. Robot path planning based on improved RRT*FN algorithm[J]. Control and Decision, 2021, 36(08): 1834-1840.)
[8]	王海芳, 张瑶, 朱亚锟, 等. 基于改进双向RRT*的移动机器人路径规划算法[J]. 东北大学学报(自然科学版), 2021, 42(8): 1065-1070, 1142. (Wang Hai-fang, Zhang Yao, Zhu Ya-kun, et al. Mobile robot path planning algorithm based on improved bidirectional RRT*[J]. Journal of Northeastern University(Natural Science), 2021, 42(8): 1065-1070, 1142.)
[9]	龙建全, 梁艳阳. 多路口环境下RRT的最优路径规划[J]. 计算机工程与应用, 2020, 56(19): 278-283. (Long Jian-quan, Liang Yan-yang. Optimal RRT path planning in multi-intersection environment[J]. Computer Engineering and applications, 2020, 56(19): 278-283.)
[10]	Adiyatov O, Varol H A. Rapidly-exploring random tree based memory efficient motion planning[C]// 2013 IEEE International Conference on Mechatronics and Automation. Takamatsu: IEEE, 2013: 354-359.
[11]	Ravankar A, Ravankar A A, Kobayashi Y, et al. Path smoothing techniques in robot navigation: state-of-the-art, current and future challenges[J]. Sensors, 2018, 18(9): 3170. DOI:10.3390/s18093170
[12]	Maekawa T, Noda T, Tamura S, et al. Curvature continuous path generation for autonomous vehicle using B-spline curves[J]. Computer-Aided Design, 2010, 42(4): 350-359. DOI:10.1016/j.cad.2009.12.007
[13]	Lin M, Kai Y, Shi C, et al. Path planning of mobile robot based on improved A* algorithm[C]// Proceedings of the 2017 29th Chinese Control and Decision Conference. Chongqing: IEEE, 2017: 3570-3576.
[14]	Elbenhawi M, Simic M, Jazar R. Continuous-curvature bounded trajectory planning using parametric splines[J]. Frontiers in Artificial Intelligence and Applications, 2014, 262: 513-522.