
 , 石运昊1, 阿力普江杰如拉2, 姜鉴晖1
, 石运昊1, 阿力普江杰如拉2, 姜鉴晖1 1. 东北大学 资源与土木工程学院,辽宁 沈阳 110819;
2. 新疆大学 建筑工程学院,新疆 乌鲁木齐 830017
收稿日期:2021-10-17
基金项目:国家自然科学基金资助项目(U1602232);中央高校基本科研业务费专项资金资助项目(N170108029);辽宁省重点研发计划项目(2019JH2/10100035)。
作者简介:王述红(1969-),男,江苏泰州人,东北大学教授,博士生导师。
摘要:自平衡试桩法因其具有方便、经济等优势而被推广起来,但目前关于该方法转换成静载法荷载-位移曲线过程中涉及到的转换系数的研究较少.在对比研究自平衡试桩法与传统单桩竖向抗压静载试验方法的基础上,依据Mindlin解, 对未考虑土体连续性时转换后得到的自平衡试桩桩顶位移与实际结果的差异进行分析,研究砂土地区试桩中的上托桩桩周土体位移对桩端沉降变化的影响,进而对现有确定自平衡试桩承载力的转换方法进行改进.通过室内模拟试验验证了该方法的可行性,将此方法应用到沈阳某高层桩基础工程试验中,发现采用考虑土体连续性的自平衡转换方法明显降低了荷载-位移曲线的拟合误差.
关键词:桩基础土体连续性堆载法自平衡法承载力
Research on the Self-balanced Method of Pile Bearing Capacity Considering Soil Continuity and Engineering Test
WANG Shu-hong1

 , SHI Yun-hao1, ALIPUJIANG Jierula2, JIANG Jian-hui1
, SHI Yun-hao1, ALIPUJIANG Jierula2, JIANG Jian-hui1 1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China;
2. College of Architecture & Civil Engineering, Xinjiang University, Urumqi 830017, China
Corresponding author: WANG Shu-hong, E-mail: wangshuhong@mail.neu.edu.cn.
Abstract: The self-balanced test pile method is gradually popularized due to its convenience and economy. However, few studies were focused on the conversion coefficient involved in the process of converting this method into the static load-displacement curve. Because the settlement on the pile top is affected by soil continuity, the displacement difference on the pile top of the self-balanced test pile and the static load pile were analyzed using the Mindlin′s formula based on the comparative study of the self-balanced test pile method and the traditional vertical compression static load test method of single pile. An equivalent conversion method to determine the bearing capacity of self-balanced test pile was proposed in order to improve the empirical formula. The rationality of the improved method was verified by indoor simulation test as well as pile foundation engineering test of a super high-rise building in Shenyang. It is found that the self-balance conversion method taking the soil continuity in to account can significantly reduced the fitting error of the load-displacement curve.
Key words: pile foundationsoil continuitystack methodself-balanced methodbearing capacity
在很多工程实践中,场地条件无法保证传统静载试验的顺利实施,Osterberg[1]提出自平衡法,并逐渐得到广泛应用[2-5],因其具有工期短、造价低等优点.在自平衡法试桩确定承载力的过程中,需要将上、下段桩的荷载-位移曲线处理后等效转换成传统受压桩的荷载-位移曲线[6].在确定单桩承载力的转换过程中,最大的难点在于将自平衡的上段桩的向下侧摩阻力值转换为向上的侧摩阻力值.自平衡试验转换方法中工程应用最为广泛的就是经验公式法,此方法是对上托桩侧摩阻力分析时考虑到上托桩受载情况特殊,引入一般小于1的转换系数γ,将修正后上托桩侧摩阻力值与下压侧摩阻力进行整合:
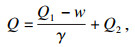 | (1) |
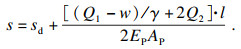 | (2) |
Li等[7]将每根试桩的上段桩在同一土层处的自平衡法测的极限侧摩阻力值与堆载法测的极限侧摩阻力值进行对比,得到了各土层自平衡法转换系数值,修正系数为上段桩各层土转换系数的加权平均值.Li等[8]以MATLAB编程为基础,采用最小二乘法对传统静载试验数据进行拟合,得到传统静载法结果拟合效果最佳的γ值.杜思义等[9]利用经验公式法求桩承载力的过程中,引入了桩侧摩阻力分布系数,对上托桩压缩量的计算进行改进.由于上段桩桩周土受剪荷载作用,产生向下的位移,所以计算桩端土体沉降时需考虑土体连续性对经验公式中转换系数的影响,本文提出一种改进的自平衡等效转换方法.
1 现有转换方法的问题自平衡法与堆载法不同的是自平衡法上、下段桩受载后移动方向不同,因此桩周土体侧摩阻力方向也不同.堆载法试桩与自平衡试桩中下压桩受到的摩阻力方向都是向上的,但与自平衡法桩中上托桩桩身受力状态却不尽一致.所以如何处理上段桩的荷载位移数据,让等效转换后的Q-S曲线更贴近传统受压桩Q-S曲线是难点所在.目前大多方法以堆载法的Q-S曲线为基准,采用MATLAB编程对其拟合,在获得与传统静载法测得结果拟合误差最小的γ值的过程中可以得知,确定上托桩分级荷载Qu与位移Su之前,要先确定下压桩的位移Sd.自平衡法下压桩位移Sd由4部分组成:①下压桩身的弹性压缩量ΔSd;②考虑土体连续性的下压桩桩周各层土体受剪荷载产生的向下位移引起的桩端土体沉降变化Swd;③上托桩桩周土体因受剪作用产生的向上位移,引起桩端土体沉降变化Swu;④由于桩端荷载,桩端土体压缩导致桩端沉降Sb为
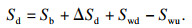 | (3) |
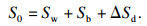 | (4) |
图 1(Fig. 1)
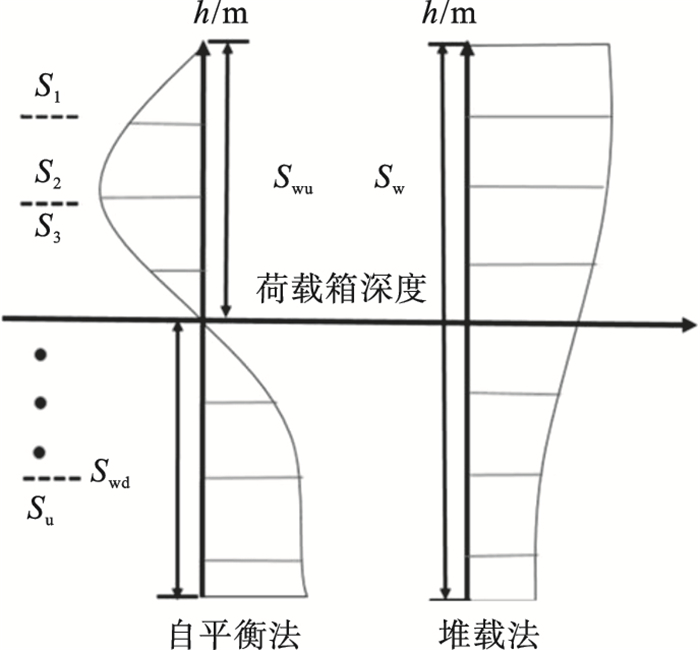 | 图 1 桩周土层因摩阻力产生的位移随深度变化图Fig.1 The displacement changes due to the friction of soil around with depth |
图 2(Fig. 2)
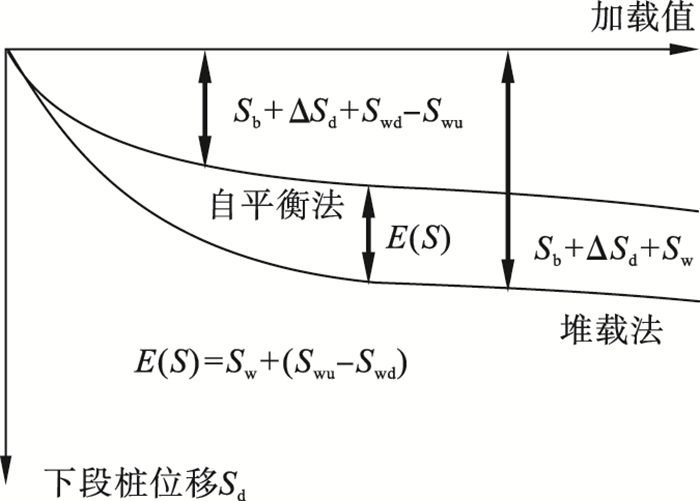 | 图 2 自平衡法与堆载法中下段桩荷载-位移曲线Fig.2 Load-displacement curves of the lower part of the pile in the self-balancing method and the stacking method |
依据广义Mindlin解可知[10],桩周各层土体产生的位移由桩土剪应力和土体竖向位移柔度系数决定,一般采用弹性半空间体内集中荷载作用下的Mindlin解来计算桩周各层土体位移,主要由桩体位移与土体位移相协调建立协调方程,从而求解桩周土体位移,自平衡法上托桩的桩周土体位移引起的桩端沉降变化为
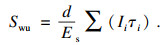 | (5) |
自平衡法下压桩的桩周土体位移引起的桩端沉降变化为
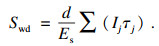 | (6) |
堆载法整根试桩桩周土体位移引起桩端沉降变化为
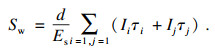 | (7) |
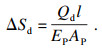 | (8) |
将式(5),式(6),式(8)代入式(3),自平衡法中下压桩的位移为
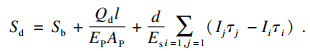 | (9) |
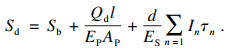 | (10) |
虽然两根试桩桩土条件一致,但由于加载位置及加载值不同,导致各土层发挥的侧摩阻力值不一样.采用Mindlin解计算同一层土体在不同加载工况下所产生的位移也不一样,若将自平衡法上托桩的桩周土体位移引起的桩端沉降变化Swu转化成堆载法桩桩周土体位移引起桩端沉降Sw时,需将对各层土体摩阻力与位移进行对应折减,其中涉及到的参数较多,过程较为复杂,所以本文从土体连续性的角度,对自平衡法转换公式中的Sd进行处理,提出一种改进的等效转换方法.
2 改进等效转换方法2.1 改进转换方法原理分析现有转换方法可知:式(2)中的下段桩位移Sd未考虑上托桩桩周土体因受剪作用产生的向上位移而引起的桩端土体沉降变化.将优化自平衡法中下压桩位移Sd按照上托桩、下压桩在自平衡试桩中的分开方法,将堆载法试桩分成上、下段桩, 上、下段桩长度分别与上托桩、下压桩一致,方便后文进行解释.先将上、下段桩分开的位置称为“虚拟荷载箱”.利用桩土条件、施工工艺、几何尺寸都相同的堆载法试桩中“虚拟荷载箱”位置的位移S0替换自平衡试桩中下压桩位移Sd.下段桩加载值Qd改为堆载法试桩中“虚拟荷载箱”位置的轴力Fn,进而对上段桩的荷载-位移曲线进行改良.之所以采用堆载法试桩中“虚拟荷载箱”位置的位移S0代替Sd, 是因为参数S0弥补了Sd没有考虑土体连续性的缺陷,S0为
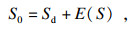 | (11) |
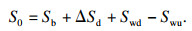 | (12) |
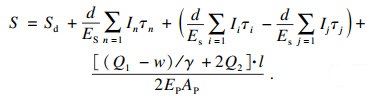 | (13) |
Fn是从堆载法桩身轴力变化曲线中获得.采用堆载法的试桩桩身是压缩变形的状态,桩身轴力从桩顶到桩端是从大到小的,是一个直角三角形,如图 3所示.
图 3(Fig. 3)
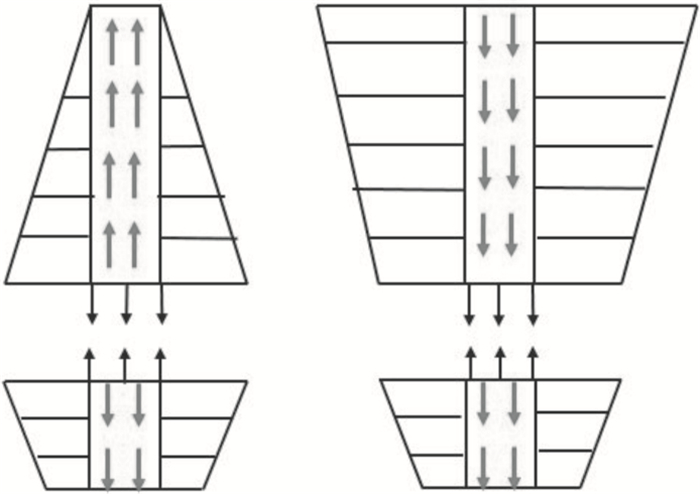 | 图 3 堆载法与自平衡法桩身轴力图Fig.3 The axial force diagram of pile by surcharge method and self-balanced method |
采用自平衡法试桩的上、下段桩相反方向的作用力,通过观察两种检测方法的桩身轴力图 3可知,上托桩的轴力从桩顶到荷载箱由小变大,而下压桩的轴力则是直角梯形, 从荷载箱到桩端由大变小.
通过沈阳砂土地区以往自平衡法对比试验数据来看,自平衡法试桩分级加载值与堆载法试桩对应每级加载情况下的桩身轴力数值接近,所以改进转换方法中将Qd替换为Fn是可行的.
混凝土强度及桩身直径很难改进转换方法中需要将自平衡法试桩中下压桩位移Sd被替换为堆载法试桩中虚拟荷载箱的位移S0.由于实际工程中,钻孔灌注桩的桩身混凝土强度,以及桩身直径很难保证一致,易形成支盘、缩径的情况,导致上段桩桩身横截面积与桩身弹性模量不一致,无法通过桩顶沉降减去上段桩弹性压缩量来获得“虚拟荷载箱”位置的桩身位移S0.为了获得准确的桩身位移S0,在受压试桩中“虚拟荷载箱”预留圆板将受压试桩分为上、下段桩,预留圆板上部连接有位移杆,为避免位移杆移动时与混凝土产生摩擦更大的误差,将位移杆放置在护管中,测量装置如图 4所示.
图 4(Fig. 4)
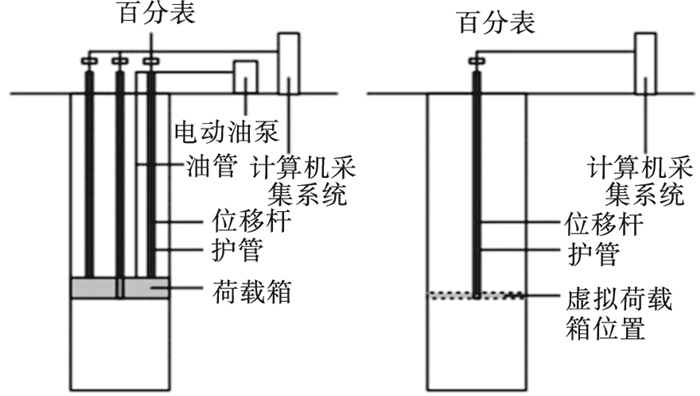 | 图 4 自平衡法与堆载法试桩桩身位移测量装置Fig.4 Pile displacement measuring devices for the self-balanced and surcharge method |
2.2 基本假定为便于推导和分析,对改进等效转换方法做出如下假定:
1) 假定自平衡法下段桩与受压桩中虚拟荷载箱位置下方的下段桩桩身条件、施工工艺、几何尺寸与标高一致.
2) 假定不考虑桩身横向变形对侧摩阻力的影响.
3) 假定自平衡试桩中的荷载箱位置是平衡点位置.
2.3 计算步骤利用埋设在堆载法试桩中的桩身位移测量装置得到虚拟荷载箱位置位移S0,替代自平衡法测得的下压桩位移Sd.因为传统堆载法桩的位移是整体一致的,所以上段桩的荷载箱每级加载取值为Su=Sd=S0时所对应的Qu-Su曲线的荷载Qu,如图 5所示.
图 5(Fig. 5)
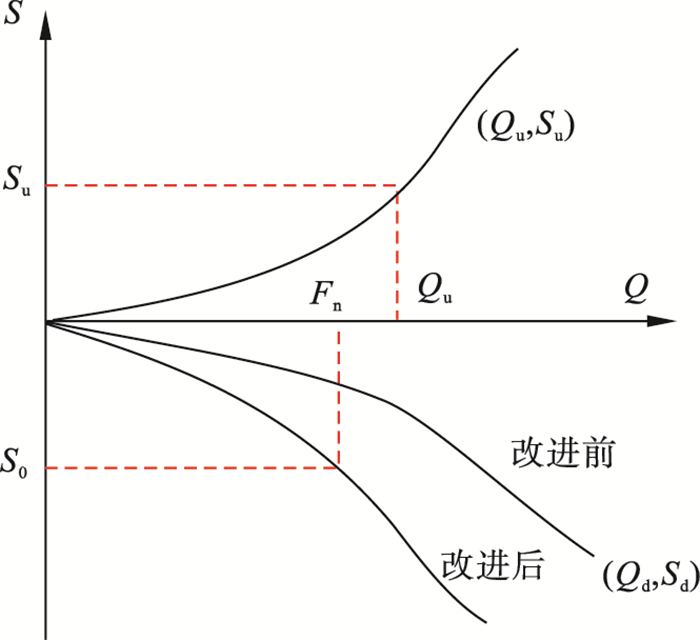 | 图 5 数据处理图Fig.5 Data processing diagram |
计算步骤如下所示:
1) 将静载试桩以“虚拟荷载箱”位置为分界点,分为上、下段桩,并用特殊的桩身位移测量装置测量得到的“虚拟荷载箱”位置位移S0替代自平衡法测得的下压桩位移Sd.
2) 将受压桩中虚拟荷载箱位置的每级加载下的桩身轴力Fn取代自平衡法下压桩的分级加载值Qd.
3) 将计算或测量的虚拟荷载箱位置的位移S0替代自平衡法测得的下压桩位移Sd.
4) 利用上述步骤得到的各级加载下的数据Qu,Su,Sd,Fn,采用最小二乘法进行拟合,进而获得拟合误差最小的转换系数.
5) 将转换系数取值代入转换式(1)与式(2)中得到修正后的单桩荷载—位移曲线.
改进的转换方法如图 6所示.
图 6(Fig. 6)
 | 图 6 改进转换方法示意图Fig.6 Schematic diagram of the improved conversion method |
3 改进方法的验证为了验证改进的自平衡法等效转换模型的可行性,引用室内模拟试验数据对其可行性验证.室内模拟试验对空间场地要求较低,可多次试验以提高试验误差精度,使测试结果更合理.为了避免实际工程中桩土材料特性、复杂边界条件等未知因素干扰,方便调整荷载箱加载值Qd和测量桩身中位移S0及节省验证本文模型的成本,为研究自平衡与静载法传递规律的差异及原因,Cai等[11]进行了相同边界条件、桩土材料特性的自平衡试桩与静压试桩室内模拟实验, 获得了两种试桩的极限承载力与桩身不同位置的位移数据以及桩身轴力随深度的变化规律.
模型试桩荷载-位移曲线如图 7所示,向上位移为正,向下位移为负,自平衡试桩与抗拔试桩Q-S曲线均存在明显突变点,呈突发性破坏.桩身轴力随桩身深度的变化关系如图 8所示.
图 7(Fig. 7)
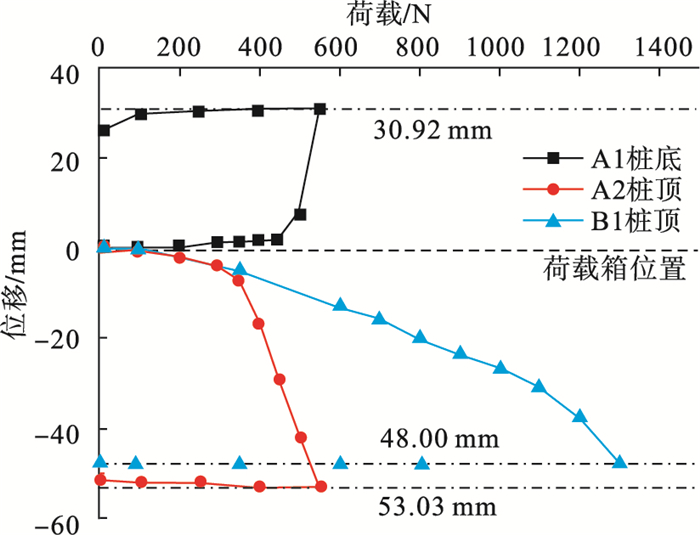 | 图 7 A1,A2,B1试桩荷载-位移曲线Fig.7 Load-displacement curves of test piles A1, A2 and B1 |
图 8(Fig. 8)
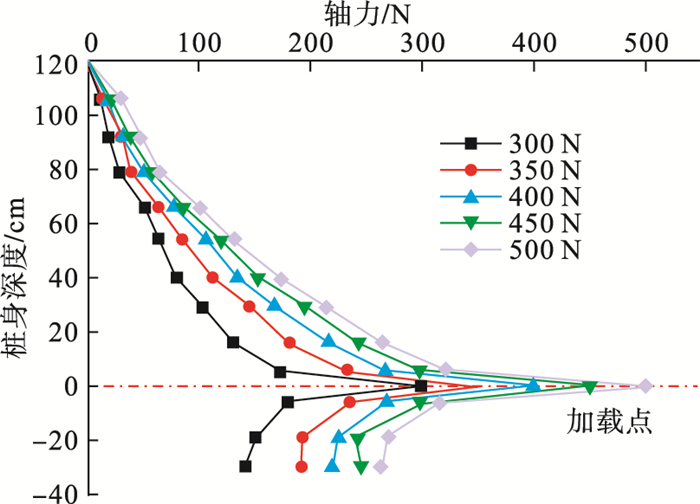 | 图 8 A1,A2桩身轴力随桩身深度变化关系Fig.8 Relationship between pile axial force A1, A2 and pile depth |
由图 8可知,荷载从加载点近端传到加载点远端,自下而上传递,加载点近端桩身轴力递减较为明显.随距离桩身顶部越来越近,轴力递减趋势逐渐放缓.轴力曲线整体向左侧凸起,表明上托桩A1桩下侧桩周土层发挥较为明显的作用.当加载值慢慢增大时,上端土层开始发挥作用.下压桩A2桩桩身轴力在0到-5 cm桩段急剧变化,-5 cm以下桩段轴力递减放缓,随荷载增加,桩端阻力逐渐发挥作用.A1,A2试桩的桩身轴力曲线整体呈人字分布.
桩身轴力随桩身深度的变化如图 9所示,传统受压试桩桩身整体轴力上大下小,桩身深度78~82 cm时,桩身轴力变化较为明显.轴力曲线大致呈反“S”型,桩端阻力大致占桩总阻力的20 %,B1桩表现为端承摩擦桩.
图 9(Fig. 9)
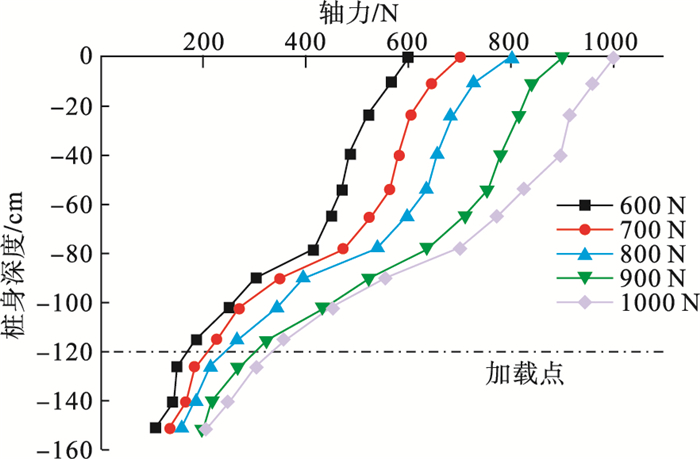 | 图 9 B1桩身轴力随桩身深度变化关系Fig.9 Relationship between pile axial force B1 and pile depth |
通过室内模拟实验可得自平衡法试桩加载点的下压桩位移Sd,与静压试桩加载点深度相同位置的桩身轴力Fn与下段桩位移S0如表 1所示.
表 1(Table 1)
| 表 1 室内模拟试验对比组数据 Table 1 Comparison on data of the indoor simulation test | ||||||||||||||||||||||||||||||||||||
考虑土体连续性的改进转换方法和未考虑土体连续性的转换方法[12]Q-S曲线结果对比如图 10所示.由Mindlin位移解可知[13],对土体连续性的改进等效转换方法对上、下段桩Q-S曲线进行拟合,得到的转换系数为0.724.按γ=0.724得到的等效转换曲线低于室内模拟实验中γ=0.573的Q-S曲线下方,相对于未考虑土体连续性的转换方法得到的转换系数取值更贴近静压试桩的Q-S曲线.这是因为将静压桩里的Fn与S0替换为自平衡法里的Qd与Sd,避免了上段桩桩周土受剪荷载产生向下位移,对桩端沉降产生影响[14].由图 10可知,采用改进等效转换方法后的Q-S曲线相比未考虑土体连续性的Q-S曲线,更贴近于受压试桩曲线.
图 10(Fig. 10)
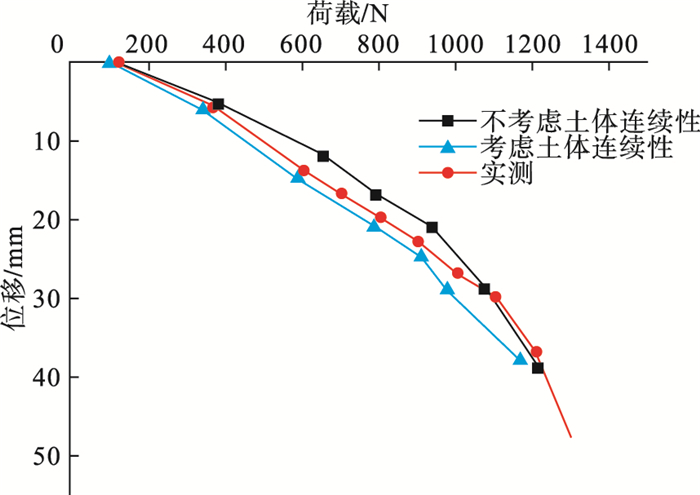 | 图 10 Q-S曲线对比图Fig.10 Comparison on Q-S curves |
4 工程应用4.1 工程概况通过室内模拟试验验证了本文改进等效转换方法理论的可行性,拟合后的等效转换曲线更贴近堆载法荷载-位移曲线.将此改进方法运用到某工程现场项目中,沈阳某高层建筑桩基础工程项目进行1号桩、2号桩两根钻孔灌注桩桩基承载力检测.桩身混凝土强度等级为C45.桩端持力层为全风化砂砾岩层,且桩端进入持力层的深度不小于2倍桩径.所有桩均变截面配筋,长度均为53 m.该工程绝对标高47.800 m,均采用旋挖钻孔灌注桩,为桩径1 000 mm的抗压桩.本项目的两根试桩:1号桩、2号桩分别采用自平衡法及传统堆载法测量极限抗压承载力,两种方法的承载力值分别为25 300,23 000 kN.
表 2给出了两根试桩的设计参数,图 11是两根桩的桩周土层分布图与荷载箱位置,图 12是试桩桩身位移S0的测量装置.
表 2(Table 2)
| 表 2 1号桩、2号桩试桩设计参数 Table 2 Test pile design parameters of No. 1, 2 pile |
图 11(Fig. 11)
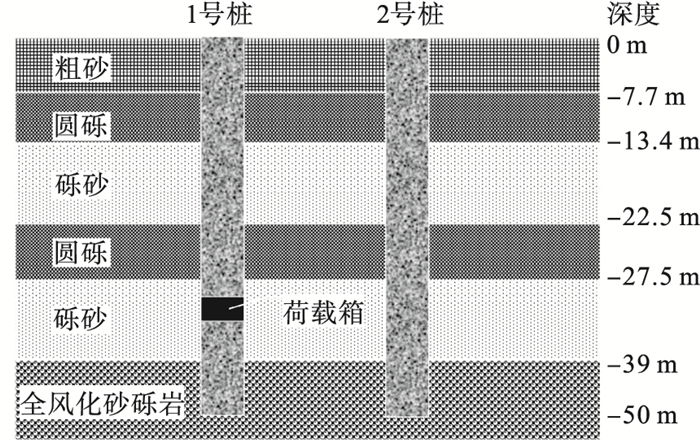 | 图 11 1, 2号试桩桩周土层分布及荷载箱位置Fig.11 The distribution of soil around pile No. 1 and No. 2 and the load box position |
图 12(Fig. 12)
 | 图 12 试桩桩身位移测量装置Fig.12 The displacement measuring device of test piles |
4.2 Q-S曲线图 13为自平衡试桩与堆载法试桩的荷载-位移曲线,两根桩的Q-S曲线都属于缓变形,在分级加载过程中,Q-S曲线并未出现突变点.1号桩与2号桩的Q-S曲线近似呈线性分布,1号桩上段桩加载到12 650 kN, 累计位移为5.71 mm; 下端桩加载到12 650 kN, 累计位移为5.15 mm, 终载时未出现桩破坏状态. 2号桩是传统受压桩,采用堆载法检验单桩极限抗压承载力,桩顶荷载加载到23 000 kN, 累计位移10.1 mm.通过观察回弹量可知,1号桩上段桩卸荷沉降量为0.51 mm, 下段桩卸荷沉降量为0.23 mm;2号桩卸荷沉降量为2.11 mm, 均未超出弹性变形.卸荷沉降量之所以小说明桩周土受上部堆载影响对其形成预压荷载,挤密地基土层,进而导致整体沉降量小,卸荷沉降量也小[15].
图 13(Fig. 13)
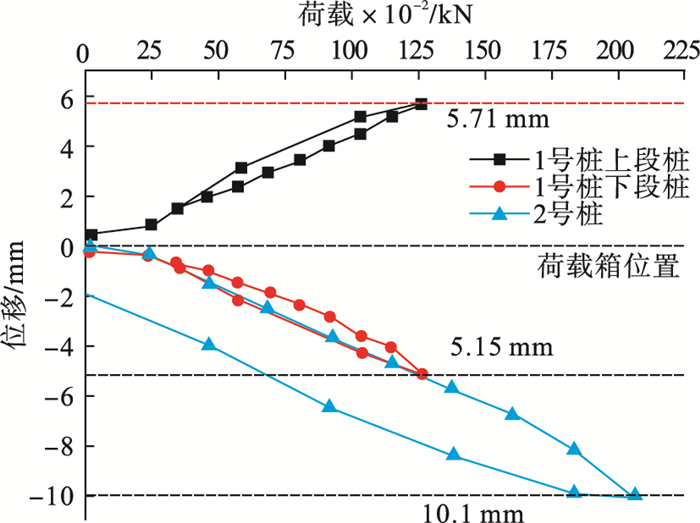 | 图 13 1,2号桩试桩荷载-位移曲线Fig.13 Load-displacement curves of pile No. 1 and No. 2 |
4.3 桩身轴力曲线1,2号桩身轴力随桩身深度的关系如图 14, 图 15所示.自平衡试桩轴力图中加载点往上的桩段为正距离,向下为负距离.由图 14可知,在桩身深度0~20 m桩段内,在各级加载下,桩身轴力均未发生明显变化,由于0~20 m深度里桩周土层为粗砂与圆砾层,因自身重力作用较小,导致土体密实度差,未发挥出理想摩阻效果[16].自平衡试桩下段桩的轴力曲线变化趋势明显大于上段桩桩身轴力曲线,这可能是因为下段桩桩周岩层主要为全风化砂砾岩,1号桩采用后注浆工艺后,桩土作用面得到明显改善,并且桩周土层与桩端岩层的反作用力使下压桩产生的泊松效应大于上托桩,明显的侧向变形导致桩土法向接触力更大,进而致使下压桩摩阻力大于上托桩摩阻力.纵向来看,自平衡法试桩桩身轴力曲线整体呈人字分布[17].
图 14(Fig. 14)
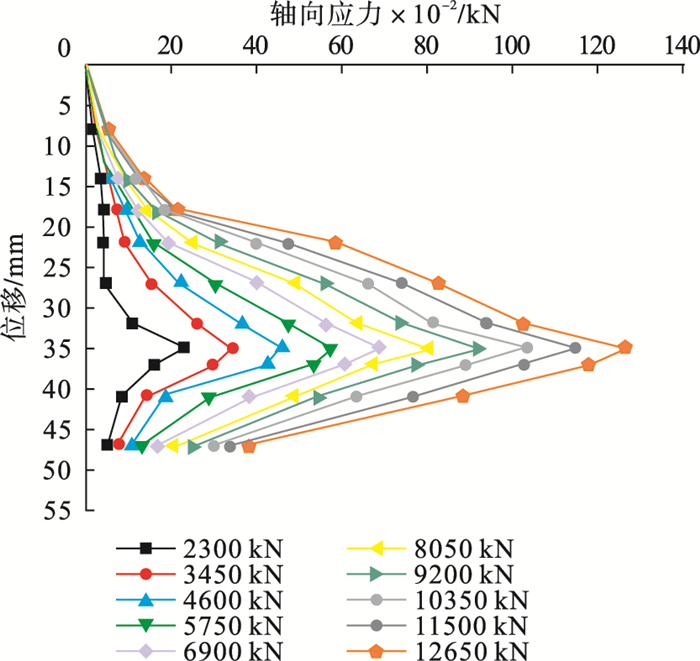 | 图 14 1号桩身轴力随桩身深度变化关系Fig.14 Relationship between axial force of pile No. 1 and the depth |
图 15(Fig. 15)
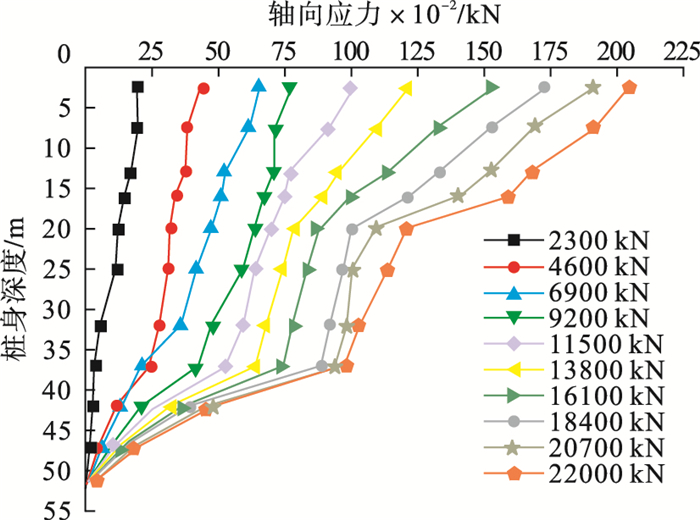 | 图 15 2号桩桩身轴力随桩身深度的变化关系Fig.15 Relationship between axial force of pile No.2 and the pile depth |
堆载法试桩桩身轴力曲线整体呈倒三角分布,上大下小,在15~20 m桩段,轴力递减较快,预估为砾砂层含砂量较大,在灌注过程中形成支盘,受力较大,导致桩身轴力出现明显变化.在20~35 m段桩处轴力变化减缓,说此桩段桩侧摩阻力未得到有效发挥.
4.4 Qd与Sd的确定考虑土体连续性的改进等效转换方法, 将堆载法试桩中虚拟荷载箱位置的桩身轴力来替代自平衡试桩的加载值,堆载法试桩中“虚拟荷载箱”位置的位移替代自平衡试桩中下压桩位移,工程试验对比组数据如表 3所示.按照改进的转换方法进行拟合得到的转换系数为0.95,通过观察图 16可知,按照γ=0.95取值得到的等效转换曲线明显低于未考虑土体连续性时γ=0.80取值得到的Q-S曲线下方,采用改进之后等效转换方法得到的Q-S曲线更接近于堆载法试桩的Q-S曲线,拟合误差相比未考虑土体连续性时也降低了13.1 %.
表 3(Table 3)
| 表 3 工程试桩对比组数据 Table 3 Comparison on data of engineering test piles | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
图 16(Fig. 16)
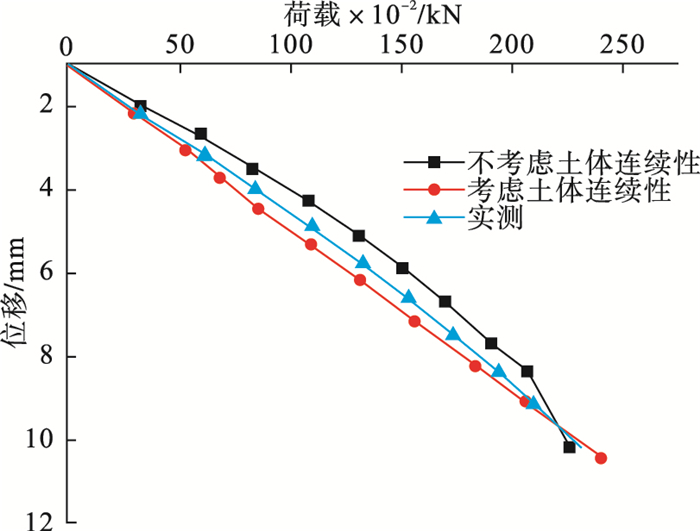 | 图 16 Q-S曲线对比图Fig.16 Comparsion on Q-S curves diagram |
5 结论1) 计算Mindlin位移解,分析桩周土体受到侧摩阻力向下传递造成的桩端沉降,发现自平衡试桩的下压桩位移在未考虑土体连续性的情况下,相比于传统受压方法检测的试桩下段桩位移偏小.
2) 通过室内模拟试验数据进行验证,发现本文提出的考虑土体连续性的桩承载力自平衡方法是正确有效的,在工程试验中具有可行性.
3) 将改进转换方法运用到沈阳砂土地区某高层的桩基工程试验中,按照优化后的转换系数取值γ=0.95计算得到的Q-S曲线与堆载法实测Q-S曲线的拟合误差更小,比改进前降低了13.1 %.
参考文献
| [1] | Osterberg J. New device for load testing driven piles and drilled shafts separates friction and end bearing[J]. Piling and Deep Foundations, 1989, 1(6): 421-427. |
| [2] | He C L, Gong C Z. Comparison and analysis on self-balanced method and anchored pile method in Qingdao Gulf Bridge[J]. Advanced Materials Research, 2013, 838/839/840/841: 1024-1027. |
| [3] | Bo L, Gong W, Dai G. Engineering application of self-balanced pile loading test using double load cells technique[J]. Building Structure, 2008(4): 35-37, 40. |
| [4] | Da I G L, Gong W M, Wang L, et al. Application of self-balanced test pile method in steel composite pile foundation of port wharf[J]. China Harbour Engineering, 2017, 37(10): 37-41. |
| [5] | Gong C Z, He C L, Gong W M, et al. Analysis of size effect on large diameter rock-socketed pile based on self-balance method[J]. Rock and Soil Mechanics, 2012, 33(8): 2403-2407. |
| [6] | Gong W, Dai G, Jiang Y, et al. Theory and practice of self-balanced loading test for pile bearing capacity[J]. Journal of Building Structures, 2002(1): 82-88. |
| [7] | Li X J, Chen X J, Dai G L, et al. Research on conversion coefficient of cast-in-situ pile in clay in self-balanced loading test[J]. Rock and Soil Mechanics, 2016, 37(sup1): 226-232, 262. |
| [8] | Li X J, Dai G L, Gong W M, et al. Research on conversion factor of self-balanced loading test in sandy soil[J]. Rock & Soil Mechanics, 2016, 37(sup1): 659-668. |
| [9] | 杜思义, 李晨辉. 自平衡试验中简单转换法的改进[J/OL]. 工业建筑: 2021, 51(5): 1-10. (Du Si-yi, Li Chen-hui. Improvement of simple conversion method in selfbalance test[J/OL]. Industrial Construction 2021, 51(5): 1-10. ) |
| [10] | Ai Z. Application extended mindlin solution to analyze a vertically loaded pile in multi-layered soil[J]. China Civil Engineering Journal, 2001, 34(2): 89-95. |
| [11] | Cai Y, Xu L R, Zhou D Q, et al. Model test research on method of self-balance and traditional static load[J]. Rock and Soil Mechanics, 2019, 40(8): 3011-3018. |
| [12] | 中国建筑科学研究院. JGJ/T403-2017建筑基桩自平衡静载试验技术规程[S]. 北京: 中国建筑工业出版社, 2017. (China Architecture Science Research Institute. JGJ/T403-2017 construction pile self-balance static carry test technical regulations[S]. Beijing: China Construction Industry Press, 2017. ) |
| [13] | 王述红, 赵贺兴, 姜磊, 等. 基于两阶段法地铁盾构开挖对邻近桩基影响分析[J]. 东北大学学报(自然科学版), 2014, 35(6): 871-874. (Wang Shu-hong, Zhao He-xing, Jiang Lei, et al. Analysis of the impact on adjacent pile caused by excavation with metro shield based on two-stage method[J]. Journal of Northeastern University(Natural Science), 2014, 35(6): 871-874. DOI:10.3969/j.issn.1005-3026.2014.06.025) |
| [14] | Zhu X R, Wang S Z, Ye J N, et al. Load transfer model and improved transition method for load-settlement curve under O-cell pile testing method[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1717-1721. |
| [15] | Kim H J, Mission J L C. Improved evaluation of equivalent top-down load-displacement curve from a bottom-up pile load test[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 137(6): 568-578. |
| [16] | Kim H J, Mission J L C. Design charts for elastic pile shortening in the equivalent top-down load settlement curve from a bidirectional load test[J]. Computers and Geotechnics, 2011, 38(2): 167-177. DOI:10.1016/j.compgeo.2010.11.001 |
| [17] | Chandler R J. The shaft friction of piles in cohesive soils in terms of effective stress[J]. Civil Engineering and Public Works Review, 1968, 63: 48-51. |
