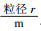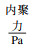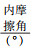郭隆基^1,2, 何满潮^1,2, 瞿定军³, 陶志刚^1,2
1. 中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室，北京 100083;
2. 中国矿业大学(北京) 力学与建筑工程学院，北京 100083;
3. 远安县燎原矿业有限责任公司，湖北 宜昌 444200
收稿日期：2021-06-12
基金项目：国家自然科学基金资助项目(41941018)。
作者简介：郭隆基(1994-)，男，河南灵宝人，中国矿业大学(北京)博士研究生;
何满潮(1956-), 男, 河南灵宝人, 中国矿业大学教授, 博士生导师, 中国科学院院士;
陶志刚(1981-)，男，河北邯郸人，中国矿业大学(北京)教授，博士生导师。

摘要：为了解决深部开采造成的冲击地压、大变形和常规锚杆/索破断失效等问题，本文以某煤矿釆区为研究试验段，基于高地应力软岩大变形破坏机理，采用FLAC3D-PFC3D耦合建模方法首次开展NPR锚杆/索动力学数值模拟研究，建立PR和NPR锚杆/索两种支护方案的数值模型，对比分析动荷载下硐室围岩以及锚杆的受力、位移情况.结果表明：25 MPa冲击荷载下，25根PR支护锚杆/索中21根已失效，围岩大面积失稳，耦合墙出现严重变形，硐室呈现内凸弧形变形破坏.而相同条件下，NPR锚杆/索均未失效，硐室围岩稳定性保持良好.
关键词：冲击地压NPR锚杆/索围岩支护FLAC3D硐室稳定性
Numerical Simulation of Dynamic Response of Surrounding Rock Anchored by NPR Bolt/Cable
GUO Long-ji^1,2, HE Man-chao^1,2, QU Ding-jun³, TAO Zhi-gang^1,2
1. State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology(Beijing), Beijing 100083, China;
2. School of Mechanics & Civil Engineering, China University of Mining and Technology(Beijing), Beijing 100083, China;
3. Yuan'an County Liaoyuan Mining Co., Ltd., Yichang 444200, China
Corresponding author: TAO Zhi-gang, E-mail: taozhigang@cumtb.edu.cn.

Abstract: In this paper, a coal mine is used as the research region to study the problems caused by deep mining, such as rock burst, large deformation and failure of conventional bolt/cable. Based on the large deformation failure mechanism of high in-situ stress soft rock, the FLAC3D-PFC3D coupling modeling method was used to carry out the dynamic numerical simulation study of NPR (negative Poisson's ratio) bolt/cable for the first time. Numerical models of two support schemes of PR and NPR bolt/cable were established, and the stress and displacement of the surrounding rock of the chamber and the bolt/cable under dynamic loads were compared and analyzed. The results show that under the impact load of 25 MPa, 21 of the 25 PR support bolts/cables failed, the surrounding rock was damaged in a large area, the coupling wall was severely deformed, and the chamber presented inner convex arc-shaped deformation and failure. Under the same conditions, none of the NPR bolts/cables failed, and the stability of the surrounding rock of the chamber remained good.
Key words: rock burstNPR bolt/cablesurrounding rock supportFLAC3Dchamber stability
我国的锚杆围岩支护已取得很大进展，但我国煤矿的软岩地层分布十分广泛，在开挖前岩体内部就已经存在大量原生节理裂隙，当处于开挖应力状态时，围岩从原来的三向受力转变为双向受力状态，迅速发生错动、扩张，承载能力也迅速下降，导致围岩大面积失稳.研究开发有效控制高应力、高地压、软岩和开采扰动等大变形巷道的锚杆及支护技术成为关键^[1].众多****结合锚杆理论研究、室内相似模型试验，对锚杆本身的静态力学性能和锚杆-围岩耦合加固机理开展了大量的研究^[2-6].Kang等^[7]以煤粉水泥胶结料为模型材料，开展以2根锚杆支护应力场模型的实验，分析了围岩应力场与支护构件自身产生应力场相互作用的影响.Bobet等^[8]给出了DMFC, CMC, CFC锚杆巷道围岩支护与钢筋锚固力间相互作用的封闭解，得出的解强烈依赖于锚杆和变形岩石之间的相对刚度，结果表明在岩石弹性变形时放置钢筋，隧道收敛性不会大幅度减少，而在岩石经历塑性变形时放置锚杆其支护变形效果最好.Hu等^[9]建立围岩-支护流变变形模型，推演围岩与锚杆支护相互作用机理，理论证实锚杆支护可应用于软岩巷道.
许多国内外****利用SHPB冲击、落锤锚杆、爆破现场试验等，进行了动态荷载下锚杆-围岩的动力响应特性研究，但是大多支护吸能锚杆并没有考虑其与围岩结合的动载相互作用^[10-15].陈士海等^[16]通过建立震源荷载实验模型，研究了爆破荷载下围岩与支护锚杆动力响应特征，发现对于全锚锚杆既存在拉伸状态，又存在压缩状态，为地下硐室支护设计提供可行的指导.王光勇等^[10]利用有限元数值软件LS_DYNA 3D，模拟爆破集中荷载装药下锚杆与应力波的相互作用，对锚杆的轴向应力分布规律进行了研究，得出拱腰锚杆都是先受压后受拉.
采用传统的锚杆支护不能满足工程稳定性要求，He等^[17-18]研发了350 kN恒阻大变形锚索，基于能量吸收和大变形控制高理论，利用350 kN高恒阻大变形锚索的吸收冲击能量特性对巷道围岩进行加强支护以期达到防治冲击地压的目的.何满潮等^[19]通过多次落锤冲击试验，得出恒阻锚索可产生拉伸变形来吸收冲击能量，其具有保持恒定阻力的特殊抗冲击力学性能.吕谦^[20]首次对NPR(negative Poisson’s ratio)高恒阻锚索的变形量和恒定阻力进行了突破性实验，并将NPR锚索应用到现场实际工程中，发现其不仅能吸收岩体内多余的变形能, 而且对岩体的大变形起控制作用, 最大程度地保证岩体的稳定性和完整性.王炯等^[21]采用理论分析及物理模型试验的方法，通过对高恒阻大变形锚索支护巷道的围岩变形试验监测值与位移计算值对比，得出高恒阻锚索有效抑制围岩变形，解决深部软岩巷道大变形问题.
1 工程背景研究试验段位于张良堡背斜南缘，林盛堡向斜西翼中段，为一轴向N35°~40°，向西南倾伏，西翼宽缓，东翼窄陡的不对称宽缓倾伏背斜.背斜倾角3°~7°，西翼倾角5°~10°，东翼以东倾角25°~40°，地层走向受倾伏背斜控制，呈半环形，向东、东南、南、西南倾，形成宽缓的扇形分布.矿井区内小构造以断层为主，按其发生时期及构造形迹和分布区域分为背斜轴部断层组、背斜东翼断层组和背斜西翼断层组三组(图 1).断层中部最大落差达70 m，向两端落差急剧减少至消失与派生的断层一起，造成井田中部位构造复杂化，对煤层破坏较严重.地层受构造作用产生的大致与之褶皱轴平行的张性断裂和相伴生的西北向断裂，属印支期的产物.
图 1(Fig. 1)

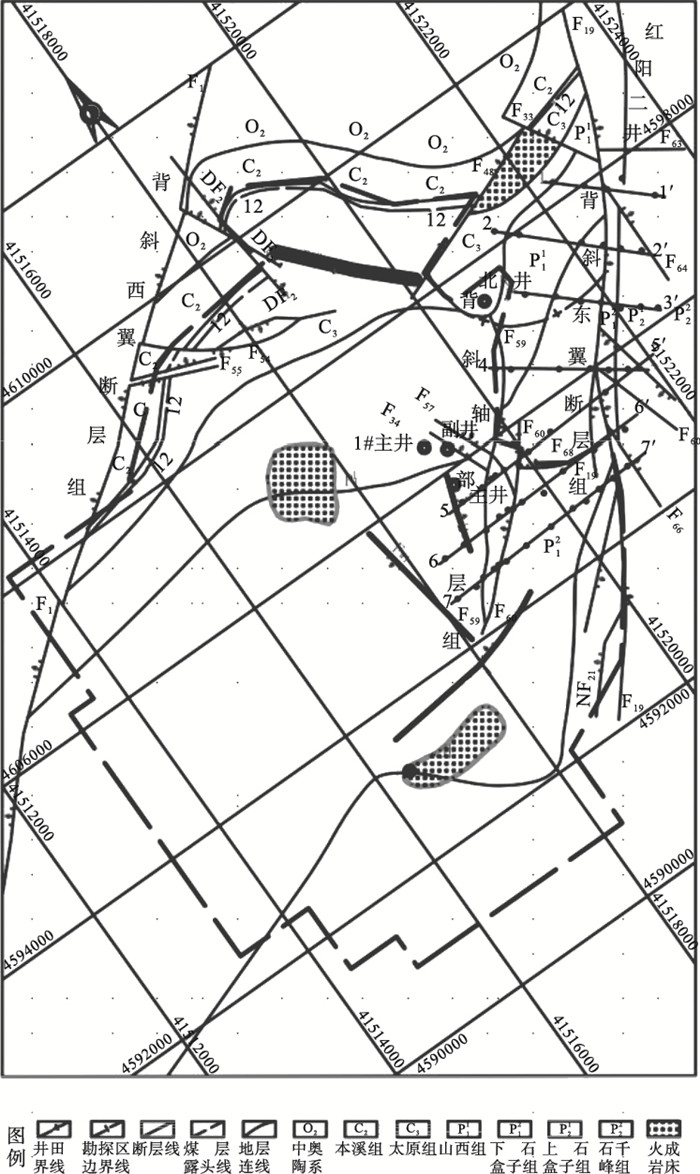图 1 研究试验段地质构造Fig.1 Geological structure for the test section region

全区被第四系冲积层覆盖，其下为上侏罗统地层不整合超覆于古生代地层之上，为隐伏煤田.本井田地层由第四系、第三系、侏罗系、二叠系、石炭系、奥陶系地层组成.本文数值模拟研究段地层系统由老至新如下：1) 上石炭统太原组由中部砂岩段和上部黑色泥岩夹薄层灰岩段组成，本组约85 m.2) 下二叠统山西组的岩性主要由灰色、灰黑色中细粒砂岩，粉砂岩与泥岩互层及煤层组成，并夹一层海相泥岩，本组厚约110 m(图 2).
图 2(Fig. 2)

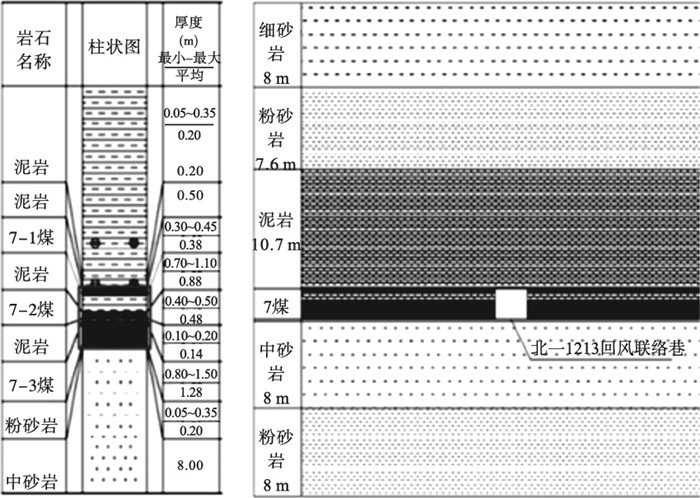图 2 试验段地层综合柱状图、岩层岩性及厚度Fig.2 Comprehensive stratigraphic histogram, lithology and thickness of the test section region

7#煤层北一釆区1213回风联络巷为数值模拟试验段如图 3所示，该段巷道埋深-769.2~-793.6 m, 总长度303 m, 地表标高+23.6 ~+24.1 m, 断面为4.2 m×2.5 m.巷道支护完整，无大断层和陷落柱.煤层坚固性系数(f)：煤，f=0.3；泥岩，f=1.8~2.9；粉砂岩, f=2.7~4.5；细砂岩，f=4~6；中砂岩，f=6.2.
图 3(Fig. 3)

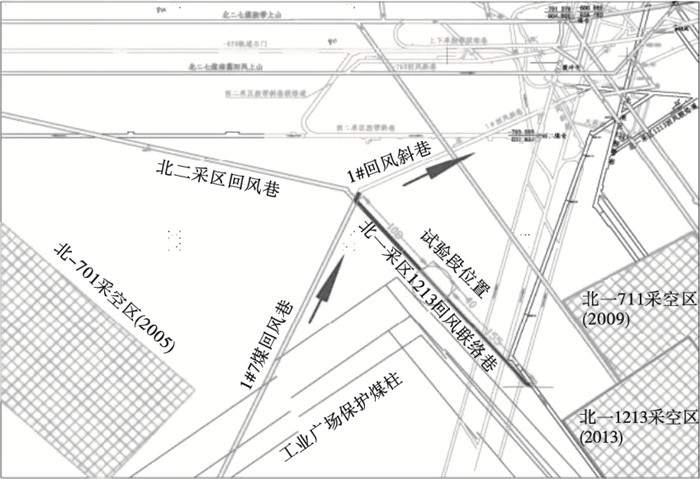图 3 1213回风联络巷平面位置示意图Fig.3 Schematic diagram of plane location of 1213 return air contact lane

2 软岩大变形软岩硐室的大变形破坏特征不仅受围岩的力学特性影响，而且受所处的地应力环境和工程因素等控制.我国许多煤矿在采深不大的情况下，坑道的变形破坏并不强烈，常规支护即可维护巷道硐室稳定.但采深加大后，某些煤矿坑道稳定性降低，变形破坏趋于强烈，常规支护锚杆/索难以维护稳定.
2.1 高应力软岩高应力软岩(high stressed soft rock，简称H型)，是指在较高应力水平(>25 MPa)条件下才发生显著大变形的中高强度的工程岩体，如表 1所示.这种软岩的强度一般高于25 MPa，其砂质成分较多，如泥质粉砂岩、泥质砂岩等.其大变形的机理是处于高应力水平时，岩石骨架中的基质(黏土矿物)发生滑移和扩容，导致发生缺陷或裂纹的扩容和滑移塑性变形，如表 2所示.
表 1(Table 1)

表 1 高应力软岩分级表Table 1 Classification of high stress soft rock 高应力软岩类型 应力水平/MPa 高应力软岩 25~50 超高应力软岩 50~75 极高应力软岩 >75

表 1 高应力软岩分级表 Table 1 Classification of high stress soft rock

表 2(Table 2)

表 2 软岩分类表Table 2 Classification of soft rock 软岩分类 泥质质量分数/% Rc/MPa 大变形特点 膨胀性软岩(称低强度软岩) >25 < 25 在工程力的作用下，沿片架状硅酸盐黏土矿物产生滑移，遇水显著膨胀等 高应力软岩 ≤25 ≥25 遇水发生少许膨胀，在高应力状态下，沿片架状黏土矿物发生滑移 节理化软岩 少含 低~中等 沿节理面等结构面产生滑移、扩容等塑性变形 复合型软岩 含 低~高 具有上述某种组合的复合型机理 注：Rc为岩体单轴抗压强度.

表 2 软岩分类表 Table 2 Classification of soft rock

2.2 软岩大变形破坏特征1) 持续时间长.软岩具有强流变性和低强度性，因此，软岩巷道硐室开挖以后围岩应力重分布.软岩巷道硐室变形破坏持续较长时间，往往长达1~2年.
2) 破坏位置不同.软岩具有强烈的各向异性，硐室所处的地应力强度因方向而异，因而变形破坏程度不同.变形破坏在方向上的差异往往导致支护结构受力不均，支护结构中产生巨大的弯矩，不利于支护结构的稳定.
3) 破坏范围大.软岩硐室中围岩强度与地应力比值很小，特别当支护不当或不及时，围岩破坏区的范围可达5倍硐室半径，甚至更大.软岩流变过程中，围岩强度降低.
3 数值模型概况试验段埋深近800 m，属高应力软岩.建立基于以PFC3D颗粒流与FLAC3D耦合墙为主体的防冲支护数值模型，嵌入NPR锚杆/索.模拟对比分析25 MPa冲击峰值压力下，PR/NPR锚杆/索支护围岩变形特征与硐室稳定性.
3.1 模型建立模型围岩地层条件如下：以砂岩为主，粉砂-中细粒结构，裂隙发育，属软岩-坚硬岩.岩层近水平状分布，岩石抗压强度60 MPa，围岩等级III级.
首先建立2D模型大小为48 m×45 m，硐室截面大小为7.0 m×7.8 m，模型以硐室中心线对称，硐室巷道截面为直墙半圆拱形式，如图 4所示.
图 4(Fig. 4)

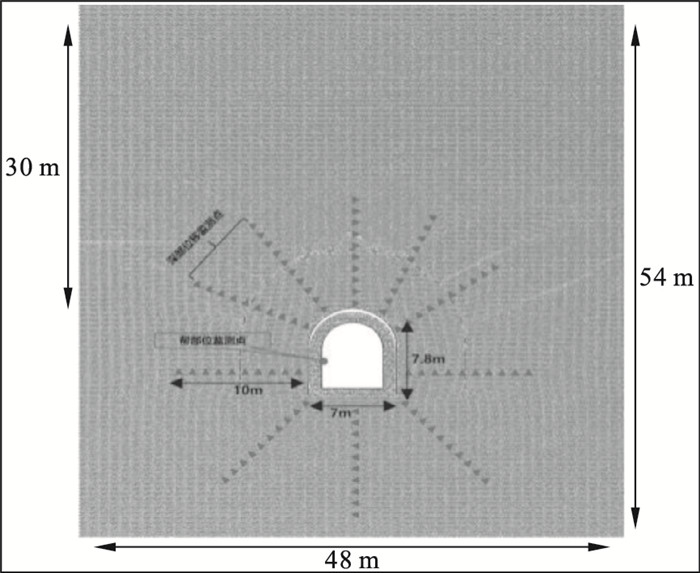图 4 硐室数值模型Fig.4 Numerical model of chamber

试验段模拟PR/NPR锚杆/索支护措施：采用恒定阻力值25 t，预紧力10 t，长度为6 m的NPR高恒阻大变形锚杆/索，在左右帮沿硐室截面对称布设25根，下部距离底板300 mm，帮部位锚杆/索间距离800 mm，拱顶锚索间距离850 mm，如表 3，图 5所示.
表 3(Table 3)

表 3 支护方案Table 3 Support scheme 方案 方案参数 锚杆/索参数(恒阻值，自由段伸长率) 锚固段长度/m 自由段长度/m 1 25 MPa+“PR锚索(6 m)+衬砌” 250 kN，1%~3% 3.0 3.0 2 25 MPa+“NPR锚索(6 m)+衬砌” 250 kN，20% 3.0 3.0

表 3 支护方案 Table 3 Support scheme

图 5(Fig. 5)

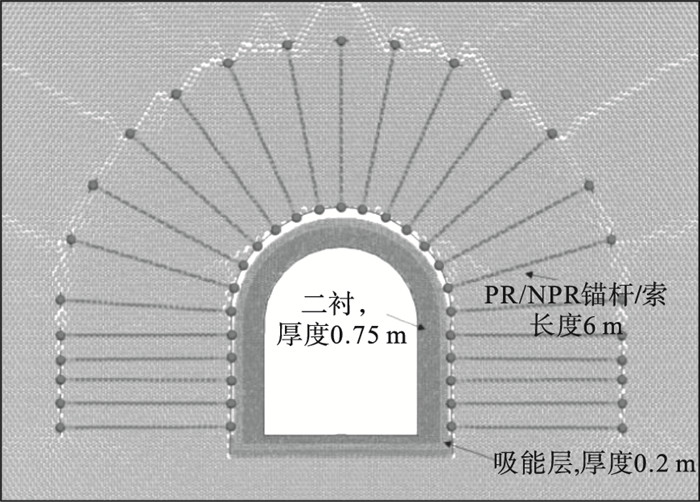图 5 数值支护模型Fig.5 Numerical support model

锚杆/索的类型为冲击荷载下的唯一变量，如图 5所示，锚杆/索临空端显示的圆点即为锚固节点(link节点)；其次，在锚杆/索群的深部锚固端设计垂直于锚杆/索的网片状弹性结构单元(shell)，长度约为20 cm，并将锚杆/索锚固端头与该网片中心节点进行刚性固定.最后，为每一根锚杆/索施加预应力，该施加过程中锚杆/索不断收缩，并牵引两端网状结构单元产生挤压移动，网状结构单元则可通过计算中的耦合墙单元(structure-wall)与围岩颗粒发生力学传导，将预应力施加给围岩.
3.2 参数反演结合Mohr-Coulomb^[22]强度理论公式，基于PFC3D离散元软件，在单轴、三轴试验结果已知情况下，对单轴剪切破坏形式主导下的黏聚力、内摩擦角以及岩石单轴抗压强度间建立关系式.调整细观参数使模型模拟的宏观现象与物理试验宏观现象相匹配.通过正反演分析法，先假定待反演的岩体参数，通过正演分析得到岩体结构的应力等，然后将其与实际的抗压强度曲线相比较，逐步逼近实测值，从而确定待反演的岩体参数，如表 4、表 5所示.
表 4(Table 4)

表 4 数值模拟细观参数Table 4 Mesoscopic parameters of numerical simulation 类型 宏观基础参数 细观反演参数 泊松比 围岩 67.4 0.1 32.7 0.2 3.5E+6 50E+6 1.15 11E+9 初衬 40 0.05 23.5 0.2 2.2E+6 50E+6 1.12 8.0E+9

表 4 数值模拟细观参数 Table 4 Mesoscopic parameters of numerical simulation

表 5(Table 5)

表 5 NPR锚杆/索力学参数Table 5 Mechanical parameters of NPR bolt/cable 弹性模量/GPa 泊松比 抗拉强度/MPa 恒阻力/kN 206 0.28 730 250

表 5 NPR锚杆/索力学参数 Table 5 Mechanical parameters of NPR bolt/cable

3.3 边界条件在初始地应力场的生成过程中，模型不设置速度边界条件，依据地应力场的分布情况在模型最外层单元施加应力边界条件，应力转化成节点力作用在模型最外层单元的节点上，向模型内部传递，并保持恒定.数值模型没有位移边界条件，平衡过程中可能会产生较大的位移，在模型达到平衡后将所有节点速度清零，来模拟围岩体在初始地应力场作用下的静力平衡状态.
数值模型具体的边界位移约束表达式如下：
1) 施加水平位移约束在模型的左右及前后，初始位移设置为零；
2) 设置模型顶部及底部边界水平、垂直初始位移均为零.
由应力条件确定该模型所处的应力条件，X方向上取水平位移约束条件，即
Y方向上取水平位移约束条件，即
顶部及底部边界设置垂直位移约束条件，即
3.4 荷载施加方式施加初始地应力，具体采用摩尔-库仑模型分阶段的弹塑性求解法，首先调整施加模型围岩颗粒较大的内聚力和抗拉强度，挤压产生初始应力场，进行弹性求解，直至平衡；再将内聚力、抗拉强度重置为初始设定值，进行开挖硐室，塑性阶段的求解，直至模型体系力平衡状态.在考虑地质构造应力的情况下，施加在模型上的载荷即为构造应力，根据现场实测数据，利用应力伺服控制程序进行初始地应力生成^[23].
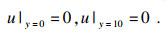冲击荷载加载，根据现场实测的应力波-时间函数曲线，确定其应力峰值.围岩地应力场水平应力为7 MPa，垂向应力为14 MPa，地层单轴抗压强度为25 MPa.通常认为应力波是以柱状和球形向四周传播，但对于大埋深地下工程，当应力波传播距离足够远时，可以近似看作是平面波，即本模拟中25 MPa应力波以平面波形式传递.
4 数值结果分析随着应力波的传递，能量逐渐传递扩散，产生位移变形.在冲击载荷施加初期，其截取时间相对较短，而在后期围岩变形速度放缓，其云图截取时间相对较长，通过反复校核云图截取效果，选定t=7，40，150 ms共3个时间节点.
4.1 硐室围岩爆破颗粒速度扩散云图冲击载荷经由地表加载后，应力波由地表处向深部及四周传递.如图 6所示PR围岩颗粒速度扩散云图，t=7 ms岩体颗粒峰值速度5.89 m/s，应力波传递首先引起硐室顶部发生震动响应，一倍硐径范围内岩体颗粒以相互碰撞等方式传递和耗散传递峰值应力；t=40 ms时峰值速度为4.7 m/s，应力经过扰动，锚杆/索衬砌受力变形；t=150 ms硐室两帮衬砌已经发生变形，拱顶下沉，判定硐室因锚杆/索衬砌等支护结构变形发生失稳破坏.
图 6(Fig. 6)

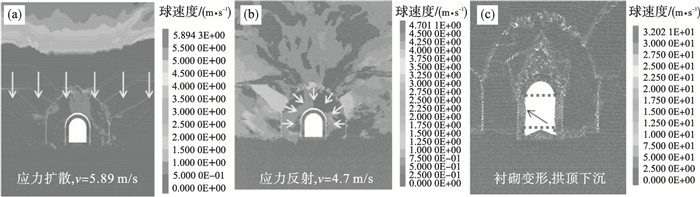图 6 PR围岩颗粒速度扩散云图Fig.6 Particle velocity diffusion cloud image of PR surrounding rock (a)—t=7 ms颗粒传递; (b)—t=40 ms颗粒反射; (c)—t=150 ms颗粒破坏.

图 7为NPR围岩颗粒速度扩散云图，t=7 ms应力波药包位置形成爆破空腔，速度最大为5.89 m/s，由边界反射再次传递至硐室围岩，引起速度场应力迅速向周边扩展.t=40 ms顶部和两帮率先受到爆破速度场的影响，围岩颗粒经过传递速度峰值为4.25 m/s，围岩体峰值能量被岩体颗粒间阻尼、颗粒间扩散、锚杆/索衬砌吸收三种方式耗散至远处，使得此时围岩体速度下降.t=150 ms时，应力波由边界反射再次传递至硐室围岩处，引起围岩体扰动, 锚杆/索衬砌未发生变形, 围岩应力基本完成重分布达到稳定，硐室NPR衬砌支护结构稳定.
图 7(Fig. 7)

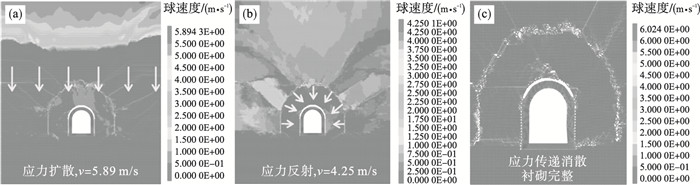图 7 NPR围岩颗粒速度扩散云图Fig.7 Particle velocity diffusion cloud image of NPR surrounding rock (a)—t=7 ms颗粒传递；(b)—t=40 ms颗粒反射；(c)—t=150 ms颗粒稳定.

4.2 硐室围岩爆破锚杆/索瞬时轴力云图圆点即代表力传递的节点，圆点消失则表示锚杆/索失效.图 8为PR锚杆/索瞬时轴力云图，当t=7 ms时轴力峰值为240 kN，随爆破引起应力波的传播，硐室帮部与顶板处的锚杆/索受力开始逐渐增加，shell单元钢片开始出现小幅度变形；当t=40 ms时，硐室顶部锚杆/索已经全部失效，右右帮部位置锚杆/索逐步出现破断效应；当t=150 ms时，左帮3根PR锚杆/索及右帮1根尚未失效，即21根锚杆/索已经失效，右帮大面积失效，导致了耦合墙严重变形，硐室呈现内凸的弧形变形破坏.
图 8(Fig. 8)

图 8 PR锚杆/索瞬时轴力云图Fig.8 Instantaneous axial force cloud diagram of surrounding rock with PR bolt/cable (a)—t=7 ms连接点消失；(b)—t=40 ms锚杆/索失效；(c)—t=150 ms锚杆/索破断硐室变形.

图 9为NPR锚杆/索瞬时轴力云图，当t=7 ms时，shell单元钢片开始出现小幅度变形；当t=40 ms时轴力达到最大值250 kN, 但仅小部分锚杆/索轴力出现骤降现象；当t=150 ms时，仅有5根锚杆/索出现范围内变形，锚杆/索全都未出现失效.
图 9(Fig. 9)

图 9 NPR锚杆/索瞬时轴力云图Fig.9 Instantaneous axial force cloud diagram of surrounding rock with NPR bolt/cable (a)—t=7 ms轴力消耗能量；(b)—t=40 ms锚杆/索受力恒定；(c)—t=150 ms硐室稳定.

4.3 硐室围岩爆破锚杆/索瞬时位移云图图 10为PR锚杆/索瞬时位移云图，当t=7 ms时，峰值位移量0.153 m，锚杆/索变形开始增加；当t=40 ms时，shell单元钢片连接开始大范围位移变形；当t=150 ms时，硐室左右两帮因锚杆/索拉断位移近100 mm, 破断大面积扭曲破坏.
图 10(Fig. 10)

图 10 PR锚杆/索瞬时位移云图Fig.10 Instantaneous displacement cloud diagram with PR bolt/cable (a)—t=7 ms锚杆/索位移滑动；(b)—t=40 ms锚杆/索位移大变形；(c)—t=150 ms锚杆/索扭曲位移.

图 11为NPR锚杆/索瞬时位移云图，当t=7 ms时，shell单元小幅度变形, 峰值位移为0.035 3 m；t=40 ms时, 左帮最大伸长量达到175 mm；当t=150 ms时，仅底板锚杆/索出现小范围内变形.
图 11(Fig. 11)

图 11 NPR锚杆/索瞬时位移云图Fig.11 Instantaneous displacement cloud diagram with NPR bolt/cable (a) —t=7 ms锚杆/索变形；(b)—t=40 ms钢片shell位移变形；(c)—t=150 ms锚杆/索位移变形.

4.4 冲击压力作用下PR/NPR锚杆/索轴力对比分析冲击压作用下，巷道顶板PR锚杆/索轴力出现波动如图 12，图 13所示.t=0.18 s，顶板锚杆/索轴力突降为0 kN，此时处于震中阶段，顶部、帮部PR锚杆/索的恒阻性均在震中阶段失效.同等条件下，NPR锚杆/索始终保持高恒阻力，帮部20# 锚杆/索出现轴力为0 kN是由于此处巷道衬砌受压，导致预紧力损失.综上，PR锚杆/索支护下巷道难以整体稳定性，但NPR锚杆/索保持高恒阻力，保证巷道整体稳定性.
图 12(Fig. 12)

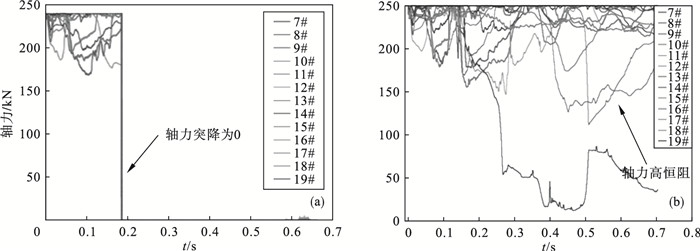图 12 顶板PR/NPR锚杆/索轴力Fig.12 Roof axial force with PR/NPR bolt /cable (a)—PR锚杆/索轴力突降；(b)—NPR锚杆/索高恒阻力.

图 13(Fig. 13)

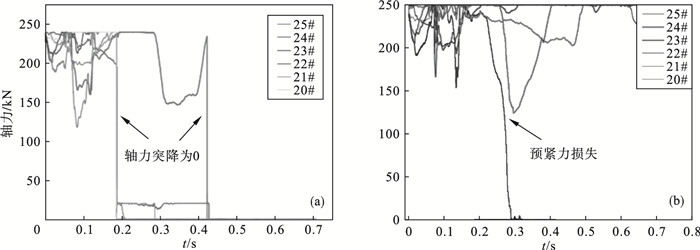图 13 帮部PR/NPR锚杆/索轴力Fig.13 Side axial force with PR/NPR bolt/ cable (a)—PR锚杆/索轴力突降；(b)—NPR锚杆/索高恒阻力.

5 结论1) FLAC3D与PFC3D联合建立模拟区域围岩体、爆破点以及支护结构的耦合模拟计算新思路和新方法，实现高冲击速率条件下的地下硐室NPR锚杆/索防冲加固模拟.
2) 基于模拟现场爆破位置及布设方式，25 MPa峰值压力模拟结果显示：冲击荷载作用下，PR锚杆/索支护巷道的右帮破坏严重，冲击前共25根锚杆/索正常支护，冲击后有21根锚杆/索失效，NPR锚杆/索支护硐室未出现NPR锚杆/索破断情况，且围岩体趋于稳定，帮部得到有效支护，防冲效果显著.
3) 通过此次数值模拟对比试验得出，在相同能量冲击试验下，普通锚杆/索产生了冲击破坏；高恒阻大变形NPR锚杆/索在冲击力作用下可吸收爆炸产生的冲击能量，同时保持恒定的阻力.表明高恒阻大变形锚杆/索比普通锚杆/索具有更好的抗冲击性能，防冲效果良好.
参考文献

[1]	漆泰岳. 锚杆与围岩相互作用的数值模拟[M]. 北京: 中国矿业大学出版社, 2002: 1-120. (Qi Tai-yue. Numerical simulation of interaction between rock bolt and surrounding rock[M]. Beijing: China University of Mining and Technology Press, 2002: 1-120.)
[2]	Kang H, Wu Y, Gao F, et al. Mechanical performances and stress states of rock bolts under varying loading conditions[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2016, 52: 138-146.
[3]	Freeman T J. The behavior of fully bonded rock bolts in the Kielder experimental tunnel[J]. Tunnels & Tunnelling, 1978, 10(5): 37-40.
[4]	Nanda B K. Study of the effect of bolt diameter and washer on damping in layered and jointed structures[J]. Journal of Sound & Vibration, 2006, 290(3/4/5): 1290-1314.
[5]	Wu Y, Gao F, Chen J, et al. Experimental study on the performance of rock bolts in coal burst-prone mines[J]. Rock Mechanics and Rock Engineering, 2019, 52: 3959-3970. DOI:10.1007/s00603-019-01794-9
[6]	Kang H, Yang J, Gao F, et al. Experimental study on the mechanical behavior of rock bolts subjected to complex static and dynamic loads[J]. Rock Mechanics and Rock Engineering, 2020, 53: 4993-5004. DOI:10.1007/s00603-020-02205-0
[7]	Kang H P, Li J Z, Yang J H, et al. Investigation on the influence of abutment pressure on the stability of rock bolt reinforced roof strata through physical and numerical modeling[J]. Rock Mechanics and Rock Engineering, 2016, 50(2): 1-15.
[8]	Bobet A, Einstein H H. Tunnel reinforcement with rockbolts[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2011, 26(1): 100-123.
[9]	Hu T, Hou G Y, Li Z H, et al. Study on the parameters of roadside support after the cantilever beam of the basic roof with height of fracture zone cut by deep-hole blasting[J]. IOP Conference Series: Earth and Environmental Science, 2019, 283(1): 12038-12048. DOI:10.1088/1755-1315/283/1/012038
[10]	王光勇, 郭晓燕, 王超, 等. 在拱腰爆炸荷载作用下锚杆动态响应数值分析[J]. 爆破, 2015, 32(2): 33-38. (Wang Guang-yong, Guo Xiaoy-an, Wang Chao, et al. Numerical analysis of dynamic response of anchor bolt under blast load of arch waist[J]. Blasting, 2015, 32(2): 33-38.)
[11]	Ming Z Q, Gu J C, Zhang X Y, et al. Study of anti-explosion effects of tunnels with different forms of bolt bolster plates[J]. Rock and Soil Mechanics, 2012, 33(10): 2991-2995.
[12]	Li C C, Doucet C. Performance of D-bolts under dynamic loading[J]. Rock Mechanics & Rock Engineering, 2012, 45(2): 193-204.
[13]	Yang Z Y, Gu J C, Yang B S, et al. Numerical analysis of reinforcement effects and response to dynamic loads characteristics of rock bolts[J]. Rock and Soil Mechanics, 2009, 30(9): 2805-2809.
[14]	Meikle I, Tadolini S C, Sainsbury B, et al. Laboratory and field testing of bolting systems subjected to highly corrosive environments[J]. International Journal of Mining Science and Technology, 2017, 27(1): 101-106. DOI:10.1016/j.ijmst.2016.11.017
[15]	Xu J M, Gu J C, Chen A M, et al. Study of anti-explosion ability of reinforced tunnels with different anchor lengths and spacings[J]. Rock and Soil Mechanics, 2012, 33(11): 3489-3496.
[16]	陈士海, 宫嘉辰, 胡帅伟. 爆破荷载下围岩及支护锚杆动力响应特征模型试验研究[J]. 岩土力学, 2020, 41(12): 3910-3918. (Chen Shi-hai, Gong Jia-chen, Hu Shuai-wei. Experimental study on dynamic response characteristics of surrounding rock and supporting bolt under blasting load[J]. Rock and Soil Mechanics, 2020, 41(12): 3910-3918.)
[17]	He M C, Gong W L, Wang J, et al. Development of a novel energy-absorbing bolt with extraordinarily large elongation and constant resistance[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 67: 29-42.
[18]	He M C, Jia X N, Coli M, et al. Experimental study of rock burst in underground quarrying of Carrara marble[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 52(1): 1-8.
[19]	何满潮, 王炯, 孙晓明, 等. 负泊松比效应锚索的力学特性及其在冲击地压防治中的应用研究[J]. 煤炭学报, 2014, 39(2): 214-221. (He Man-chao, Wang Jiong, Sun Xiao-ming, et al. Mechanics characteristics and applications of prevention and control rock bursts of the negative Poisson's ratio effect anchor[J]. Journal of China Coal Society, 2014, 39(2): 214-221.)
[20]	吕谦. 静力拉伸条件下NPR锚索力学特性实验研究[D]. 北京: 中国矿业大学(北京), 2018. (Lyu Qian. Experimental study on mechanical properties of NPR anchor cable under static tensile condition[D]. Beijing: China University of Mining and Technology(Beijing), 2018. )
[21]	王炯, 张正俊, 朱天赐, 等. 恒阻大变形锚索支护巷道变形机制模型试验研究[J]. 岩石力学与工程学报, 2020, 39(5): 927-937. (Wang Jiong, Zhang Zheng-jun, Zhu Tian-ci, et al. Model test study on deformation mechanisms of roadways supported by constant resistance and large deformation anchor cables[J]. Journal of Rock Mechanics and Engineering, 2020, 39(5): 927-937.)
[22]	Carranza T C, Fairhurst C. The elastoplastic response of underground excavations in rock masses that obey the Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(6): 777-809. DOI:10.1016/S0148-9062(99)00047-9
[23]	Meng Z G, Hou Y L, Guo L J, et al. Discrete element simulation analysis of the bending and toppling failure mechanisms of high rock slopes[J]. Geofluids, 2021, 2021(84): 1-12.