
 , 许继谦2, 巩云鹏1
, 许继谦2, 巩云鹏1 1. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819;
2. 东北大学 机器人科学与工程学院,辽宁 沈阳 110169
收稿日期:2021-08-02
基金项目:辽宁省中央引导地方科技发展专项项目(2021JH6/10500132)。
作者简介:高跃(1991-),男,辽宁朝阳人,东北大学博士研究生;
房立金(1965-),男,辽宁沈阳人,东北大学教授,博士生导师。
摘要:基于双电机伺服驱动的关节设计制造了一种7-DOF协作机械臂,建立了该型机械臂末端执行器的几何误差模型,并且基于原始参数误差独立作用原理对参数误差进行分析与合成.基于数理统计大数定律,利用蒙特卡洛的方法对几何位置误差影响因素的灵敏度进行了数值仿真计算分析,找出对机械臂几何位置误差影响程度相对较大的参数误差.通过对机械臂末端执行器的几何位置误差计算分析,可知误差在工作空间内服从瑞利分布.经过实验测量,机械臂的重复定位误差不超过0.059 1 mm,并且绝对定位误差服从瑞利分布是显著性的,证明了双电机伺服驱动关节具有回差小、传动精度高的特点和误差分析的正确性,为机械臂的精度设计与应用提供理论依据.
关键词:7-DOF机械臂结构设计误差模型敏感性分析误差分析
Structural Design of a 7-DOF Manipulator and Its Geometric Position Error Analysis
GAO Yue1, FANG Li-jin2

 , XU Ji-qian2, GONG Yun-peng1
, XU Ji-qian2, GONG Yun-peng1 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. School of Robot Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: FANG Li-jin, E-mail: ljfang@mail.neu.edu.cn.
Abstract: A 7-DOF cooperative manipulator was designed and manufactured based on the joint driven by dual motor servo. The geometric error model of the end-effector of the manipulator was established, and the parameter errors were analyzed and synthesized based on the principle of independent action of the original parameter errors. Based on the law of large numbers of mathematical statistics and Monte Carlo method, the sensitivity of influencing factors of the geometric position errors was analyzed by numerical simulation, and the parameter errors which have relatively greater influence on the geometric position errors of the manipulator were found. Through the calculation and analysis of the geometric position errors of the end-effector of the manipulator, it was found that the errors obey the Rayleigh distribution in the workspace of the manipulator. The experimental measurement showed that the repeated positioning error of the manipulator is less than 0.059 1 mm, and the absolute positioning error obeys Rayleigh distribution significantly. It proved that the double motor servo-driven joint has the characteristics of small return errors and high transmission accuracy, and the error analysis is correct, which provides a theoretical basis for the precision design and application of the manipulator.
Key words: 7-DOF manipulatorstructural designerror modelsensitivity analysiserror analysis
传统的工业机械臂通常最多具有6自由度,6个自由度是具有完成空间定位能力的最小自由度数,因其机构属性,当其末端位姿轨迹规定之后,不可避免地存在一些问题,比如无法避障、运动灵活性差、不能克服关节运动极限、动力学性能偏弱等天然弱点.而增加自由度便可改善机械臂的运动学和动力学特性,7自由度是机械臂对人类手臂最真实的还原,它能够在不改变末端位姿状态下实现有效避障.另外,冗余的自由度还具有容错性,这对于很多特殊环境的应用场合有着极其重要的实用价值[1].
随着工业机械臂的应用拓展与深入,在钻铆、铣削、打磨、铺丝、装配等高精度作业领域中对机器人提出了更高精度技术要求.目前对于提高机械臂定位精度方法的研究主要是通过标定技术对参数修正补偿,对于如何从设计阶段即从误差源头消除误差来提高机器人精度的研究还比较少.文献[2-3]通过正运动学建立了机械臂几何位置误差数学模型,Shiakolas等[4]通过对机械臂的定位精度分析得出机器人构件结构参数的几何误差是引起机器人绝对定位误差的主要影响因素,Chen等[5]对五轴机床的误差进行了敏感性分析,文献[6-9]对并联机器人进行了几何误差建模及灵敏度分析,找出了对并联机器人精度影响的主要因素.本文在建立7-DOF机械臂几何位置误差模型的基础上,基于原始误差独立作用原理对参数误差进行合成.为了找到各参数对机械臂几何位置误差的影响程度,进行了敏感性分析.通过对机械臂末端执行器的几何位置误差分析,得到了其在工作空间内服从瑞利分布的结论,为机械臂的精度设计与应用提供理论依据.
1 机械臂的结构设计由文献[10-12]可知,双电机伺服驱动的机械臂关节具有回差小、传动精度高、承载能力强等优点.本文设计制造了一种闭环伺服控制的双电机驱动关节,驱动原理及样机如图 1所示.利用双电机伺服驱动渐开线齿轮机构替代高精度旋转矢量(rotate vector, RV)减速器或者谐波减速器来实现关节传动系统的高精度传动,具有启动转矩小、附加转矩小、寿命长、噪音小、成本低等优点.
图 1(Fig. 1)
 | 图 1 双电机伺服驱动的原理图及样机Fig.1 Schematic diagram and prototype of the dual motor servo-driven (a)—原理图;(b)—样机. |
双电机伺服驱动控制具有消除间隙和共同负载驱动两种模式.双电机伺服驱动关节消除间隙的实质是传动系统的阻抗控制,即在输出轴上预加定值反向力矩,使轮系保持单面啮合,通过将两台驱动电机按照对称结构带动两个主动轮共同驱动从动轮,在伺服系统起动或换向过程中,对两台驱动电机的输出转矩进行联动控制,使得至少有一个驱动轮与从动轮相啮合,保证系统无间隙传动.双电机驱动伺服系统通过编码器实现闭环控制确保输出轴的准确度.
基于双电机伺服驱动关节,设计制造了一款结构紧凑、质量轻的7自由度机械臂样机,其系统坐标图及其样机如图 2所示.由于双电机驱动的关节质量以及结构特点,该机械臂的腰关节、肩关节、肘关节拟采用双电机伺服驱动关节,其他关节拟采用质量轻、结构紧凑等带有谐波减速器的关节,以提高灵活性.
图 2(Fig. 2)
 | 图 2 7-DOF机械臂的系统坐标图及其样机Fig.2 System coordinate diagram of the 7-DOF manipulator and the prototype (a)—系统坐标图;(b)—样机. |
机械臂的每个连杆可以用连杆长度ai、连杆转角αi、连杆偏移量di和关节角度θi来描述,称为D-H参数[13].由文献[2]所述,ai为沿着Xi轴,从Zi-1移动到Zi的距离;αi为绕着Xi轴,从Zi-1旋转到Zi的角度;di为沿着Zi-1轴,从Xi-1移动到Xi的距离;θi为绕着Zi-1轴,从Xi-1旋转到Xi的角度.对于转动关节,θi为关节变量,其他三个连杆参数是固定不变的,本文所述机械臂的D-H参数见表 1.
表 1(Table 1)
| 表 1 机械臂的D-H参数 Table 1 D-H parameters of the manipulator |
2 误差模型及误差合成2.1 几何位置误差的数学模型如果定义了连杆坐标系和相应的连杆参数,则每个关节的齐次变换矩阵可以描述为
 | (1) |
 |
 | (2) |
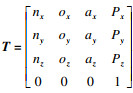
向量n, o, a相互重直,分别表示机械臂末端坐标系相对基坐标系的法线、指向和接近向量;向量P表示末端坐标系原点相对于基坐标系的位置.
由于机械臂零件的加工制造等原因,D-H参数的实际值与名义值都会有一定偏差,根据机械臂的正运动学方程,机械臂几何位置误差可以表示为
 | (3) |
根据原始误差独立作用原理,即原始误差叠加原理,机械臂几何位置误差可以表示为几何位置表达式对各原始误差的偏导数和,忽略高阶误差的影响,式(3)可以表示为
 | (4) |
 | (5) |
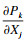
 | (6) |
 | (7) |
 | (8) |
 | (9) |
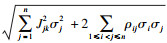
机械臂末端执行器几何位置误差的极限值:
 | (10) |
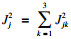
当参数误差相互独立或弱相关时,各参数几何误差引起机械臂几何误差的标准偏差为
 | (11) |
 | (12) |
由于参数误差ΔX中所有元素在统计意义下独立且均值为零,显然机械臂几何位置误差的方向分量ΔPk的期望值为E(ΔPk)=0,k=x, y, z.则ΔPk的方差为
 | (13) |
 | (14) |
 | (15) |
 | (16) |
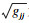
 | (17) |
 | (18) |
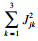
 | (19) |
 | (20) |
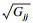
 | (21) |
图 3(Fig. 3)
 | 图 3 不同方向灵敏度系数Fig.3 Sensitivity coefficients in different directions (a)—x方向;(b)—y方向;(c)—z方向. |
由几何位置误差各方向分量的灵敏度评价指标的计算结果可知,各参数误差对机械臂末端执行器x,y方向的几何位置误差的影响程度类似,4个关节的连杆偏角误差和关节角误差对末端执行器位置误差影响程度相对较大,Δd1,Δα7和Δθ7对x,y方向几何位置误差没有影响;Δa1,Δd2,Δα7和Δθ1对z方向几何位置误差没有影响,Δd1对z方向几何位置误差的影响按同比传递到末端.
根据图 4几何位置误差灵敏度评价指标的计算结果,可知关节连杆偏角误差Δα7和关节角误差Δθ7对机械臂腕关节的几何位置误差没有影响;每个关节的连杆长度和偏距误差对机械臂几何位置误差大小的影响程度相对较小,按原始误差的大小同比传到末端;第i个关节的连杆偏角误差和关节角误差对几何位置误差影响程度大小几乎相同,影响程度由大到小依次为Δα2和Δθ2,Δα1和Δθ1,Δα4和Δθ4,Δα3和Δθ3,Δα5和Δθ5,Δα6和Δθ6,其中前4个关节的连杆偏角误差和关节角误差对末端执行器位置误差影响程度相对较大,在参数公差分配中应该严格控制其公差范围.
图 4(Fig. 4)
 | 图 4 几何位置误差的灵敏度系数Fig.4 Sensitivity coefficients of geometric position errors |
由各个参数误差敏感性系数的最大、最小值以及标准偏差可知,机械臂在不同位姿状态下,每个参数误差对几何位置误差的影响程度是不同的.其中Δα2和Δθ2,Δα1和Δθ1,Δα4和Δθ4,Δα3和Δθ3的敏感性系数变化范围相对较大,并且最大值远远高于其他参数的最大值.在参数的公差分配时,应该格外考虑在它们的敏感性系数取最大值时所对应的机械臂位姿状态下的几何位置误差不超过精度的设计要求.
4 误差分析在机械臂的设计阶段,需要根据机械臂的精度设计要求,合理地分配各参数的公差,确保机械臂末端执行器在工作空间中的最大几何位置误差满足设计要求.为此,找到参数误差与几何位置误差最佳映射关系的位姿以及确定几何位置误差的分布情况,为机械臂精度设计提供重要的参考.
4.1 几何位置误差的分布假设7-DOF机械臂的D-H参数的误差取值如表 2所示,在关节空间内随机选取足够多的关节角服从均匀分布,利用蒙特卡洛数值计算的方法计算机械臂末端执行器的几何位置误差.
表 2(Table 2)
| 表 2 D-H参数的几何误差 Table 2 Geometric errors for D-H parameters |
随机选取1000个位姿分别计算机械臂末端执行器的几何位置误差,几何位置误差及其各方向分量的平均值、最大值、均方差(RMSE)见表 3,误差的频率分布如图 5所示.由计算结果可知,在机械臂工作空间内,末端执行器的几何位置误差随着位姿状态不同而不同,并且几何位置误差在多个位姿状态下接近或者达到最大值.对机械臂末端执行器的综合几何位置误差进行正态分布和瑞利分布函数拟合,由拟合曲线可知瑞利分布更为显著,几何位置误差在x,y,z各方向的分量服从正态分布.
表 3(Table 3)
| 表 3 机械臂末端执行器几何位置误差分布的数字特征值 Table 3 Digital characteristics of the geometric position error distribution of the end-effector of the manipulator |
图 5(Fig. 5)
 | 图 5 末端执行器几何位置误差的频率分布Fig.5 Geometric position error distribution of the end-effector (a)—x方向误差;(b)—y方向误差;(c)—z方向误差;(d)—综合误差. |
4.2 实验验证本文用LTD 500激光跟踪测量系统对机械臂末端执行器的位置误差进行测量,测量系统与机械臂的相对位姿如图 6所示.
图 6(Fig. 6)
 | 图 6 机械臂与LTD 500测量系统的相对位姿Fig.6 Relative posture of the manipulator and the LTD 500 measurement system |
4.2.1 重复定位精度GB/T 12642—2013工业机器人性能规范及其实验方法中规定,机械臂重复定位精度为
 | (22) |
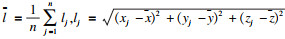
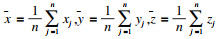
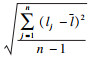
在机械臂的灵活工作空间内选取一个平面内的5个点测量其位置坐标,重复测量30次.根据式(22)求解各点的重复定位精度,见表 4.该机械臂在测量点P3的重复定位误差最大,不超过0.059 1 mm,证明了双电机伺服驱动关节具有回差小、传动精度高的特点.
表 4(Table 4)
| 表 4 不同测量点的机械臂重复定位精度 Table 4 Repetitive positioning accuracy of the manipulatorat different measuring points ? | ||||||||||||||||||||||||||||||||||||||||||||||||
4.2.2 绝对定位精度在机械臂工作空间内随机测量了165个位姿状态下的末端执行器的位置误差,误差的平均值|ΔP|mean=5.805 5 mm,最大值|ΔP|max=17.180 6 mm,均方差|ΔP|RMSE=3.603 0 mm,其频率分布如图 7所示.对实验测量的机械臂末端误差进行正态分布和瑞利分布拟合,由拟合曲线可知机械臂末端执行器的位置误差服从瑞利分布更为显著,与仿真计算所得的结果相符,验证了机械臂几何位置误差模型以及参数误差分布假设的准确性.
图 7(Fig. 7)
 | 图 7 末端执行器几何位置误差的频率分布Fig.7 Geometric position error distribution of the end-effector |
5 结论1) 本文基于双电机伺服驱动关节设计制造了一款7-DOF机械臂.通过对该型机械臂参数误差的敏感性分析,可知前4个连杆偏角误差和关节转角误差对机械臂末端执行器的几何位置误差影响较大,在参数公差分配中应该严格控制其公差范围.
2) 利用蒙特卡洛的方法对机械臂末端执行器的几何位置误差计算分析,通过拟合曲线分析可知其在工作空间内服从瑞利分布.
3) 经过实验测量,机械臂的重复定位误差不超过0.059 1 mm,并且绝对定位误差服从瑞利分布是显著性的.证明了双电机伺服驱动关节具有回差小、传动精度高的特点和误差分析的正确性,为机械臂的精度设计提供理论依据.
4) 在机械臂的精度设计中如何分配参数的公差以及通过标定技术提高机械臂的定位精度是在未来的工作中需要进一步探讨的问题.
参考文献
| [1] | 卢月品, 张含阳. 破局七轴工业机器人发展[J]. 机器人产业, 2016(2): 35-41. (Lu Yue-pin, Zhang Han-yang. Breaking the seven axis industrial robot development[J]. Robotics Industry, 2016(2): 35-41.) |
| [2] | Wu C H. A kinematic CAD tool for the design and control of a robot manipulator[J]. The International Journal of Robotics Research, 1984, 3(1): 58-67. DOI:10.1177/027836498400300105 |
| [3] | Veitschegger W K, Wu C H. Robot accuracy analysis based on kinematics[J]. IEEE Journal on Robotics and Automation, 1986, 2(3): 171-179. DOI:10.1109/JRA.1986.1087054 |
| [4] | Shiakolas P S, Conrad K L, Yih T C. On the accuracy, repeatability, and degree of influence of kinematics parameters for industrial robots[J]. International Journal of Modelling & Simulation, 2002, 22(4): 245-254. |
| [5] | Chen G, Liang Y, Sun Y, et al. Volumetric error modeling and sensitivity analysis for designing a five-axis ultra-precision machine tool[J]. International Journal of Advanced Manufacturing Technology, 2013, 68(9/10/11/12): 2525-2534. |
| [6] | 李思维, 黄田. 一种含平行四边形支链的3自由度并联机构姿态精度综合与装配工艺设计[J]. 机械工程学报, 2003, 39(7): 38-42. (Li Si-wei, Huang Tian. Attitude precision synthesis and assembly process design of a 3-DOF parallel mechanism with parallelogram branch chain[J]. Chinese Journal of Mechanical Engineering, 2003, 39(7): 38-42. DOI:10.3321/j.issn:0577-6686.2003.07.008) |
| [7] | 郑辉, 唐国宝. Delta并联机械手几何误差建模及灵敏度分析[J]. 哈尔滨工业大学学报, 2009, 41(7): 252-255. (Zheng Hui, Tang Guo-bao. Geometric error modeling and sensitivity analysis of delta parallel manipulator[J]. Journal of Harbin Institute of Technology, 2009, 41(7): 252-255.) |
| [8] | Lee S C, Zeng Q, Ehmann K F. Error modeling for sensitivity analysis and calibration of the tri-pyramid parallel robot[J]. The International Journal of Advanced Manufacturing Technology, 2017, 93(5): 1319-1332. |
| [9] | Ni Y, Shao C, Zhang B, et al. Error modeling and tolerance design of a parallel manipulator with full-circle rotation[J]. Advances in Mechanical Engineering, 2016, 8(5): 1-16. |
| [10] | 房立金, 孙龙飞. 双电机驱动系统消隙特性研究[J]. 中国机械工程, 2012, 23(24): 2991-2996. (Fang Li-jin, Sun Long-fei. Research on clearance characteristics of dual motor drive system[J]. China Mechanical Engineering, 2012, 23(24): 2991-2996. DOI:10.3969/j.issn.1004-132X.2012.24.019) |
| [11] | 孙龙飞, 房立金. 一种新型差动驱动A/B双摆头设计[J]. 东北大学学报(自然科学版), 2016, 37(9): 1269-1273. (Sun Long-fei, Fang Li-jin. Design of a novel A/B birotary head based on differential drive[J]. Journal of Northeastern University(Natural Science), 2016, 37(9): 1269-1273. DOI:10.3969/j.issn.1005-3026.2016.09.012) |
| [12] | 程登元. 一种双电机消隙伺服系统[J]. 雷达科学与技术, 2009(5): 72-76. (Cheng Deng-yuan. Research on clearance characteristics of dual motor drive system[J]. Radar Science and Technology, 2009(5): 72-76.) |
| [13] | Craig J J. Introduction to robotics: mechanics and control[M]. London: Pearson Education Inc, 1986. |
| [14] | 石则昌. 机构精确度[M]. 北京: 高等教育出版社, 1995. (Shi Ze-chang. Institutional precision[M]. Beijing: Higher Education Press, 1995.) |
