
 , 唐亮, 何平
, 唐亮, 何平 东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004
收稿日期:2021-05-21
基金项目:国家自然科学基金资助项目(11705122);河北省自然科学基金资助项目(F2020501040)。
作者简介:马淑华(1967-),女,河北秦皇岛人,东北大学秦皇岛分校教授。
摘要:针对密度峰值聚类(density peak clustering, DPC)算法不能根据数据集自适应选取聚类中心和截断距离dc, 从而不能自适应聚类的问题, 提出了一种自适应的密度峰值聚类(adaptive density peak clustering, ADPC)算法.首先,提出了一个综合考虑局部密度ρi和相对距离δi的参数μi, 根据μi的排列顺序及下降趋势trend自动确定聚类中心.然后,基于基尼系数G对截断距离dc做了自适应选择.最后, 对ADPC算法做出了实验验证, 并与DPC算法和K-means算法进行了对比.实验结果表明, ADPC算法具有较高的ARI,NMI和AC值, 具有较好的聚类效果.
关键词:聚类自适应聚类中心截断距离下降趋势基尼系数
An Adaptive Density Peak Clustering Algorithm
MA Shu-hua, YOU Hai-rong

 , TANG Liang, HE Ping
, TANG Liang, HE Ping School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: YOU Hai-rong, E-mail: hairongyou@qq.com.
Abstract: The density peak clustering algorithm cannot adaptively cluster because it cannot adaptively select the clustering center and cutoff distance dc according to data set, so that an adaptive density peak clustering(ADPC) algorithm was proposed. Firstly, a parameter μi that comprehensively considers the local density ρi and cutoff distance δi was proposed, and the cluster center was automatically determined according to the sorting and downtrend of μi. Then, an adaptive selection of dc was made based on the concept of Gini coefficient. Finally, the ADPC algorithm was verified and compared with the DPC and K-means algorithm. The experimental results show that the ADPC algorithm has higher ARI, NMI and AC values, and has a better clustering effect.
Key words: clusteringadaptiveclustering centercutoff distancedownward trendGini coefficient
随着计算机技术的发展, 数据和信息呈现井喷式增加, 使得大数据技术日趋成熟.其中数据挖掘技术是在海量的数据中挖掘有价值的信息, 使数据实现价值最大化, 在当今时代显得尤为重要.聚类算法是数据挖掘技术中的一个重要领域, 用以描述事物之间的差异及相似性, 因此对聚类算法进行研究具有十分重要的价值和意义.当前的聚类算法大致可分为以下6类:
1) 基于划分的聚类算法.基于划分的聚类算法原理是首先创建k个类别, 挑选初始中心后根据启发式算法进行更新迭代从而获取最优效果[1].这类算法中最常见的就是K-means算法, 后续又演变出K-medoids, K-modes, K-medians, kernel K-means等算法[2-7].这类算法简单高效, 但是容易出现局部最优的情况, 并且对初始值和噪声十分敏感.
2) 基于层次的聚类算法.基于层次的聚类算法分为合并和分裂两种.前者的基本原理是从底层开始, 合并相似的聚类构建上一层聚类, 直到所有数据都合并成一层聚类时终止.后者恰恰相反, 从一类包含所有数据的类别开始, 即从顶层开始, 然后从上而下进行类别分裂,直到一个数据点为一个类别结束[8].常见的此类算法有平衡迭代削减聚类(BIRCH)算法等[9].这类算法可解释性好, 但是时间复杂度十分高.
3) 基于网络的聚类算法.此类算法原理比较简单, 就是将数据划分为网格空间, 然后判断网格空间是否符合高密度的条件, 如果是, 将相邻的两个高密度单元定为一簇[10].常见的基于网格的聚类算法有数据信息网格(STING)算法、集群查询(CLIQUE)算法等[11].此类算法速度很快, 但其对参数敏感, 并且不适用于不规则的数据.
4) 基于模型的聚类算法.基于模型的聚类算法首先为数据假设了一个模型, 然后寻找最佳拟合模型, 大多采用基于概率的模型[12].这一类别常用的算法有高斯混合模型[13].此类算法对类的划分不是十分死板, 但是执行效率不高.
5) 基于模糊的聚类算法.基于模糊的聚类算法是根据隶属度对数据进行划分的, 克服了传统聚类算法非此即彼的缺点, 但是该算法依赖已有的初始聚类中心, 因此还需要其他聚类算法进行配合[14].常见的此类算法有模糊C均值聚类(FCM)算法[15].
6) 基于密度的聚类算法.基于密度的聚类算法基本原理是画圈, 基于圈的半径和圈的最小容量两个参数进行划分[16].此类算法中最常用的算法是带噪声的基于密度的应用程序空间聚类(DBSCAN)[17], 最典型的基于密度的聚类算法是密度峰值聚类(density peak clustering, DPC)算法[18].此类算法可以应用于不规则形状的聚类, 并且对噪声不敏感, 但是聚类结果受参数影响比较大.
基于以上分析可以得知, 基于密度的聚类算法性能最好, 但是受参数影响比较大, 聚类效果的好坏取决于参数选取是否精确.因此本文对密度峰值聚类算法进行了参数的自适应改进, 从而进一步实现聚类算法的优化.
1 DPC算法密度峰值聚类算法是基于密度的聚类算法, 其基本思想是聚类中心在其邻域内具有最高的密度值, 并且与其他聚类中心距离较远.该算法基于以下两个参量: 局部密度ρi和相对距离δi[18].
定义1??? 局部密度ρi.局部密度根据数据的离散和连续分为截断核和高斯核两种计算方式, 其中截断核适用于离散数据, 计算公式为
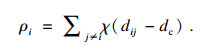 | (1) |
χ(x)定义如下:
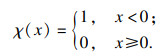 | (2) |
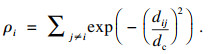 | (3) |
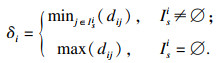 | (4) |
图 1(Fig. 1)
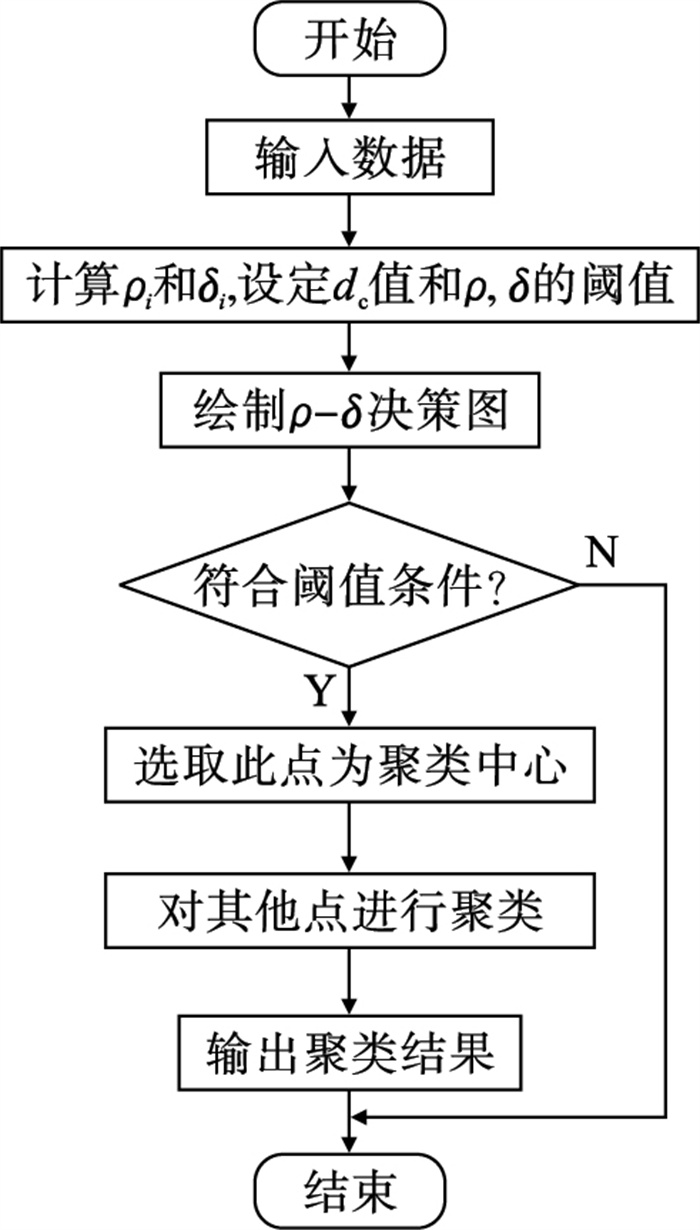 | 图 1 DPC算法的流程图Fig.1 The flowchart of DPC algorithm |
2 ADPC算法传统的密度峰值聚类算法对参数依赖性比较强, 通常情况下密度峰值聚类算法依靠人工选定聚类中心和截断距离dc值, 比较耗费时间, 并且在参数选择不恰当时, 聚类效果与预期效果大相径庭.因此, 本文对DPC算法的聚类中心的选择和dc参数进行了自适应改进.
2.1 聚类中心的自适应选择首先, 设计了一个综合考虑局部密度ρi和相对距离δi的参数μi:
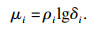 | (5) |
定义3??? 下降趋势:
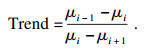 | (6) |
获取到下降趋势之后, 取下降趋势最大的点及前面的几个点作为聚类中心.
2.2 dc参数的自适应选择DPC算法通常是经过实验验证或者凭借经验获得dc值, 具有很大的不确定性, 通常好的聚类算法划分的同种类别的差异较小, 因此选取dc值可以根据综合衡量元素差异来获取, 本文正是采用衡量元素差距的参数——基尼系数去约束dc值, 即求取基尼系数最小时的dc值.
定义4??? 基尼系数G.传统的基尼系数是用来衡量一个国家的居民收入差距的[19], 本文采用该指标衡量聚类结果中每种类别内元素的差异.定义如下:
 | (7) |
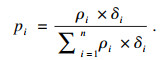 | (8) |
2.3 ADPC算法整体流程ADPC算法过程如表 1所示.
表 1(Table 1)
| 表 1 自适应密度峰值聚类算法过程 Table 1 ADPC algorithm process |
3 结果及评价所有实验均在Lenovo-Y7000P笔记本上进行, 操作系统为Windows 10, Intel i5-9300H CPU, 实验平台为Matlab R2018a.
3.1 数据集和评价指标为了避免实验结果的偶然性, 本文选取了6组典型的聚类数据集进行了ADPC算法测试, 包括: D31, Data1, Data2, Aggregation, Spiral, Fish数据集.重点对D31数据集聚类过程进行了详细分析, 对其数据集的聚类效果进行了展示, 并且与DPC聚类算法以及最常用的K-means聚类算法进行了聚类效果对比.
本文采用常用的评估聚类效果的3项指标进行衡量, 分别是调整兰德指数ARI、标准化互信息NMI以及准确度AC.
3.2 ADPC算法聚类过程实现以D31数据集为例对ADPC算法进行详细说明及分析:
1) 首先将dc=1作为初始值, 计算D31数据集的局部密度ρi和相对距离δi, 并绘制决策图, 如图 2所示.
图 2(Fig. 2)
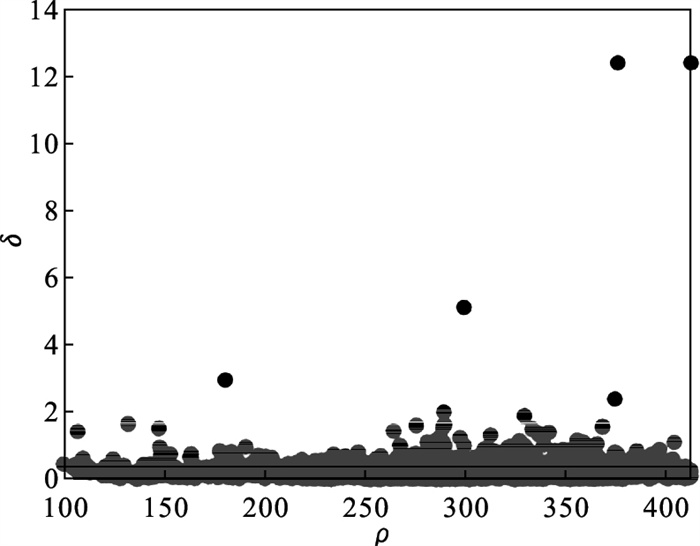 | 图 2 D31数据集的决策图Fig.2 Decision graph of D31 dataset |
2) 改变dc的值, 并计算每个dc值对应的基尼系数, 绘制dc和基尼系数的关系图, 如图 3所示.
图 3(Fig. 3)
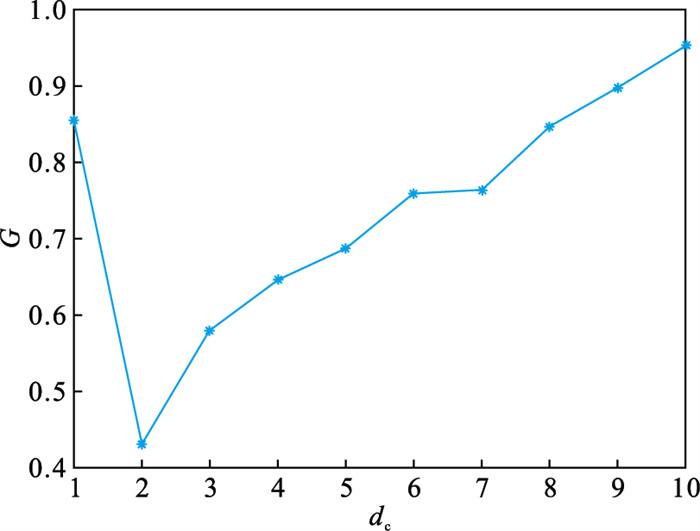 | 图 3 基尼系数和dc的关系图Fig.3 Gini coefficient and dc relationship diagram |
3) 根据图 3, 当dc=2时, 基尼系数具有最小值, 因此令dc=2, 重新绘制ρ-δ分布图, 新的分布图如图 4所示, 可以看出, 新的分布图具有更高的规律性, 具有较大的局部密度ρi和相对距离δi的点分布比较集中.
图 4(Fig. 4)
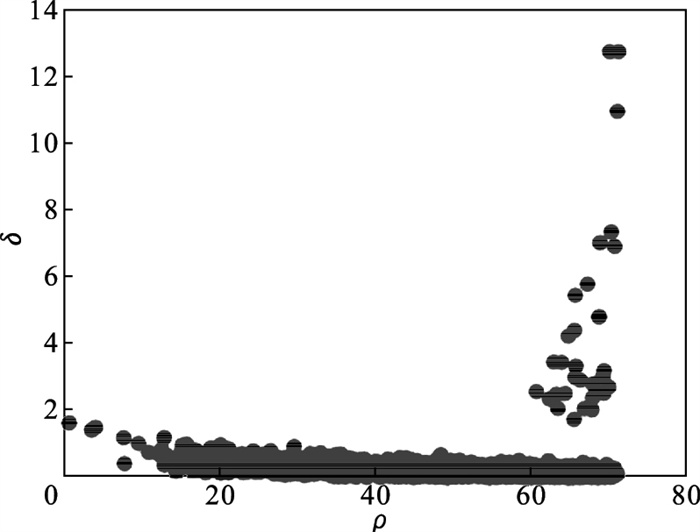 | 图 4 改进后的决策图Fig.4 Improved decision graph |
4) 根据式(5)计算μi的值, 并将其降序排列, 绘制μi降序图, 如图 5所示.根据式(6)下降趋势的定义, 计算μi对应的下降趋势值, 并绘制下降趋势图如图 6所示, 图 6中第31个点具有最高的下降趋势, 因此选取前31个点作为聚类中心点, 聚类中心的选择如图 7所示.
图 5(Fig. 5)
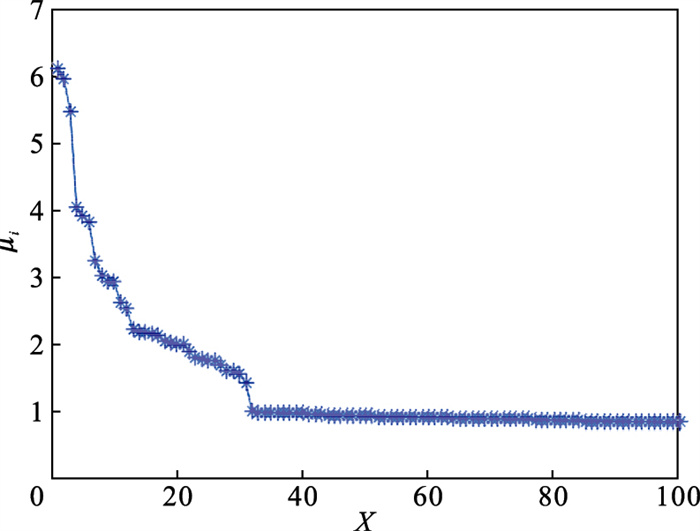 | 图 5 μi值的分布Fig.5 The values distribution of μi |
图 6(Fig. 6)
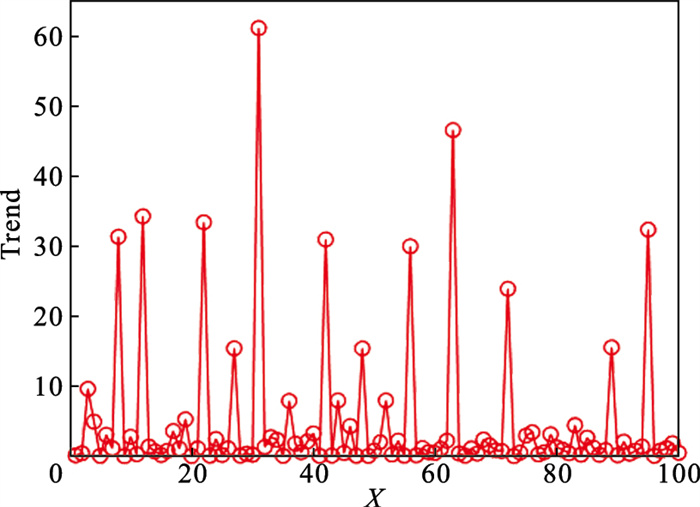 | 图 6 下降趋势图Fig.6 The values distribution of Trend |
图 7(Fig. 7)
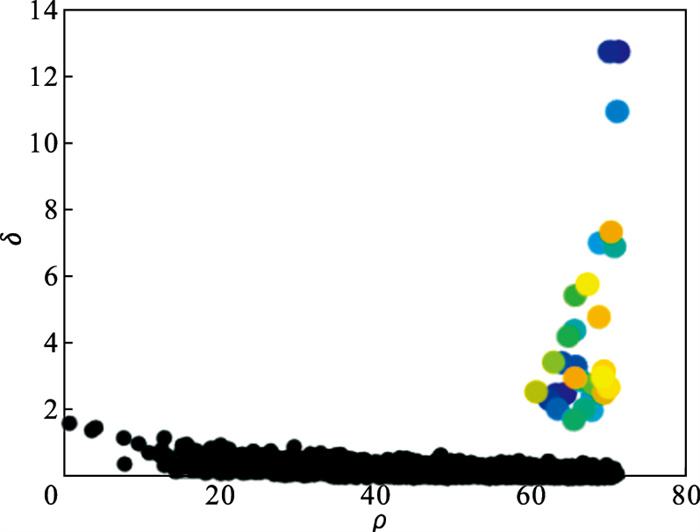 | 图 7 聚类中心的选择Fig.7 Selection of cluster centers |
5) 根据已选好的聚类中心和dc值进行聚类, 最终聚类结果如图 8所示, 可以看出聚类效果较好.
图 8(Fig. 8)
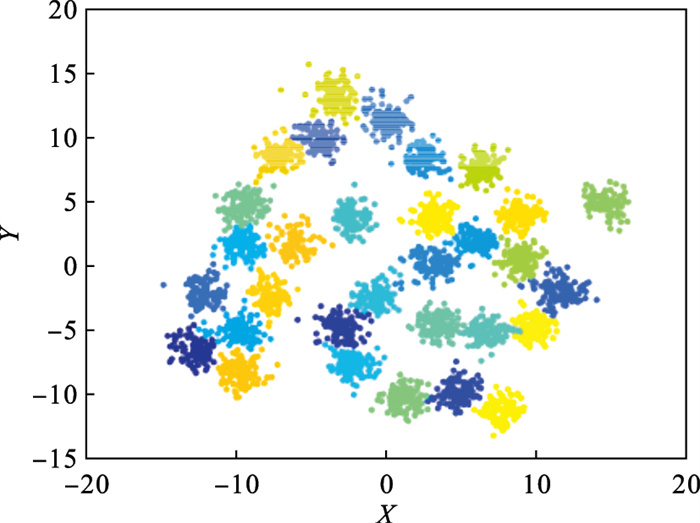 | 图 8 聚类结果Fig.8 Clustering result |
3.3 与DPC算法和K-means算法比较3.3.1 聚类效果对比本文将ADPC聚类算法与DPC算法和K-means算法进行了对比, D31, Data1, Data2, Aggregation, Spiral以及Fish数据集在3种聚类算法下的聚类结果如图 9~图 14所示.由聚类结果可以看出, Data1, Data2两种数据集下, 3种算法具有差不多的效果, 聚类均比较精确, 但是在Aggregation、Spiral和Fish数据集下, 3种算法的聚类效果差异较大.
图 9(Fig. 9)
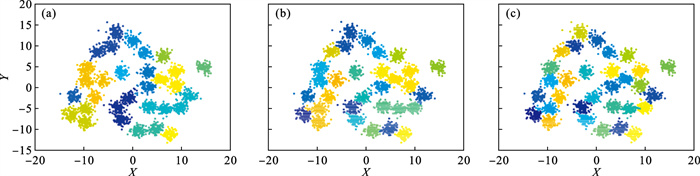 | 图 9 D31数据集Fig.9 D31 data set (a)—DPC; (b)—K-means; (c)—ADPC. |
图 10(Fig. 10)
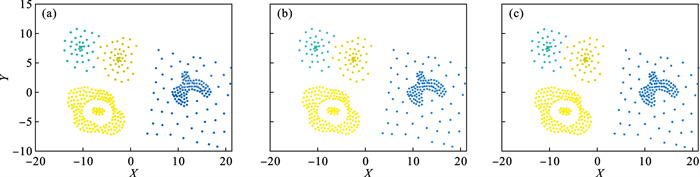 | 图 10 Data1数据集Fig.10 Data1 data set (a)—DPC; (b)—K-means; (c)—ADPC. |
图 11(Fig. 11)
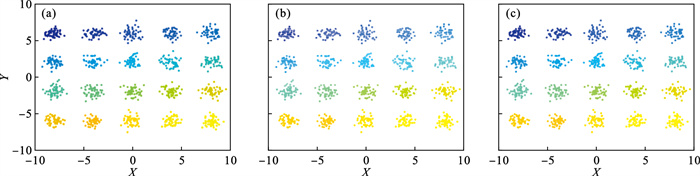 | 图 11 Data2数据集Fig.11 Data2 data set (a)—DPC; (b)—K-means; (c)—ADPC. |
图 12(Fig. 12)
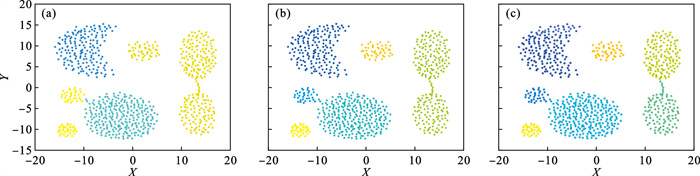 | 图 12 Aggregation数据集Fig.12 Aggregation data set (a)—DPC; (b)—K-means; (c)—ADPC. |
图 13(Fig. 13)
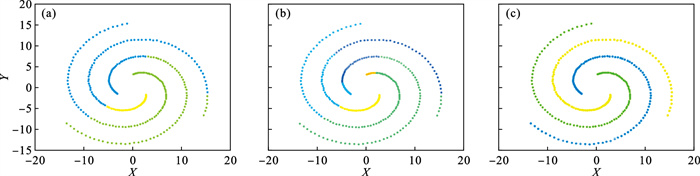 | 图 13 Spiral数据集Fig.13 Spiral data set (a)—DPC; (b)—K-means; (c)—ADPC. |
图 14(Fig. 14)
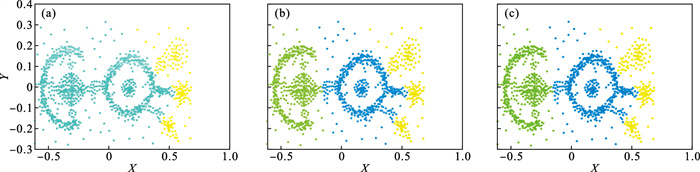 | 图 14 Fish数据集Fig.14 Fish data set (a)—DPC; (b)—K-means; (c)—ADPC. |
Aggregation数据集的聚类效果如图 12所示, 图 12a为DPC算法的聚类效果, 在DPC算法下的聚类类别的区分不够明显, 左下角黄色的类别以及右侧黄色的类别没有得到划分.如图 12b所示,K-means算法中左下角的两种类别被划分很精确, 但是右侧的两种类别依然没有被划分开.ADPC算法的聚类效果见图 12c, 所有类别均被识别.
Spiral数据集在聚类数据集中比较具有代表性, 与普通数据集不同的是, 该数据集以环形分布, 并且两种类别的聚类比较近, 不具有明显的区别性.3种聚类算法的聚类效果见图 13, 可以看出图 13a DPC算法和图 13b K-means算法的聚类效果较差, 图 13c ADPC算法的聚类效果比较精确.
Fish数据集的聚类效果见图 14, 可以看出K-means算法和ADPC算法的聚类效果较好.
综上, 针对一些容易区分的数据集, 如Data1和Data2数据集, DPC, K-means和ADPC三种算法均有较好的聚类效果.但是对于一些不容易区分的数据集, 如Aggregation, Spiral和Fish数据集, ADPC算法具有更好的聚类效果.
3.3.2 聚类效果评价ARI指标的值在[-1, 1]之间, 值越大代表划分程度越高, 说明聚类效果越好.DPC, K-means以及ADPC算法在6种数据集下的ARI值如图 15所示.由图 15可以看出, ADPC相比DPC和K-means算法具有更高的ARI值.
图 15(Fig. 15)
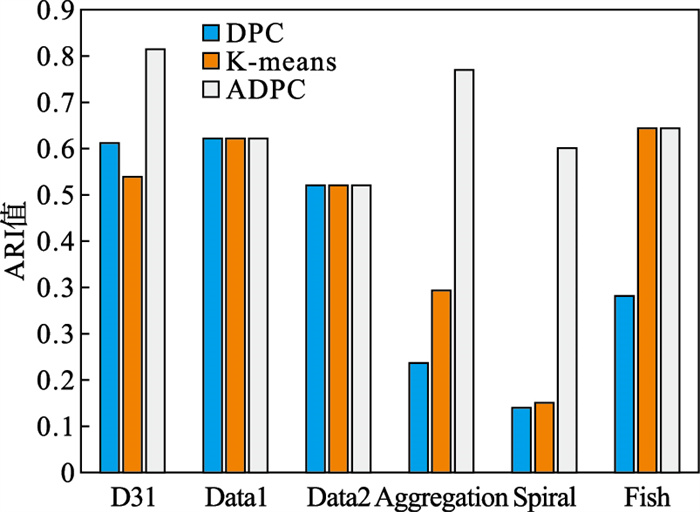 | 图 15 ARI值对比Fig.15 Comparison of ARI values |
NMI指标是度量两个类别相似程度的指标, 在[0, 1]之间取值, 指标值越大代表聚类效果越好.DPC、K-means以及ADPC算法在6种数据集下的NMI值如图 16所示, 由图 16可以看出, ADPC相比于DPC和K-means算法在绝大部分情况下具有更高的NMI值.
图 16(Fig. 16)
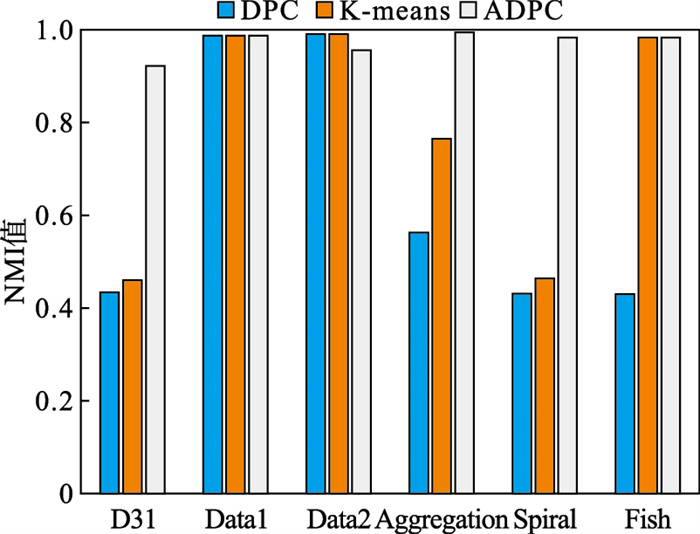 | 图 16 NMI值对比Fig.16 Comparison of NMI value |
AC指标是衡量聚类准确度的指标, 在[0, 1]之间取值, 越接近1代表精确度越高.DPC、K-means以及ADPC算法在6种数据集下的AC值如图 17所示, 由图 17可以看出, ADPC相比DPC和K-means算法具有更高的AC值.
图 17(Fig. 17)
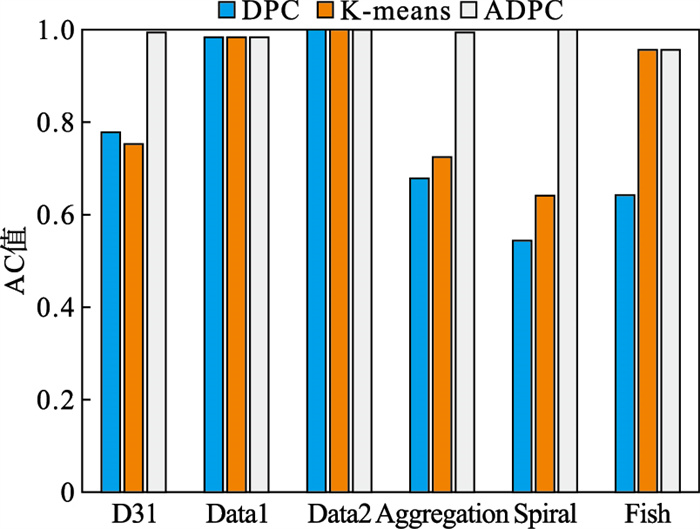 | 图 17 AC值对比Fig.17 Comparison of AC values |
综上, 对ARI,NMI和AC三个指标的值进行整理, 并计算平均值, 如图 18所示, 结果显示, ADPC算法与DPC算法和K-means算法相比除了在Data2数据集中的NMI值低0.02以外, 其他情况下均具有更高的ARI, NMI和AC值, 并且具有更高的ARI平均值、NMI平均值和AC平均值.因此, ADPC算法具有相对于DPC算法和K-means算法更好的聚类效果.
图 18(Fig. 18)
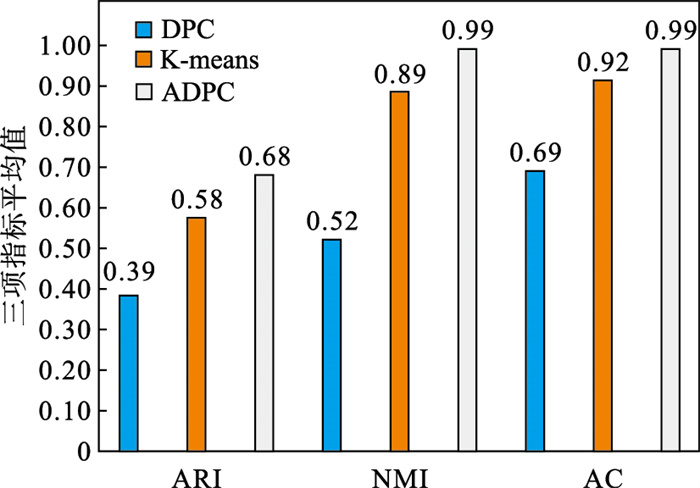 | 图 18 三项指标的平均值Fig.18 Average of three indicators |
4 结语本文对密度峰值聚类算法做出了改进, 针对其不能自动选择聚类中心的缺点, 重新定义了综合衡量局部密度ρi和δi相对距离的参量μi, 针对其不能自动确定dc的问题, 通过基尼系数去衡量dc的最佳值.选取了6组具有代表性的数据集进行了算法测试, 首先根据D31数据集的聚类结果对自适应的聚类算法的聚类过程进行了详细介绍, 最后将6组数据集的聚类效果与DPC聚类算法和K-means算法进行了对比, 并分别分析了ARI, NMI和AC三个指标.结果表明, ADPC算法具有较好的聚类效果.
参考文献
| [1] | Boomija M D, Phil M. Comparison of partition based clustering algorithms[J]. Journal of Computer Applications, 2008, 1(4): 18-21. |
| [2] | Krishna K, Narasimha Murty M. Genetic K-means algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B(Cybernetics), 1999, 29(3): 433-439. DOI:10.1109/3477.764879 |
| [3] | Park H S, Jun C H. A simple and fast algorithm for K-medoids clustering[J]. Expert Systems with Applications, 2009, 36(2): 3336-3341. DOI:10.1016/j.eswa.2008.01.039 |
| [4] | Huang Z, Ng M K. A fuzzy K-modes algorithm for clustering categorical data[J]. IEEE Transactions on Fuzzy Systems, 1999, 7(4): 446-452. DOI:10.1109/91.784206 |
| [5] | 彭春春, 陈燕俐, 荀艳梅. 支持本地化差分隐私保护的K-modes聚类方法[J]. 计算机科学, 2021, 48(2): 105-113. (Peng Chun-chun, Chen Yan-li, Xun Yan-mei. K-modes clustering guaranteeing local differential privacy[J]. Computer Science, 2021, 48(2): 105-113.) |
| [6] | Cardot H, Cénac P, Monnez J M. A fast and recursive algorithm for clustering large datasets with K-medians[J]. Computational Statistics & Data Analysis, 2012, 56(6): 1434-1449. |
| [7] | Tzortzis G F, Likas A C. The global kernel K-means algorithm for clustering in feature space[J]. IEEE Transactions on Neural Networks, 2009, 20(7): 1181-1194. DOI:10.1109/TNN.2009.2019722 |
| [8] | Wang J, Li M, Chen J, et al. A fast hierarchical clustering algorithm for functional modules discovery in protein interaction networks[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2010, 8(3): 607-620. DOI:10.1142/S0219720010004677 |
| [9] | Zhang T, Ramakrishnan R, Livny M. BIRCH: an efficient data clustering method for very large databases[J]. ACM Sigmod Record, 1996, 25(2): 103-114. DOI:10.1145/235968.233324 |
| [10] | Kamal S, Burk L I. FACT: a new neural network-based clustering algorithm for group technology[J]. International Journal of Production Research, 1996, 34(4): 919-946. DOI:10.1080/00207549608904943 |
| [11] | Rani P. A survey on STING and CLIQUE grid based clustering methods[J]. International Journal of Advanced Research in Computer Science, 2017, 8(5): 1510-1512. |
| [12] | Meilǎa M, Heckerman D. An experimental comparison of model-based clustering methods[J]. Machine Learning, 2001, 42(1): 9-29. |
| [13] | Zhang J, Yin Z, Wang R. Pattern classification of instantaneous cognitive task-load through gmm clustering, Laplacian eigen map, and ensemble svms[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2016, 14(4): 947-965. |
| [14] | Kumar P, Varma K I, Sureka A. Fuzzy based clustering algorithm for privacy preserving data mining[J]. International Journal of Business Information Systems, 2011, 7(1): 27-40. DOI:10.1504/IJBIS.2011.037295 |
| [15] | Bezdek J C, Ehrlich R, Full W. FCM: the fuzzy C-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2/3): 191-203. |
| [16] | Parimala M, Lopez D, Senthilkumar N C. A survey on density based clustering algorithms for mining large spatial databases[J]. International Journal of Advanced Science and Technology, 2011, 31(1): 59-66. |
| [17] | Schubert E, Sander J, Ester M, et al. DBSCAN revisited, revisited: why and how you should(still)use DBSCAN[J]. ACM Transactions on Database Systems, 2017, 42(3): 1-21. |
| [18] | Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [19] | Milanovic B. A simple way to calculate the Gini coefficient, and some implications[J]. Economics Letters, 1997, 56(1): 45-49. DOI:10.1016/S0165-1765(97)00101-8 |
