
 , 刘相华
, 刘相华 东北大学 轧制技术及连轧自动化国家重点实验室, 辽宁 沈阳 110819
收稿日期:2021-07-26
基金项目:国家自然科学基金资助项目(U1460107, 51704065);科技部国际合作专项资助项目(2015DFA50780)。
作者简介:张思佳(1990-),男,河北张家口人,东北大学博士研究生;
刘相华(1953-),男,黑龙江双鸭山人,东北大学教授,博士生导师。
摘要:分析了轧制差厚板的显微组织和力学性能存在差异性的原因.针对差厚板方盒件的拉深成形过程建立有限元模型, 探讨了其变厚度特性及性能差异化特征的建模方法.通过对比实验及模拟条件下方盒件的成形结果, 证明了有限元模型的可靠性.根据验证后的有限元模型, 以极限拉深高度和过渡区中心线偏移量为评价标准, 分析了差厚板的几何参数(过渡区长度、过渡区位置、薄区与厚区的厚度差)对其拉深成形的影响.结果表明, 过渡区越长、厚区占比越大、薄区与厚区的厚度差越小, 则差厚板的拉深成形性能越好.确定差厚板的几何参数时, 需综合考虑板料的成形性能和轻量化效果.
关键词:轧制差厚板方盒件拉深成形实验有限元模拟轻量化
Experimental and Simulation Study on Deep Drawing of Square Box Made from Tailor Rolled Blank
ZHANG Si-jia, HU Xian-lei

 , LIU Xiang-hua
, LIU Xiang-hua State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China
Corresponding author: HU Xian-lei, E-mail: hu_xianlei@263.net.
Abstract: The microstructure and mechanical properties of different parts in tailor rolled blanks(TRBs)were studied and the differentiation was explained. A finite element model was established to simulate deep drawing process of the square box from TRB and the effects of the thickness and non-uniformly distributed mechanical properties on the model setup were discussed. After comparison the experimental and simulation results, the reliability of the numerical model was verified. Taking the limit drawing height and the offset of thickness transition zone(TTZ)as the evaluation criteria, the effects of the geometric parameters(i.e. the length and position of the TTZ, and the thickness difference between the thin and thick area)on the formability of TRB were analyzed. The results show that when the TTZ length is longer, the distance between the TTZ and thin area is smaller and the thickness difference between thin and thick areas is smaller, the formability of TRB is better. Therefore, determining the geometric parameters of TRB need to consider the formability and light-weight effect.
Key words: tailor rolled blank(TRB)square boxdeep drawing testfinite element simulationlight weight
国家“十三五”规划中指出, “改革、调整、绿色、创新”是钢铁行业未来的发展主线[1].在这种背景下, 节能减排和高端制造成为钢铁行业的主要发展方向.传统方法轧制钢板追求厚度均匀, 但是钢板在服役过程中所承受的载荷往往分布不均匀, 以均匀的厚度承载不均匀的外力, 势必造成材料浪费[2].基于负荷裕量优化分配理论, 通过轧辊在垂直方向的刚性位移速度和轧辊旋转速度相互配合, 制备厚度与载荷相匹配的变厚度板材, 称为轧制差厚板(以下简称差厚板)[3-5].使用差厚板代替等厚度板, 可以实现“节能、减排、降成本”的目标, 已经被广泛应用于汽车工业[6].
由于差厚板沿轧制方向的厚度和力学性能分布不均匀, 使其在成形过程中的应力应变分布、金属流动规律以及各区域变形速度等成形特征变得更加复杂.因此, 差厚板的成形规律不同于传统等厚度板, 也无法完全借鉴局部加强板和激光拼焊板等变厚度板材[7].
20世纪90年代, 差厚板在德国亚琛工业大学被成功开发出来后, 科研人员投入了对其成形性能的研究, 主要探究应用差厚板制备复杂零件的可行性.Kleiner等[8]总结了差厚板的成形技术, 包括柔性模具可调系统、快速分段模具系统以及液压胀形等.Urban等[9]将液压胀形技术应用于差厚板, 成功地试制了变厚度盖板和变厚度横梁.Puteen等[10]对差厚板液压胀形工艺进行了有限元分析, 优化了相关工艺流程.我国对差厚板成形性能的研究起步较晚.Jiang等[11]对差厚板进行拉深成形模拟, 指出差厚板盒形件的薄壁圆角和过渡区底部容易发生开裂.Li等[12]和Zhang等[13]通过有限元方法分别研究了差厚板的部分几何参数对其成形性能的影响.
差厚板冷轧后需要进行退火处理, 从而消除部分加工硬化, 以利于进一步深加工.在变厚度轧制过程中不同厚度对应不同的压下率, 因此退火处理后差厚板的力学性能表现出明显的差异化[14-15].然而在对差厚板的成形性能进行有限元分析时, 文献[10-11]默认差厚板力学性能均匀, 采用等厚度材料的力学性能参数; 文献[12-13]则默认差厚板力学性能单调变化, 以板厚为变量, 对薄区材料和厚区材料的力学性能参数进行线性插值, 从而构建过渡区的应力应变关系, 忽略了差厚板的力学性能差异化特性.
本文研究了差厚板经退火处理后显微组织及力学性能的分布规律, 分析了造成差异化的原因.介绍了差厚板变厚度特性及性能变化特征的建模方法.对差厚板方盒件的拉深成形过程进行了数值模拟, 对比实验及模拟条件下的成形结果, 验证了有限元模型的可靠性.根据验证后的有限元模型, 以极限拉深高度和过渡区中心线偏移量为评价标准, 分析了过渡区长度、过渡区位置、薄区与厚区的厚度差对差厚板方盒件拉深成形性能的影响.
1 实验材料1.1 轧制差厚板制备以厚度为2.2 mm的CR340钢板为实验材料, 其化学成分(质量分数, %)为: C 0.080, Si 0.204, Mn 0.882, P 0.025, S 0.018, Al 0.047.利用四辊冷轧机, 通过在线调节轧辊辊缝的方法制备差厚板.将冷轧后的差厚板进行620 ℃保温60 min的退火处理以获得实验用差厚板, 其几何尺寸如图 1所示.
图 1(Fig. 1)
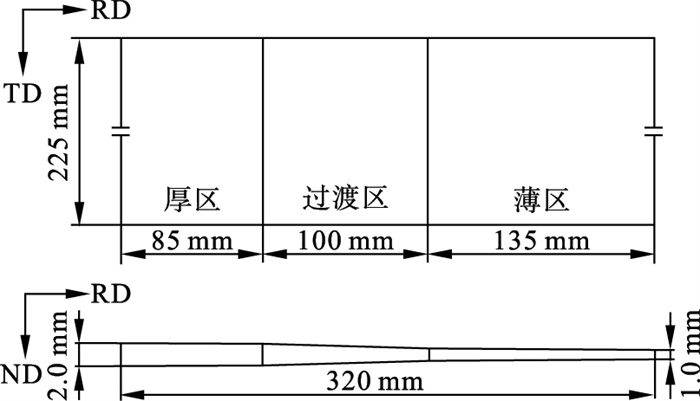 | 图 1 实验用差厚板的几何尺寸Fig.1 Schematic of geometric dimension of TRB in experiment |
1.2 差厚板的显微组织和力学性能差厚板是由一整块等厚度板经过变厚度轧制以及退火处理制备而成的, 不同区域的材料具有相同的化学成分和原始组织.在制备差厚板的过程中, 沿轧制方向连续变化的压下量以及退火工艺参数对其显微组织和力学性能的分布情况有显著影响.
图 2给出了实验用差厚板沿轧制方向的组织变化, 其中红色组织为变形晶粒, 黄色组织为亚晶结构晶粒, 蓝色组织为再结晶晶粒.可以看出, 差厚板的显微组织形貌存在显著差异, 且变形晶粒、亚晶结构晶粒和再结晶晶粒的体积分数发生明显变化.这是因为CR340钢板的显微组织为等轴状再结晶晶粒, 在变厚度冷轧过程中, 随着压下率增加, 亚晶粒逐渐在晶粒内部形成, 且晶粒内部的平均取向差逐渐增大, 原始组织中的再结晶晶粒首先转变为亚晶结构晶粒, 并最终转变为变形晶粒, 因此冷轧态差厚板内再结晶晶粒的体积分数随着压下率的增加而减小, 变形晶粒的体积分数随着压下率的增加而增大.在随后的退火过程中, 厚区金属(压下率9 %)储存的畸变能不足以驱动其发生再结晶, 因此显微组织只发生回复, 晶粒的形貌几乎不发生变化.薄区金属(压下率54 %)具有足够的畸变能驱动其发生完全再结晶, 从而使纤维状变形晶粒完全被新生成的等轴状再结晶晶粒所取代.过渡区(9 % < 压下率 < 54 %) 内金属的组织转变介于薄区与厚区之间, 显微组织在退火过程中发生不完全再结晶, 最终由扁平的变形晶粒、亚晶结构晶粒以及等轴状再结晶晶粒共同构成, 且压下率越大, 再结晶晶粒的体积分数越大.需要注意的是, 图 2c~图 2f中的再结晶晶粒为退火过程中新形成的再结晶晶粒, 而图 2a和2b中的再结晶晶粒为从原始组织中再结晶晶粒.
图 2(Fig. 2)
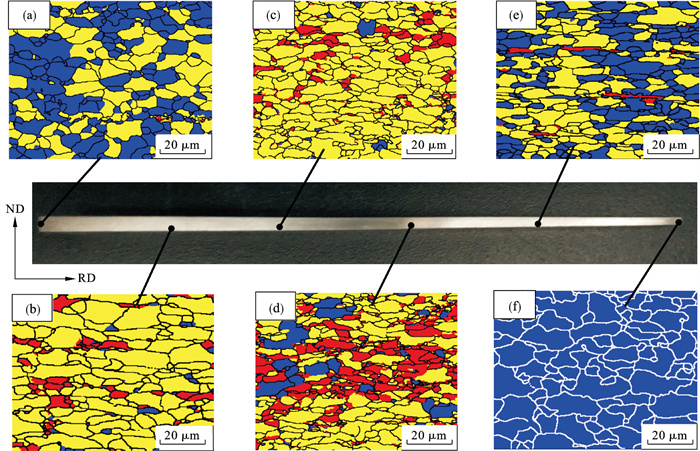 | 图 2 实验用差厚板不同压下率对应的显微组织Fig.2 Microstructure of the experimental TRBs after different reductions (a)—9 %; (b)—18 %; (c)—27 %; (d)—36 %; (e)—45 %; (f)—54 %. |
通过单向拉伸实验检测差厚板压下率为9 %,18 %,27 %,36 %,45 % 和54 % 时材料与轧制方向成0°,45°和90°角的力学性能.如图 3所示, 沿轧制方向差厚板的力学性能分布不均匀, 随着压下率的增加, 屈服和抗拉强度均先升高后降低, 在压下率为36 % 时达到峰值, 均匀延伸率的变化趋势与之相反.这是因为CR340钢板在变厚度冷轧过程中发生不同程度的加工硬化, 随着压下率的增加, 冷轧态差厚板的强度单调升高而塑性单调降低.经过620 ℃/60 min退火处理后, 差厚板厚区金属只发生回复, 其力学性能几乎不发生变化; 薄区金属发生完全再结晶, 其力学性能恢复至轧制前的状态; 过渡区内金属发生不完全再结晶, 显微组织由变形晶粒、亚晶结构晶粒和再结晶晶粒组成, 其力学性能与不同类型晶粒的体积分数有关, 即再结晶晶粒的体积分数越高, 则强度越低, 塑性越高.综上所述, 在加工硬化和再结晶软化效应的共同作用下, 经过620 ℃/60 min退火处理的差厚板的力学性能表现出不均匀的特点.
图 3(Fig. 3)
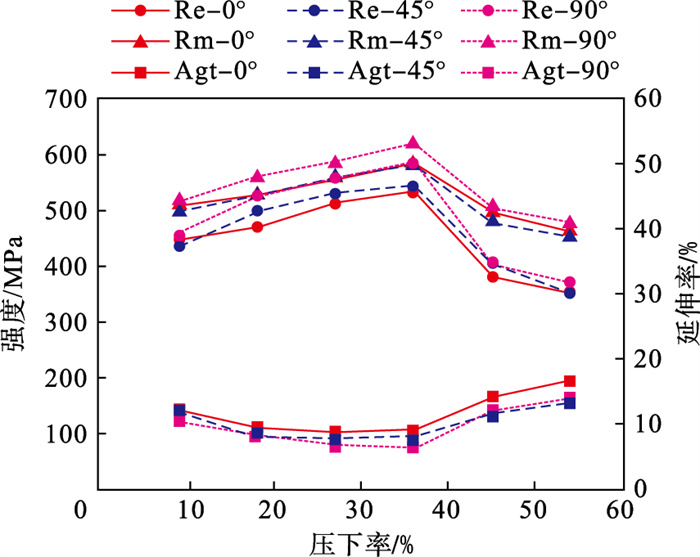 | 图 3 实验用差厚板的力学性能分布Fig.3 Distribution of mechanical properties of experimental TRB |
2 实验设备及有限元模型2.1 实验设备及参数图 4为用于方盒件拉深成形实验的万能薄板成形实验机及拉深模具装配示意图.凹模边长为90 mm, 底部圆角半径为6 mm, 厚区侧壁圆角半径和薄区侧壁圆角半径均为12 mm.凸模底部圆角半径为6 mm, 厚区侧壁圆角半径和薄区侧壁圆角半径分别为9.8 mm和10.9 mm.凸模与凹模间隙为1.1倍板料厚度.凹模和压边圈的板料接触表面与差厚板的厚度变化相适应.压边力选用120 kN, 凸模移动速度为6 mm/min.板料选用直径为180 mm的差厚板, 其圆心与差厚板过渡区的中心重合.
图 4(Fig. 4)
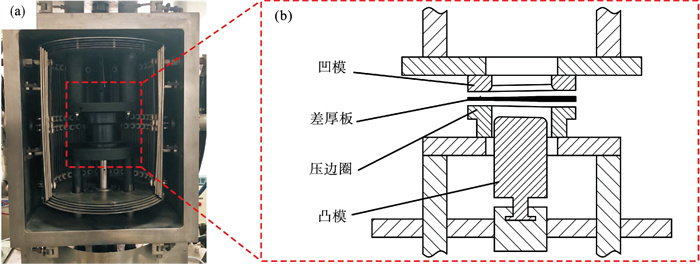 | 图 4 差厚板方盒件拉深成形实验设备及模具Fig.4 Schematic diagram of equipment and die for deep drawing of square box made from TRB (a)—拉深成形实验设备;(b)—拉深成形模具装配示意图. |
2.2 有限元模型采用数值模拟软件ABAQUS 2016对差厚板方盒件的拉深成形过程进行模拟研究.差厚板采用CR340材料, 密度ρ=7 850 kg/m3, 杨氏模量E=210 GPa, 泊松比ν=0.3.基于不同压下率材料的力学性能数据, 使用拉格朗日插值法, 以板料厚度为变量进行插值, 可获得如图 5所示的差厚板过渡区的真应力、真应变与厚度之间的关系.利用软件的前处理功能, 通过引入场变量, 使不同压下率材料的力学性能对应不同的场变量值, 从而实现材料模型的导入.
图 5(Fig. 5)
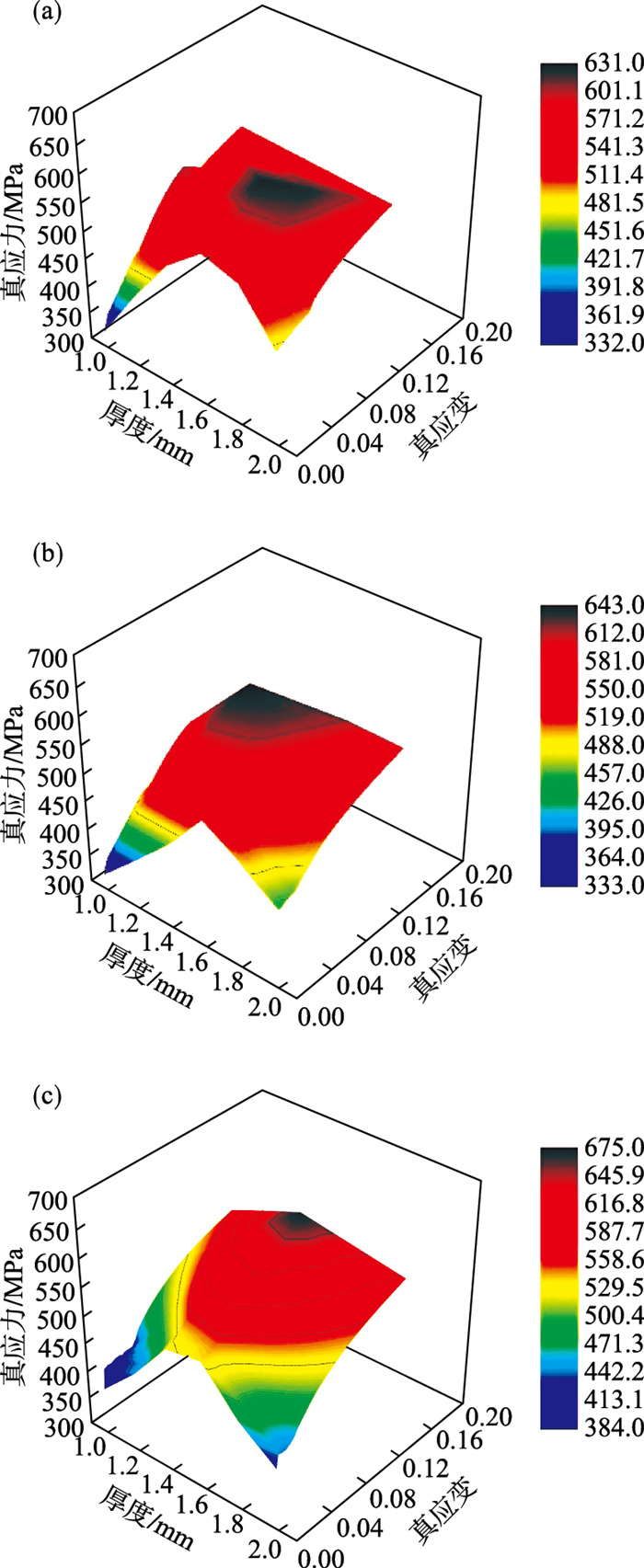 | 图 5 差厚板过渡区的真应力、真应变与厚度之间的三维曲面关系Fig.5 Relationships among the true stress, true strain and thickness of the transition zone of TRB (a)—平行于轧制方向;(b)—与轧制方向成45°;(c)—垂直于轧制方向. |
图 6为差厚板方盒件拉深成形模拟的几何模型, 采用二分之一模型.凸模、凹模和压边圈为离散刚体, 几何尺寸与实验用模具相同.由于与平面尺寸相比, 差厚板的厚度很小, 因此使用壳单元模拟差厚板, 单元类型为S4R, 网格尺寸为2 mm×2 mm.通过解析场中的映射方法实现沿轧制方向变化厚度的赋予.压边力及凸模移动速度均与实验相同, 分别为120 kN和6 mm/min, 摩擦系数选用0.12, 质量放大因子为1 000.
图 6(Fig. 6)
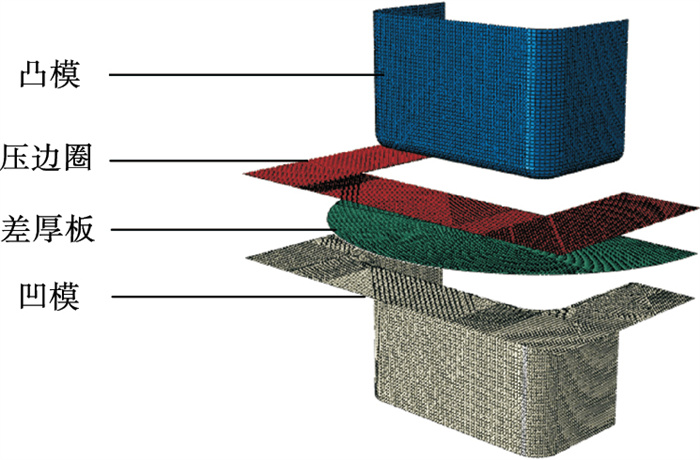 | 图 6 差厚板方盒件拉深成形模拟的几何模型Fig.6 Geometric model to simulate deep drawing of square box made from TRB |
3 有限元模拟与实验结果对比图 7给出了差厚板方盒件拉深成形的数值模拟与实验结果.可以看出, 由于沿轧制方向差厚板的厚度连续变化且力学性能分布不均匀, 在拉深成形过程中薄侧与厚侧的变形程度不同.由图 3可知, 与厚区相比, 薄区材料具有较低的强度和较好的塑性, 同时厚度较小, 在相同外力作用下所受应力较大.因此, 在压边力一定的条件下, 差厚板薄侧首先发生变形, 且金属更容易流动.随着拉深过程的进行, 由于厚侧板料金属流动性较差, 导致应变分布不均匀, 又因为与薄区相比, 厚区材料的塑性较低.因此, 在拉深成形过程中差厚板厚侧直壁与底部之间的过渡圆角处首先破裂.
图 7(Fig. 7)
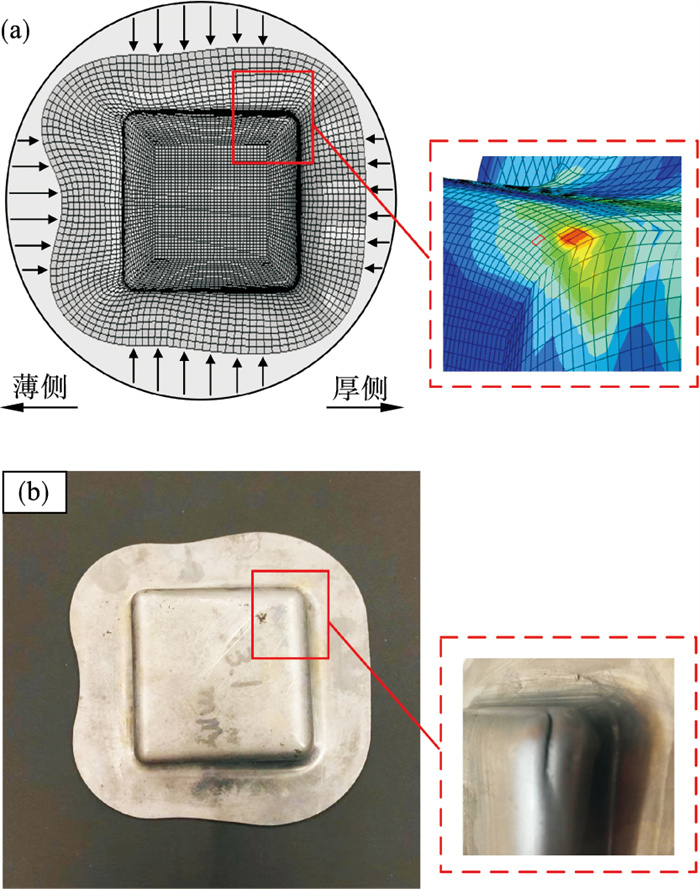 | 图 7 差厚板方盒拉深成形的数值模拟与实验结果Fig.7 Experimental and simulation results of deep drawing of square box made from TRB (a)—有限元模拟;(b)—实验. |
对比图 7a和图 7b可以看出, 数值模拟和实验后方盒件的形貌和尺寸基本吻合, 且开裂部位均位于方盒件厚侧的底部圆角附近, 说明有限元模型能够很好地预测差厚板拉深过程中的变形行为和金属流动情况.图 8给出了实验和模拟条件下凸模的力-位移曲线, 可以看出有限元模型所预测的载荷水平及整体变化趋势与实验结果基本吻合. 此外, 测量三次实验后方盒件的拉深高度分别为23.1, 21.6和22.8 mm, 平均值为22.5 mm; 数值模拟方盒件的拉深高度为23.4 mm.经计算, 实验与数值模拟的误差为4.0 %.由此可见, 本文构建的差厚板拉深成形有限元模型具有较高的可靠性和准确性, 能够有效预测差厚板方盒件的拉深成形过程.
图 8(Fig. 8)
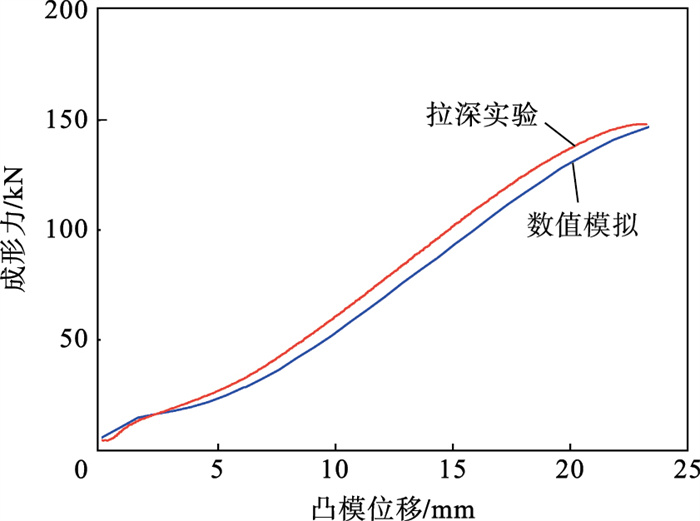 | 图 8 实验和模拟条件下凸模的力-位移曲线对比Fig.8 Comparison of the force-displacement curves of punching from experiment and simulation |
4 几何参数对方盒件拉深成形性能和轻量化效果的影响4.1 差厚板方盒件拉深成形性能的评价标准采用极限拉深高度h和过渡区中心线偏移量Δl作为差厚板方盒件拉深性能的评价标准, 研究在力学性能分布不均匀的情况下, 差厚板的几何参数(过渡区长度、过渡区位置、薄区与厚度的厚度差)对其拉深成形性能的影响.
极限拉深高度是评价板料成形性能的常用指标, 指板料在不发生破裂和起皱的前提下, 可以达到的最大拉深高度.极限拉深高度越大, 说明板料的成形性能越好.差厚板方盒件的极限拉深高度主要受到板料破裂位置的影响.过渡区中心线偏移量是用于评价差厚板成形性能的另一重要指标, 指在达到极限拉深高度时, 差厚板过渡区中心线沿轧制方向的位移, 测量方法如图 9所示(将过渡区中心线向厚侧移动的位移记作正值, 向薄侧移动的位移记作负值).过渡区中心线偏移量能够有效地反映差厚板的成形精度, 过渡区内应变分布越均匀, 则过渡区中心线偏移量越小, 说明差厚板成形后零件的厚度分布与板料厚度分布越接近, 有利于差厚板的结构设计.
图 9(Fig. 9)
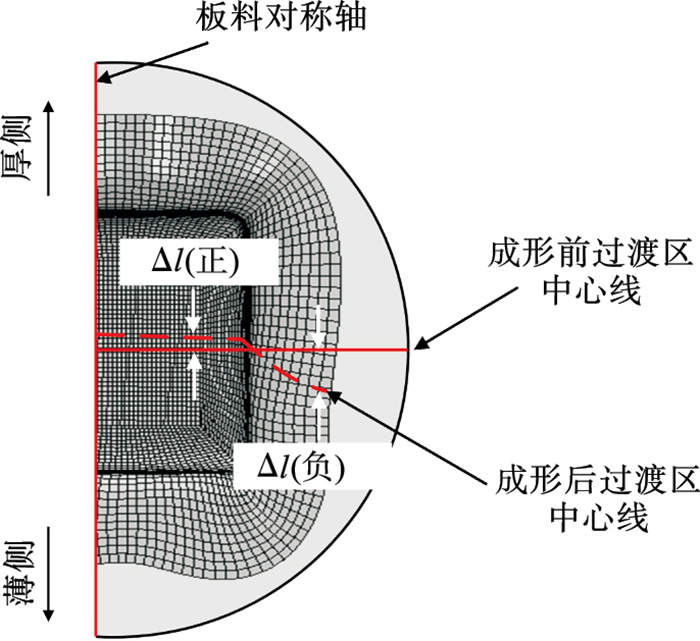 | 图 9 过渡区中心线上各点偏移量的测量方法Fig.9 Measuring the displacement of each point on the center line of TTZ |
4.2 过渡区长度对方盒件拉深成形性能的影响在过渡区位置和厚度差一定的条件下, 对过渡区长度分别为60,80,100,120和140 mm的差厚板进行方盒件拉深成形模拟, 图 10给出了不同过渡区长度对应的极限拉深高度以及过渡区中心线上各点偏移量.由图 10a可以看出, 随着过渡区长度的增加, 极限拉深高度先减小, 后增大, 当长度为100 mm时, 拉深高度最低, 分别为25.6 mm(60 mm),23.4 mm(100 mm)和24.1 mm(140 mm).当过渡区长度小于方盒件的边长时, 凸模圆角分别与等厚度的薄区和厚区接触, 变形主要集中在等厚度区域, 而过渡区内应变较小.此时过渡区越长, 则薄区和厚区占比越小, 从而导致成形过程中能够发生流动的金属减少, 方盒件的极限拉深高度降低.当过渡区长度大于方盒件边长时, 凸模圆角与过渡区接触, 成形过程中过渡区和等厚度区域均发生较大变形.此时过渡区越长, 沿轧制方向差厚板的厚度及力学性能变化越平缓, 从而导致成形过程中应变分布的不均匀程度降低, 能够发生流动的金属增多, 方盒件的极限拉深高度升高.
图 10(Fig. 10)
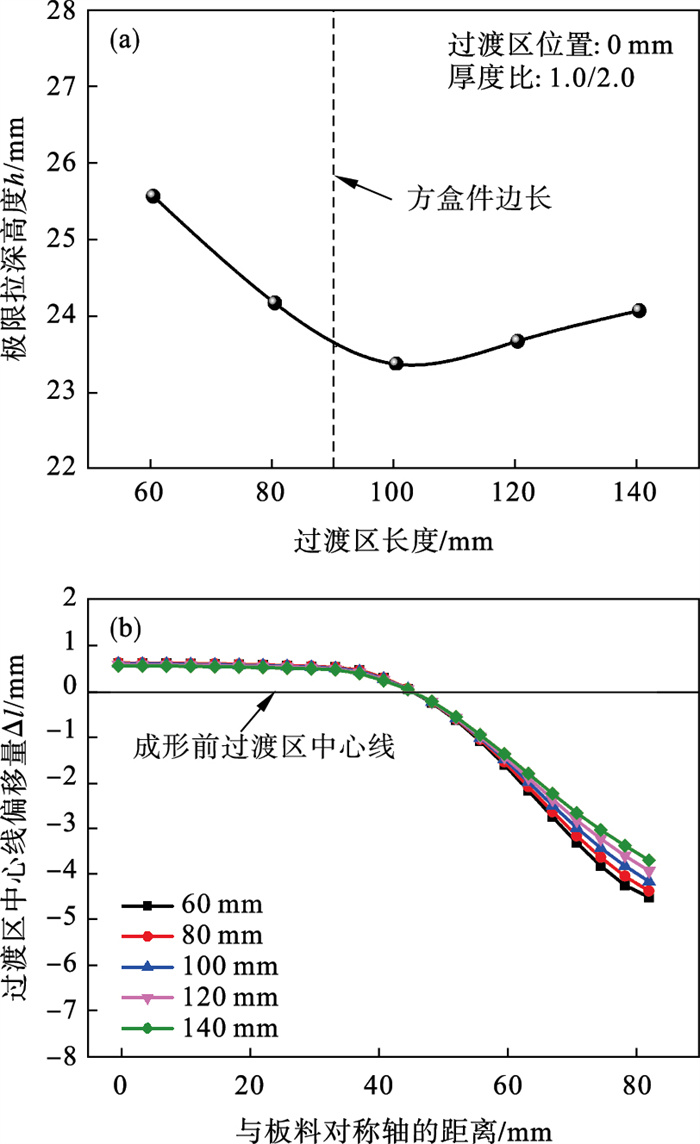 | 图 10 不同过渡区长度对应的差厚板方盒件的极限拉深高度和过渡区中心线上各点偏移量Fig.10 Limit drawing height and the offset of TTZ at different lengths of TTZ (a)—极限拉深高度;(b)—过渡区中心线上各点偏移量. |
由图 10b可以看出, 位于方盒件底部的过渡区向厚侧移动, 而位于方盒件法兰处的过渡区向薄侧移动.这是由方盒件成形过程中金属流动方向和流量决定的: 1)法兰处的部分金属分别向薄侧圆角和厚侧圆角流动, 而侧壁处的部分金属向底部流动; 2)薄侧厚度较小且强度较低, 成形时更容易发生变形, 所以薄侧流入凹模及其底部的金属更多.此外, 随着过渡区长度增加, 过渡区中心线偏移量减小.由图 10b还可以看出, 具有不同长度过渡区的方盒件, 中心线偏移量相差不大, 说明过渡区长度对过渡区移动的影响较小.
4.3 过渡区位置对方盒件拉深成形性能的影响在过渡区的长度和厚度差一定的条件下, 对过渡区位置分别为-10, -5, 0, 5, 10 mm的差厚板进行方盒件拉深成形模拟(采用过渡区中心线与板料中心线之间的距离表述过渡区位置, 过渡区靠近厚侧时, 距离值为正; 反之, 距离值为负).图 11给出了不同过渡区位置对应的极限拉深高度以及过渡区中心线上各点偏移量.可以看出, 随着过渡区由厚侧向薄侧移动, 方盒件的极限拉深高度逐渐上升,由24.3 mm升至26.6 mm; 同时, 过渡区中心线的偏移量显著减小.这是因为与薄区相比, 厚区材料强度高而塑性低(屈服强度高91 MPa, 均匀延伸率低4.2 %), 拉深过程中厚区金属流动性相对较差, 盒形件首先在厚区底部圆角位置处破裂.当过渡区靠近薄区时, 板料内厚区所占比例较大, 厚区金属受到外力而发生的塑性应变可以分散到更多区域内进行.因此, 随着板料内厚区所占比例增加, 板料内应变分布的均匀程度有所升高, 从而导致极限拉深高度增加, 过渡区中心线的偏移量降低.
图 11(Fig. 11)
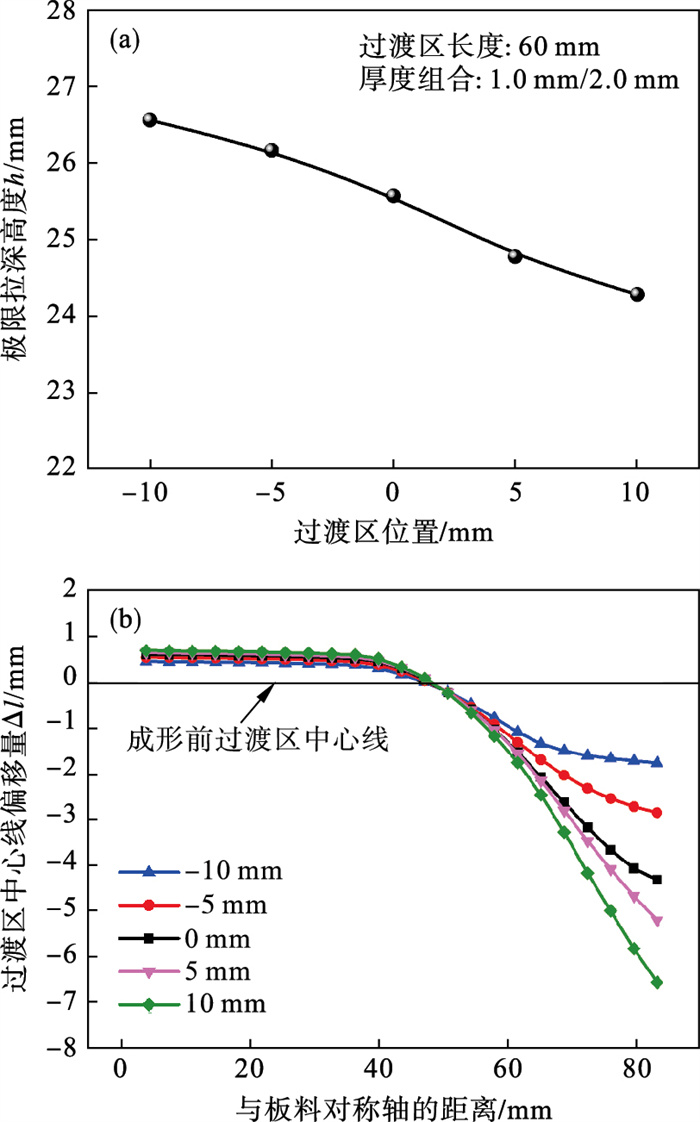 | 图 11 不同过渡区位置对应的差厚板方盒件的极限拉深高度以及过渡区中心线上各点偏移量Fig.11 Limit drawing height and the offset of TTZ at different positions of TTZ (a)—极限拉深高度;(b)—过渡区中心线上各点偏移量. |
4.4 厚度差对方盒件拉深成形性能的影响在过渡区的长度和位置一定的条件下, 对厚度组合分别为1.0 mm/2.0 mm, 1.2 mm/2.0 mm, 1.4 mm/2.0 mm, 1.6 mm/2.0 mm和1.8 mm/2.0 mm的差厚板进行方盒件拉深成形模拟, 以研究厚度差对极限拉深高度以及过渡区中心线上各点偏移量的影响.如图 12所示, 随着薄区与厚区的厚度差减小, 方盒件的极限拉深高度上升,由25.6 mm升高至27.1 mm.同时, 过渡区中心线的偏移量显著减小.造成这种现象的原因是: 随着厚度差的减小, 板料厚度和力学性能的不均匀程度降低, 在拉深成形过程中, 板料薄厚两侧的厚度和力学性能越接近, 则应变分布越均匀, 金属流动越充分, 各区域的变形更加同步.因此, 随着厚度差的减小, 差厚板成形过程中的变形方式更加接近等厚度板, 从而导致极限拉深高度增加, 过渡区中心线偏移量减小.
图 12(Fig. 12)
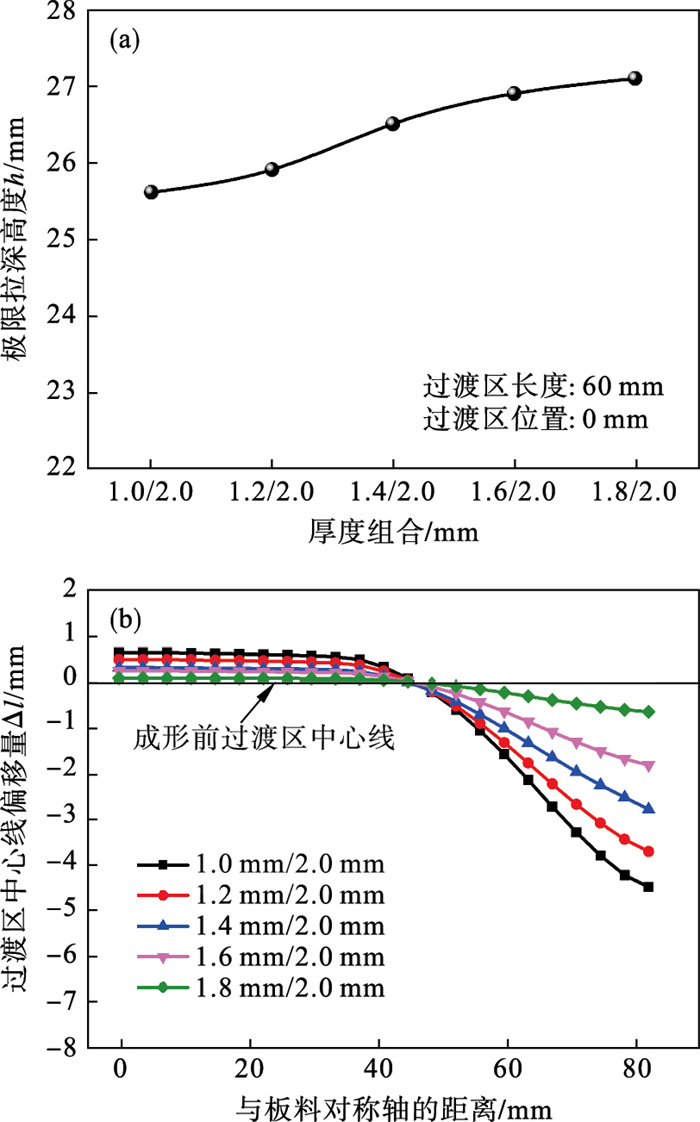 | 图 12 不同厚度组合对应的差厚板方盒件的极限拉深高度以及过渡区中心线上各点偏移量Fig.12 Limit drawing height and the offset of TTZ at different thickness combinations (a)—极限拉深高度;(b)—过渡区中心线上各点偏移量. |
4.5 几何参数对方盒件轻量化效果的影响表 1给出了典型差厚板的几何参数、极限拉深高度和质量.可以看出, 实验用差厚板(TRB-1)方盒件的极限拉深高度为23.4 mm, 质量约为0.299 5 kg.将过渡区长度由100 mm缩短至60 mm(TRB-2), 可以在不改变方盒件质量的前提下, 使其拉深高度上升约9.1 %.在此基础上,采用将过渡区向薄侧移动或增加薄区厚度的方法均会使方盒件的极限拉深高度进一步提升, 使其轻量化效果降低.经计算, 将过渡区向薄侧移动10 mm(TRB-3), 可使拉深高度上升3.9 %, 同时方盒件质量增加8.1 %; 将薄区厚度由1.0 mm增加至1.8 mm(TRB-4), 可使拉深高度上升5.9 %, 同时方盒件质量增加26.7 %.
表 1(Table 1)
| 表 1 典型差厚板的几何参数、极限拉深高度和质量 Table 1 Geometric parameters, limit drawing height and mass of the typical TRBs |
因此, 确定差厚板的几何参数时, 需根据实际工况, 综合考虑板料的成形性能和轻量化效果, 从而在满足性能要求的前提下, 获得良好的节材减重效果.
5 结论1) 差厚板显微组织及力学性能的分布情况由轧制压下率和退火工艺参数决定.当压下率范围为9 % ~54 %, 退火工艺为620 ℃, 保温60 min时, 厚区发生静态回复, 薄区发生完全再结晶, 过渡区则发生不完全再结晶, 且压下率越大, 再结晶晶粒的体积分数越大.随着压下率的增大, 差厚板的强度呈现先升高后降低的趋势; 塑性呈现先降低后升高的趋势.
2) 建立了差厚板方盒件拉深成形的有限元模型, 采用引入场变量的方法导入材料模型, 采用解析场中构建映射关系的方法赋予工件厚度变化.模拟和实验结果基本吻合, 说明有限元模型能够有效地预测差厚板方盒件的拉深成形过程.
3) 对于力学性能分布不均匀的差厚板, 其方盒件的拉深成形性能与板料几何参数有关.随着过渡区长度的增加, 极限拉深高度呈现先减小、后增大的趋势; 过渡区中心线偏移量减小.随着过渡区由厚侧向薄侧移动, 极限拉深高度增加; 过渡区中心线偏移量减小.随着板料薄区与厚区厚度差的减小, 极限拉深高度增加; 过渡区中心线偏移量减小.
参考文献
| [1] | 李新创, 郜学, 姜晓东. 我国钢铁工业"十三五"节能潜力分析[C]// 第十届中国钢铁年会暨第六届宝钢学术年会论文集. 上海, 2015: 1-5. (Li Xin-chuang, Gao Xue, Jiang Xiao-dong. Analysis on potential of energy conservation of Chinese steel industry in the 13th five-year period[C] // The 10th CSM Steel Congress & The 6th Baosteel Biennial Academic Conference. Shanghai, 2015: 1-5. ) |
| [2] | Zhang S J, Liu X H, Liu L Z. A tensile specimen of tailor rolled blanks with equal probability in yield and its mechanical behavior analysis[J]. Materials, 2018, 11(5): 693-711. DOI:10.3390/ma11050693 |
| [3] | Liu X H, Zhao Q L, Liu L L. Recent development on theory and application of variable gauge rolling: a review[J]. Acta Metallurgica Sinica(English Letters), 2014, 27(3): 483-493. DOI:10.1007/s40195-014-0065-z |
| [4] | 张华伟. 轧制差厚板成形性能研究[D]. 大连: 大连理工大学, 2012. (Zhang Hua-wei. Research on formability of tailor rolled blank[D]. Dalian: Dalian University of Technology, 2012. ) |
| [5] | Merklein M, Johannes M, Lechner M, et al. A review on tailored blanks — production, applications and evaluation[J]. Journal of Materials Processing Technology, 2014, 214(2): 151-164. DOI:10.1016/j.jmatprotec.2013.08.015 |
| [6] | Liu X H. Prospects for variable gauge rolling: technology, theory and application[J]. Journal of Iron & Steel Research International, 2011, 18(1): 1-7. |
| [7] | Lu R H, Liu X H, Fu S T, et al. Experiment and simulation for the crushing of tailor rolled tubes with various geometric parameters[J]. International Journal of Mechanical Sciences, 2018, 136: 371-395. DOI:10.1016/j.ijmecsci.2017.12.043 |
| [8] | Kleiner M, Chatti S, Klaus A. Metal forming techniques for lightweight construction[J]. Journal of Materials Processing Technology, 2006, 177: 2-7. DOI:10.1016/j.jmatprotec.2006.04.085 |
| [9] | Urban M, Krahn M, Hirt G, et al. Numerical research and optimization of high pressure sheet metal forming of tailor rolled blanks[J]. Journal of Materials Processing Technology, 2006, 177: 360-363. DOI:10.1016/j.jmatprotec.2006.03.195 |
| [10] | Putten K V, Urban M, Kopp R. Computer aided product optimization of high pressure sheet metal formed tailor rolled blanks[J]. Steel Research International, 2005, 76(12): 897-904. DOI:10.1002/srin.200506113 |
| [11] | Jiang Y F, Fang L, Li Z F, et al. Formability window of tailor rolled blanks at blank holder force[J]. Advanced Materials Research, 2011, 156(156/157): 488-491. |
| [12] | Li Y H, Du J T. Research of geometric parameters related to TRB uniaxial tension[J]. Advanced Materials Research, 2010, 97: 268-272. |
| [13] | Zhang H W, Liu X H, Liu L Z, et al. Forming limit and thickness transition zone movement for tailor rolled blank during drawing process[J]. Journal of Iron and Steel Research International, 2016, 23(3): 185-189. DOI:10.1016/S1006-706X(16)30032-2 |
| [14] | 杨兵, 高永生, 张文, 等. 变厚板(VRB)冲压成形数值模拟[J]. 塑性工程学报, 2015, 22(1): 88-93. (Yang Bing, Gao Yong-sheng, Zhang Wen, et al. Numerical simulation technology of stamping of variable-thickness rolled blank(VRB)[J]. Journal of Plasticity Engineering, 2015, 22(1): 88-93. DOI:10.3969/j.issn.1007-2012.2015.01.017) |
| [15] | Zhang S J, Hu X L, Niu C L, et al. Annealing of HC340LA tailor rolled blanks—Control of mechanical properties and formability[J]. Journal of Materials Processing Technology, 2020, 281: 116581. DOI:10.1016/j.jmatprotec.2019.116581 |
