周逸夫^1,2, 李鹤^1,2
1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动 及控制教育部重点实验室, 辽宁 沈阳 110819
收稿日期：2021-08-10
基金项目：国家自然科学基金资助项目(51675091)。
作者简介：周逸夫(1995-)，男，辽宁沈阳人，东北大学博士研究生;
李鹤(1975-)，男，河南方城人，东北大学教授，博士生导师。

摘要：转向节的作用是传递和承受汽车的前部载荷, 支承和驱动前轮绕主销转动, 使汽车转向.针对仍处于开发阶段的某麦弗逊式转向节的疲劳失效问题, 提出了一种对其台架试验结果进行评估的方法, 根据转向节在系统中的实际连接情况分多工况进行了疲劳台架试验, 利用Weibull分布理论结合N_50%, N_90%标准对转向节的失效循环次数分布进行了评价, 同时推导了一种局部疲劳裂纹尺寸的概率分布预测模型, 并利用实测试验数据验证了所推导预测模型的适用性.
关键词：转向节前悬系统疲劳试验Weibull分布裂纹尺寸分布
Fatigue Life Assessment of a Vehicle Steering Knuckle and Probability Distribution of Its Local Crack Size
ZHOU Yi-fu^1,2, LI He^1,2
1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion System, Ministry of Education, Northeastern University, Shenyang 110819, China
Corresponding author: LI He, E-mail: hli@mail.neu.edu.cn.

Abstract: The steering knuckle is used to transfer and bear the front load of the vehicle, support and drive the front wheel to rotate around the kingpin to make the automotive turn. Aimed at the fatigue failure of a McPherson-type steering knuckle which is still at the development stage, a method is proposed to evaluate the rig test results based on its actual connection situation in the system, and the fatigue rig test is carried out under multiple working conditions. The failure cycle number distribution of the steering knuckle is evaluated by using Weibull distribution theory and N_50% and N_90% criteria. At the same time, a probability distribution prediction model of local fatigue crack size is derived, and the applicability of the proposed prediction model is verified by the experimental data.
Key words: steering knucklefront suspension systemfatigue testWeibull distributioncrack size distribution
随着人们对舒适性和操控性要求的不断提高, 汽车悬架系统的性能表现也得到了消费者更高的关注.目前, 汽车设计师致力于使产品轻量化, 在节约成本的同时保证产品的安全性.轻量化悬架部件顺应了汽车工业节能减排的趋势, 也将提高汽车的操控性能, 这对于传统能源汽车和新能源汽车都有很高的匹配价值.前悬架系统通过连接底盘框架和车轴来支撑车辆, 同时还吸收车轮引起的振动^[1].转向节是汽车前悬架系统的重要部件之一.根据转向节在前悬架系统之间的装配关系, 转向节需要承受加速、制动、碰撞等引起的循环载荷和扭矩.因此, 要求其具有较高的疲劳强度.传统上, 转向节采用球墨铸铁制造, 但近年来, 铝合金零部件在转向节中的渗透率逐年升高, 宝马等多数豪华品牌在很多车型上都采用了铝合金转向节, 以减少簧下质量.
对于仍处在开发环节的汽车底盘零部件而言, 使用台架零部件试验代替部分整车测试是一种更为高效且经济的方式.Chang等^[2]对发动机支架的动态强度进行了台架试验, 并优化了一种发动机支架的疲劳强度评估方法.Han等^[3]建立了半挂车发动机台架试验耐久性评估方法, 同时对发动机台架试验的损伤进行了测量并优化了台架试验方法.Meyer等^[4]和Esmaeili等^[5]分别通过台架试验和多轴疲劳分析, 研究了预紧力对铝合金螺栓连接疲劳强度的影响和剪切循环载荷下的疲劳裂纹扩展问题, 他们的研究在包含螺栓连接的汽车部件仿真分析中具有一定的应用前景, 但其建模方法在模拟螺栓预紧力和空间约束对局部破坏机制的影响方面仍存在一定的局限性.另外, 疲劳寿命的评估也是汽车零部件设计过程中的一个主要问题, Weibull分布是进行寿命评估的重要方法之一, Cordeiro等^[6]推导了一种体现特征和最薄弱环节尺寸效应的材料疲劳概率模型.在其基础上, Caiza等^[7]完善了该模型, 给出了Weibull分布的概率加权矩的一般表达式, 将其应用于疲劳参数的估计, 得到了准确的估计结果.
为保证疲劳强度的设计要求, 往往规定要从生产线中随机抽取样品进行疲劳试验, 根据疲劳试验中出现的裂纹位置、尺寸来判别、认可产品的制造质量.同一失效准则下疲劳裂纹尺寸的分布是进行结构耐久性设计和分析的主要依据之一^[8].为了对部件失效循环次数和裂纹尺寸进行数理统计, Khalili等^[9]利用贝叶斯理论来更新裂纹尺寸等不确定参数的概率分布, 修正裂纹尺寸分布后, 可以提高接头可靠性估计的准确性.顾怡等^[8]从疲劳裂纹扩展的规律和随机性出发, 讨论了裂纹尺寸的随机分布, 其研究结果证实了裂纹尺寸服从类似于对数正态分布.Co等^[10]建立了一种多项式随机疲劳裂纹扩展模型.研究了该模型的对数正态随机变量和对数正态白噪声两种极端情况, 得到了任意服役时间随机裂纹尺寸分布函数的解析解和达到规定裂纹尺寸的随机时间分布函数.Solomos等^[11]研究了疲劳裂纹扩展过程中裂纹尺寸的分布规律，通过疲劳裂纹扩展规律引入了裂纹的马尔可夫模型, 建立了相应的Fokker-Planck方程, 并对其边界条件进行了详细的描述.Wang等^[12]基于弹塑性断裂力学方法研究短裂纹疲劳寿命关联方程, 得到了计算疲劳裂纹起裂尺寸的基本模型.通过引入疲劳裂纹萌生寿命、疲劳总寿命和失效时裂纹尺寸的计算方法, 进一步完善了疲劳裂纹萌生尺寸预测模型.在实际测试工况下, 对于一批结构相同的零部件, 由于材料和加工工艺等因素不可避免存在微小的差异, 导致裂纹的扩展速率不尽相同.因此对同一批零部件采用同一确定的裂纹扩展速率预估部件的疲劳裂纹尺寸显然是不合理的, 有必要针对测试结果的裂纹尺寸的概率分布展开研究.
在前悬系统中, 可以根据每个部件具体的工作方式将台架试验分解为多个受载模式.每个受载模式相对独立, 可以分别独立地进行台架试验.本文以某麦弗逊式独立悬架系统中的转向节为研究对象, 提出了一种针对其疲劳失效循环次数的评价方法.首先考虑其在前悬系统中与其他部件的实际连接关系, 分多种疲劳工况对其进行了疲劳台架试验.将试验数据进行双参数Weibull分布后, 利用N_50%, N_90%标准对其进行了评价.随后, 基于裂纹的扩展速率始终大于零这一共性, 利用超值概率分布推导了随机分布的裂纹尺寸预测方法, 利用试验结果对所提出的裂纹尺寸的概率预测模型进行了验证.本文研究成果可为汽车零部件的疲劳台架试验和裂纹尺寸估计提供理论和现实参考.
1 基于Weibull分布的寿命评价方法Weibull分布是以瑞典物理学家W. Weibull的名字命名的, 由其分析材料强度时在经验的基础上推导而来, 通常包含2个或3个参数.双参数Weibull分布模型广泛应用于机械零件的寿命预测.本文采用线性最小二乘法估计试验的可靠失效循环次数, 每个试验结果的出现频率确定如下:

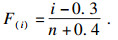(1)

式中: F为完整数据分布函数的经验取值; n为试验样本数, i=1 ~n.Weibull分布的最小二乘法一般采用逆变换法, 其累积分布函数有如下形式^[13]:

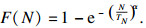(2)

式中: T_N是负载循环的特征数, 是标度参数.α是形状参数, N是采样周期数.失效循环的数据是从最小到最大排序的, 因此回归模型的自变量N₁, N₂, …, N_n也是从最小到最大排序的.对于具有未审查数据的试样, 可使用近似中值秩公式来估计每个失效循环数的失效概率:

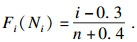(3)

由式(3)可得因变量序列Y₁, Y₂, …, Y_n, 然后用最小二乘原理估计回归系数a和b:

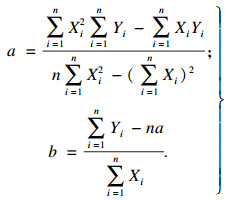(4)

通过反变换获得形状和尺寸参数的估计值:

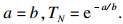(5)

最后, 10%, 50%和90%失效可靠度下的载荷循环数为

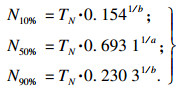(6)

利用计算得到的评价参数, 本文为转向节设计疲劳试验方案, 并对试验结果进行评估的流程图如图 1所示.
图 1(Fig. 1)

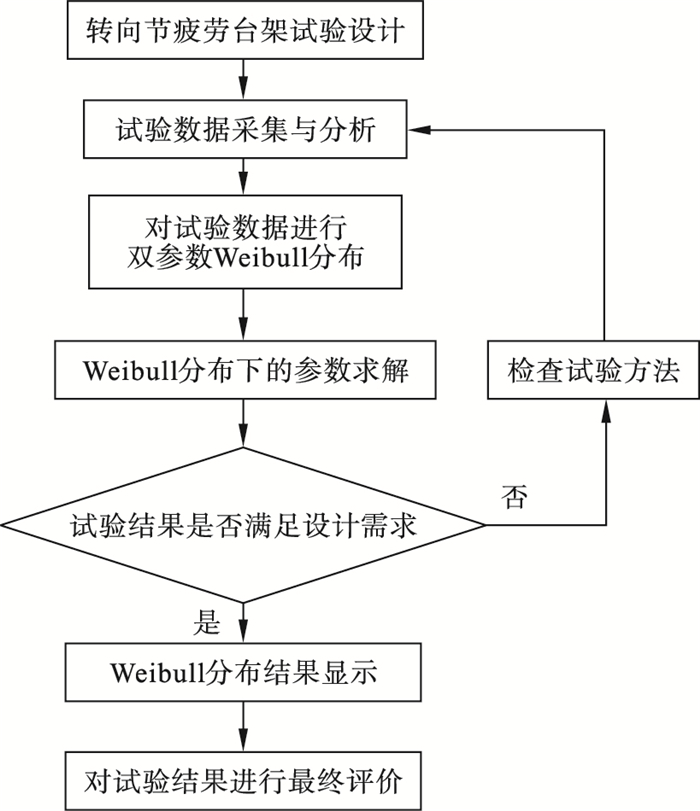图 1 对转向节疲劳试验结果进行评价的流程图Fig.1 Flow chart for evaluating the fatigue test results of steering knuckles

2 转向节的疲劳强度测试方案疲劳失效一般指的是由循环载荷引起的材料损伤过程.对于转向节而言, 其失效位置取决于加载条件和它的几何结构.处于开发设计阶段的转向节属于正向设计, 需根据周边部件与其连接情况布置后续的疲劳台架试验, 通过试验结果来验证转向节是否达到设计要求.本文将根据某麦弗逊式独立悬架系统中转向节的实际连接情况, 分多种工况设计转向节的疲劳台架测试方案.
2.1 转向节在前悬系统中的实际连接情况如图 2所示, 本文研究的麦弗逊式独立悬架的主要特点为: 转向节分别与转向横拉杆、下控制臂、制动卡钳和减震器连接并且其受到的载荷主要来自于横拉杆、下控制臂和减震器.当悬架弹性变形或方向盘偏转导致它们相对于车架跳动时, 转向节与横拉杆也在相对空间内运动, 为避免发生运动干扰, 它们之间通过球头螺栓进行连接.减震器上端与车架铰链连接, 下端与转向节连接.下控制臂的内端与车架铰链连接, 外端与转向节连接, 同样是通过球头螺栓进行连接.转向节通过球头螺栓与上述部件连接的部位在工作时需要承受巨大的扭矩, 因此, 转向节在此类区域的失效概率较大.
图 2(Fig. 2)

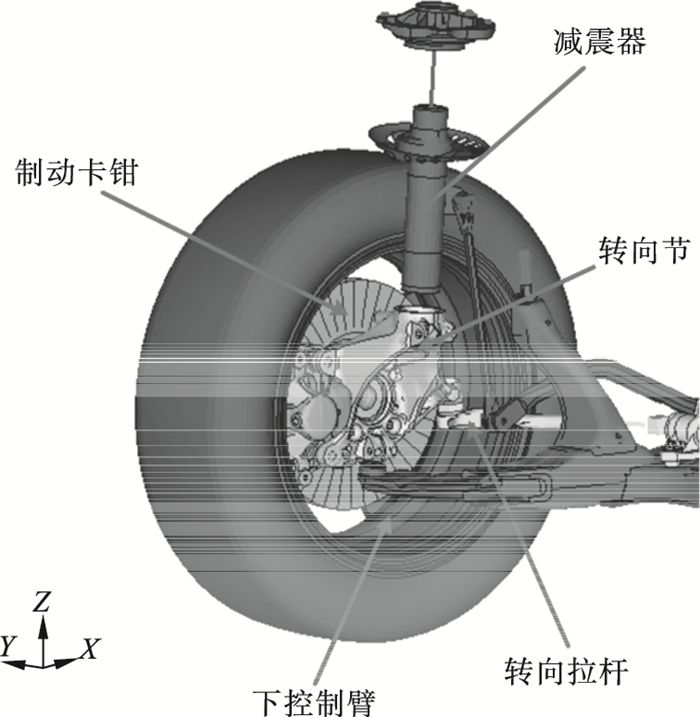图 2 前悬系统中转向节的连接关系示意图Fig.2 The connection situation of steering knuckle in the front suspension system

本文仅关注转向节的疲劳失效问题, 故基于上述结构件之间的连接关系, 在本文设计的台架试验方案中将使用直拉杆替代转向拉杆、下控制臂等连接部件, 并通过如图 3所示的球头螺栓结构将连接部件的载荷传递到转向节上.使用钢板代替原制动卡钳, 通过螺栓连接与转向节一起拧紧固定在夹具上, 但需要注意的是, 转向节与试验装置的接触方式需要与原部件间的接触方式保持一致.
图 3(Fig. 3)

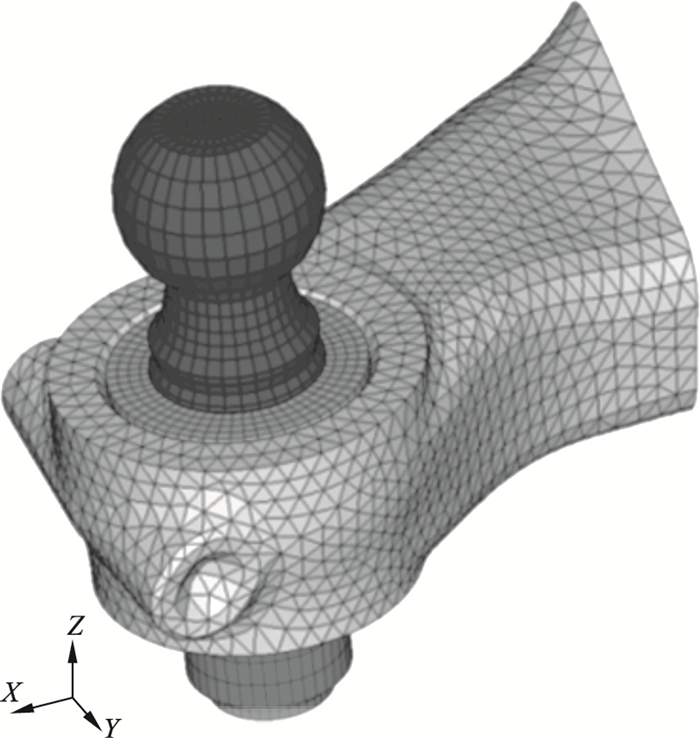图 3 转向节与直拉杆连接方式Fig.3 The connection mode of steering knuckle and tie rod

2.2 不同连接工况下转向节的疲劳试验方案如上所述, 对于转向节而言, 由球头螺栓连接的部位更容易出现疲劳失效现象, 本文将针对转向节的三类连接工况, 分别制定其疲劳失效的试验方案.
为保证拉杆连接与转向节之间的接触方式与原工作方式保持一致, 载荷的作用点及方向也需与原工作方式保持一致, 图 4为载荷施加在转向节臂的三种试验工况.
图 4(Fig. 4)

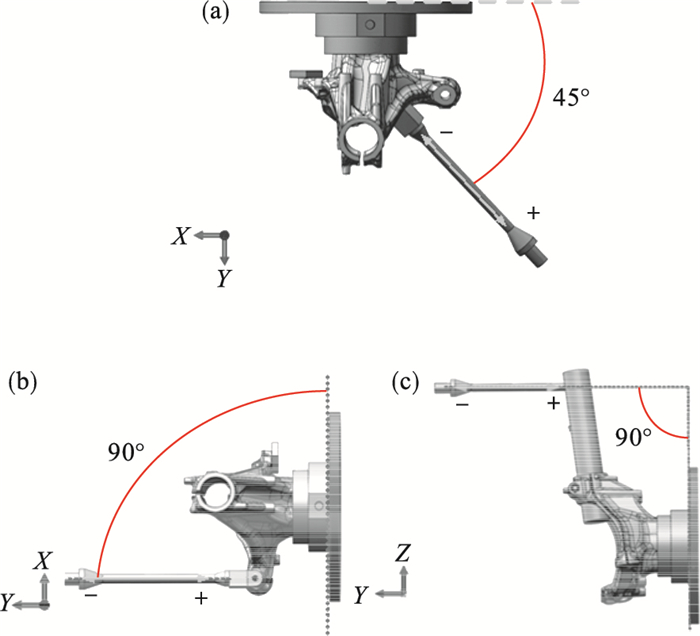图 4 施加载荷的位置及方向Fig.4 Position and direction of the applied loads (a)—下控制臂工况; (b)—横拉杆工况; (c)—减震器工况.

如图 4a所示, 在下控制臂侧向工况中, 载荷与固定夹具成45°角, 在X-Y平面上与夹紧面成45°(与XZ平面成45°角).如图 4b所示, 在横拉杆垂直工况中, 转向节横拉杆将承受拉压载荷, 载荷位于Y-Z平面(垂直于XZ平面, 平行于XY平面).如图 4c所示, 在减震器垂直工况下, 拉压载荷将施加在减震器上, 载荷位于Y-Z平面(垂直于XZ平面, 平行于XY平面).
试验台的载荷数据基于真实车辆测量和虚拟车辆的运行载荷仿真.根据上述实际测量载荷通过多体动力学软件迭代到转向节后, 分别在转向节与下控制臂连接处、横拉杆连接处与减震器连接处布置了6种载荷工况.
为符合实际设计需求, 要求如果采用10%的存活率, 试验载荷必须大于存活率为10%的S-N曲线上循环次数对应的100 000次循环的载荷值, 循环次数也必须大于100 000次.如果使用50%的存活率, 则试验载荷必须大于与存活率为50%的S-N曲线上循环次数对应的170 000次循环的载荷值, 并且循环次数也必须大于170 000次.为验证转向节是否符合设计需求, 从首批试制样件中随机抽取了一批转向节分三组进行了疲劳测试.
3 疲劳试验数据的采集与分析所提出试验台的搭建方式如图 5所示, 通过地脚螺栓与夹具等零件将液压作动器和转向节固定在试验台架上, 根据已经调好的转向节的位置, 调节液压作动器的位置, 并保证作动器水平加载.本试验采用MOOG公司的电液伺服阀和MTS公司生产的线性作动器, 最大动态试验力为±100 kN, 最大行程范围为±150 mm.用球头螺栓将液压作动器与转向节的下控制臂、转向拉杆和减振套筒连接处进行连接, 并利用液压作动器的前后运动对转向节的连接端施加纵向载荷.所有的载荷工况采用正弦往复加载, 载荷工况如表 1所示.一般地, 底盘部件的台架测试频率在1~30 Hz之间, 在此区间增大试验的试验频率对试验结果一般不产生影响.本文依据德国BAB(Bauteil Auslegungs Blatt)工程测试标准, 在所有负载情况下, 频率均采用10 Hz恒定.采用位移传感器, 该传感器布置在适配器连接端, 并与弯曲杆轴连接, 测量施力方向位移, 参考初始BAB载荷水平的停机标准, 即在试验过程中, 以测点处的0.2 mm位移作为停机标准, 此时视为转向节已发生疲劳失效, 作动器停止加载, 试验立即停止.如果运行至340 000次循环时仍未达到停机标准, 则初始载荷+10%继续进行试验; 重复上述过程, 直到达到停机标准为止.
图 5(Fig. 5)

图 5 疲劳试验平台Fig.5 Fatigue test bench

表 1(Table 1)

表 1 不同连接位置的载荷工况Table 1 Load cases of different connection positions 载荷位置 载荷方案 大小/kN 频率/Hz 下控制臂 Load case 1 9.75±22.5 10 下控制臂 Load case 2 10.5±24.5 10 横拉杆 Load case 3 ±17 10 横拉杆 Load case 4 ±16 10 减震器 Load case 5 2±8.5 10 减震器 Load case 6 2.5±10 10

表 1 不同连接位置的载荷工况 Table 1 Load cases of different connection positions

表 1为转向节施加的所有载荷工况, 所有工况的载荷频率均为10 Hz, 默认的正方向为拉伸方向.按照所述的试验方案, 对表 1中的载荷工况进行疲劳试验.为了使试验结果足够可信且便于统计, 本文将对随机抽取的42个转向节在每个工况下分7组进行试验, 试验结果如图 6所示.
图 6(Fig. 6)

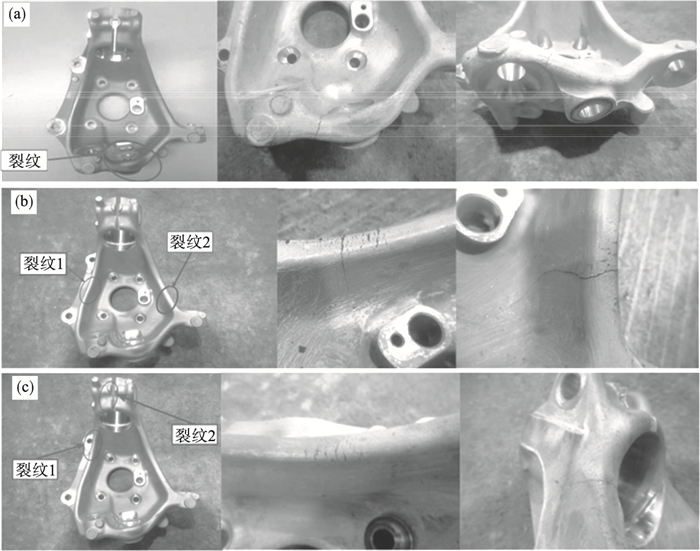图 6 疲劳试验结果Fig.6 Fatigue test results (a)—下控制臂工况; (b)—横拉杆工况; (c)—减震器工况.

如图 6所示, 在满足停机标准后, 转向节表面均出现了疲劳裂纹, 且在同一工况下, 观察到的裂纹尺寸不一, 但发生位置全部一致.从图 6a可以发现, 对于下控制臂端的连接工况, 裂纹的发生位置处于下控制臂连接处的外缘.从图 6b可以发现, 对于横拉杆端的连接工况, 转向节的表面出现了两个裂纹, 分别处于转向节与横拉杆的接触部位和外壁.通过图 6c发现, 对于减震器端的连接工况, 转向节同样出现了两个裂纹, 其中一个位于外壁边缘, 另一个位于转向节与销连接的接触部位.
图 7为下控制臂端、横拉杆端和减震器端疲劳工况失效循环次数的统计图.其中, LS 10%和LS 50%分别代表 10%和50%的存活率要求, K值代表幂函数形式下试件S-N曲线斜率的负倒数.为使统计结果更加直观, 首先以第3章所述的100 000和170 000次的失效循环次数标准作为横坐标, 以BAB规定的最小载荷幅值作为纵坐标确定两个点, 过这两点分别作两条斜率为幂函数形式下试件S-N曲线斜率的直线, 再将纵轴转换为非幂函数形式后作为评价试件的两种标准线.从分布结果来看, 所有结果不仅能满足10%存活率的试验要求, 还能满足50%存活率的试验要求, 即满足了一般以50%存活率作为设计准则的要求.下面将对转向节的失效循环次数进行Weibull分布并以50%失效可靠度进行评价, 最后对转向节表面裂纹尺寸的概率分布进行评价.
图 7(Fig. 7)

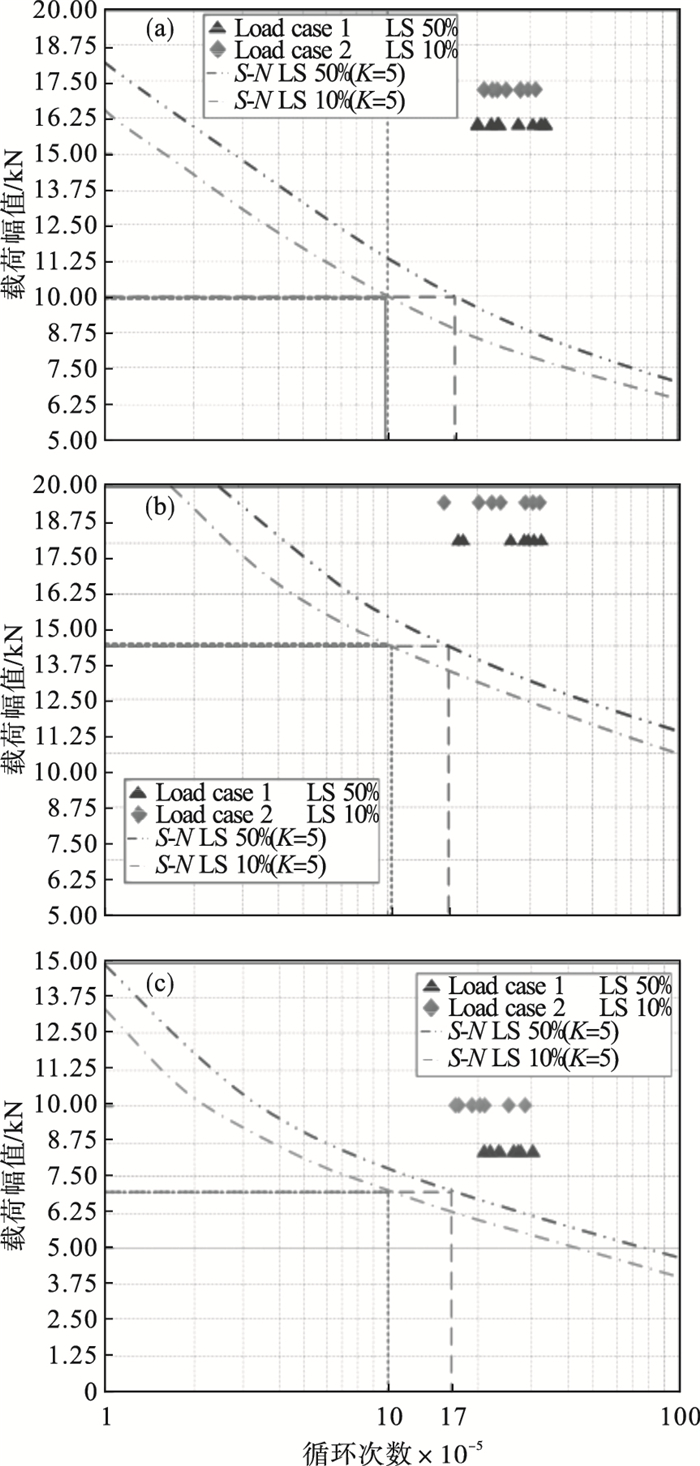图 7 疲劳失效循环次数分布Fig.7 Distribution of fatigue failure cycles (a)—下控制臂工况; (b)—横拉杆工况; (c)—减震器工况.

从图 7的分布结果可以看出, 所有试验结果都满足了50%存活率的试验要求.对转向节的失效循环次数进行Weibull分布, 分布结果如图 8所示.
图 8(Fig. 8)

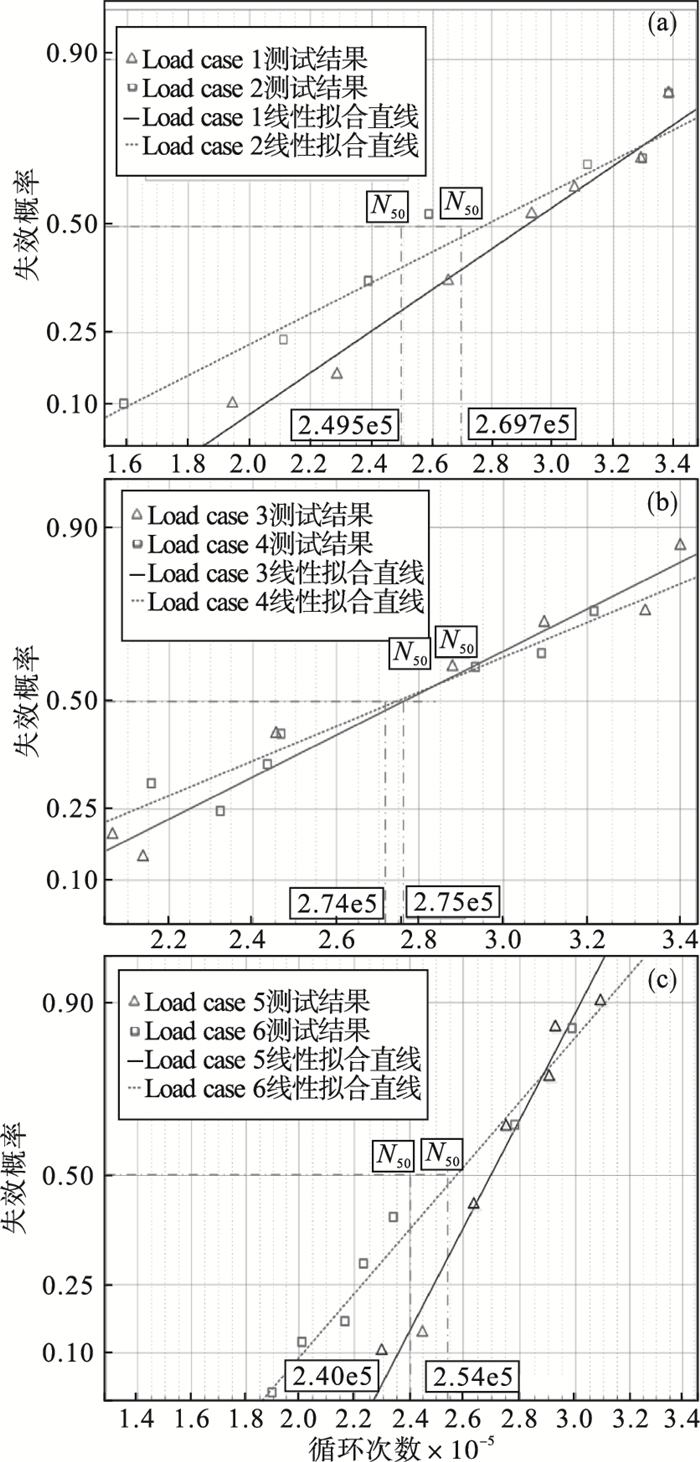图 8 试验结果的Weibull线性分布Fig.8 Weibull linear distribution of the test results (a)—下控制臂工况; (b)—横拉杆工况; (c)—减震器工况.

如图 8所示的统计结果, 转向节的疲劳寿命服从以N_50%为标准的Weibull分布.根据德国汽车工业质量标准, 试验应考虑散射的N_90%/N_10%是否大于5.如果是这种情况, 应检查试验台.经检验, 本次试验结果的N_90%/N_10%均小于5, 符合设计要求.
4 疲劳裂纹尺寸的概率分布模型由试验结果可知, 由于加载系统的波动及转向节本身制造工艺的差异性等因素, 在转向节达到疲劳失效终止条件时, 转向节表面出现的裂纹长度也属于随机分布.即使在实验室测试中采用良好控制的确定性加载, 疲劳裂纹扩展数据依然表现出显著的统计变异性.使用概率方法来预测结构单元的疲劳裂纹扩展是更具说服力的.令随机变量A_n表示疲劳寿命为n时的裂纹长度, 取值为a_n.裂纹扩展规律可以用Paris公式^[14]描述:

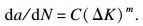(7)

其中: da/dN为每循环应力周期裂纹长度的平均增量; C和m为材料参数; ΔK为应力强度因子范围, 可以表示为

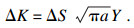(8)

式中：ΔS为外载；Y为裂纹形状系数, 一般在1~2之间, 则式(7)可变为

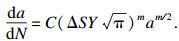(9)

设转向节的疲劳裂纹长度在第k次循环时的长度为A_k, 则由式(9)得

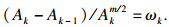(10)

其中, ω_k是一个只与ΔS和C相关的随机变量, 对其进行求和并写成积分形式:

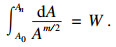(11)

由中心极限定理^[9]可知收敛于正态分布N(μ₀, σ₀²), 其概率密度函数h(ω)为

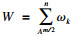
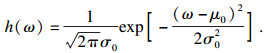(12)

对同一批转向节进行疲劳失效试验, 取A₀为定值a₀.A_n服从对数正态分布ln(μ₀+lna₀, σ₀²), 对于m≠2的工况, 其概率密度函数为

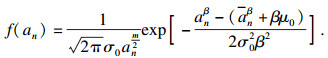(13)

则其概率为

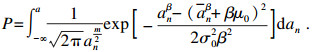(14)

可转化为

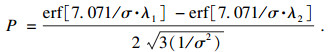(15)

其中: ; λ₂=0.01μ₀-a_n^0.1+0.794 3.
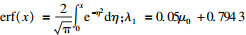
在试验达到停机标准后, 对转向节表面的裂纹尺寸a_n进行了观测.通过图 6所示的实验结果可以发现, 转向节发生疲劳失效时, 转向拉杆工况和减震器工况分别出现了两处明显的裂纹, 裂纹的具体尺寸分布如表 2所示.其中, 工况号代表该工况采用的载荷方案号.工况1, 2为下控制臂侧向测试工况, 工况3, 4为横拉杆垂直工况, 工况5, 6为减震器垂直工况.每个工况号中的载荷分别用CL1和CL2表示.选取6种疲劳工况中代表最大疲劳损伤的Load case 1(CL2), Load case 4, Load case 5(CL1), 利用平均秩公式分配其经验概率, 与本文推导出的失效概率预测值的对比结果如图 9所示.
表 2(Table 2)

表 2 六种工况下的裂纹尺寸Table 2 Crack size under six load cases? mm 工况 样本1 样本2 样本3 样本4 样本5 样本6 样本7 1 CL1-10/CL2-42 CL1-5/ CL2-30 CL1-7/CL2-40 CL1-8/CL2-62 CL1-8/CL2-46 CL1-5/CL2-33 CL1-10/CL2-62 2 CL1-3/ CL2-75 CL1-3/ CL2-45 CL1-2/CL2-45 CL1-3/CL2-48 CL1-2/CL2-40 CL1-2/CL2-53 CL-1-3/CL2-50 3 53 65 41 39 30 32 47 4 42 47 41 45 52 40 58 5 CL1-50/CL2-30 CL1-30/CL2-20 CL1-36/CL2-12 CL1-40/CL2-12 CL1-47/CL2-20 CL1-32/CL2-14 CL1-60/CL2-62 6 CL1-58/ CL2-8 CL1-43/CL2-15 CL1-41/CL2-10 CL1-40/CL2-5 CL1-34/CL2-8 CL1-28/CL2-12 CL-1-3/CL2-50

表 2 六种工况下的裂纹尺寸 Table 2 Crack size under six load cases?

图 9(Fig. 9)

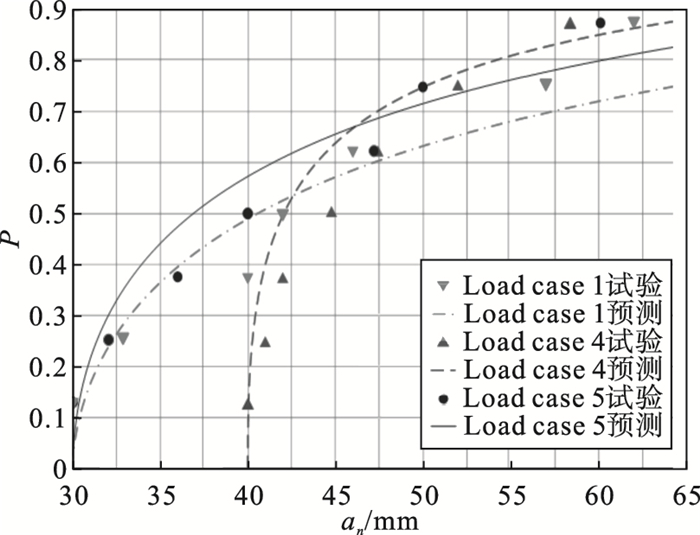图 9 多工况下裂纹尺寸的分布Fig.9 Distribution of crack size under multi-working conditions

如图 9所示, 从代表不同连接处的对比结果来看, 转向节发生局部失效时的裂纹尺寸与预测结果吻合良好, 本文推导的尺寸概率模型可以预测转向节发生失效时疲劳裂纹的尺寸分布.相比于整车失效的可靠性试验, 进行零部件级的试验无疑针对性更为明显且更容易操作.对于发生疲劳失效时裂纹的尺寸分布, 本文推导的裂纹尺寸分布概率预测模型可以进一步缩短试验周期, 节约研发成本.
5 结论1) 对于转向节的疲劳台架试验, 使用拉杆连接, 并通过球头螺栓与转向节臂相连接的方式可以较好地模拟原下控制臂、转向拉杆及减震器与转向节的连接关系, 但需要保证转向节与试验装置的接触方式必须与原连接件保持一致.
2) 在所有工况下, 转向节的疲劳寿命服从双参数Weibull分布.通过寿命的分布结果可以发现, 所有试验结果不仅满足最低试验标准, 而且满足50%存活率的设计标准.
3) 在发生疲劳失效时, 转向节表面的疲劳裂纹尺寸服从对数正态分布, 本文推导出的疲劳裂纹尺寸概率模型具有良好的预测效果.
参考文献

[1]	Chang Y S, Lee J. Reliability-based design optimization of knuckle component using conservative method of moving least squares meta-models[J]. Probabilistic Engineering Mechanics, 2011, 26(2): 364-379. DOI:10.1016/j.probengmech.2010.09.004
[2]	Chang J W, Lee Y S. Topology optimization of compressor bracket[J]. Journal of Mechanical Science& Technology, 2008, 22(9): 1668-1676.
[3]	Han Y, Lin Y, Zhang C, et al. Customer-related durability test of semi-trailer engine based on failure mode[J]. Engineering Failure Analysis, 2021, 120: 105095. DOI:10.1016/j.engfailanal.2020.105095
[4]	Meyer J J, Adams D E. Theoretical and experimental evidence for using impact modulation to assess bolted joints[J]. Nonlinear Dynamic, 2015, 81(1/2): 103-117.
[5]	Esmaeili F, Chakherlou T N, Zehsaz M. Prediction of fatigue life in aircraft double lap bolted joints using several multiaxial fatigue criteria[J]. Materials & Design, 2014, 59(7): 430-438.
[6]	Cordeiro G M, Gomes A E, Da-Sliva C Q, et al. The beta exponentiated Weibull distribution[J]. Journal of Statistical Computation & Simulation, 2013, 83(1): 114-138.
[7]	Caiza P, Ummenhofer T. General probability weighted moments for the three-parameter Weibull distribution and their application in S-N curves modelling[J]. International Journal of Fatigue, 2011, 33(12): 1533-1538. DOI:10.1016/j.ijfatigue.2011.06.009
[8]	顾怡, 姚卫星. 疲劳裂纹尺寸的随机分布[J]. 机械强度, 1992, 14(1): 30-32. (Gu Yi, Yao Wei-xing. Random distribution of fatigue crack size[J]. Mechanical Strength, 1992, 14(1): 30-32.)
[9]	Khalili H, Oterkus S, Barltrop N, et al. Different Bayesian methods for updating the fatigue crack size distribution in a tubular joint[J]. Journal of Offshore Mechanics and Arctic Engineering, 2020, 143(2): 1-28.
[10]	Co N, Burns J T. Effects of micro-scale corrosion damage feature and local microstructure on fatigue crack initiation location[J]. International Journal of Fatigue, 2021, 150(4): 106301.
[11]	Solomos G P, Lucia A C. Markov approximation to fatigue crack size distribution[J]. Fatigue & Fracture of Engineering Materials & Structures, 1990, 13(5): 457-471.
[12]	Wang H, Liu X, Wang X, et al. Numerical method for estimating fatigue crack initiation size using elastic-plastic fracture mechanics method[J]. Applied Mathematical Modelling, 2019, 73(9): 365-377.
[13]	Almalki S J, Nadarajah S. Modification of the Weibull distribution: a review[J]. Reliability Engineering & System Safety, 2014, 124: 32-55.
[14]	Liu C T. Critical analysis of crack growth data[J]. Journal of Propulsion & Power, 1990, 6(5): 519-524.