
 , 孙琦, 寇晓宇, 王立夫
, 孙琦, 寇晓宇, 王立夫 东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004
收稿日期:2021-07-15
基金项目:中央高校基本科研业务费专项资金资助项目(N2023022)。
作者简介:孔芝(1979-),女,辽宁北镇人,东北大学秦皇岛分校副教授。
摘要:现有的节点重要度排序方法大多只针对网络的拓扑结构进行研究, 忽视了网络节点自身所包含的属性信息.然而这些属性信息至关重要, 却广泛存在不完备性, 这些不完备属性信息与节点的重要性密切相关.针对这一问题, 提出一种基于优势粗糙集理论和TOPSIS方法的网络节点重要度分析方法, 融合网络结构特性和节点属性信息, 克服了单一从拓扑结构分析的局限.最后, 将本文所提出的方法应用于微博社交网络中的用户重要度评价, 并与其他方法进行比较, 结果表明, 该方法的排序结果对节点在属性信息和结构特性的重要性进行了较好的综合, 能全面地体现出各节点的重要程度.
关键词:复杂网络节点重要度微博网络属性重要度结构重要度
Research on the Importance of Network Nodes Based on Attribute Information and Structural Characteristics
KONG Zhi

 , SUN Qi, KOU Xiao-yu, WANG Li-fu
, SUN Qi, KOU Xiao-yu, WANG Li-fu School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: KONG Zhi, E-mail: kongz@neuq.edu.cn.
Abstract: Most of the existing node importance ranking methods only study the topology of the network, ignoring the attribute information contained in the network nodes themselves. Attribute information is very important, but there is widespread incompleteness. Incomplete attribute information is closely related to the importance of nodes. Aiming at these problems, a network node importance analysis method based on superior rough set theory and TOPSIS method is proposed, which combines network structure characteristics and node attribute information and overcomes the limitations of single topological structure analysis. Finally, the proposed method is applied to the user importance evaluation in Weibo social network and compared with other methods. The results show that the ranking results of this method can well synthesize the importance of each node in attribute information and structural characteristics and can fully reflect the importance of each node.
Key words: complex networknode importanceWeibo networkattribute importancestructure importance
随着互联网的高速发展, 人们的日常生活中充斥着各种各样的网络, 如通信网络、生物网络、交通网络、电力网络、社交网络等.网络中节点之间存在着错综复杂的关系, 当某些节点遭到破坏时, 其影响会迅速波及整个网络, 甚至导致网络瘫痪.因此, 对网络重要节点的评估与挖掘意义重大, 这对网络可靠性和鲁棒性的研究具有重要意义[1].
现有的重要节点挖掘方法, 主要考虑网络的拓扑结构来进行分析.常用的节点中心性指标主要有节点的度中心性[2]、接近中心性[3]、介数中心性[4]、特征向量中心性、H指数[5]与k-shell中心性[6]等.另外通过移除网络中的一些节点, 移除后对网络的破坏性即为节点的重要性, 研究人员提出了节点删除法[7]、节点收缩法[8]、节点凝聚法[9]和最大连通子图法等[10].单一结构性指标不能很好地评价节点的重要程度, 因此研究人员综合多种指标研究该问题.于会等[11]综合局部和全局的中心性指标进行多属性决策, 更为全面准确地得到了评价结果.Liu等[12]将k-shell指标进行改进, 并将其作为新的指标, 提出了一种基于与理想对象相似度排序的多属性排序方法.Lu等[13]针对传统TOPSIS方法的不足, 利用相对熵来解决不能有效区分正、负理想解中的垂直线节点的问题, 使得排序结果更为准确.从网络拓扑结构进行分析应考虑节点的局部信息以及全局信息, 因此研究人员从不同的角度展开了研究.胡钢等[14]通过分析关联节点的影响以及节点之间的传输能力, 构建了重要度传输矩阵, 同时考虑了节点的局部、全局信息, 综合评估节点的重要度.黄丽亚等[15]分别将网络中所有节点设置为传染源, 进行传染病传播, 定义K-阶传播数为网络中已感染的节点数量, 最终通过比较不同K值下的K-阶传播数的大小来对节点重要度进行评估.
以上关于节点重要度排序问题的研究, 主要考虑节点在网络中的结构特性, 忽视了网络节点自身的关键属性.而节点的自身属性密切影响着节点的重要程度.网络的拓扑结构只能体现网络中节点与节点之间的连接情况, 无法体现出每个节点的属性特征.因此只利用网络中的结构特性来挖掘重要节点, 具有一定的单一性和局限性.
而在实际网络中, 节点属性信息通过测量工具采集、传输、存储等方式获得, 由于传感器故障或数据保存失败等因素, 导致部分数据无法获得, 而数据缺失现象是无法避免的客观存在的问题.当节点属性信息不完备时, 如何对节点重要度进行排序, 是广泛存在的实际问题.
针对上述问题, 本文基于优势粗糙集理论和TOPSIS方法, 提出融合网络节点自身属性和网络结构特性的节点重要度排序方法, 能有效克服单一从拓扑结构分析的局限, 使评价结果更具合理性.最后, 将本文所提出的方法应用于微博社交网络中的用户重要度的评价问题.利用蓄意攻击及传染病模型对该方法进行测试, 并将该方法与单一中心性指标、TOPSIS方法和PageRank(PR)方法进行比较, 结果表明本文所提出的方法排序结果更具合理性.
1 基础知识粗糙集理论是处理不完备和不确定性问题的一种有效工具, 它是通过等价关系来对论域进行划分的, 广泛应用于机器学习、数据挖掘、知识发现等领域.而在实际问题中, 数据缺失现象经常发生, 针对不完备的信息系统, 利用优势关系代替等价关系来处理缺失数据, 具有一定的优势.下面将介绍本文所涉及到的与优势粗糙集相关的几个概念.
定义1[16](对象xi在属性c上优于对象xj的概率)??对于一个不完备序信息系统S≥*=(U, A, V, f), A为属性集, ?a∈A, ?xi∈U, xj∈U, 则对象xi关于属性a优于对象xj的概率表示为
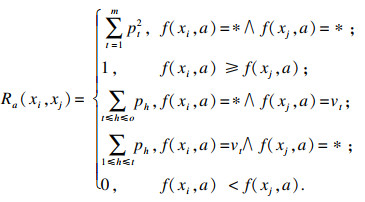 |
定义2[16](优势类)??给定一个不完备序信息系统S≥*=(U, A, V, f), 对于?xi∈U, ?xj∈U, 关于属性集A的α优势关系定义为
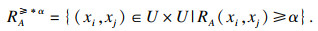 |
2 属性信息不完备的节点重要度排序方法在实际网络中, 因节点属性信息暂时无法获取或信息被遗漏等因素, 节点信息中常含有未知的数据, 而数据缺失现象是无法避免的客观存在的问题.如何解决节点属性信息含有缺失数据的重要度排序问题, 是实际复杂网络问题中亟待解决的关键问题.本文采用优势粗糙集方法, 分析节点自身的属性特征.
2.1 节点属性不完备信息描述利用不完备粗糙集描述该复杂网络G*=(U*, E, C), C为每个节点的属性集, 假设节点ui对应属性cj的属性值vj(ui)=vij=*, 不完备复杂网络信息表如表 1所示.
表 1(Table 1)
| 表 1 属性值不完备关系 Table 1 Incomplete relation of attribute value |
2.2 节点属性不完备信息与结构信息融合的排序方法分析复杂网络节点重要度, 由于其属性值部分信息缺失, 属性信息不完备, 因此采用优势粗糙集方法分析该问题.下面详细阐述该方法.
第1步??设定阈值αl(l=1, …, q), 计算不同阈值αl下节点关于属性集C的优势类:
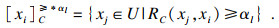 | (1) |
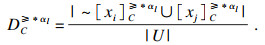 | (2) |
 | (3) |
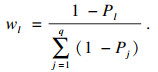 | (4) |
第5步??计算节点关于属性集C的平均综合优势度DC(xi)(i=1, …, n), 即为节点xi的属性重要度:
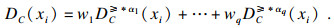 | (5) |
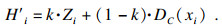 | (6) |
算法伪代码如下:
输入: 不完备序信息系统S≥*=(U, A, V, f), α1, α2, …, αq.
输出: 节点属性不完备时全序化排序结果.
1.??For i, j=1:n do
2.????For l=1:q do
3.??????利用式(1)计算不同阈值αl下节点关于属性集C的优势类[xi]C≥*αl,
4.??????利用式(2)计算不同阈值αl下每对节点关于属性集C的优势度DC≥*αl,
5.??????利用式(3)计算不同阈值αl下节点i关于属性集C的整体优势度DC≥*αl(xi),
6.????End for
7.??End for
8.??For l=1:q do
9.??????利用式(4)确定阈值αl下节点i整体优势度DC≥*αl(xi)的权重wl,
10.End for
11.For i=1:n do
12.????????利用式(5)计算节点xi的不完备属性重要度DC(xi),
13.End for
14.For i=1:n do
15.????????通过TOPSIS算法[11]计算节点xi的结构重要度Zi,
16.????????利用式(6)计算节点xi的属-结重要度, 返回运算结果,
17.End for
2.3 举例分析为验证新方法的合理性和可行性, 以具有17个节点的防空化网络为例, 分析节点重要度排序问题, 其中节点重要度是指该节点对我方作战意图的贡献程度和对敌方的威胁程度.在防空化网络中, 每个节点代表一个作战单元, 不同的符号代表不同的作战单元, 主要包括指挥控制、传感器、火力打击单元等.节点与节点之间的连边表示各节点之间的物理、逻辑联系, 箭头方向为信息、能量流动的方向.网络示意图如图 1所示.
图 1(Fig. 1)
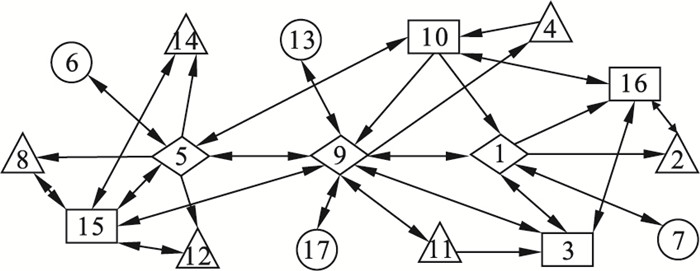 | 图 1 网络化防空系统Fig.1 Networked air defense system |
分析防空化网络节点自身的属性特征, 设定节点的属性集C={c1对敌方威胁程度, c2对我方作战影响, c3与作战意图一致度, c4抗毁能力, c5修复难度}, 各节点的属性描述如表 2所示, 其中*为未知数据.
表 2(Table 2)
| 表 2 防空化网络节点的属性值 Table 2 Attribute values of air defense network node |
由于属性值的缺失不会对网络的结构造成影响, 因此只需考虑节点属性重要度对节点重要度的影响, 利用优势粗糙集方法分析节点属性重要度, 选取α1=0.1, α2=0.5, α3=0.9, k=0.8, 不完备防空化网络节点属-结重要度排序结果对比如表 3所示.
表 3(Table 3)
| 表 3 不完备防空化网络节点重要性top10排序结果 Table 3 Top 10 ranking results of incomplete air defense network node importance |
从表 3可以看出, 在排序结果的top10中, 重要度最高的节点均为节点9.不完备属-结重要度与结构重要度的排序结果大致相同.在不完备属-结重要度与结构重要度的排序中, 节点10与节点17的差异最大, 观察表 2不完备防空化网络节点各属性值, 可以发现节点10的与作战意图一致度远远大于节点17, 且经计算可知节点10的优势度高于节点17.此外, 从网络的拓扑结构中也可以发现, 相较于节点17, 节点10与其他节点的联系更加紧密, 因此节点10的不完备属-结排序结果优于节点17是合理的.
根据以上的示例说明, 选择k∈(0, 1), 步长为0.05, 讨论k的变化对排名结果的影响, 结果如表 4所示.由表 4可知, k的变化会导致排名的变化, 但不同k的最优选择变化不变, 即节点9.因此, 验证了本文所提方法的稳定性.
表 4(Table 4)
| 表 4 不同k值的排序结果 Table 4 Sort results of different k values |
3 微博社交网络节点重要度分析3.1 数据获取本文以新浪微博作为数据源, 读取了2020年10—11月份某大学的官方微博数据, 获得7 509名微博用户的信息, 选取其中200个节点构建有向社交网络.获取用户的基本信息如下: 用户名、用户ID、关注数、粉丝数、会员等级、是否认证、认证方式、微博数, 每条博文的点赞数、转发数、评论数等.
根据用户之间的交互关系来构建社交网络模型, 将微博用户抽象为节点, 用户与用户之间的关注关系抽象为边(如果用户ui是用户uj的粉丝, 那么就存在一条边从用户ui指向用户uj), 用有向图G*=(U*, E, C)来表示, U*为节点集合, E是直接相连用户边的集合, C为节点自身属性集合, 节点的拓扑图如图 2所示.
图 2(Fig. 2)
 | 图 2 微博社交网络拓扑图Fig.2 Weibo social network topology map |
本文选取用户的粉丝数量、近期微博质量(包含被转发数、被评论数、被点赞数)、用户被信服程度(主要包括用户所发微博数, 以及近一个月内的活跃程度, 与其他用户的交互程度)[17]、用户等级、认证程度5个方面作为用户的属性特征, 以15%的概率随机删除节点属性特征表中的数据, 并对数据进行离散化处理, 不完备微博网络属性值离散等级划分表如表 5所示, 其中属性c1, c4, c5根据数据读取, c2, c3利用文献[17]的方法得出, 部分节点属性特征如表 6所示.
表 5(Table 5)
| 表 5 不完备微博网络属性值离散等级划分表 Table 5 Incomplete Weibo network attribute value discrete grade classification table |
表 6(Table 6)
| 表 6 微博部分用户属性特征 Table 6 Some user attribute characteristics of Weibo |
3.2 对比分析利用优势粗糙集方法对该微博网络节点的属性信息进行分析.
3.2.1 对比其他重要度排序方法本文根据2.3节中实验得出的经验, 在本节实验中依旧选取k值为0.8, 然后将本文所提出的排序结果与三种单指标方法DC, BC, Ci, TOPSIS方法和PR方法排序结果进行比较, 6种方法挖掘出的top 20节点如表 7所示.
表 7(Table 7)
| 表 7 不确定微博网络节点重要性top 20排序结果 Table 7 Top 20 sort results of the importance of uncertain Weibo network nodes |
从表 7可以看出, 在微博社交网络中本文提出的方法与TOPSIS方法有17个相同的节点(其中11个节点名次完全相同), 与DC, BC, Ci分别有15, 10, 6个相同的结果, 与PR方法有6个相同的结果.本文提出方法与其他方法的节点重要度排序结果基本一致, 体现了本文方法的可行性.与TOPSIS方法相比, 排序结果发生变化的有节点58↑, 159↑, 76↓等, 节点58, 159的排序名次比较靠前, 这是因为这两名用户的粉丝数较高, 并且最近一个月内的活跃度较高, 所发微博原创度高, 获得其他用户转发、点赞、评论数高, 从而获得了较高的重要度; 节点76的排序下降是因为尽管节点76有着较高的度数,即节点76的邻居节点较多, 但由于该用户粉丝数较少, 用户被信服程度的属性值较低, 没有认证, 从而导致了节点76的不完备属-结重要度下降.
3.2.2 蓄意攻击方法利用三种单指标方法(DC, BC, Ci),TOPSIS方法、PR方法和本文所提出的方法分别对节点重要性进行排序, 本文以排序结果所对应的节点顺序进行蓄意攻击[18], 被攻击到的节点不会再对信息传播起到任何作用, 而当社交网络中的某些节点失去传播能力时, 网络的传播效率必然会受到影响.因此, 本文选取网络稳健性为指标进行节点重要度的验证, 以此来衡量微博社交网络中重要节点的传播效率.
网络稳健性指的是受到攻击后的网络效率与初始效率的比值, 即ε=E/E′, E为受到攻击后网络效率, E′为初始效率.其中, 网络效率定义为网络中两两节点之间最短距离倒数之和的平均值, 有向网络中, 节点之间的最短路径需要同时考虑入边和出边, 表达式为
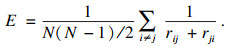 | (7) |
按照节点重要度的顺序, 由高到低依次对网络进行攻击, 通过对不同方法以及随机攻击下网络稳健性的下降情况进行对比, 结果体现出本文所提方法的可行性及优越性.如图 3所示, 为网络稳健性随着移除关键节点数量的变化情况.
图 3(Fig. 3)
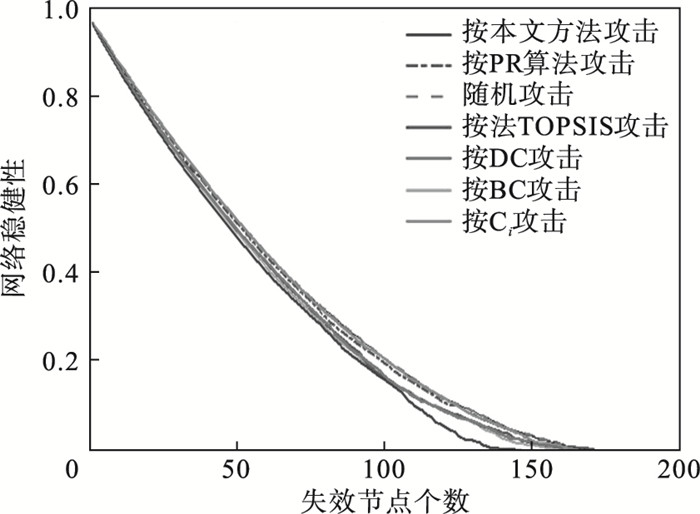 | 图 3 网络稳健性对比图Fig.3 Network robustness comparison chart |
从图 3中可以看出, 网络稳健性与移除节点的个数大体上呈现出反比的趋势, 并且网络稳健性的下降速率由快到慢, 这是因为起初的节点重要度较高, 失效后对网络的影响较大, 网络稳健性下降速率较快, 随着节点不断地失效, 节点重要度开始减小, 因此网络稳健性的下降速率也开始逐渐降低.相比之下, 利用本文算法检测出的关键节点失效后对网络影响更大, 其受到攻击后网络稳健性的下降速率相比于其他6种攻击方法较为明显, 网络结构瓦解得更快.
3.2.3 SI传染病模型利用传染病模型对本文方法进行验证, 在传染病模型的SI模型中, S代表易感染者, I代表感染者, 感染者以一定的概率将病毒传染给易感染者.社交网络中的信息传播类似于该种机制, 如二级传播理论, 信息首先到达舆论领袖那里, 舆论领袖再把他们得到的内容与信息传达给受他们影响的人.因此, 本文将排序结果的TOP10节点作为感染者I, 剩余其他的全部节点作为易感染者S, 每个节点都有相同的概率接收到信息.
对比本文方法与TOPSIS方法、三种单指标方法DC, BC, Ci以及PR方法下传播的情况以及达到全部传播所需的时间, 如表 8所示.在微博社交网络中, 本文提出的方法节点完全感染所需时间最短, 并且在每一时刻被感染节点数最多, 感染范围最大, 说明本文算法找出的关键节点更为合理, 通过控制这些节点, 将信息首先传播给这些关键节点, 可以提高网络传播的效率.由于TOPSIS方法综合了DC, BC, Ci三种方法, 因此每一时刻感染节点数以及最终用时与其他方法接近.
表 8(Table 8)
| 表 8 不确定微博网络SI传染结果对比 Table 8 Comparison of SI infection results on uncertain Weibo networks |
4 结论1) 对比本文所提出的方法与其他方法, 利用蓄意攻击进行验证, 结果表明本文所提出的方法的关键节点对网络影响更大, 网络结构瓦解得更快; 利用传染病模型进行验证, 结果表明本文所提出方法的传播时间要小于其他方法.
2) 本文所提出的方法可以有效识别网络中的重要节点, 对控制信息传播以及网络稳健性均起到了良好的作用.
参考文献
| [1] | Lin Z, Wen F, Xue Y. A restorative self-healing algorithm for transmission systems based on complex network theory[J]. IEEE Transactions on Smart Grid, 2017, 7(4): 2154-2162. |
| [2] | Yang Z Y, Hu M, Huang T Y. Influential nodes identification in complex networks based on global and local information[J]. Chinese Physics B, 2020, 29(8): 572-578. |
| [3] | Farzaneh N A, Foad M P, Balabhaskar B. Detecting a most closeness-central clique in complex networks[J]. European Journal of Operational Research, 2020, 283(2): 461-475. DOI:10.1016/j.ejor.2019.11.035 |
| [4] | Newman M. A measure of betweenness centrality based on random walks[J]. Social Networks, 2005, 27(1): 39-54. DOI:10.1016/j.socnet.2004.11.009 |
| [5] | Li Z, Yan X, Zhang G J. Bi-directional h-index: a new measure of node centrality in weighted and directed networks[J]. Journal of Informetrics, 2018, 12(1): 299-314. DOI:10.1016/j.joi.2018.01.004 |
| [6] | Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2010, 6(11): 888-893. DOI:10.1038/nphys1746 |
| [7] | Wen X X, Tu C L, Wu M G. Node importance evaluation in aviation network based on "no return" node deletion method[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 503(8): 546-559. |
| [8] | 刘娜, 沈江, 于鲲鹏. 基于改进节点收缩法的加权供应链网络节点重要度评估[J]. 天津大学学报, 2018, 51(10): 64-72. (Liu Na, Shen Jiang, Yu Kun-peng. Weighted supply chain network node importance evaluation based on improved node shrinkage method[J]. Journal of Tianjin University, 2018, 51(10): 64-72.) |
| [9] | Yu J F, Gilbert B A, Oviatt B M. Effects of alliances, time, and network cohesion on the initiation of foreign sales by new ventures[J]. Strategic Management Journal, 2010, 32(4): 424-446. |
| [10] | Ping H, Fan W, Mei S. Identifying node importance in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 429(4): 169-176. |
| [11] | 于会, 刘尊, 李勇军. 基于多属性决策的复杂网络节点重要性综合评价方法[J]. 物理学报, 2013, 62(2): 54-62. (Yu Hui, Liu Zun, Li Yong-jun. Comprehensive evaluation method of node importance in complex network based on multi-attribute decision-making[J]. Acta Physica Sinica, 2013, 62(2): 54-62.) |
| [12] | Liu Z, Jiang C, Wang J, et al. The node importance in actual complex networks based on a multi-attribute ranking method[J]. Knowledge-Based Systems, 2015, 84(8): 56-66. |
| [13] | Lu M. Node importance evaluation based on neighborhood structure hole and improved TOPSIS[J]. Computer Networks, 2020, 178(9): 107336. |
| [14] | 胡钢, 高浩, 徐翔, 等. 基于重要度传输矩阵的复杂网络节点重要性辨识方法[J]. 电子学报, 2020, 48(12): 116-122. (Hu Gang, Gao Hao, Xu Xiang, et al. Importance identification method of complex network nodes based on importance transmission matrix[J]. Acta Electronica Sinica, 2020, 48(12): 116-122.) |
| [15] | 黄丽亚, 汤平川, 霍宥良, 等. 基于加权K-阶传播数的节点重要性[J]. 物理学报, 2019, 68(12): 1-11. (Huang Li-ya, Tang Ping-chuan, Huo You-liang, et al. Node importance based on weighted K-order propagation number[J]. Acta Physica Sinica, 2019, 68(12): 1-11.) |
| [16] | 李佳, 梁吉业, 庞天杰. 基于加权α优势关系的多属性决策排序方法[J]. 模式识别与人工智能, 2017, 30(8): 91-98. (Li Jia, Liang Ji-ye, Pang Tian-jie. Multi-attribute decision ranking method based on weighted alpha dominance relation[J]. Pattern Recognition and Artificial Intelligence, 2017, 30(8): 91-98.) |
| [17] | 王新胜, 马树章. 融合用户自身因素与互动行为的微博用户影响力计算方法[J]. 计算机科学, 2020, 47(1): 102-107. (Wang Xin-sheng, Ma Shu-zhang. Microblog user influence calculation method integrating user's own factors and interactive behavior[J]. Computer Science, 2020, 47(1): 102-107.) |
| [18] | 赵海, 郑春阳, 王进法. 面向蓄意攻击的网络异常检测方法[J]. 东北大学学报(自然科学版), 2020, 41(10): 1376-1381. (Zhao Hai, Zheng Chun-yang, Wang Jin-fa. Network anomaly detection method for deliberate attacks[J]. Journal of Northeastern University(Natural Science), 2020, 41(10): 1376-1381. DOI:10.12068/j.issn.1005-3026.2020.10.002) |
