李建华¹, 朱泽阳¹, 徐礼胜^1,2, 孙国哲³
1. 东北大学 医学与生物信息工程学院, 辽宁 沈阳 110169;
2. 沈阳东软智能医疗科技研究院有限公司, 辽宁 沈阳 110167;
3. 中国医科大学附属第一医院 心血管内科, 辽宁 沈阳 110001
收稿日期：2021-07-13
基金项目：国家自然科学基金资助项目(61773110); 中央高校基本科研业务费专项资金资助项目(N2119007, N2119008)；沈阳市科学技术计划基金资助项目(20201410); 沈阳东软智能医疗科技研究院有限公司会员课题项目(MCMP062002)。
作者简介：李建华(1973-)，男，河北怀来人，东北大学讲师;
徐礼胜(1975-)，男，安徽安庆人，东北大学教授，博士生导师。

摘要：电子病历数据经常存在缺失, 严重影响分析结果.基于MIMIC数据库中的重症监护单元(intensive care unit, ICU)患者数据研究缺失值插补, 数据集由23组临床常用生理变量以及不存在缺失的5 260例样本构成.提出了一种基于深度嵌入聚类的K近邻插值方法.该方法以深度嵌入聚类为核心, 通过多次聚类构造样本邻近度矩阵, 再选择缺失样本的K个近邻样本, 以这些近邻样本的平均值填补缺失.与均值插补、中值插补、后验分布估算插补和条件均值插补相比, 该方法插补后的结果与原数据相似度更高, 且更好地保留了样本间的差异性.
关键词：重症监护单元电子病历缺失值插补深度嵌入聚类邻近度矩阵
Interpolation of Missing Physiological Data of ICU Patients Based on Deep Embedded Clustering
LI Jian-hua¹, ZHU Ze-yang¹, XU Li-sheng^1,2, SUN Guo-zhe³
1. School of Medicine and Biological Information Engineering, Northeastern University, Shenyang 110169, China;
2. Neusoft Research of Intelligent Healthcare Technology, Co., Ltd., Shenyang 110167, China;
3. Department of Cardiovascular Medicine, The First Hospital of China Medical University, Shenyang 110001, China
Corresponding author: XU Li-sheng, E-mail: xuls@bmie.neu.edu.cn.

Abstract: The data in electronic medical records are often missing, significantly affecting the analysis results. The ICU(intensive care unit)patients' data in MIMIC database were analyzed for missing value interpolation, and the dataset consists of 23 groups of commonly used clinical physiological variables and 5 260 samples without missing values. A K-nearest neighbor interpolation method was proposed based on deep embedded clustering. This method takes deep embedded clustering as the core, constructs the sample proximity matrix through multiple clustering, and then regards the average value of K-nearest neighbor of missing samples as the missing values. Compared with mean interpolation, median interpolation, a posteriori distribution estimation interpolation and conditional mean interpolation, the proposed method obtains higher similarity between the interpolated results and the original data, and better retains the differences between various samples.
Key words: intensive care unit(ICU)electronic medical recordmissing value interpolationdeep embedded clusteringproximity matrix
重症监护单元(intensive care unit, ICU)是监护和抢救危重症患者的特殊医疗单元, 被称为生命的最后一道防线^[1].自电子病历出现以来, 重症领域的研究者们可以借助于回顾性的ICU患者生理数据开展相关的研究, 例如死亡风险评估、生存期预测、器官衰竭预测等^[2].这些研究都是依托于电子病历, 因此数据质量对研究结果影响很大.
对ICU患者数据而言, 存在缺失是常见现象.造成数据缺失的原因是多样的, 常见的有人为原因和设备故障等^[3].数据缺失会造成样本信息大量损失, 进而影响数据分析的结果, 因此处理数据缺失是数据分析任务的重中之重.目前相关研究中对缺失值的处理相对简单, El-Rashidy等^[4]在进行ICU患者死亡预测模型的研究中, 将存缺的样本直接剔除, 使用无缺失的样本构建模型, 这种做法虽然简单, 但是浪费了大量的可用信息.在更多的相关研究中^[5-7], 均值插补法被用于缺失值插补, 这种方法确实能减少缺失对样本的影响, 但是如果缺失的样本较多, 会造成样本间的差异性被缩小.
针对这些问题, 本文提出基于深度嵌入聚类构造邻近度矩阵的缺失值插补算法, 本算法可以有效地控制用于替代缺失值的样本数量, 更适用于ICU患者数据.
1 实验数据与方法1.1 实验数据本研究的所有样本均来自于MIMIC(medical information mart for intensive care)数据库^[8].该数据库由贝斯以色列女执事医疗中心、麻省理工学院、牛津大学和麻省总医院的急诊科医生、重症科医生、计算机科学专家等共同建立.本文使用的MIMIC-III V1.4版本包括了2001—2012年期间在贝斯以色列女执事医疗中心重症监护室内接受治疗的约40 000名患者的数据, 以关系型数据库表格形式存储, 共计26张数据表, 包括了人口统计学信息、生理数据、精神状态、用药信息、治疗方式、患病史等重要数据.
从数据库中选择了23组临床常用的生理变量^[9], 包括: 碳酸氢根(HCO₃^-)、肌酐(Creatinine)、红细胞压积(HCT)、血红蛋白(Hemoglobin)、血小板(Platelet)、血清钾离子浓度(K⁺)、血清钠离子浓度(Na⁺)、凝血激活酶时间(PTT)、凝血酶原时间(PT)、国际标准化比值(INR)、血尿素(BUN)、白细胞计数(WBC)、Glasgow昏迷评分(GCS)、尿量(URINE)、是否进行肾脏替代治疗(RRT)、年龄(Age)、心率(HR)、收缩压(SYSbp)、舒张压(DIAbp)、平均动脉压(MAP)、呼吸频率(BR)、体温(Temperature)、血氧饱和度(SPO₂).在23组变量中, 4个变量取单个值, 12个变量分别取最大、最小值, 7个变量分别取最大、最小和平均值, 因此特征的总数是49个.
此23组变量均存在不同程度的缺失, 图 1描述了这些特征的缺失情况, 图中缺失率由式(1)定义:

(1)

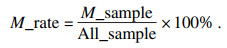图 1(Fig. 1)

图 1 所选特征的缺失情况Fig.1 The missing values of the selected features

其中: M_rate为缺失率; M_sample为存在缺失的样本数量; All_sample是样本总数.
本文选取了数据库中23组特征均不存在缺失的5 260例样本作为研究对象, 首先生成多组缺失率不同的人造缺失数据, 然后使用不同方法生成插补后的数据, 比较这些数据与原始数据的相似性, 进而比较插补方法性能.
本文提出一种基于深度嵌入聚类的K近邻插值算法.本算法以深度嵌入聚类为核心, 通过多次聚类构造样本邻近度矩阵, 再自适应地选择缺失样本的K个近邻样本, 用这些近邻样本的平均值填补缺失.本算法无需手动选择K值或聚类的簇数, 且能有效控制存缺样本的邻居数量, 从而有效解决均值插补方法缩小样本间差异的问题.
1.2 K近邻插值法在死亡率预测的相关研究中, 研究者大多使用均值插补缺失值, 因为均值插补计算简单, 效果尚可.均值插补很容易降低样本间的差异性, 而K近邻数据填充法可以弥补这一不足.K近邻数据填充法的核心思想是利用与含缺失值样本近似的其他样本的值来填补缺失值, 常见方法是先根据某种距离度量计算得到样本的“邻居”, 然后用K个近邻样本的均值来替代缺失值.求解K近邻的过程也可以视作聚类的过程, 先对数据聚类, 再在类内做插补.
1.3 栈式自编码器在解决聚类任务时, 一般步骤为先将高维特征映射到低维空间, 再对低维特征使用聚类算法.因为在高维空间中, 样本间的距离难以衡量, 即使距离较远的两个样本在某个平面上也可能是近邻^[10], 所以降维是聚类前的必要步骤.主成分分析(principal component analysis, PCA)是一种常用的降维方法, 其基本思想是在特征空间中找到一条轴, 使特征空间的点映射到这条轴上后的方差最大化.PCA作为一种基本的线性降维方法, 没有参数的限制, 大大降低了计算成本, 但是学习到的特征较为简单.
自动编码器(auto encoder, AE)作为一种深度神经网络, 在限制了隐含层的维度后, 可以学习到比PCA更全面的特征.由于AE学习到的特征是原特征空间在连续非交叉曲面上的投影, 相比于PCA学习到的低维超平面投影, AE的隐含层表达包含原特征的更多信息^[11].在这种考虑下, 诞生了深度聚类网络, 即先使用AE学习特征的低维表征, 再使用聚类器完成聚类.深度聚类网络(deep clustering net, DCN)本质上是一个分步模型, 降维和聚类是两个独立的步骤.深度嵌入聚类则是在DCN的基础上, 使用聚类模型的损失函数训练AE的编码过程, 使AE能够学习到对聚类任务友好的低维特征^[12].图 2为深度嵌入聚类模型的结构, 其中X_i表示输入特征, f(x)表示编码函数, g(x)表示解码函数, l(X, Y)是自编码器输入和输出的重构误差函数, f(X_i)是原特征在自编码器隐含层的表征, 也可以看作是降维后的特征, 聚类器为K-means.
图 2(Fig. 2)

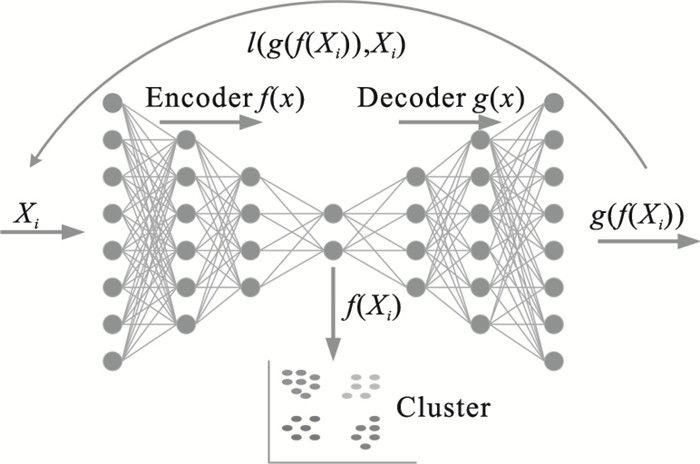图 2 深度嵌入聚类模型结构图Fig.2 Structure of deep embedded clustering model

AE是一种无监督学习技术, 其训练过程可以理解为通过编码函数对输入X进行表征学习得到原始特征的编码, 再使用解码函数将编码映射到原特征空间得到重构的X′, 并使X≈X′.AE相当于重构了输入, 其损失函数为重构误差, 如式(2)所示:

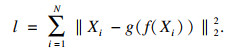(2)

其中: N为样本个数; X_i表示输入特征; f(x)表示编码函数; g(x)表示解码函数.
因为AE的训练是最小化重构误差的过程, 为了避免其简单地将输入复制给输出, 考虑限制隐含层的输出维数, 即限制隐含层的神经元个数, 使隐含层的输出维度小于输入维度, 限制各层之间能够传递的信息量, 以此强制AE学习到有效的信息^[13].而栈式自编码器(stacked auto encoder, SAE)则是增加隐含层的个数, 扩大网络容量, 使编码更复杂.
1.4 K-means聚类K-means选用欧氏距离作为相似性度量, 其目标函数是最小化类内样本到聚类中心的距离^[14].对于样本X, 假设将其分为K类, 类别记作{C₁, C₂, …, C_K}, K-means的目标函数表示为

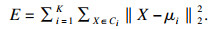(3)

其中, μ_i表示类C_i的聚类中心点.
K-means最小化目函数的过程是通过迭代完成的, 其步骤为
1) 在样本中随机选择K个点作为聚类中心记作μ_i, K为指定的聚类簇数.
2) 对于n=1, 2, …, N, N为样本的总个数.
① 初始化聚类簇, 使C_i=?.
② 计算样本X_n到每个簇的中心的欧氏距离, 将该样本归入距离最小的聚类中心所在的类.
③ 将所有样本分类完成后, 重新计算每个簇的聚类中心, 即该簇中所有样本的均值向量.
④ 如果聚类中心发生变化, 重复步骤①到③, 直至聚类中心不再发生变化或达到最大迭代次数, 结束迭代.
3) 输出聚类簇.
1.5 深度嵌入聚类网络训练深度嵌入聚类网络(deep embedded clustering, DEC)将SAE的编码函数加入K-means的损失函数中, 编码函数如式(4)所示:

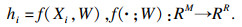(4)

其中: h_i是输入X_i通过多层编码后的瓶颈层输出; 在此过程中特征由M维降低到R维; W记录f的全部参数, 参数包括连接各层神经元的权重和每个隐含层的偏差.
将h_i作为输入, 更新K-means的目标函数如式(5)所示:

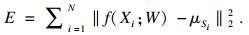(5)

其中, S_i表示X_i所属的聚类.
随后将此目标函数作为正则项加入SAE的重构误差函数, 如式(6)所示:

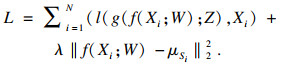(6)

其中: λ取1;g(X_i; Z)是解码函数; Z是由隐含层变换到输出层的参数; l是自编码器的重构误差.
SAE的训练过程如下, 首先训练一个自编码器, 得到隐含层的输出, 再使用第一个自编码器的隐含层输出作为输入训练第二个自编码器, 最后将所有自编码器堆叠, 得到最终的栈式自编码器.如图 2所示, 本研究使用的SAE共5个隐含层, 编码器的三个隐含层维数分别设置为30, 20, 10, 即瓶颈层输出维度为10.通过预训练得到的瓶颈层输出训练K-means, 得到初始化的聚类簇和聚类中心点, 然后在求最优聚类簇和聚类中心的过程中同时优化参数W和Z, 最终得到对聚类任务友好的特征表征h_i.
1.6 K-means++初始化K-means++初始化是K-means初始聚类中心选取的优化方案^[15], 根据K-means的聚类思想, 每个样本到类中心点的距离要尽量近, 并且聚类中心点之间要尽量远, K-means++算法就是考虑选取距离最远的点作为初始聚类中心.K-means++算法步骤如下:
1) 随机选择第一个点作为聚类中心, 记作C₁.
2) 计算每个样本X_n到C₁的距离, 记作D(X), 计算每个样本点被选为下一个聚类中心的概率p(C_X), p由式(7)定义:

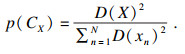(7)

3) 累加p, 得到每个点被选为下一个聚类中心的概率区间, 然后随机生成一个0~1之间的数, 其所属的区间对应的点就被选作下一个聚类中心.
4) 重复步骤2)和3), 直至选出所有聚类中心, 初始化完成.需要注意, 当进行步骤2)时已经产生了多个聚类中心, 则需要计算样本到每个聚类中心的距离, 并选择其中最小的值作为D(X).
2 实验过程2.1 基于邻近度矩阵的K近邻插值法本方法结合DEC与集成学习思想构造邻近度矩阵.对包含n个样本的数据X, 多次使用DEC, 因为聚类初始化点是随机选取的, 这样多次聚类会得到不同的划分结果.假设进行了m次聚类, 最终得到m个划分, 定义同类别矩阵N(n×n), N_ij=N_ji表示样本i和样本j在m次聚类中被划分在同一类中的次数; 式(8)定义了邻近度矩阵D.D度量了一个样本与其他样本被多次划分为同一类的概率, 邻近指数D_ij越接近1, 样本i和j越有可能是近邻.

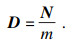(8)

邻近度矩阵是一个对称矩阵, 图 3给出了矩阵示例, 每行表示一个样本与其他样本的邻近程度, 数值越大则两样本是近邻的概率越大, 对角线元素为1.
图 3(Fig. 3)

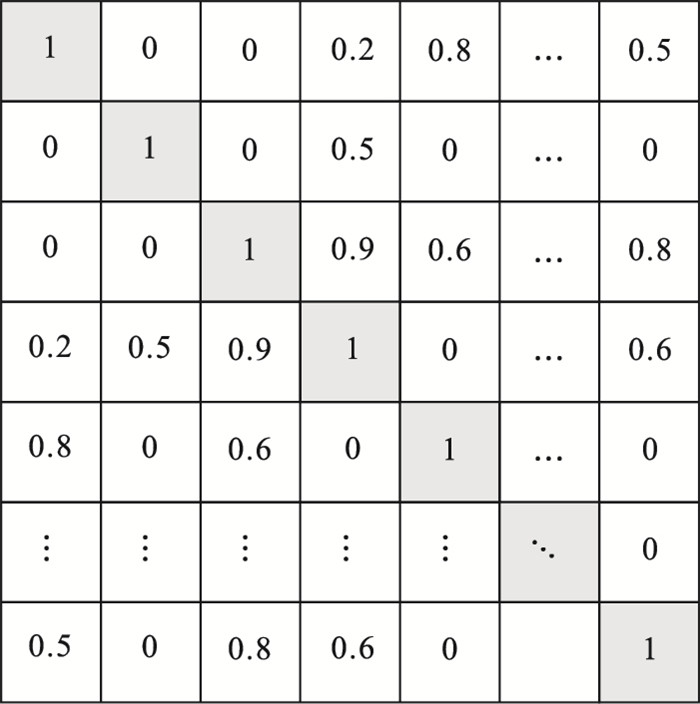图 3 典型的邻近度矩阵Fig.3 Example of typical proximity matrix

将样本及其特征构成的矩阵称为特征矩阵.对缺失值的插补算法过程如下, 对特征矩阵中的每一列特征进行如下操作.
1) 计算当前特征存在缺失的样本行号, 对应邻近度矩阵D的行号.
2) 对D中相应的行从高到低排序, 取前K个值, 计算其对应的样本在特征矩阵中的行号, 获取这些样本对应的特征值.
3) 检查这K个特征值中是否存在缺失, 若存在, 用D中第K+1个样本对应的特征值替换, 重复此步骤至此K个特征中不含有缺失值.
4) 用此K个特征值的均值代替缺失值.
相比于直接在聚类簇内使用均值插补, 本方法可以通过参数K的选取控制用于计算插补值的样本数量, 相当于控制聚类簇中的样本数量, 同时保证了每个簇中只有一个缺失值.本方法主要参数有聚类划分次数m, 每次划分的聚类簇数C以及用于计算缺失特征替代值的近邻样本个数K; 根据集成聚类的相关研究^[16], C取近似于m的值效果较好, 一般C=m+1, 本文根据重复实验选取m值为20.对K值的选取主要依据每个样本的高近邻样本的个数来选取, 根据对样本的观察, 选取邻近指数在[0.9, 1]之间的样本作为邻近样本, 邻近样本个数K由缺失样本在规定区间内的邻居个数决定.
2.2 评估指标本文主要使用插补后数据和原数据的相似性以及样本集内样本之间的差异性来衡量插补方法的性能.
使用余弦相似度作为相似性指标, 两个n维向量A和B的余弦相似度S_θ由式(9)定义, S_θ越接近1说明两个向量越相似, 使用特征矩阵行向量余弦相似度的均值表示两个矩阵的相似度.

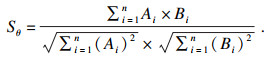(9)

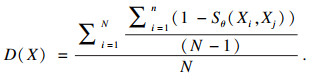式(10)定义了一个样本集的总体差异性指标, 对一个含有N个样本集X, 每个样本为X_i(i=1, 2, …, N), 其含义为每个样本与其他样本的差异性的平均值.

(10)

3 结果与讨论3.1 数据缺失对样本的影响为了直观地展示数据缺失对样本的影响, 本文使用PCA方法将原始特征映射到三维空间以便于观察, 将三个维度的特征命名为f1, f2和f3.以此三个特征建立空间坐标系, 其中图 4是1 000个无缺失样本的空间分布, 图 5是原始样本人工加入5%缺失数据后在特征空间的分布情况.
图 4(Fig. 4)

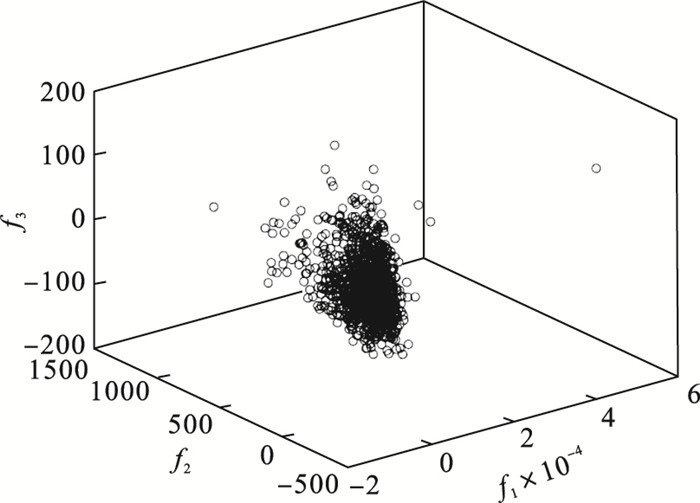图 4 1 000例无缺样本在三维特征空间的分布图Fig.4 The distribution of 1 000 samples without missing data in the three-dimensional feature space

图 5(Fig. 5)

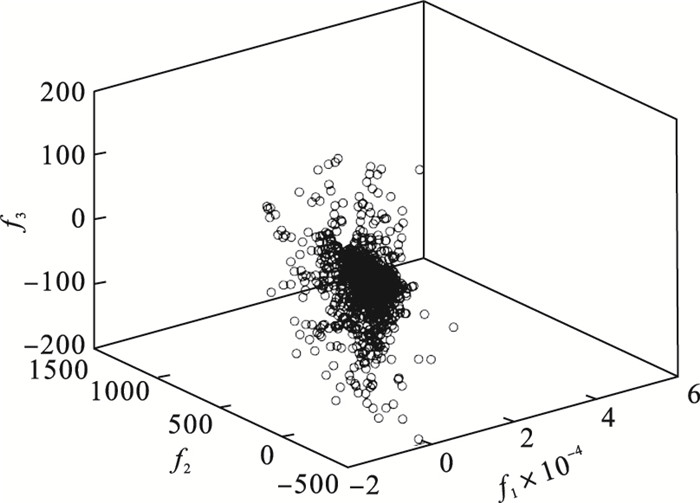图 5 加入5%缺失后1 000例样本在三维特征空间的分布图Fig.5 The distribution of 1 000 samples with 5% missing data in the three-dimensional feature space

如图 5所示, 在无缺失原始样本中人为地添加缺失值后, 样本发生了肉眼可见的偏移, 且样本更加分散.
3.2 插补后与原数据的相似度对比在PCA降维后的三维特征空间中, 图 6~图 8分别是均值插补、中值插补和本算法插补后的数据在三维特征空间内的分布情况.
图 6(Fig. 6)

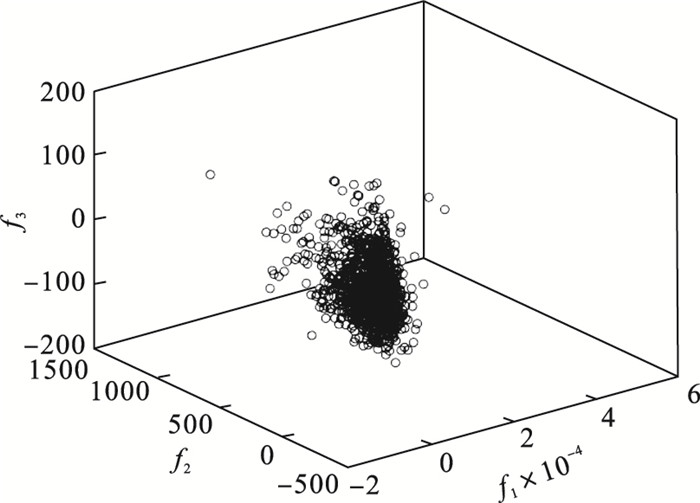图 6 使用均值插补法补缺后样本在三维特征空间的分布图Fig.6 The data distribution interpolated by mean interpolation method in the three-dimensional feature space

图 7(Fig. 7)

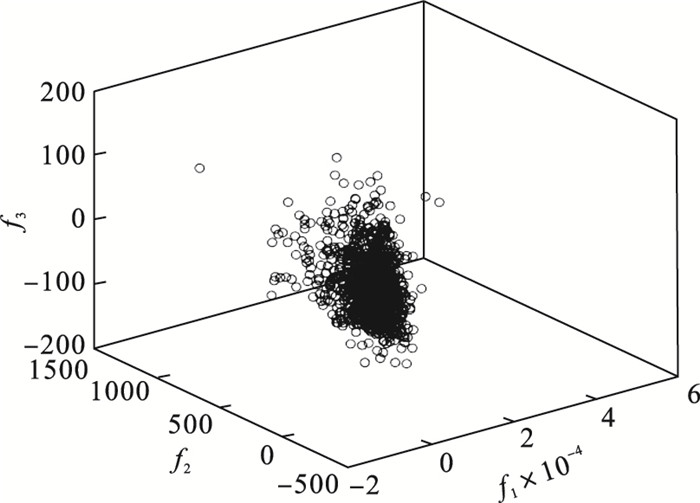图 7 使用中值插补法补缺的数据在三维特征空间的分布图Fig.7 The data distribution interpolated by median interpolation method in the three-dimensional feature space

图 8(Fig. 8)

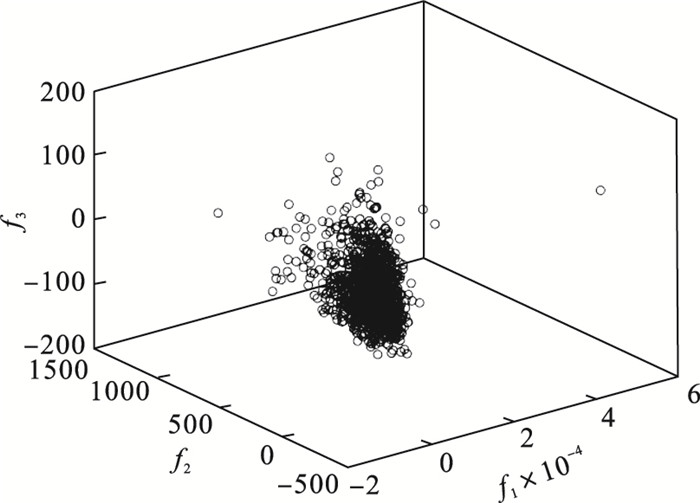图 8 使用邻近度矩阵插值法补缺后样本在三维特征空间的分布图Fig.8 The data distribution interpolated by the proximity matrix interpolation method in the three-dimensional feature space

由图 6~图 8可知, 经过插补的数据与原数据分布近乎一致, 证明插补是一种有效的预处理手段, 但是与本文的方法相比, 均值插补和中值插补后的数据存在细节上的不足, 一些离群点出现失真.
以余弦相似度作为度量, 表 1比较了均值插补、中值插补、后验分布估算插补、条件均值插补和基于邻近度矩阵的插值的性能.从表中可见, 本文的方法插值得到的数据更接近真实数据, 在缺失率较高时这种优势更加明显.例如, 当缺失率从5%升至15%时, 作为对照的4种方法中性能最好的条件均值插补法, 余弦相似度从0.993 2降至0.975 4, 下降了1.79%;本文方法, 相应从0.994 8降至0.987 5, 仅下降0.73%.
表 1(Table 1)

表 1 使用不同插补方法得出的数据与原数据的余弦相似度Table 1 The cosine similarity between the data obtained by different interpolation methods and the original data 缺失程度/% 均值插补 中值插补 后验分布估算插补 条件均值插补 本文方法 1 0.996 4 0.996 8 0.996 0 0.997 0 0.998 4 2 0.995 2 0.994 9 0.993 6 0.996 2 0.998 1 5 0.980 0 0.982 6 0.977 9 0.993 2 0.994 8 10 0.976 0 0.975 7 0.972 1 0.980 0 0.992 2 15 0.968 1 0.965 9 0.963 7 0.975 4 0.987 5

表 1 使用不同插补方法得出的数据与原数据的余弦相似度 Table 1 The cosine similarity between the data obtained by different interpolation methods and the original data

3.3 样本间差异性分析计算可得5 260例样本的总体差异度为0.869 7, 表 2给出不同插补方法得出的数据的总体样本间差异度.以均值插补法为例, 对于缺失率大于10%的样本, 得到的补缺数据样本间差异度明显小于原始数据.当大量样本存在缺失时, 均值插补、中值插补等方法为所有的缺失值都给定相同的替代值, 这种计算方法会缩小样本间差异, 对后续的数据分析任务带来难度.相比之下, 提出的方法在低缺失率时, 可以很好地还原数据, 样本间差异度十分接近原始数据; 而在高缺失率时, 样本差异性的缩小并不明显, 说明本算法很好地还原了数据的真实情况.例如, 当缺失率从5%升至15%时, 4种方法中后验分布估计插补的总体样本间差异度变化最小, 从0.853 9降至0.835 6, 下降了2.14%;本文的方法, 相应地从0.867 0降至0.860 5, 仅下降0.75%, 较好地保持了样本间的差异性.
表 2(Table 2)

表 2 使用不同插补方法得出的数据的总体样本间差异度Table 2 The total sample difference of data obtained by different interpolation methods 缺失程度/% 均值插补 中值插补 后验分布估算插补 条件均值插补 本文方法 1 0.864 4 0.865 2 0.864 7 0.864 4 0.869 1 2 0.863 9 0.864 3 0.862 7 0.863 6 0.868 8 5 0.854 3 0.855 3 0.853 9 0.854 6 0.867 0 10 0.837 6 0.838 0 0.838 1 0.838 4 0.864 5 15 0.835 0 0.835 6 0.835 6 0.836 0 0.860 5

表 2 使用不同插补方法得出的数据的总体样本间差异度 Table 2 The total sample difference of data obtained by different interpolation methods

4 结语ICU患者的回顾性生理数据中存在缺失值是一种常见现象, 在使用数据进行统计分析时, 缺失值会产生不利影响.缺失值插补是使用估计值代替缺失值, 因为ICU患者生理数据本身具有变异性, 生理参数值很可能不在正常值范围内, 对其缺失值的插补是一项具有挑战性的工作.
本文提出了一种基于深度嵌入聚类构造邻近度矩阵的缺失值插补算法.与ICU患者回顾性数据分析的相关研究中常用的插补方法相比, 本算法插补后的数据与原始数据近似程度较高.本算法能够有效地确定替代样本的数量, 根据样本间差异性的对比, 更好地保留了原样本的数据特性.
此外, 本研究还可以在数据方面做深入工作.因为MIMIC数据库中不包含中国人的数据, 对国内的ICU患者数据是否效果较好还需要进一步验证.未来将与医院积极合作, 进一步验证本算法的适用性.
参考文献

[1]	Digiovine B, Chenoweth C, Watts C, et al. The attributable mortality and costs of primary nosocomial bloodstream infections in the intensive care unit[J]. American Journal of Respiratory and Critical Care Medicine, 1999, 160(3): 976-981. DOI:10.1164/ajrccm.160.3.9808145
[2]	侯明曙. 重症监护病房的发展现状[J]. 现代医药卫生, 1995(2): 40. (Hou Ming-shu. Development status of intensive care unit[J]. Modern Medicine and Health, 1995(2): 40.)
[3]	Idri A, Benhar H, Fernández-Alemán J L, et al. A systematic map of medical data preprocessing in knowledge discovery[J]. Computer Methods and Programs Biomedicine, 2018, 162: 69-85. DOI:10.1016/j.cmpb.2018.05.007
[4]	El-Rashidy N, EI-Sappagh S, Abuhmed T, et al. Intensive care unit mortality prediction: an improved patient-specific stacking ensemble model[J]. IEEE Access, 2020, 8: 133541-133564. DOI:10.1109/ACCESS.2020.3010556
[5]	Macas M, Kuzilek J, Odstrcilik T, et al. Linear Bayes classification for mortality prediction[C]// 2012 Computing in Cardiology. Krakow: IEEE, 2012: 473-476.
[6]	Kim S, Kim W, Park R W. A comparison of intensive care unit mortality prediction models through the use of data mining techniques[J]. Healthcare Informatics Research, 2011, 17(4): 232-243. DOI:10.4258/hir.2011.17.4.232
[7]	Liu J, Chen X, Fang Z, et al. ICU mortality prediction using modified cost-sensitive PCA and chaos PSO[C]// 2017 IEEE the 19th International Conference on e-Health Networking, Applications and Services(Healthcom). Dalian: IEEE, 2017: 1-6.
[8]	Johnson A E, Pollard T J, Shen L, et al. MIMIC-Ⅲ, a freely accessible critical care database[J]. Scientific Data, 2016, 3: 160035. DOI:10.1038/sdata.2016.35
[9]	Pickering B W, Gajic O, Ahmed A, et al. Data utilization for medical decision making at the time of patient admission to ICU[J]. Critical Care Medicine, 2013, 41(6): 1502-1510. DOI:10.1097/CCM.0b013e318287f0c0
[10]	Peng X, Feng J, Zhou J T, et al. Deep subspace clustering[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(12): 5509-5521. DOI:10.1109/TNNLS.2020.2968848
[11]	Vincent P, Larochelle H, Bengio Y, et al. Extracting and composing robust features with denoising autoencoders[C]//Proceedings of the 25th International Conference on Machine Learning. Helsinki, 2008: 1096-1103.
[12]	Yang B, Fu X, Sidiropoulos N D, et al. Towards k-means-friendly spaces: simultaneous deep learning and clustering[C]//Proceedings of the 34th International Conference on Machine Learning. Sydney, 2017: 3861-3870.
[13]	Masci J, Meier U, Ciresan D, et al. Stacked convolutional auto-encoders for hierarchical feature extraction[C]//Proceedings of the 21th International Conference on Artificial Neural Networks. Espoo, 2011: 52-59.
[14]	Jain A K. Data clustering: 50 years beyond k-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666. DOI:10.1016/j.patrec.2009.09.011
[15]	Dasuki Y D, Sheng O C, Hee L M, et al. A hybrid k-means-GMM machine learning technique for turbomachinery condition monitoring[C]//MATEC Web of Conferences. Sabah, 2019: 06008.
[16]	Fred A L N, Jain A K. Combining multiple clusterings using evidence accumulation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(6): 835-850. DOI:10.1109/TPAMI.2005.113