
 , 樊星, 李凯, 张凌越
, 樊星, 李凯, 张凌越 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期:2021-07-15
基金项目:国家自然科学基金资助项目(51875092); 宁夏回族自治区自然科学基金资助项目(2020AAC03279)。
作者简介:李小彭(1976-),男,江西宁都人,东北大学教授,博士生导师。
摘要:巡检机器人进行越障时, 受负载时变影响, 会出现控制超调、振动等现象.在考虑负载惯量时变特性的情况下, 研究了一种用于分析巡检机器人越障状态下动态性能的方法.对双臂线路巡检机器人的回转机构建立了基于双惯量模型的动力学方程, 使用改进D-H法与拉格朗日法对机器人建模, 具体包括分配坐标系, 求解拉格朗日方程, 利用惯性矩阵计算负载转动惯量等.通过选择合适的阻尼系数设计了控制器参数, 利用阻尼系数与固有角频率的变化分析了机器人的动态性能变化.研究成果有助于对双臂巡检机器人越障时的动态性能进行分析, 并可用于机器人的伺服控制参数调试.
关键词:线路巡检机器人负载时变双惯量系统动态性能伺服控制
Dynamic Performance Analysis of Line Inspecting Robots Considering Time-Varying Loads
LI Xiao-peng

 , FAN Xing, LI Kai, ZHANG Ling-yue
, FAN Xing, LI Kai, ZHANG Ling-yue School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: LI Xiao-peng, E-mail: xpli@me.neu.edu.cn.
Abstract: When the power transmission line inspection robots(PTLIRs)cross obstacles, the phenomenon of control overshoot and vibration will appear due to the influence of time-varying loads. A method for analyzing the dynamic performance of PTLIRs in obstacle crossing state is studied considering the time-varying characteristics of load inertia. The dynamics equations of the slewing mechanism of the dual-arm PTLIR are established with the two-inertia-system, and further the kinematics and dynamics modeling are carried out based on the modified D-H method and Lagrangian mechanics, including assigning coordinate system, solving Lagrange's equation, using inertia matrix to calculate the load moment of inertia, etc. The controller parameters are designed by selecting appropriate damping coefficient, and the changes of the damping coefficient and the natural angular frequency are used to analyze the dynamic performance of the PTLIR. The research results are helpful to analyze the dynamic performance of the dual-arm PTLIR affected by the time-varying load inertia when crossing obstacles, and can be used to debug the servo parameters of the robot.
Key words: power transmission line inspection robottime-varying loadtwo-inertia-systemdynamic performanceservo sontrol
传统对输电线路定期巡检的方法大多为人工检测, 包括: 爬行检测、地面监测和使用望远镜检测等.但随着电力系统的发展, 这些检测方法表现出较大的限制性[1].相比人工检测, 使用机器人检测的成本更低、速度更快、安全性更高, 已成为国内外许多****和机构的研究热点[2].目前对巡检机器人的研究多数集中于构型创新设计[3-5]与电力检测识别方面(如: 电力系统组件[6]、线路[7]、电力塔[8]).考虑到机器人在工作中需要通过变换关节(如: 旋转关节(R)、移动关节(P))姿态改变位姿来跨越诸如防振锤、悬垂线夹、绝缘子等线路障碍, 而这个过程作为一个动态过程, 受参数时变影响较大, 所以需要对越障过程的动态性能进行分析.
对机器人的动态性能分析的传统方法通常为提出适当的指标评价惯量用以衡量系统的动态性能, 如用于评价机械臂动力学性能的GIE方法[9]和DME方法[10].虽然惯量对机器人来说是影响动态性能的重要因素[11], 但机器人作为一个机电系统, 工作时的动态性能除受到动力学特性如惯性特性的影响, 更与控制特性(如: 控制结构与控制参数)密切相关[12], 所以上述方法无法很好地使用在巡检机器人上.伺服电机作为机器人的驱动器, 与控制特性密切相关.对伺服电机的很多研究, 虽然传统控制模型中考虑了负载惯性, 但只是将其作为扰动, 很大程度上不会影响机电系统的稳定性和性能[13-14], 所以使用这一类传统的模型的动态性能分析准确性不够.相比传统的控制模型, 一些研究使用负载惯性控制为半闭环控制的双惯量模型更符合实际情况[15-16].以巡检机器人为例, 负载惯性在关节空间与机器人的姿态有关, 具有时变性, 但基于双惯量模型同时考虑负载参数时变性方面研究却很少.
本文利用双惯量控制模型, 在考虑负载惯量时变特性的情况下, 研究了一种完整的动态性能分析方法.首先对机器人的关节臂建立了基于双惯量系统的控制模型与动力学方程.使用改进D-H参数法与拉格朗日法进行了机器人的运动学、动力学建模, 从而使机器人越障时负载的时变性得到考虑.分析时主要通过研究负载惯量的变化对定常系统的影响来对动态性能进行分析, 并给出了分析的步骤流程.最后, 进行了包括速度端阶跃响应、位移端轨迹跟踪、系统关键参数变化等一系列仿真.
1 机构描述及控制系统模型建立1.1 机构描述图 1为双臂输电线巡检机器人的三维模型.整机由两个关节臂与连接部件组成, 每个关节臂包含了行走、旋转、升降、回转、平移机构; 连接部件则由机架与重心调节机构组成.各机构由伺服电机驱动, 通过传感器测量各机构实际的运行, 控制器再通过误差对电机发出指令.整机共包含7个关节, 可实现7个自由度的活动.
图 1(Fig. 1)
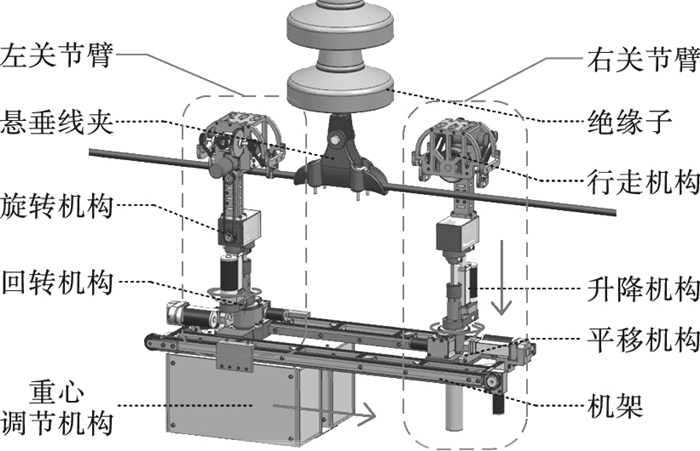 | 图 1 越障中的双臂输电线巡检机器人Fig.1 Dual-arm PTLIR crossing obstacles |
在巡检机器人执行输电线巡检任务时, 需要跨越诸如防震锤、悬垂线夹、空中警示球等障碍物.越障作为一个动态过程, 存在很强的时变性.
1.2 基于双惯量系统的关节控制模型的建立关节空间控制为机器人主要的控制方法之一[13], 为分析越障时负载端时变性对机器人造成的影响, 首先需要对回转关节建立基于双惯量系统的控制模型, 如图 2所示.
图 2(Fig. 2)
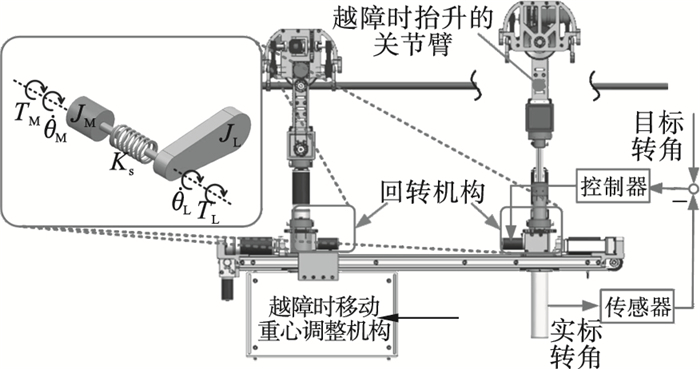 | 图 2 回转机构的双惯量模型Fig.2 Two-inertia-system of slewing mechanism |
图 2中:
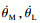
基于双惯量模型, 得到如式(1)所示的动力学方程.
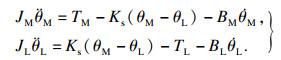 | (1) |
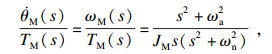 | (2) |
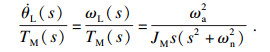 | (3) |
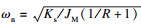
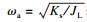
2 动力学建模2.1 改进D-H参数法建模双臂式巡检机器人多数为开环链式结构.建立坐标系时, 将越障时抓住导线的行走机构视为基座, 此时另一端脱离线路越过障碍的行走机构视为末端执行器.使用改进D-H参数法由基座起始依次建立共7个连杆坐标系, 如图 3所示.
图 3(Fig. 3)
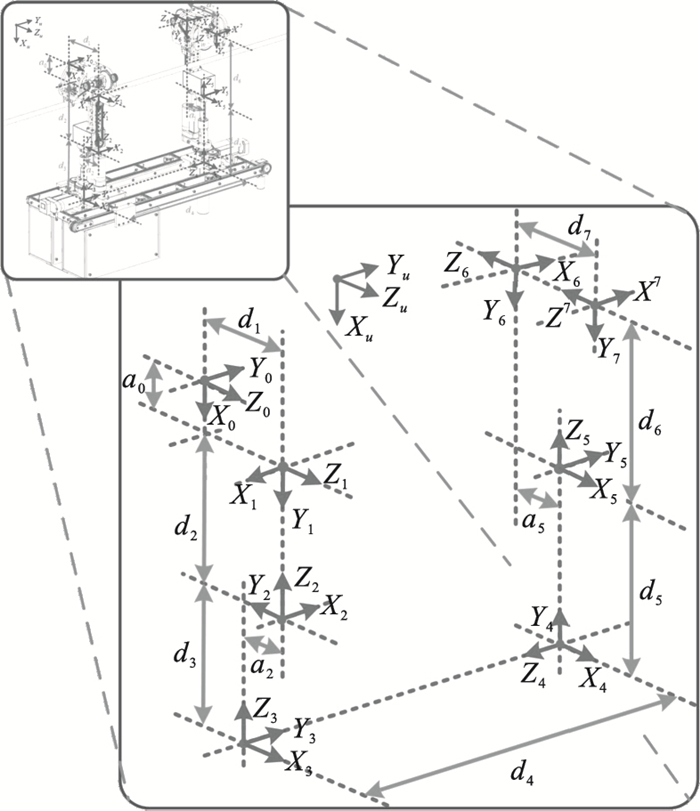 | 图 3 双臂巡检机器人D-H连杆坐标系Fig.3 D-H link coordinate system of the dual-arm PTLIR |
改进D-H参数法是通过4个参数即ai-1, αi-1, θi, di来描述从第i-1个连杆到第i个连杆的齐次变换矩阵, 其中矩阵的形式如式(4)所示.
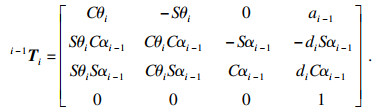 | (4) |
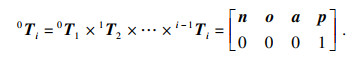 | (5) |
2.2 动力学方程通过拉格朗日法对机器人的动力学进行分析.首先定义拉格朗日函数如式(6)所示.
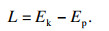 | (6) |
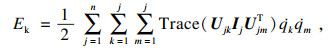 | (7) |
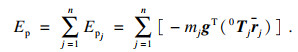 | (8) |
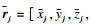
由广义坐标下的拉格朗日方程可建立机器人的动力学方程, 如式(9)所示.
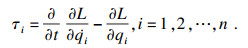 | (9) |
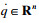
根据式(9), 得到巡检机器人的动力学方程如式(10)所示.
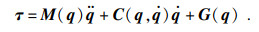 | (10) |
 |
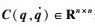
3 考虑负载时变性的动态性能分析机器人回转机构的双惯量模型下的控制结构框图如图 4所示, 具体包含位置环、速度环和电流环.图中速度环控制器和电流环控制器为PI控制器, 位置环控制器为P控制器.由于速度外环与电流内环的带宽差距, 可认为在速度外环调节时, 电流内环的调节已经完成, 所以在下文中将Kt视为1进行分析[16].
图 4(Fig. 4)
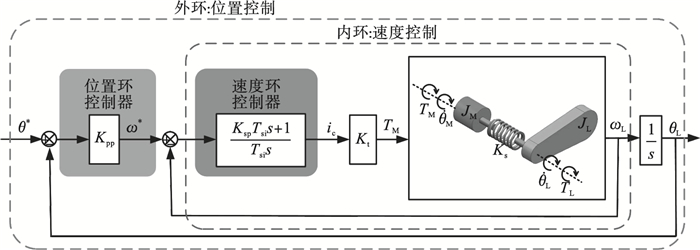 | 图 4 双惯量模型的控制结构框图Fig.4 Block diagram of control structure of the two-inertia-system |
根据图 4得到从ωL到ω*的传递函数, 如式(11)所示.
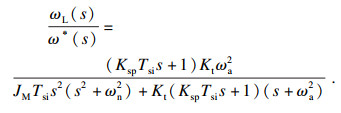 | (11) |
同样位置控制下从θL到θ*的传递函数, 如式(12)所示.
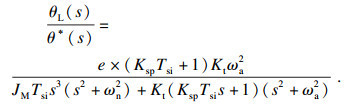 | (12) |
由式(11)、式(12)可知转速ωL、转角θL与反谐振频率ωa、谐振频率ωn相关.所以具有时变性的负载参数会影响控制效果而影响机器人稳定.
对动态性能变化分析前需要计算控制器参数.将闭环传递函数式(11)化简为形式为式(13)所示传递函数与形式为分母包含2个二阶环节组合的如式(14)所示传递函数.
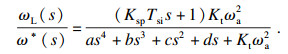 | (13) |
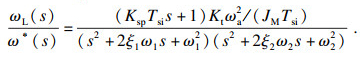 | (14) |
令传递函数(13)、(14)的特征方程逐项相等得到式(15)~式(18).其中, 式(15)、式(16)为控制器参数计算表达式; 式(17)、式(18)为极点的限制方程.因为方程存在4个极点, 而控制器参数只有2个, 所以极点不能自由配置, 需要其他限制条件.
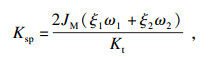 | (15) |
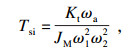 | (16) |
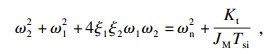 | (17) |
 | (18) |
将ξ1=ξ2=ξ代入限制方程(17)、方程(18)可解出ω1, ω2表达式如式(19)所示.
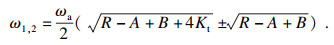 | (19) |
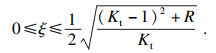 | (20) |
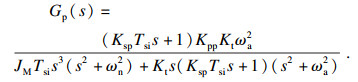 | (21) |
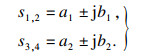 | (22) |
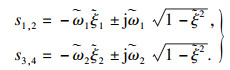 | (23) |
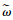
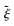
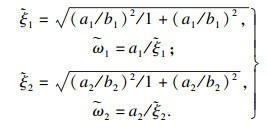 | (24) |
图 5(Fig. 5)
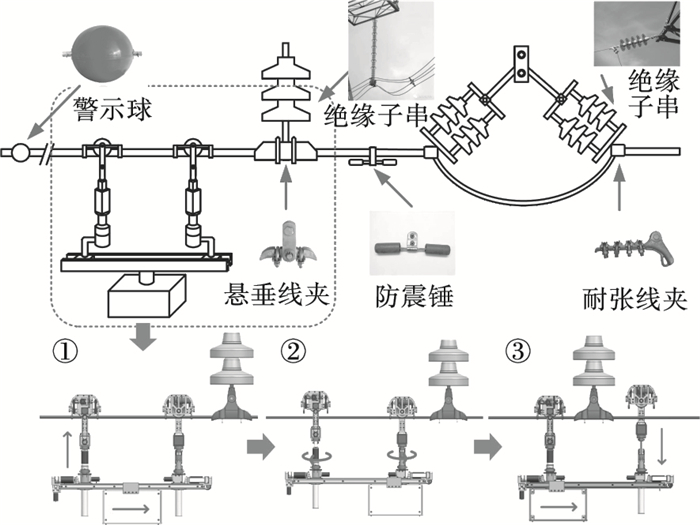 | 图 5 机器人越障工况示意图Fig.5 Schematic diagram of robots crossing obstacles |
越障作为一个动态过程受负载时变性影响较大.由图 5可知在越障第②步姿态变化时, 线路上仅有一个行走机构, 此时受负载时变影响较大, 容易造成工作时动态性能的不稳定.
4.1 负载惯量的参数计算将动力学方程中惯量矩阵M(q) 最大奇异值作为不同姿态下伺服电机的负载转动惯量值[13], 计算得到以关节3与关节5角度值为自变量参数下的负载惯量值与惯量比的变化结果, 如图 6所示.
图 6(Fig. 6)
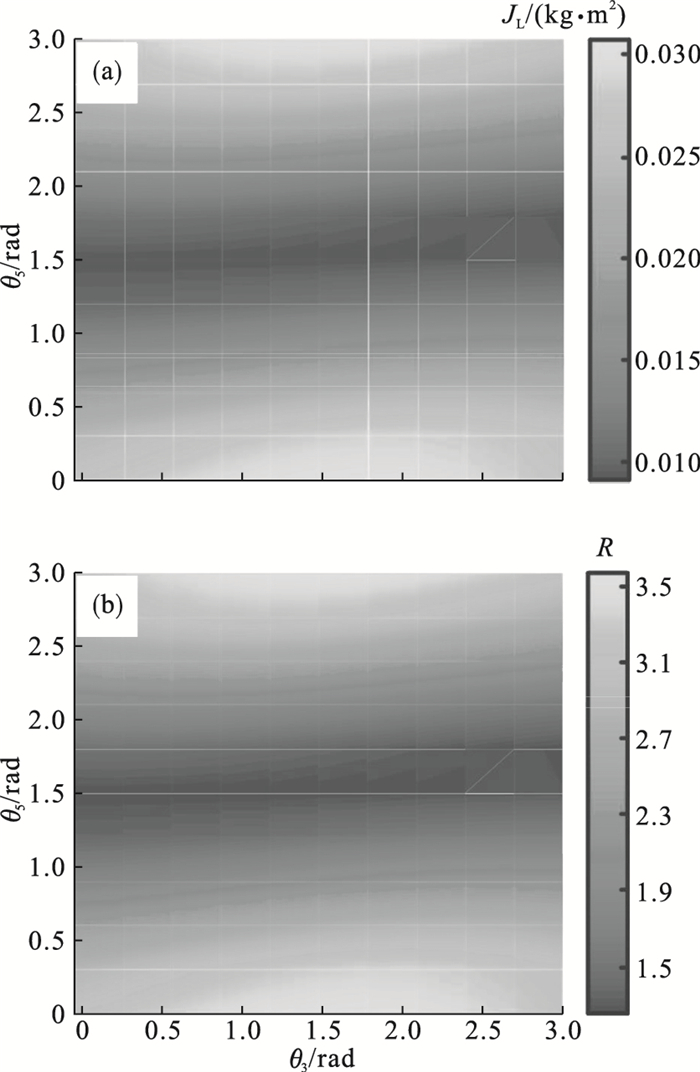 | 图 6 惯量及惯量比计算结果Fig.6 Calculation results of the inertia and inertia ratio (a)—负载惯量;(b)—惯量比. |
由图可知, 在越障时发生的机器人姿态变化会导致负载转动惯量的变化, 具体变化范围为从小于0.01 kg · m2到大于0.03 kg · m2; 对应惯量比的变化范围为从小于1.5到大于3.5.即越障时负载惯量会因机器人姿态的变化而表现出强烈的参数时变性.
4.2 负载端速度的仿真分析仿真前先计算控制器参数, 由图 6按照最大、中等、最小的次序分别以负载转动惯量JL1=0.032 2 kg · m2(R=3.788), JL2=0.016 7 kg · m2(R=1.965)及JL3=0.009 8 kg · m2(R=1.153)为参考, 对不同惯量下负载端速度变化进行仿真分析.
仿真所需各项参数如表 1所示.以最大负载转动惯量和最小负载转动惯量为参考数值计算控制器参数分别如表中参数1、参数2所示.
表 1(Table 1)
| 表 1 仿真参数 Table 1 Simulation parameters |
仿真负载端速度阶跃响应如图 7所示.图 7为在参数1、参数2下的控制器参数进行仿真的阶跃响应图.
图 7(Fig. 7)
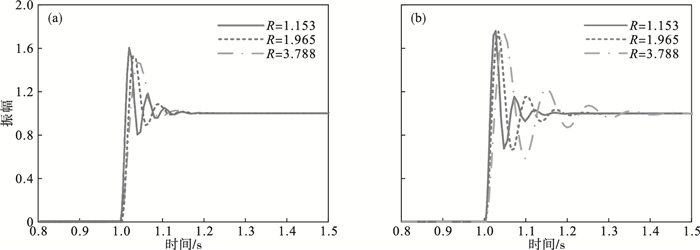 | 图 7 速度阶跃响应Fig.7 Step response of angular velocity (a)—控制器参数1;(b)—控制器参数2. |
由图可知, 无论采用哪一组控制参数, 越障时负载参数的变化会导致机器人动态性能都会发生变化, 尤其是振动幅值的变化; 对比图 7a与图 7b, 可得较大惯量参数计算得到的仿真参数下的阶跃响应相比另一种, 总体振动幅值更小.
4.3 负载端位移的仿真分析根据位置环开环传递函数绘制系统根轨迹图, 如图 8所示.图中箭头方向为增益参数变大方向, 依据根轨迹图选择能满足系统稳定性的比例增益参数, 结果为Kpp=40.由图可知, 虽然使用的控制结构相同, 但受负载惯性参数变化的影响, 根轨迹是不同的, 动态性能也是不同的.
图 8(Fig. 8)
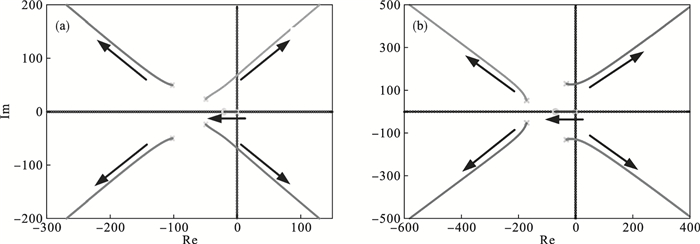 | 图 8 根轨迹图Fig.8 Root locus diagrams (a)—最大负载惯量参数;(b)—最小负载惯量参数. |
输入正弦函数作为参考轨迹, 位置环的轨迹跟踪误差曲线如图 9所示.受负载惯量时变性的影响, 两图在最大转动惯量即R=3.788的初始阶段存在较为明显的振动; 此外, 由较大的负载惯量确定的控制参数下系统的跟踪性能更好.
图 9(Fig. 9)
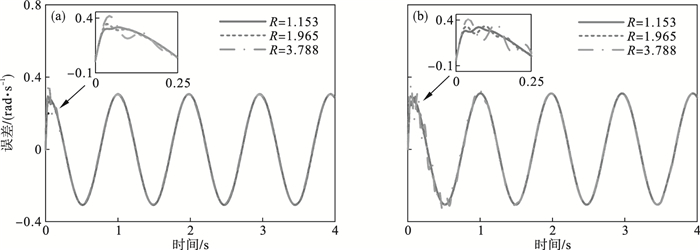 | 图 9 位移轨迹误差曲线Fig.9 Trajectory tracking error of displacement (a)—控制器参数1;(b)—控制器参数2. |
4.4 考虑负载时变下的关键参数变化分析机器人在越障时发生姿态变化会导致动态性能的变化.观察系统特征方程可知, 其根本原因在于系统的阻尼比与固有角频率的变化.
由式(22)~式(24)计算机器人越障时整个工作空间中在表 1中参数1、参数2下负载时变引起的系统阻尼系数ξ和固有角频率ω的变化规律, 结果分别如图 10、图 11所示.
图 10(Fig. 10)
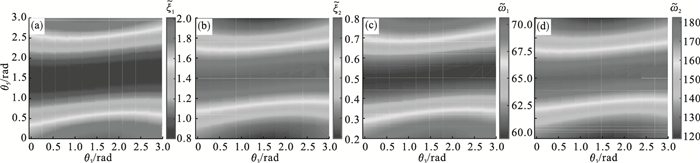 | 图 10 参数1下关键参数变化图Fig.10 Key parameter change diagram under parameter 1  |
图 11(Fig. 11)
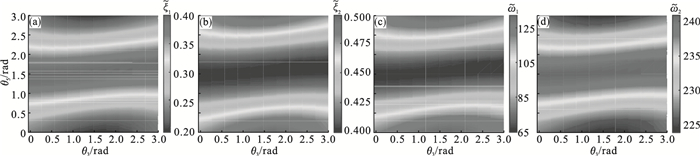 | 图 11 参数2下关键参数变化图Fig.11 Key parameter change diagram under parameter 2  |
由图 10可知, 参数1下阻尼系数ξ和自然角频率ω会随关节角的变化而变化.其中阻尼系数变化范围分别为从0.8到大于2和从小于0.2到0.8;自然角频率的变化范围分别为从小于60到大于70和小于120到大于180.图 11中参数2阻尼系数ξ和自然角频率ω同样随关节角的变化而变化.其中阻尼系数变化范围分别为从小于0.2到0.4和0.4到大于0.5;自然角频率的变化范围分别为从小于65到大于125和小于225到大于240.
所以固定控制参数不能保证系统的动态性能, 由姿态变化引起的阻尼系数和自然角频率的变化会导致特征多项式根的变化, 从而进一步影响机器人的动态性能.
5 结论1) 研究了一种用于双臂式输电线巡检机器人在越障时, 分析负载惯量参数变化如何对机器人动态性能影响的方法.具体包括基于双惯量控制系统的建模、机器人整机动力学建模、控制器参数设计计算以及系统参数变化的分析.
2) 负载惯量的时变性对机器人动态性能有较大影响, 具体表现为越障时位姿变化导致的负载惯量变化会加大机身振动程度, 所以固定控制参数不能很好保证系统的动态性能; 此外选择控制器参数时, 计算范围内较大的阻尼系数下的控制器参数总体控制效果更好.
3) 研究成果可用于评价越障时机器人的动力学特性, 并可用于机器人电机伺服参数调试过程以提高机器人的动态性能.
参考文献
| [1] | Chen M H, Tian Y N, Xing S Y, et al. Environment perception technologies for power transmission line inspection robots[J]. Journal of Sensors, 2021, 2021(2): 1-16. |
| [2] | Menendez O, Cheein F A, Perez M, et al. Robotics in power systems: enabling a more reliable and safe grid[J]. IEEE Industrial Electronics Magazine, 2017, 11(2): 22-34. |
| [3] | Richard P L, Pouliot N, Morin F, et al. LineRanger: analysis and field testing of an innovative robot for efficient assessment of bundled high-voltage powerlines[C]//2019 International Conference on Robotics and Automation(ICRA). Montreal, 2019: 9130-9136. |
| [4] | Yue X, Wang H G, Jiang Y. A novel 110 kV power line inspection robot and its climbing ability analysis[J]. International Journal of Advanced Robotic Systems, 2017, 14(3): 172988141771046. |
| [5] | Tao G H, Fang L J. A multi-unit serial inspection robot for power transmission lines[J]. Industrial Robot, 2019, 46(2): 223-234. DOI:10.1108/IR-09-2018-0195 |
| [6] | Sampedro C, Rodriguez-Vazquez J, Rodriguez-Ramos A, et al. Deep learning-based system for automatic recognition and diagnosis of electrical insulator strings[J]. IEEE Access, 2019, 7(99): 101283. |
| [7] | Hui X L, Jiang B, Zhao X G, et al. Vision-based autonomous navigation approach for unmanned aerial vehicle transmission-line inspection[J]. International Journal of Advanced Robotic Systems, 2018, 15(1): 172988141775282. |
| [8] | Miralles F, Hamelin P, Lambert G, et al. LineDrone technology: landing an unmanned aerial vehicle on a power line[C]//2018 IEEE International Conference on Robotics and Automation(ICRA). Brisbane, 2018: 6545-6552. |
| [9] | Haruhiko A. A geometrical representation of manipulator dynamics and its application to arm design[J]. Journal of Dynamic Systems Measurement and Control, 1983, 105(3): 131. DOI:10.1115/1.3140644 |
| [10] | Yoshikawa T. Dynamic manipulability of robot manipulators[C]// 1985 IEEE International Conference on Robotics and Automation. St. Louis, 1985: 1033-1038. |
| [11] | 王冬, 吴军, 王立平, 等. 3-PRS并联机器人惯量耦合特性研究[J]. 力学学报, 2016, 48(4): 804-812. (Wang Dong, Wu Jun, Wang Li-ping, et al. Research on the inertia coupling property of a 3-PRS parallel robot[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 804-812.) |
| [12] | Wang L P, Wang D, Wu J. Dynamic performance analysis of parallel manipulators based on two-inertia-system[J]. Mechanism and Machine Theory, 2019, 137: 237-253. DOI:10.1016/j.mechmachtheory.2019.03.023 |
| [13] | Wu J, Wang D, Wang L P. A control strategy of a two degrees-of-freedom heavy duty parallel manipulator[J]. Journal of Dynamic Systems Measurement & Control, 2015, 137(6): 061007. |
| [14] | Hanifzadegan M, Nagamune R. Contouring control of CNC machine tools based on linear parameter-varying controllers[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(5): 2522-2530. DOI:10.1109/TMECH.2016.2560765 |
| [15] | Kawai Y, Yokokura Y, Ohishi K, et al. High-robust force control for environmental stiffness variation based on duality of two-inertia system[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 850-860. |
| [16] | 李小彭, 尚东阳, 李凡杰, 等. 输电线巡检机器人位姿变化的柔性关节控制策略[J]. 东北大学学报(自然科学版), 2020, 41(11): 59-65. (Li Xiao-peng, Shang Dong-yang, Li Fan-jie, et al. Flexible joint control strategy based on posture change of transmission line inspection robots[J]. Journal of Northeastern University(Natural Science), 2020, 41(11): 59-65.) |
