罗忠^1,2,3, 刘家希^1,2, 刘凯宁^1,2, 孙凯^1,2
1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动及控制教育部 重点实验室, 辽宁 沈阳 110819;
3. 东北大学 佛山研究生院, 广东 佛山 528312
收稿日期：2021-06-14
基金项目：国家自然科学基金资助项目(11872148); 广东省基础与应用基础研究基金联合基金资助项目(2020B1515120015); 中央高校基本科研业务费专项资金资助项目(N180703018，N2003012，N2003013)。
作者简介：罗忠(1978-)，男，内蒙古集宁人，东北大学教授，博士生导师。

摘要：针对用于航空发动机转子系统中的弹性环式支承结构刚度特性问题, 开展其动刚度分析和实验测试以及其对转子系统固有特性影响分析研究.首先, 建立弹性环式支承结构有限元模型, 对其动刚度进行计算, 并进行动刚度测试与验证, 经实验所得测试结果与仿真计算的结果趋势一致, 证明了对弹性环式支承结构的动刚度分析方法的有效性.然后, 建立了带弹性环式支承结构的转子系统有限元模型, 研究了转子系统在静刚度和动刚度条件下对临界转速的影响.结果表明, 弹性环式支承结构动刚度对临界转速的影响较为明显, 其中一阶临界转速降低了26 %, 且产生了新的共振频率, 因此分析转子系统固有特性时应充分考虑支承结构的动刚度影响.
关键词：弹性环式支承结构动刚度有限元仿真转子系统临界转速
Analysis of Dynamic Stiffness of the Elastic Ring Support Structure and Its Influence on the Rotor System
LUO Zhong^1,2,3, LIU Jia-xi^1,2, LIU Kai-ning^1,2, SUN Kai^1,2
1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion System, Ministry of Education, Northeastern University, Shenyang 110819, China;
3. Foshan Graduate School, Northeastern University, Foshan 528312, China
Corresponding author: LUO Zhong, E-mail: zhluo@mail.neu.edu.cn.

Abstract: Aiming at the stiffness characteristics of the elastic ring support structure used in the aero-engine rotor system, the dynamic stiffness analysis and experimental tests as well as the analysis of its influence on the natural characteristics of the rotor system are carried out. First, a finite element model of the elastic ring support structure is established to calculate its dynamic stiffness, then the dynamic stiffness testing and verification is conducted. The experimental test results are basically consistent with the simulation results, which verify the correctness of the finite element analysis method of the elastic ring structure. Then, a finite element model is built which includes the rotor system and the elastic ring structure. Besides, the influence of the rotor system on the critical speed under the conditions of static and dynamic stiffness is studied. The results show that the dynamic stiffness of the elastic ring support structure has a significant impact on the critical speed. The first-order critical speed is reduced by 26 %, and a new resonance frequency is generated. Therefore, the dynamic stiffness of the support structure should be fully considered when analyzing the natural characteristics of the rotor system.
Key words: elastic ring support structuredynamic stiffnessfinite element simulationrotor systemcritical speed
现代航空发动机设计的核心技术之一便是对发动机转子-支承系统的设计, 其中弹性环式支承结构由于体积小, 易于装配, 在航空发动机中, 得到了越来越广泛的应用, 它已逐渐成为航空发动机转子-支承系统中常见的弹性支承类型.为了保证航空发动机稳定安全地运行^[1], 需要对航空发动机转子的临界转速进行准确合理的设计, 可通过设计弹性支承的刚度来调节转子的临界转速.工程实践表明^[2]弹性环式支承结构的刚度会在动态激励下发生变化而不是恒定不变的, 即称为动刚度^[3].弹性支承结构的动刚度会导致转子临界转速的变化, 造成较大影响.为准确地对航空发动机临界转速进行设计, 亟需开展考虑支承动刚度对转子系统的动力学特性影响的研究.
国内外****针对转子-支承系统的动刚度开展了大量的研究工作.Gupta等^[4]对轴承刚度的时变特性进行了分析, 证明了轴承刚度的水平分量随转速而增加, 而垂直分量几乎保持不变; 龙伦等^[5]分析了某型涡轴发动机燃气发生器转子的临界转速受支承系统动刚度的影响, 证明了支承动刚度条件下转子的各阶临界转速均有不同程度的下降; Hong等^[6-7]分析了在考虑机匣支承动刚度与鼠笼刚度耦合作用下的转子系统动力学特性, 发现考虑机匣支承动刚度的模型结果要更加接近于整机模型结果; Ma等^[8]采用激振器对含金属橡胶弹性环动力学特性进行了实验研究; Son等^[9]对比分析了低压转子实验台模型在只考虑支承静刚度、支承动刚度以及整机模型条件下的动力学特性, 发现了附加共振峰现象; 乔留春等^[10]通过建立弹性支承结构的有限元模型, 进行动刚度计算与实验验证; 赵文涛等^[11]通过力锤敲击法和正弦扫描法分别得到了航空发动机转子实验器垂向测点和横向测点的幅频特性曲线, 且两种方法所得结果趋势一致, 并用锤击法测得不同测点不同激励点的动刚度曲线.但目前, 针对航空发动机转子系统中弹性环式支承结构的计算与实验测试研究尚少, 弹性环式支承结构的动刚度特性及其影响规律尚不清晰, 因此对于弹性环式支承结构的动刚度特性的研究, 及其动刚度对转子系统临界转速的影响需要进一步展开.
根据上述情况, 采用有限元方法对建立的弹性环式支承结构进行动刚度计算得到动刚度值, 并进行实验验证, 对简化的转子-支承系统进行有限元模型的建立, 应用该转子-支承系统模型, 分析了弹性环式支承结构的动刚度对转子-支承系统的影响, 结果表明在航空发动机临界转速的详细设计阶段需考虑支承系统动刚度的影响.
1 动刚度计算方法航空发动机的转子在工作时, 转子会产生基频及倍频载荷周期性变化的简谐激励, 进而传递到支承系统中, 持续地受到大小和方向随着时间周期变化的简谐激励, 导致支承系统的变形也会在频域范围内不断变化, 转子的周期性载荷激励与支承系统动态变化量可通过以下公式得到^[12].

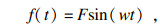(1)

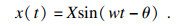(2)

其中: F和X分别是动态力和运动变化量的幅值; θ表示运动的相位角.支承系统的复杂动刚度K^*:

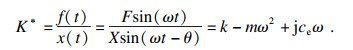(3)

其中: m表示振动的质量; ω表示激励的循环频率.可以从式(3)中看出, 系统的静刚度值、质量、频率和阻尼影响其动刚度的值.K^*的实部和虚部给出了支承的刚度k和等效黏性阻尼系数c表达式:

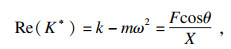(4)

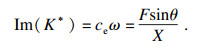(5)

2 弹性环式支承结构动刚度计算2.1 弹性环式支承结构有限元模型的建立图 1为本文所研究的弹性环式支承结构中弹性环的具体结构示意图, 它是一种环形结构, 内外两侧均匀加工若干个凸台, 有着改善支承位置的应变能分布, 方便调整的特点, 其内表面凸台与轴承外圈配合, 外表面凸台一般与轴承座或机匣配合^[13].
图 1(Fig. 1)

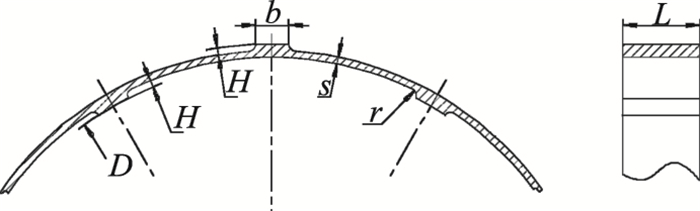图 1 弹性环结构示意图Fig.1 Diagram of the elastic ring structure

根据特定的支承1与支承2处的空间以及相应的刚度值, 所设计左右支承处的弹性环结构参数尺寸与材料如表 1所示, 内外衬套的尺寸如表 2所示.
表 1(Table 1)

表 1 弹性环结构主要结构参数Table 1 Main structure parameters of the elastic ring 参数 支承1数值 支承2数值 内直径D/mm 190 210 凸台个数 10 10 凸台长度b/mm 5 5 凸台高度H/mm 0.2 0.2 壁厚s/mm 2.3 3.9 宽度L/mm 24 33 材料 9Cr18 9Cr18 弹性模量E/MPa 2.19×105 2.19×105 泊松比 0.3 0.3

表 1 弹性环结构主要结构参数 Table 1 Main structure parameters of the elastic ring

表 2(Table 2)

表 2 衬套结构主要结构参数Table 2 Main structure parameters of the bush 参数 支承1 支承2 内衬套 外衬套 内衬套 外衬套 外径/mm 190 208 210 228 内径/mm 180 195.4 200 218.6 宽度/mm 24 24 33 33 材料 9Cr18 9Cr18 9Cr18 9Cr18

表 2 衬套结构主要结构参数 Table 2 Main structure parameters of the bush

根据表 1与表 2中弹性环式支承结构的空间参数, 设计弹性环式支承结构的有限元分析模型, 使用SOLID186单元建立弹性环式支承结构组件的三维模型, 其中弹性环结构与内衬套、外衬套的有限元分析模型如图 2所示.
图 2(Fig. 2)

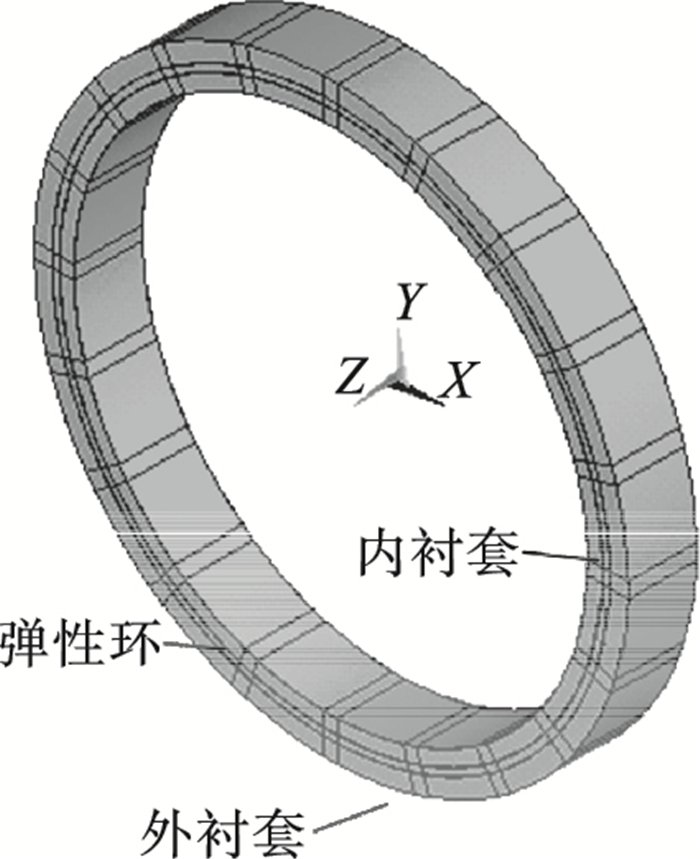图 2 有限元分析模型Fig.2 Finite element analytical model

根据弹性环式支承结构工作的工况, 设置的边界条件如图 3所示, 约束外衬套外圈表面上所有节点的自由度以模拟外衬套外圈受轴承座约束的状态, 为了加载时不造成局部变形, 对内衬套内圈表面上所有节点的平移自由度进行耦合, 从而使载荷均匀加载到弹性环式支承结构的内衬套上, 各节点一起联动, 同时对弹性环所有节点施加轴向和周向位移约束, 使弹性环只能有径向位移.为了使仿真结果具有更高的可靠性及真实度, 在外衬套内圈与弹性环外凸台间、内衬套外圈与弹性环内凸台之间进行接触设置, 采用CONTA172单元和TARGE169面-面接触单元对内外衬套与凸台间的接触情况进行模拟^[14-15].
图 3(Fig. 3)

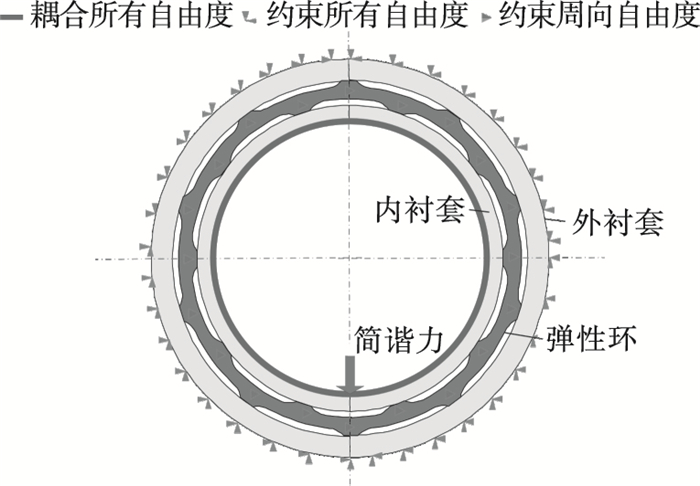图 3 弹性环式支承结构边界条件Fig.3 Boundary conditions of the elastic ring support

2.2 动刚度分析将弹性环式支承结构简化为弹簧质量单元, 施加简谐激励于其外部, 弹性环式支承结构本身会产生相应频率的简谐振动位移, 弹性环式支承结构的动刚度即为外部施加的简谐激励与相应的弹性环式支承结构本身所产生的简谐振动位移的比值, 根据上述思路对弹性环式支承结构进行动刚度分析, 其动刚度仿真计算与测试流程如图 4所示.
图 4(Fig. 4)

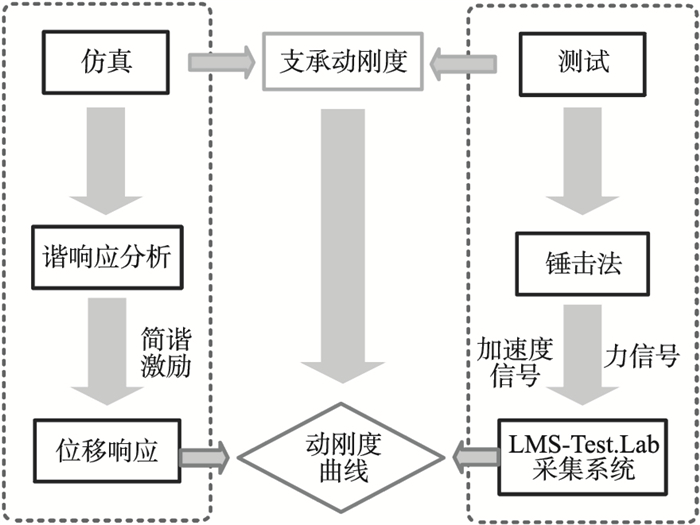图 4 动刚度计算与测试流程Fig.4 Dynamic stiffness calculation and test process

在0~500 Hz频率范围内, 按照图 3对两组弹性环式支承结构施加边界条件后, 采取谐响应分析的方法, 选取内衬套内圈最下方节点, 对该节点在径向施加简谐力500 N.因为弹性环式支承结构阻尼数值较低, 设置材料的阻尼比为0.003, 提取最下方节点的位移响应, 经计算得到两组弹性环式支承结构的内衬套对应节点的幅频曲线, 结果如图 5所示.由图可知支承1与支承2处两组弹性环式支承结构的固有频率分别为340 Hz与360 Hz, 支承1处的弹性环式支承结构位移响应更大.
图 5(Fig. 5)

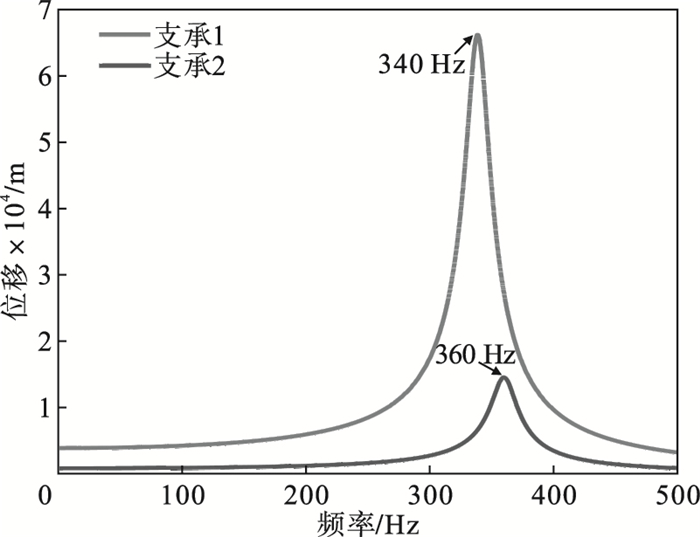图 5 弹性环式支承结构的幅频曲线Fig.5 Amplitude-frequency curves of the elastic ring support

将图 5的幅频曲线数据结果导出, 将所添加的简谐力与幅频曲线进行处理后得到弹性环式支承结构的动刚度曲线.如图 6所示, 可以看出动刚度曲线在0~500 Hz范围内可以分为三个阶段: 在频率范围0~100 Hz内的低频段, 两组弹性环式支承结构的动刚度在数值上变化很小, 为准静态区, 动刚度值与静刚度值较为接近, 静刚度值分别为1.27×10⁷ N/m与5.69×10⁷ N/m; 当激励频率接近弹性环式支承结构的固有频率附近的频率范围时, 该区域为阻尼控制区且阻尼比影响共振的峰值, 动刚度主要取决于固有频率值和阻尼比, 弹性环式支承结构产生共振现象, 导致振动的位移增大, 动刚度值因此降低, 即出现刚度退化的现象; 当激励频率大于固有频率时, 为质量控制区, 动刚度主要取决于弹性环式支承结构的质量, 在该特定频率范围内动刚度值逐步增大, 其中动刚度值也可能高于静刚度值, 这主要是由惯性效应引起的.
图 6(Fig. 6)

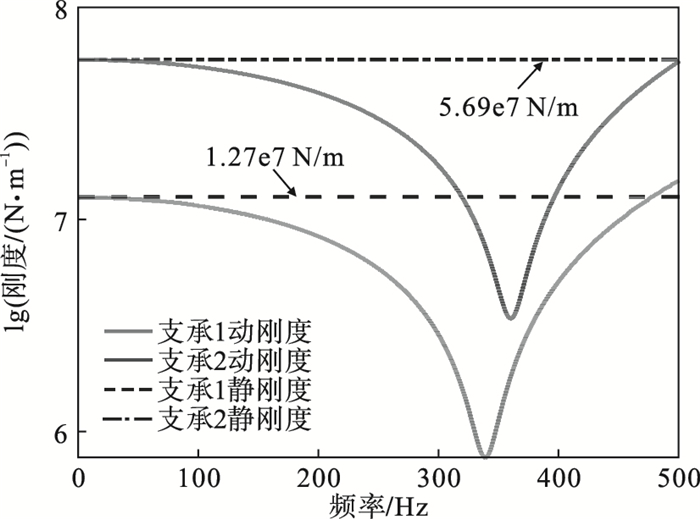图 6 弹性环式支承结构的动刚度Fig.6 Dynamic stiffness curves of the elastic ring support

3 弹性环式支承结构动刚度实验验证为验证弹性环式支承结构动刚度仿真结果的正确性, 通过锤击法对支承1处的弹性环式支承结构进行动刚度实验测试.实验的测试方案为通过力锤与加速度传感器分别来测试弹性环式支承结构所受到的激振力信号与结构的加速度振动信号.对所得加速度信号进行二次积分计算, 得到弹性环式支承结构的位移响应, 最终通过LMS系统对信号进行处理, 即可得到弹性环式支承结构的频响函数与动刚度曲线^[16], 试验所用测试系统LMS如图 7所示.
图 7(Fig. 7)

图 7 LMS测试系统Fig.7 LMS test system

现场测试情况如图 8所示, 锤击实验过程, 为模拟仿真过程中的边界条件, 设计工装以约束外衬套外圈所有自由度.在装配过程中保证弹性环式支承结构中弹性环结构的外凸台位于正下方位置, 采取与图 3相同的位置施加简谐力并提取位移响应.因此在内衬套内圈粘贴加速度传感器, 并使用力锤敲击内衬套内圈的最下方位置, 选定500 Hz频率分析范围, 得到弹性环式支承结构的三组实验测试幅频曲线的结果如图 9所示, 与图 5所示出现峰值的频率一致.可见峰值出现在340~360 Hz范围内, 在误差范围内, 与仿真结果趋于一致, 验证了图 5所示对弹性环式支承结构谐响应分析的正确性, 从而可进一步验证图 6所示弹性环式支承结构动刚度分析的正确性.
图 8(Fig. 8)

图 8 锤击法测试现场Fig.8 Scene drawing of the hammering test

图 9(Fig. 9)

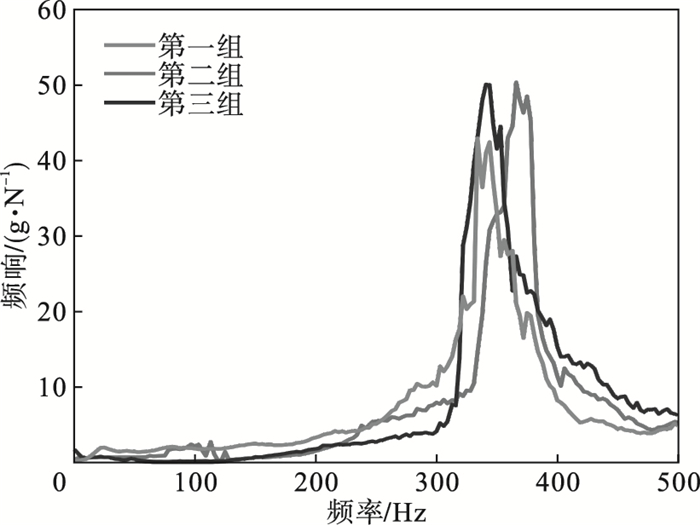图 9 实测幅频曲线Fig.9 Testing results of amplitude-frequency

再根据图 4所示的动刚度测试流程与上述测试方案, 对实验所得动刚度曲线绘制拟合曲线, 如图 10所示.试验测试、拟合结果与仿真结果在刚度数值与峰值出现的位置上趋势基本一致, 证明了对弹性环式支承结构的动刚度有限元计算的正确性, 也证明了针对航空发动机临界转速的准确设计需计算支承结构的动刚度, 以更贴近真实工况, 满足实际工作的要求.
图 10(Fig. 10)

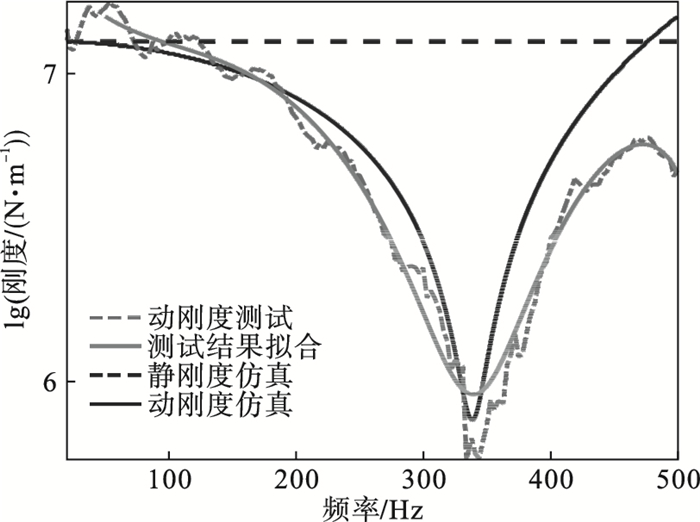图 10 实测动刚度曲线Fig.10 Testing results of the dynamic stiffness

但在细节的对应上仍有一定的差异存在, 分析其原因为以下三点: 首先, 锤击法测试本身不仅会得到弹性环式支承结构整体的固有频率, 还会得到其部件的固有频率, 然而在有限元计算时, 只能得到整体固有频率, 锤击法易造成局部响应, 激励能量在低频处可能不足造成影响; 其次, 弹性环式支承结构组件与组件之间, 组件与工装之间存在着配合方式的影响, 与有限元分析时的配合方式不一致, 造成一定误差; 最后, 由于阻尼比的设置不明确, 与实物有一定的误差, 造成共振时峰值的差异.
4 动刚度对转子临界转速的影响通过对弹性环式支承结构动刚度的研究, 可进一步用于分析转子系统与支承系统之间的动态耦合的关系, 转子-支承系统的动力学特性会随着转子转速变化, 受到支承系统的固有频率特性的影响.建立如图 11所示的转子-支承系统^[17], 该转子两个支点的支承系统采用滚动轴承与弹性环式支承结构组成, 且弹性环式支承结构的支承刚度远小于滚动轴承的刚度, 由串联刚度计算公式可知组合弹性支承结构的刚度主要取决于弹性环式支承结构的刚度, 因此该转子系统的固有特性受弹性环式支承结构的刚度影响极大.
图 11(Fig. 11)

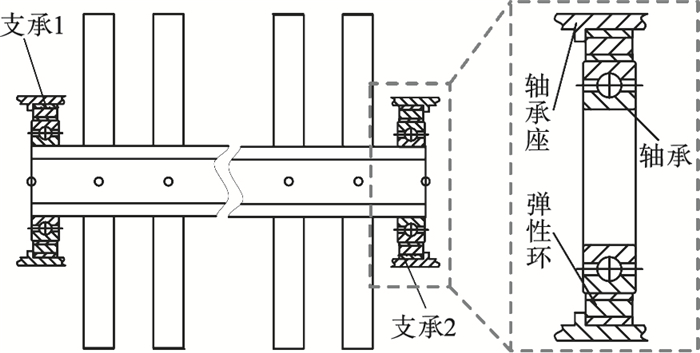图 11 转子-支承系统结构简图Fig.11 Structural diagram of the rotor-support system

对上述转子-支承系统进行有限元建模, 转子系统的具体参数如表 3所示, 其中支承1与支承2处的弹性支承采用上述分析的两组弹性环式支承结构, 并在ANSYS中对该转子-支承系统进行建模求解.转轴采用Beam188单元, 集中质量采用Mass21单元, 支承采用Matrix单元, 通过ANSYS求解该转子-支承系统的临界转速.
表 3(Table 3)

表 3 转子系统的结构参数Table 3 Structural parameters of the rotor system 轴段 长度/m 内径/m 外径/m 转盘质量/kg 直径转动惯量/(kg·m2) 极转动惯量/(kg·m2) 1 0.033 50 0.038 1 0.050 8 0.000 0.000 00 0.000 00 2 0.034 59 0.038 1 0.050 8 1.663 5 0.003 67 0.007 34 3 0.122 79 0.038 1 0.050 8 1.663 5 0.003 67 0.007 34 4 0.024 64 0.038 1 0.050 8 1.138 5 0.002 43 0.004 86 5 0.038 48 0.038 1 0.050 8 1.138 5 0.002 43 0.004 86

表 3 转子系统的结构参数 Table 3 Structural parameters of the rotor system

假设轴承刚度为定值, 在计算转子的耦合支承动刚度时仅考虑弹性环式支承结构的支承动刚度的影响, 分别计算转子-支承系统在弹性环式支承结构静刚度与动刚度条件下的临界转速, 其中对应得到的Campbell图分别如图 12与图 13所示.由两个图对比可看出, 在0~500 Hz范围内, 两种刚度条件下的转子-支承系统的临界转速有较大差异, 静刚度条件下转子的第一阶临界转速为19 294 r/min, 且在该频率范围内第二阶固有频率与原点引出的射线没有出现交点, 实际上的第二阶临界转速为56 065 r/min, 图 13中由于受弹性环式支承结构动刚度的影响, 该转子-支承系统的一阶临界转速出现下降趋势, 变为14 280 r/min且下降幅度为26 %.由图 6可知, 左右支承的弹性环式支承结构动刚度的刚度最低值出现在340 Hz与360 Hz处, 在此范围内出现了刚度降低的情况, 从Campbell图可以看出, 当转子转速接近弹性环式支承结构的固有频率时, 弹性环式支承结构的动刚度对转子系统的固有特性造成较大影响.与静刚度条件下不同, 第二阶固有频率由于支承刚度的变化与原点引出的射线产生两个新的交点, 出现了新的临界转速^[8], 分别为20 880与22 440 r/min.
图 12(Fig. 12)

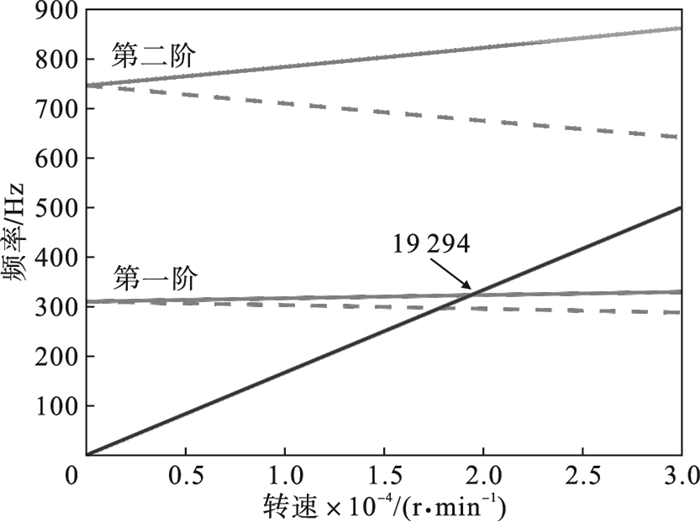图 12 静刚度条件下的Campbell图Fig.12 Campbell diagram with the static stiffness

图 13(Fig. 13)

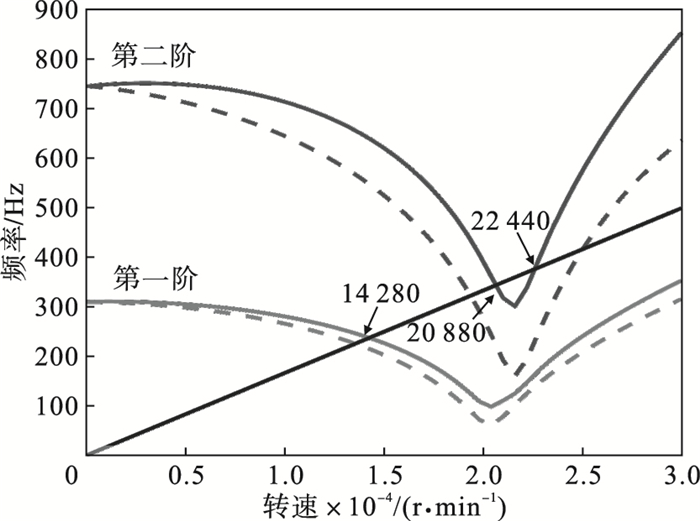图 13 动刚度条件下的Campbell图Fig.13 Campbell diagram with the dynamic stiffness

为进一步分析该转子-支承系统的振动特性, 分别计算了在弹性环式支承结构静刚度与动刚度条件下的幅频曲线.由图 14的幅频曲线对比可得出, 动刚度条件下会造成转子-支承系统第一阶临界转速的提前, 共振峰值的降低, 受弹性环式支承结构动刚度值降低的影响, 产生了新的共振峰值, 且峰值的位移较低, 峰值出现的位置与Campbell图交点一致.为验证文中所得结论, 与文献[18]中搭建的转子-弹性环支承测试系统的幅频特性曲线进行对比, 其支承系统受固有频率的影响, 动刚度值降低, 导致实验所得幅频特性曲线产生新的共振频率, 并且测试所得临界转速小于静刚度条件下仿真所得临界转速, 验证了文中支承系统的动刚度特性对转子-支承系统的振动特性的影响.
图 14(Fig. 14)

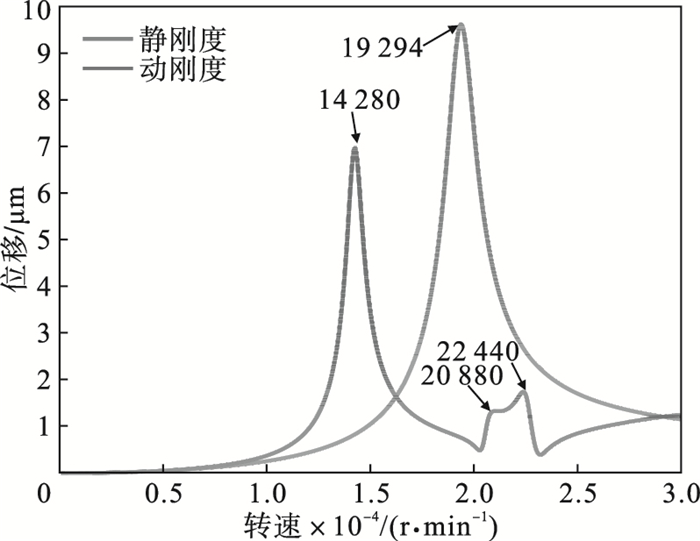图 14 动刚度条件下的幅频曲线Fig.14 Amplitude-frequency curves with the dynamic stiffness

综上, 在对航空发动机临界转速进行设计时, 为准确计算转子-支承系统的临界转速, 且保证转子-支承系统的临界转速有足够的安全裕度以保证运行的安全性, 需要充分考虑支承系统动刚度的影响.由于航空发动机支承系统结构、装配关系复杂, 各部件间常常相互耦合, 且目前对支承系统阻尼值的分析还不成熟, 很难准确地给出支承系统动刚度对转子临界转速的影响, 对该方面的研究仍需要进一步开展.
5 结论1) 建立了弹性环式支承结构的有限元模型, 通过谐响应分析, 得到了左右支承处弹性环式支承结构的动刚度曲线, 并开展实验测试, 测试结果与仿真值较为吻合.
2) 由弹性环式支承结构的动刚度曲线可知, 在低频处弹性环式支承结构的动刚度数值上变化很小与静刚度值较为接近; 激励频率达到固有频率时, 结构产生共振, 动刚度降低; 当激励频率大于固有频率时, 其动刚度值随频率的增大而有所回升.
3) 考虑弹性环式支承结构动刚度时的转子临界转速相较于仅考虑静刚度, 一阶临界转速下降了26 %, 二阶临界转速受支承动刚度影响较大, 产生新的共振峰值.
参考文献

[1]	Childs D W. Rotor dynamics of turbo machinery[C] // Proceedings of the Sixth International Conference on Rotor dynamics. Sydney, 2000: 66-70.
[2]	Bai C Q, Xu Q Y, Wang J Y. Effects of flexible support stiffness on the nonlinear dynamic characteristics and stability of a turbopump rotor system[J]. Nonlinear Dynamics, 2011, 64: 237-252. DOI:10.1007/s11071-010-9858-4
[3]	Luo H T, Fu J, Yu C S. Numerical simulation and experimental testing of dynamic stiffness of angular contact ball bearing[J]. Advances in Mechanical Engineering, 2018, 10(9): 1-14.
[4]	Gupta T C. Parametric studies on dynamic stiffness of ball bearings supporting: a flexible rotor[J]. Journal of Vibration and Control, 2019, 25(15): 2175-2188. DOI:10.1177/1077546319856147
[5]	龙伦, 吕彪, 袁巍. 支承动刚度对某涡轴发动机燃气发生器转子临界转速影响分析[J]. 风机技术, 2018, 60(2): 66-70. (Long Lun, Lyu Biao, Yuan Wei. Analysis of influence of supporting dynamic stiffness on critical rotational speed of a turboshaft engine gas generator rotor[J]. Fan Technology, 2018, 60(2): 66-70.)
[6]	Hong J, Chen M, Liu S. Application of whole engine finite element models in aero-engine rotordynamic simulation analysis[C]//ASME Turbo Exposition. Montreal, 2007: 771-778.
[7]	Hong J, Wang H, Xiao D, et al. Effects of dynamic stiffness of rotor bearing on rotor dynamic characteristics[J]. Aeroengine, 2008, 34(1): 23-27.
[8]	Ma Y H, Zhu H, Zhang D, et al. Experimental envestigation on dynamic mechanical behavior of the elastic ring support with metal rubber[C]//ASME 2013 International Mechanical Engineering Congress and Exposition. San Diego, 2013: 53-60.
[9]	Song H Y, Wang S H, Sun K. Rotordynamic characteristics analysis for an aero-engine low pressure rotor rig test model[C]//Commercial Aircraft Engine Conferences. Shanghai, 2018, 179(9): 03012.
[10]	乔留春. 弹支结构用异型轴承刚度特性分析及试验研究[D]. 大连: 大连理工大学, 2018. (Qiao Liu-chun. Analysis and experimental research on stiffness characteristics of special bearing for elastic-supported structure[D]. Dalian: Dalian University of Technology, 2018. )
[11]	赵文涛. 考虑实测支承动刚度的航空发动机整机振动建模及验证[D]. 南京: 南京航空航天大学, 2012. (Zhao Wen-tao. Vibration modeling and verification of aircraft engine considering measurements of supporting dynamic stiffness[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. )
[12]	马艳红, 陆宏伟, 朱海雄, 等. 弹性环金属橡胶支承结构刚度设计与试验验证[J]. 航空学报, 2013, 34(6): 1301-1308. (Ma Yan-hong, Lu Hong-wei, Zhu Hai-xiong, et al. Structural stiffness design and experimental verification of metal rubber bearing with elastic ring[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1301-1308.)
[13]	刘闯, 陈国栋, 杨阳, 等. 基于有限元仿真的弹性环刚度特性分析[J]. 沈阳航空航天大学学报, 2019, 36(3): 8-13. (Liu Chuang, Chen Guo-dong, Yang Yang, et al. Stiffness analysis of elastic ring based on finite element simulation[J]. Journal of Shenyang Aerospace University, 2019, 36(3): 8-13.)
[14]	Diligenskiy D, Novikov D. Studying of manufacturing tolerance influence on the performance of GTE rotor elastic rings[J]. Procedia Engineering, 2017, 176: 483-497. DOI:10.1016/j.proeng.2017.02.348
[15]	Zhang W, Ding Q. Elastic ring deformation and pedestal contact status analysis of elastic ring squeeze film damper[J]. Journal of Sound Vibration, 2015, 346: 314-327.
[16]	Lu E O, Ripin Z M. Dynamic stiffness and loss factor measurement of engine rubber mount by impact test[J]. Materials & Design, 2011, 32(4): 1880-1887.
[17]	黄宇熙. 耦合双转子-组合支承系统非线性动力特性分析[D]. 大连: 大连海事大学, 2018. (Huang Yu-xi. Analysis of nonlinear dynamic characteristics of coupled double rotor and combined bearing system[D]. Dalian: Dalian Maritime University, 2018. )
[18]	王震林. 弹性环式挤压油膜阻尼器动力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. (Wang Zhen-lin. Research on the dynamic characteristics of elastic ring squeeze film damper[D]. Harbin: Harbin Institute of Technology, 2019. )