
 , 于天彪, 王宛山
, 于天彪, 王宛山 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期:2021-07-15
基金项目:国家重点研发计划项目(2017YFA0701201)。
作者简介:李奇(1986-),男,吉林四平人,东北大学博士研究生,工程师;
于天彪(1968-),男,吉林长春人,东北大学教授,博士生导师;
王宛山(1946-),男,辽宁沈阳人,东北大学教授,博士生导师。
摘要:根据光学元件的加工工艺特点对光学自由曲面铣床进行了设计, 并对光学自由曲面铣床进行了有限元(FE)建模及静动态特性分析.结果表明: 在重力载荷条件下铣床原点位置时, 重力平衡装置未工作时导轨直线度为0.7 μm, 重力平衡装置工作时导轨直线度为0.035 μm, 重力平衡装置未工作时丝杠直线度为2.3 μm, 重力平衡装置工作时丝杠直线度为0.2 μm.提取了不同结构方案及材料方案光学自由曲面铣床的固有频率, 振型显示影响加工精度的铣床首阶振型为第三阶, 最优的动态特性设计方案为铣床Z轴电机安装在顶板上及铣床结构材料采用天然花岗岩, 铣床结构材料采用天然花岗岩相比于铸铁可以显著提升铣床动态特性.
关键词:光学自由曲面铣床静动态特性力学分流重力平衡有限元
Research on Static and Dynamic Characteristics of the Optical Free-Form Milling Machine
LI Qi

 , YU Tian-biao, WANG Wan-shan
, YU Tian-biao, WANG Wan-shan School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: LI Qi, E-mail: liqi_neu@163.com.
Abstract: An optical free-form milling machine is designed according to the technological characteristics of optical component manufacturing and the finite element(FE)modeling and static and dynamic characteristics analysis of the optical free-form surface milling machine are carried out. The results show that, at the original position under gravity load, when the gravity balance device is not working, the straightness of guide rail is 0.7 μm, and when the gravity balance device is working, the straightness of guide rail is 0.035 μm, when the gravity balance device is not working, the straightness of lead screw is 2.3 μm, and when the gravity balance device is working, the straightness of lead screw is 0.2 μm. The natural frequencies of the optical free-form surface milling machine with different structural schemes and material schemes are extracted, and the vibration mode shows that the first vibration mode of the milling machine that affects the machining precision is the third order, the optimal design scheme of dynamic characteristics is that the Z-axis motor of the milling machine is installed on the roof and the milling machine structure material uses natural granite, and the milling machine structure material using natural granite compared with cast iron can significantly improve the dynamic characteristics of the milling machine.
Key words: optical free-form surface milling machinestatic and dynamic characteristicsmechanical shuntgravity balancefinite element(FE)
在光学曲面加工整个工艺链中, 精密铣削对光学自由曲面的表面及亚表面质量影响很大, 其加工效果将直接决定磨削、抛光等后续加工的效率及可行性.因此, 研制光学自由曲面铣床成为提高光学自由曲面制造能力的关键因素之一, 而光学自由曲面铣床设计中存在的高刚度、大阻尼及长效稳定性等多因素耦合也使其成为当前极复杂、风险极高的工程问题之一[1-3].
针对机床悬空部重力对机床精度的影响, Han等[4]通过优化横梁结构, 提高横梁静刚度, 减小横梁在重力作用下的变形; 张伯鹏等[5]通过建立机床横梁重力变位自演进补偿系统来降低横梁重力变形, 提高机床横梁部分导轨所在运动轴的几何精度; 胡东方等[6]通过对机床床身、立柱等基础大件的筋板、结构形式等进行改进的方法, 降低了由于机床自身重力导致的机床变形; Ibaraki等[7]通过有限元仿真计算和建立并联机床的运动学模型来计算各轴的重力变形, 最终通过误差补偿来补偿掉这部分误差.在机床动力学研究方面, 王岩等[8]对超声振动工作台进行了模态分析和动态特性优化;应申舜等[9]通过试验获取了拉床床台的模态参数并进行了拓扑优化;黄华等[10]基于切削动力学对一台数控加工中心进行结构优化设计;Luo等[11]提出一种机床运动部件不同位置时机床固有频率预测方法;Chen等[12]基于动力学提出一种超精密机床集成设计系统.
本文设计了Z轴立柱采用力学分流设计的光学自由曲面铣床.通过设置重力平衡装置可有效地降低铣床悬空部重力引起的整机结构静变形误差问题.建立了光学自由曲面铣床有限元模型, 对铣床进行了静动态特性分析.
1 光学自由曲面铣床设计图 1a为光学自由曲面铣床三维主视图, 图 1b为机床防护门未开启时光学自由曲面铣床三维人机工程图, 图 1c为光学自由曲面铣床防护门开启时三维人机工程图, 图 2为光学自由曲面铣床主体结构各部件明细.
图 1(Fig. 1)
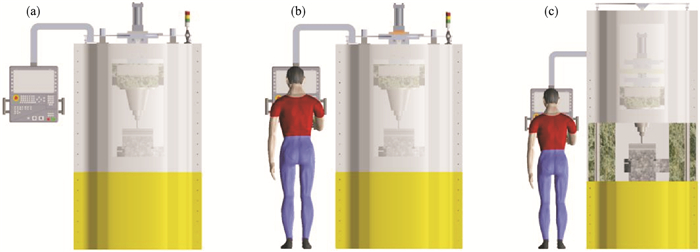 | 图 1 光学自由曲面铣床Fig.1 Optical free-form surface milling machine (a)—三维主视图; (b)—防护门未开启时三维人机工程图; (c)—防护门开启时三维人机工程图. |
图 2(Fig. 2)
 | 图 2 光学自由曲面铣床主体结构示意图Fig.2 Schematic diagram of the main structure of the optical free-form surface milling machine 1-铣床底座; 2-铣床底板; 3-Z轴运动机构; 4-工件; 5-铣床顶板; 6-Y轴运动机构; 7-重力平衡装置; 8-X轴运动机构; 9-主轴箱; 10-主轴组件; 11-工件夹具; 12-摇篮工作台. |
重力传递路径是指铣床结构中悬空部重力的力流路径.重力平衡装置的提升力为溜板重力、X轴运动机构重力、Y轴运动机构重力和主轴组件重力之和.图 3a为铣床重力平衡装置未工作时、Z轴电机设置在顶板上时光学自由曲面铣床重力传递路径.图 3b为铣床重力平衡装置工作时、Z轴电机设置在顶板上时光学自由曲面铣床重力传递路径.图 3c为铣床重力平衡装置未工作时、Z轴电机设置在立柱上时光学自由曲面铣床重力传递路径.图 3d为铣床重力平衡装置工作时、Z轴电机设置在立柱上时光学自由曲面铣床重力传递路径.
图 3(Fig. 3)
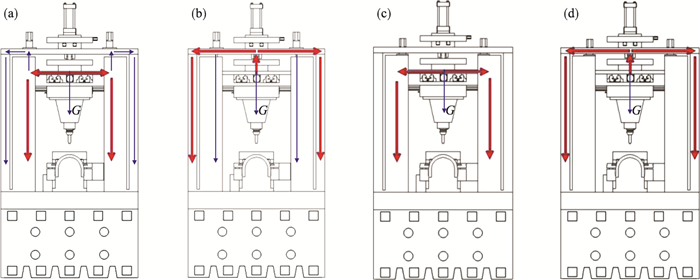 | 图 3 光学自由曲面铣床重力传递路径Fig.3 Gravity transfer path of the optical free-form surface milling machine (a)—顶板+重力平衡未工作; (b)—顶板+重力平衡工作; (c)—立柱+重力平衡未工作; (d)—立柱+重力平衡工作. |
Z轴电机设置在顶板上使铣床内框和外框互联, 可以增加铣床静动态刚度, 但会产生力学回流效应(会有小部分力从相对路径流出), 降低铣床Z轴运动精度.Z轴电机设置在立柱上不会产生力学回流效应, 因此铣床Z轴运动精度高.
图 4a为固定重力平衡装置工作原理, 固定重力平衡装置由油缸及其连接组件组成, 采用固定重力平衡装置可以平衡掉铣床悬空部重力, 但由于铣床X轴、Y轴的运动, 铣床悬空部重心不断变化, 产生的重力矩会影响铣床精度.图 4b为二维运动重力平衡装置工作原理, 二维运动重力平衡装置由油缸及其连接组件、二维主运动平台及二维随动运动平台组成, 工作时二维主运动平台根据计算的重心位置运动, 保证铣床悬空部重心始终在油缸的轴线上, 二维运动重力平衡装置相比于固定重力平衡装置不但可以平衡掉铣床悬空部重力, 也可以消除重力矩对铣床精度的影响, 但铣床运动轴数量多, 因此对控制系统要求较高.图 5为光学自由曲面铣床结构拓扑图, 拓扑图可以表明铣床运动的传递关系.
图 4(Fig. 4)
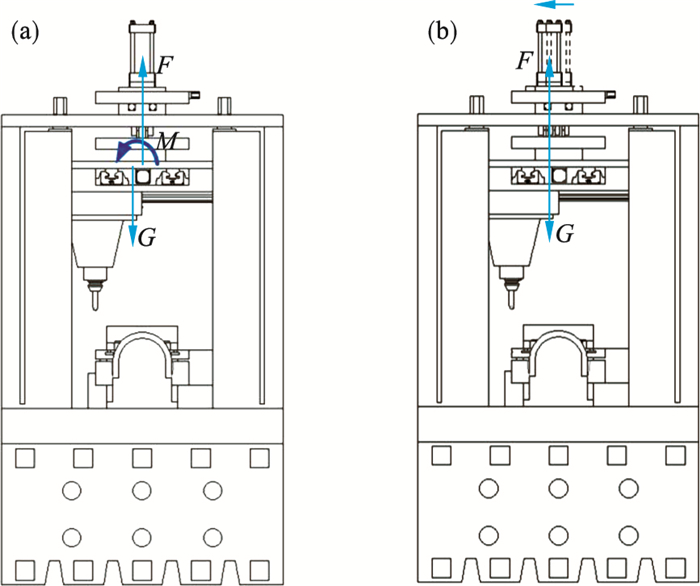 | 图 4 重力平衡装置工作原理Fig.4 Working principle of the gravity balance device (a)—固定重力平衡装置工作原理; (b)—二维运动重力平衡装置工作原理. |
图 5(Fig. 5)
 | 图 5 光学自由曲面铣床结构拓扑图Fig.5 Structure topology graph of the optical free- form surface milling machine |
2 光学自由曲面铣床功能说明2.1 光学自由曲面铣床的特征1) 光学自由曲面铣床主体结构尺寸为1 400 mm×2 000 mm×1 200 mm, X轴、Y轴和Z轴行程分别为400, 400和280 mm.
2) 光学自由曲面铣床Z轴为封闭结构, Z轴立柱采用力学分流设计, 并设有重力平衡装置.铣床基础应设有隔振装置, 在恒温恒湿条件下工作.
3) Z轴立柱由上部一分为二形成两个立柱同时共用Z轴立柱下部制作而成, 位于内侧的立柱设置有Z轴导轨滑块安装槽, 位于外侧的立柱与铣床顶板连接, Z轴立柱与铣床顶板的连接面高于内测立柱的上端面.
4) 防护门是自动门, 通过数控系统进行控制.启闭动力由铣床前立柱后端的气缸提供, 通过防护门升降板与防护门进行连接.
5) 防护门与铣床高度比为黄金分割比.铣床前下侧防护涂装成黄色, 其余皆涂装成白色.防护门采用造型设计.
2.2 光学自由曲面铣床的优点1) 铣床Z轴为封闭结构, 并设置重力平衡装置, 相对于悬臂式结构, 铣床具有良好的刚度、强度和稳定性, Z轴立柱采用力学分流设计, 铣床上部重力从Z轴立柱局部传出, 不影响Z轴精度.
2) 铣床结构材料当采用天然花岗岩时, 该材料经过长期自然时效, 采用该材料的铣床具有优异的结构稳定性和精度保持性, 并且该材料具有优良的振动阻尼性和低热膨胀系数, 能够提高光学自由曲面的制造精度[13].
3) 铣床当采用二维运动重力平衡装置时, 可以提高光学自由曲面的制造精度.
4) 铣床结构对称设计, 可以降低热量对制造精度影响.
5) 铣床各运动部件受力状态好.
3 有限元模型的建立有限元模型的建立分为三个阶段, 首先根据图纸的要求建立简化后的光学自由曲面铣床的三维几何模型.然后进行材料属性定义、网格划分、接触单元生成等工作(考虑结合面的刚度和阻尼特性), 生成等效的有限元模型.最后根据光学自由曲面铣床的工作状态和受力情况加载边界约束条件和力载荷, 生成力学模型.
采用有限元软件ABAQUS静力学模块对Z轴电机设置在立柱上光学自由曲面铣床进行静力学建模分析, 铣床主体结构材料采用天然花岗岩, 天然花岗岩弹性模量为55 GPa, 泊松比为0.3, 密度为2 800 kg/m3.载荷加载情况: 当光学自由曲面铣床仅受重力的作用时, 对整个模型施加重力载荷, 载荷方向沿Z轴方向向下.当光学自由曲面铣床在重力载荷条件及切削载荷共同作用时, 除了施加重力载荷, 同时施加切削载荷Fx=100 N, Fy=100 N, Fz=100 N.根据重力平衡装置是否工作, 施加平衡力, 平衡力大小为所平衡部重力.采用有限元软件ABAQUS动力学模块对Z轴电机设置在立柱上和顶板上光学自由曲面铣床进行模态分析, 铣床主体结构材料采用灰铸铁或天然花岗岩, 灰铸铁弹性模量为120 GPa, 泊松比为0.25, 密度为7 300 kg/m3.约束情况: 对铣床底座的下表面作全约束处理.
4 静力学分析结果4.1 在重力载荷下铣床仿真结果与分析静力变形反应结构的静刚度特性, 重力平衡未工作时(等同于非分流设计)光学自由曲面铣床在重力载荷作用下空间误差如图 6a所示, 铣床最大空间误差为32 μm, 最大空间误差部位在铣床主轴处.重力平衡工作时光学自由曲面铣床在重力载荷作用下空间误差如图 6b所示, 铣床最大空间误差为54 μm, 最大空间误差部位在铣床顶板处, 其中蓝色区域为空间误差小的区域, 红色区域为空间误差大的区域, 黄色区域为中间区域.
图 6(Fig. 6)
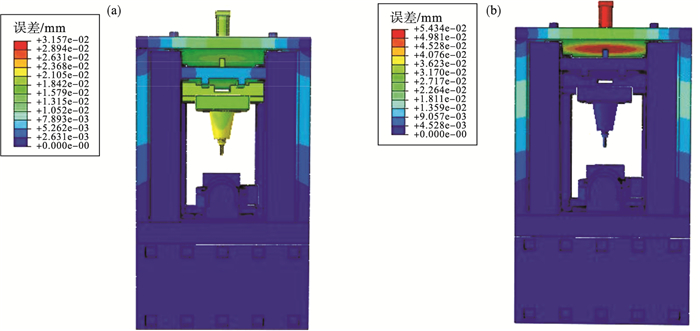 | 图 6 光学自由曲面铣床空间误差Fig.6 Space error of the optical free-form surface milling machine (a)—重力平衡未工作时; (b)—重力平衡工作时. |
图 7为Z=0, X轴和Y轴最大行程时, 在重力平衡未工作、固定重力平衡工作和二维运动重力平衡工作时Z轴导轨和丝杠的空间误差, 可知重力平衡工作时可以极大降低Z轴导轨和丝杠直线度, 二维运动重力平衡工作时相比固定重力平衡工作时可以进一步降低Z轴导轨和丝杠直线度.
图 7(Fig. 7)
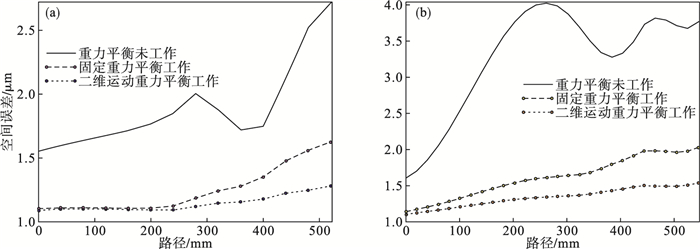 | 图 7 导轨和丝杠空间误差Fig.7 Space error of the guide rail and lead screw (a)—导轨; (b)—丝杠. |
通过导轨和丝杠沿路径的空间误差曲线计算出Z轴导轨和丝杠的直线度, 图 8为重力平衡装置是否工作在铣床原点位置时铣床Z轴导轨和丝杠直线度.可知重力平衡装置未工作时导轨直线度为0.7 μm, 重力平衡装置工作时导轨直线度为0.035 μm, 直线度误差降低95 %; 可知重力平衡装置未工作时丝杠直线度为2.3 μm, 重力平衡装置工作时丝杠直线度为0.2 μm, 直线度误差降低91 %.
图 8(Fig. 8)
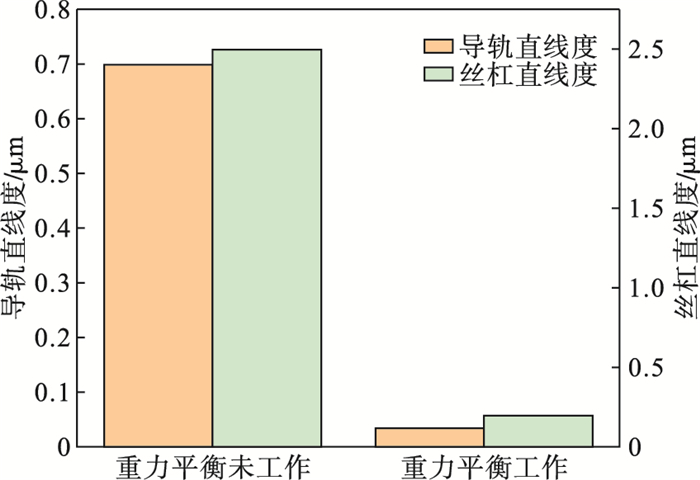 | 图 8 导轨和丝杠直线度Fig.8 Straightness of the guide rail and lead screw |
图 9为重力平衡未工作时、固定重力平衡工作时及二维运动重力平衡工作时Z=0, X轴和Y轴不同工作位置主轴端空间误差, 可知重力平衡未工作时主轴端最大空间误差为24 μm, 固定重力平衡工作时主轴端最大空间误差为6 μm, 二维运动重力平衡工作时主轴端最大空间误差为4 μm.
图 9(Fig. 9)
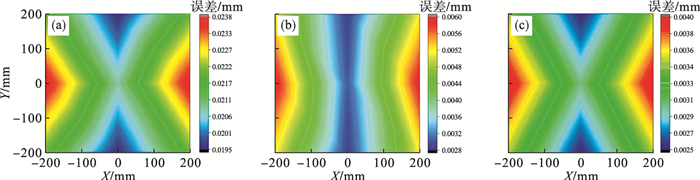 | 图 9 不同工作位置时主轴端空间误差(重力载荷)Fig.9 Space error of the spindle end in different working positions(gravity load) (a)—重力平衡未工作时; (b)—固定重力平衡工作时; (c)—二维运动重力平衡工作时. |
4.2 在重力载荷及切削载荷下铣床仿真结果与分析图 10为重力平衡未工作时、固定重力平衡工作时及二维运动重力平衡工作时Z=0, X轴和Y轴不同工作位置主轴端空间误差, 可知重力平衡未工作时主轴端最大空间误差为24.5 μm, 固定重力平衡工作时主轴端最大空间误差为8.5 μm, 二维运动重力平衡工作时主轴端最大空间误差为4.5 μm.在原点位置时铣床主轴端三个方向刚度分别为Kx=124 N/μm, Ky=73 N/μm, Kz=44 N/μm.
图 10(Fig. 10)
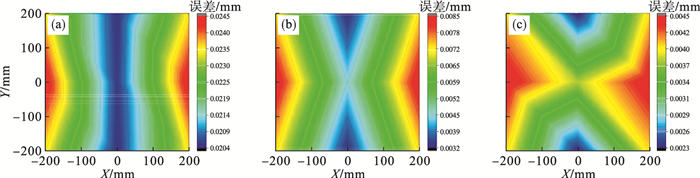 | 图 10 不同工作位置时主轴端空间误差(重力载荷+切削载荷)Fig.10 Space error of the spindle end in different working positions(gravity load + cutting load) (a)—重力平衡未工作时; (b)—固定重力平衡工作时; (c)—二维运动重力平衡工作时. |
5 动力学分析结果从能量的角度讲, 前几阶固有频率集中了铣床振动的大部分能量, 对工件的加工精度影响较大, 因此重点分析光学自由曲面铣床的低阶固有频率.采用ABAQUS软件提取了具有约束条件下光学自由曲面铣床的固有频率.分析Z轴电机安装在立柱上时光学自由曲面铣床前9阶振型如图 11所示, 影响加工精度的铣床首阶振型为第三阶, 其中第一阶、第二阶、第四阶及第九阶振型为铣床外框振动, 其余阶振型为铣床内框振动.不同结构方案及材料方案光学自由曲面铣床前9阶固有频率如图 12所示.
图 11(Fig. 11)
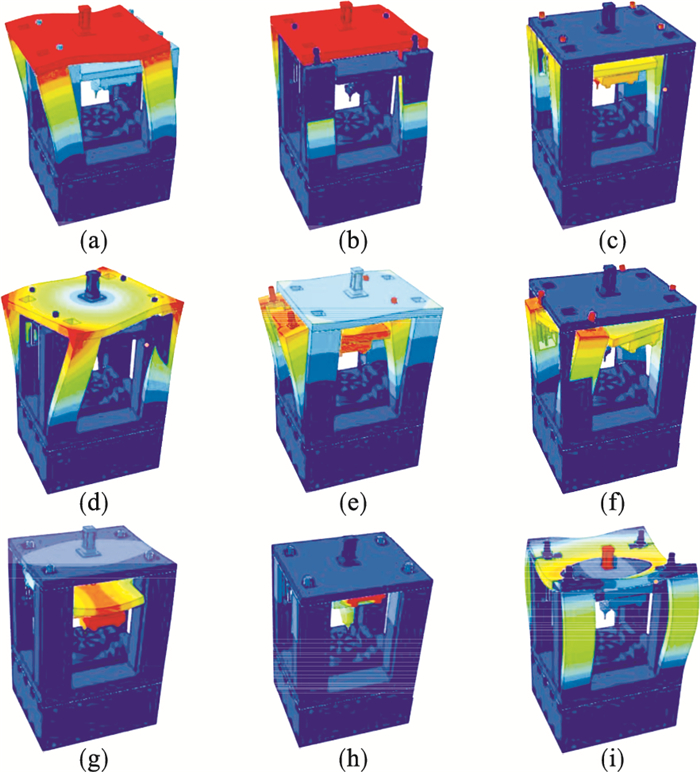 | 图 11 光学自由曲面铣床前九阶振型图Fig.11 First nine mode shapes of the optical free- form surface milling machine |
图 12(Fig. 12)
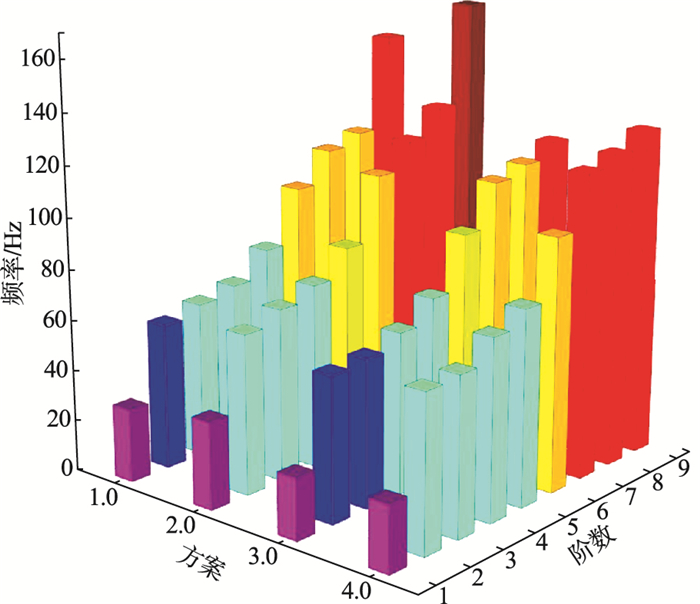 | 图 12 光学自由曲面铣床前九阶固有频率Fig.12 First nine natural frequencies of the optical free-form surface milling machine (1.0—方案: 顶板+铸铁, 2.0—方案: 顶板+天然花岗岩, 3.0—方案: 立柱+铸铁, 4.0—方案: 立柱+天然花岗岩.) |
6 结论1) 创新设计了一种Z轴立柱采用力学分流设计的光学自由曲面铣床(专利号: ZL 2020 1 0008995.1).阐明了光学自由曲面铣床力学分流功能原理.采用有限元技术获取了铣床的静动态特性数据.
2) 研究了重力平衡装置是否工作时光学自由曲面铣床在重力载荷条件下静变形误差对Z轴导向精度、驱动精度及末端精度的影响.结果表明: 光学自由曲面铣床具有优良的静力学特性, 在铣床原点重力平衡装置未工作时导轨直线度为0.7 μm, 重力平衡装置工作时导轨直线度为0.035 μm, 直线度误差降低95 %.重力平衡装置未工作时丝杠直线度为2.3 μm, 重力平衡装置工作时丝杠直线度为0.2 μm, 直线度误差降低91 %.在整个工作空间内重力平衡未工作时主轴端最大空间误差为24 μm, 固定重力平衡工作时主轴端最大空间误差为6 μm, 空间误差降低75 %, 二维运动重力平衡工作时主轴端最大空间误差为4 μm, 空间误差降低83 %.
3) 研究了重力平衡装置是否工作时光学自由曲面铣床在重力载荷、切削载荷共同作用条件下静变形误差对末端精度的影响.结果表明: 重力平衡未工作时主轴端最大空间误差为25 μm, 固定重力平衡工作时主轴端最大空间误差为8.5 μm, 二维运动重力平衡工作时主轴端最大空间误差为4.5 μm.在原点位置时铣床主轴端三个方向刚度分别为Kx=124 N/μm, Ky=73 N/μm, Kz=44 N/μm.
4) 研究了不同结构方案及材料方案光学自由曲面铣床的固有频率.结果表明: 影响加工精度的铣床首阶振型为第三阶, 最优的动态特性设计方案为铣床Z轴电机安装在顶板上及铣床结构材料采用天然花岗岩, 影响加工精度的铣床首阶固有频率为68 Hz.
参考文献
| [1] | 洪海波. 大型非球面超精密光学磨床设计关键技术研究[D]. 上海: 上海交通大学, 2016. (Hong Hai-bo. Research on key technology of large aspheric ultra-precision optical grinding machine design[D]. Shanghai: Shanghai Jiaotong University, 2016. ) |
| [2] | 曹义. 超精密铣削加工自由曲面光学元件误差补偿方法[J]. 组合机床与自动化加工技术, 2018, 11(1): 96-98. (Cao Yi. Error correction methodology for ultra-precision milling of freeform optics[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2018, 11(1): 96-98.) |
| [3] | 刘现磊, 张效栋, 徐航宇, 等. 基于光学性能评价自由曲面离轴三反系统加工误差分析[J]. 光学学报, 2017, 37(8): 184-192. (Liu Xian-lei, Zhang Xiao-dong, Xu Hang-yu, et al. Machining error analysis of freeform surface off-axis three-mirror system based on optical performance evaluation[J]. Acta Optica Sinica, 2017, 37(8): 184-192.) |
| [4] | Han G, Gao B, Shao J, et al. Structural analysis and optimization on crossbeam of heavy NC gantry moving boring & milling machine[C]// Electronic and Mechanical Engineering and Information Technology(EMEIT), 2011 International Conference on IEEE. Harbin, 2011: 1586-589. |
| [5] | 张伯鹏, 张年松. 机床横梁重力变位的自演进补偿[J]. 清华大学学报(自然科学版), 2006, 46(2): 191-193. (Zhang Bo-peng, Zhang Nian-song. Self-evolutionary compensation of machine tool crossbeam deformation induced by gravity[J]. Journal of Tsinghua University(Science and Technology), 2006, 46(2): 191-193. DOI:10.3321/j.issn:1000-0054.2006.02.009) |
| [6] | 胡东方, 张文博. 数控机床结构有限元分析方法[J]. 机械强度, 2015, 37(1): 166-170. (Hu Dong-fang, Zhang Wen-bo. Finite element analytical method for numerical control machine tool structure[J]. Journal of Mechanical Strength, 2015, 37(1): 166-170.) |
| [7] | Ibaraki S, Okuda T, Kakino Y, et al. Compensation of gravity-induced errors on a hexapod-type parallel kinematic machine tool[J]. JSME International Journal, 2004, 47(1): 160-167. DOI:10.1299/jsmec.47.160 |
| [8] | 王岩, 林彬. 附件化超声振动工作台设计及有限元优化分析[J]. 北京航空航天大学学报, 2019, 45(8): 1589-1596. (Wang Yan, Lin Bin. Attached ultrasonic vibration table design and finite element optimization analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(8): 1589-1596.) |
| [9] | 应申舜, 林绿高, 计时鸣. 基于模态参数验证的机床结构件优化设计[J]. 浙江大学学报(自然科学版), 2018, 52(10): 1880-1887. (Ying Shen-shun, Lin Lyu-gao, Ji Shi-ming. Optimization design to machine tool structures using experimental verification of modal parameters[J]. Journal of Zhejiang University(Engineering Science), 2018, 52(10): 1880-1887.) |
| [10] | 黄华, 张树有. 基于切削动力学及其不确定特性的数控机床结构参数分析优化[J]. 振动与冲击, 2016, 35(18): 82-90. (Huang Hua, Zhang Shu-you. Analysis and optimization of parameters of machine tool in structure design based on the cutting dynamics with uncertainty[J]. Journal of Vibration and Shock, 2016, 35(18): 82-90.) |
| [11] | Luo B, Pan D W, Cai H, et al. A method to predict position-dependent structural natural frequencies of machine tool[J]. International Journal of Machine Tools & Manufacture, 2015, 92(1): 72-84. |
| [12] | Chen W Q, Luo X C, Su H, et al. An integrated system for ultra-precision machine tool design in conceptual and fundamental design stage[J]. The International Journal of Advanced Manufacturing Technology, 2016, 84(1): 1177-1183. |
| [13] | Zhou C A, Yang B, Guo K, et al. Shear behavior of artificial and natural granite fractures after heating and water-cooling treatment[J]. Rock Mechanics and Rock Engineering, 2020, 53(1): 5429-5449. |
